Next Article in Journal
Numerical Simulation of a Single and Double-Rotor Impact Crusher Using Discrete Element Method
Next Article in Special Issue
Investigating the Shallow to Mid-Depth (>100–300 °C) Continental Crust Evolution with (U-Th)/He Thermochronology: A Review
Previous Article in Journal
Reply to Skublov et al. Comment on “Volodichev et al. Archean Zircons with Omphacite Inclusions from Eclogites of the Belomorian Province, Fennoscandian Shield: The First Finding. Minerals 2021, 11, 1029”
Previous Article in Special Issue
Apatite U-Pb Thermochronology: A Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 12
Issue 2
10.3390/min12020145
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Zircon (U-Th)/He Closure Temperature Lower Than Apatite Thermochronometric Systems: Reconciliation of a Paradox

by
Benjamin Gérard
1,2,*,
Xavier Robert
1,
Djordje Grujic
3,
Cécile Gautheron
4,
Laurence Audin
1,
Matthias Bernet
1 and
Mélanie Balvay
1
1
Université Grenoble Alpes, Université Savoie Mont Blanc, CNRS, IRD, IFSTTAR, ISTerre, 38000 Grenoble, France
2
GET, Université de Toulouse, CNRS, IRD, UPS, 31400 Toulouse, France
3
Department of Earth and Environmental Sciences, Dalhousie University, Halifax, NS B3H 4R2, Canada
4
Université Paris-Saclay, CNRS, GEOPS, 91405 Orsay, France
*
Author to whom correspondence should be addressed.
Minerals 2022, 12(2), 145; https://doi.org/10.3390/min12020145
Submission received: 12 December 2021 / Revised: 19 January 2022 / Accepted: 23 January 2022 / Published: 25 January 2022
(This article belongs to the Special Issue Thermochronology at Temperatures Higher than 150 °C)
Browse Figures
Review Reports Versions Notes

Abstract

:
Here, we present seven new zircon (U-Th)/He (ZHe) ages and three new zircon fission track (ZFT) ages analyzed from an age-elevation profile (Machu Picchu, Peru). ZFT data present ages older than those obtained with other thermochronological data, whereas the ZHe data interestingly present ages similar to those obtained with apatite (U-Th)/He (AHe). It has been proposed that He retention in zircon is linked to the damage dose, with an evolution of the closure temperature from low values associated with a low α-dose (<1016 α/g), subsequently increasing before decreasing again at a very high α-dose (>1018 α/g). Studies have focused on He diffusion behavior at high α-dose, but little is known at low doses. We propose that the ZHe closure temperature at α-dose ranging from 6 × 1015 to 4 × 1016 α/g is in the range of ~60–80 °C. This value is lower than that proposed in the current damage model ZRDAAM and demonstrates that the ZHe and AHe methods could have similar closure temperatures at low α-dose (i.e., similar ages). These new data strengthen our previous geological conclusions and even highlight a cooling rate approximately twice as important as that deduced from AHe and apatite fission track data alone at Machu Picchu.

1. Introduction

To quantitatively unravel the tectonics and/or relief evolution of a given region, low-temperature thermochronology methods such as (U-Th)/He and fission track dating of apatite (AHe and AFT, respectively) or zircon (ZHe and ZFT, respectively) are often used together e.g., [1,2]. The ZFT and ZHe methods are generally known to record higher temperatures or deeper processes than the AFT and AHe methods [3,4] because of their higher closure temperatures [5,6,7,8]. Additionally, for a given mineral, (U-Th)/He thermochronometry is generally considered more sensitive to lower temperatures than fission track thermochronology [1,5]. Today, these techniques are routinely applied, and numerous studies are published each year for exhumation quantification purposes. However, for over a decade, methodological studies have highlighted that He diffusion in apatites and zircons is strongly dependent on the radiation damage dose, increasing the range of the closure temperature, as important age dispersion with positive AHe-age, and positive and negative ZHe-ages correlations are now often observed e.g., [8,9] for zircons, e.g., [10,11,12,13,14] for apatites.
Regarding the ZHe method, the He diffusion behavior in zircon is still debated. Based on age-effective uranium concentration (eU) correlations, [15,16] proposed that radiation damage produced during U and Th decay influences He retention and loss in zircons, and proposed the ZRDAAM algorithm to model damage production, annealing and He diffusion in damaged zircons similar to RDAAM for apatite [13]. In this model, damage first traps He until a threshold at which point damages coalesce, leading to damage connectivity and the creation of fast He diffusion pathways [15]. In addition, several studies have discussed damage model parameters such as the threshold value e.g., [16,17] or fail to numerically reproduce highly damaged zircons with this classic He kinetic model as the minerals appear to be more He retentive than predicted [10].
On the other hand, [18] proposed a trapping model and a nonlinear relationship between the closure temperature and the increase in α-damage, illustrating the importance of the α-dose for determining the closure temperature. The α-dose corresponds to the total radiation damage that had accumulated in the crystal lattice, mostly due to α recoil. It depends on both eU and the time since when the mineral began to accumulate damage. This model explains not only zircon data presenting age-eU and age-diffusion domain (ESR) correlations, but also data with no such correlation. In the range of geologically possible α-doses, this model predicts closure temperatures consistent with settings within the middle to high range of α-doses (1017 to 5 × 1018 α/g), but there do not exist enough available data in low α-dose settings to confirm the model at any existing α-dose. The author of [18] only indirectly suggests a closure temperature for a low α-dose range (<1 × 1015 α/g) of 60–100 °C with the volcanic zircon data of [19].
In this article, we propose to provide new data with low α-doses to fill the current knowledge gap and improve the above-mentioned model with direct observations. Based on new ZHe, ZFT, and published AHe and AFT data from a Machu Picchu (Peru) vertical profile [20] (Figure 1), we show that in the case of low α-doses, ZHe closure temperatures are closer to AHe closure temperatures than previously proposed, and thus present younger ages than AFT and sometimes even younger than AHe, as predicted by the [18] model. This article does not specifically focus on the geological interpretation of these data but briefly discusses the implications of our results for the geological evolution of the region where samples were collected.

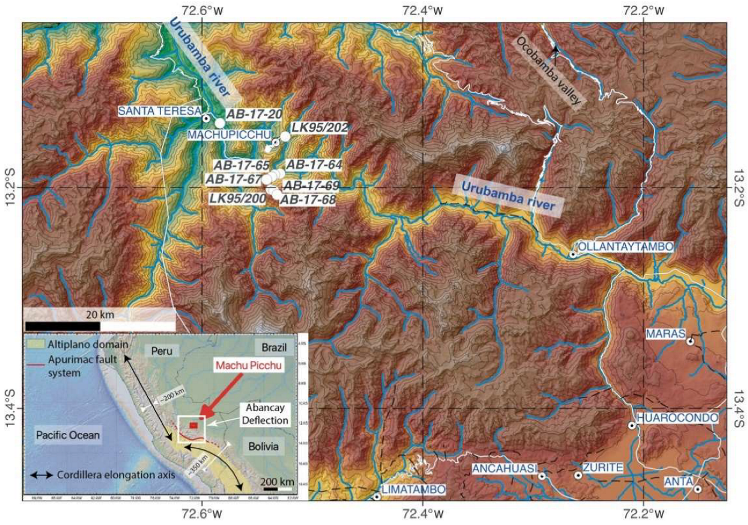
2. Geological Settings

The Machu Picchu age-elevation profile is located at the center of an Andean morphotectonic peculiarity: The Abancay Deflection [21]. The Abancay Deflection tectonically delimits the Bolivian Orocline to the south (Eocene–early Miocene rotation of up to ~65°) and the straight and narrow Andes to the north in Peru, Figure 1; [20,21,22]. It partly lies in the Eastern Cordillera (northern part of the Abancay Deflection), where numerous Permo-Triassic batholiths emplaced into Paleozoic metasedimentary rocks of the Marañon complex [23]. Among them, the granitic Machu Picchu Batholith we sampled (Figure 1) emplaced at 222 ± 7 Ma in the core of the Abancay Deflection [24]. The Eastern Cordillera shows high elevation and relief. The author of [25] proposed that it has been a long-lived structural high because of the absence of a Meso-Cenozoic sedimentary cover. Young AFT and AHe ages were obtained along a quasi-vertical transect of the Machu Picchu Batholith; however, evidence of an unexpected rapid and recent exhumation at a rate of 1.2 km/Myr, initiated at ~5 Ma was observed [26,27]. This exhumation phase is also evidenced in another vertical profile 30 km farther east in the Ocobamba valley, still in the core of the Abancay Deflection [27]. In the southern part of the Abancay Deflection, the Altiplano domain is tectonically decoupled from the Eastern Cordillera along the regional crustal-scale Apurimac fault system, Figure 1; [26,27]. In the Altiplano, Eocene plutons (50–30 Ma) [28,29] emplaced into Meso-Cenozoic sediments [30]. Unlike the core of the Abancay Deflection (Eastern Cordillera), the Altiplano did not experience recent exhumation acceleration, but rather slow and constant exhumation (~0.2 km/Myr) since 40 Ma [27,31]. Because of the differential exhumation pattern, with higher exhumation rates identified at the core of the Abancay Deflection, the active tectonics and curved fault patterns, it has been proposed that the Abancay Deflection should be a tectonic syntaxis comparable to those described in the Himalayan system, for instance [27].

3. Materials and Methods

We collected seven samples along a 1.9 km quasivertical profile in the Machu Picchu batholith (Table 1). We performed ZHe and ZFT dating from the same samples presented in [20]. In the field, we collected the freshest in situ rocks to avoid sampling near traces of fluid circulation. The samples were crushed and sieved to extract the 100–160 µm fractions in the Géode laboratory (Lyon, France). Zircon crystals were consequently concentrated using standard magnetic and heavy-liquid separation techniques at the GTC laboratory (ISTerre, Grenoble, France).
The zircons were processed at the Dalhousie Noble Gas Extraction Laboratory (Halifax, Canada) for (U-Th)/He dating. They were analyzed following the methods described in [4,5,32]. In parallel, 2 Fish Canyon Tuff standards, 28.48 ± 0.06 Ma; [33] were also analyzed (zFCT-61 and zFCT62 in Table 1). For each sample, 3 single zircon aliquots were run with transparent euhedral grain radii higher than 70 µm, possibly without inclusions and/or fractures. After measurement of their dimensions for α-correction [34] and imaging, each grain was packed into a Nb foil envelope. 4He was then extracted from each pack in an in-house built He extraction line with successive 15-min-heatings under a focused beam of a 45 W diode laser (1250 °C), until 4He yields were under 1% of total. After adding a known amount of purified 3He spike, 3He/4He ratios were measured with a Pfiffer Vaccuum Prisma quadrupole mass spectrometer. Typical errors are in range of 1.5–2% (1 σ). Samples were analyzed in groups of 36. In each group, 2 Fish Canyon Tuff (FTC) zircon standards were included to ensure accuracy, reproducibility, and reliability of the data. After He extraction, zircons were dissolved in high-pressure dissolution vessels with concentrated HF and HNO3 at 200 °C for 96 h. Prior to dissolution, samples were spiked with mixed 235U, 230Th, and 149Sm spikes. Isotopic ratios were measured with iCAP Q inductively coupled plasma mass spectrometry (ICP-MS). Additional blank analyses controlled the analytical accuracy. The raw data were reduced using an Helios software package (R. Kislitsyn and S. Stockli). To test different scenarios, we computed the α-dose (Dα) [35] for each zircon dated with ZHe methodology according to the first equation presented in [36].
For ZFT dating at the GTC laboratory, zircon crystals were mounted in PFA Teflon® and polished [37]. Spontaneous fission tracks were revealed by etching the grain mounts with a NaOH:KOH melt at 228 °C in a covered Teflon dish heated by a laboratory oven for ~22–37 h. The criterion for stopping etching was when well-etched tracks were revealed in the majority of the grains in the grain mount. Zircon etching time should be longer [38,39] for low-damaged crystals; however, given the relatively high U-concentrations of 500–800 ppm (Table 2), it is possible to reveal countable tracks in zircons with 10 Ma cooling ages even with intermediate etch times of 15–30 h [37]. Using the external detector method, the samples were irradiated at the FRM II reactor (Garching, Germany). Fission tracks were counted dry on internal grain surfaces at the GTC platform with an Olympus BH2 microscope at 1250x magnification. ZFT central ages were calculated with RadialPlotter software [40], using a ζ-value of 131.49 +/− 5.4 (M. Bernet) for the IRMM-541 uranium dosimeter glass (50 μ g / g U).

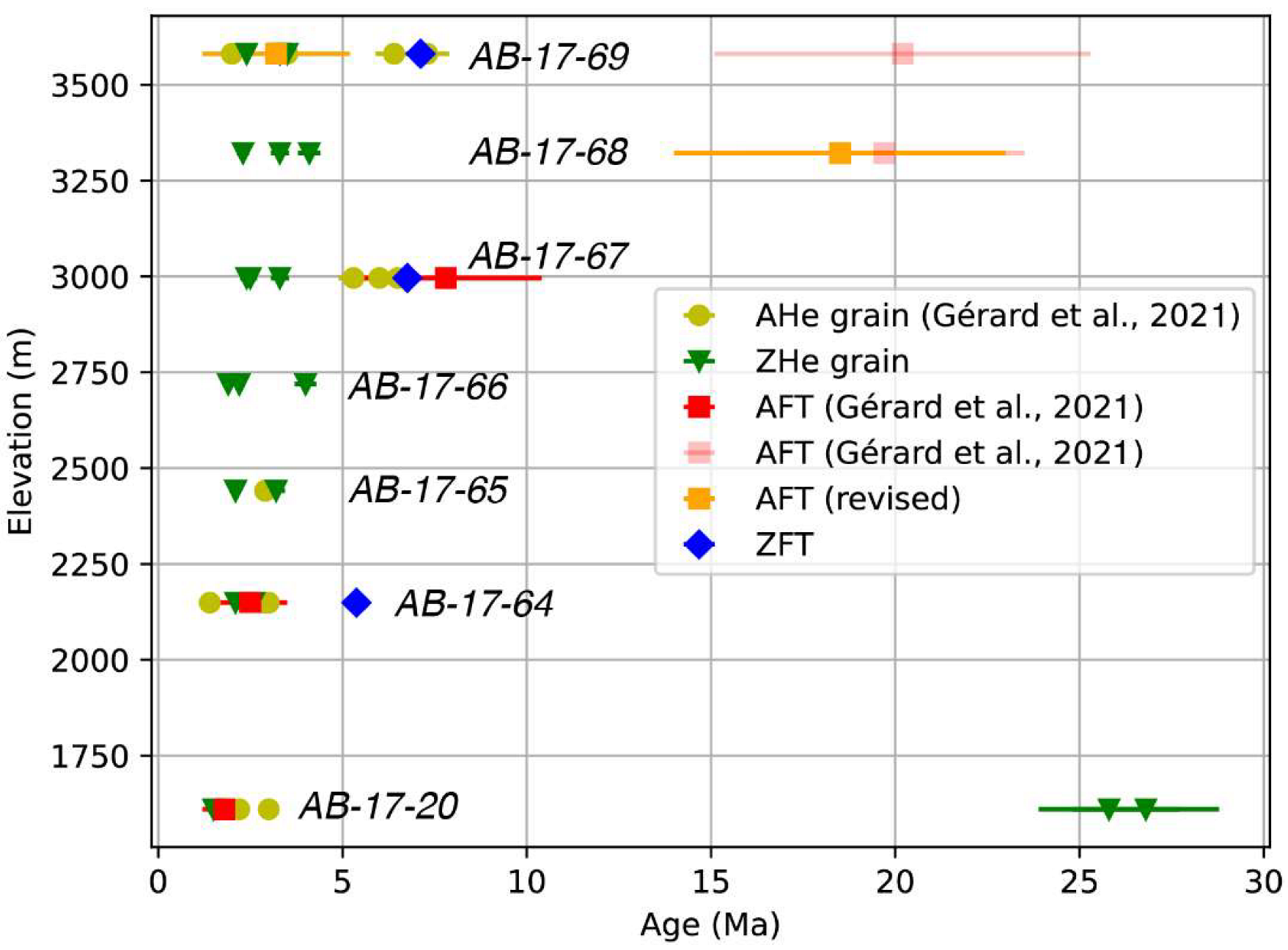
4. Results

The six samples collected along the Inca trail (AB-12-64 to AB-17-69) analyzed with ZHe yield mean ages ranging from 2.4 ± 0.3 to 3.2 ± 0.9 Ma, giving a self-consistent age-elevation trend (Table 1; Figure 2). The aliquots of each sample are also consistent themselves. In contrast, the lowest and 6-km-laterally offset sample (AB-17-20) is less consistent: 1 aliquot is young (1.5 ± 0.1 Ma) and fit with the age-elevation trend, whereas the two other aliquots present consistent old ages of ~25 Ma (Figure 2). In addition, the ZHe data do not show any age-effective uranium (eU) content or age-equivalent sphere radius (ESR) correlation (Figure 3).
The three new ZFT data range from 5.4 ± 0.3 Ma (AB-17-64) to 7.1 ± 0.4 (AB-17-68) (Table 2), are consistent with the other thermochronometers following the same age-elevation trend (Figure 2; supplementary materials Figures S3–S5).
These new ZHe and ZFT data are much younger and thus apparently incompatible with the two highest AFT ages (AB-17-68 and AB-17-69 from [20]) in the profile. We thus revised the counting of these two AFT samples (Figure 2; Supplementary Materials Figures S1 and S2). In fact, both of the highest AFT samples are difficult to date because of poor apatite quality (fractures, inclusions), as mentioned in [20]; thus, these two samples yield unreliable AFT ages. After revision, the highest sample (AB-17-69) gives an AFT age more compatible with the zircon data (3.1 + 3.2 − 1.6 Ma) but still not reliable because of the few grains (10) dated and because of the low apatite quality and U zonation. The second highest sample (AB-17-68) with a central age of 18.5 + 5.1 − 4.0 Ma remains older than the other samples in the profile. Here, also, the very low counts question the validity of this age (Table 3). For these reasons, we will not base the following discussion on the highest fission track data in the profile.

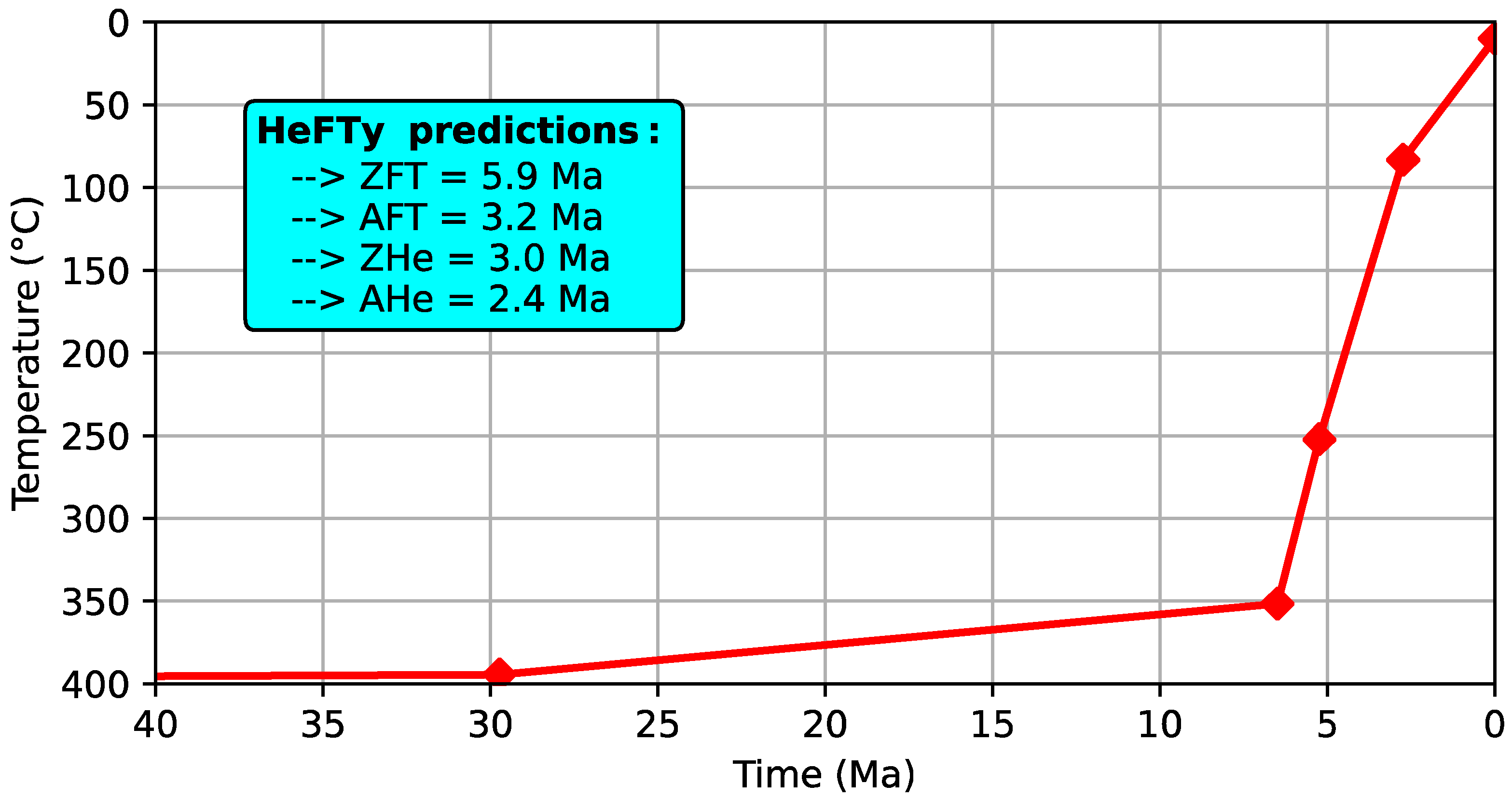
5. Discussion

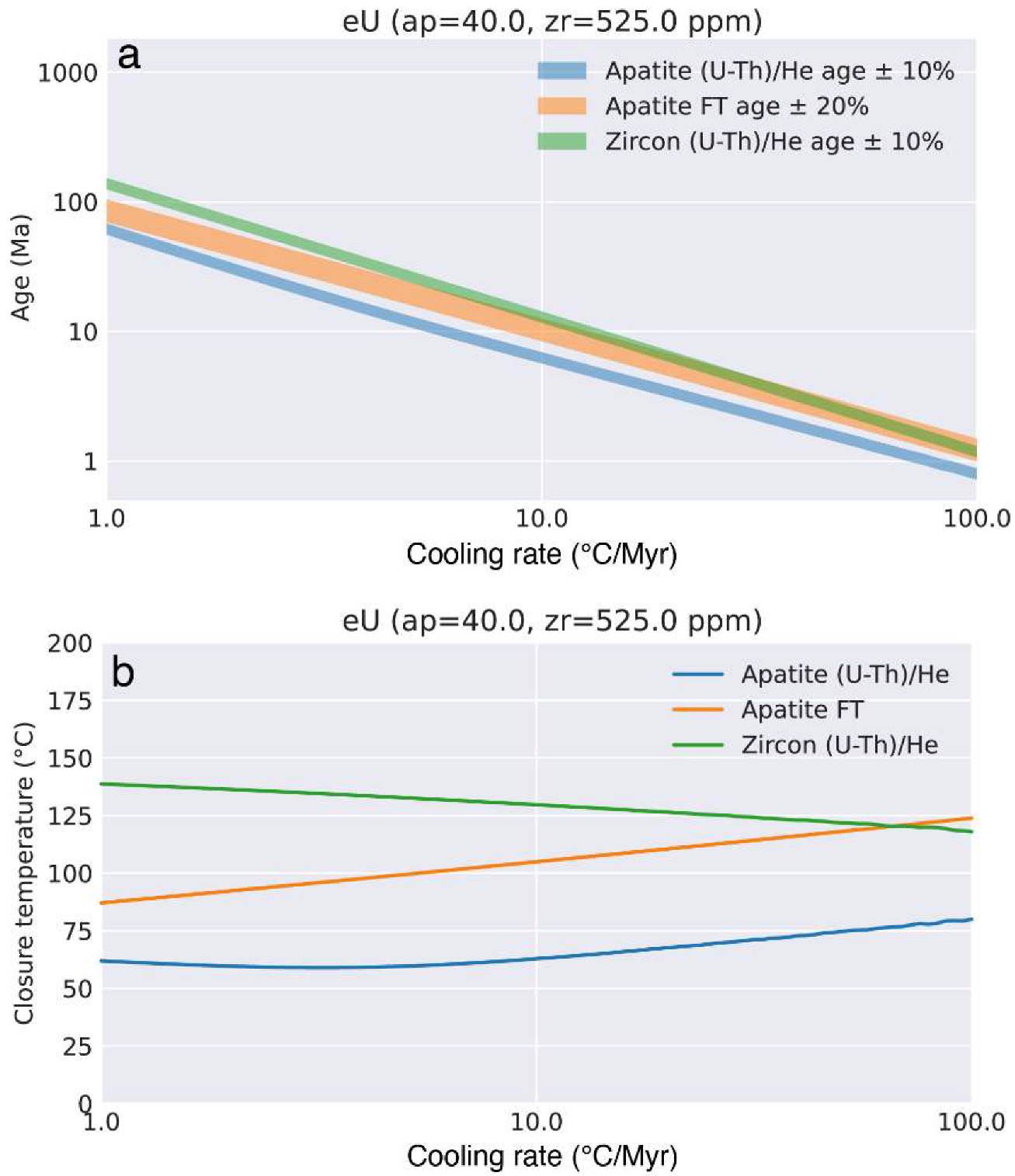
5.1. Revisiting the ZHe Temperature Sensitivity

The new ZHe and ZFT age-elevation trends are consistent with the ones obtained with AHe and AFT data by indicating relatively recent rapid cooling, and curiously, the ZHe data are younger or equivalent than usually lower closure temperature thermochronometers such as AHe and AFT (Figure 2). Given the low eU and Dpar values observed in our AHe and AFT data, not abnormally high AHe and AFT closure temperatures should be expected. The ZFT data are consistent with previous data (AHe and AFT; Figure 2) and confirm previous geological interpretations [20,27]. Whereas all ZHe ages, at the exception of the lowest and more distant sample (AB-17-20), are younger than AFT and AHe dates from the same samples (Figure 2). This suggests that those samples present a ZHe closure temperature of ~80 °C similar to the AHe system, which is lower than the classically expected, 100–200 °C [1]. One can argue that an analytic issue occurred during the analysis. However, the two Fish Canyon Tuff zircons standards analysis (zFCT-6x in Table 1) give acceptable results (30.7 ± 2.3 Ma and 29.8 ± 2.2 Ma for a 28.48 ± 0.06 Ma age reference [33]), ruling out any strong analytical bias.
Similar observations have been made by [15], who developed the ZRDAAM model, based on correlations between ZHe ages and effective uranium content. They proposed that low closure temperatures are due to middle-low (~1016 α/g with a Tc = ~120 °C) or high annealing damage (>>1018 α/g). Using the software developed by [43] to implement the ZRDAAM model, we calculated the expected ZHe, AFT, and AHe ages and closure temperatures in function of cooling rates (Figure 4). Modelling yields observed ZHe ages (same or younger than the AFT ages) for cooling rates between 30 and 50 °C/Ma, and indicates that ZHe closure temperature for our samples becomes lower than for the AFT at cooling rates of about 40 °C/Ma. This suggests that the Pliocene cooling might have been faster than previously modelled [20].
To further test the ZRDAAM model [15], we used the HeFTy model [44] in forward mode in an attempt to reproduce the AHe, AFT, ZHe, and ZFT ages we obtained. We fed the model with a time-temperature history compatible with the one proposed by [20,27]. Modelling reveals that ZHe ages are younger than ZFT ages and close to AHe and AFT ages, but still older than AHe ages (Figure 5). The current ZHe model is thus not sufficiently accurate for very low α-doses and cannot robustly explain the observations. Ref. [18] proposed a model similar to the ZRDAAM model in terms of the Tc/α-dose relationship independent of any age/eU or age/ESR correlation or any annealing damage effects. The latter model extends the α-dose range to the low values and indirectly proposes a lower ZHe closure temperature than the ZRDAAM model for very low α-doses, based on volcanic zircon data previously published [19].
In batholiths that cool rapidly, the α-dose upper limit could be approximated by its crystallization age. However, here, the high α-dose could not be geologically explained by the age of the sampled pluton. The granitic Machu Picchu Batholith emplaced at 222 ± 7 Ma [24]. The corresponding α-dose computed for each dated zircon with this emplacement age is between 2.5 × 1017 and ~1 × 1018 α/g if we assume that all produced α -damage is preserved in the zircon crystals (Table 4). Following the trapping model [18], this value is still too low to allow the ZHe closure temperature to be lower than 80 °C. However, it is interesting to note that the ZFT ages produced on the same samples present young ages <7 Ma, indicating that all fission tracks produced since the crystallization have been annealed. The relatively low observed spontaneous track densities <1.4 × 106 tracks/cm2 despite the relatively high U concentration (600–800 μg/g) of the analyzed zircons indicates that the accumulation of α -radiation damage may not be significant (<4 × 1016  α /g) in the Machu Picchu batholith zircons (Table 2; Figure 6; [45]), because of relatively high temperatures (i.e., >300 °C) before ~7 Ma. Although we do not have direct α-dose measurements for the exact same zircons that were dated with the ZHe method, we can use the spontaneous track density of the ZFT mounts of the exact same sample to obtain an approximate estimate of the likely mean α-dose for a given sample [45]. Future research would need the use of Raman spectroscopy on zircons (processed for ZHe dating) to obtain more direct information on accumulated α-dose. Nonetheless, the above interpretation is also supported by the fact that the analyzed zircons were colorless. The author of [46] showed that color in zircon is related to the accumulation of α -damage, but that color is lost when zircons are heated or reside at ambient temperatures of 325–475 °C, with full color resetting possible; therefore, annealing of α -damage is possible at temperatures as low as 350 °C [47]. Consequently, following the conclusions derived from the ZFT data, we can consider that the α -damage produced since crystallization has been annealed and only started accumulating since approximately <7 Ma. In that case, the oldest ZFT age at ~7 Ma indicates that it should have begun to cool before this date. Cooling initiation at 7 Ma would induce an α-dose of approximately 6 × 1015 to 4 × 1016 α/g (Figure 7). Consequently, we propose that at a very low damage dose, the ZHe closure temperature is close to 80 °C (Figure 8). This result agrees with the prediction from [18] made using the theoretical approach of the diffusion behavior in zircon (Figure 8). This result has major implications because it demonstrates that the ZHe method has a large range of temperature sensitivities. A low closure temperature, similar to AHe, should be considered for zircons having a low damage dose (Figure 8). To further document and refine the models from field-based verification, it would be useful to integrate young plutons and/or young thermochronological data (few Ma; e.g., [48,49,50]) with as little inheritance as possible in such approach.

5.2. Geological Implication

In a relatively old batholith such as the Machu Picchu Batholith, two geological processes could explain a low α-dose: (1) an important reheating >300 °C that reset all α-doses before ~7 Ma could induce such a low α-dose, or (2) the batholith stayed at a relatively important temperature until recently, preventing any radiation damage effects until this date. Interestingly, previous studies [20,27], did not find evidence of any recent important reheating. Moreover, our ZFT data are not reset and show a low number of tracks. The author of [54] demonstrated that annealing of ZFT is much more temperature- and time-sensitive than healing of radiation damage in zircons. In our setting, zircon samples accumulated very little radiation damage in their lattice before a minimum of 7 Ma, suggesting that no important reheating occurred recently. We speculate that the batholith was at temperatures of ~400 °C at 40 Ma (Figure 5). We are not able to validate or disclaim if the Machu Picchu batholith experienced a reheating prior to 40 Ma with the dataset. Given that the intrusion age is ~222 Ma, it is likely that the rocks experienced reheating at some point, but clearly before the rapid cooling starting at about ~7 Ma. In such context, partial annealing of α -damage and full annealing of spontaneous fission tracks is very likely at temperatures of 300–400 °C and above e.g., [46]. Full annealing of α -damage is likely at temperatures above 530 °C. Without other higher temperature thermochronological data, we cannot well constrain that part of the thermal history. Nonetheless, our combined low-temperature thermochronology dataset does not indicate any reheating since ~7 Ma. The simplest explanation, close to the time-temperature path used in Figure 5, is that the batholith stayed at a temperature higher than ~300 °C until recently (before ~7 Ma, oldest age of our dataset) before cooling below that temperature. AHe and AFT data in the southern part of the Abancay Deflection indicate a cooling acceleration at 5 ± 2 Ma from 100–150 °C [27]. Our ZHe and ZFT data show that this cooling acceleration may have initiated at least sometimes before 7 Ma and from a higher temperature (300 °C) than previously proposed. This suggests a higher cooling rate (>43 °C/Myr) than the one deduced from AHe and AFT data (21±6 °C/Myr) [20]. The AHe- and AFT-derived exhumation rates range between 0.6 and 1.9 km/Myr [20]. Taking into account ZFT data, it leads to an exhumation rate within the range of 1.3 and 3.0 km/Myr since ~7 Ma, assuming end-member values for geothermal gradients of 26 ± 8 °C/km [55] or 18 ± 4 °C/km [27]. Our new data complete and strengthen the previous interpretations of the exhumation rates and further validate the tectonic syntaxis implications for the Abancay Deflection, as proposed in [27].

6. Conclusions

We provide new zircon fission track and zircon (U-Th)/He data for the Machu Picchu (Abancay Deflection, Peru) age–elevation profile. The new zircon ages are young (<7 Ma), reinforcing our previous interpretation of a young exhumation pulse (~5 Ma) and further favoring the interpretation of the Abancay Deflection as a tectonic syntaxis.
The ZHe system shows closure temperatures lower than those for apatite fission-track and apatite (U-Th)/He systems. This apparent contradiction, explained by low radiation damage in the zircons, is due to a simple time–temperature history with a longer stay at elevated temperature before cooling than to the age of the Machu Picchu batholith itself. In the present geological setting, these new data (1) demonstrate that the ZHe system is a thermochronometer not only sensitive to temperatures higher than 150 °C, but, in some cases, to temperatures lower than 100–110 °C or even 80 °C, and (2) complete the description of a setting (young ZHe ages, very low α-dose) that was predicted, but not observed by recent modelling. Our work highlights the importance of being aware of both the α-dose and the time since when damage accumulates to avoid biases when interpreting thermochronological data. In summary, our ZHe data open a door to designing further experiments and gaining a better understanding of He behavior in low radiation-damaged zircons.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/min12020145/s1, Figure S1: binomfit output file for sample AB-17-68 (AFT dating), Figure S2: binomfit output file for sample AB-17-69 (AFT dating), Figure S3: binomfit output file for sample AB-17-64 (ZFT dating), Figure S4: binomfit output file for sample AB-17-67 (ZFT dating), Figure S5: binomfit output file for sample AB-17-68 (ZFT dating).

Author Contributions

Conceptualization: X.R., C.G. and L.A.; methodology: C.G. and M.B. (Matthias Bernet), M.B. (Mélanie Balvay), D.G. and B.G.; software: X.R., D.G. and M.B. (Matthias Bernet) and M.B. (Mélanie Balvay); validation: B.G., X.R. and C.G.; investigation: B.G., X.R., L.A. and M.B. (Matthias Bernet), C.G. and D.G.; writing—original draft preparation: X.R.; writing—review and editing: X.R., B.G., C.G., D.G., L.A. and M.B. (Matthias Bernet); visualization: X.R., C.G., M.B. (Matthias Bernet) and B.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the Agence Nationale de la Recherche (12-NS06-0005-01 for He analyses), Institut de Recherche pour le Développement, l’Institut des Sciences de la Terre and Institut national des Sciences de l’Univers (INSU–CNRS), and the Natural Sciences and Engineering Research Council of Canada (NSERC) grant RGPIN/05658-2020 to D.G.

Data Availability Statement

Datasets for this research are included in this paper (and its supporting information file). [Creative Commons Attribution License].

Acknowledgments

We thank SERNANP, INGEMMET (Cuzco-PATA convenio 006-2016-Fondecyt), and F. Astete (National Archaeological Park of Machu Picchu) for permission to work along the Inca trail and for provided facilities. We thank F. Delgado and C. Benavente for field assistance, and P.H. Leloup, G. Mahéo (Géode laboratory, Lyon) and the GTC platform (F. Coeur and F. Sénebier, ISTerre, Grenoble) for sample processing, as well as R. Pinna-Jamme and F. Haurine for assistance during AFT, ZFT, and AHe dating. We also thank two anonymous reviewers for their helpful feedback.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ault, A.K.; Gautheron, C.; King, G.E. Innovations in (U–Th)/He, Fission Track, and Trapped Charge Thermochronometry with Applications to Earthquakes, Weathering, Surface-Mantle Connections, and the Growth and Decay of Mountains. Tectonics 2019, 38, 3705–3739. [Google Scholar] [CrossRef] [Green Version]
  2. Reiners, P.W.; Brandon, M.T. Using Thermochronology to Understand Orogenic Erosion. Annu. Rev. Earth Planet. Sci. 2006, 34, 419–466. [Google Scholar] [CrossRef] [Green Version]
  3. Reiners, P.W.; Farley, K.A.; Hickes, H.J. He Diffusion and (U–Th)/He Thermochronometry of Zircon: Initial Results from Fish Canyon Tuff and Gold Butte. Tectonophysics 2002, 349, 297–308. [Google Scholar] [CrossRef]
  4. Reiners, P.W.; Spell, T.L.; Nicolescu, S.; Zanetti, K.A. Zircon (U-Th)/He Thermochronometry: He Diffusion and Comparisons with 40Ar/39Ar Dating. Geochim. Cosmochim. Acta 2004, 68, 1857–1887. [Google Scholar] [CrossRef]
  5. Reiners, P.W. Zircon (U-Th)/He Thermochronometry. Rev. Mineral. Geochem. 2005, 58, 151–179. [Google Scholar] [CrossRef]
  6. Bernet, M. A Field-Based Estimate of the Zircon Fission-Track Closure Temperature. Chem. Geol. 2009, 259, 181–189. [Google Scholar] [CrossRef]
  7. Brandon, M.T.; Roden-Tice, M.K.; Garver, J.I. Late Cenozoic Exhumation of the Cascadia Accretionary Wedge in the Olympic Mountains, Northwest Washington State. Geol Soc Am Bull 1998, 110, 985–1009. [Google Scholar] [CrossRef]
  8. Ketcham, R.A. Fission-Track Annealing: From Geologic Observations to Thermal History Modeling. In Fission-Track Thermochronology and Its Application to Geology; Malusà, M., Fitzgerald, P., Eds.; Springer Textbooks in Earth Sciences, Geography and Environment; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
  9. Guenthner, W.R.; Reiners, P.W.; Tian, Y. Interpreting Date—EU Correlations in Zircon (U-Th)/He Datasets: A Case Study from the Longmen Shan, China. Earth Planet. Sci. Lett. 2014, 403, 328–339. [Google Scholar] [CrossRef]
  10. Johnson, J.E.; Flowers, R.M.; Baird, G.B.; Mahan, K.H. “Inverted” Zircon and Apatite (U-Th)/He Dates from the Front Range, Colorado: High-Damage Zircon as a Low-Temperature (<50 °C) Thermochronometer. Earth Planet. Sci. Lett. 2017, 466, 80–90. [Google Scholar] [CrossRef]
  11. Shuster, D.L.; Flowers, R.M.; Farley, K.A. The Influence of Natural Radiation Damage on Helium Diffusion Kinetics in Apatite. Earth Planet. Sci. Lett. 2006, 249, 148–161. [Google Scholar] [CrossRef]
  12. Flowers, R.M.; Shuster, D.L.; Wernicke, B.P.; Farley, K.A. Radiation Damage Control on Apatite (U-Th)/He Dates from the Grand Canyon Region, Colorado Plateau. Geology 2007, 35, 447–450. [Google Scholar] [CrossRef]
  13. Flowers, R.M.; Ketcham, R.A.; Shuster, D.L.; Farley, K.A. Apatite (U-Th)/He Thermochronometry Using a Radiation Damage Accumulation and Annealing Model. Geochim. Cosmochim. Acta 2009, 73, 2347–2365. [Google Scholar] [CrossRef]
  14. Gautheron, C.; Tassan-Got, L.; Barbarand, J.; Pagel, M. Effect of Alpha-Damage Annealing on Apatite (U–Th)/He Thermochronology. Chem. Geol. 2009, 266, 157–170. [Google Scholar] [CrossRef]
  15. Guenthner, W.R.; Reiners, P.W.; Ketcham, R.A.; Nasdala, L.; Giester, G. Helium Diffusion in Natural Zircon: Radiation Damage, Anisotropy, and the Interpretation of Zircon (U-Th)/He Thermochronology. Am. J. Sci. 2013, 313, 145. [Google Scholar] [CrossRef]
  16. Guenthner, W.R. Implementation of an Alpha Damage Annealing Model for Zircon (U-Th)/He Thermochronology with Comparison to a Zircon Fission Track Annealing Model. Geochem. Geophys. Geosyst. 2021, 22, e2019GC008757. [Google Scholar] [CrossRef]
  17. Ternois, S.; Odlum, M.; Ford, M.; Pik, R.; Stockli, D.; Tibari, B.; Vacherat, A.; Bernard, V. Thermochronological Evidence of Early Orogenesis, Eastern Pyrenees, France. Tectonics 2019, 38, 1308–1336. [Google Scholar] [CrossRef]
  18. Gautheron, C.; Djimbi, D.M.; Roques, J.; Balout, H.; Ketcham, R.A.; Simoni, E.; Pik, R.; Seydoux-Guillaume, A.-M.; Tassan-Got, L. A Multi-Method, Multi-Scale Theoretical Study of He and Ne Diffusion in Zircon. Geochim. Cosmochim. Acta 2020, 268, 348–367. [Google Scholar] [CrossRef]
  19. Farley, K.A.; Kohn, B.P.; Pillans, B. The Effects of Secular Disequilibrium on (U–Th)/He Systematics and Dating of Quaternary Volcanic Zircon and Apatite. Earth Planet. Sci. Lett. 2002, 201, 117–125. [Google Scholar] [CrossRef]
  20. Gérard, B.; Audin, L.; Robert, X.; Gautheron, C.; van der Beek, P.; Bernet, M.; Benavente, C.; Delgado, F. Pliocene River Capture and Incision of the Northern Altiplano: Machu Picchu, Peru. J. Geol. Soc. 2021, 178, jgs2020–jgs2100. [Google Scholar] [CrossRef]
  21. Marocco, R. Etude géologique de la chaîne andine au niveau de la déflexion d’Abancay (Pérou). Cah. ORSTOM.Série Géologie 1971, 3, 45–57. [Google Scholar]
  22. Roperch, P.; Carlotto, V.; Ruffet, G.; Fornari, M. Tectonic Rotations and Transcurrent Deformation South of the Abancay Deflection in the Andes of Southern Peru. Tectonics 2011, 30. [Google Scholar] [CrossRef] [Green Version]
  23. Mišković, A.; Spikings, R.A.; Chew, D.M.; Košler, J.; Ulianov, A.; Schaltegger, U. Tectonomagmatic Evolution of Western Amazonia: Geochemical Characterization and Zircon U-Pb Geochronologic Constraints from the Peruvian Eastern Cordilleran Granitoids. GSA Bull. 2009, 121, 1298–1324. [Google Scholar] [CrossRef]
  24. Carlier, G.; Grandin, G.; Laubacher, G.; Marocco, R.; Mégard, F. Present Knowledge of the Magmatic Evolution of the Eastern Cordillera of Peru. Earth-Sci. Rev. 1982, 18, 253–283. [Google Scholar] [CrossRef]
  25. Perez, N.D.; Horton, B.K.; Carlotto, V. Structural Inheritance and Selective Reactivation in the Central Andes: Cenozoic Deformation Guided by Pre-Andean Structures in Southern Peru. Tectonophysics 2016, 671, 264–280. [Google Scholar] [CrossRef] [Green Version]
  26. Kennan, L. Fission Track Ages and Sedimentary Provenance Studies in Peru, and Their Implications for Andean Paleogeographic Evolution, Stratigraphy and Hydrocarbon Systems. VI INGEPET 2008, 13, 17. [Google Scholar]
  27. Gérard, B.; Robert, X.; Audin, L.; Valla, P.G.; Bernet, M.; Gautheron, C. Differential Exhumation of the Eastern Cordillera in the Central Andes: Evidence for South-Verging Backthrusting (Abancay Deflection, Peru). Tectonics 2021, 40, e2020TC006314. [Google Scholar] [CrossRef]
  28. Carlier, G.; Lorand, J.P.; Liégeois, J.P. Potassic-Ultrapotassic Mafic Rocks Delineate Two Lithospheric Mantle Blocks beneath the Southern Peruvian Altiplano. Geology 2005, 33, 601–604. [Google Scholar] [CrossRef]
  29. Mamani, M.; Wörner, G.; Sempere, T. Geochemical Variations in Igneous Rocks of the Central Andean Orocline (13° S to 18° S): Tracing Crustal Thickening and Magma Generation through Time and Space. Geol. Soc. Am. Bull. 2010, 122, 162–182. [Google Scholar] [CrossRef]
  30. Carlier, G.; Lorand, J.-P.; Bonhomme, M.; Carlotto, V. A Reappraisal of the Cenozoic Inner Arc Magmatism in Southern Peru: Consequences for the Evolution of the Central Andes for the Past 50 Ma; ISAG: St. Malo, France, 1996; pp. 551–554. [Google Scholar]
  31. Ruiz, G.M.H.; Carlotto, V.; van Heiningen, P.V.; Andriessen, P.A.M. Steady-State Exhumation Pattern in the Central Andes—SE Peru. In Thermochronological Methods: From Paleotemperature Constraints to Landscape evolution Models; Lisker, F., Ventura, B., Glasmacher, U.A., Eds.; Geological Society, Special Publications: London, UK, 2009; Volume 307, pp. 307–316. [Google Scholar]
  32. Landry, K.R.; Coutand, I.; Whipp, D.M.; Grujic, D.; Hourigan, J.K. Late Neogene Tectonically Driven Crustal Exhumation of the Sikkim Himalaya: Insights from Inversion of Multithermochronologic Data. Tectonics 2016, 35, 833–859. [Google Scholar] [CrossRef] [Green Version]
  33. Schmitz, M.D.; Bowring, S.A. U-Pb Zircon and Titanite Systematics of the Fish Canyon Tuff: An Assessment of High-Precision U-Pb Geochronology and Its Application to Young Volcanic Rocks. Geochim. Cosmochim. Acta 2001, 65, 2571–2587. [Google Scholar] [CrossRef]
  34. Farley, K.A.; Wolf, R.; Silver, L. The Effect of Long Alpha-Stopping Distances on (U-Th)/He Dates. Geochim. Cosmochim. Acta 1996, 60, 4223–4229. [Google Scholar] [CrossRef]
  35. Farley, K.A. (U-Th)/He Dating: Techniques, Calibrations, and Applications. Rev. Mineral. Geochem. 2002, 47, 819–844. [Google Scholar] [CrossRef]
  36. Nasdala, L.; Hanchar, J.M.; Kronz, A.; Whitehouse, M.J. Long-Term Stability of Alpha Particle Damage in Natural Zircon. Chem. Geol. 2005, 220, 83–103. [Google Scholar] [CrossRef]
  37. Bernet, M.; Garver, J.I. Fission-Track Analysis of Detrital Zircon. Rev. Mineral. Geochem. 2005, 58, 205–237. [Google Scholar] [CrossRef]
  38. Hasebe, N.; Tagami, T.; Nishimura, S. Towards Zircon Fission-Track Thermochronology: Reference Framework for Confined Track Length Measurements. Chem. Geol. 1994, 112, 169–178. [Google Scholar] [CrossRef]
  39. Garver, J.I. Etching Zircon Age Standards for Fission-Track Analysis. Radiat. Meas. 2003, 37, 47–53. [Google Scholar] [CrossRef]
  40. Vermeesch, P. RadialPlotter: A Java Application for Fission Track, Luminescence and Other Radial Plots. Radiat. Meas. 2009, 44, 409–410. [Google Scholar] [CrossRef]
  41. Galbraith, R.F.; Laslett, G.M. Statistical Models for Mixed Fission Track Ages. Nucl. Tracks Radiat. Meas. 1993, 21, 459–470. [Google Scholar] [CrossRef]
  42. Ehlers, T.A.; Chaudhri, T.; Kumar, S.; Fuller, C.W.; Willett, S.D.; Ketcham, R.A.; Brandon, M.T.; Belton, D.X.; Kohn, B.P.; Gleadow, A.J.W.; et al. Computational Tools for Low-Temperature Thermochronometer Interpretation. Rev. Mineral. Geochem. 2005, 58, 589–622. [Google Scholar] [CrossRef]
  43. Whipp, D.; Kellett, D.; Coutand, I. Short Communication: Modelling Competing Effects of Cooling Rate, Grain Size and Radiation Damage in Low Temperature Thermochronometers. Geochronol. Discuss. 2021; 1–13, in review. [Google Scholar] [CrossRef]
  44. Ketcham, R.A. Forward and Inverse Modelling of Low-Temperature Thermochronology Data. Rev. Mineral. Geoch. 2005, 84, 1235–1255. [Google Scholar]
  45. Bernet, M.; Brandon, M.T.; Garver, J.I.; Molitor, B.R. Fundamentals of Detrital Zircon Fission-Track Analysis for Provenance and Exhumation Studies with Examples from the European Alps. In Detrital thermochronology—Provenance Analysis, Exhumation, and Landscape Evolution of Mountain Belts; Bernet, M., Spiegel, C., Eds.; Geological Society of America: Boulder, CO, USA, 2004; Volume 378, pp. 25–36. ISBN 978-0-8137-2378-5. [Google Scholar]
  46. Garver, J.I.; Kamp, P.J.J. Integration of Zircon Color and Zircon Fission-Track Zonation Patterns in Orogenic Belts: Application to the Southern Alps, New Zealand. Tectonophysics 2002, 349, 203–219. [Google Scholar] [CrossRef] [Green Version]
  47. Gordon Gastil, R.; DeLisle, M.; Morgan, J. Some Effects of Progressive Metamorphism on Zircons. GSA Bull. 1967, 78, 879–906. [Google Scholar] [CrossRef]
  48. Herman, F.; Seward, D.; Valla, P.G.; Carter, A.; Kohn, B.; Willett, S.D.; Ehlers, T.A. Worldwide Acceleration of Mountain Erosion under a Cooling Climate. Nature 2013, 504, 423–426. [Google Scholar] [CrossRef] [PubMed]
  49. Yamada, K.; Tagami, T. Postcollisional Exhumation History of the Tanzawa TonaliteComplex, Inferred from (U-Th)/He Thermochronologyand Fission Track Analysis. J. Geophys. Res. 2008, 113, 1–10. [Google Scholar] [CrossRef] [Green Version]
  50. Spencer, C.J.; Danišík, M.; Ito, H.; Hoiland, C.; Tapster, S.; Jeon, H.; McDonald, B.; Evans, N.J. Rapid Exhumation of Earth’s Youngest Exposed Granites Driven by Subduction of an Oceanic Arc. Geophys. Res. Lett. 2019, 46, 1259–1267. [Google Scholar] [CrossRef]
  51. Ketcham, R.A.; Carter, A.; Donelick, R.A.; Barbarand, J.; Hurford, A. Improved Measurement of Fission-Track Annealing in Apatite Using c-Axis Projection. Am. Mineral. 2007, 92, 789–798. [Google Scholar] [CrossRef]
  52. Bosch, G.; Teixell, A.; Jolivet, M.; Labaume, P.; Stockli, D.; Domènech, M.; Monié, P. Timing of Eocene—Miocene Thrust Activity in the Western Axial Zone and Chaînons Béarnais (West-Central Pyrenees) Revealed by Multi-Method Thermochronology. Rift. Mt. Build. Pyrenean Belt 2016, 348, 246–256. [Google Scholar] [CrossRef]
  53. Vacherat, A.; Mouthereau, F.; Pik, R.; Bellahsen, N.; Gautheron, C.; Bernet, M.; Daudet, M.; Balansa, J.; Tibari, B.; Pinna Jamme, R.; et al. Rift-to-Collision Transition Recorded by Tectono-Thermal Evolution of the Northern Pyrenees. Tectonics 2016, 35, 907–933. [Google Scholar] [CrossRef] [Green Version]
  54. Ginster, U.; Reiners, P.W.; Nasdala, L.; Chanmuang, N.C. Annealing Kinetics of Radiation Damage in Zircon. Geochim. Cosmochim. Acta 2019, 249, 225–246. [Google Scholar] [CrossRef]
  55. Barnes, J.B.; Ehlers, T.A.; McQuarrie, N.; O’Sullivan, P.B.; Tawackoli, S. Thermochronometer Record of Central Andean Plateau Growth, Bolivia (19.5 °S). Tectonics 2008, 27. [Google Scholar] [CrossRef] [Green Version]
Minerals 12 00145 g001 550
Figure 1. Location of the thermochronologic data (white dots) close to the Machu Picchu archaeological site in the Urubamba valley (Peru). The inset shows the location of the main map in Peru.
Figure 1. Location of the thermochronologic data (white dots) close to the Machu Picchu archaeological site in the Urubamba valley (Peru). The inset shows the location of the main map in Peru.
Minerals 12 00145 g001
Minerals 12 00145 g002 550
Figure 2. Age elevation of the Machu Picchu profile with AHe, ZHe, AFT, and ZFT data [20]; this study. The two upper AFT ages (pink squares) outside of the age-elevation trend were revised for this study.
Figure 2. Age elevation of the Machu Picchu profile with AHe, ZHe, AFT, and ZFT data [20]; this study. The two upper AFT ages (pink squares) outside of the age-elevation trend were revised for this study.
Minerals 12 00145 g002
Minerals 12 00145 g003 550
Figure 3. ZHe grain age of all the samples from the Machu Picchu vertical profile as a function of the equivalent uranium concentration (eU; left panel) and the equivalent sphere radius (ESR, right panel). Error bars are mostly smaller than the size of the points. There are no clear trends.
Figure 3. ZHe grain age of all the samples from the Machu Picchu vertical profile as a function of the equivalent uranium concentration (eU; left panel) and the equivalent sphere radius (ESR, right panel). Error bars are mostly smaller than the size of the points. There are no clear trends.
Minerals 12 00145 g003
Minerals 12 00145 g004 550
Figure 4. Predicted thermochronometer ages (a), and closure (or annealing) temperatures (b) for our samples. The model parameters are based on the mean values of our samples: the eU concentration is 40 μg/g for apatite and 525 μg/g for zircon, the ESR is 65 μm and 60 μm for apatite and zircon grains respectively. The plots were made with thermochron_plotter [43] and comprise 1203 forward models.
Figure 4. Predicted thermochronometer ages (a), and closure (or annealing) temperatures (b) for our samples. The model parameters are based on the mean values of our samples: the eU concentration is 40 μg/g for apatite and 525 μg/g for zircon, the ESR is 65 μm and 60 μm for apatite and zircon grains respectively. The plots were made with thermochron_plotter [43] and comprise 1203 forward models.
Minerals 12 00145 g004
Minerals 12 00145 g005 550
Figure 5. Time-temperature path used in HeFTy [44] to predict AHe, ZHe, AFT, and ZFT ages (in the blue box) using the model and model parameters of RDAMM [13], ZRDAAM [15,51] and the parallel curvilinear model of [51], respectively. This time–temperature path is an adaptation for higher closure temperature systems of the time temperature paths proposed for the southern Abancay Deflection by [27].
Figure 5. Time-temperature path used in HeFTy [44] to predict AHe, ZHe, AFT, and ZFT ages (in the blue box) using the model and model parameters of RDAMM [13], ZRDAAM [15,51] and the parallel curvilinear model of [51], respectively. This time–temperature path is an adaptation for higher closure temperature systems of the time temperature paths proposed for the southern Abancay Deflection by [27].
Minerals 12 00145 g005
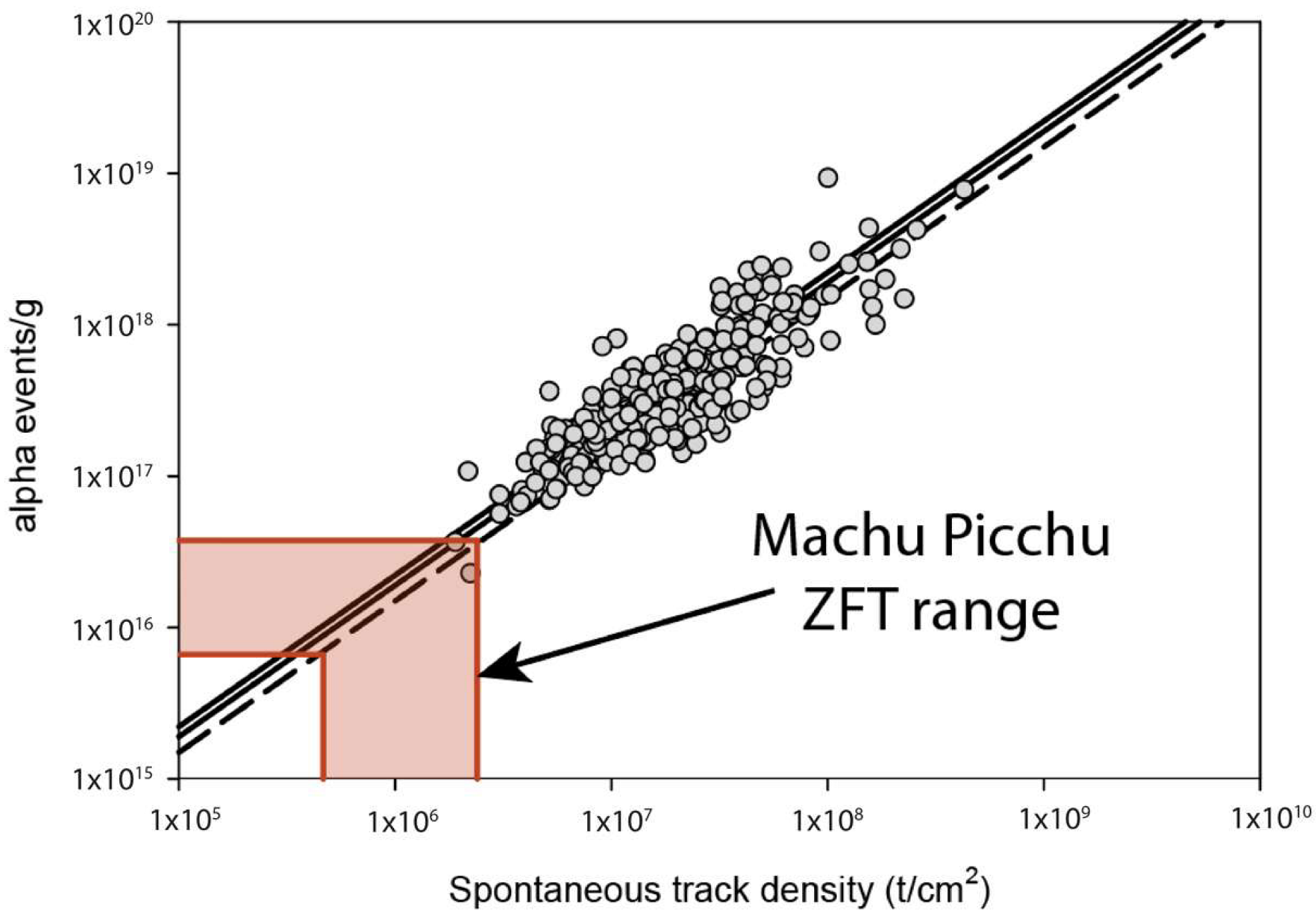
Minerals 12 00145 g006 550
Figure 6. Plot of the Machu Picchu ZFT data (light red area) in the simplified spontaneous track density ( ρ s) and α-dose relationship from [45]. Grey dots are the 336 zircons they analyzed, and the dashed and full lines represent the approximate and full relationships they computed, respectively. Spontaneous track densities from the Machu Picchu zircons indicate α-doses below 4 × 1016 α/g.
Figure 6. Plot of the Machu Picchu ZFT data (light red area) in the simplified spontaneous track density ( ρ s) and α-dose relationship from [45]. Grey dots are the 336 zircons they analyzed, and the dashed and full lines represent the approximate and full relationships they computed, respectively. Spontaneous track densities from the Machu Picchu zircons indicate α-doses below 4 × 1016 α/g.
Minerals 12 00145 g006
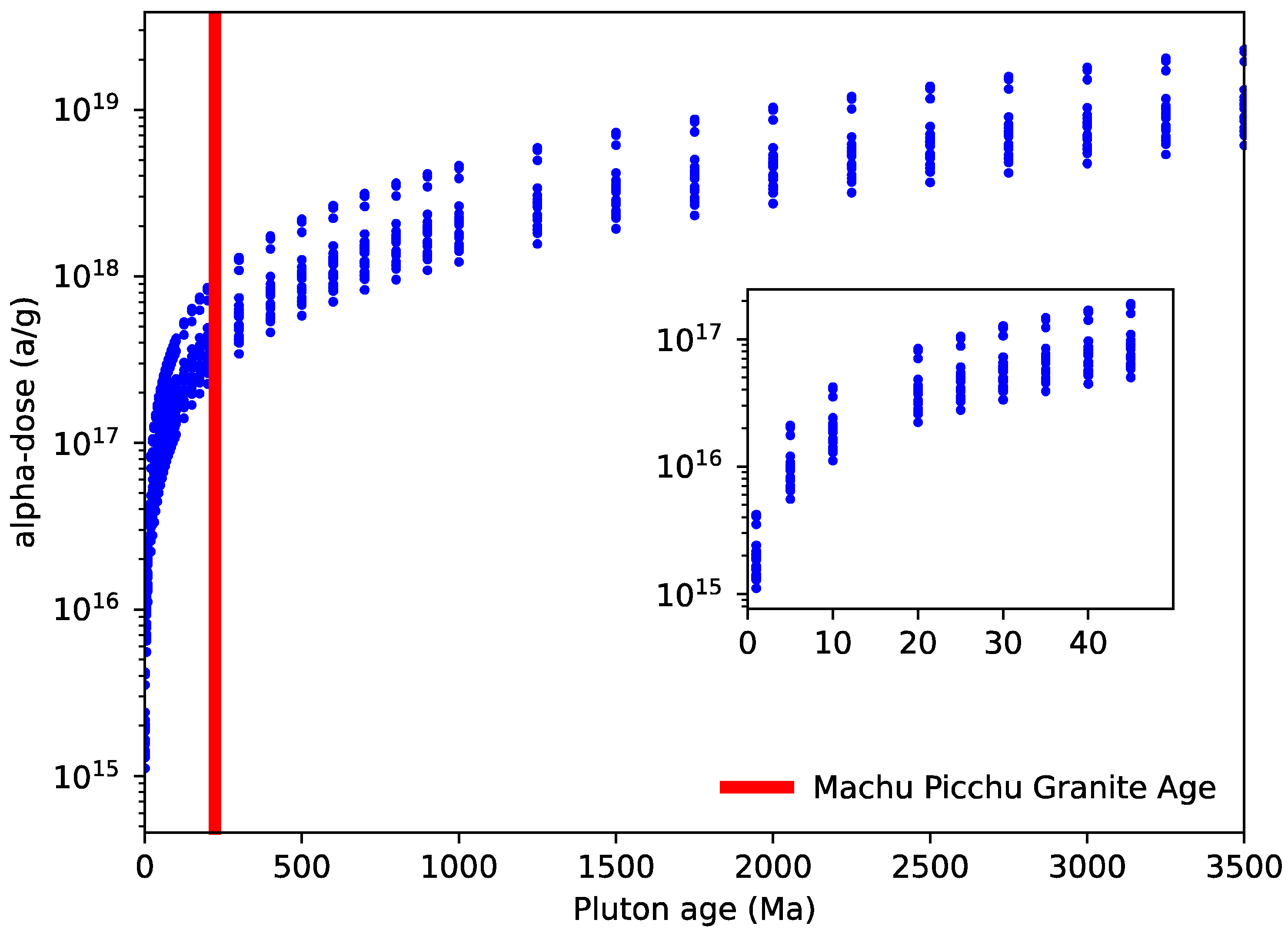
Minerals 12 00145 g007 550
Figure 7. α-dose as a function of the age of a pluton computed for the samples of the Machu Picchu vertical profile (blue dots). The thick red vertical line corresponds to the ages of the Machu Picchu batholith, ~222 Ma, [23]. Light red horizontal bands show the α-dose values that are compatible with the ZHe data from Machu Picchu. We estimated them with the relationship between the ZHe closure temperature, the α-dose, and the estimated ZHe closure temperature from the Machu Picchu. The inset is an enlargement of the first part of the graph.
Figure 7. α-dose as a function of the age of a pluton computed for the samples of the Machu Picchu vertical profile (blue dots). The thick red vertical line corresponds to the ages of the Machu Picchu batholith, ~222 Ma, [23]. Light red horizontal bands show the α-dose values that are compatible with the ZHe data from Machu Picchu. We estimated them with the relationship between the ZHe closure temperature, the α-dose, and the estimated ZHe closure temperature from the Machu Picchu. The inset is an enlargement of the first part of the graph.
Minerals 12 00145 g007
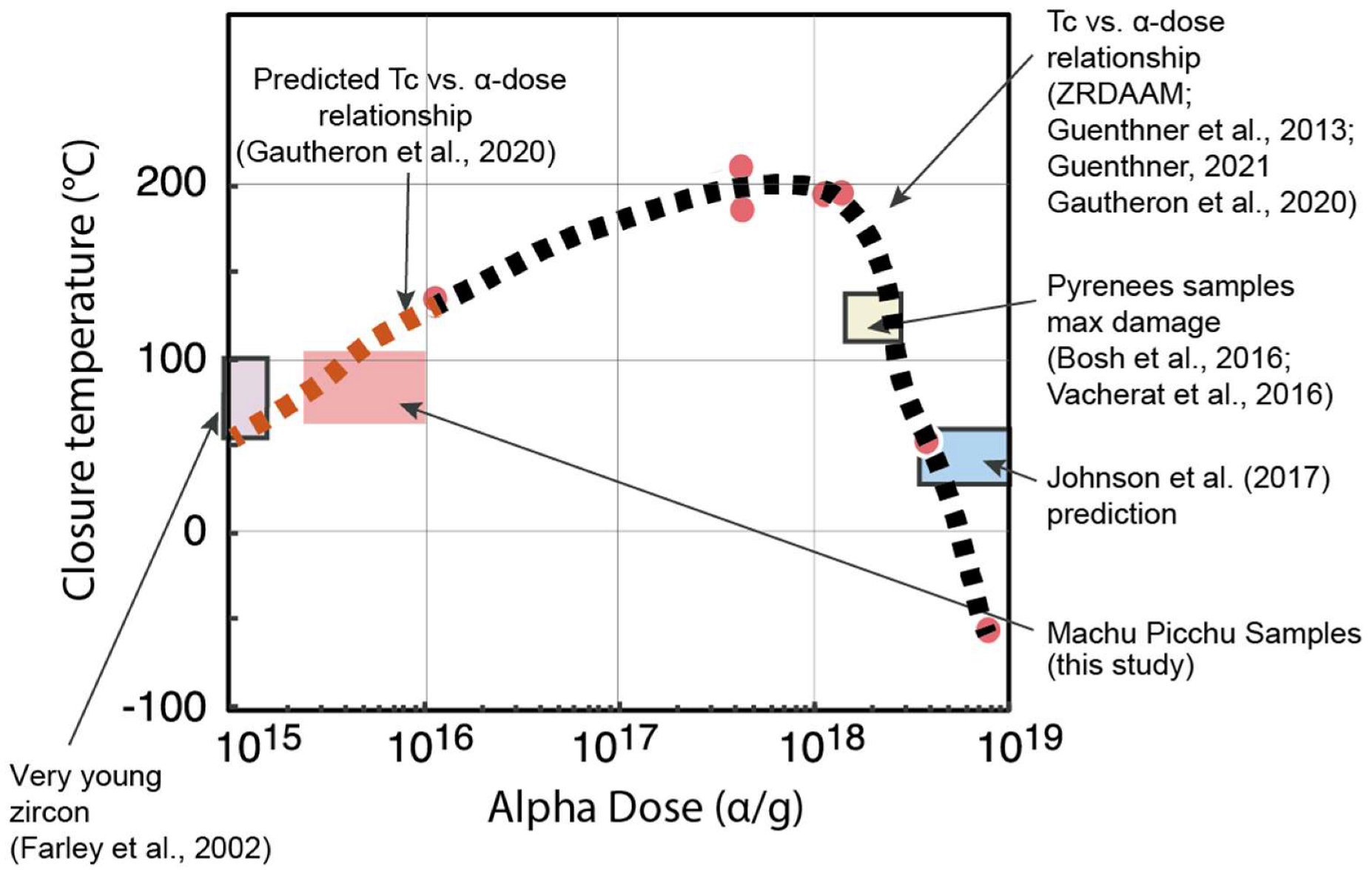
Minerals 12 00145 g008 550
Figure 8. Update of the coevolution of the closure temperature and the α-dose from [18] with our new data from the Machu Picchu profile (red square). Red circles correspond to [15] data recalculated with the density functional theory results (see details in [18]), the yellow box places Pyrenean samples [52,53], and the blue box represents [10] highly damaged zircons. The black dashed line shows the shape of the closure-temperature/α-dose relationship presented in previous models. We added an estimation of the closure-temperature/α-dose relationship inferred from [18] (red dashed line), and the estimated closure temperature of the ZHe from Machu Picchu (this study, red square).
Figure 8. Update of the coevolution of the closure temperature and the α-dose from [18] with our new data from the Machu Picchu profile (red square). Red circles correspond to [15] data recalculated with the density functional theory results (see details in [18]), the yellow box places Pyrenean samples [52,53], and the blue box represents [10] highly damaged zircons. The black dashed line shows the shape of the closure-temperature/α-dose relationship presented in previous models. We added an estimation of the closure-temperature/α-dose relationship inferred from [18] (red dashed line), and the estimated closure temperature of the ZHe from Machu Picchu (this study, red square).
Minerals 12 00145 g008
Table
Table 1. Zircon (U-Th)/He data.
Table 1. Zircon (U-Th)/He data.
Sample
Number		Latitude (° S)Longitude (° W)Elevation (m)Age (Ma) 1 σ   Err   ( Ma ) U 2 (μg/g)U 2 (ng)Th 2 (μg/g)Th 2 (ng)147Sm 2 (μg/g)eU (μg/g)Th/UHe 2 (nmol/g)Err. He (nmol/g)Mass (µg)Ft ESR   3
(μm) 		Raw Age (Ma)Err. (Ma)
zFCT-61 1 30.72.3373.02.3191.91.20.0417.10.553.04.26.10.849.823.51.7
zFCT-62 1 29.82.2315.31.9168.21.00.0354.00.544.03.56.20.851.523.01.7
zAB1720-113.1418272.58376161025.81.9470.44.5400.73.80.0562.60.962.25.09.60.857.220.41.5
zAB1720-21.50.1403.14.832.30.40.0410.50.12.80.211.90.862.51.30.1
zAB1720-326.82.0452.75.0332.83.60.0529.30.761.74.911.00.861.421.51.6
zAB1764-113.1874772.5293121492.10.2516.06.9248.13.30.0573.10.55.40.413.30.865.51.70.1
zAB1764-22.60.2675.28.5272.73.40.0738.00.48.40.712.60.864.32.10.2
zAB1764-32.40.2440.26.1152.52.10.1475.40.35.10.413.80.866.72.00.1
zAB1765-113.1883372.5342824413.20.2541.94.3298.82.40.1610.70.68.30.77.90.855.52.50.2
zAB1765-22.10.2597.04.7149.21.20.0631.30.25.50.47.90.855.71.60.1
zAB1765-32.10.2459.15.2147.91.70.0493.20.34.60.411.40.864.31.70.1
zAB1766-113.1903472.536927194.00.3503.93.3312.42.00.0575.90.69.60.86.50.851.33.10.2
zAB1766-22.20.2364.32.9237.41.90.1419.00.74.00.38.10.857.11.80.1
zAB1766-31.90.1403.03.1141.01.10.0435.50.33.60.37.60.854.01.50.1
zAB1767-113.1928872.5415729962.50.2464.84.0182.41.60.0506.80.45.40.48.60.857.92.00.1
zAB1767-23.30.2313.72.4115.90.90.0340.40.44.70.47.80.855.82.60.2
zAB1767-32.40.2613.77.0220.02.50.1664.30.47.10.611.40.863.52.00.1
zAB1768-113.202972.5349733222.30.21017.08.7270.92.30.01079.40.310.50.88.60.858.51.80.1
zAB1768-24.10.3353.61.5182.20.80.0395.50.56.60.54.40.746.53.10.2
zAB1768-33.30.21130.68.2486.03.50.11242.60.417.31.47.20.855.42.60.2
zAB1769-113.2065272.5320435813.50.3508.55.8257.93.00.0567.90.58.80.711.40.862.92.90.2
zAB1769-23.30.2538.37.3247.13.40.1595.20.58.60.713.60.866.02.70.2
zAB1769-32.40.21176.39.3489.73.90.01289.10.413.31.17.90.855.91.90.1
1 Fish Canyon Tuff standards. 2 Typical errors of the U, Th, Sm, and He measurements are in the range of 1.5–2% (1σ). The reproducibility for zircons is based on ongoing measurements of standards and is at 7.3%. 3 ESR is the age-diffusion domain (equivalent sphere radius).
Table
Table 2. Zircon fission track data 1.
Table 2. Zircon fission track data 1.
Samplenρs
(106 cm−2)		Nsρi
(106 cm−2)		Niρd
105 cm−2)		P
(χ2)		Dispersion
(%)		Age
(Ma)		 ± 1 σ U
(μg/g)		 ± 2 σ
AB-17-64201.45876.728513.910.111.95.40.385841
AB-17-67201.14674.117763.959.20.76.80.452829
AB-17-68201.24184.415103.978.60.37.10.455932
1 Fission-track age is given as the central age [41] calculated with Radialplotter software [40]. Samples were counted dry with a BH2 Olympus microscope at 1250x magnification. Ages were calculated using a ζ -value of 131.49 ± 5.4 for the IRMM 541 uranium dosimeter glass (50 μg/g U). n: number of grains analyzed; ρ s: spontaneous track density; Ns: number of spontaneous tracks; ρ i: induced track density; Ni: number of induced tracks; ρ d: dosimeter track density; P( χ 2): probability of obtaining the χ 2 value for n degrees of freedom (n = N° of crystals—1).
Table
Table 3. Revised apatite fission-track data for the Machu Picchu profile 1.
Table 3. Revised apatite fission-track data for the Machu Picchu profile 1.
Samplenρs
(105 cm−2)		Nsρi
(105 cm−2)		Niρd
(105 cm−2)		P
(χ2)		Dispersion
(%)		Central Age
(Ma)		 ± 2 σ U
(μg/g)		 ± 1 σ n
Dpar 2		 MDpar
( μ m ) 2		n
TL 2		 MTL
( μ m ) 2
AB-17-68104.87853.385114.369.40.218.55.1534741.5N.D. 3N.D. 3
AB-17-69113.0819.352214.445.213.63.13.2192421.0311.9
1 Fission track age is reported as the central age [41]. Samples were counted dry with a BX51 Olympus microscope at 1250x magnification. Ages were calculated with the BINOMFIT program [42], using a ζ -value of 270.90 ± 9.61 and the IRMM 540 uranium glass standard (15 μg/g U). n: number of grains analyzed; ρ s: spontaneous track density; Ns: number of spontaneous tracks; ρ i: induced track density; Ni: number of induced tracks; ρ d: dosimeter track density; P( χ 2): probability of obtaining the χ 2 value for n degrees of freedom (n = N° of crystals—1); n Dpar: number of Dpar values measured; MDpar: mean Dpar value, i.e., average etch pit diameter of fission track; n TL: number of track lengths measured; MTL: mean track lengths of horizontally confined tracks. 2 Reported from [20]. 3 No data.
Table
Table 4. Closure temperature (Tc) estimation with a scenario implying rapid cooling initiated between 5 and 7 Ma (case 1) and a simple scenario where the α-dose received is only due to the age of the Permo-Triasic, pluton 222 Ma; [23], (case 2) or of a >1 Ga pluton (case 3). Tc is estimated for each aliquot by reporting the computed α-dose for each case in Figure 8.
Table 4. Closure temperature (Tc) estimation with a scenario implying rapid cooling initiated between 5 and 7 Ma (case 1) and a simple scenario where the α-dose received is only due to the age of the Permo-Triasic, pluton 222 Ma; [23], (case 2) or of a >1 Ga pluton (case 3). Tc is estimated for each aliquot by reporting the computed α-dose for each case in Figure 8.
Case 1: 5–7 Ma CoolingCase 2: Permo-Triasic Pluton Emplacement (222 Ma) without ReheatingCase 3: 1 Ga Pluton Emplacement
without Reheating
Sample
Number		Time
(106 yr)		α -dose
(α/g)		Estimated Tc Range (°C) 1Time
(106 yr)		α-Dose
(α/g)		Estimated Tc Range (°C) 1Time
(109 yr)		α-Dose
(α/g)		Estimated Tc Range (°C) 1
zAB1720-25 6 . 7 × 10 15 50–100222 3.0 × 10 17 150–2001 1.5 × 10 18 110–130
zAB1764-15 9.4 × 10 15 70–110222 4.2 × 10 17 150–2001 2.1 × 10 18 100–120
zAB1764-25 1.2 × 10 16 100–140222 5.5 × 10 17 150–2001 2.7 × 10 18 100–120
zAB1764-35 7.8 × 10 15 70–110222 3.5 × 10 17 150–2001 1.7 × 10 18 100–130
zAB1765-15 1.0 × 10 16 70–110222 4.5 × 10 17 150–2001 2.2 × 10 18 100–120
zAB1765-25 1.0 × 10 16 100–140222 4.7 × 10 17 150–2001 2.3 × 10 18 100–120
zAB1765-35 8.1 × 10 15 70–110222 3.7 × 10 17 150–2001 1.8 × 10 18 100–130
zAB1766-15 9.4 × 10 15 70–110222 4.3 × 10 17 150–2001 2.1 × 10 18 100–120
zAB1766-25 6.9 × 10 15 70–110222 3.1 × 10 17 150–2001 1.5 × 10 18 100–130
zAB1766-35 7.1 × 10 15 70–110222 3.2 × 10 17 150–2001 1.6 × 10 18 100–130
zAB1767-16 9.9 × 10 15 70–110222 3.8 × 10 17 150–2001 1.8 × 10 18 100–130
zAB1767-26 6.7 × 10 15 70–110222 2.5 × 10 17 150–2001 1.2 × 10 18 120–190
zAB1767-36 1.3 × 10 16 100–140222 4.9 × 10 17 150–2001 2.4 × 10 18 100–120
zAB1768-17 2.5 × 10 16 100–140222 8.0 × 10 17 150–2001 3.9 × 10 18 30–60
zAB1768-27 9.1 × 10 15 70–110222 2.9 × 10 17 150–2001 1.4 × 10 18 100–130
zAB1768-37 2.8 × 10 16 100–140222 9.2 × 10 17 150–2001 4.5 × 10 18 30–60
zAB1769-18 1.5 × 10 16 100–140222 4.2 × 10 17 150–2001 2.0 × 10 18 100–120
zAB1769-28 1.6 × 10 16 100–140222 4.4 × 10 17 150–2001 2.1 × 10 18 100–120
zAB1769-38 3.4 × 10 16 100–140222 9.5 × 10 17 150–2001 4.6 × 10 18 30–60
1 Tc estimated from [18], using α-dose values.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Gérard, B.; Robert, X.; Grujic, D.; Gautheron, C.; Audin, L.; Bernet, M.; Balvay, M. Zircon (U-Th)/He Closure Temperature Lower Than Apatite Thermochronometric Systems: Reconciliation of a Paradox. Minerals 2022, 12, 145. https://doi.org/10.3390/min12020145

AMA Style

Gérard B, Robert X, Grujic D, Gautheron C, Audin L, Bernet M, Balvay M. Zircon (U-Th)/He Closure Temperature Lower Than Apatite Thermochronometric Systems: Reconciliation of a Paradox. Minerals. 2022; 12(2):145. https://doi.org/10.3390/min12020145

Chicago/Turabian Style

Gérard, Benjamin, Xavier Robert, Djordje Grujic, Cécile Gautheron, Laurence Audin, Matthias Bernet, and Mélanie Balvay. 2022. "Zircon (U-Th)/He Closure Temperature Lower Than Apatite Thermochronometric Systems: Reconciliation of a Paradox" Minerals 12, no. 2: 145. https://doi.org/10.3390/min12020145

APA Style

Gérard, B., Robert, X., Grujic, D., Gautheron, C., Audin, L., Bernet, M., & Balvay, M. (2022). Zircon (U-Th)/He Closure Temperature Lower Than Apatite Thermochronometric Systems: Reconciliation of a Paradox. Minerals, 12(2), 145. https://doi.org/10.3390/min12020145

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop