Deciphering Igneous Rock Crystals: Unveiling Multifractal Patterns in Crystal Size Dynamics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Number–Length (N-LoC) Fractal Geometry Method
2.2. Sample Description and Data Acquisition
3. Results
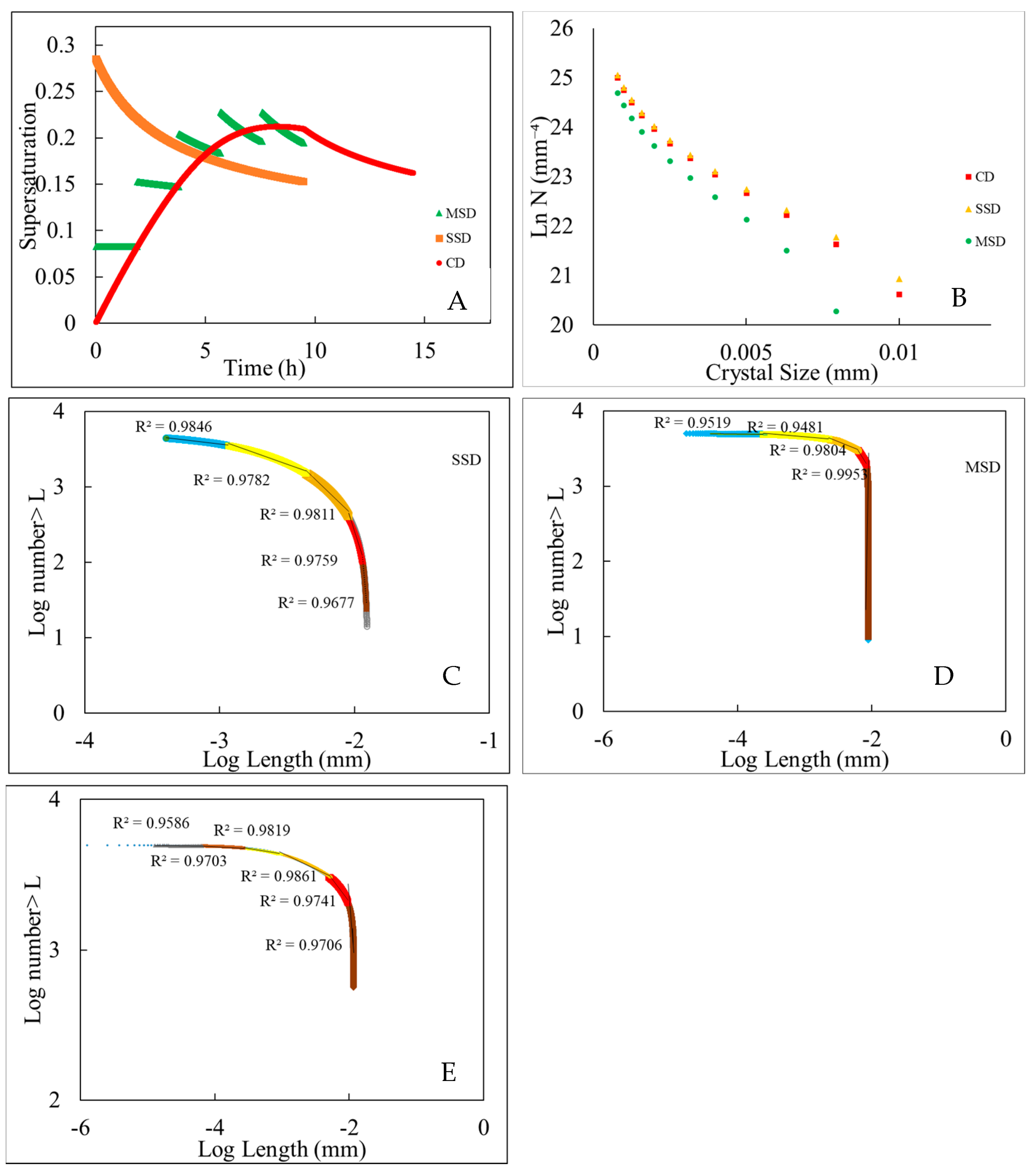
3.1. Multifractal Analysis of Experimental Samples
3.2. Multifractal Analysis of Natural Samples
3.3. Multifractal Analysis of Numerical Modeling Results
4. Discussion
4.1. Cooling-Driven Crystallization
4.2. Decompression-Induced Crystallization
4.3. Applications and Volcanic Hazard Implications
4.4. Multifractal and CSD Methods: Limitations and Future Trends
5. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Marsh, B.D. Crystal Size Distribution (CSD) in Rocks and the Kinetics and Dynamics of Crystallization I. Theory. Contrib. Mineral. Petrol. 1988, 99, 277–291. [Google Scholar] [CrossRef]
- Cashman, K.V.; Marsh, B.D. Crystal Size Distribution (CSD) in Rocks and the Kinetics and Dynamics of Crystallization II: Makaopuhi Lava Lake. Contrib. Mineral. Petrol. 1988, 99, 292–305. [Google Scholar] [CrossRef]
- Higgins, M.D. Measurement of Crystal Size Distributions. Am. Mineral. 2000, 85, 1105–1116. [Google Scholar] [CrossRef]
- Cashman, K.V. Crystallization of Mount St. Helens 1980–1986 Dacite: A Quantitative Textural Approach. Bull. Volcanol. 1988, 50, 194–209. [Google Scholar] [CrossRef]
- Marsh, B.D. On the Interpretation of Crystal Size Distributions in Magmatic Systems. J. Petrol. 1998, 39, 553–599. [Google Scholar] [CrossRef]
- Muir, D.D.; Blundy, J.D.; Rust, A.C. Multiphase Petrography of Volcanic Rocks Using Element Maps: A Method Applied to Mount St. Helens, 1980–2005. Bull. Volcanol. 2012, 74, 1101–1120. [Google Scholar] [CrossRef]
- Salisbury, M.J.; Bohrson, W.A.; Clynne, M.A.; Ramos, F.C.; Hoskin, P. Multiple Plagioclase Crystal Populations Identified by Crystal Size Distribution and In Situ Chemical Data: Implications for Timescales of Magma Chamber Processes Associated with the 1915 Eruption of Lassen Peak, CA. J. Petrol. 2008, 49, 1755–1780. [Google Scholar] [CrossRef]
- Ni, H.; Keppler, H.; Walte, N.; Schiavi, F.; Chen, Y.; Masotta, M.; Li, Z. In Situ Observation of Crystal Growth in a Basalt Melt and the Development of Crystal Size Distribution in Igneous Rocks. Contrib. Mineral. Petrol. 2014, 167, 1003. [Google Scholar] [CrossRef]
- Befus, K.S.; Andrews, B.J. Crystal Nucleation and Growth Produced by Continuous Decompression of Pinatubo Magma. Contrib. Mineral. Petrol. 2018, 173, 92. [Google Scholar] [CrossRef]
- Pupier, E.; Duchene, S.; Toplis, M.J. Experimental Quantification of Plagioclase Crystal Size Distribution during Cooling of a Basaltic Liquid. Contrib. Mineral. Petrol. 2008, 155, 555–570. [Google Scholar] [CrossRef]
- Andrews, B.J.; Befus, K.S. Supersaturation Nucleation and Growth of Plagioclase: A Numerical Model of Decompression-Induced Crystallization. Contrib. Mineral. Petrol. 2020, 175, 23. [Google Scholar] [CrossRef]
- Hammer, J.E.; Rutherford, M.J. An Experimental Study of the Kinetics of Decompression-Induced Crystallization in Silicic Melt. J. Geophys. Res. Solid Earth 2002, 107, ECV 8-1–ECV 8-24. [Google Scholar] [CrossRef]
- Higgins, M.D. Textural Coarsening in Igneous Rocks. Int. Geol. Rev. 2011, 53, 354–376. [Google Scholar] [CrossRef]
- Higgins, M.D. Magma Dynamics beneath Kameni Volcano, Thera, Greece, as Revealed by Crystal Size and Shape Measurements. J. Volcanol. Geotherm. Res. 1996, 70, 37–48. [Google Scholar] [CrossRef]
- Witter, M.; Furman, T.; Lafemina, P.; Feineman, M. Understanding Magmatic Processes at Telica Volcano, Nicaragua: Crystal Size Distribution and Textural Analysis. Am. Mineral. 2016, 101, 1052–1060. [Google Scholar] [CrossRef]
- Preece, K.; Gertisser, R.; Barclay, J.; Charbonnier, S.J.; Komorowski, J.C.; Herd, R.A. Transitions between Explosive and Effusive Phases during the Cataclysmic 2010 Eruption of Merapi Volcano, Java, Indonesia. Bull. Volcanol. 2016, 78, 54. [Google Scholar] [CrossRef]
- Innocenti, S.; del Marmol, M.A.; Voight, B.; Andreastuti, S.; Furman, T. Textural and Mineral Chemistry Constraints on Evolution of Merapi Volcano, Indonesia. J. Volcanol. Geotherm. Res. 2013, 261, 20–37. [Google Scholar] [CrossRef]
- van der Zwan, F.M.; Chadwick, J.P.; Troll, V.R. Textural History of Recent Basaltic-Andesites and Plutonic Inclusions from Merapi Volcano. Contrib. Mineral. Petrol. 2013, 166, 43–63. [Google Scholar] [CrossRef]
- Brugger, C.R.; Hammer, J.E. Crystal Size Distribution Analysis of Plagioclase in Experimentally Decompressed Hydrous Rhyodacite Magma. Earth Planet. Sci. Lett. 2010, 300, 246–254. [Google Scholar] [CrossRef]
- Mangler, M.F.; Humphreys, M.C.S.; Wadsworth, F.B.; Iveson, A.A.; Higgins, M.D. Variation of Plagioclase Shape with Size in Intermediate Magmas: A Window into Incipient Plagioclase Crystallisation. Contrib. Mineral. Petrol. 2022, 177, 64. [Google Scholar] [CrossRef]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Bölviken, B.; Stokke, P.R.; Feder, J.; Jössang, T. The Fractal Nature of Geochemical Landscapes. J. Geochem. Explor. 1992, 43, 91–109. [Google Scholar] [CrossRef]
- Cheng, Q.; Agterberg, F.P. Multifractal Modeling and Spatial Statistics. Math. Geol. 1996, 28, 1–16. [Google Scholar] [CrossRef]
- Cheng, Q.; Agterberg, F.P.; Ballantyne, S.B. The Separation of Geochemical Anomalies from Background by Fractal Methods. J. Geochem. Explor. 1994, 51, 109–130. [Google Scholar] [CrossRef]
- De Rosa, R.; Donato, P.; Ventura, G. Fractal Analysis of Mingled/Mixed Magmas: An Example from the Upper Pollara Eruption (Salina Island, Southern Tyrrhenian Sea, Italy). Lithos 2002, 65, 299–311. [Google Scholar] [CrossRef]
- Diego, P.; Giampiero, P. Chaotic Dynamics and Fractals in Magmatic Interaction Processes: A Different Approach to the Interpretation of Mafic Microgranular Enclaves. Earth Planet. Sci. Lett. 2000, 175, 93–103. [Google Scholar] [CrossRef]
- Armienti, P.; Tarquini, S. Power Law Olivine Crystal Size Distributions in Lithospheric Mantle Xenoliths. Lithos 2002, 65, 273–285. [Google Scholar] [CrossRef]
- Peternell, M.; Kruhl, J.H. Automation of Pattern Recognition and Fractal-Geometry-Based Pattern Quantification, Exemplified by Mineral-Phase Distribution Patterns in Igneous Rocks. Comput. Geosci. 2009, 35, 1415–1426. [Google Scholar] [CrossRef]
- Sadeghi, B.; Moarefvand, P.; Afzal, P.; Yasrebi, A.B.; Saein, L.D. Application of Fractal Models to Outline Mineralized Zones in the Zaghia Iron Ore Deposit, Central Iran. J. Geochem. Explor. 2012, 122, 9–19. [Google Scholar] [CrossRef]
- Sadeghi, B. Concentration-Concentration Fractal Modelling: A Novel Insight for Correlation between Variables in Response to Changes in the Underlying Controlling Geological-Geochemical Processes. Ore Geol. Rev. 2021, 128, 103875. [Google Scholar] [CrossRef]
- Sadeghi, B.; Cohen, D.R. Category-Based Fractal Modelling: A Novel Model to Integrate the Geology into the Data for More Effective Processing and Interpretation. J. Geochem. Explor. 2021, 226, 106783. [Google Scholar] [CrossRef]
- Sadeghi, B. Concentration-Area Plot. In Encyclopedia of Mathematical Geosciences; Daya Sagar, B.S., Cheng, Q., McKinley, J., Agterberg, F., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 169–175. ISBN 978-3-030-85040-1. [Google Scholar]
- Sadeghi, B. Spectrum-Area Method. In Encyclopedia of Mathematical Geosciences; Daya Sagar, B.S., Cheng, Q., McKinley, J., Agterberg, F., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 1398–1403. ISBN 978-3-030-85040-1. [Google Scholar]
- Sadeghi, B.; Cohen, D. Concentration-Distance from Centroids (C-DC) Multi-Fractal Model: A Model to Recognize Geochemical Anomalies Based on the Distance of Samples from the Known Mineralization Areas. In Proceedings of the IAMG 2019–20th Annual Conference of the International Association for Mathematical Geosciences, State College, PA, USA, 10–16 August 2019. [Google Scholar]
- Sadeghi, B. Simulated-Multifractal Models: A Futuristic Review of Multifractal Modeling in Geochemical Anomaly Classification. Ore Geol. Rev. 2021, 139, 104511. [Google Scholar] [CrossRef]
- Agterberg, F. Multifractal Modelling of the Sizes and Grades of Giant and Supergiant Deposits. Glob. Tecton. Metallog. 1996, 6, 131–136. [Google Scholar] [CrossRef]
- Sadeghi, B.; Khalajmasoumi, M.; Afzal, P.; Moarefvand, P. Discrimination of Iron High Potential Zones at the Zaghia Iron Ore Deposit, Bafq, Using Index Overlay GIS Method. Iran. J. Earth Sci. 2015, 6, 91–98. [Google Scholar]
- Agterberg, F.P.; Cheng, Q.; Brown, A.; Good, D. Multifractal Modeling of Fractures in the Lac Du Bonnet Batholith, Manitoba. Comput Geosci 1996, 22, 497–507. [Google Scholar] [CrossRef]
- Cashman, K.V. Crystal Size Distribution (CSD) Analysis of Volcanic Samples: Advances and Challenges. Front. Earth Sci. 2020, 8, 291. [Google Scholar] [CrossRef]
- Giuliani, L.; Iezzi, G.; Vetere, F.; Behrens, H.; Mollo, S.; Cauti, F.; Ventura, G.; Scarlato, P. Evolution of Textures, Crystal Size Distributions and Growth Rates of Plagioclase, Clinopyroxene and Spinel Crystallized at Variable Cooling Rates from a Mid-Ocean Ridge Basaltic Melt. Earth Sci. Rev. 2020, 204, 103165. [Google Scholar] [CrossRef]
- Zieg, M.J.; Marsh, B.D. Multiple Reinjections and Crystal-Mush Compaction in the Beacon Sill, McMurdo Dry Valleys, Antarctica. J. Petrol. 2012, 53, 2567–2591. [Google Scholar] [CrossRef]
- Frey, H.M.; Manon, M.R.; Barclay, J.; Davies, B.V.; Walters, S.A.; Cole, P.D.; Christopher, T.E.; Joseph, E.P. Petrology of the Explosive Deposits from the April 2021 Eruption of La Soufrière Volcano, St Vincent: A Time-Series Analysis of Microlites. Geol. Soc. Lond. Spec. Publ. 2024, 539, 201–230. [Google Scholar] [CrossRef]
- Brugger, C.R.; Hammer, J.E. Crystallization Kinetics in Continuous Decompression Experiments: Implications for Interpreting Natural Magma Ascent Processes. J. Petrol. 2010, 51, 1941–1965. [Google Scholar] [CrossRef]
- Riker, J.M.; Cashman, K.V.; Rust, A.C.; Blundy, J.D. Experimental Constraints on Plagioclase Crystallization during H2O- and H2O–CO2-Saturated Magma Decompression. J. Petrol. 2015, 56, 1967–1998. [Google Scholar] [CrossRef]
- Brandeis, G.; Jaupart, C.; Allegre, C.J. Nucleation, Crystal Growth and the Thermal Regime of Cooling Magmas. J. Geophys. Res. 1984, 89, 10161–10177. [Google Scholar] [CrossRef]
- Hammer, J.E. Experimental Studies of the Kinetics and Energetics of Magma Crystallization. Rev. Mineral. Geochem. 2008, 69, 9–59. [Google Scholar] [CrossRef]
- Mollo, S.; Hammer, J. Dynamic Crystallization in Magmas. EMU Notes Miner. 2017, 16. [Google Scholar] [CrossRef]
- Schiavi, F.; Walte, N.; Keppler, H. First in Situ Observation of Crystallization Processes in a Basaltic-Andesitic Melt with the Moissanite Cell. Geology 2009, 37, 963–966. [Google Scholar] [CrossRef]
- Le Gall, N.; Arzilli, F.; La Spina, G.; Polacci, M.; Cai, B.; Hartley, M.E.; Vo, N.T.; Atwood, R.C.; Di Genova, D.; Nonni, S.; et al. In Situ Quantification of Crystallisation Kinetics of Plagioclase and Clinopyroxene in Basaltic Magma: Implications for Lava Flow. Earth Planet. Sci. Lett. 2021, 568, 117016. [Google Scholar] [CrossRef]
- Polacci, M.; Arzilli, F.; La Spina, G.; Le Gall, N.; Cai, B.; Hartley, M.E.; Di Genova, D.; Vo, N.T.; Nonni, S.; Atwood, R.C.; et al. Crystallisation in Basaltic Magmas Revealed via in Situ 4D Synchrotron X-Ray Microtomography. Sci. Rep. 2018, 8, 8377. [Google Scholar] [CrossRef]
- Burkhard, D.J.M. Nucleation and Growth Rates of Pyroxene, Plagioclase and Fe-Ti Oxides in Basalt [Abs.]. In Eos, Transactions, American Geophysical Union; Wiley: Hoboken, NJ, USA, 2003; Volume 84. [Google Scholar]
- Kile, D.E.; Eberl, D.D. On the Origin of Size-Dependent and Size-Independent Crystal Growth: Influence of Advection and Diffusion. Am. Mineral. 2003, 88, 1514–1521. [Google Scholar] [CrossRef]
- Cabane, H.; Laporte, D.; Provost, A. An Experimental Study of Ostwald Ripening of Olivine and Plagioclase in Silicate Melts: Implications for the Growth and Size of Crystals in Magmas. Contrib. Mineral. Petrol. 2005, 150, 37–53. [Google Scholar] [CrossRef]
- Armienti, P.; Pareschi, M.T.; Innocenti, F.; Pompilio, M. Effects of Magma Storage and Ascent on the Kinetics of Crystal Growth. Contrib. Mineral. Petrol. 1994, 115, 402–414. [Google Scholar] [CrossRef]
- Hammer, J.E.; Cashman, K.V.; Hoblitt, R.P.; Newman, S. Degassing and Microlite Crystallization during Pre-Climactic Events of the 1991 Eruption of Mt. Pinatubo, Philippines. Bull. Volcanol. 1999, 60, 355–380. [Google Scholar] [CrossRef]
- Cashman, K.V.; McConnell, S.M. Multiple Levels of Magma Storage during the 1980 Summer Eruptions of Mount St. Helens, WA. Bull. Volcanol. 2005, 68, 57. [Google Scholar] [CrossRef]
- Shea, T.; Hammer, J.E. Kinetics of Cooling- and Decompression-Induced Crystallization in Hydrous Mafic-Intermediate Magmas. J. Volcanol. Geotherm. Res. 2013, 260, 127–145. [Google Scholar] [CrossRef]
- Mujin, M.; Nakamura, M. A Nanolite Record of Eruption Style Transition. Geology 2014, 42, 611–614. [Google Scholar] [CrossRef]
- Higgins, M.D. Verification of Ideal Semi-Logarithmic, Lognormal or Fractal Crystal Size Distributions from 2D Datasets. J. Volcanol. Geotherm. Res. 2006, 154, 8–16. [Google Scholar] [CrossRef]
- Higgins, M.D. Numerical Modeling of Crystal Shapes in Thin Sections: Estimation of Crystal Habit and True Size. Am. Mineral. 1994, 79, 113–119. [Google Scholar]
- Morgan, D.J.; Jerram, D.A. On Estimating Crystal Shape for Crystal Size Distribution Analysis. J. Volcanol. Geotherm. Res. 2006, 154, 1–7. [Google Scholar] [CrossRef]
- Jerram, D.A.; Mock, A.; Davis, G.R.; Field, M.; Brown, R.J. 3D Crystal Size Distributions: A Case Study on Quantifying Olivine Populations in Kimberlites. Lithos 2009, 112, 223–235. [Google Scholar] [CrossRef]
- Zellmer, G.F. Gaining Acuity on Crystal Terminology in Volcanic Rocks. Bull. Volcanol. 2021, 83, 78. [Google Scholar] [CrossRef]
- Jeffery, A.J.; Gertisser, R.; Troll, V.R.; Jolis, E.M.; Dahren, B.; Harris, C.; Tindle, A.G.; Preece, K.; O’Driscoll, B.; Humaida, H.; et al. The Pre-Eruptive Magma Plumbing System of the 2007–2008 Dome-Forming Eruption of Kelut Volcano, East Java, Indonesia. Contrib. Mineral. Petrol. 2013, 166, 275–308. [Google Scholar] [CrossRef]
- Cashman, K.; Blundy, J. Petrological Cannibalism: The Chemical and Textural Consequences of Incremental Magma Body Growth. Contrib. Mineral. Petrol. 2013, 166, 703–729. [Google Scholar] [CrossRef]
- Morgan, D.J.; Jerram, D.A.; Chertkoff, D.G.; Davidson, J.P.; Pearson, D.G.; Kronz, A.; Nowell, G.M. Combining CSD and Isotopic Microanalysis: Magma Supply and Mixing Processes at Stromboli Volcano, Aeolian Islands, Italy. Earth Planet. Sci. Lett. 2007, 260, 419–431. [Google Scholar] [CrossRef]
- Hammer, J.E.; Cashman, K.V.; Voight, B. Magmatic Processes Revealed by Textural and Compositional Trends in Merapi Dome Lavas. J. Volcanol. Geotherm. Res. 2000, 100, 165–192. [Google Scholar] [CrossRef]
- Gualda, G.A.R.; Ghiorso, M.S.; Lemons, R.V.; Carley, T.L. Rhyolite-MELTS: A Modified Calibration of MELTS Optimized for Silica-Rich, Fluid-Bearing Magmatic Systems. J. Petrol. 2012, 53, 875–890. [Google Scholar] [CrossRef]
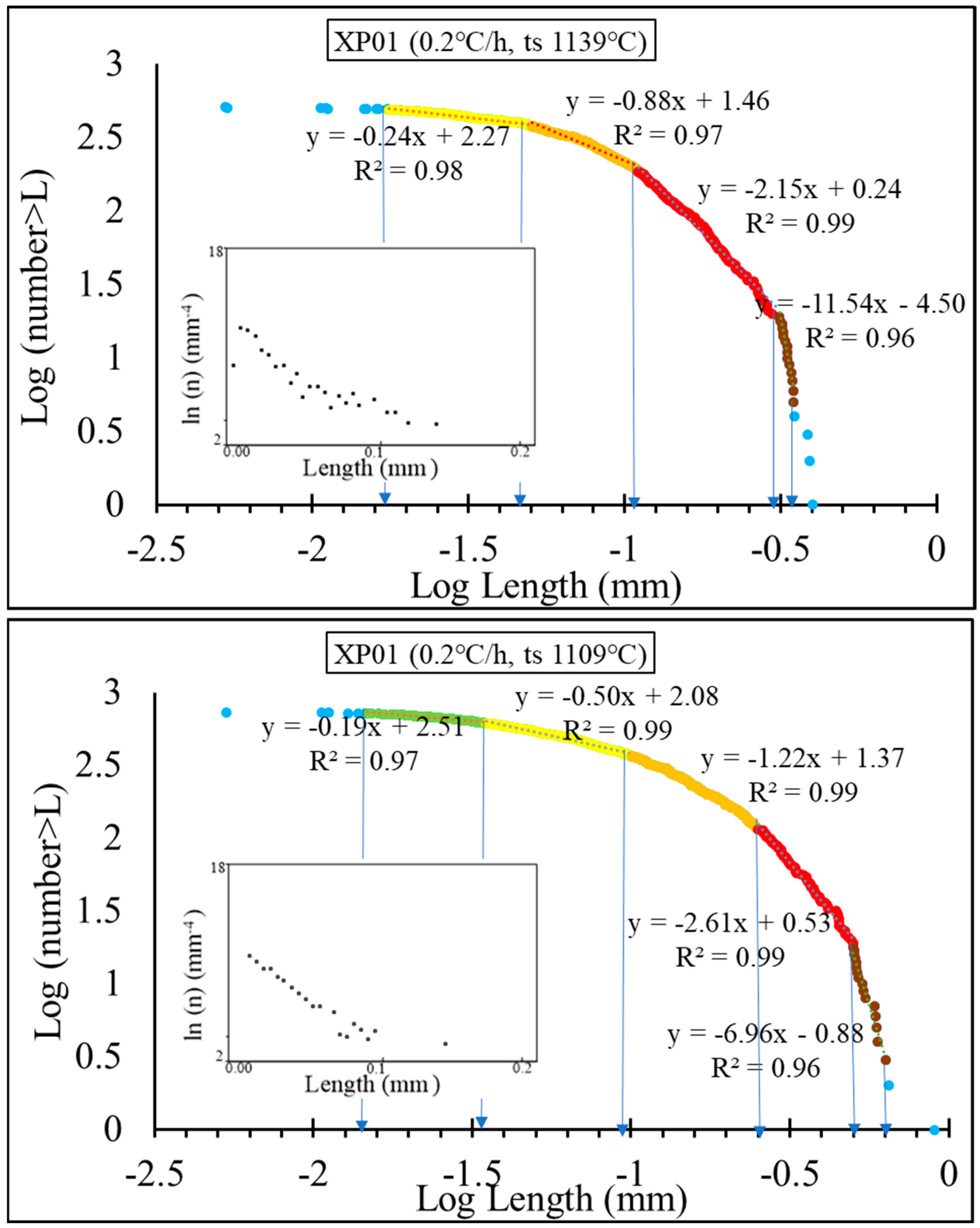
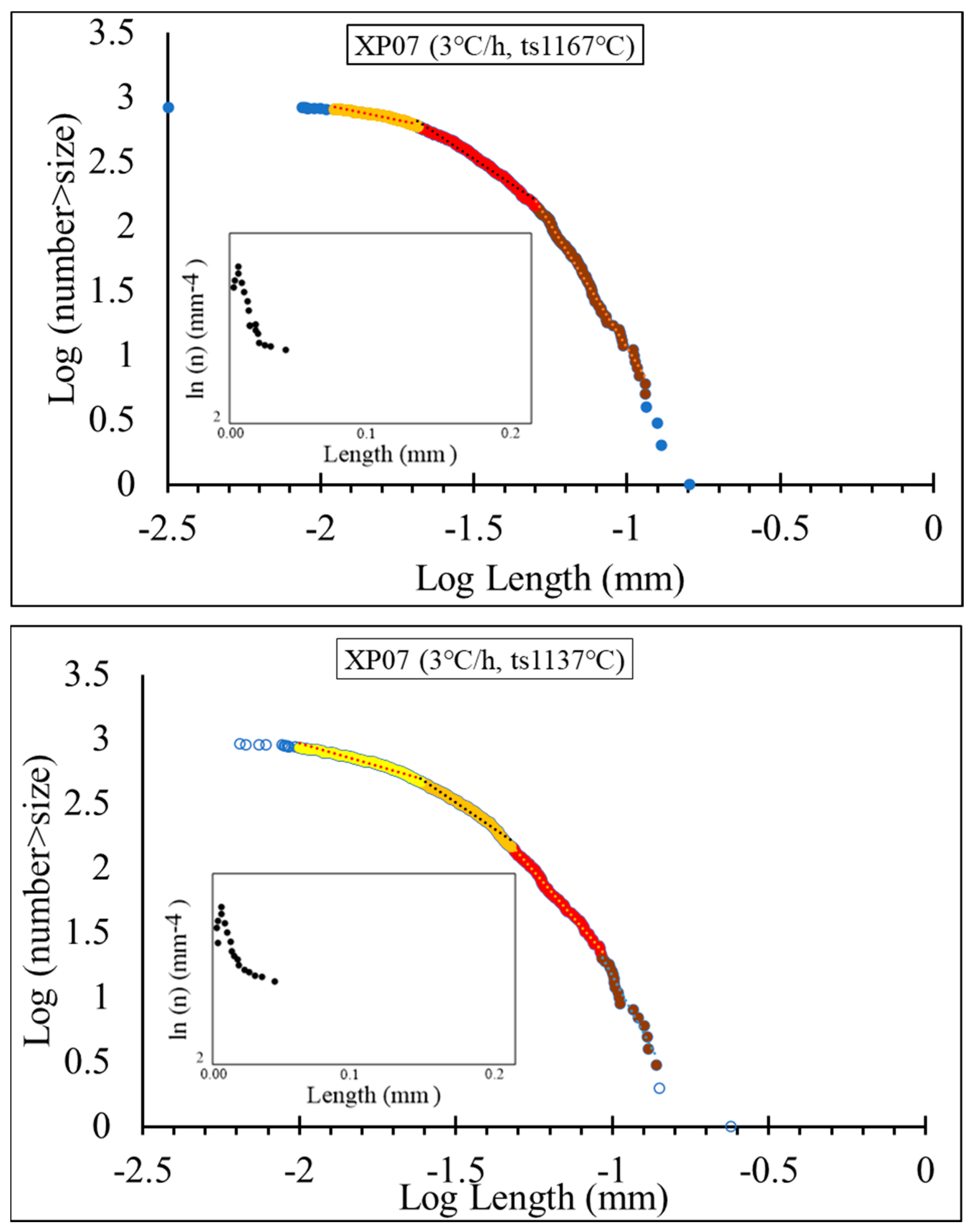
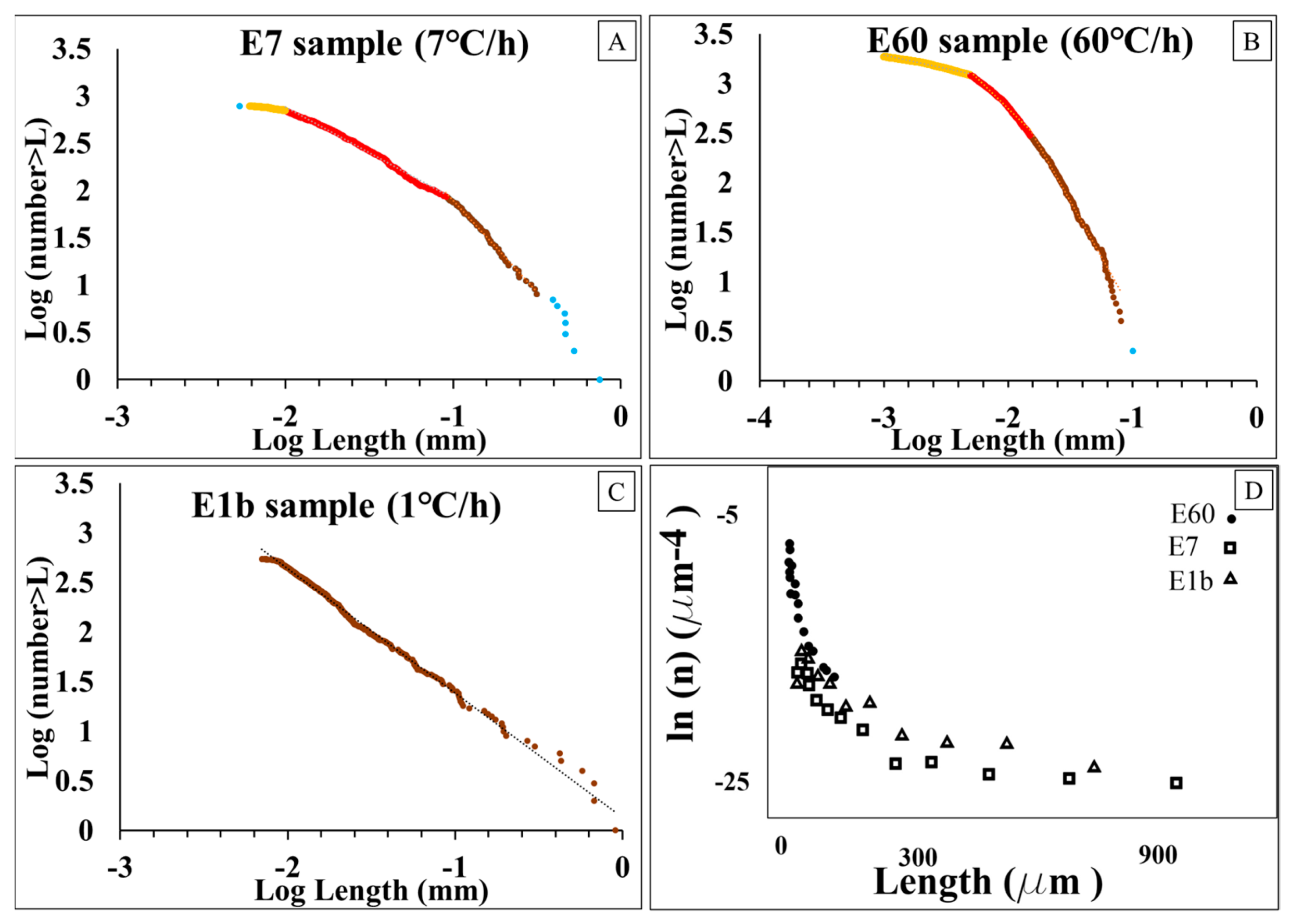
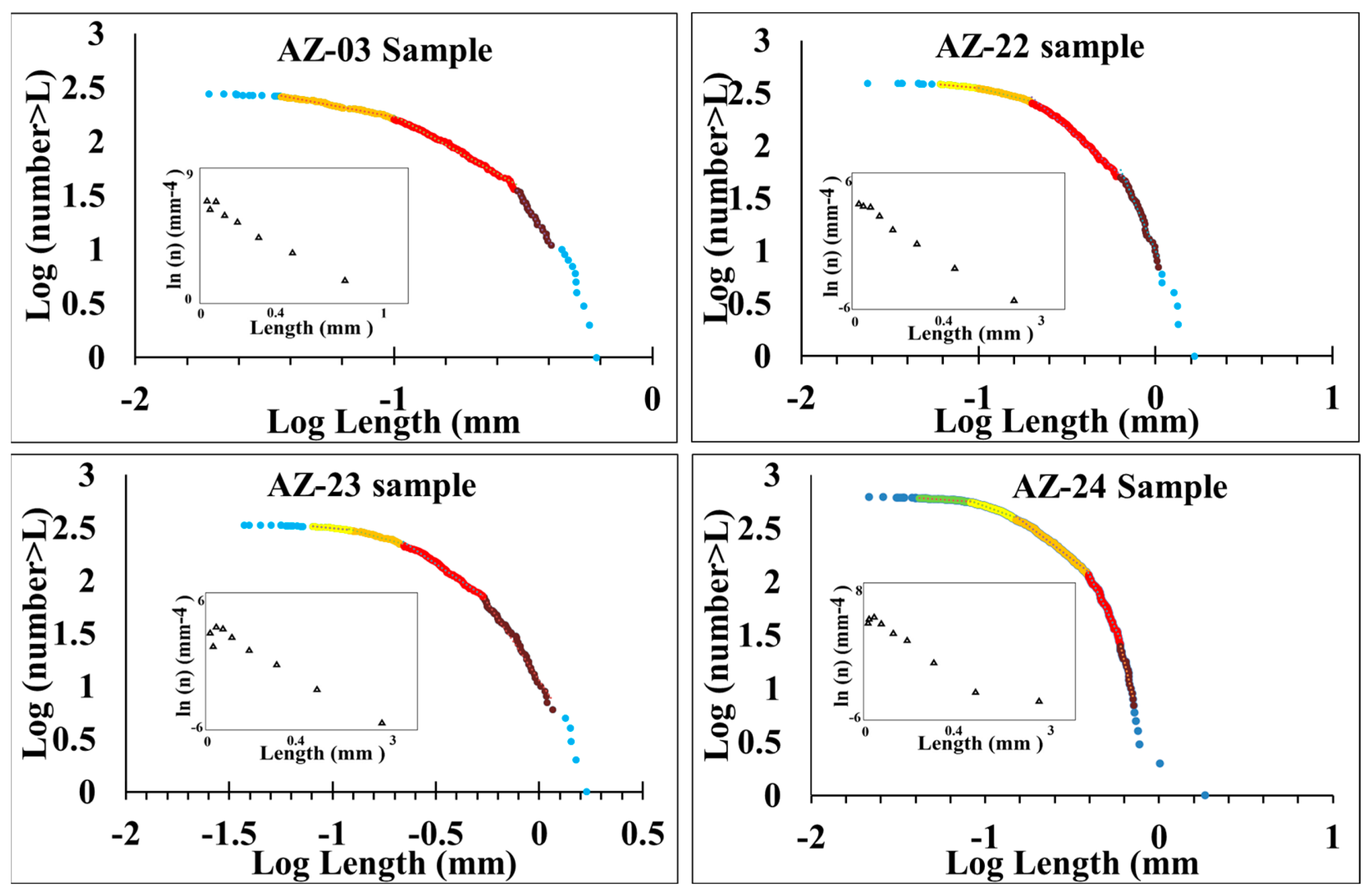

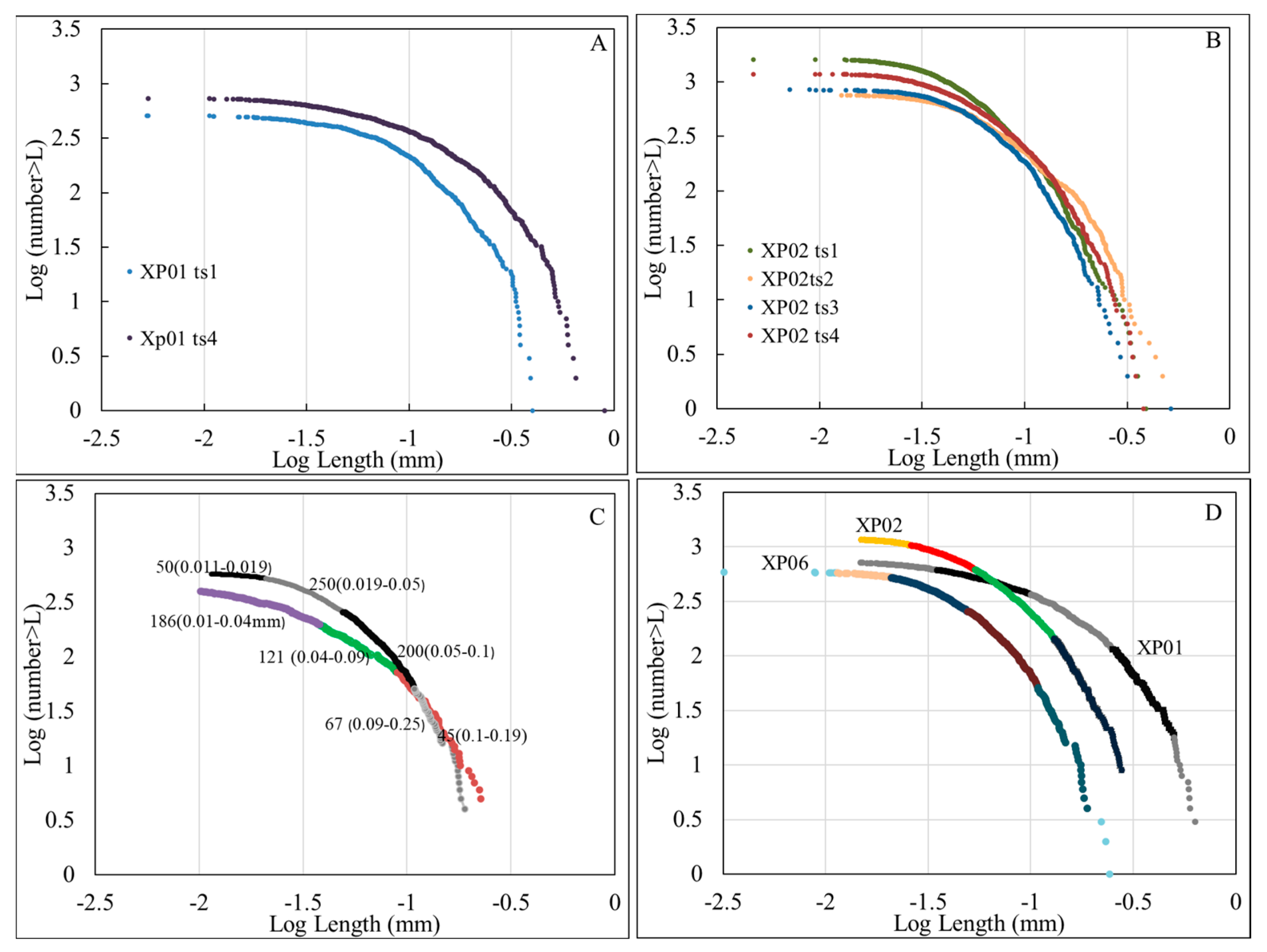

| XP01 (ts 1139 °C) | XP01 (ts 1109 °C) | ||||
|---|---|---|---|---|---|
| t (mm) | n | p (%) | t (mm) | n | P (%) |
| 0.02 | 16 | 3.23 | 0.01 | 12 | 1.74 |
| 0.05 | 107 | 21.57 | 0.03 | 88 | 12.74 |
| 0.11 | 188 | 37.90 | 0.10 | 230 | 33.29 |
| 0.30 | 169 | 34.07 | 0.25 | 255 | 36.90 |
| 0.33 | 14 | 2.82 | 0.50 | 97 | 14.04 |
| 0.40 | 5 | 1.01 | 0.63 | 3 | 0.43 |
| 0.9 | 2 | ||||
| XP07 (ts 1167 °C) | XP07 (1137 °C) | ||||
|---|---|---|---|---|---|
| t (mm) | n | p | t (mm) | n | p |
| 0.01 | 15 | 2.07 | 0.01 | 16 | 2.41 |
| 0.02 | 158 | 21.85 | 0.03 | 246 | 36.99 |
| 0.05 | 408 | 56.43 | 0.05 | 280 | 42.11 |
| 0.11 | 137 | 18.95 | 0.09 | 140 | 21.05 |
| 0.16 | 6 | 0.83 | 0.13 | 18 | 2.71 |
| 0.23 | 6 | 0.90 | |||
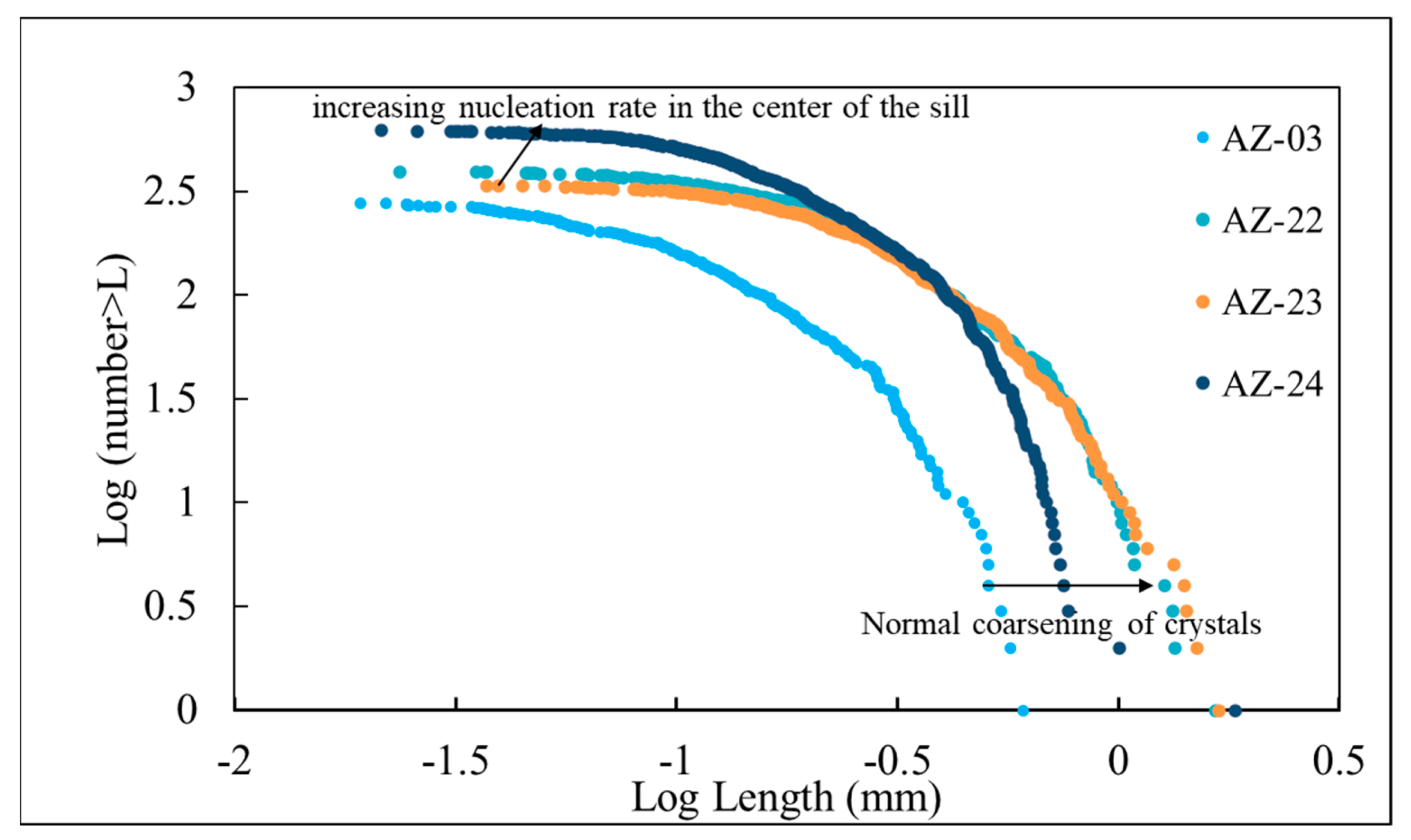
| AZ-03 | AZ-22 | AZ-23 | AZ-24 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| t (mm) | n | p | t (mm) | n | p | t (mm) | n | p | t (mm) | n | p |
| 0.04 | 21 | 7.6 | 0.06 | 16 | 4.1 | 0.08 | 19 | 5.7 | 0.04 | 17 | 2.8 |
| 0.10 | 99 | 35.6 | 0.10 | 31 | 8.0 | 0.13 | 25 | 7.5 | 0.08 | 51 | 8.5 |
| 0.29 | 124 | 44.6 | 0.20 | 89 | 22.9 | 0.22 | 78 | 23.4 | 0.15 | 159 | 26.6 |
| 0.42 | 23 | 8.3 | 0.63 | 207 | 53.2 | 0.54 | 142 | 42.5 | 0.38 | 256 | 42.9 |
| 0.61 | 11 | 4.0 | 1.12 | 41 | 10.5 | 1.12 | 65 | 19.5 | 0.60 | 90 | 15.1 |
| 1.66 | 6 | 1.5 | 1.69 | 5 | 1.5 | 0.71 | 18 | 3.0 | |||
| 1.8 | 6 | 1.0 | |||||||||
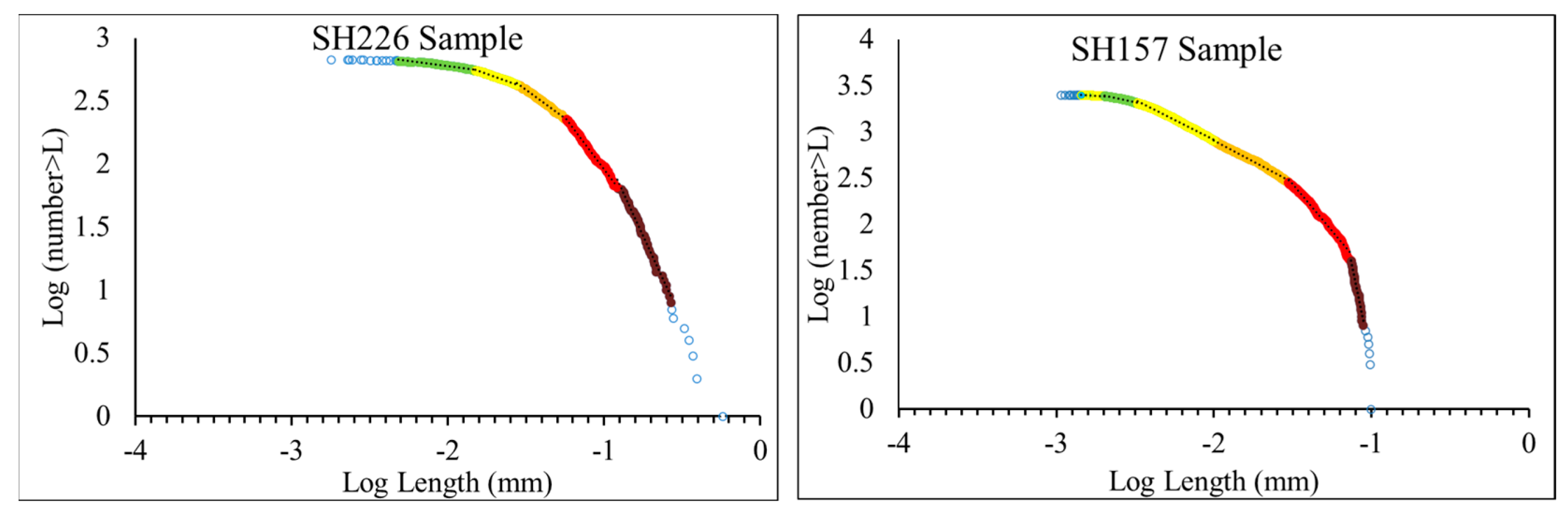
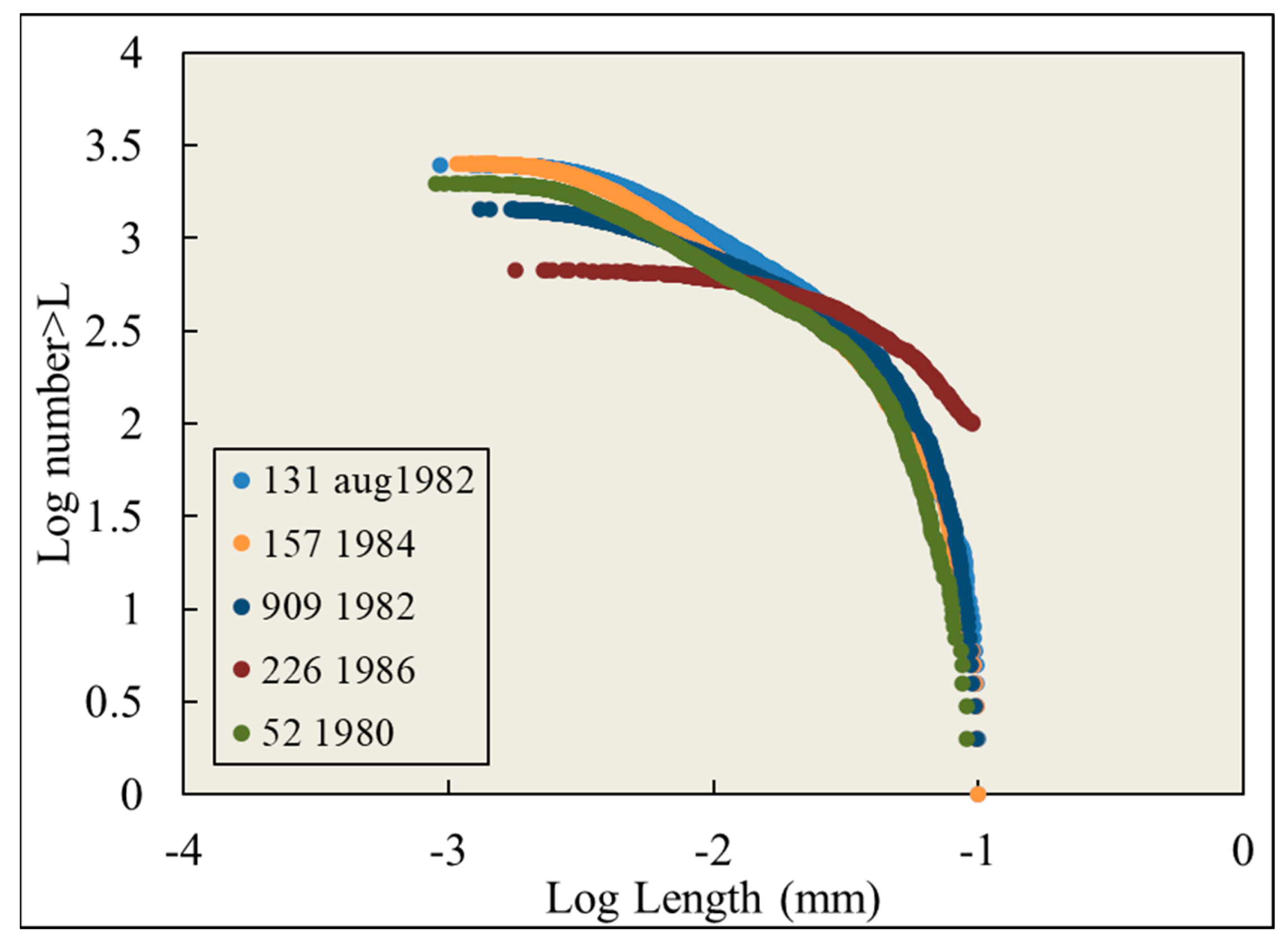
| SH226 | SH157 | ||||
|---|---|---|---|---|---|
| t (mm) | n | p | t (mm) | n | p |
| 0.005 | 7 | 1.0 | 0.001 | 14 | 0.6 |
| 0.013 | 105 | 15.7 | 0.002 | 61 | 2.8 |
| 0.028 | 122 | 18.3 | 0.003 | 306 | 13.9 |
| 0.054 | 196 | 29.4 | 0.010 | 1029 | 46.8 |
| 0.126 | 160 | 24.0 | 0.030 | 511 | 23.2 |
| 0.263 | 58 | 8.7 | 0.071 | 244 | 11.1 |
| 0.577 | 8 | 1.2 | 0.089 | 32 | 1.5 |
| 0.099 | 8 | 0.4 | |||
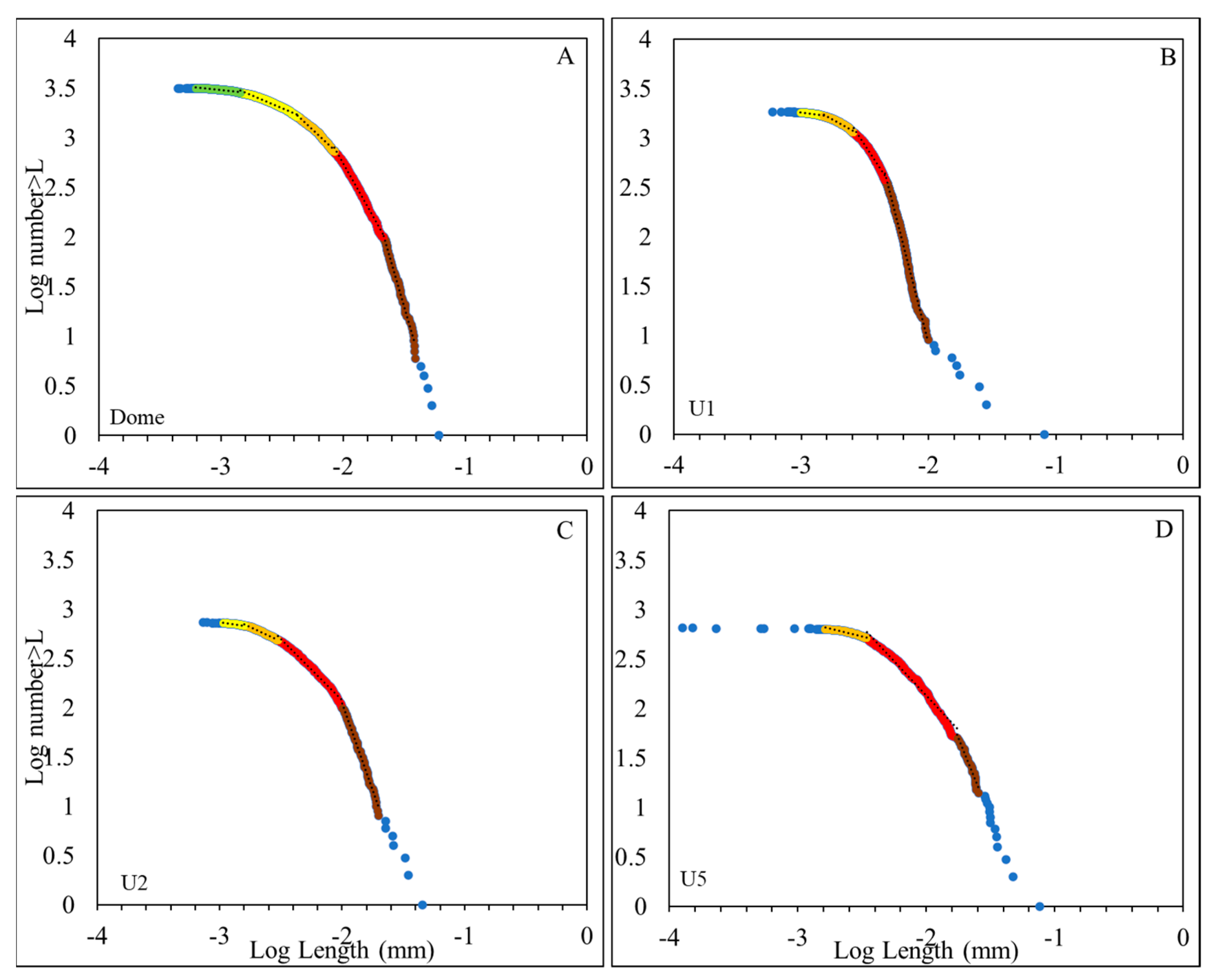
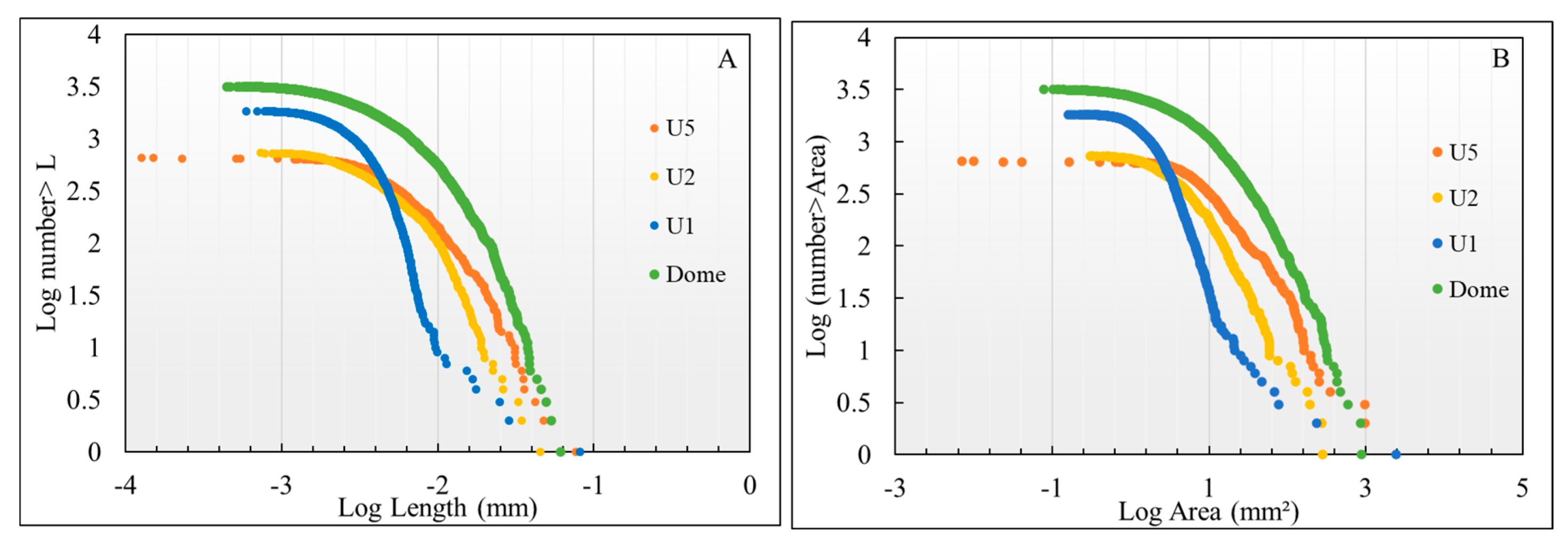
| DOME | U1 | U2 | U5 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| t (mm) | n | p | T (mm) | n | p | t (mm) | n | p | t (mm) | n | p |
| 0.00158 | 16 | 0.58 | 0.00089 | 30 | 1.93 | 0.00100 | 8 | 1.1 | 0.001585 | 16 | 2.6 |
| 0.00398 | 250 | 9.04 | 0.00158 | 121 | 7.80 | 0.00158 | 40 | 5.7 | 0.003981 | 110 | 17.6 |
| 0.00794 | 1000 | 36.15 | 0.00282 | 400 | 25.79 | 0.00282 | 180 | 25.8 | 0.017783 | 450 | 71.9 |
| 0.01995 | 800 | 28.92 | 0.00490 | 650 | 41.91 | 0.01000 | 372 | 53.3 | 0.028184 | 36 | 5.8 |
| 0.03981 | 600 | 21.69 | 0.01000 | 342 | 22.05 | 0.01995 | 90 | 12.9 | 0.079433 | 14 | 2.2 |
| 0.06310 | 94 | 3.40 | 0.07943 | 8 | 0.52 | 0.04467 | 8 | 1.1 | |||
| 0.07943 | 5 | 0.18 | |||||||||
| CSD Analysis | Multifractal Analysis | ||
|---|---|---|---|
| Advantages | Disadvantages | Advantages | Disadvantages |
| Calculation of kinetic parameters | Assuming a constant crystal shape | Independent from crystal shape | Using 2D size and area measurements |
| Obtaining 3D size intervals | Several assumptions | A few assumptions | Requires a large number of crystal measurements (recommended > 500 measurements) |
| Widely used method | Single population for all phenocrysts | Sensitivity to subtle J/G rates | Less efficient for large crystals |
| Overestimation of the number density of small crystals | Fast delineation of crystal populations | ||
| Applicable in the classification of the size, area, and volume of crystals | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eskandari, A.; Sadeghi, B. Deciphering Igneous Rock Crystals: Unveiling Multifractal Patterns in Crystal Size Dynamics. Minerals 2024, 14, 660. https://doi.org/10.3390/min14070660
Eskandari A, Sadeghi B. Deciphering Igneous Rock Crystals: Unveiling Multifractal Patterns in Crystal Size Dynamics. Minerals. 2024; 14(7):660. https://doi.org/10.3390/min14070660
Chicago/Turabian StyleEskandari, Amir, and Behnam Sadeghi. 2024. "Deciphering Igneous Rock Crystals: Unveiling Multifractal Patterns in Crystal Size Dynamics" Minerals 14, no. 7: 660. https://doi.org/10.3390/min14070660
APA StyleEskandari, A., & Sadeghi, B. (2024). Deciphering Igneous Rock Crystals: Unveiling Multifractal Patterns in Crystal Size Dynamics. Minerals, 14(7), 660. https://doi.org/10.3390/min14070660





