Inertial Accelerated Algorithm for Fixed Point of Asymptotically Nonexpansive Mapping in Real Uniformly Convex Banach Spaces

Abstract

In this work, we introduce a new inertial accelerated Mann algorithm for finding a point in the set of fixed points of asymptotically nonexpansive mapping in a real uniformly convex Banach space. We also establish weak and strong convergence theorems of the scheme. Finally, we give a numerical experiment to validate the performance of our algorithm and compare with some existing methods. Our results generalize and improve some recent results in the literature.

1. Introduction

Let X be a real Banach space and C a nonempty closed and convex subset of X. Let $T:C\to C$ be a mapping. A point $x\in C$ is called a fixed point of T if $Tx=x$. We denote by $Fix\left(T\right)$ the set of all fixed points of T, that is, $Fix\left(T\right):=\{x\in C:Tx=x\}$. Then, the mapping $T:C\to C$ is said to be:

(i)

Nonexpansive if $\left|\right|Tx-Ty\left|\right|\le \left|\right|x-y\left|\right|\forall x,y\in C;$

(ii)

Asymptotically nonexpansive (see [1] ) if there exists a sequence $\left\{k_n\right\}\subset [0,\infty )$, with ${\displaystyle \underset{n\to \infty }{lim}}{k}_n=0$ such that

$$\left|\right|T^{n}x-T^{n}y\left|\right|\le (1+k_n)\left|\right|x-y\left|\right|\forall x,y\in Cand\forall n\ge 1;$$

and

(iii)

Uniformly L-Lipschitzian if there exists a constant $L>0$ such that, for all $x,y\in C$, $\left|\right|T^{n}x-T^{n}y\left|\right|\le L\left|\right|x-y\left|\right|\forall n\ge 1.$

The class of asymptotically nonexpansive mappings was first introduced and studied by Goebel and Kirk [1] as a generalization of the class of nonexpansive mappings. They proved that if C is a nonempty closed convex and bounded subset of a real uniformly convex Banach space and T is an asymptotically nonexpansive mapping on C, then T has a fixed point.

Many problems in pure and applied sciences, like those related to the theory of differential equations, optimization, game theory, image recovery, and signal processing (see [2,3,4,5,6] and the references contained therein) can be formulated as fixed-point problems of nonexpansive mappings. Iterative methods for approximating fixed points of nonexpansive and asymptotically nonexpansive mappings using Mann and Ishikawa iterative processes have been studied by many authors. Mann and Ishikawa methods were first studied for nonexpansive mappings and later modified to study the convergence analysis of fixed points of asymptotically nonexpansive mappings; see for example [7,8,9,10,11] and references therein. In 1978, Bose [12] started the study of iterative methods for approximating fixed points of asymptotically nonexpansive mapping in a bounded closed convex nonempty subset C of a uniformly convex Banach space which satisfies Opial’s condition. Bose [12] proved that the sequence $\left\{T^{n}x\right\}$ of asymptotically nonexpansive mapping converges weakly to the fixed point of asymptotically nonexpansive mapping T, provided T is asymptotically regular at $x\in C$; that is, ${\displaystyle \underset{n\to \infty }{lim}}\left|\right|T^{n+1}x-T^{n}x\left|\right|=0$. Later, Schu [13,14] was the first to study the following modified Mann iteration process for approximating the fixed point of an asymptotically nonexpansive mapping T on nonempty closed convex and bounded subsets C of both Hilbert space and (resp.) uniformly convex Banach space with Opial’s condition. The modified Mann sequence $\left\{x_n\right\}$ generated with any arbitrary $x_1\in C$ and for any control sequence $\left\{{\alpha }_n\right\}$ in $[0,1]$ is as follows:

$$x_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_n{T}^n{x}_n,n\ge 1.$$

(1)

In 2000, Osilike and Aniagbosor [15] proved that the theorems of Schu [13,14] remain true without the boundedness condition imposed on C provided that the fixed-points set of asymptotically nonexpansive mapping is nonempty. Later, in 2015, Dong and Yuan [16] studied the accelerated convergence rate of Mann’s iterative method [9] by combining Picard’s method [10] with the conjugate gradient methods [17]. Consequently, they obtained the following fast algorithm for nonexpansive mapping in Hilbert space:

$$\left\{\begin{array}{c}{d}_{n+1}=\frac{1}{\lambda }\left(T\left(x_n\right)-x_n\right) + {\beta }_n{d}_n\hfill \\ y_n=x_n+\lambda d_{n+1}\hfill \\ x_{n+1}=\mu {\gamma }_n{x}_n+(1-\mu {\gamma }_n)y_n,\forall n\ge 0,\hfill \end{array}\right.$$

(2)

where $\mu \in (0,1]$, $\lambda >0$, and $\left\{{\gamma }_n\right\}$ and $\left\{{\beta }_n\right\}$ are real nonnegative sequences. They proved weak convergence of the sequence $\left\{x_n\right\}$ in (2) under the following conditions:

(C1)

${\sum }_{n=0}^{\infty }\mu {\gamma }_n(1-\mu {\gamma }_n)=\infty$.

(C2)

${\sum }_{n=0}^{\infty }{\beta }_n<\infty$.

(C3)

$\left\{T\left(x_n\right)-x_n\right\}$ is bounded.

Finally, they provided some numerical examples to validate that the accelerated Mann algorithm (2) is more efficient than the Mann algorithm.

On the other hand, in the light of inertial-type iterative methods which are based upon a discrete version of a second-order dissipative dynamical system [18,19,20], it has been proved that the procedure improves the performance and increases the rate of convergence of the iterative sequence (see [21,22,23,24,25,26] and the references therein). In [22], Dong et al. proposed the following modified inertial Mann algorithm for nonexpansive mappings for Hilbert space, by combining the accelerated Mann algorithm (2) and an inertial-type extrapolation method. Consequently, they studied the following accelerated Mann algorithm:

$$\left\{\begin{array}{c}{x}_0,x_1\in H,\hfill \\ w_n=x_n+{\alpha }_n(x_n-x_{n-1}),\hfill \\ d_{n+1}=\frac{1}{\lambda }\left(T\left(w_n\right)-w_n\right)+{\beta }_n{d}_n\hfill \\ y_n=w_n+\lambda d_{n+1}\hfill \\ x_{n+1}=\mu {\gamma }_n{w}_n+(1-\mu {\gamma }_n)y_n,\forall n\ge 1,\hfill \end{array}\right.$$

(3)

where ${\alpha }_n\in [0,\alpha ]$ is nonincreasing with ${\alpha }_1=0$ and $0\le \alpha <1$, $\left\{{\gamma }_n\right\}$ satisfies

$$\delta >\frac{{\alpha }^2(1+\alpha )+\alpha \delta }{1-{\alpha }^2}$$

and

$$0<1-\mu \gamma \le 1-\mu {\gamma }_n\le \frac{\delta -\alpha \left[\alpha \right(1+\alpha )+\alpha \delta +\sigma ]}{\delta +\alpha \left[\alpha \right(1+\alpha )+\alpha \delta +\sigma ]}$$

where $\gamma ,\sigma ,\delta >0.$ Under the assumption that the sequence $\left\{w_n\right\}$ satisfies:

• (D1) $\{T{w}_n-w_n\}$ is bounded; and
• (D2) $\{T{w}_n-y\}$ is bounded for any $y\in Fix\left(T\right)$

They proved that $\left\{x_n\right\}$ converges weakly to a point in $Fix\left(T\right)$.

Inspired and motivated by the above results, it is our purpose in this paper to extend and generalize the result of Dong et al. [22] from nonexpansive mapping to asymptotically nonexpansive mapping in the setting of real uniformly convex Banach space, which is more general than Hilbert space. We use an inertial parameter which is different from the one in [22]. Finally, we give some numerical examples to validate the convergence of our algorithm.

2. Preliminaries

We use the following notations:

(i)

$\rightharpoonup$ for weak convergence and → for strong convergence.

(ii)

${\omega }_w\left(x_n\right)=\{x:\exists x_{n_k}\rightharpoonup x\}$ to denote the set of w-weak cluster limits of $\left\{x_n\right\}$.

Definition 1.

A normed linear space X is said to be a uniformly convex Banach space if for any $ϵ\in (0,2]$ there exists a $\delta \left(ϵ\right)>0$ such that for any $x,y\in X$ with $\left|\right|x\left|\right|\le 1$, $\left|\right|y\left|\right|\le 1$ and $\left|\right|x-y\left|\right|\ge ϵ$, then, $\left|\right|\frac{x+y}{2}\left|\right|\le 1-\delta \left(ϵ\right)$.

Remark 1.

We oberve from Definition 1 that every Hilbert space is a uniformly convex Banach space.

Definition 2.

Let X be a Banach space and $X^{\ast }$ be its dual space. A mapping $J_{\phi }:X\to 2^{X^{\ast }}$ associated with a gauge function φ defined by

$$J_{\phi }\left(x\right)=\{x^{\ast }\in X^{\ast }:⟨x,x^{\ast }⟩=\left|\right|x\left|\right|\left|\right|x^{\ast }\left|\right|,\left|\right|x^{\ast }\left|\right|=\phi \left(\right|\left|x\right|\left|\right)\}$$

is called the generalized duality mapping where φ is defined by $\phi \left(t\right)=t^{p-1}$ for all $t\ge 0$ and $1<p<\infty$. In particular, if $p=2$, $J_2$ is known as the normalized duality map written as J, which is defined by

$$J\left(x\right)=\{x^{\ast }\in X^{\ast }:⟨x,x^{\ast }⟩=|\left|x\right|{|}^2,\left|\right|x^{\ast }\left|\right|=\left|\right|x\left|\right|\}.$$

The space X is said to have a weakly sequentially continuous duality map if $J_{\phi }$ is single-valued and sequentially continuous from X with weak topology to $X^{\ast }$ with weak${}^{\ast }$ topology.

Definition 3

(Browder, [27]). The duality mapping J is said to be weakly sequentially continuous if for any sequence $\left\{x_n\right\}$ in E such that $x_n\rightharpoonup x$, implies $J\left(x_n\right)\stackrel{\ast }{\rightharpoonup }J\left(x\right)$, where $\stackrel{\ast }{\rightharpoonup }$ means weak${}^{\ast }$ convergence.

Definition 4.

(1) 

Demiclosed at $y_0\in C$, if for any sequence $\left\{x_n\right\}$ in C which converges weakly to $x_0\in C$ and $T{x}_n\to y_0$, it holds that $T{x}_0=y_0$.

(2) 

Semicompact, if for any bounded sequence $\left\{x_n\right\}$ in C such that ${\displaystyle \underset{n\to \infty }{lim}}\left|\right|x_n-T{x}_n\left|\right|=0$ there exists a subsequence $\left\{x_{n_k}\right\}\subset \left\{x_n\right\}$ such that $x_{n_k}\to x^{\ast }\in C$.

The following lemmas will be needed in the proof of the main results.

Lemma 1

(see [28] Opial’s property). If in a Banach space X having a weakly continuous duality mapping J, the sequence $\left\{x_n\right\}$ is weakly convergent to $x_0$, then for any $x\in X$:

$$\underset{n\to \infty }{lim\; inf}\left|\right|x_n-x\left|\right|\ge \underset{n\to \infty }{lim\; inf}\left|\right|x_n-x_0\left|\right|.$$

(4)

In particular, if the space X is uniformly convex, then equality holds if and only if $x=x_0$.

It is known that in every Hilbert space and ${\ell }_p$ space, $1\le p<\infty$ satisfies!Opial’s condition. However $L_p$ with $p\ne 2$ does not satisfy this condition; (see [29] for more details). Additionally, it is clear in [30] that every Banach space with weakly sequentially continuous duality mapping satisfies Opial’s condition. An example of a space with a weakly sequentially continuous duality map is ${\ell }_p(1<p<\infty )$ space.

Lemma 2

(see [11]). Let X be a real uniformly convex Banach space, let C be a nonempty closed convex subset of X, and $T:C\to C$ an asymptotically nonexpansive mapping with a sequence $\left\{k_n\right\}\subset [0,\infty )$ and ${\displaystyle \underset{n\to \infty }{lim}}{k}_n=0$. Then, the mapping $(I-T)$ is demiclosed at zero.

Lemma 3

(see [15] Lemma 1). Let $\left\{a_n\right\}$, $\left\{b_n\right\}$, and $\left\{c_n\right\}$ be nonnegative sequences such that

$$a_{n+1}\le (1+c_n)a_n+b_n$$

with ${\sum }_{n=0}^{\infty }{b}_n<+\infty$ and ${\sum }_{n=0}^{\infty }{c}_n<+\infty$ $\forall n\ge 0$. Then

(i) 

The sequence $\left\{a_n\right\}$ converges.

(ii) 

In particular, if ${\displaystyle \underset{n\to \infty }{lim\; inf}}{a}_n=0$, then ${\displaystyle \underset{n\to \infty }{lim}}{a}_n=0$.

Lemma 4

(see [31]). Let $r>0$ be a fixed number. Then, a real Banach space X is uniformly convex if and only if there exists a continuous and strictly increasing function $g:[0,\infty )\to [0,\infty )$ with $g\left(0\right)=0$, such that;

$$\left|\right|\lambda x+{(1-\lambda )y\left|\right|}^2\le {\lambda \left|\right|x\left|\right|}^2+{(1-\lambda )\left|\right|y\left|\right|}^p-\lambda (1-\lambda )g\left(\right||x-y\left|\right|)$$

for all $x,y$ in $B_r=\{x\in X:|\left|x\right||\le r\}$ and $\lambda \in [0,1]$.

3. Main Results

In this section, we prove weak and strong convergence theorems for asymptotically nonexpansive mapping in real uniformly convex Banach space.

Weak Convergence Theorem

Assumption 1.

Let X be a real uniformly convex Banach space.

(i) 

Choose sequences $\left\{{\alpha }_n\right\}\subset (0,1)$, $\left\{{\beta }_n\right\},\left\{{\delta }_n\right\}\subset [0,\infty )$ and ${\sum }_{n=1}^{\infty }{\delta }_n<\infty$ with ${\delta }_n=\circ \left({\beta }_n\right)$ which means ${\displaystyle \underset{n\to \infty }{lim}}\frac{{\delta }_n}{{\beta }_n}=0$.

(ii) 

Let $x_0,x_1\in X$ be arbitrary points, for the iterates $x_{n-1}$ and $x_n$ for each $n\ge 1$, choose ${\theta }_n$ such that $0\le {\theta }_n\le {\overline{\theta }}_n$ where, for any $\eta \ge 3$

$$\begin{array}{c}\hfill {\overline{\theta }}_n:=\left\{\begin{array}{c}min\left\{\frac{n-1}{n+\eta -1},\frac{{\delta }_n}{\left|\right|x_n-x_{n-1}\left|\right|}\right\}, if x_n\ne x_{n-1};\hfill \\ \\ \frac{n-1}{n+\eta -1},Otherwise.\hfill \end{array}\right.\end{array}$$

This idea was obtained from the recent inertial extrapolation step introduced in [32].

Remark 2.

It is easy to see from Assumption 1 that for each $n\ge 1$, we have

$${\theta }_n\left|\right|x_n-x_{n-1}\left|\right|\le {\delta }_n,$$

which together with ${\sum }_{n=1}^{\infty }{\delta }_n<\infty$ and ${\displaystyle \underset{n\to \infty }{lim}}\frac{{\delta }_n}{{\beta }_n}=0$, we respectively obtain

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|<\infty \end{array}$$

(5)

and

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\frac{{\theta }_n}{{\beta }_n}\left|\right|x_n-x_{n-1}\left|\right|\le {\displaystyle \underset{n\to \infty }{lim}}\frac{{\delta }_n}{{\beta }_n}=0.\end{array}$$

(6)

Theorem 1.

Let X be a real uniformly convex Banach space with Opial’s property. Let $T:X\to X$ be an asymptotically nonexpansive mapping with sequence $\left\{k_n\right\}\subset [0,\infty )$ such that ${\sum }_{n=0}^{\infty }{k}_n<\infty$ and $Fix\left(T\right)\ne \varnothing$. Let $\left\{x_n\right\}$ be the sequence generated as follows:

$$\left\{\begin{array}{c}{x}_0,x_1\in X,\hfill \\ w_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ d_{n+1}=\frac{1}{\lambda }\left(T^n\left(w_n\right)-w_n\right)+{\beta }_n{d}_n\hfill \\ y_n=w_n+\lambda d_{n+1}\hfill \\ x_{n+1}=\mu {\alpha }_n{w}_n+(1-\mu {\alpha }_n)y_n,n\ge 1,\hfill \end{array}\right.$$

(7)

where $\mu \in (0,1]$, $\lambda >0$, assuming that Assumption 1 holds and set $d_1=\frac{1}{\lambda }(T^1{w}_0-w_0)$. Then, the sequence $\left\{x_n\right\}$ converges weakly to a point $x\in Fix\left(T\right)$, provided that the following conditions hold:

(C1) ${\sum }_{n=0}^{\infty }{\beta }_n<\infty$.

(C2) ${\displaystyle \underset{n\to \infty }{lim\; inf}}\mu {\alpha }_n(1-\mu {\alpha }_n)>0$.

Moreover, $\left\{w_n\right\}$ satisfies

(C3) $\{T^n{w}_n-w_n\}$is bounded.

Proof. 

We divide the proof into the following steps:

Step (i): We show that $\left\{d_n\right\}$ is bounded.

We have from (C1) that ${\displaystyle \underset{n\to \infty }{lim}}{\beta }_n=0$; thus, there exists $n_0\in \mathbb{N}$ such that ${\beta }_n\le \frac{1}{2}$ for all $n\ge n_0$. Let $M_1$ be defined as follows:

$$M_1:=max\left\{\underset{1\le k\le n_0}{max}\left|\right|d_k\left|\right|,\left(\frac{2}{\lambda }\right)\underset{n\in \mathbb{N}}{sup}\left|\right|T^n{w}_n-w_n\left|\right|\right\}.$$

Then, by (C3), we have $M_1<\infty$. Assume that $\left|\right|d_n\left|\right|\le M_1$ for some $n\ge n_0$, then

$$\begin{array}{ccc}\hfill \left|\right|d_{n+1}\left|\right|& =& \left|\right|\frac{1}{\lambda }(T^n{w}_n-w_n)+{\beta }_n{d}_n\left|\right|\hfill \\ & \le & \frac{1}{\lambda }\left|\right|T^n{w}_n-w_n\left|\right|+{\beta }_n\left|\right|d_n\left|\right|\hfill \\ & \le & M_1.\hfill \end{array}$$

This implies that

$$\left|\right|d_n\left|\right|\le M_{1}foralln\ge 0,$$

(8)

and consequently $\left\{d_n\right\}$ is bounded.

Step (ii): We show that ${\displaystyle \underset{n\to \infty }{lim}}\left|\right|x_n-p\left|\right|$ exists for any $p\in Fix\left(T\right)$.

From the scheme (7), we have

$$\begin{array}{ccc}\hfill y_n& =& w_n+\lambda d_{n+1}\hfill \\ & =& w_n+\lambda \left(\frac{1}{\lambda }(T^n{w}_n-w_n)+{\beta }_n{d}_n\right)\hfill \\ & =& T^n{w}_n+\lambda {\beta }_n{d}_n.\hfill \end{array}$$

(9)

By (8), (9), and for any $p\in Fix\left(T\right)$, we have

$$\begin{array}{ccc}\hfill \left|\right|y_n-p\left|\right|& =& \left|\right|T^n{w}_n+\lambda {\beta }_n{d}_n-p\left|\right|\hfill \\ & \le & \left|\right|T^n{w}_n-p\left|\right|+\lambda {\beta }_n\left|\right|d_n\left|\right|\hfill \\ & \le & (1+k_n)\left|\right|w_n-p\left|\right|+\lambda M_1{\beta }_n.\hfill \end{array}$$

(10)

Additionally,

$$\begin{array}{ccc}\hfill \left|\right|w_n-p\left|\right|& =& \left|\right|x_n-p+{\theta }_n(x_n-x_{n-1})\left|\right|\hfill \\ & \le & \left|\right|x_n-p\left|\right|+{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|.\hfill \end{array}$$

(11)

Combining (10) and (11), we obtain

$$\begin{array}{ccc}\hfill \left|\right|y_n-p\left|\right|& \le & (1+k_n)\left|\right|x_n-p\left|\right|+{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|+\lambda M_1{\beta }_n\hfill \\ & =& (1+k_n)\left|\right|x_n-p\left|\right|+{\beta }_n\left[(1+k_n)\frac{{\theta }_n}{{\beta }_n}\left|\right|x_n-x_{n-1}\left|\right|+\lambda M_1\right].\hfill \end{array}$$

By (6) in Remark 2, we know that the sequence $\left\{\frac{{\delta }_n}{{\beta }_n}\left|\right|x_n-x_{n-1}\left|\right|\right\}$ converges, and since ${\sum }_{n=1}^{\infty }{k}_n<\infty$, then it converges, so there exists some constant say $M_2>0$ such that for all $n\ge 1$

$$(1+k_n)\frac{{\theta }_n}{{\beta }_n}\left|\right|x_n-x_{n-1}\left|\right|+\lambda M_1\le M_2$$

thus

$$\begin{array}{c}\hfill \left|\right|y_n-p\left|\right|\le (1+k_n)\left|\right|x_n-p\left|\right|+{\beta }_n{M}_2.\end{array}$$

(12)

Now, using (10), (12), and for some $M_3>0$, any $p\in Fix\left(T\right)$, we have

$$\begin{array}{ccc}\hfill \left|\right|x_{n+1}-p\left|\right|& =& \left|\right|\mu {\alpha }_n{w}_n+(1-\mu {\alpha }_n)y_n-p\left|\right|\hfill \\ & \le & \mu {\alpha }_n\left|\right|w_n-p\left|\right|+(1-\mu {\alpha }_n)\left|\right|y_n-p\left|\right|\hfill \\ & \le & \mu {\alpha }_n\left|\right|w_n-p\left|\right|+\mu {\alpha }_n{\theta }_n\left|\right|y_n-p\left|\right|\hfill \\ & & +(1-\mu {\alpha }_n)[(1+k_n)\left|\right|x_n-p\left|\right|+{\beta }_n{M}_2]\hfill \\ & \le & [1+(1-\mu {\alpha }_n)k_n]\left|\right|x_n-p\left|\right|+{\beta }_n{M}_3.\hfill \end{array}$$

Therefore,

$$\left|\right|x_{n+1}-p\left|\right|\le (1+k_n)\left|\right|x_n-p\left|\right|+{\beta }_n{M}_3.$$

(13)

Hence, using the fact that ${\sum }_{n=1}^{\infty }{k}_n<\infty$, together with condition (C1) and Lemma 3 in (13), we get that ${\displaystyle \underset{n\to \infty }{lim}}\left|\right|x_n-p\left|\right|$ exists. Consequently, the sequence $\left\{x_n\right\}$ is bounded.

Step (iii): Next we show that ${\displaystyle \underset{n\to \infty }{lim}}\left|\right|x_n-T{x}_n\left|\right|=0.$

Since the sequence $\left\{x_n\right\}$ is bounded, it follows that $\left\{w_n\right\}$ is bounded and consequently $\left\{T^n{w}_n\right\}$ is bounded. Let $r={\displaystyle \underset{n\ge 1}{sup}}\left\{\right||w_n\left|\right|,\left|\right|T^n{w}_n\left|\right|\}$. Then, for any $p\in Fix\left(T\right)$ and since X is a uniformly convex Banach space, by Lemma 4, there exists a continuous and strictly increasing function $g:[0,\infty )\to [0,\infty )$ with $g\left(0\right)=0$ such that

$$\left|\right|\lambda x+{(1-\lambda )y\left|\right|}^2\le {\lambda \left|\right|x\left|\right|}^2+{(1-\lambda )\left|\right|y\left|\right|}^p-\lambda (1-\lambda )g\left(\right||x-y\left|\right|)$$

for all $x,y$ in $B_r=\{x\in X:|\left|x\right||\le r\}$ and $\lambda \in [0,1]$.

Therefore,

$$\begin{array}{ccc}\hfill \left|\right|x& {}_{n+1}\hfill & -{p\left|\right|}^2=\left|\right|\mu {\alpha }_n{w}_n+(1-\mu {\alpha }_n)y_n-p{\left|\right|}^2\hfill \\ & =& \left|\right|\mu {\alpha }_n{w}_n+(1-\mu {\alpha }_n)(T^n{w}_n+\lambda {\beta }_n{d}_n)-p{\left|\right|}^2\hfill \\ & =& \left|\right|\mu {\alpha }_n(w_n-p)+(1-\mu {\alpha }_n)(T^n{w}_n-p)+(1-\mu {\alpha }_n)\lambda {\beta }_n{d}_n{\left|\right|}^2\hfill \\ & \le & {\left(\left|\right|\mu {\alpha }_n(w_n-p)+(1-\mu {\alpha }_n)(T^n{w}_n-p)\left|\right|+(1-\mu {\alpha }_n)\lambda {\beta }_n\left|\right|d_n\left|\right|\right)}^2\hfill \\ & =& \left|\right|\mu {\alpha }_n(w_n-p)+(1-\mu {\alpha }_n)(T^n{w}_n-p){\left|\right|}^2+{(1-\mu {\alpha }_n)}^2{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \\ & & +2(1-\mu {\alpha }_n)\lambda {\beta }_n\left|\right|d_n\left|\right|\left|\right|\mu {\alpha }_n(w_n-p)+(1-\mu {\alpha }_n)(T^n{w}_n-p)\left|\right|\hfill \\ & \le & \mu {\alpha }_n\left|\right|w_n-{p\left|\right|}^2+(1-\mu {\alpha }_n)\left|\right|T^n{w}_n-{p\left|\right|}^2-\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2(1-\mu {\alpha }_n)\lambda {\beta }_n\left|\right|d_n\left|\right|\left|\right|\mu {\alpha }_n(w_n-p)+(1-\mu {\alpha }_n)(T^n{w}_n-p)\left|\right|\hfill \\ & & +{(1-\mu {\alpha }_n)}^2{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \end{array}$$

$$\begin{array}{ccc}& \le \mu {\alpha }_n& \left|\right|w_n-{p\left|\right|}^2+(1-\mu {\alpha }_n){(1+k_n)}^2\left|\right|w_n-p{\left|\right|}^2\hfill \\ & & -\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2(1-\mu {\alpha }_n)\lambda {\beta }_n\left|\right|d_n\left|\right|\left(\mu {\alpha }_n\left|\right|w_n-p\left|\right|+(1-\mu {\alpha }_n)\left|\right|T^n{w}_n-p\left|\right|\right)\hfill \\ & & +(1-2\mu {\alpha }_n+{\mu }^2{\alpha }_n^2){\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \\ & \le & \mu {\alpha }_n\left|\right|w_n-{p\left|\right|}^2+(1-\mu {\alpha }_n)(1+2k_n+k_n^2)\left|\right|w_n-p{\left|\right|}^2\hfill \\ & & -\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)+{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \\ & & +2(1-\mu {\alpha }_n)\lambda {\beta }_n\left|\right|d_n\left|\right|\left(\mu {\alpha }_n\left|\right|w_n-p\left|\right|+(1-\mu {\alpha }_n)(1+k_n)\left|\right|w_n-p\left|\right|\right)\hfill \\ & & -2\mu {\alpha }_n{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2+{\mu }^2{\alpha }_n^2{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \\ & \le & \left|\right|w_n-{p\left|\right|}^2+2k_n\left|\right|w_n-{p\left|\right|}^2+k_n^2\left|\right|w_n-{p\left|\right|}^2-\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2(1-\mu {\alpha }_n)\lambda {\beta }_n\left|\right|d_n\left|\right|\left(\left|\right|w_n-p\left|\right|+k_n\left|\right|w_n-p\left|\right|-\mu {\alpha }_n{k}_n\left|\right|w_n-p\left|\right|\right)\hfill \\ & & +{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2+{\mu }^2{\lambda }^2{\alpha }_n^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \end{array}$$

$$\begin{array}{ccc}& =& \left|\right|w_n-{p\left|\right|}^2+2k_n\left|\right|w_n-{p\left|\right|}^2+k_n^2\left|\right|w_n-{p\left|\right|}^2-\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2\lambda {\beta }_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|+2\lambda {\beta }_n{k}_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|-2\lambda {\beta }_n\mu {\alpha }_n{k}_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|\hfill \\ & & -2\mu {\alpha }_n\lambda {\beta }_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|-2\mu {\alpha }_n\lambda {\beta }_n{k}_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|+{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \\ & & +2{\mu }^2{\alpha }_n^2\lambda {\beta }_n{k}_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|+{\mu }^2{\alpha }_n^2{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \\ & \le & \left|\right|w_n-{p\left|\right|}^2+2k_n\left|\right|w_n-{p\left|\right|}^2+k_n^2\left|\right|w_n-{p\left|\right|}^2-\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2\lambda {\beta }_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|+2\lambda {\beta }_n{k}_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|+{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2+{\mu }^2{\alpha }_n^2{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2\hfill \\ & \le & \left|\right|w_n-{p\left|\right|}^2+2k_n\left|\right|w_n-{p\left|\right|}^2+k_n^2\left|\right|w_n-{p\left|\right|}^2-\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2\lambda {\beta }_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|+2\lambda {\beta }_n{k}_n\left|\right|d_n\left|\right|\left|\right|w_n-p\left|\right|+2{\lambda }^2{\beta }_n^2\left|\right|d_n{\left|\right|}^2.\hfill \end{array}$$

Since ${\displaystyle \underset{n\to \infty }{lim}}\left|\right|x_n-p\left|\right|$ exists for any $p\in Fix\left(T\right)$, then using (5) it follows from (11) that there exists $L>0$ such that $\left|\right|w_n-p\left|\right|\le L$ for any $p\in Fix\left(T\right)$, and using (8), we have

$$\begin{array}{ccc}& & \hfill {\displaystyle \left|\right|x_{n+1}-{p\left|\right|}^2\le \left|\right|w_n-p{\left|\right|}^2+2L^2{k}_n+L^2{k}_n^2}\\ & & -\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2\lambda M_{1}L{\beta }_n+2\lambda M_{1}L{k}_n{\beta }_n+2{\lambda }^2{M_1}^2{\beta }_n^2\hfill \\ & \le & \left(\right||x_n-p\left|\right|+{\theta }_n\left|\right|x_n-x_{n-1}{\left|\right|)}^2+2L^2{k}_n\hfill \\ & & +L^2{k}_n^2-\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2\lambda M_{1}L{\beta }_n+2\lambda M_{1}L{k}_n{\beta }_n+2{\lambda }^2{M_1}^2{\beta }_n^2\hfill \\ & =& \left|\right|x_n-{p\left|\right|}^2+2{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|x_n-p\left|\right|\hfill \\ & & +({\theta }_n\left|\right|x_n-x_{n-1}{\left|\right|)}^2+2L^2{k}_n\hfill \\ & & +L^2{k}_n^2-\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2\lambda M_{1}L{\beta }_n+2\lambda M_{1}L{k}_n{\beta }_n+2{\lambda }^2{M_1}^2{\beta }_n^2.\hfill \end{array}$$

Since ${\displaystyle \underset{n\to \infty }{lim}}\left|\right|x_n-p\left|\right|$ exists for any $p\in Fix\left(T\right)$, then $\left\{\left|\right|x_n-p\left|\right|\right\}$ is bounded; therefore, there exists $H>0$ such that $\left|\right|x_n-p\left|\right|\le H$ for all $n\ge 1$. Hence,

$$\begin{array}{ccc}\hfill \left|\right|x_{n+1}-p{\left|\right|}^2& \le & \left|\right|x_n-{p\left|\right|}^2+2{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|H+({\theta }_n\left|\right|x_n-x_{n-1}{\left|\right|)}^2+2L^2{k}_n\hfill \\ & & +L^2{k}_n^2-\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\hfill \\ & & +2\lambda M_{1}L{\beta }_n+2\lambda M_{1}L{k}_n{\beta }_n+2{\lambda }^2{M_1}^2{\beta }_n^2.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill \mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)& \le & \left|\right|x_n-{p\left|\right|}^2-\left|\right|x_{n+1}-{p\left|\right|}^2+2H{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|\hfill \\ & & +({\theta }_n\left|\right|x_n-x_{n-1}{\left|\right|)}^2+2L^2{k}_n+L^2{k}_n^2\hfill \\ & & +2\lambda M_{1}L{\beta }_n+2\lambda M_{1}L{k}_n{\beta }_n+2{\lambda }^2{M_1}^2{\beta }_n^2.\hfill \end{array}$$

Hence,

$$\begin{array}{ccc}& \sum _{n=0}^{\infty }\hfill & {\displaystyle \mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)\le \sum _{n=0}^{\infty }\left(\right||x_n-{p\left|\right|}^2-\left|\right|x_{n+1}-{p\left|\right|}^2)}\hfill \\ & & +2H\sum _{n=0}^{\infty }{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|+\sum _{n=0}^{\infty }({\theta }_n\left|\right|x_n-x_{n-1}{\left|\right|)}^2+2L^2\sum _{n=0}^{\infty }{k}_n\hfill \\ & & +L^2\sum _{n=0}^{\infty }{k}_n^2+2\lambda M_{1}L\sum _{n=0}^{\infty }{\beta }_n+2\lambda M_{1}L\sum _{n=0}^{\infty }{k}_n{\beta }_n+2{\lambda }^2{M_1}^2\sum _{n=0}^{\infty }{\beta }_n^2\hfill \\ & \le & \left|\right|x_0-{p\left|\right|}^2+2H\sum _{n=0}^{\infty }{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|+\sum _{n=0}^{\infty }({\theta }_n\left|\right|x_n-x_{n-1}{\left|\right|)}^2+2L^2\sum _{n=0}^{\infty }{k}_n\hfill \\ & & +L^2\sum _{n=0}^{\infty }{k}_n^2+2\lambda M_{1}L\sum _{n=0}^{\infty }{\beta }_n+2\lambda M_{1}L\sum _{n=0}^{\infty }{k}_n{\beta }_n+2{\lambda }^2{M_1}^2\sum _{n=0}^{\infty }{\beta }_n^2.\hfill \end{array}$$

Using (C1), (5), and ${\sum }_{n=0}^{\infty }{k}_n<\infty$, we obtain

$$\sum _{n=0}^{\infty }\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)<\infty ,$$

which implies that

$$\underset{n\to \infty }{lim}\mu {\alpha }_n(1-\mu {\alpha }_n)g\left(\right||w_n-T^n{w}_n\left|\right|)=0.$$

By (C2), we have

$$\underset{n\to \infty }{lim}g\left(\right||w_n-T^n{w}_n\left|\right|)=0.$$

Using the property of g, we have

$${\displaystyle \underset{n\to \infty }{lim}}\left|\right|w_n-T^n{w}_n\left|\right|=0.$$

(14)

Now,

$$\begin{array}{ccc}\hfill \left|\right|w_n-x_n\left|\right|& =& \left|\right|x_n+{\theta }_n(x_n-x_{n-1})-x_n\left|\right|\hfill \\ & =& {\theta }_n\left|\right|x_n-x_{n-1}\left|\right|.\hfill \end{array}$$

Taking the sum over n of both sides and considering (5), we have

$$\sum _{n=0}^{\infty }\left|\right|w_n-x_n\left|\right|=\sum _{n=0}^{\infty }{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|<\infty ,$$

which implies that

$$\underset{n\to \infty }{lim}\left|\right|w_n-x_n\left|\right|=0.$$

(15)

Since T is asymptotically nonexpansive, we obtain

$$\begin{array}{c}\hfill {\displaystyle \left|\right|x_n-T^n{x}_n\left|\right|=\left|\right|x_n-w_n+w_n-T^n{w}_n+T^n{w}_n-T^n{x}_n\left|\right|}\\ \le \left|\right|x_n-w_n\left|\right|+\left|\right|w_n-T^n{w}_n\left|\right|+\left|\right|T^n{w}_n-T^n{x}_n\left|\right|\hfill \\ \le \left|\right|x_n-w_n\left|\right|+\left|\right|w_n-T^n{w}_n\left|\right|+(1+k_n)\left|\right|w_n-x_n\left|\right|\hfill \\ =(2+k_n)\left|\right|w_n-x_n\left|\right|+\left|\right|w_n-T^n{w}_n\left|\right|.\hfill \end{array}$$

(16)

Using (14) and (15) in (16), we have

$$\underset{n\to \infty }{lim}\left|\right|x_n-T^n{x}_n\left|\right|=0.$$

(17)

On the other hand,

$$\begin{array}{ccc}\hfill \left|\right|w_n-y_n\left|\right|& =& \left|\right|w_n-(w_n+\lambda d_{n+1})\left|\right|\hfill \\ & =& \left|\right|\lambda d_{n+1}\left|\right|\hfill \\ & =& \lambda \left|\right|d_{n+1}\left|\right|\hfill \\ & \le & \lambda \left(\frac{1}{\lambda }\left|\right|w_n-T^n{w}_n\left|\right|+{\beta }_n\left|\right|d_n\left|\right|\right)\hfill \\ & =& \left|\right|w_n-T^n{w}_n\left|\right|+\lambda {\beta }_n\left|\right|d_n\left|\right|\hfill \\ & \le & \left|\right|w_n-T^n{w}_n\left|\right|+\lambda M_1{\beta }_n.\hfill \end{array}$$

Using (14) and (C1), we have

$$\underset{n\to \infty }{lim}\left|\right|w_n-y_n\left|\right|=0.$$

(18)

Similarly, using (8), we have

$$\begin{array}{c}{\displaystyle \left|\right|x_{n+1}-T^n{x}_{n+1}\left|\right|=\left|\right|\mu {\alpha }_n{w}_n+(1-\mu {\alpha }_n)y_n-T^n{x}_{n+1}\left|\right|}\hfill \\ =\left|\right|\mu {\alpha }_n(w_n-T^n{w}_n)+(1-\mu {\alpha }_n)\lambda {\beta }_n{d}_n+(T^n{w}_n-T^n{x}_{n+1})\left|\right|\hfill \\ \le \mu {\alpha }_n\left|\right|w_n-T^n{w}_n\left|\right|+(1-\mu {\alpha }_n)\lambda {\beta }_n\left|\right|d_n\left|\right|+\left|\right|T^n{w}_n-T^n{x}_{n+1}\left|\right|\hfill \\ \le \mu {\alpha }_n\left|\right|w_n-T^n{w}_n\left|\right|+\lambda {\beta }_n\left|\right|d_n\left|\right|+(1+k_n)\left|\right|w_n-x_{n+1}\left|\right|\hfill \\ =\mu {\alpha }_n\left|\right|w_n-T^n{w}_n\left|\right|+\lambda {\beta }_n\left|\right|d_n\left|\right|+(1+k_n)(1-\mu {\alpha }_n)\left|\right|w_n-y_n\left|\right|\hfill \\ \le \mu {\alpha }_n\left|\right|w_n-T^n{w}_n\left|\right|+\lambda M_1{\beta }_n+(1+k_n)\left|\right|w_n-y_n\left|\right|.\hfill \end{array}$$

(19)

It follows from (14), (18), and (C1) that

$$\underset{n\to \infty }{lim}\left|\right|x_{n+1}-T^n{x}_{n+1}\left|\right|=0.$$

(20)

Thus,

$$\begin{array}{ccc}\hfill \left|\right|x_{n+1}-T{x}_{n+1}\left|\right|& =& \left|\right|x_{n+1}+T^{n+1}{x}_{n+1}-T^{n+1}{x}_{n+1}-T{x}_{n+1}\left|\right|\hfill \\ & \le & \left|\right|x_{n+1}-T^{n+1}{x}_{n+1}\left|\right|+\left|\right|T{x}_{n+1}-T^{n+1}{x}_{n+1}\left|\right|\hfill \\ & =& \left|\right|x_{n+1}-T^{n+1}{x}_{n+1}\left|\right|+\left|\right|T{x}_{n+1}-T\left(T^n{x}_{n+1}\right)\left|\right|\hfill \\ & \le & \left|\right|x_{n+1}-T^{n+1}{x}_{n+1}\left|\right|+k_1\left|\right|x_{n+1}-T^n{x}_{n+1}\left|\right|.\hfill \end{array}$$

From (17) and (20), we have

$$\underset{n\to \infty }{lim}\left|\right|x_n-T{x}_n\left|\right|=0.$$

(21)

This completes the proof of (iii).

Since $\left\{x_n\right\}$ is bounded and X is a reflexive Banach space, there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ which converges weakly to a point where $p\in X$. Therefore, from (21), it follows that ${\displaystyle \underset{k\to \infty }{lim}}\left|\right|x_{n_k}-T{x}_{n_k}\left|\right|=0$ and consequently by Lemma 2 we have $Tp=p$. Therefore, we obtain that ${\omega }_w\left(x_n\right)\subset Fix\left(T\right)$.

Now, to prove that the sequence $\left\{x_n\right\}$ converges weakly to a fixed point of T, it suffices to show that ${\omega }_w\left(x_n\right)$ is a singleton. To do that, we proceed as follows.

By our assumption that X satisfies Opial’s property, using Lemma 1, taking $p_1,p_2\in {\omega }_w\left(x_n\right)$ and let $\left\{x_{n_i}\right\}$ and $\left\{x_{n_j}\right\}$ be subsequences of $\left\{x_n\right\}$ such that $x_{n_i}\rightharpoonup p_1$ and $x_{n_j}\rightharpoonup p_2$. Then for $p_1\ne p_2$, we have

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}\left|\right|x_n-p_1\left|\right|& =& \underset{i\to \infty }{lim}\left|\right|x_{n_i}-p_1\left|\right|\hfill \\ & <& \underset{i\to \infty }{lim\; inf}\left|\right|x_{n_i}-p_2\left|\right|\hfill \\ & =& \underset{n\to \infty }{lim}\left|\right|x_n-p_2\left|\right|\hfill \\ & =& \underset{j\to \infty }{lim\; inf}\left|\right|x_{n_j}-p_2\left|\right|\hfill \\ & <& \underset{j\to \infty }{lim\; inf}\left|\right|x_{n_j}-p_1\left|\right|\hfill \\ & =& \underset{n\to \infty }{lim}\left|\right|x_n-p_1\left|\right|.\hfill \end{array}$$

This is a contradiction, showing that ${\omega }_w\left(x_n\right)$ is a singleton. This completes the proof. □

Now we prove strong convergence theorem.

Theorem 2.

If in addition to all the hypotheses of Theorem 1, the map T is semicompact, then the iterative sequence $\left\{x_n\right\}$ generated by (7) converges strongly to a fixed point of T.

Proof. 

Assume that T is semicompact. Since from step (ii) and step (iii) in the proof of Theorem 1, we know that the sequence $\left\{x_n\right\}$ is bounded and ${\displaystyle \underset{k\to \infty }{lim}}\left|\right|x_n-T{x}_n\left|\right|=0$, then there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $x_{n_k}\to x^{\ast }$ as $k\to \infty$. Therefore $x_{n_k}\rightharpoonup x^{\ast }$ and so $x^{\ast }\in {\omega }_w\left(x_n\right)\subseteq Fix\left(T\right)$. From step (ii) in the proof of Theorem 1, ${\displaystyle \underset{n\to \infty }{lim}}\left|\right|x_n-x^{\ast }\left|\right|$ exists, then

$$\underset{n\to \infty }{lim}\left|\right|x_n-x^{\ast }\left|\right|=\underset{k\to \infty }{lim}\left|\right|x_{n_k}-x^{\ast }\left|\right|=0,$$

which means that $x_n\to x^{\ast }\in Fix\left(T\right)$. This completes the proof. □

If in Theorem 1 we assume that T is nonexpansive, we obtain the following corollary.

Corollary 1.

Let X be a real uniformly convex Banach space with Opial’s property and $T:X\to X$ be nonexpansive mapping with $Fix\left(T\right)\ne Ø$. Let $\left\{x_n\right\}$ be the sequence generated as follows:

$$\left\{\begin{array}{c}{x}_0,x_1\in X,\hfill \\ w_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ d_{n+1}=\frac{1}{\lambda }\left(T\left(w_n\right)-w_n\right)+{\beta }_n{d}_n\hfill \\ y_n=w_n+\lambda d_{n+1}\hfill \\ x_{n+1}=\mu {\alpha }_n{w}_n+(1-\mu {\alpha }_n)y_n,n\ge 1,\hfill \end{array}\right.$$

(22)

where $\mu \in (0,1]$, $\lambda >0$, assuming that Assumption 1 holds, and set $d_0:=\frac{1}{\lambda }(T{w}_0-w_0)$. Then, the sequence $\left\{x_n\right\}$ converges weakly to a point $x\in Fix\left(T\right)$, provided that the following conditions hold:

(C1) ${\sum }_{n=0}^{\infty }{\beta }_n<\infty$.

(C2) ${\displaystyle \underset{n\to \infty }{lim\; inf}}\mu {\alpha }_n(1-\mu {\alpha }_n)>0$.

Moreover, $\left\{w_n\right\}$ satisfies

(C3) $\{T{w}_n-w_n\}$ is bounded.

If in Theorem 1 we assume that X is a real Hilbert space, we get the following corollary.

Corollary 2.

Let H be a real Hilbert space. Let $T:H\to H$ be an asymptotically nonexpansive mapping with sequence $\left\{k_n\right\}\subset [0,\infty )$ such that ${\sum }_{n=0}^{\infty }{k}_n<\infty$ and $Fix\left(T\right)\ne \varnothing$. Let $\left\{x_n\right\}$ be the sequence generated as follows:

$$\left\{\begin{array}{c}{x}_0,x_1\in H,\hfill \\ w_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ d_{n+1}=\frac{1}{\lambda }\left(T^n\left(w_n\right)-w_n\right)+{\beta }_n{d}_n\hfill \\ y_n=w_n+\lambda d_{n+1}\hfill \\ x_{n+1}=\mu {\alpha }_n{w}_n+(1-\mu {\alpha }_n)y_n,n\ge 1,\hfill \end{array}\right.$$

(23)

where $\mu \in (0,1]$, $\lambda >0$, assuming that Assumption 1 holds and set $d_0:=\frac{(T{w}_0-w_0)}{\lambda }$. Then, the sequence $\left\{x_n\right\}$ converges weakly to a point $x\in Fix\left(T\right)$, provided that the following conditions hold:

(C1) ${\sum }_{n=0}^{\infty }{\beta }_n<\infty$.

(C2) ${\displaystyle \underset{n\to \infty }{lim\; inf}}\mu {\alpha }_n(1-\mu {\alpha }_n)>0$.

Moreover, $\left\{w_n\right\}$ satisfies

(C3) $\{T^n{w}_n-w_n\}$ is bounded.

If in Corollary 2 we assume that T is nonexpansive, we obtain the following Corollary.

Corollary 3.

Let H be a real Hilbert space and $T:H\to H$ be nonexpansive mapping with $Fix\left(T\right)\ne \varnothing$. Let $\left\{x_n\right\}$ be the sequence generated as follows

$$\left\{\begin{array}{c}{x}_0,x_1\in H,\hfill \\ w_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ d_{n+1}=\frac{1}{\lambda }\left(T\left(w_n\right)-w_n\right)+{\beta }_n{d}_n\hfill \\ y_n=w_n+\lambda d_{n+1}\hfill \\ x_{n+1}=\mu {\alpha }_n{w}_n+(1-\mu {\alpha }_n)y_n,n\ge 1,\hfill \end{array}\right.$$

(24)

where $\mu \in (0,1]$, $\lambda >0$, assuming the Assumption 1 holds and set $d_0:=\frac{(T{x}_0-x_0)}{\lambda }$. Then, the sequence $\left\{x_n\right\}$ converges weakly to a point $x\in Fix\left(T\right)$, provided that the following conditions hold;

(C1) ${\sum }_{n=0}^{\infty }{\beta }_n<\infty$.

(C2) ${\displaystyle \underset{n\to \infty }{lim\; inf}}\mu {\alpha }_n(1-\mu {\alpha }_n)>0$.

Moreover, $\left\{w_n\right\}$ satisfies

(C3) $\{T{w}_n-w_n\}$ is bounded.

Remark 3.

Our results extend and generalize many results in the literature for this important class of nonlinear mappings. In particular, Theorem 1 extends Theorem 3.1 of Dong et al. [22] to a more general class of asymptotically nonexpansive mappings in the setting of a real uniformly convex Banach space, more general than a real Hilbert space.

4. Numerical Examples

In this section, we present a numerical example to illustrate the behavior of the sequences generated by the iterative scheme (7). The numerical implementation is done with the aid of MATLAB 2019b programming on a PC with Processor AMD Ryzen 53500 U, 2.10 GHz, 8.00 GB RAM.

Example 1.

Let $X={\ell }_4\left(\mathbb{R}\right),$ where

$${\ell }_4\left(\mathbb{R}\right)=\left\{u=(u_1,u_2,\dots ,u_k,\dots ),u_k\in \mathbb{R}:\sum _{k=1}^{\infty }{\left|u_k\right|}^4<\infty \right\},$$

with

$${\parallel u\parallel }_{{\ell }_4}={\left(\sum _{k=1}^{\infty }{\left|u_k\right|}^4\right)}^{\frac{1}{4}},forallu\in {\ell }_4\left(\mathbb{R}\right).$$

The duality mapping with respect to ${\ell }_4\left(\mathbb{R}\right)$ is defined by (see [33])

$$J_p\left(u\right)=\left(|u_1{|}^{3}sgn\left(u_1\right),{\left|u_2\right|}^{3}sgn\left(u_2\right),\dots \right).$$

More so, X is not a real Hilbert space. Let $T:X\to X$ be defined by $T^{n}u=\left(\frac{10n^2+1}{10n^2}\right)u.$ We take $\mu =\frac{1}{13},\lambda =5,$${\alpha }_n=\frac{1}{2}+\frac{1}{n},$${\theta }_n=\frac{1}{n^2+1},$${\beta }_n=\frac{97n-1}{100(n+1)}.$ Then, all the conditions of Theorem 1 are satisfied with $k_n=\frac{10n^2+1}{10n^2}.$ Then, from (7) we get

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_0,x_1\in X,\hfill \\ w_n=x_n+\frac{1}{n^2+1}(x_n-x_{n-1}),\hfill \\ d_{n+1}=\frac{w_n}{50n^2}+\left(\frac{97n-1}{100n}\right)d_n,\hfill \\ y_n=w_n+5d_{n+1},\hfill \\ x_{n+1}=\left(\frac{n+2}{26n}\right)w_n+\left(\frac{25n-2}{26n}\right)y_n,n\in \mathbb{N},\hfill \end{array}\right.\end{array}$$

(25)

where $d_1=\frac{w_1}{50}.$ We compare the performance of (25) with the methods of Pan and Wang [34] and Vaish and Ahmad [35], which are given respectively by

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f\left(x_n\right)+{\gamma }_n{T}^n(t_n{x}_n+(1-t_n)x_{n+1}),n\in \mathbb{N}$$

(26)

and

$$x_{n+1}={\rho }_{n}g\left(x_n\right)+{\sigma }_n{x}_n+{\delta }_n{T}^n({\eta }_n{x}_n+(1-{\eta }_n)x_{n+1}),n\in \mathbb{N},$$

(27)

where ${\alpha }_n,{\beta }_n,{\gamma }_n,t_n,{\rho }_n,{\sigma }_n,{\delta }_n,$ and ${\eta }_n$ are sequences in $(0,1)$ such that ${\alpha }_n+{\beta }_n+{\gamma }_n=1$, ${\rho }_n+{\sigma }_n+{\delta }_n=1$, $f:X\to X$ is a Meir–Keeler contraction mapping and $g:X\to X$ is a contraction mapping with coefficient $\alpha \in (0,1).$ In our computation, we take $t_n={\eta }_n=\frac{3n}{3n+1},$${\alpha }_n={\rho }_n=\frac{2n}{10(n+1)},$${\gamma }_n={\delta }_n=\frac{97n-1}{100(n+1)},$${\beta }_n=1-{\alpha }_n-{\gamma }_n,$${\sigma }_n=1-{\rho }_n-{\delta }_n$, $f\left(x\right)=\frac{x}{20},$ and $g\left(x\right)=\frac{x}{8}.$ We test the iterative methods for the following initial points:

Case I:

$x_0=\left(\frac{1}{2},\frac{1}{3},\frac{1}{4},\dots \right)$ and $x_1=\left(1,\frac{1}{\sqrt{2}},\frac{1}{\sqrt{3}},\dots \right);$

Case II:

$x_0=(2,2,2,\dots )$ and $x_1=(5,5,5,\dots );$

Case III:

$x_0=(1,3,5,\dots )$ and $x_1=\left(-\frac{1}{4},\frac{1}{16},-\frac{1}{64},\dots \right);$

Case IV:

$x_0=(3,9,27,\dots )$ and $x_1=(2,4,8,\dots ).$

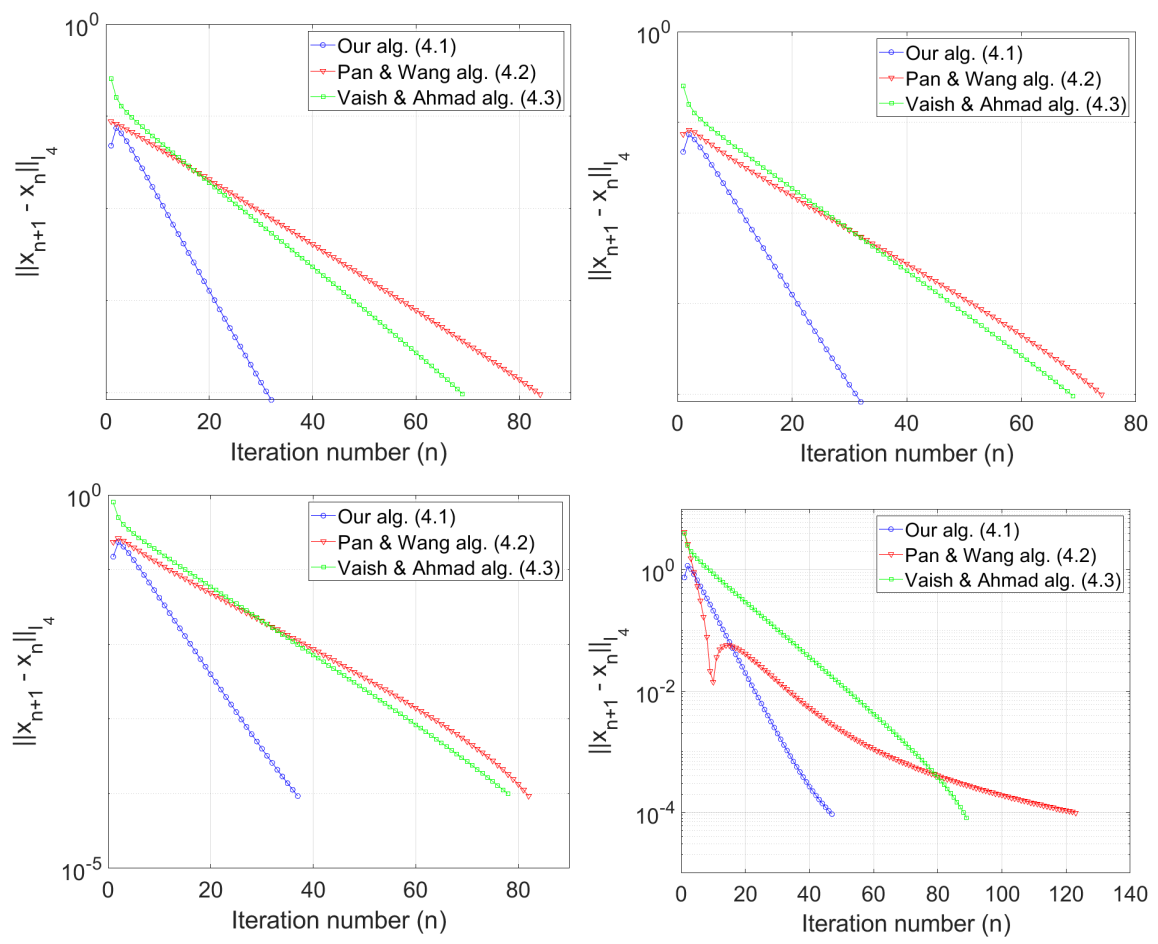
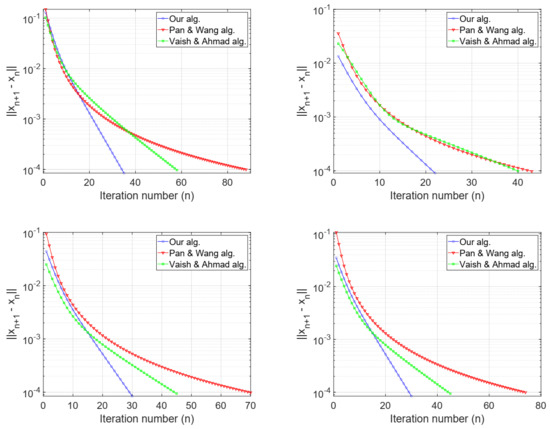
We used $\parallel x_{n+1}-x_n{\parallel }_{{\ell }_4}<{10}^{-4}$ as the stopping criterion for all the algorithms. The numerical results are shown in Table 1 and Figure 1.

Table 1. Computational results showing the performance of the algorithms.

	Alg. (25)		Alg. (26)		Alg. (27)
	Iter.	CPU (sec)	Iter.	CPU (sec)	Iter.	CPU (sec)
Case I	32	0.0063	84	0.0750	69	0.0102
Case II	33	0.0065	74	0.0724	69	0.0120
Case III	38	0.0084	87	0.0847	78	0.0103
Case IV	48	0.0095	123	0.0781	89	0.0131

Figure 1. Example 1. Top left: Case I; top right: Case II; bottom left: Case III; bottom right: Case IV.

Example 2.

Let $X={\mathbb{R}}^4$, endowed with the inner product $⟨x,y⟩=x_1{y}_1+x_2{y}_2+x_3{y}_3+x_4{y}_4$ and the norm $\left|\right|x\left|\right|={\left({\sum }_{i=1}^4{\left|x_i\right|}^2\right)}^{\frac{1}{2}}$ for all $x=(x_1,x_2,x_3,x_4)$, $y=(y_1,y_2,y_3,y_4)\in {\mathbb{R}}^4$. Define $T:{\mathbb{R}}^4\to {\mathbb{R}}^4$ as follows:

$$Tx=\left(x_1,1+\frac{x_2}{2},1+\frac{x_3}{3},\frac{x_4}{2}\right),\forall x=(x_1,x_2,x_3,x_4)\in {\mathbb{R}}^4.$$

Then, clearly $Fix\left(T\right)=\left\{(0,2,\frac{3}{2},0)\right\}$ and for all $x,y\in {\mathbb{R}}^4$, it is easy to see that

$$T^{2}x=T\left(Tx\right)=\left(x_1,1+\frac{1}{2}+\frac{x_2}{2^2},1+\frac{1}{3}+\frac{x_3}{3^2},\frac{x_4}{2^2}\right).$$

In general, for any $n\ge 1$ we have

$$T^{n}x=\left(x_1,\sum _{j=0}^{n-1}\frac{1}{2^j}+\frac{x_2}{2^n},\sum _{j=0}^{n-1}\frac{1}{3^j}+\frac{x_3}{3^n},\frac{x_4}{2^n}\right).$$

So

$$\begin{array}{ccc}\left|\right|T^{n}x-T^{n}y\left|\right|\hfill & =\hfill & {\left(|x_1-y_1{|}^2+{\left(\frac{1}{2^n}\right)}^2|x_2-y_2{|}^2+{\left(\frac{1}{3^n}\right)}^2|x_3-y_3{|}^2+{\left(\frac{1}{2^n}\right)}^2{|x_4-y_4|}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le \hfill & {\left(|x_1-y_1{|}^2+{\left(\frac{1}{2^n}\right)}^2|x_2-y_2{|}^2+{\left(\frac{1}{2^n}\right)}^2|x_3-y_3{|}^2+{\left(\frac{1}{2^n}\right)}^2{|x_4-y_4|}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le \hfill & {\left(\left(1+\frac{1}{2^n}\right)\left[|x_1-y_1{|}^2+|x_2-y_2{|}^2+|x_3-y_3{|}^2+{|x_4-y_4|}^2\right]\right)}^{\frac{1}{2}}\hfill \\ \hfill & =\hfill & {\left(1+\frac{1}{2^n}\right)}^{\frac{1}{2}}\left|\right|x-y\left|\right|\hfill \\ \hfill & =\hfill & \left(1+\frac{1}{2}\times \frac{1}{2^n}+\frac{\frac{1}{2}(\frac{1}{2}-1)}{2!}\times {\left(\frac{1}{2^n}\right)}^2+\frac{\frac{1}{2}(\frac{1}{2}-1)\frac{1}{2}-2)}{3!}\times {\left(\frac{1}{2^n}\right)}^3+\dots \right)\left|\right|x-y\left|\right|\hfill \\ \hfill & \le \hfill & \left(1+\frac{1}{2^n}+{\left(\frac{1}{2^n}\right)}^3+{\left(\frac{1}{2^n}\right)}^5+\dots \right)\left|\right|x-y\left|\right|\hfill \\ \hfill & =\hfill & \left(1+\frac{\frac{1}{2^n}}{1-{\left(\frac{1}{2^n}\right)}^2}\right)\left|\right|x-y\left|\right|\hfill \\ \hfill & \le \hfill & \left(1+\frac{1}{2^n}\right)\left|\right|x-y\left|\right|.\hfill \end{array}$$

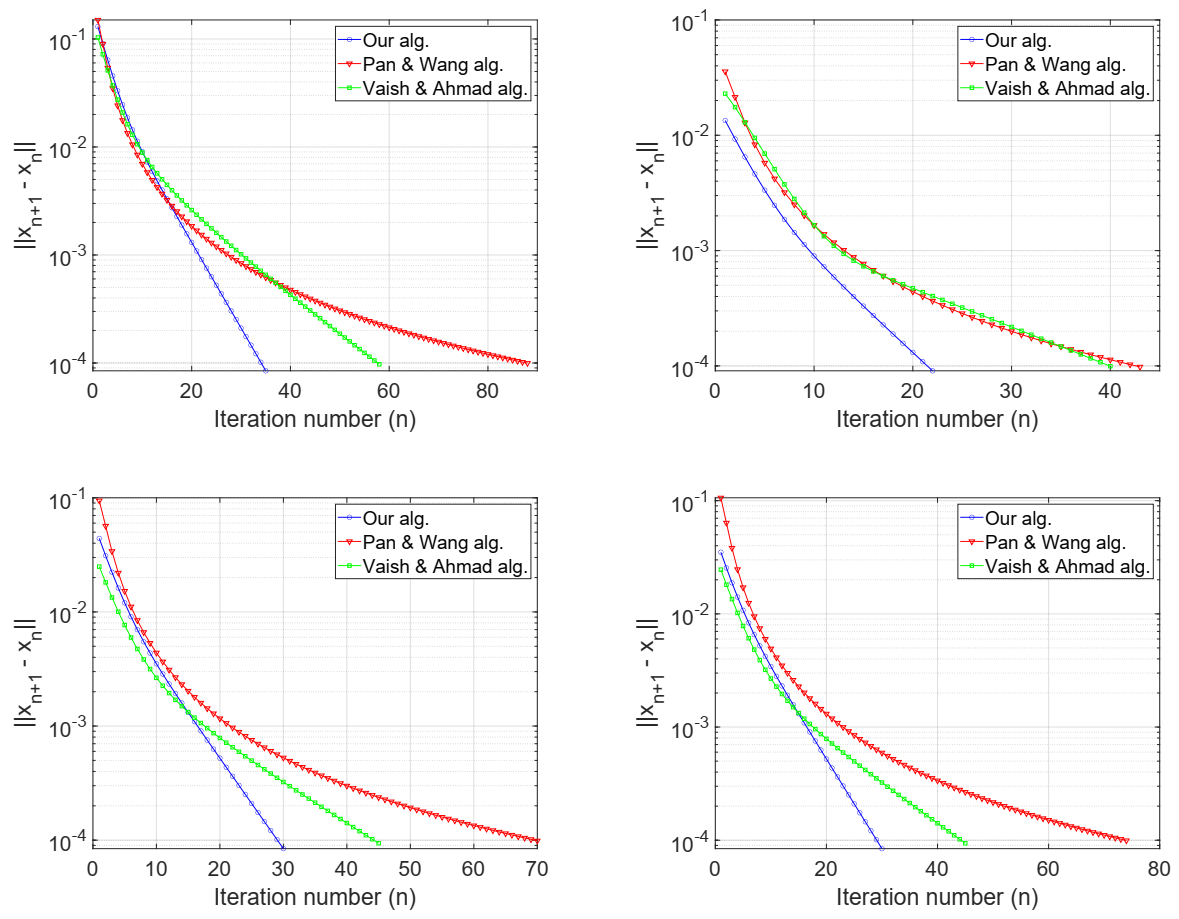
This implies that T is an asymptotically nonexpansive mapping with $k_n=\frac{1}{2^n}\to 0$ as $n\to \infty$. Similarly, we compare the performance of (7) with that of Pan and Wang [34] and Vaish and Ahmad [35]. For (7), we choose $\mu =\frac{1}{8},\lambda =2,{\delta }_n=\frac{1}{n+1},{\beta }_n={\delta }_n^2$. For the Pan and Wang algorithm, we take $f\left(x\right)=\frac{2}{\sqrt{x}},{\beta }_n=\frac{1}{5(n+1)},{\alpha }_n=\frac{2n}{5n+8},t_n=\frac{n}{3(n+1)}.$ For the Vaish and Ahmad algorithm, we take $g\left(x\right)=\frac{x}{2},{\rho }_n=\frac{2n}{5n+8},{\sigma }_n=\frac{1}{10(n+1)},{\delta }_n=1-{\sigma }_n-{\rho }_n,{\eta }_n=\frac{n}{3n+3}.$ We test the algorithm using the following initial points:

Case I:

$x_0={(2,2,2,2)}^{\prime },x_1={(5,5,5,5)}^{\prime };$

Case II:

$x_0={(1,3,3,1)}^{\prime },x_1={(0.5,1,1.5,3)}^{\prime };$

Case III:

$x_0={(2,0,0,2)}^{\prime },x_1={(8,3,3,8)}^{\prime };$

Case IV:

$x_0={(3,3,3,3)}^{\prime },x_1={(10,10,10,10)}^{\prime }.$

We use $\left|\right|x_{n+1}-x_n\left|\right|<{10}^{-4}$ as the stopping criterion. The numerical results are shown in Table 2 and Figure 2.

Table 2. Computational results showing the performance of the algorithms for Example 2.

	Our Alg.		Pan and Wang Alg.		Vaish and Ahmad Alg.
	Iter.	CPU (sec)	Iter.	CPU (sec)	Iter.	CPU (sec)
Case I	35	0.0103	88	0.0382	58	0.0156
Case II	22	0.0067	43	0.0163	40	0.0104
Case III	30	0.0090	70	0.0487	45	0.0175
Case IV	30	0.0072	74	0.0368	45	0.0175

Figure 2. Example 2. Top left: Case I; top right: Case II; bottom left: Case III; bottom right: Case IV.

Example 3.

Finally, we apply our algorithm to solve an image restoration problem which involves the reconstruction of an image degraded by blur and additive noise. We solve the $l_1$-norm regularization problem, that is, find a solution to the following continuous optimization problem:

$$\underset{x\in {\mathbb{R}}^N}{min}\left\{{\parallel x\parallel }_1:Ax=b\right\},$$

(28)

where b is a vector in ${\mathbb{R}}^M,$ A is a matrix of dimension $M\times N$ ($M<<N$), and ${\parallel x\parallel }_1={\sum }_{i=1}^N\left|x_i\right|$ is the $l_1$-norm of $x.$ The expression in (28) can be reformulated as the following least absolute selection and shrinkage operator (LASSO) problem [36,37]:

$$\underset{x\in {\mathbb{R}}^N}{min}\left\{{\omega \parallel x\parallel }_1+\frac{1}{2}{\parallel b-Ax\parallel }_2^2\right\},$$

(29)

where $\omega >0$ is a balancing parameter. Clearly, (29) is a convex unconstrained minimization problem which appears in compress sensing and image reconstruction, where the original signal (or image) is sparse in some orthogonal basis by the process

$$b=Ax+\eta ,$$

where x is the original signal (or image), A is the blurring operator, η is a noise, and b is the degraded or blurred data which needs to be recovered. Many iterative methods have been proposed for solving (29), with the earliest being the projection method by Figureido et al. [36]. Note that the LASSO problem (29) can be expressed as a variational inequality problem, that is, finding $x\in {\mathbb{R}}^N$ such that $⟨F\left(x\right),y-x⟩\ge 0,$ for all $y\in {\mathbb{R}}^N$, where $F=A^T(Ax-b)$ (see [38]). Equivalently, we can rewrite (29) as a fixed point problem with $T\equiv P_{{\mathbb{R}}^N}(I-\lambda F)$ (for $\lambda >0$) which is nonexpansive. Our aim here is to recover the original image x given the data of the blurred image b. We consider the greyscale image of M pixels width and N pixels height, where each value is known to be in the range $[0,255]$. Let $D=M\times N.$ The quality of the restored image is measured by the signal-to-noise ratio defined as

$$SNR=20\times {log}_{10}\left(\frac{{\parallel x\parallel }_2}{\parallel x-x^{\ast }{\parallel }_2}\right),$$

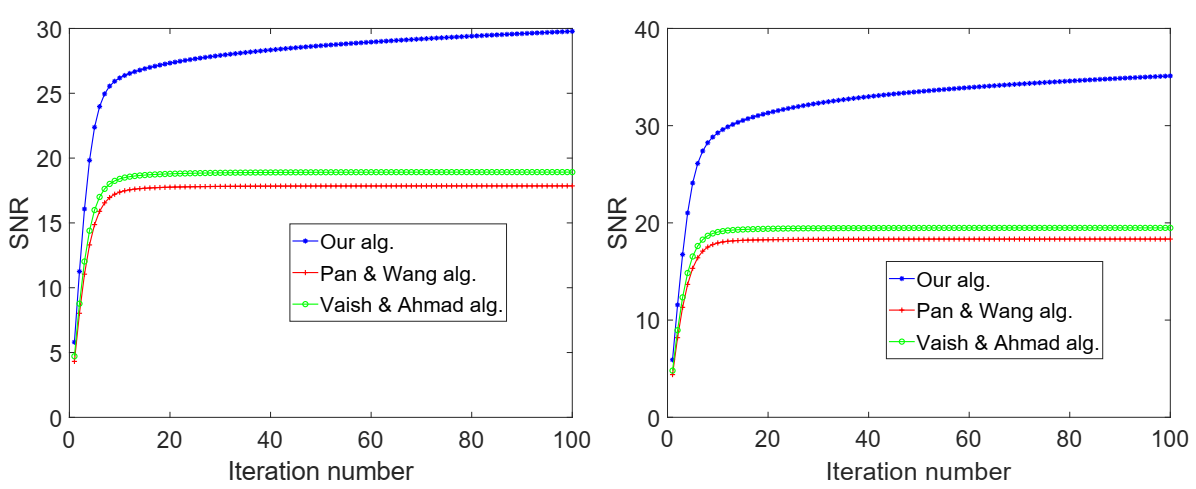
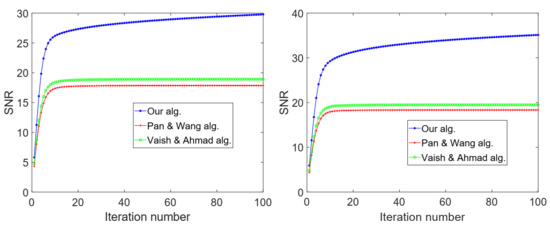
where x is the original image and $x^{\ast }$ is the restored image. Typically, the larger the $SNR$, the better the quality of the restored image. In our experiments, we use the greyscale test images Cameraman ($256\times 256$) and Pout ($291\times 240$) in the Image Processing Toolbox in MATLAB, and each test image is degraded by a Gaussian $7\times 7$ blur kernel with standard deviation $4.$ For our iterative scheme (7), we choose ${\alpha }_n=\frac{1}{2n+1},\mu =\frac{1}{8},{\beta }_n=\frac{1}{n^{0.5}},{\delta }_n={\beta }_n^2,\eta =3.5,$ while for the Pan and Wang algorithm [34] and the Vaish and Ahmad algorithm [35] we take $t_n={\eta }_n=\frac{19n}{20n+21},$${\gamma }_n={\delta }_n=\frac{1}{2}+\frac{5n}{19n+20},$${\alpha }_n={\rho }_n=\frac{1}{n+1},$${\beta }_n=1-{\alpha }_n-{\gamma }_n,$${\sigma }_n=1-{\rho }_n-{\delta }_n,$$f\left(x\right)=\frac{2}{\sqrt{x}},g\left(x\right)=\frac{x}{2}.$ The initial values are chosen by ${\mathbf{x}}_{\mathbf{0}},{\mathbf{x}}_{\mathbf{1}}\in {\mathbb{R}}^{\mathbf{D}}.$ Figure 3 and Figure 4 shows the original, blurred, and restored images using the algorithms. Figure 5 shows the graphs of SNR against number of iterations for each algorithm, and in Table 3 we report the time (in seconds) for each algorithm in the experiments.

Figure 3. Example 2. The top row shows the original Cameraman image (left) and the degraded Cameraman image (right). The bottom row shows the images recovered by our algorithm, by the algorithm of Pan and Wang, and by that of Vaish and Ahmad.

Figure 4. Example 2. The top row shows the original Pout image (left) and the degraded Pout image (right). The bottom row shows the images recovered by our algorithm, by that of Pan and Wang, and by that of Vaish and Ahmad.

Figure 5. Example 2: Graphs of signal-to-noise ratio (SNR) values against the number of iterations for Cameraman (left)and Pout (right).

Table 3. Time (s) for restoring the images for each algorithm.

	Our Alg.	Pan and Wang Alg.	Vaish and Ahmad Alg.
Cameraman image	2.7928	2.6422	2.6709
Pout image	4.8237	4.4248	3.45630

From the numerical results, we observe that all the algorithms are able to restore the degraded images. Algorithm (7) performs better than the other algorithms in terms of the SNR (quality) of the restored image, but with more time taken.

5. Conclusions

We studied a modified inertial accelerated Mann algorithm in real uniformly convex Banach spaces. A strong convergence theorem was proved for approximating a fixed point of asymptotically nonexpansive mapping. Finally, we applied our results to study an image restoration problem and presented some numerical experiments to demonstrate and clarify the efficiency of our proposed iterative method compared to some existing methods in the literature.