Novel Concept of Energy in Bipolar Single-Valued Neutrosophic Graphs with Applications
Abstract
:1. Introduction
2. Preliminaries
- ;
- ;
- .
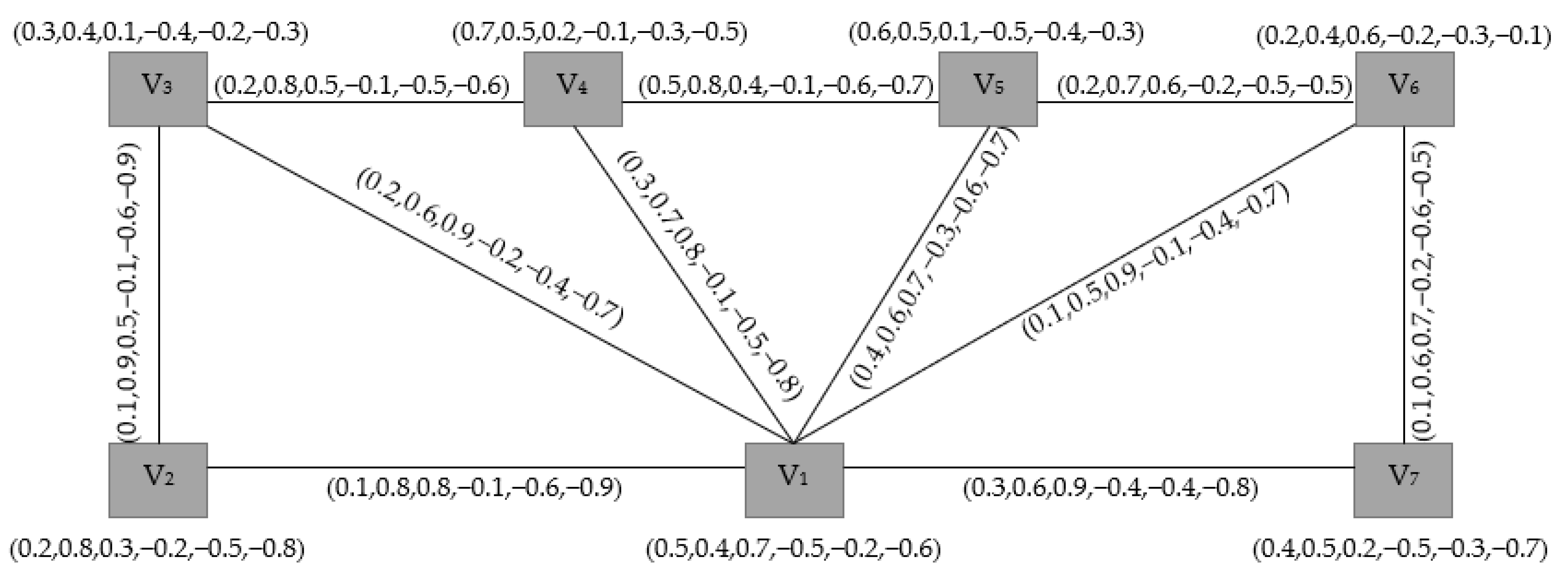
3. Energy of Bipolar Single-Valued Neutrosophic Graphs
- and .
- and
- Since is a symmetric matrix with zero traces, its eigenvalues are real with a sum equal to zero.
- By trace properties of a matrix, we havewhere
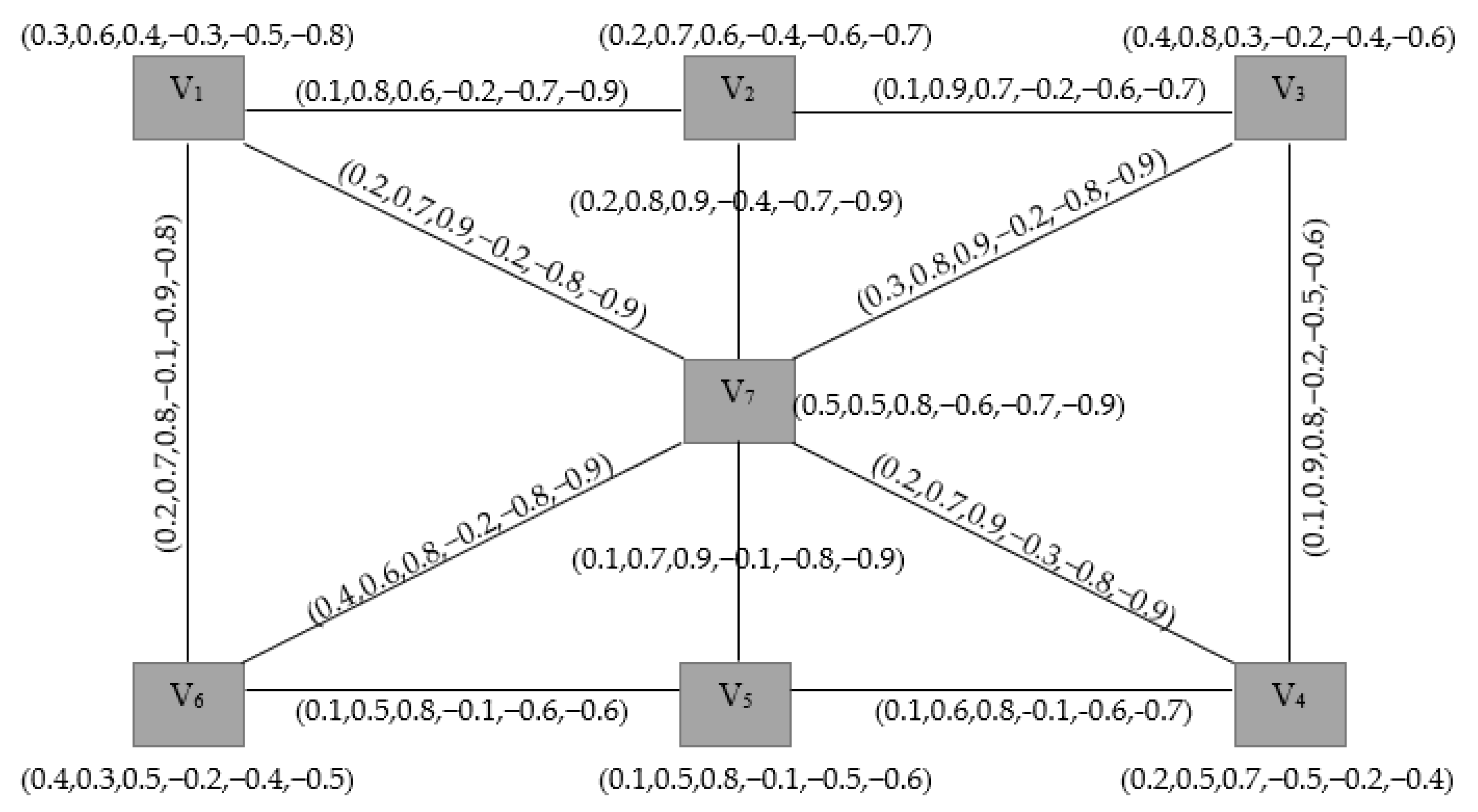
4. Laplacian Energy of Bipolar Single-Valued Neutrosophic Graphs (BSVNG)
- and .
- and
5. Signless Laplacian Energy of BSVNG
6. Relation between Energy, Laplacian Energy and Signless Laplacian Energy of BSVNG
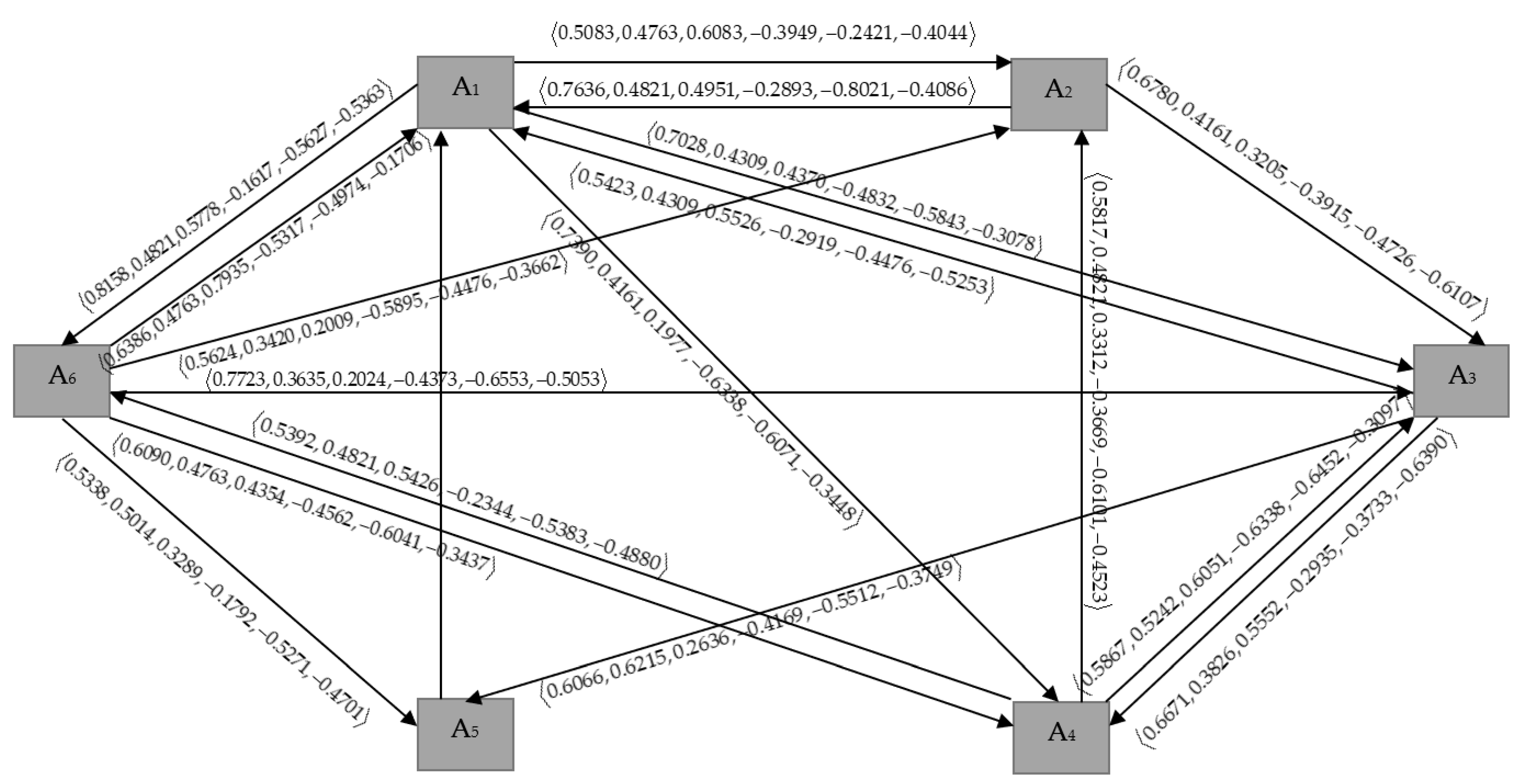
7. Application of Energy of BSVNG
Selection of the Most Compatible Renewable Energy Source
8. Comparative Study
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gutman, I. The energy of a graph. Ber. Math. Stat. Sekt. Forsch. Graz. 1978, 103, 1–22. [Google Scholar]
- Gutman, I.; Zhou, B. Laplacian energy of a graph. Linear Algebra Appl. 2006, 414, 29–37. [Google Scholar] [CrossRef] [Green Version]
- Gutman, I. The Energy of a Graph: Old and New Results. Algebraic Combinatorics and Applications; Springer: Berlin/Heidelberg, Germany, 2001; pp. 196–211. [Google Scholar]
- Gutman, I.; Kiani, D.; Mirzakhah, M.; Zhou, B. On incidence energy of a graph. Linear Algebra Appl. 2009, 431, 1223–1233. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Gutman, I.; Aleksic, T. A note on Laplacian energy of graphs. MATCH Commun. Math. Comput. Chem. 2008, 60, 441–446. [Google Scholar]
- Gutman, I.; Wagner, S. The matching energy of a graph. Discret. Appl. Math. 2012, 160, 2177–2187. [Google Scholar] [CrossRef] [Green Version]
- So, W.; Robbiano, M.; de Abreu, N.M.M.; Gutman, I. Applications of a theorem by Ky Fan in the theory of graph energy. Linear Algebra Appl. 2010, 432, 2163–2169. [Google Scholar] [CrossRef] [Green Version]
- Abreu, N.; Cardoso, D.M.; Gutman, I.; Martins, E.A.; Robbiano, M. Bounds for the signless Laplacian energy. Linear Algebra Appl. 2011, 435, 2365–2374. [Google Scholar] [CrossRef] [Green Version]
- Adiga, C.; Bayad, A.; Gutman, I.; Srinivas, S.A. The minimum covering energy of a graph. Kragujev. J. Sci. 2012, 34, 39–54. [Google Scholar]
- Das, K.C.; Mojallal, S.A. Relation between energy and (signless) Laplacian energy of graphs. Match 2015, 74, 359–366. [Google Scholar]
- Das, K.C.; Mojallal, S.A. Relation between signless Laplacian energy, energy of graph and its line graph. Linear Algebra Appl. 2016, 493, 91–107. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Kauffman, A. Introduction a la Theorie des Sous-Emsembles Flous; Masson et Cie: Paris, France, 1973. [Google Scholar]
- Rosenfeld, A. Fuzzy Graph. Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Elsevier: Amsterdam, The Netherlands, 1975; pp. 77–95. [Google Scholar]
- Zhang, W.R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis. In NAFIPS/IFIS/NASA’94, Proceedings of the First International Joint Conference of the North American Fuzzy Information Processing Society Biannual Conference, the Industrial Fuzzy Control and Intellige; IEEE: Washington, DC, USA, 1995; pp. 305–309. [Google Scholar]
- Smarandache, F. A unifying field in logics. In Neutrosophy: Neutrosophic Probability, Set, and Logic; American Research Press: Rehoboth, DE, USA, 1999. [Google Scholar]
- Anjali, N.; Mathew, S. Energy of a fuzzy graph. Ann. Fuzzy Math. Inform. 2013, 6, 455–465. [Google Scholar]
- Shabaf, S.R.; Fayazi, F. Laplacian Energy of a Fuzzy Graph. Iran. J. Math. Chem. 2014, 5, 1–10. [Google Scholar]
- Praba, B.; Chandrasekaran, V.M.; Deepa, G. Energy of an intuitionistic fuzzy graph. Ital. J. Pure Appl. Math. 2014, 32, 431–444. [Google Scholar]
- Basha, S.S.; Kartheek, E. Laplacian energy of an intuitionistic fuzzy graph. Indian J. Sci. Technol. 2015, 8, 1–7. [Google Scholar]
- Akram, M.; Naz, S. Energy of Pythagorean fuzzy graphs with applications. Mathematics 2018, 6, 136. [Google Scholar] [CrossRef] [Green Version]
- Murugesan, R.; Venkatesh, K.A. Laplacian energy of bipolar fuzzy. Int. J. Emerg. Technol. Innov. Res. 2018, 5, 1235–1239. [Google Scholar]
- Naz, S.; Ashraf, S.; Karaaslan, F. Energy of a bipolar fuzzy graph and its application in decision making. Ital. J. Pure Appl. Math. 2018, 2018, 339–352. [Google Scholar]
- Ramesh, O.; Basha, S.S. The Implementation of Cosine Similarity Measures in Decision-Making Problems by Signless Laplacian Energy of an Intuitionistic Fuzzy Graph. Eur. J. Mol. Clin. Med. 2020, 7, 239–251. [Google Scholar]
- Ramesh, O.; Basha, S.S. Group decision making of selecting partner based on signless laplacian energy of an intuitionistic fuzzy graph with topsis method: Study on matlab programming. Adv. Math. Sci. J. 2020, 9, 5849–5859. [Google Scholar] [CrossRef]
- Broumi, S.; Talea, M.; Bakali, A.; Singh, P.K.; Broumi, S.; Smarandache, F. Energy and Spectrum Analysis of Interval Valued Neutrosophic Graph using MATLAB. Neutrosophic Sets Syst. 2019, 24, 46–60. [Google Scholar]
- Khan, M.; Umar, S.; Broumi, S. Laplacian Energy of a Complex. Neutrosophic Graph; Springer: Cham, Switzerland, 2019; pp. 203–232. [Google Scholar]
- Naz, S.; Akram, M.; Smarandache, F. Certain Notions of Energy in Single-Valued Neutrosophic Graphs. Axioms 2018, 7, 50. [Google Scholar] [CrossRef] [Green Version]
- Mullai, M.; Broumi, S. Dominating Energy in Neutrosophic graphs. Int. J. Neutrosoph. Sci. 2020, 5, 38–58. [Google Scholar]
- Deli, I.; Ali, M.; Smarandache, F. Bipolar Neutrosophic Sets And Their Application Based On Multi-Criteria Decision Making Problems. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems, Beijing, China, 22–24 August 2015. [Google Scholar]
- Broumi, S.; Smarandache, F.; Talea, M.; Bakali, A. An Introduction to Bipolar Single Valued Neutrosophic Graph Theory. Appl. Mech. Mater. 2016, 841, 184–191. [Google Scholar] [CrossRef] [Green Version]
- Broumi, S.; Talea, M.; Bakali, A.; Smarandache, F. On Bipolar Single Valued Neutrosophic Graphs. J. New Theory 2016, 11, 84–102. [Google Scholar]
- Ali, M.; Son, L.H.; Deli, I.; Tien, N.D. Bipolar neutrosophic soft sets and applications in decision making. J. Intell. Fuzzy Syst. 2017, 33, 4077–4087. [Google Scholar] [CrossRef] [Green Version]
- Akram, M.; Luqman, A. A new decision-making method based on bipolar neutrosophic directed hypergraphs. J. Appl. Math. Comput. 2018, 57, 547–575. [Google Scholar] [CrossRef]
- Akram, M.; Shumaiza; Smarandache, F. Decision-making with bipolar neutrosophic TOPSIS and bipolar neutrosophic ELECTRE-I. Axioms 2018, 7, 33. [Google Scholar] [CrossRef] [Green Version]
- Uluçay, V.; Deli, I.; Şahin, M. Similarity measures of bipolar neutrosophic sets and their application to multiple criteria decision making. Neural Comput. Appl. 2018, 29, 739–748. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Basset, M.; Mohamed, M.; Elhoseny, M.; Son, L.H.; Chiclana, F.; Zaied, A.E.N.H. Cosine similarity measures of bipolar neutrosophic set for diagnosis of bipolar disorder diseases. Artif. Intell. Med. 2019, 101, 101735. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Ye, J.; Feng, S.; Fan, E.; Hu, K. Multi-criteria decision-making method using heronian mean operators under a bipolar neutrosophic environment. Mathematics 2019, 7, 97. [Google Scholar] [CrossRef] [Green Version]
- Abdel-Basset, M.; Gamal, A.; Son, L.H.; Smarandache, F. A bipolar neutrosophic multi criteria decision making framework for professional selection. Appl. Sci. 2020, 10, 1202. [Google Scholar] [CrossRef] [Green Version]
- Rahim, N.; Abdullah, L.; Yusoff, B. A border approximation area approach considering bipolar neutrosophic linguistic variable for sustainable energy selection. Sustainability 2020, 12, 3971. [Google Scholar] [CrossRef]
- Karaşan, A.; Kahraman, C. Selection of the Most Appropriate Renewable Energy Alternatives by Using a Novel Interval-Valued Neutrosophic ELECTRE I Method. Informatica 2020, 31, 225–248. [Google Scholar] [CrossRef] [Green Version]

| Author and References | Year | Fuzzy/Neutrosophic Sets | Significance Influences |
|---|---|---|---|
| Akram and Naz [21] | 2018 | Pythagorean fuzzy sets | Introduce the energy and Laplacian energy in Pythagorean fuzzy graphs and Pythagorean fuzzy digraphs. |
| Rajeshwari et al. [22] | 2018 | Bipolar fuzzy sets | Introduce Laplacian energy for a bipolar fuzzy graph. |
| Naz et al. [23] | 2018 | Bipolar fuzzy sets | Introduce the concept of energy in bipolar fuzzy graph (BFG) and bipolar fuzzy digraphs (BFDGs). |
| Naz et al. [28] | 2018 | Single-valued neutrosophic sets | Introduce the concept of energy, Laplacian energy and signless Laplacian energy in single-valued neutrosophic graphs (SVNGs). |
| Broumi et al. [26] | 2019 | Interval-valued neutrosophic sets | Compute the spectrum and energy of interval-valued neutrosophic graph (IVNG). |
| Mohsin et al. [27] | 2019 | Complex neutrosophic set | Compute Laplacian energy of a complex neutrosophic graph in terms of its adjacency matrix. |
| Ramesh and Basha [24] | 2020 | Intuitionistic fuzzy sets | Solve decision-making problem by signless Laplacian energy of intuitionistic fuzzy graph and cosine similarity measure. |
| Ramesh and Basha [25] | 2020 | Intuitionistic fuzzy sets | Solve group decision-making problem by signless Laplacian energy of intuitionistic fuzzy graph. |
| Mullai and Broumi [29] | 2020 | Single-valued neutrosophic sets | Introduce dominating sets and dominating numbers for energy graphs in single-valued neutrosophic graphs. |
| 0.5 | 0.2 | 0.3 | 0.7 | 0.6 | 0.2 | 0.4 | |
| 0.4 | 0.8 | 0.4 | 0.5 | 0.5 | 0.4 | 0.5 | |
| 0.7 | 0.3 | 0.1 | 0.2 | 0.1 | 0.6 | 0.2 | |
| −0.5 | −0.2 | −0.4 | −0.1 | −0.5 | −0.2 | −0.5 | |
| −0.2 | −0.5 | −0.2 | −0.3 | −0.4 | −0.3 | −0.3 | |
| −0.6 | −0.8 | −0.3 | −0.5 | −0.3 | −0.1 | −0.7 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.1 | 0.3 | 0.1 | 0.2 | 0.5 | 0.2 | 0.1 | |
| 0.8 | 0.6 | 0.7 | 0.6 | 0.5 | 0.6 | 0.9 | 0.8 | 0.8 | 0.7 | 0.6 | |
| 0.8 | 0.9 | 0.8 | 0.7 | 0.9 | 0.9 | 0.5 | 0.5 | 0.4 | 0.6 | 0.7 | |
| −0.1 | −0.2 | −0.1 | −0.3 | −0.1 | −0.4 | −0.1 | −0.1 | −0.1 | −0.2 | −0.2 | |
| −0.6 | −0.4 | −0.5 | −0.6 | −0.4 | −0.4 | −0.6 | −0.5 | −0.6 | −0.5 | −0.6 | |
| −0.9 | −0.7 | −0.8 | −0.7 | −0.7 | −0.8 | −0.9 | −0.6 | −0.7 | −0.5 | −0.5 |
| 0.3 | 0.2 | 0.4 | 0.2 | 0.1 | 0.4 | 0.5 | |
| 0.6 | 0.7 | 0.8 | 0.5 | 0.5 | 0.3 | 0.5 | |
| 0.4 | 0.6 | 0.3 | 0.7 | 0.8 | 0.5 | 0.8 | |
| −0.3 | −0.4 | −0.2 | −0.5 | −0.1 | −0.2 | −0.6 | |
| −0.5 | −0.6 | −0.4 | −0.2 | −0.5 | −0.4 | −0.7 | |
| −0.8 | −0.7 | −0.6 | −0.4 | −0.6 | −0.5 | −0.9 |
| 0.1 | 0.2 | 0.2 | 0.1 | 0.2 | 0.1 | 0.3 | 0.1 | 0.2 | 0.1 | 0.1 | 0.4 | |
| 0.8 | 0.7 | 0.7 | 0.9 | 0.8 | 0.9 | 0.8 | 0.6 | 0.7 | 0.5 | 0.7 | 0.6 | |
| 0.6 | 0.8 | 0.9 | 0.7 | 0.9 | 0.8 | 0.9 | 0.8 | 0.9 | 0.8 | 0.9 | 0.8 | |
| −0.2 | −0.1 | −0.2 | −0.2 | −0.4 | −0.2 | −0.2 | −0.1 | −0.3 | −0.1 | −0.1 | −0.2 | |
| −0.7 | −0.9 | −0.8 | −0.6 | −0.7 | −0.5 | −0.8 | −0.6 | −0.8 | −0.6 | −0.8 | −0.8 | |
| −0.9 | −0.8 | −0.9 | −0.7 | −0.9 | −0.6 | −0.9 | −0.7 | −0.9 | −0.6 | −0.9 | −0.9 |
| 0.2 | 0.7 | 0.1 | 0.5 | 0.3 | 0.4 | 0.8 | |
| 0.6 | 0.1 | 0.3 | 0.2 | 0.4 | 0.6 | 0.7 | |
| 0.4 | 0.5 | 0.2 | 0.1 | 0.7 | 0.7 | 0.6 | |
| −0.4 | −0.1 | −0.3 | −0.4 | −0.5 | −0.2 | −0.5 | |
| −0.6 | −0.3 | −0.2 | −0.5 | −0.3 | −0.4 | −0.4 | |
| −0.1 | −0.6 | −0.5 | −0.2 | −0.4 | −0.1 | −0.3 |
| 0.2 | 0.1 | 0.1 | 0.4 | 0.3 | 0.1 | 0.2 | 0.3 | 0.4 | 0.2 | 0.3 | |
| 0.7 | 0.6 | 0.4 | 0.3 | 0.5 | 0.5 | 0.5 | 0.7 | 0.8 | 0.8 | 0.7 | |
| 0.6 | 0.5 | 0.6 | 0.7 | 0.8 | 0.8 | 0.7 | 0.8 | 0.6 | 0.8 | 0.8 | |
| −0.1 | −0.2 | −0.1 | −0.1 | −0.1 | −0.3 | −0.3 | −0.2 | −0.3 | −0.4 | −0.1 | |
| −0.8 | −0.7 | −0.4 | −0.6 | −0.4 | −0.5 | −0.6 | −0.7 | −0.5 | −0.5 | −0.6 | |
| −0.7 | −0.5 | −0.6 | −0.8 | −0.7 | −0.5 | −0.4 | −0.3 | −0.4 | −0.5 | −0.4 |
| M | A1 | A2 | A3 |
| A1 | |||
| A2 | |||
| A3 | |||
| A4 | |||
| A5 | |||
| A6 | |||
| A4 | A5 | A6 | |
| A1 | |||
| A2 | |||
| A3 | |||
| A4 | |||
| A5 | |||
| A6 |
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| A6 |
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| A6 |
| A1 | ||||||
| A2 | ||||||
| A3 | ||||||
| A4 | ||||||
| A5 | ||||||
| A6 |
| M | A1 | A2 | A3 |
| A1 | |||
| A2 | |||
| A3 | |||
| A4 | |||
| A5 | |||
| A6 | |||
| A4 | A5 | A6 | |
| A1 | |||
| A2 | |||
| A3 | |||
| A4 | |||
| A5 | |||
| A6 |
| Alternatives | Weight/Score Function | Rank |
|---|---|---|
| Biomass energy plant (A1) | 0.5778 | 2 |
| Geothermal energy plant (A2) | 0.5056 | 5 |
| Hydro power plant (A3) | 0.5667 | 3 |
| Solar power plant (A4) | 0.5556 | 4 |
| Wave power plant (A5) | 0.4910 | 6 |
| Wind power plant (A6) | 0.5860 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamad, S.N.F.; Hasni, R.; Smarandache, F.; Yusoff, B. Novel Concept of Energy in Bipolar Single-Valued Neutrosophic Graphs with Applications. Axioms 2021, 10, 172. https://doi.org/10.3390/axioms10030172
Mohamad SNF, Hasni R, Smarandache F, Yusoff B. Novel Concept of Energy in Bipolar Single-Valued Neutrosophic Graphs with Applications. Axioms. 2021; 10(3):172. https://doi.org/10.3390/axioms10030172
Chicago/Turabian StyleMohamad, Siti Nurul Fitriah, Roslan Hasni, Florentin Smarandache, and Binyamin Yusoff. 2021. "Novel Concept of Energy in Bipolar Single-Valued Neutrosophic Graphs with Applications" Axioms 10, no. 3: 172. https://doi.org/10.3390/axioms10030172
APA StyleMohamad, S. N. F., Hasni, R., Smarandache, F., & Yusoff, B. (2021). Novel Concept of Energy in Bipolar Single-Valued Neutrosophic Graphs with Applications. Axioms, 10(3), 172. https://doi.org/10.3390/axioms10030172







