Advanced Proportional-Integral-Derivative Control Compensation Based on a Grey Estimated Model in Dynamic Balance of Single-Wheeled Robot
Abstract
:1. Introduction
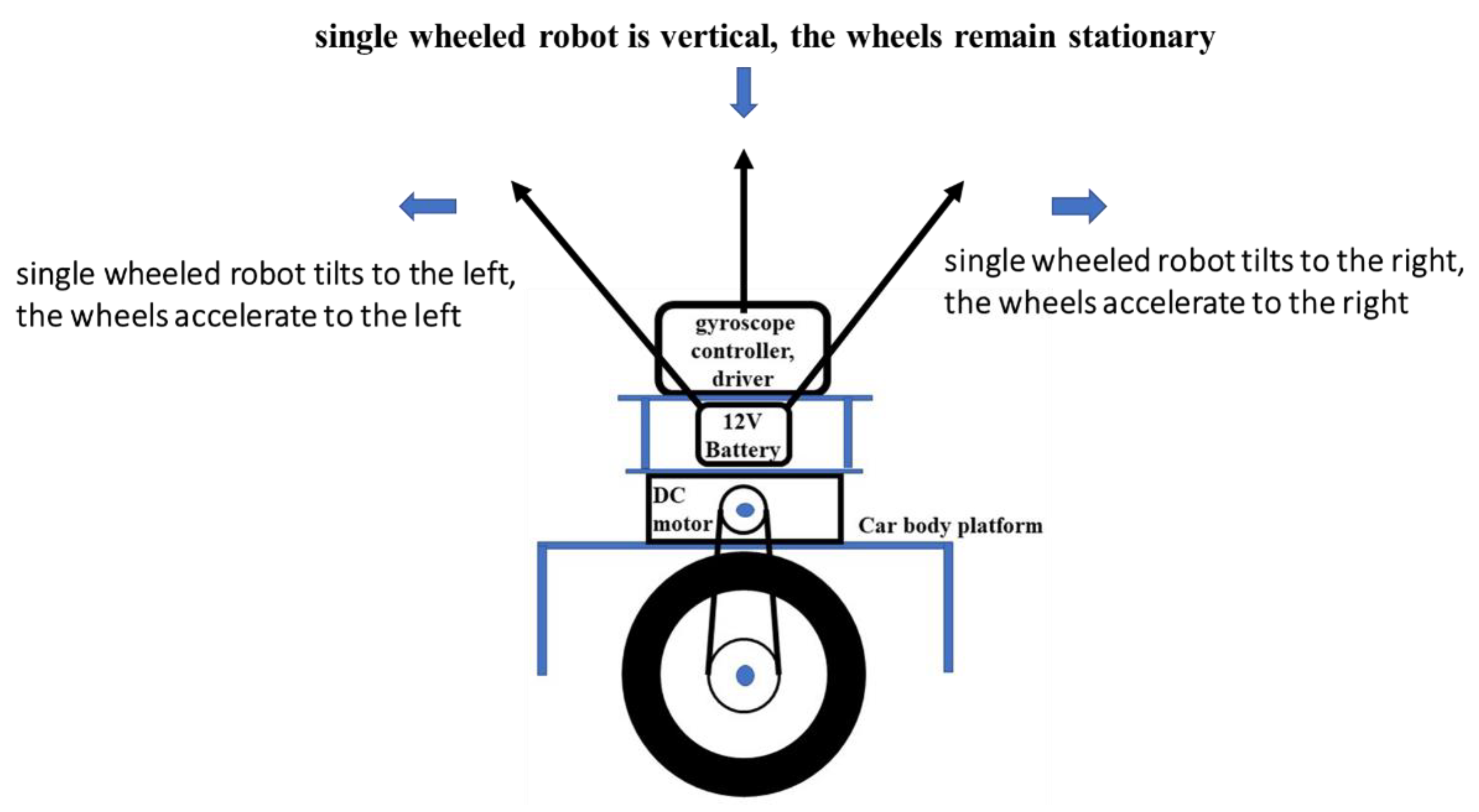
2. Mathematical Model of the One-Wheeled Robot
2.1. Analysis of Robot Load-Carrying Capability
2.2. Equation of Robot System Dynamics
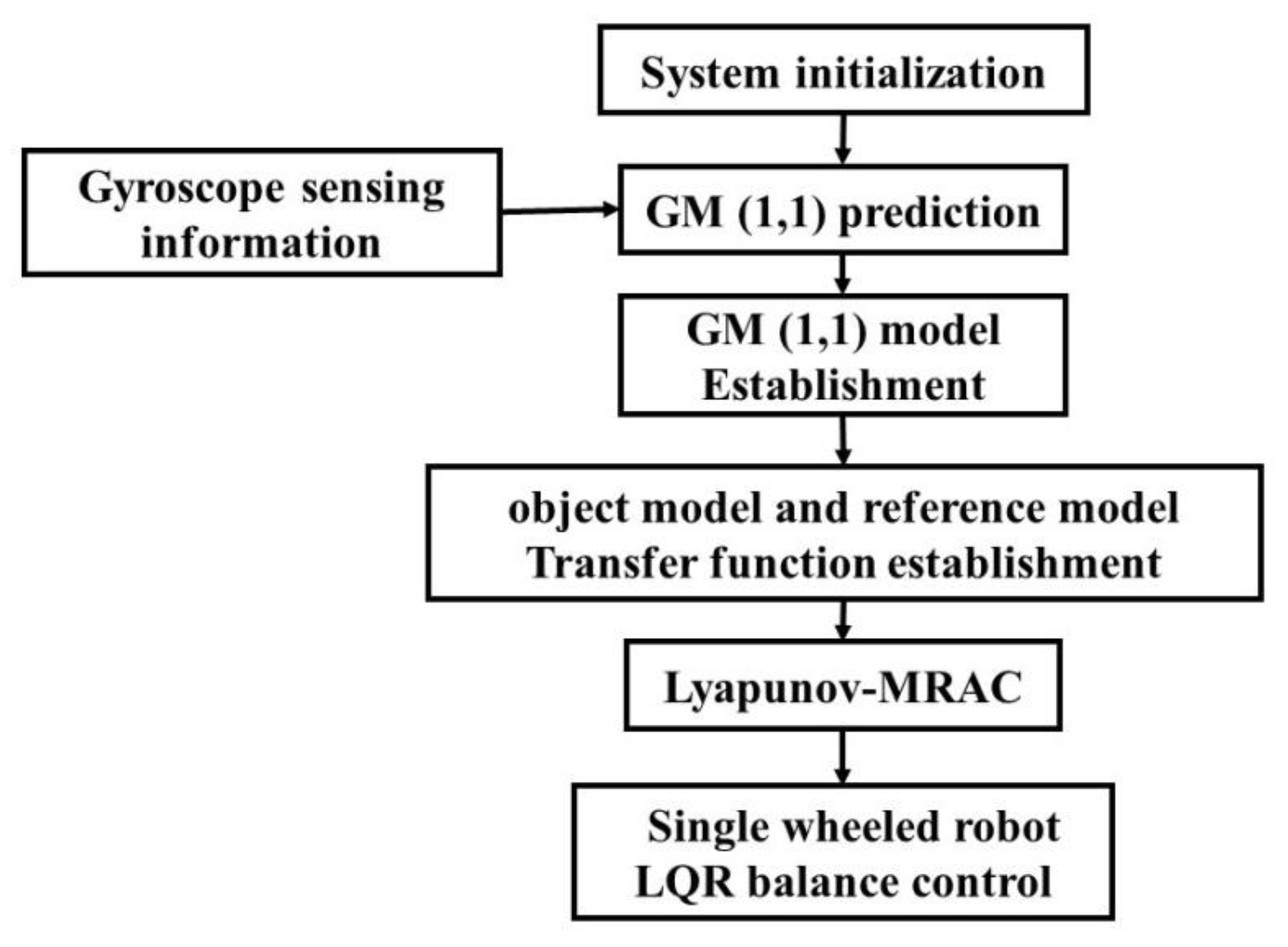
3. Grey Prediction Model
3.1. The Establishment of the GM (1,1) Model
- x is the background value of , also called the initial value.
- a and u are the grey parameters to be calculated, where a is the development coefficient, reflecting the development trend of x
- u is the grey effect value, which reflects the changing relationship among the data.
- Calculating an accumulation sequence from the original data sequence ;
- Establishing a data vector, Y, and a data matrix, B;
- Calculating the inverse matrix for the least square method;
- Estimating and , according to
- Calculating the fitting value with the time response equation, and then restoring it with the post subtraction operation, that is:
- Following the accuracy test, prediction is corrected until the error becomes minimal.
3.2. The Checking of GM (1,1) and Residual
- Residual test, calculated separately:Residual: ;Relative residual: .
- A posteriori error test, calculated separately:mean value: ;variance: ;Mean value of residuals: ;The variance of residuals: ;Posterior error ratio: ;Small error probability: .
- The comparison table of prediction accuracy grades is shown in Table 2.
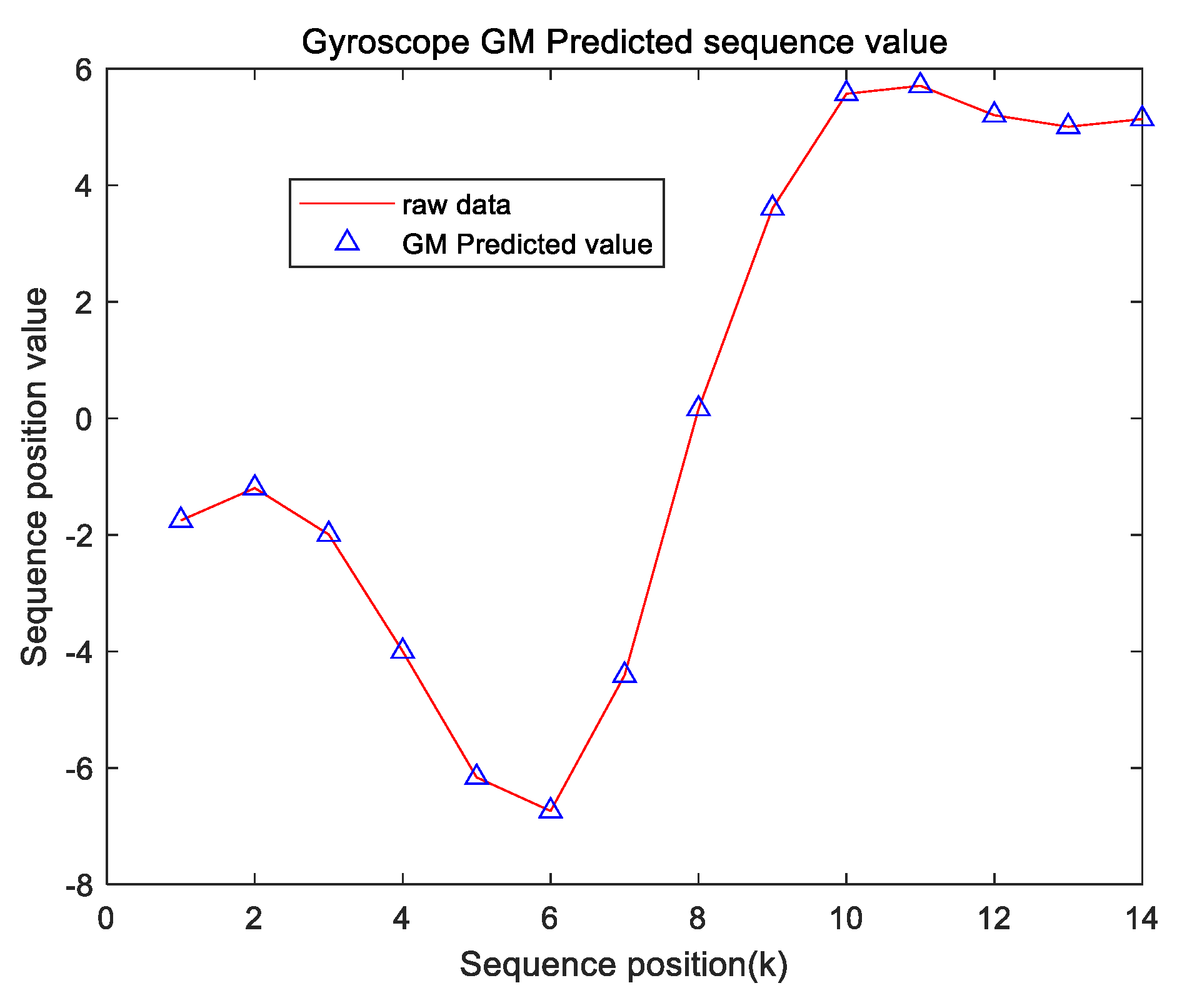
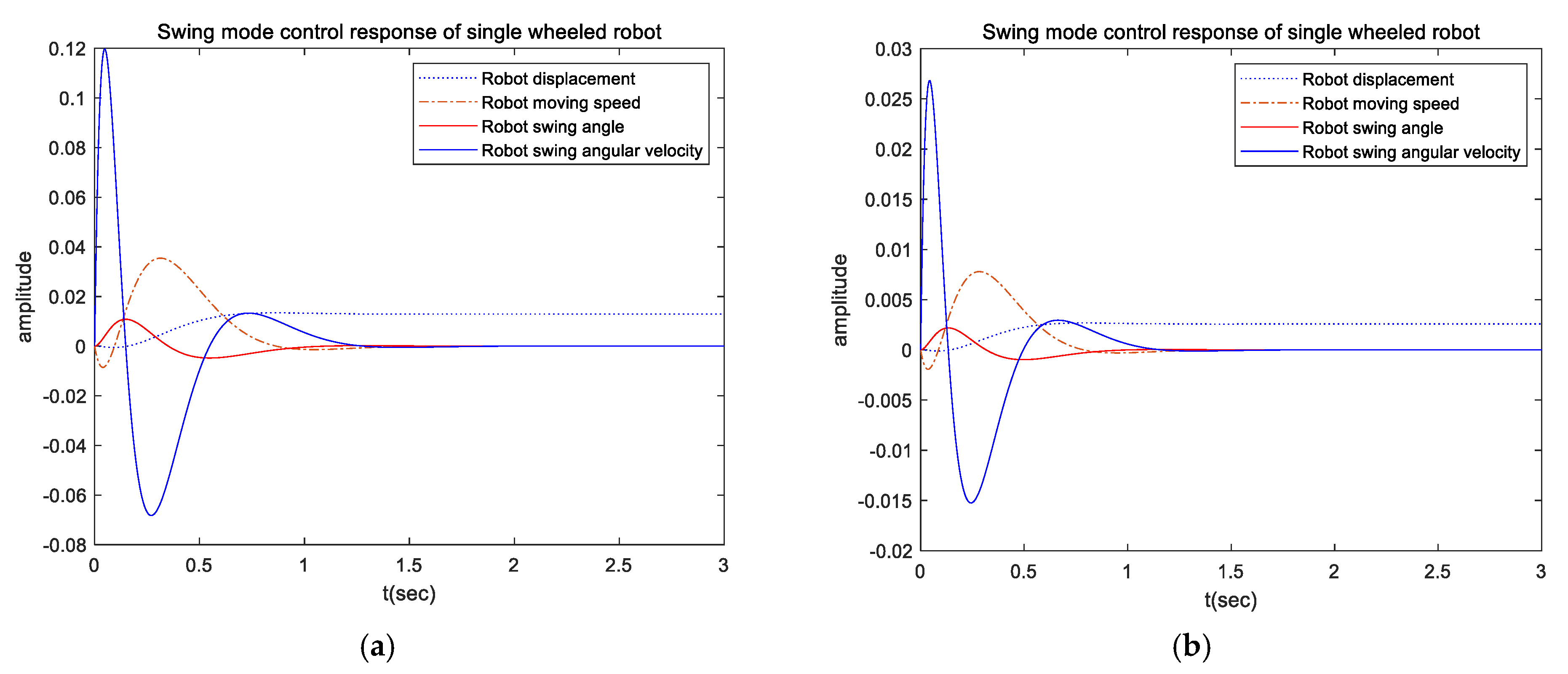
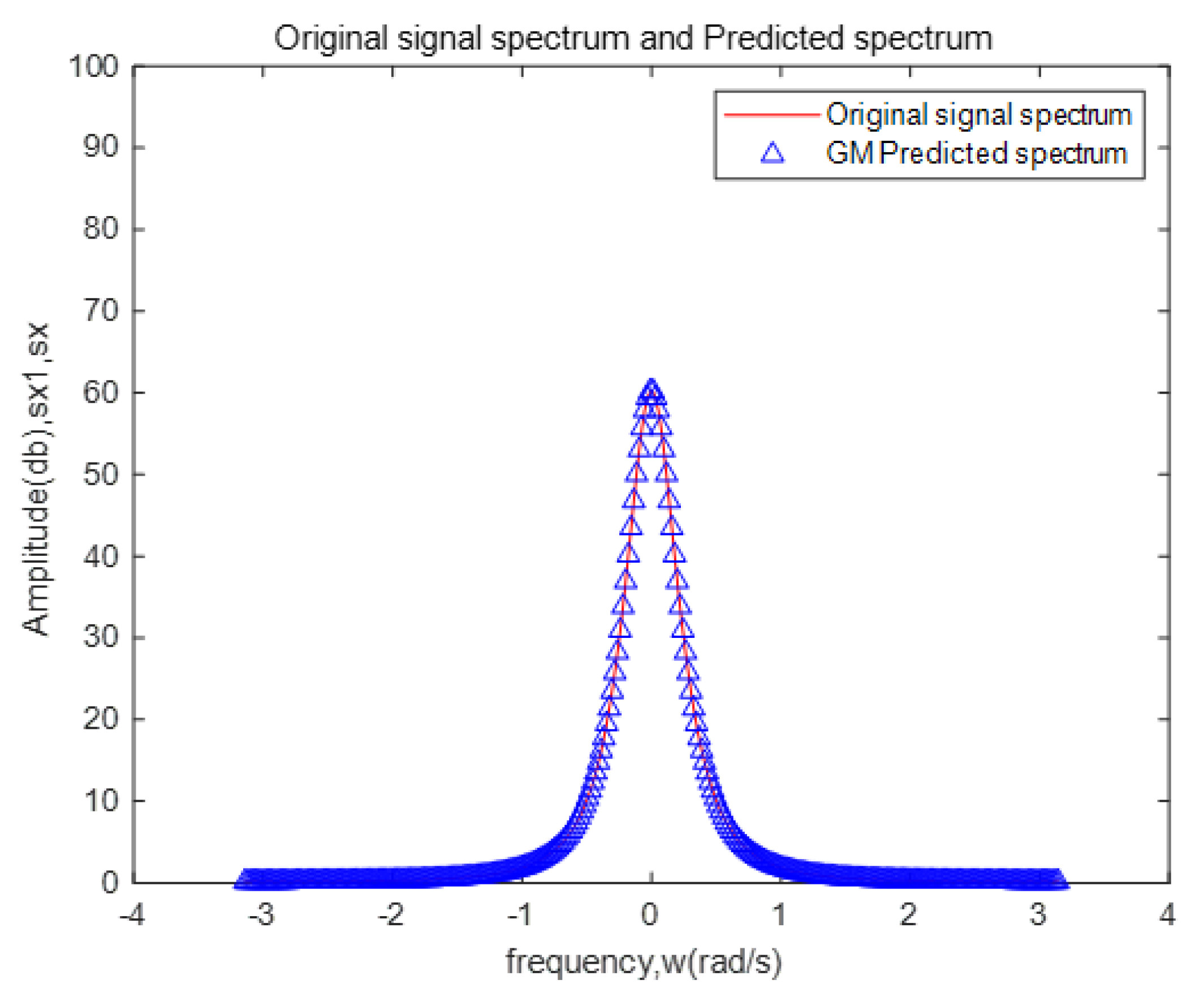
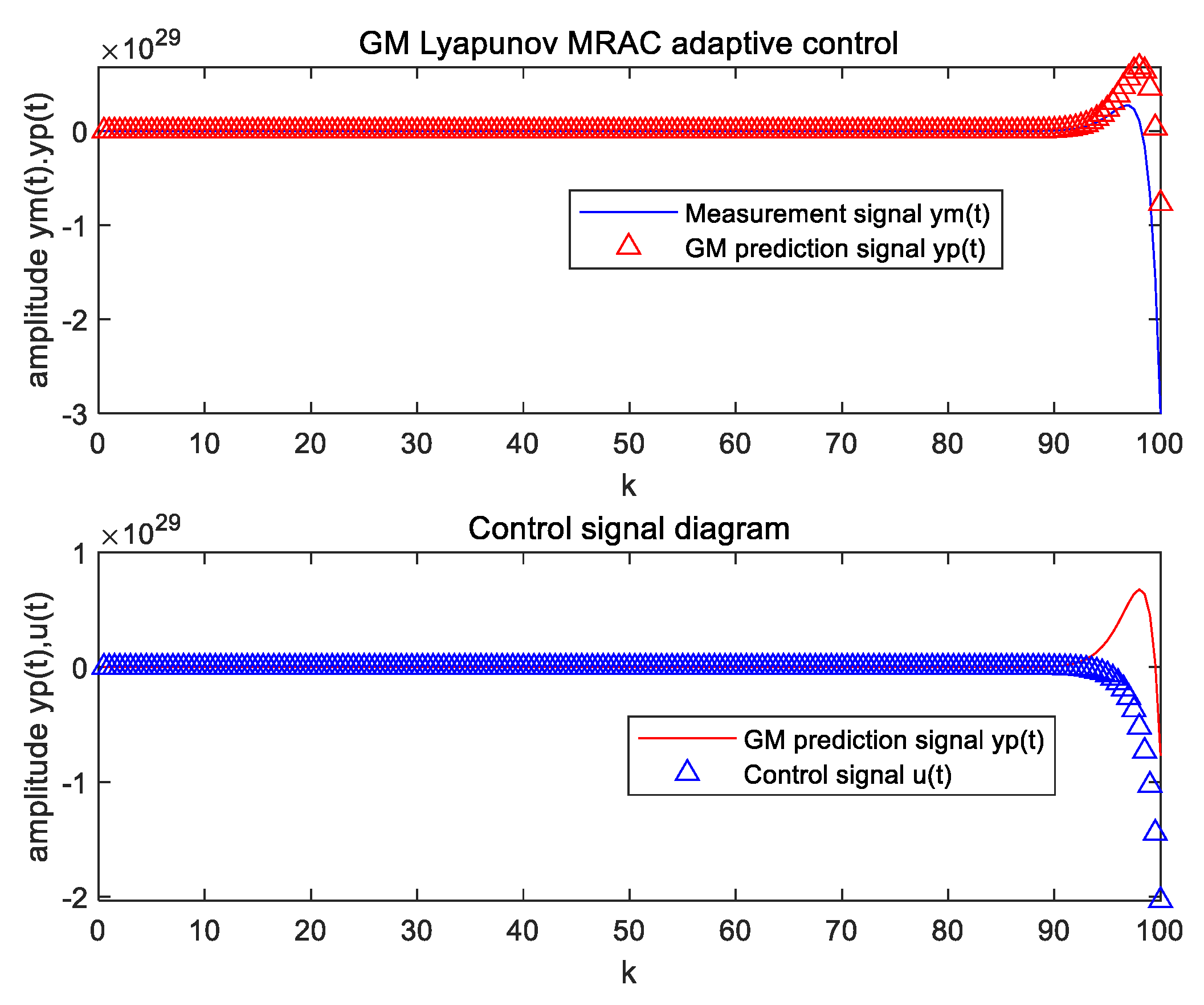
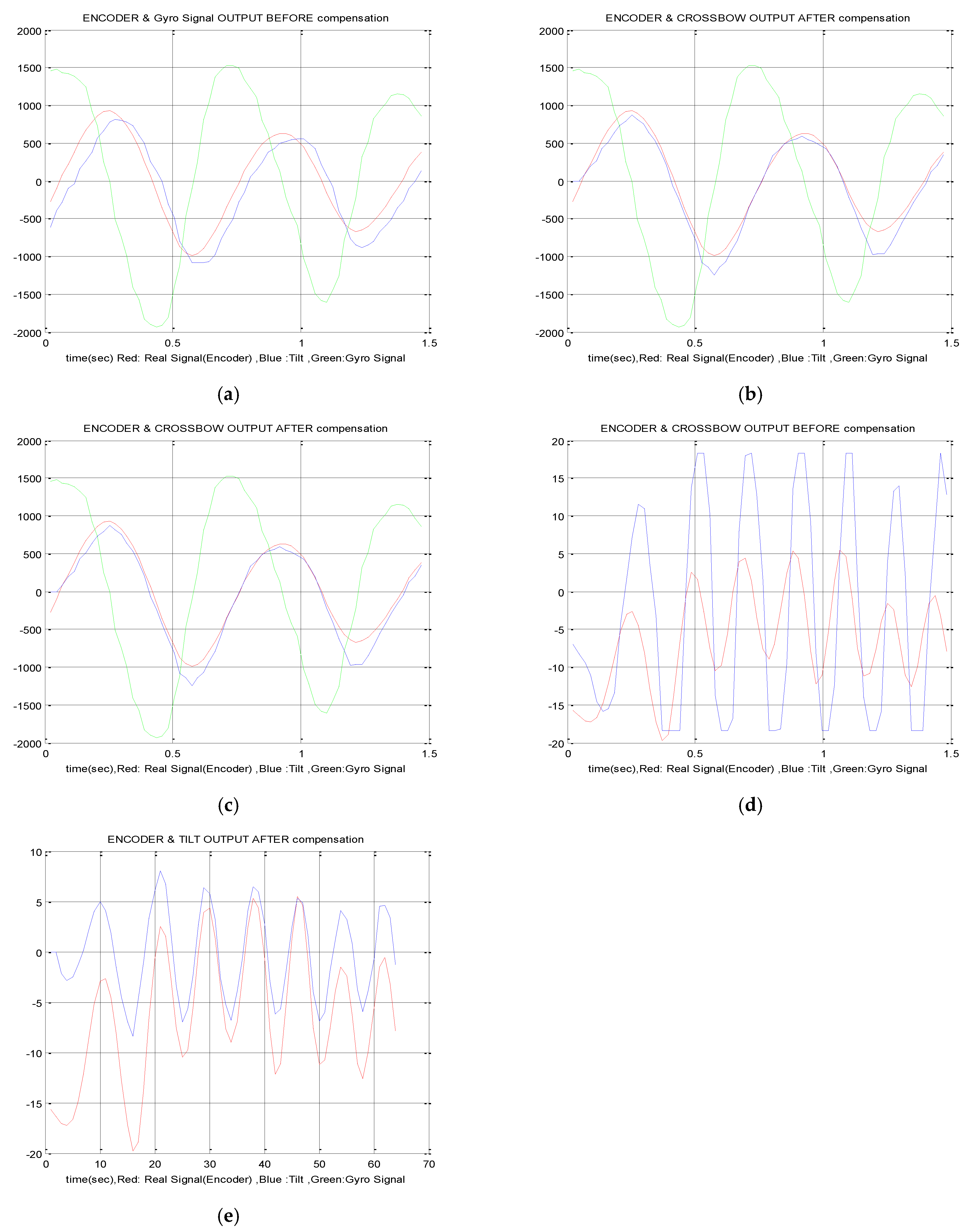
4. Simulation and Verification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, H.B.; Xu, Y. A single-wheel, gyroscopically stabilized robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; pp. 3658–3663. [Google Scholar]
- Nakajima, R.; Tsubouchi, T.; Yuta, S.; Koyanagi, E. A development of a new mechanism of an autonomous unicycle. In Proceedings of the the 1997 IEEE/RSJ International Conference on Intelligent Robot and Systems, Innovative Robotics for Real-World Applications, IROS’97, Grenoble, France, 11 September 1997; pp. 906–912. [Google Scholar]
- Okumura, J.; Takei, T.; Tsubouchi, T. Path tracking of an unicycle robot with a wide-type wheel aimed for navigation. In Proceedings of the 2010 11th IEEE International Workshop on Advanced Motion Control (AMC), Nagaoka, Japan, 21March 2010; pp. 268–272. [Google Scholar]
- Wu, C.-W.; Hwang, C.-K. A novel spherical wheel driven by Omni wheels. In Proceedings of the 2008 International Conference on Machine Learning and Cybernetics, Kunming, China, 12–15 July 2008; pp. 3800–3803. [Google Scholar]
- Wu, C.-W.; Huang, K.-S.; Hwang, C.-K. A novel spherical wheel driven by chains with guiding wheels. In Proceedings of the 2009 International Conference on Machine Learning and Cybernetics, Baoding, China, 12–15 July 2009; pp. 3242–3245. [Google Scholar]
- Patel, N.P.; Parikh, D.R.; Patel, D.A.; Patel, R.R. AI and web-based human-like interactive university chatbot (UNIBOT). In Proceedings of the 2019 3rd International conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 148–150. [Google Scholar]
- Ram, R.; Pathak, P.; Junco, S. Inverse kinematics of mobile manipulator using bidirectional particle swarm optimization by manipulator decoupling. Mech. Mach. Theory 2019, 131, 385–405. [Google Scholar] [CrossRef]
- Wang, L.; Pei, W.; Li, X.; Zhou, J. Research on Distributed Integrated Control Method for Wheeled Mobile Robot with Skid Steering. In Proceedings of the ISCSIC 2020: 2020 4th International Symposium on Computer Science and Intelligent Control, Newcastle upon Tyne, UK, 17–19 November 2020. [Google Scholar]
- Xu, Y.; Ou, Y. Control of Single Wheel Robots; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Wheeler, N.J.; Jones, K.S. Kinematics affect people’s judgments of a wheeled robot’s ability to climb a stair. Int. J. Soc. Robot. 2021, 13, 117–128. [Google Scholar] [CrossRef]
- Bayar, G.; Ozturk, S. Investigation of The Effects of Contact Forces Acting on Rollers Of a Mecanum Wheeled Robot. Mechatronics 2020, 72, 102467. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, W.; Zou, Y.; Ou, B.; Xun, Z. Piezoelectric-driven miniature wheeled robot based on flexible transmission mechanisms. Microsyst. Technol. 2018, 24, 943–950. [Google Scholar] [CrossRef]
- Li, Z.; Deng, J.; Lu, R.; Xu, Y.; Bai, J.; Su, C.-Y. Trajectory-tracking control of mobile robot systems incorporating neural-dynamic optimized model predictive approach. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 740–749. [Google Scholar] [CrossRef]
- Mathew, N.J.; Rao, K.K.; Sivakumaran, N. Swing Up and Stabilization Control of a Rotary Inverted Pendulum. IFAC Proc. Vol. 2013, 46, 654–659. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Kwon, S. Dynamic modeling of a two-wheeled inverted pendulum balancing mobile robot. Int. J. Control. Autom. Syst. 2015, 13, 926–933. [Google Scholar] [CrossRef]
- Anoohya, B.B.; Padhi, R. Trajectory Tracking of Autonomous Mobile Robots Using Nonlinear Dynamic Inversion. IFAC-PapersOnLine 2018, 51, 202–207. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, X.; Xiao, Y.; Huang, J. Sensorimotor self-learning model based on operant conditioning for two-wheeled robot. J. Shanghai Jiaotong Univ. (Sci.) 2017, 22, 148–155. [Google Scholar] [CrossRef]
- Ruan, X.; Chen, J.; Dai, L. Motor Learning Based on the Cooperation of Cerebellum and Basal Ganglia for a Self-Balancing Two-Wheeled Robot. Intell. Control. Autom. 2011, 2, 12. [Google Scholar] [CrossRef] [Green Version]
- El-Bardini, M.; El-Nagar, A.M. Interval type-2 fuzzy PID controller for uncertain nonlinear inverted pendulum system. ISA Trans. 2014, 53, 732–743. [Google Scholar] [CrossRef]
- Liu, X.; Peng, H.; Bai, Y.; Zhu, Y.; Liao, L. Tourism Flows Prediction based on an Improved Grey GM(1,1) Model. Procedia-Soc. Behav. Sci. 2014, 138, 767–775. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Luo, W.; Wang, Z.; Meng, H. Research on Highway Tunnel Ventilation Control Based on Internet of Things and Grey Prediction Algorithm. In Proceedings of the 2020 International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 25–27 September 2020. [Google Scholar]
- Wardana, A.A.; Takaki, T.; Jiang, M.; Ishii, I. Development of a single-wheeled inverted pendulum robot capable of climbing stairs. Adv. Robot. 2020, 34, 674–688. [Google Scholar] [CrossRef]
- Jin, H.; Wang, T.; Yu, F.; Zhu, Y.; Zhao, J.; Lee, J. Unicycle Robot Stabilized by the Effect of Gyroscopic Precession and Its Control Realization Based on Centrifugal Force Compensation. IEEE/ASME Trans. Mechatron. 2016, 21, 2737–2745. [Google Scholar] [CrossRef]
- Forouhar, M.; Abedin-Nasab, M.H.; Liu, G. Introducing GyroSym: A single-wheel robot. Int. J. Dyn. Control 2020, 8, 404–417. [Google Scholar] [CrossRef]
- Lee, S.; Jung, S. Detection and control of a gyroscopically induced vibration to improve the balance of a single-wheel robot. J. Low Freq. Noise Vib. Act. Control 2017, 37, 443–455. [Google Scholar] [CrossRef]
- Nguyen, P.L.; Nguyen, T.P.; Ngo, T.M. Balancing control for single-wheel unicycle Robot using the Sliding mode controller. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1109, 012020. [Google Scholar] [CrossRef]
- Zarei, F.; Moosavian, S.A.A.; Najafi, A. Force Analysis of a Spherical Single-wheeled Robot. In Proceedings of the 2018 6th RSI International Conference on Robotics and Mechatronics (IcRoM), Tehran, Iran, 23–25 October 2018; pp. 542–547. [Google Scholar]
- Ashwani, K.; Piyush, D.; Priyanka, S. Anti-Swing and Position Control of Single Wheeled Inverted Pendulum Robot (SWIPR). Int. J. Appl. Evol. Comput. (IJAEC) 2018, 9, 37–47. [Google Scholar] [CrossRef]
- Zad, H.S.; Ulasyar, A. Adaptive control of self-balancing two-wheeled robot system based on online model estimation. In Proceedings of the 2017 10th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017; pp. 876–880. [Google Scholar]
- George, T.; Ganesan, V. Optimal tuning of PID controller in time delay system: A review on various optimization techniques. J.Chem. Prod. Process. Model. 2020, 20202001. [Google Scholar] [CrossRef]
- Venugopal, K.R.; Srinivasa, K.G.; Patnaik, L.M. Soft Computing for Data Mining Applications; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Qian, Q.; Wu, J.; Wang, Z. Dynamic balance control of two-wheeled self-balancing pendulum robot based on adaptive machine learning. Int. J. Wavelets Multiresolut. Inf. Process. 2020, 18, 1941002. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Li, D.-D.; Zheng, H.-H. Model comparison of GM(1,1) and DGM(1,1) based on Monte-Carlo simulation. Phys. A Stat. Mech. Appl. 2020, 542, 123341. [Google Scholar] [CrossRef]
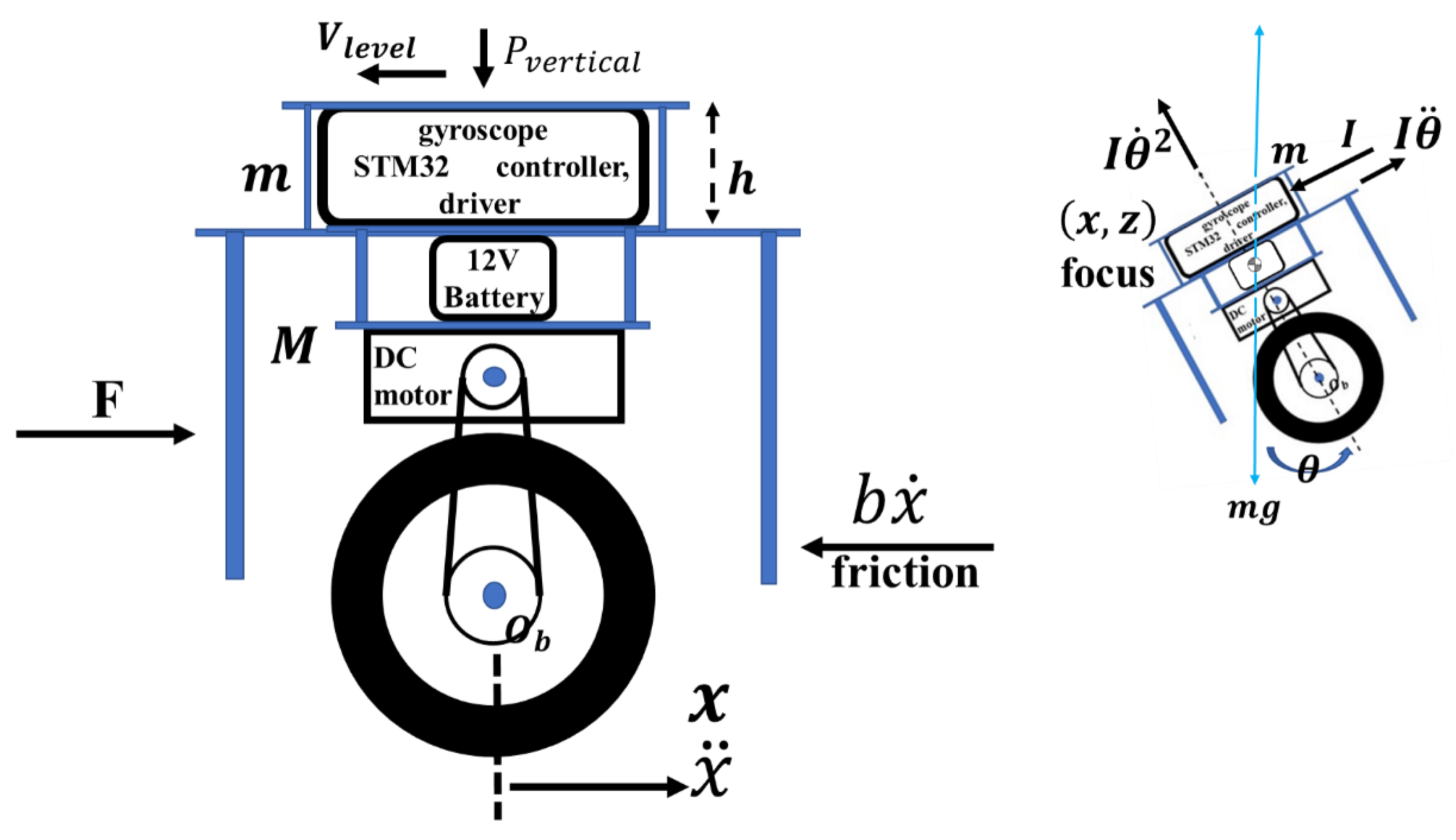


| Name of Parameters | Unit |
|---|---|
| Robot body Weight (m) | Kg |
| Robot lower body weight (M) | Kg |
| Operating friction coefficient (b) | N/(m/s) |
| Vehicle body to center Swing length (h) | M |
| Body swing inertia (I) | Kg |
| Vehicle body External force pushed (F) | N |
| Robot position (x) | kg |
| Robot body Swing angle (θ) | rad |
| Gravitational acceleration (g) | m/s2 |
| Prediction Accuracy Level | Probe | C |
|---|---|---|
| good | >0.95 | <0.35 |
| qualified | >0.80 | <0.45 |
| reluctantly | >0.70 | <0.50 |
| unqualified | ≤0.70 | ≥0.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.-L.; Chen, C.-Y.; Wen, C.-H.; Liao, P.-H.; Chen, K.-J. Advanced Proportional-Integral-Derivative Control Compensation Based on a Grey Estimated Model in Dynamic Balance of Single-Wheeled Robot. Axioms 2021, 10, 326. https://doi.org/10.3390/axioms10040326
Chen M-L, Chen C-Y, Wen C-H, Liao P-H, Chen K-J. Advanced Proportional-Integral-Derivative Control Compensation Based on a Grey Estimated Model in Dynamic Balance of Single-Wheeled Robot. Axioms. 2021; 10(4):326. https://doi.org/10.3390/axioms10040326
Chicago/Turabian StyleChen, Mao-Lin, Chun-Yen Chen, Chien-Hung Wen, Pin-Hao Liao, and Kai-Jung Chen. 2021. "Advanced Proportional-Integral-Derivative Control Compensation Based on a Grey Estimated Model in Dynamic Balance of Single-Wheeled Robot" Axioms 10, no. 4: 326. https://doi.org/10.3390/axioms10040326
APA StyleChen, M.-L., Chen, C.-Y., Wen, C.-H., Liao, P.-H., & Chen, K.-J. (2021). Advanced Proportional-Integral-Derivative Control Compensation Based on a Grey Estimated Model in Dynamic Balance of Single-Wheeled Robot. Axioms, 10(4), 326. https://doi.org/10.3390/axioms10040326






