New Estimation Method of an Error for J Iteration

Abstract

The major aim of this article is to show how to estimate direct errors using the J iteration method. Direct error estimation of iteration processes is being investigated in different journals. We also illustrate that an error in the J iteration process can be controlled. Furthermore, we express J iteration convergence by using distinct initial values.

1. Introduction

Fixed point theory combines analysis, topology, and geometry in a unique way. Fixed point technology in particular applies to biology, chemistry, economics, gaming, and physics. Once the existence of a fixed point of a mapping has been established, determining the value of that fixed point is a difficult task, which is why we employ iteration procedures to do so. Iterative algorithms are utilized for the computation of approximate solutions of stationary and evolutionary problems associated with differential equations. A lot of iterative processes have been established, and it is difficult to cover each one. A famous Banach’s contraction theorem uses Picard’s iterative procedure to approach a fixed point. Other notable iterative methods can be found in references [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Fastest convergent methodes can be seen in references [15,16,17,18,19,20,21,22,23,24,25]. Also for errors, stability and Data dependency of different iteration proess can be seen in references [26,27,28].

In an iteration process, “rate of convergence”, “stability”, and “error” all play important roles. According to Rhoades [4], the Mann iterative model converges faster than the Ishikawa iterative procedure for decreasing functions, whereas the Ishikawa iteration method is preferable for increasing functions. In addition, it appears that the Mann iteration process is unaffected by the starting prediction. Liu [2] first proposed the Mann iteration procedure with errors in 1995. One of the authors, Xu [6], recently pointed out that Liu’s definition, which is based on the convergence of error terms, is incompatible with randomness because error terms occur at random. As a result, Xu created new types of random error Mann and Ishikawa iterative processes. Agarwal [3] demonstrated results for contraction mappings, where the Agarwal iteration process converges at the same rate as the Picard iteration process and quicker than the Mann iteration process. For quasi-contractive operators in Banach spaces, Chugh [7] defined that the CR iteration process is equivalent to and faster than the Picard, Mann, Ishikawa, Agarwal, Noor, and SP iterative processes. The authors in [5] demonstrated that for the class of contraction mappings, the CR iterative process converges faster than the $S^{*}$ iterative process. The authors showed in [18] that for the class of Suzuki generalized nonexpansive mappings, the Thakur iteration process converges quicker than the Picard, Mann, Ishikawa, Agarwal, Noor, and Abbas iteration processes. Abbas [1] offers numerical examples to illustrate that their iterative process is more quickly convergent than existing iterative processes for non-expansive mapping. In [19], the study shows that the $M^{*}$ iterative method has superior convergence than the iterative procedures in [1]. In [20], another iteration technique, M, is proposed, and its convergence approach was better than to those of Agarwal and [1]. In [11], a new iterative algorithm, known as the K iterative algorithm, was introduced, demonstrating that it is faster than the previous iterative techniques in achieving convergence. The study also demonstrated that their method is T-stable. In [17], the authors devised a novel iterative process termed “$K^{*}$” and demonstrated the convergence rate and stability of their iterative method. Recently, in [12], a new iterative scheme, namely, the “J” iterative algorithm, was developed. They have proved the convergence rate and stability for their iteration process.

The following question arises: Is the direct error estimate of the iterative process in [12] bounded and controllable?

The error of the “J” iteration algorithm is estimated in this article, and it is shown that this estimation for the iteration process in [12] is also bounded and controlled. Furthermore, as shown in [4], certain iterative processes converge to increase function while others converge to decrease function. The initial value selection affects the convergence of these iterative processes. For any initial value, we present a numerical example to support the analytical finding and to demonstrate that the J iteration process has a higher convergence rate than the other iteration methods mentioned above.

2. Preliminaries

Definition 1

([15]). If for each $ϵ\in$ (0,2] $\exists \delta >$ 0 s.t for r,s $\in X$ having $\parallel r\parallel \le 1$ and $\parallel s\parallel \le 1,\parallel r-s\parallel >ϵ$ $\Rightarrow \parallel \frac{r+s}{2}\parallel \le \delta$, then X is called uniformly convex.

Definition 2

([17]). Let ${\left\{u_n\right\}}_{n=0}^{\infty }$ be a random sequence in M. The iteration technique $r_{n+1}=f(F,r_n)$ is said to be F-stable if it converges to a fixed point p. Consider for ${ϵ}_n=\parallel t_n+1-f(F:u_n)\parallel ,n\in N$, $\Rightarrow li{m}_{n\to \infty }ϵ=0$ if $li{m}_{n\to \infty }{u}_n=p$.

Definition 3

([10]). Consider F and $\tilde{F}:X\to X$ are contraction map. If for some $ϵ>$ 0, then $\tilde{F}$ is an approximate contraction for F. We have $\parallel Fx-\tilde{F}x\parallel \le ϵ$ for all $x\in X$.

Definition 4

([10]). Let ${\left\{r_n\right\}}_{n=0}^{\infty }$ and ${\left\{s_n\right\}}_{n=0}^{\infty }$ be two different fixed point I.M that approach to unique fixed point p and $\parallel r_n-p\parallel \le j_n$ and $\parallel s_n-p\parallel \le k_n$, for all $n\ge$ 0. If the sequence ${\left\{j_n\right\}}_{n=0}^{\infty }$ and ${\left\{k_n\right\}}_{n=0}^{\infty }$ approaches to j and k, respectively, and $li{m}_{n\to \infty }\frac{\parallel j_n-j\parallel }{\parallel k_n-k\parallel }=0$, then ${\left\{r_n\right\}}_{n=0}^{\infty }$ approaches faster than ${\left\{s_n\right\}}_{n=0}^{\infty }$ to p.

3. Estimation of an Error for J Scheme

We will suppose all through this section that $(X,|.\left|\right)$ is a real-valued Banach space that can be selected randomly. S is a subspace of X, which is closed as well as convex, also let a mapping F: S → S, which is nonexpensive, and ${\left\{{\alpha }_n\right\}}_{n=0}^{\infty }$ and ${\left\{{\beta }_n\right\}}_{n=0}^{\infty }\in$ [0 1] are parameter sequences that satisfy specific control constraints.

We primarily wish to assess the J iterative method’s error estimates in X, defined in [12].

$$\left\{\begin{array}{cc}{x}_0\in C& \\ z_n=F((1-{\beta }_n)x_n+{\beta }_{n}F{x}_n)& \\ y_n=F((1-{\alpha }_n)z_n+{\alpha }_{n}F{z}_n)& \\ x_{n+1}=F\left(y_n\right)\end{array}\right.$$

(1)

Many researchers have come close to achieving this goal in a roundabout way. A few publications in the literature have recently surfaced in terms of their direct computations (estimation). As direct error estimation in [15,16,28]. In reference [9], the authors have calculated direct error estimation for the iteration process defined in [28]. We have established an approach for the direct estimate of the J iteration error in terms of accumulation in this article. It should be emphasized that this method’s direct error calculations are significantly more complex than the iteration process as in [26,27].

Define the errors of $F{x}_n,F{y}_n$, and $F{z}_n$ by:

$$p_n=F{x}_n-\overline{F{x}_n},q_n=F{y}_n-\overline{F{y}_n},r_n=F{z}_n-\overline{F{z}_n}$$

(2)

for all $n\in \mathbf{N}$, where $\overline{F{x}_n},\overline{F{y}_n}$, and $\overline{F{z}_n}$ are the exact values of $F{x}_n,F{y}_n$, and $F{z}_n$, respectively, that is, $F{x}_n,F{y}_n$, and $F{z}_n$ are approximate values of $\overline{F{x}_n},\overline{F{y}_n}$, and $\overline{F{z}_n}$, respectively. The theory of errors implies that ${\left\{p_n\right\}}_{n=0}^{\infty },{\left\{q_n\right\}}_{n=0}^{\infty }$, and ${\left\{r_n\right\}}_{n=0}^{\infty }$ are bounded. Set:

$$M=max\{M_p,M_q,M_r\}$$

(3)

where $M_p={sup}_{n\in N}\parallel p_n\parallel ,M_q={sup}_{n\in N}\parallel q_n\parallel$ and $M_r={sup}_{n\in N}\parallel r_n\parallel$ are the absolute error boundaries of ${\left\{F{x}_n\right\}}_{n=0}^{\infty },{\left\{F{y}_n\right\}}_{n=0}^{\infty }$, and ${\left\{F{z}_n\right\}}_{n=0}^{\infty }$, respectively, and (1) has accumulated errors as a result of $p_n,q_n$, and $r_n$, hence we can set:

$$\left\{\begin{array}{cc}\overline{x_0}\in C,& \\ \overline{z_n}=\overline{F}((1-{\beta }_n)\overline{x_n}+{\beta }_n\overline{F{x}_n}),& \\ \overline{y_n}=\overline{F}((1-{\alpha }_n)\overline{z_n}+{\alpha }_n\overline{F{z}_n}),& \\ \overline{x_{n+1}}=\overline{F{y}_n}.\end{array}\right.$$

(4)

where $\overline{x_n},\overline{y_n}$, and $\overline{z_n}$ are exact values of $x_n,y_n$, and $z_n$, respectively. Obviously, each iteration error will affect the next (n+1) steps. Now, for the initial step in x, y, z, we have:

$$\parallel x_0\parallel =\parallel \overline{x_0}\parallel .$$

(5)

Now for the z term we have:

$$\begin{array}{c}\parallel z_0-\overline{z_0}\parallel =\parallel F((1-{\beta }_0)x_0+{\beta }_{0}F{x}_0)-\overline{F}((1-{\beta }_0)\overline{x_0}+{\beta }_0\overline{F{x}_0})\parallel \hfill \\ =\parallel F((1-{\beta }_0)x_0+{\beta }_{0}F{x}_0)-F((1-{\beta }_0)\overline{x_0}+{\beta }_0\overline{F{x}_0})+F((1-{\beta }_0)\overline{x_0}\hfill \\ +{\beta }_0\overline{F{x}_0})-\overline{F}((1-{\beta }_0)\overline{x_0}+{\beta }_0\overline{F{x}_0})\parallel \hfill \\ \le \parallel F((1-{\beta }_0)x_0+{\beta }_{0}F{x}_0)-F((1-{\beta }_0)\overline{x_0}+{\beta }_0\overline{F{x}_0})\parallel +\parallel F((1-{\beta }_0)\overline{x_0}\hfill \\ +{\beta }_0\overline{F{x}_0})-\overline{F}((1-{\beta }_0)\overline{x_0}+{\beta }_0\overline{F{x}_0})\parallel \hfill \\ \le \parallel F((1-{\beta }_0)x_0+{\beta }_{0}F{x}_0)-F((1-{\beta }_0)\overline{x_0}+{\beta }_0\overline{F{x}_0})\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel z_0-\overline{z_0}\parallel =\parallel ((1-{\beta }_0)x_0+{\beta }_{0}F{x}_0)-((1-{\beta }_0)\overline{x_0}+{\beta }_0\overline{F{x}_0})\parallel +ϵ\hfill \\ =\parallel ((1-{\beta }_0)(x_0-\overline{x_0})+{\beta }_0(F{x}_0-\overline{F{x}_0})\parallel +ϵ,\hfill \end{array}$$

from (2) and (5) we have:

$$\parallel z_0-\overline{z_0}\parallel ={\beta }_0\parallel p_0\parallel +ϵ.$$

(6)

Now, for the y term, we have:

$$\begin{array}{c}\parallel y_0-\overline{y_0}\parallel =\parallel F((1-{\alpha }_0)z_0+{\alpha }_{0}F{z}_0)-\overline{F}((1-{\alpha }_0)\overline{z_0}+{\alpha }_0\overline{F{z}_0})\parallel \hfill \\ =\parallel F((1-{\alpha }_0)z_0+{\alpha }_{0}F{z}_0)-F((1-{\alpha }_0)\overline{z_0}+{\alpha }_0\overline{F{z}_0})+F((1-{\alpha }_0)\overline{z_0}\hfill \\ +{\alpha }_0\overline{F{z}_0})-\overline{F}((1-{\alpha }_0)\overline{z_0}+{\alpha }_0\overline{F{z}_0})\parallel \hfill \\ \le \parallel F((1-{\alpha }_0)z_0+{\alpha }_{0}F{z}_0)-F((1-{\alpha }_0)\overline{z_0}+{\alpha }_0\overline{F{z}_0})\parallel +\parallel F((1-{\alpha }_0)\overline{z_0}\hfill \\ +{\alpha }_0\overline{F{z}_0})-\overline{F}((1-{\alpha }_0)\overline{z_0}+{\alpha }_0\overline{F{z}_0})\parallel \hfill \\ \le \parallel F((1-{\alpha }_0)z_0+{\alpha }_{0}F{z}_0)-F((1-{\alpha }_0)\overline{z_0}+{\alpha }_0\overline{F{z}_0})\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel y_0-\overline{y_0}\parallel =\parallel ((1-{\alpha }_0)z_0+{\alpha }_{0}F{z}_0)-((1-{\alpha }_0)\overline{z_0}+{\alpha }_0\overline{F{z}_0})\parallel +ϵ\hfill \\ =\parallel (1-{\alpha }_0)(z_0-\overline{z_0})+{\alpha }_0(F{z}_0-\overline{F{z}_0})\parallel +ϵ,\hfill \end{array}$$

from (2) and (6), we have:

$$\begin{array}{c}\parallel y_0-\overline{y_0}\parallel =(1-{\alpha }_0)({\beta }_0\parallel p_0\parallel +ϵ)+{\alpha }_0\parallel r_0\parallel +ϵ\hfill \\ =(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel +(1-{\alpha }_0)ϵ+ϵ\hfill \\ =(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel +{ϵ}^{{}^{\prime }},\hfill \end{array}$$

hence:

$$\parallel y_0-\overline{y_0}\parallel =(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel +ϵ.$$

(7)

Now, for an error in the first step of x, y, z, we have the following:

Firstly, for x, we have:

$$\begin{array}{c}\parallel x_1-\overline{x_1}\parallel =\parallel F{y}_0-\overline{F{y}_0}\parallel \hfill \\ =\parallel F{y}_0-F\overline{y_0}+F\overline{y_0}-\overline{F{y}_0}\parallel \hfill \\ \le \parallel F{y}_0-F\overline{y_0}\parallel +|F\overline{y_0}-\overline{F{y}_0}\parallel \hfill \\ \le \parallel F{y}_0-F\overline{y_0}\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\parallel x_1-\overline{x_1}\parallel =\parallel y_0-\overline{y_0}\parallel +ϵ,$$

from (2) and (7), we have:

$$\begin{array}{c}\parallel x_1-\overline{x_1}\parallel =(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel +ϵ+ϵ\hfill \\ =(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel +{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\parallel x_1-\overline{x_1}\parallel =(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel +ϵ.$$

(8)

Now, for y, we have:

$$\begin{array}{c}\parallel y_1-\overline{y_1}\parallel =\parallel F((1-{\alpha }_1)z_1+{\alpha }_{1}F{z}_1)-\overline{F}((1-{\alpha }_1)\overline{z_1}+{\alpha }_1\overline{F{z}_1})\parallel \hfill \\ =\parallel F((1-{\alpha }_1)z_1+{\alpha }_{1}F{z}_1)-F((1-{\alpha }_1)\overline{z_1}+{\alpha }_1\overline{F{z}_1})+F((1-{\alpha }_1)\overline{z_1}+\hfill \\ {\alpha }_1\overline{F{z}_1})-\overline{F}((1-{\alpha }_1)\overline{z_1}+{\alpha }_1\overline{F{z}_1})\parallel \hfill \\ \le \parallel F((1-{\alpha }_1)z_1+{\alpha }_{1}F{z}_1)-F((1-{\alpha }_1)\overline{z_1}+{\alpha }_1\overline{F{z}_1})\parallel +\parallel F((1-{\alpha }_1)\overline{z_1}\hfill \\ +{\alpha }_1\overline{F{z}_1})-\overline{F}((1-{\alpha }_1)\overline{z_1}+{\alpha }_1\overline{F{z}_1})\parallel \hfill \\ \le \parallel F((1-{\alpha }_1)z_1+{\alpha }_{1}F{z}_1)-F((1-{\alpha }_1)\overline{z_1}+{\alpha }_1\overline{F{z}_1})\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel y_1-\overline{y_1}\parallel =\parallel ((1-{\alpha }_1)z_1+{\alpha }_{1}F{z}_1)-((1-{\alpha }_1)\overline{z_1}+{\alpha }_1\overline{F{z}_1})\parallel +ϵ\hfill \\ =(1-{\alpha }_1)\parallel z_1-\overline{z_1}\parallel +{\alpha }_1\parallel F{z}_1-\overline{F{z}_1}\parallel +ϵ,\hfill \end{array}$$

from (2) and (8), we have:

$$\begin{array}{c}\parallel y_1-\overline{y_1}\parallel =(1-{\alpha }_1)((1-{\alpha }_1)(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +(1-{\beta }_1){\alpha }_0\parallel r_0\parallel +{\beta }_1\parallel p_1\parallel +ϵ)\hfill \\ +{\alpha }_1\parallel r_1\parallel +ϵ\hfill \\ ={\alpha }_1\parallel r_1\parallel +(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_1)(1-{\alpha }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]\hfill \\ +(1-{\alpha }_1)ϵ+ϵ\hfill \\ ={\alpha }_1\parallel r_1\parallel +(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_1)(1-{\alpha }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\begin{array}{c}\parallel y_1-\overline{y_1}\parallel ={\alpha }_1\parallel r_1\parallel +(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel \\ +{\alpha }_0\parallel r_0\parallel ]+ϵ.\end{array}$$

(9)

Now, for z we have,

$$\begin{array}{c}\parallel z_1-\overline{z_1}\parallel =\parallel F((1-{\beta }_1)x_1+{\beta }_{1}F{x}_1)-\overline{F}((1-{\beta }_1)\overline{x_1}+{\beta }_1\overline{F{x}_1})\parallel \hfill \\ =\parallel F((1-{\beta }_1)x_1+{\beta }_{1}F{x}_1)-F((1-{\beta }_1)\overline{x_1}+{\beta }_1\overline{F{x}_1})+F((1-{\beta }_1)\overline{x_1}\hfill \\ +{\beta }_1\overline{F{x}_1})-\overline{F}((1-{\beta }_1)\overline{x_1}+{\beta }_1\overline{F{x}_1})\parallel \hfill \\ \le \parallel F((1-{\beta }_1)x_1+{\beta }_{1}F{x}_1)-F((1-{\beta }_1)\overline{x_1}+{\beta }_1\overline{F{x}_1})\parallel +\parallel F((1-{\beta }_1)\overline{x_1}\hfill \\ +{\beta }_1\overline{F{x}_1})-\overline{F}((1-{\beta }_1)\overline{x_1}+{\beta }_1\overline{F{x}_1})\hfill \\ \le \parallel F((1-{\beta }_1)x_1+{\beta }_{1}F{x}_1)-F((1-{\beta }_1)\overline{x_1}+{\beta }_1\overline{F{x}_1})\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel z_1-\overline{z_1}\parallel =\parallel ((1-{\beta }_1)x_1+{\beta }_{1}F{x}_1)-((1-{\beta }_1)\overline{x_1}+{\beta }_1\overline{F{x}_1})\parallel +ϵ\hfill \\ =\parallel ((1-{\beta }_1)(x_1-\overline{x_1})+{\beta }_1(F{x}_1-\overline{F{x}_1})\parallel +ϵ,\hfill \end{array}$$

from (2) and (9), we have:

$$\begin{array}{c}\parallel z_1-\overline{z_1}\parallel =(1-{\beta }_1)((1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel +ϵ)+{\beta }_1\parallel p_1\parallel +ϵ\hfill \\ =(1-{\beta }_1)(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +(1-{\beta }_1){\alpha }_0\parallel r_0\parallel +{\beta }_1\parallel p_1\parallel +(1-{\beta }_1)ϵ+ϵ\hfill \\ =(1-{\beta }_1)(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +(1-{\beta }_1){\alpha }_0\parallel r_0\parallel +{\beta }_1\parallel p_1\parallel +{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\parallel z_1-\overline{z_1}\parallel =(1-{\beta }_1)(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +(1-{\beta }_1){\alpha }_0\parallel r_0\parallel +{\beta }_1\parallel p_1\parallel +ϵ.$$

(10)

Now, for an error in the second step of x, y, z, we have the following:

$$\begin{array}{c}\parallel x_2-\overline{x_2}\parallel =\parallel F{y}_1-\overline{F{y}_1}\parallel \hfill \\ =\parallel F{y}_1-F\overline{y_1}+F\overline{y_1}-\overline{F{y}_1}\parallel \hfill \\ \le \parallel F{y}_1-F\overline{y_1}\parallel +|F\overline{y_1}-\overline{F{y}_1}\parallel \hfill \\ \le \parallel F{y}_1-F\overline{y_1}\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\parallel x_2-\overline{x_2}\parallel =\parallel y_1-\overline{y_1}\parallel +ϵ,$$

from (2) and (10), we have:

$$\begin{array}{c}\parallel x_2-\overline{x_2}\parallel ={\alpha }_1\parallel r_1\parallel +(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel \hfill \\ +{\alpha }_0\parallel r_0\parallel ]+ϵ+ϵ\hfill \\ ={\alpha }_1\parallel r_{1}lo\parallel +(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel \hfill \\ +{\alpha }_0\parallel r_0\parallel ]+{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\begin{array}{c}\parallel x_2-\overline{x_2}\parallel ={\alpha }_1\parallel r_1\parallel +(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel \\ +{\alpha }_0\parallel r_0\parallel ]+ϵ.\end{array}$$

(11)

$$\begin{array}{c}\parallel z_2-\overline{z_2}\parallel =\parallel F((1-{\beta }_2)x_2+{\beta }_{2}F{x}_2)-\overline{F}((1-{\beta }_2)\overline{x_2}+{\beta }_2\overline{F{x}_2})\parallel \hfill \\ =\parallel F((1-{\beta }_2)x_2+{\beta }_{2}F{x}_2)-F((1-{\beta }_2)\overline{x_2}+{\beta }_2\overline{F{x}_2})+F((1-{\beta }_2)\overline{x_2}\hfill \\ +{\beta }_2\overline{F{x}_2})-\overline{F}((1-{\beta }_2)\overline{x_2}+{\beta }_2\overline{F{x}_2})\parallel \hfill \\ \le \parallel F((1-{\beta }_2)x_2+{\beta }_{2}F{x}_2)-F((1-{\beta }_2)\overline{x_2}+{\beta }_2\overline{F{x}_2})\parallel +\parallel F((1-{\beta }_2)\overline{x_2}\hfill \\ +{\beta }_2\overline{F{x}_2})-\overline{F}((1-{\beta }_2)\overline{x_2}+{\beta }_2\overline{F{x}_2})\parallel \hfill \\ \le \parallel F((1-{\beta }_2)x_2+{\beta }_{2}F{x}_2)-F((1-{\beta }_2)\overline{x_2}+{\beta }_2\overline{F{x}_2})\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel z_2-\overline{z_2}\parallel =\parallel ((1-{\beta }_2)x_2+{\beta }_{2}F{x}_2)-((1-{\beta }_2)\overline{x_2}+{\beta }_2\overline{F{x}_2})\parallel +ϵ\hfill \\ =\parallel ((1-{\beta }_2)(x_2-\overline{x_2})+{\beta }_2(F{x}_2-\overline{F{x}_2})\parallel +ϵ,\hfill \end{array}$$

from (2) and (11) we have:

$$\begin{array}{c}\parallel z_2-\overline{z_2}\parallel =(1-{\beta }_2)({\alpha }_1\parallel r_1\parallel +(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel \hfill \\ +{\alpha }_0\parallel r_0\parallel ]+ϵ)+{\beta }_2\parallel p_2\parallel +ϵ\hfill \\ ={\beta }_2\parallel p_2\parallel +(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+(1-{\beta }_2)ϵ+ϵ\hfill \\ ={\beta }_2\parallel p_2\parallel +(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\begin{array}{c}\parallel z_2-\overline{z_2}\parallel ={\beta }_2\parallel p_2\parallel +(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \\ +(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+ϵ.\end{array}$$

(12)

$$\begin{array}{c}\parallel y_2-\overline{y_2}\parallel =\parallel F((1-{\alpha }_2)z_2+{\alpha }_{2}F{z}_2)-\overline{F}((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})\parallel \hfill \\ =\parallel F((1-{\alpha }_2)z_2+{\alpha }_{2}F{z}_2)-F((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})+F((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})\hfill \\ -\overline{F}((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})\parallel \hfill \\ \le \parallel F((1-{\alpha }_2)z_2+{\alpha }_{2}F{z}_2)-F((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})\parallel +\parallel F((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})\hfill \\ -\overline{F}((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})\parallel \hfill \\ \le \parallel F((1-{\alpha }_2)z_2+{\alpha }_{2}F{z}_2)\hfill \\ -F((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel y_2-\overline{y_2}\parallel =\parallel ((1-{\alpha }_2)z_2+{\alpha }_{2}F{z}_2)-((1-{\alpha }_2)\overline{z_2}+{\alpha }_2\overline{F{z}_2})\parallel +ϵ\hfill \\ =\parallel (1-{\alpha }_2)(z_2-\overline{z_2})+{\alpha }_2(F{z}_2-\overline{F{z}_2})\parallel +ϵ,\hfill \end{array}$$

from (2) and (12), we have:

$$\begin{array}{c}\parallel y_2-\overline{y_2}\parallel =(1-{\alpha }_2)({\beta }_2\parallel p_2\parallel +(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+ϵ)+{\alpha }_2\parallel r_2\parallel +ϵ\hfill \\ ={\alpha }_2\parallel r_2\parallel +(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel \hfill \\ +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)\hfill \\ [(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+(1-{\alpha }_2)ϵ+ϵ\hfill \\ ={\alpha }_2\parallel r_2\parallel +(1-{\alpha }_2){\beta }_2\parallel p_2\parallel \hfill \\ +(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\begin{array}{c}\parallel y_2-\overline{y_2}\parallel ={\alpha }_2\parallel r_2\parallel +(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel \hfill \\ +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)\hfill \\ [(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+ϵ.\hfill \end{array}$$

(13)

Now, we calculate an error in third step of x, y, z as follows:

$$\begin{array}{c}\parallel x_3-\overline{x_3}\parallel =\parallel F{y}_2-\overline{F{y}_2}\parallel \hfill \\ =\parallel F{y}_2-F\overline{y_2}+F\overline{y_2}-\overline{F{y}_2}\parallel \hfill \\ \le \parallel F{y}_2-F\overline{y_2}\parallel +|F\overline{y_2}-\overline{F{y}_2}\parallel \hfill \\ \le \parallel F{y}_2-F\overline{y_2}\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel x_3-\overline{x_3}\parallel =\parallel y_2-\overline{y_2}\parallel +ϵ,\hfill \end{array}$$

from (2) and (13), we have:

$$\begin{array}{c}\parallel x_3-\overline{x_3}\parallel ={\alpha }_2\parallel r_2\parallel +(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\alpha }_2)(1-{\beta }_2)\hfill \\ (1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+ϵ+ϵ\hfill \\ ={\alpha }_2\parallel r_2\parallel +(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\alpha }_2)(1-{\beta }_2)\hfill \\ (1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\begin{array}{c}\parallel x_3-\overline{x_3}\parallel ={\alpha }_2\parallel r_2\parallel +(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\alpha }_2)\hfill \\ (1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)\hfill \\ [(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+ϵ.\hfill \end{array}$$

(14)

$$\begin{array}{c}\parallel z_3-\overline{z_3}\parallel =\parallel F((1-{\beta }_3)x_3+{\beta }_{3}F{x}_3)-\overline{F}((1-{\beta }_3)\overline{x_3}+{\beta }_3\overline{F{x}_3})\parallel \hfill \\ =\parallel F((1-{\beta }_3)x_3+{\beta }_{3}F{x}_3)-F((1-{\beta }_3)\overline{x_3}+{\beta }_3\overline{F{x}_3})+F((1-{\beta }_3)\overline{x_3}+{\beta }_3\overline{F{x}_3})\hfill \\ -\overline{F}((1-{\beta }_3)\overline{x_3}+{\beta }_3\overline{F{x}_3})\parallel \hfill \\ \le \parallel F((1-{\beta }_3)x_3+{\beta }_{3}F{x}_3)-F((1-{\beta }_3)\overline{x_3}+{\beta }_3\overline{F{x}_3})\parallel +\parallel F((1-{\beta }_3)\overline{x_3}\hfill \\ +{\beta }_3\overline{F{x}_3})-\overline{F}((1-{\beta }_3)\overline{x_3}+{\beta }_3\overline{F{x}_3})\parallel \hfill \\ \le \parallel F((1-{\beta }_3)x_3+{\beta }_{3}F{x}_3)-F((1-{\beta }_3)\overline{x_3}+{\beta }_3\overline{F{x}_3})\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel z_3-\overline{z_3}\parallel =\parallel ((1-{\beta }_3)x_3+{\beta }_{3}F{x}_3)-((1-{\beta }_3)\overline{x_3}+{\beta }_3\overline{F{x}_3})\parallel +ϵ\hfill \\ =\parallel ((1-{\beta }_3)(x_3-\overline{x_3})+{\beta }_3(F{x}_3-\overline{F{x}_3})\parallel +ϵ.\hfill \end{array}$$

Now, by using (2) and (14), we have:

$$\begin{array}{c}\parallel z_3-\overline{z_3}\parallel =(1-{\beta }_3)({\alpha }_2\parallel r_2\parallel +(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\alpha }_2)\hfill \\ (1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel \hfill \\ +{\alpha }_0\parallel r_0\parallel ]+ϵ)+{\beta }_3\parallel p_3\parallel +ϵ\hfill \\ ={\beta }_3\parallel p_3\parallel +(1-{\beta }_3){\alpha }_2\parallel r_2\parallel +(1-{\beta }_3)(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\beta }_3)(1-{\alpha }_2)\hfill \\ (1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]\hfill \\ +(1-{\beta }_3)ϵ+ϵ\hfill \\ ={\beta }_3\parallel p_3\parallel +(1-{\beta }_3){\alpha }_2\parallel r_2\parallel +(1-{\beta }_3)(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\beta }_3)(1-{\alpha }_2)\hfill \\ (1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\begin{array}{c}\parallel z_3-\overline{z_3}\parallel ={\beta }_3\parallel p_3\parallel +(1-{\beta }_3){\alpha }_2\parallel r_2\parallel +(1-{\beta }_3)(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\beta }_3)\hfill \\ (1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel \hfill \\ +{\alpha }_0\parallel r_0\parallel ]+ϵ.\hfill \end{array}$$

(15)

$$\begin{array}{c}\parallel y_3-\overline{y_3}\parallel =\parallel F((1-{\alpha }_3)z_3+{\alpha }_{3}F{z}_3)-\overline{F}((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})\parallel \hfill \\ =\parallel F((1-{\alpha }_3)z_3+{\alpha }_{3}F{z}_3)-F((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})+F((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})\hfill \\ -\overline{F}((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})\parallel \hfill \\ \le \parallel F((1-{\alpha }_3)z_3+{\alpha }_{3}F{z}_3)-F((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})\parallel +\parallel F((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})\hfill \\ -\overline{F}((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})\parallel \hfill \\ \le \parallel F((1-{\alpha }_3)z_3+{\alpha }_{3}F{z}_3)-F((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})\parallel +ϵ.\hfill \end{array}$$

As F is nonexpansive, we have:

$$\begin{array}{c}\parallel y_3-\overline{y_3}\parallel =\parallel ((1-{\alpha }_3)z_3+{\alpha }_{3}F{z}_3)-((1-{\alpha }_3)\overline{z_3}+{\alpha }_3\overline{F{z}_3})\parallel +ϵ\hfill \\ =\parallel (1-{\alpha }_3)(z_3-\overline{z_3})+{\alpha }_3(F{z}_3-\overline{F{z}_3})\parallel +ϵ,\hfill \end{array}$$

from (2) and (15), we have:

$$\begin{array}{c}\parallel y_3-\overline{y_3}\parallel =(1-{\alpha }_3)({\beta }_3\parallel p_3\parallel +(1-{\beta }_3){\alpha }_2\parallel r_2\parallel +(1-{\beta }_3)(1-{\alpha }_2){\beta }_2\parallel p_2\parallel \hfill \\ +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+ϵ)\hfill \\ +{\alpha }_3\parallel r_3\parallel +ϵ\hfill \\ ={\alpha }_3\parallel r_3\parallel +(1-{\alpha }_3){\beta }_3\parallel p_3\parallel +(1-{\alpha }_3)(1-{\beta }_3){\alpha }_2\parallel r_2\parallel +(1-{\alpha }_3)(1-{\beta }_3)\hfill \\ (1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_3)(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\alpha }_3)(1-{\beta }_3)\hfill \\ (1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_3)(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)\hfill \\ (1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+(1-{\alpha }_3)ϵ+ϵ\hfill \\ ={\alpha }_3\parallel r_3\parallel +(1-{\alpha }_3){\beta }_3\parallel p_3\parallel +(1-{\alpha }_3)(1-{\beta }_3){\alpha }_2\parallel r_2\parallel +(1-{\alpha }_3)(1-{\beta }_3)\hfill \\ (1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_3)(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel +(1-{\alpha }_3)(1-{\beta }_3)\hfill \\ (1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_3)(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)\hfill \\ (1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+{ϵ}^{\prime },\hfill \end{array}$$

hence:

$$\begin{array}{c}\parallel y_3-\overline{y_3}\parallel ={\alpha }_3\parallel r_3\parallel +(1-{\alpha }_3){\beta }_3\parallel p_3\parallel +(1-{\alpha }_3)(1-{\beta }_3){\alpha }_2\parallel r_2\parallel +(1-{\alpha }_3)\hfill \\ (1-{\beta }_3)(1-{\alpha }_2){\beta }_2\parallel p_2\parallel +(1-{\alpha }_3)(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2){\alpha }_1\parallel r_1\parallel \hfill \\ +(1-{\alpha }_3)(1-{\beta }_3)(1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1){\beta }_1\parallel p_1\parallel +(1-{\alpha }_3)(1-{\beta }_3)\hfill \\ (1-{\alpha }_2)(1-{\beta }_2)(1-{\alpha }_1)(1-{\beta }_1)[(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]+ϵ.\hfill \end{array}$$

(16)

Repeating the above process, we have:

$$\begin{array}{c}\parallel x_{n+1}-\overline{x_n+1}\parallel =\sum _{k=0}^n[(1-{\alpha }_k){\beta }_k\parallel p_k\parallel +{\alpha }_k\parallel r_k\parallel ]\left[\prod _{i=k+1}^n(1-{\alpha }_i)(1-{\beta }_i)\right]+ϵ.\hfill \end{array}$$

(17)

$$\begin{array}{c}\parallel y_n-\overline{y_n}\parallel ={\alpha }_n\parallel r_n\parallel +(1-{\alpha }_n){\beta }_n\parallel p_n\parallel +(1-{\alpha }_n)(1-{\beta }_n)\times \sum _{k=0}^n[(1-{\alpha }_k)\hfill \\ {\beta }_k\parallel p_k\parallel +{\alpha }_k\parallel r_k\parallel ]\left[\prod _{i=k+1}^n(1-{\alpha }_i)(1-{\beta }_i)\right]+ϵ\hfill \\ ={\alpha }_n\parallel r_n\parallel +(1-{\alpha }_n){\beta }_n\parallel p_n\parallel +(1-{\alpha }_n)(1-{\beta }_n)\parallel x_n-\overline{x_n}\parallel +ϵ.\hfill \end{array}$$

(18)

$$\begin{array}{c}\parallel z_n-\overline{z_n}\parallel ={\beta }_n\parallel p_n\parallel +(1-{\beta }_n)\times \sum _{k=0}^n[(1-{\alpha }_k){\beta }_k\parallel p_k\parallel +{\alpha }_k\parallel r_k\parallel \left]\right[\prod _{i=k+1}^n(1-{\alpha }_i)\hfill \\ (1-{\beta }_i)]+ϵ\hfill \\ ={\beta }_n\parallel p_n\parallel +(1-{\beta }_n)\parallel x_n-\overline{x_n}\parallel +ϵ.\hfill \end{array}$$

(19)

Define:

$$\begin{array}{c}{E}_n^{\left(1\right)}:=\parallel x_{n+1}-\overline{x_n+1}\parallel =\sum _{k=0}^n[(1-{\alpha }_k){\beta }_k\parallel p_k\parallel +{\alpha }_k\parallel r_k\parallel \left]\right[\prod _{i=k+1}^n(1-{\alpha }_i)\hfill \\ (1-{\beta }_i)]+ϵ.\hfill \end{array}$$

(20)

$$\begin{array}{c}{E}_n^{\left(2\right)}:=\parallel y_n-\overline{y_n}\parallel ={\alpha }_n\parallel r_n\parallel +(1-{\alpha }_n){\beta }_n\parallel p_n\parallel +(1-{\alpha }_n)(1-{\beta }_n)E_{n-1}^{\left(1\right)}+ϵ.\hfill \end{array}$$

(21)

$$\begin{array}{c}{E}_n^{\left(3\right)}:=\parallel z_n-\overline{z_n}\parallel ={\beta }_n\parallel p_n\parallel +(1-{\beta }_n)E_{n-1}^{\left(1\right)}+ϵ.\hfill \end{array}$$

(22)

We discovered that in the J iterative scheme, the error grew to (n + 1) iterations, defined as $E_n^{\left(1\right)},E_n^{\left(2\right)}$ and $E_n^{\left(3\right)}$.

Next we present the following outcomes.

Theorem 1.

Let S, F, M, $E_n^{\left(1\right)},E_n^{\left(2\right)}$, and $E_n^{\left(3\right)}$be as defined above and ϵ be a positive fixed real number:

(i) 

If ${\sum }_{i=0}^{\infty }{\alpha }_i=+\infty$ or ${\sum }_{=0}^{\infty }{\beta }_i=+\infty$, then the errors estimation of (1) is bounded and cannot exceed the number N;

(ii) 

If ${\sum }_{i=0}^{\infty }[(1-{\alpha }_i){\beta }_i+{\alpha }_i]<+\infty ,{lim}_{n\to \infty }{\alpha }_n=0$and${lim}_{n\to \infty }{\beta }_n=0$, then random errors of (1) are controllable.

Proof. 

(i) It is well known that ${\sum }_{i=0}^{\infty }{\beta }_i=+\infty$ implies ${\prod }_{i=0}^{\infty }(1-{\beta }_i)=0$, by (Remark 2.1 of [18]). By using this fact and the above inequalities, we have:

$$\begin{array}{c}\parallel E_n^{\left(1\right)}\parallel =\parallel [(1-{\alpha }_0){\beta }_0{p}_0+{\alpha }_0{r}_0]\prod _{i=1}^n(1-{\alpha }_i)(1-{\beta }_i)+[(1-{\alpha }_1){\beta }_1{p}_1\hfill \\ +{\alpha }_1{r}_1]\prod _{i=2}^n(1-{\alpha }_i)(1-{\beta }_i)+...+(1-{\alpha }_n){\beta }_n{p}_n+{\alpha }_n{r}_n+ϵ\parallel ,\hfill \\ \le \parallel [(1-{\alpha }_0){\beta }_0{p}_0+{\alpha }_0{r}_0]\prod _{i=1}^n(1-{\alpha }_i)(1-{\beta }_i)\parallel +\parallel [(1-{\alpha }_1){\beta }_1{p}_1+{\alpha }_1{r}_1]\hfill \\ \prod _{i=2}^n(1-{\alpha }_i)(1-{\beta }_i)\parallel +...+\parallel (1-{\alpha }_n){\beta }_n{p}_n+{\alpha }_n{r}_n\parallel +ϵ,\hfill \\ \le [(1-{\alpha }_0){\beta }_0\parallel p_0\parallel +{\alpha }_0\parallel r_0\parallel ]\prod _{i=1}^n(1-{\alpha }_i)(1-{\beta }_i)+[(1-{\alpha }_1){\beta }_1\parallel p_1\parallel \hfill \\ +{\alpha }_1\parallel r_1\parallel ]\prod _{i=2}^n(1-{\alpha }_i)(1-{\beta }_i)+...+(1-{\alpha }_n){\beta }_n\parallel p_n\parallel +{\alpha }_n\parallel r_n\parallel +ϵ,\hfill \end{array}$$

which implies:

$$\begin{array}{c}\parallel E_n^{\left(1\right)}\parallel \le M\{\prod _{i=0}^n(1-{\alpha }_i)(1-{\beta }_i)\hfill \\ [(1-{\alpha }_0){\beta }_0+{\alpha }_0]\prod _{i=1}^n(1-{\alpha }_i)(1-{\beta }_i)\hfill \\ [(1-{\alpha }_1){\beta }_1+{\alpha }_1]\prod _{i=2}^n(1-{\alpha }_i)(1-{\beta }_i)\hfill \\ +...+(1-{\alpha }_n){\beta }_n+{\alpha }_n\hfill \\ -\prod _{i=0}^n(1-{\alpha }_i)(1-{\beta }_i)\}+ϵ,\hfill \\ =M[1-\prod _{i=0}^n(1-{\alpha }_i)(1-{\beta }_i)]+ϵ,\hfill \\ =M[1-\prod _{i=0}^n(1-{\alpha }_i)\prod _{i=0}^n(1-{\beta }_i)]+ϵ,\hfill \\ \le M[1-\prod _{i=0}^{\infty }(1-{\alpha }_i)\prod _{i=0}^{\infty }(1-{\beta }_i)]+ϵ=M+ϵ=N.\hfill \end{array}$$

(23)

$$\begin{array}{c}\parallel E_n^{\left(2\right)}\parallel =\parallel {\alpha }_n{r}_n+(1-{\alpha }_n){\beta }_n{p}_n+(1-{\alpha }_n)(1-{\beta }_n)E_{n-1}^{\left(1\right)}+ϵ\parallel ,\hfill \\ \le {\alpha }_n\parallel r_n\parallel +(1-{\alpha }_n){\beta }_n\parallel p_n\parallel +(1-{\alpha }_n)(1-{\beta }_n)\parallel E_{n-1}^{\left(1\right)}\parallel +ϵ,\hfill \\ \le M[{\alpha }_n+(1-{\alpha }_n){\beta }_n+(1-{\alpha }_n)(1-{\beta }_n)]+ϵ=M+ϵ=N.\hfill \end{array}$$

(24)

$$\begin{array}{c}\parallel E_n^{\left(3\right)}\parallel =\parallel {\beta }_n{p}_n+(1-{\beta }_n)E_{n-1}^{\left(1\right)}+ϵ\parallel ,\hfill \\ \le {\beta }_n\parallel p_n\parallel +(1-{\beta }_n)\parallel E_{n-1}^{\left(1\right)}\parallel +ϵ,\hfill \\ \le M[{\beta }_n+(1-{\beta }_n)]+ϵ=M+ϵ=N.\hfill \end{array}$$

(25)

Hence, we have ${max}_{n\in N}[\parallel E_n^{\left(1\right)}\parallel ,\parallel E_n^{\left(2\right)}\parallel ,\parallel E_n^{\left(3\right)}\parallel ]\le N$.

Indeed, ${\sum }_{i=0}^{\infty }[(1-{\alpha }_i){\beta }_i+{\alpha }_i]<+\infty$ implies the following:

$$\begin{array}{c}\prod _{i=0}^{\infty }\left([(1-{\alpha }_i){\beta }_i+{\alpha }_i]\right),\hfill \\ =\prod _{i=0}^{\infty }(1-{\alpha }_i)(1-{\beta }_i)\in (0,1).\hfill \end{array}$$

Let 1-${\prod }_{i=0}^{\infty }(1-{\alpha }_i)(1-{\beta }_i)=l\in (0,1).$

We have:

$$\parallel E_n^{\left(1\right)}\parallel \le M[1-\prod _{i=0}^n(1-{\alpha }_i)(1-{\beta }_i)]+ϵ.$$

On the other hand, the conditions ${lim}_{n\to \infty }{\alpha }_n=0$ and ${lim}_{n\to \infty }{\beta }_n=0\Rightarrow {lim}_{n\to \infty }({\alpha }_n+{\beta }_n-{\alpha }_n{\beta }_n)=0$ $\Rightarrow \exists$ and $n_0\in \mathbf{N}$ s.t ∀$n\ge n_0$, we have ${\alpha }_n+{\beta }_n-{\alpha }_n{\beta }_n\le \frac{l}{1-l}$. Using this fact, we obtain:

$$\begin{array}{c}\parallel E_n^{\left(2\right)}\parallel \le M[{\alpha }_n+(1-{\alpha }_n){\beta }_n+(1-{\alpha }_n)(1-{\beta }_n)l]+ϵ,\hfill \\ =M[l+({\alpha }_n+{\beta }_n-{\alpha }_n{\beta }_n)(1-l)]+ϵ,\hfill \\ \le M[l+\frac{l}{1-l}(1-l)]+ϵ,\hfill \\ =2lM+ϵ.\hfill \end{array}$$

Similarly, the condition ${lim}_{n\to \infty }{\beta }_n$ = 0 $\Rightarrow \exists$ and $n_0\in$N s.t ∀ n $\ge n_0$, we have ${\beta }_n\le \frac{l}{1-l}.$ Now, we have:

$$\begin{array}{c}\parallel E_n^{\left(3\right)}\parallel \le {\beta }_n\parallel p_n\parallel +(1-{\beta }_n)\parallel E_{n-1}^{\left(1\right)}\parallel +ϵ,\hfill \\ \le {\beta }_{n}M(1-l)+Ml,\hfill \\ \le \frac{l}{1-l}M(1-l)+Ml,\hfill \\ =2lM+ϵ \mathrm{for} \mathrm{all} n\ge n_0.\hfill \end{array}$$

Thus, we conclude that $\parallel E_n^{\left(1\right)}\parallel$, $\parallel E_n^{\left(2\right)}\parallel$ and $\parallel E_n^{\left(3\right)}\parallel$ can be controlled for suitable choice of the parameter sequences ${\left\{{\alpha }_n\right\}}_{n=0}^{\infty }$ and ${\left\{{\beta }_n\right\}}_{n=0}^{\infty }$ for all $n\ge n_0$. □

Remark 1.

Theorem 1 indicates that the direct error estimation for an iterative algorithm defined in [12] is controllable and bounded, which is the actual aim of our research. The following example illustrates that not only is the direct error in the iterative algorithm defined in [12] controlled and bounded, but it is also independent of the initial value selection. The efficiency of the J iteration approach is represented in both tables and graphs.

Example 1.

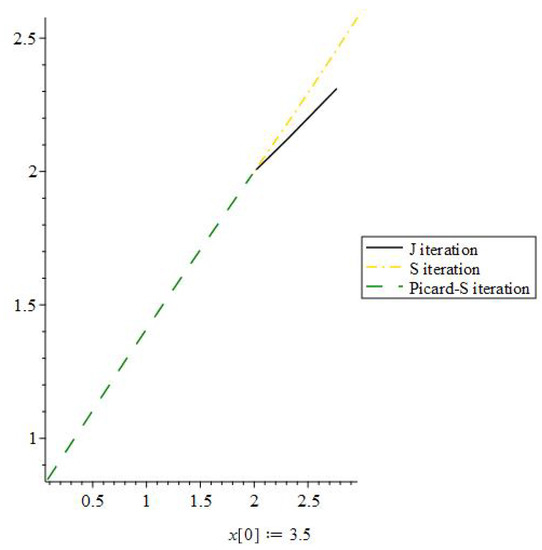
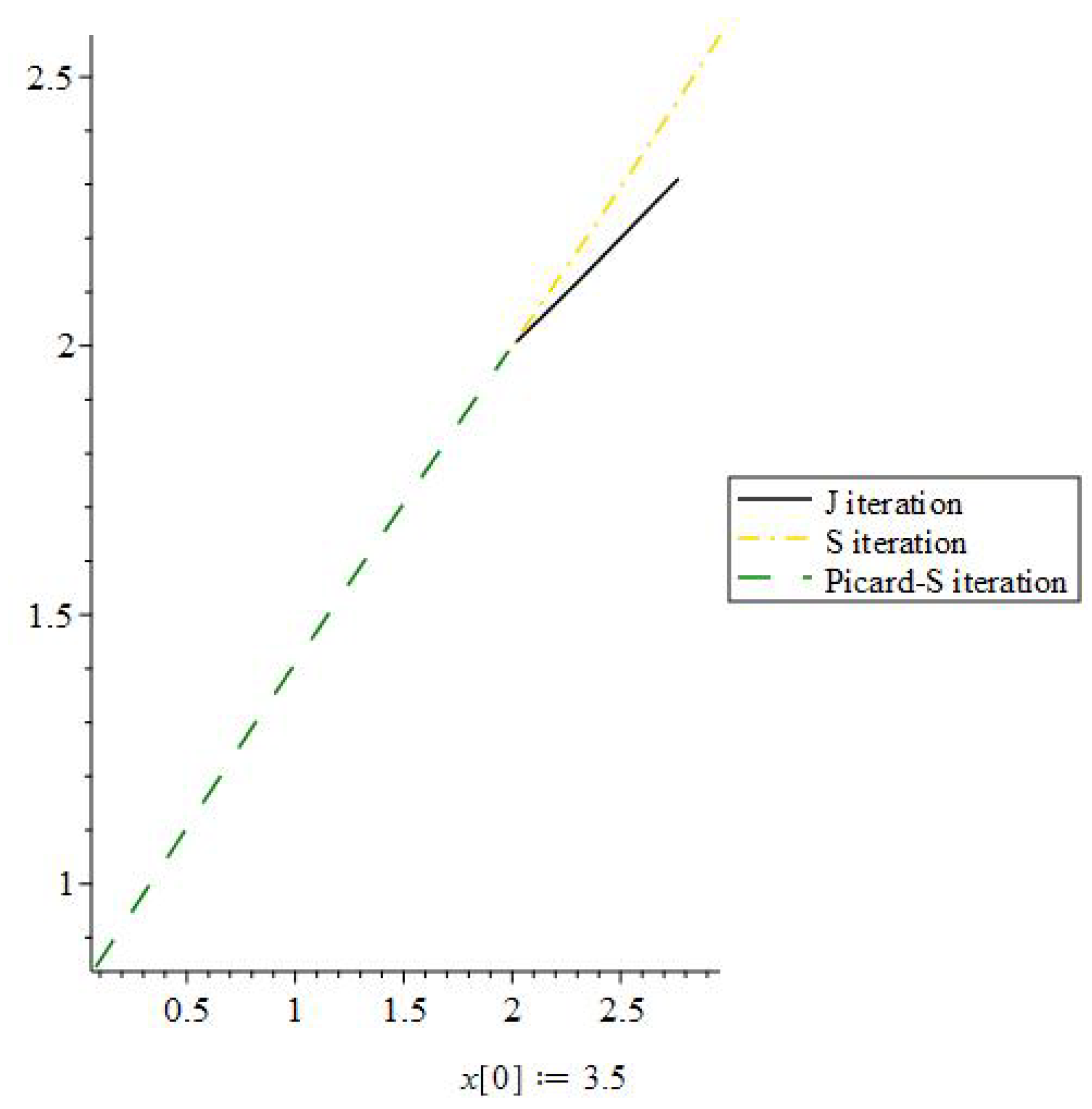
Let us start by defining a function $Q:R\to R$ by $Q\left(x\right)=(4x+2)/5.$ Then, Q is definitely a contraction mapping. Let ${\alpha }_n=2n/(3n+1)$ and ${\beta }_n=3n/(4n+1).$ The iterative values for $x_0=3.5$ are given in Table 1. The convergence graph can be seen in Figure 1. The effectiveness of the J iteration method is undeniable.

Table 1. Sequence formed by J, Picard-S, and S Iteration methods, having initial value $x_0=3.5$ for contraction mapping Q of Example 1.

	S	Picard-S	J
$x_0$	3.5	3.5	3.5
$x_1$	3.2	2.96	2.31142
$x_2$	2.9024	2.57754	2.12239
$x_3$	2.66692	2.34146	2.04751
$x_4$	2.48921	2.20038	2.05893
$x_5$	2.35737	2.1171	2.01832
$x_6$	2.26037	2.06825	2.00703
$x_7$	2.18935	2.03971	2.00269
$x_8$	2.13752	2.02307	2.00102
$x_9$	2.09977	2.01339	2.00039
$x_{10}$	2.07233	2.00777	2.00014
$x_{11}$	2.05248	2.00456	2.00005
$x_{12}$	2.03794	2.00261	2.00002
$x_{13}$	2.02746	2.00151	2
$x_{14}$	2.01987	2.00087	2
$x_{15}$	2.01437	2.00051	2
$x_{16}$	2.01039	2.00029	2
$x_{17}$	2.00751	2.00017	2
$x_{18}$	2.00543	2.0001	2
$x_{19}$	2.00392	2.00006	2
$x_{20}$	2.00283	2.00003	2

Figure 1. J iteration process convergence when the initial value is 3.5.

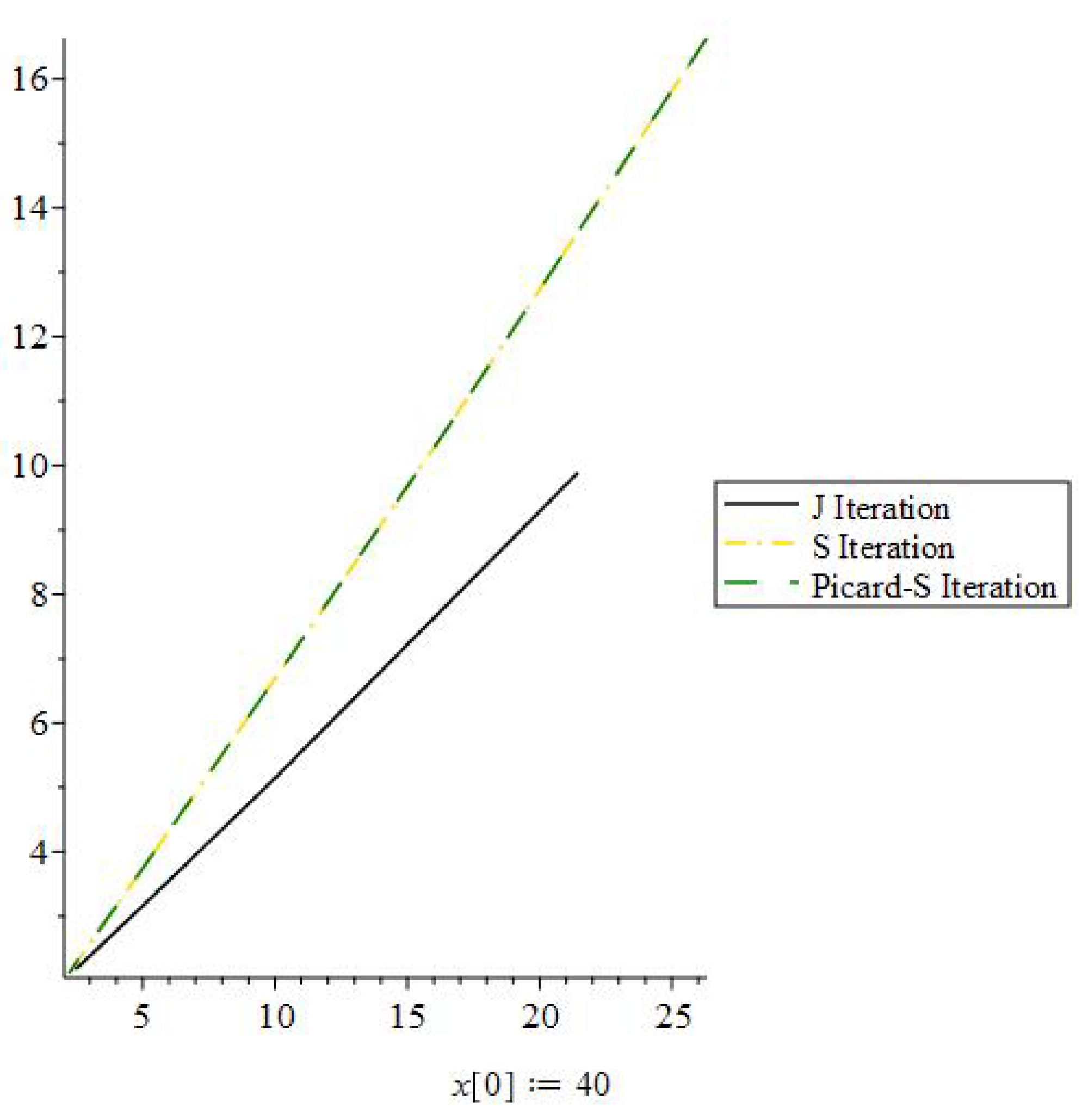
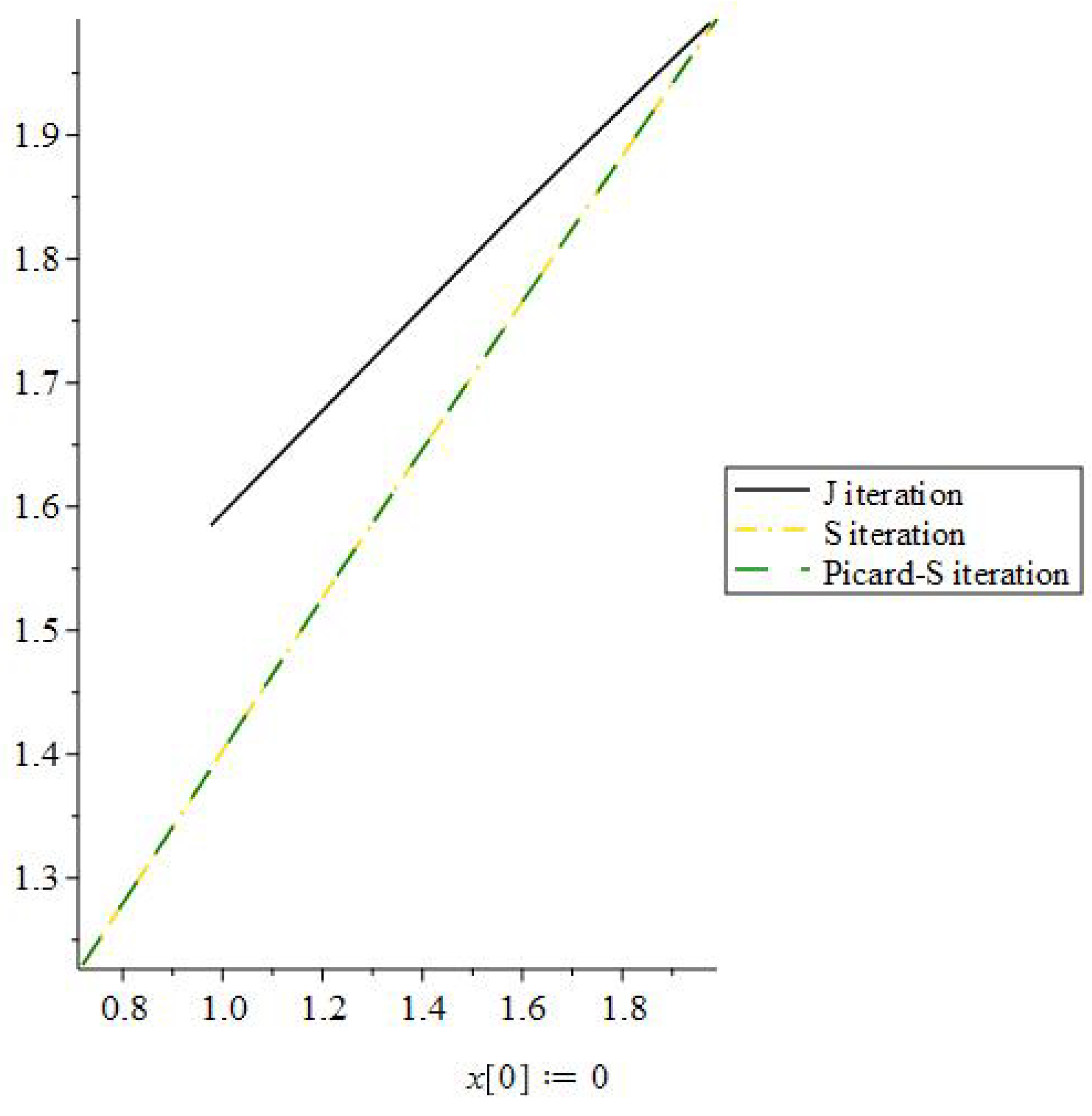
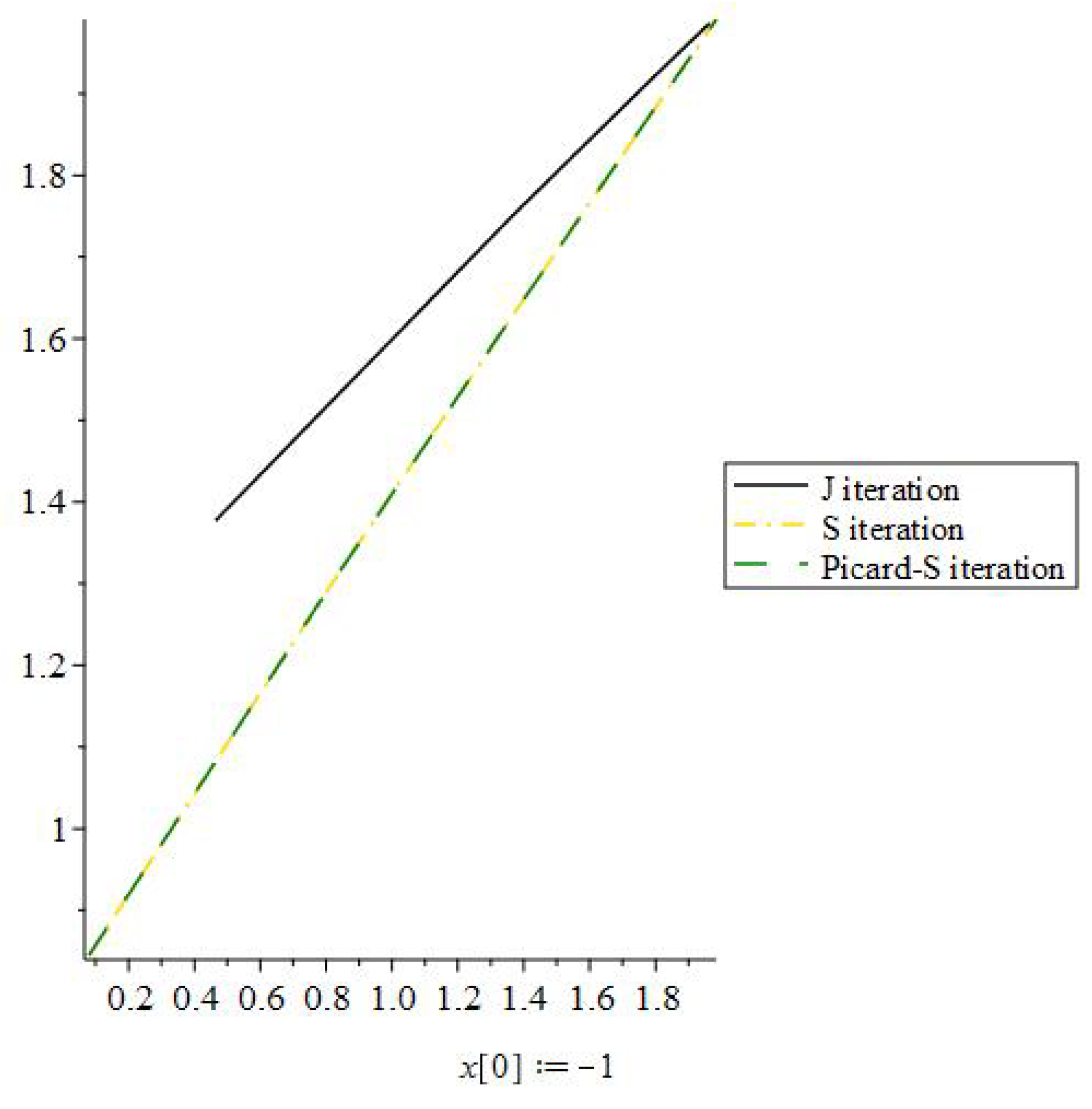
In Table 1, it is shown that the J iterative process is more efficient than other iterative algorithm in terms of approaching a fixed point quickly. Following that, we show some graphs demonstrating that the J iteration strategy is effective for any initial value. Figure 1, Figure 2, Figure 3 and Figure 4, J, Picard-S, and S Iteration process approach 2, which is fixed point of Q, by utilizing different initial guesses for mapping Q in Example 1.

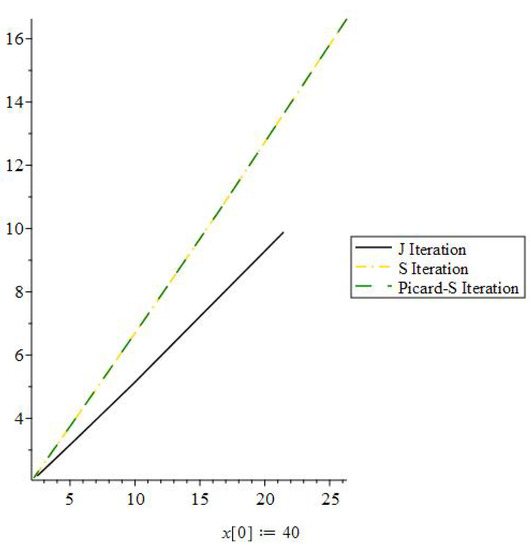
Figure 2. J iteration process convergence when the initial value is 40.

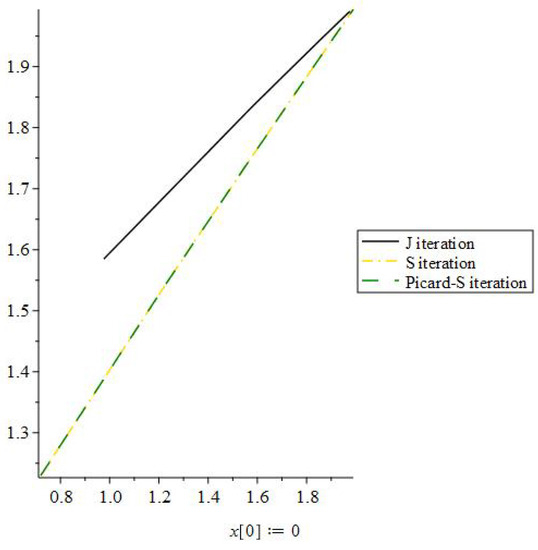
Figure 3. J iteration process convergence when the initial value is 0.

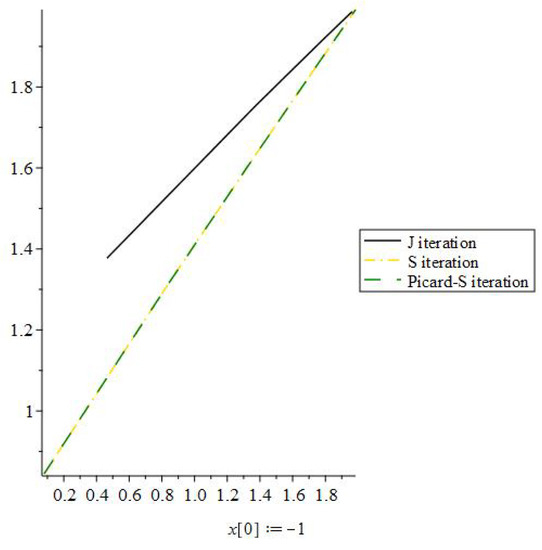
Figure 4. J iteration process convergence when the initial value is −1.

In this graph, we have compared the rate of convergence of the J iteration process, the S iteration process, and the Picard-S iteration process, letting 3.5 be the initial value. From the graph, the efficiency of the J iteration method is clear. Next, we consider 40 to be an initial value.

We compared the rate of converge of the J iteration process, S iteration process, and Picard-S iteration process in this graph, using 40 as the beginning value. The efficiency of the J iteration method is shown in the graph. Next, we will use 0 as a starting point.

In this graph, we used 0 as the starting value to compare the rate of convergence of the J iteration process, S iteration process, and Picard-S iteration process. The graph depicts the efficiency of the J iteration approach. Now, as a starting point, we will choose −1.

To compare the rate of convergence of the J iteration process, S iteration process, and Picard-S iteration process, we utilized −1 as the starting value in this graph. The efficiency of the J iteration strategy is depicted in the graph.

All of the graphs above, as well as Table 1, show that the J iteration approach has a fast convergence rate and is not affected by the initial value selection.

4. Conclusions

Applying specific criteria on parametric sequences is a typical practice for the iteration method described in the articles “Data dependence for Ishikawa iteration when dealing with contractive like operators”, “On estimation and control of errors of the Mann iteration process”, and “On the rate of convergence of Mann, Ishikawa, Noor and SP iterations for continuous functions on an arbitrary interval” such as ${\left\{{\alpha }_n\right\}}_{n=0}^{\infty }$ and ${\left\{{\beta }_n\right\}}_{n=0}^{\infty }$ and ${\sum }_{i=0}^{\infty }{\left\{{\alpha }_n\right\}}_{n=0}^{\infty }=\infty$ and ${\sum }_{i=0}^{\infty }{\left\{{\beta }_n\right\}}_{n=0}^{\infty }=\infty$ for all n∈ N for broad I.M to acquire the rate of convergence, stability, and dependency on initial guesses in findings and also estimate their error directly. In our corresponding results, none of these conditions were employed. Generalizing this, we proved that the direct error estimation of (1) is controllable as well as bounded. Consequently, our analysis more precise in terms of all of the preceding comparisons. Moreover, the graphical analyses of the rate of convergence of the J iteration for different initial values chosen were above or below the fixed point.