Computational Experiments with the Roots of Fibonacci-like Polynomials as a Window to Mathematics Research

Abstract

Fibonacci-like polynomials, the roots of which are responsible for a cyclic behavior of orbits of a second-order two-parametric difference equation, are considered. Using Maple and Wolfram Alpha, the location of the largest and the smallest roots responsible for the cycles of period p among the roots responsible for the cycles of periods 2^kp (period-doubling) and kp (period-multiplying) has been determined. These purely computational results of experimental mathematics, made possible by the use of modern digital tools, can be used as a motivation for confirmation through not-yet-developed methods of formal mathematics.

1. Introduction

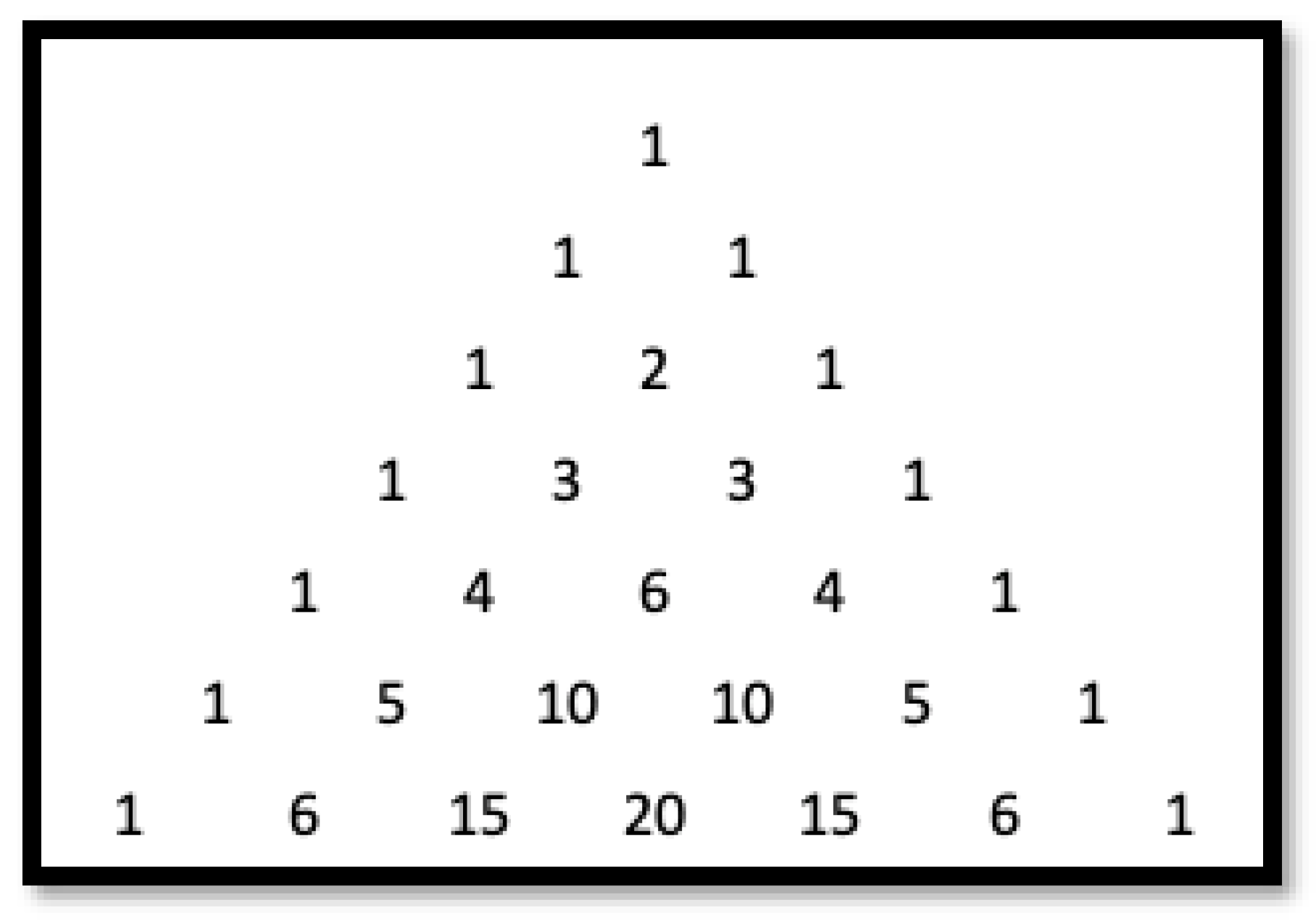
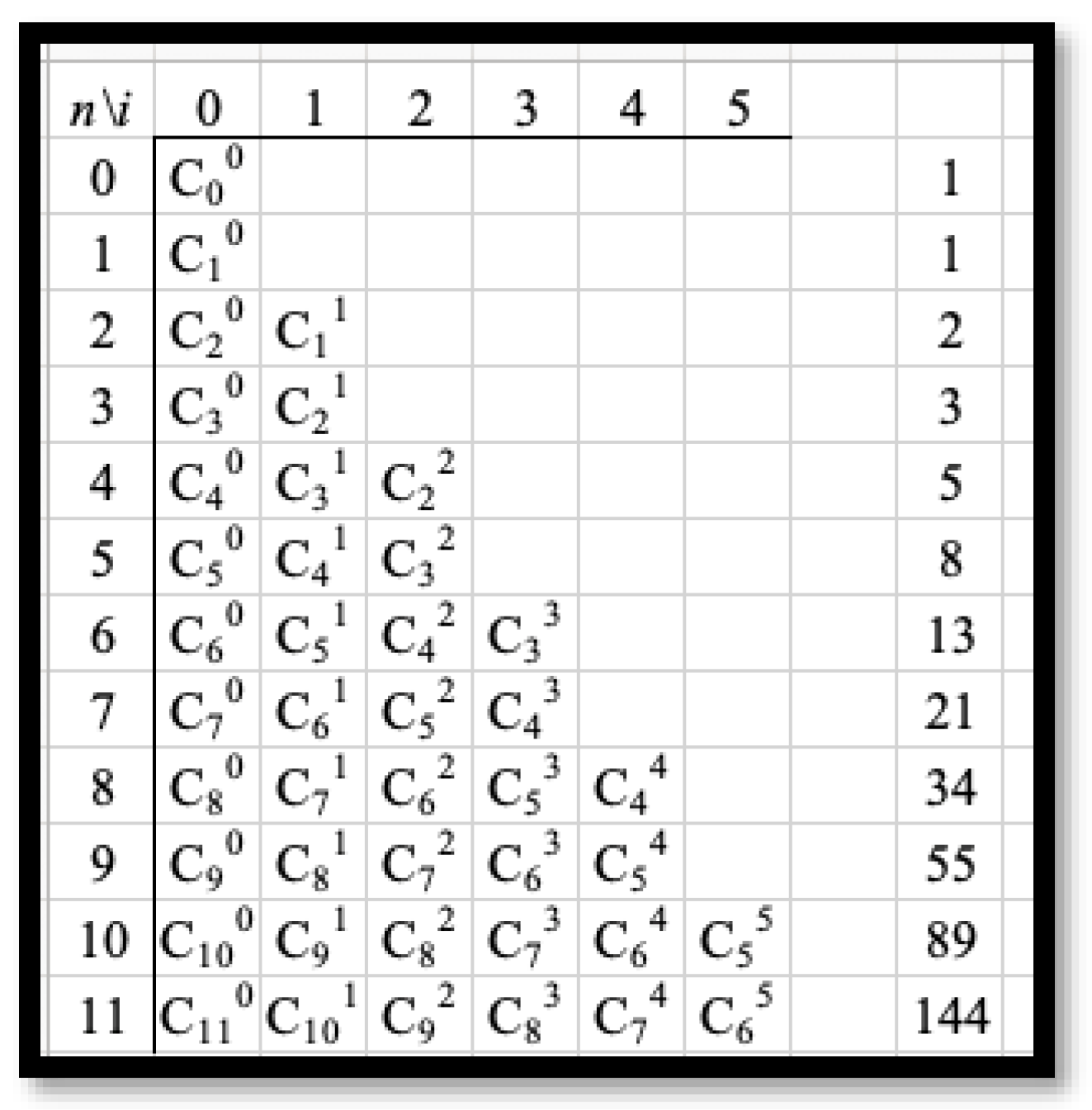
The main results of this paper are purely computational, carried out in the contexts of Maple and Wolfram Alpha. The paper deals with locating the roots of the Fibonacci-like polynomials of degree k among the roots of the Fibonacci-like polynomials of degree m > k. Before proceeding further, the Fibonacci-like polynomials discussed in detail in ref. [1] have to be introduced. To this end, one may recall that in Pascal’s triangle (Figure 1), which, according to ref. [2], was used by Pascal to record the sample spaces of experiments involving the tossing of n coins for different values of n, Fibonacci numbers can be found when adding the entries of the triangle along the so-called shallow diagonals [3]. The entries of Pascal’s triangle can be rearranged as shown in Figure 2, where the first column is comprised of ones located either on the left side of Pascal’s triangle or on its right side. The second, third, fourth, and so on columns are the diagonals parallel, respectively, to the first one shifted by two rows down along the column on its immediate left. Through this process, the numbers on the shallow diagonals form rows of the rearranged Pascal’s triangle so that the sums of numbers in these rows are Fibonacci numbers (Figure 2). Furthermore, the rows go in pairs: two rows with one number, two rows with two numbers, two rows with three numbers, and so on. Using these pairs of numbers as coefficients of the polynomials of degrees zero, one, two, and so on, the following polynomials can be formed:

$$P_{-1}\left(x\right)=1,P_0\left(x\right)=1,P_1\left(x\right)=x+1, P_2\left(x\right)=x+2, P_3\left(x\right)=x^2+3x+1,$$

$$P_4\left(x\right)=x^2+4x+3, \dots , P_8\left(x\right)=x^4+8x^3+21x^2+20x+5,$$

$$P_9\left(x\right)=x^5+9x^4+28x^3+35x^2+15x+1, P_{10}\left(x\right)=x^5+10x^4+36x^3+56x^2+35x+6.$$

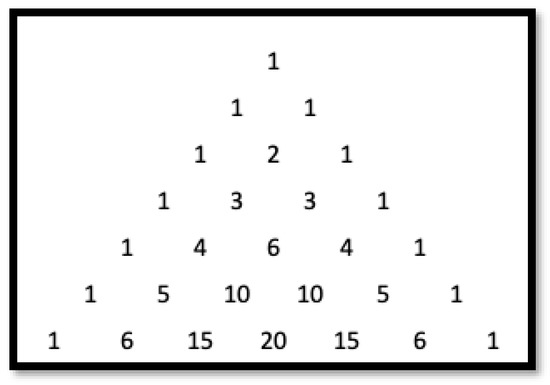
Figure 1. Pascal’s triangle.

Figure 2. Rearranged Pascal’s triangle and Fibonacci numbers.

The above polynomials are called Fibonacci-like polynomials; the term Fibonacci polynomial has been used for another class of polynomials associated with Fibonacci numbers found in a number of publications; for example, in refs. [4,5]. What is special about Fibonacci-like polynomials is that any Fibonacci-like polynomial of degree n has exactly n different real roots. For example, using Wolfram Alpha (Figure 3), one can factor the polynomial P₁₀(x) into the product (x + 1)(x + 2) (x + 3)(x² + 4x + 1), so that:

P₁₀(x) = P₁(x) P₂(x) (x + 3) (x² + 4x + 1).

Figure 3. Factoring a Fibonacci-like polynomial.

This factorization shows that all the roots of the polynomial P₁₀(x) are real numbers, some of which coincide with the roots of P₁(x) and P₂(x). Furthermore, one can note that

P₄(x) = P₂(x) + P₃(x), P₃(x) = xP₂(x) + P₁(x) and P₈(x) = P₁₀(x) − P₉(x) = x⁴ + 8x³ + 21x² + 20x + 5.

Noting that entries of Pascal’s triangle are binomial coefficients, the triangle shown in Figure 2 can be rewritten as shown in Figure 4. All these observations can be generalized, making it possible to define Fibonacci-like polynomials through the following recursive formula [1]:

$$P_n\left(x\right)=x^{mod\left(n,2\right)}{P}_{n-1}\left(x\right)+P_{n-2}\left(x\right), P_{-1}\left(x\right)=P_0\left(x\right)=1$$

(1)

where mod(n,2) = 0 when n is even and mod(n,2) = 1 when n is odd. Drawing coefficients of the Fibonacci-like polynomials from the triangle shown in Figure 4 results in the following closed formulas involving binomial coefficients [1]:

$$P_{2n-1}\left(x\right)={\displaystyle \sum }_{i=0}^n{C}_{2n-i}^i{x}^{n-i}$$

(2)

and

$$P_{2n}\left(x\right)={\displaystyle \sum }_{i=0}^n{C}_{2n-i+1}^i{x}^{n-i}$$

(3)

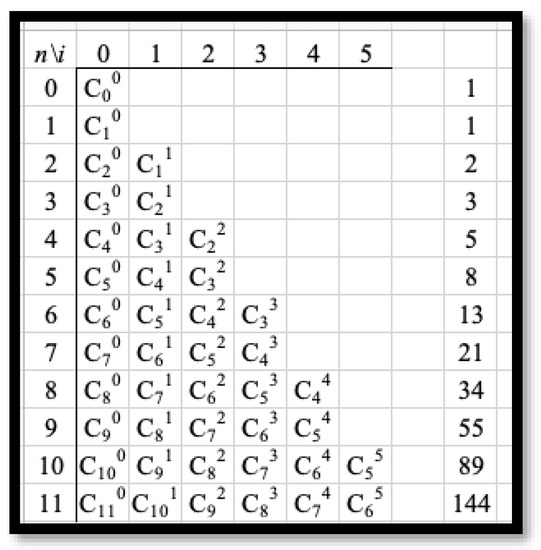
Figure 4. An alternative representation of the rearranged Pascal’s triangle.

2. Connecting Fibonacci-like Polynomials to Cycles Formed by Generalized Golden Ratios

When Fibonacci-like polynomials are defined through the entries of the rearranged Pascal’s triangle, they have no apparent connection to any difference equations like the one that defines Fibonacci numbers. In order to demonstrate this connection, consider a parametric generalization of the well-known Fibonacci recursion in the form of the difference equation:

$$f_{n+1}=a{f}_n+b{f}_{n-1}, f_0=f_1=1$$

(4)

where a and b are real numbers. Equation (4) can be explored in terms of the behavior of the ratios $\frac{f_{n+1}}{f_n}$ as n increases, and also by their dependence on the parameters. Such ratios are called generalized golden ratios [1]. It was found in ref. [6] that when $a^2+4b<0$, for certain values of parameters a and b the ratios form cycles of different periods. By exploring the recursive equation:

$$g_{n+1}=a+\frac{b}{g_n}, g_1=1$$

(5)

in which $a^2+4b<0$ the cycles that attracted the ratios $g_{n+1}=\frac{f_{n+1}}{f_n}$ can be connected to Fibonacci-like polynomials. For example, in order to find a relation between the parameters a and b that enables these ratios to form cycles of period five (alternatively, for the ratios to be attracted by those cycles), the condition $g_6=g_1=1$ was set, resulting in the relation $a^4+3a^{2}b+b^2=0,$ which, under the substitution $\frac{a^2}{b}=x,$ is equivalent to the quadratic equation $x^2+3x+1=0$. The left-hand side of this equation is the Fibonacci-like polynomial $P_3\left(x\right),$ the coefficients of which are located in the fifth line of the rearranged Pascal’s triangle. In other words, when the right-hand side of the relation $\frac{a^2}{b}=x$ is a root of the Fibonacci-like polynomial $P_3\left(x\right), \mathrm{the}$ recursive Equation (5) generates cycles of period five. Furthermore, one can check to see that both roots of $P_3\left(x\right)$ can be found among the roots of $P_8\left(x\right)=x^4+8x^3+21x^2+20x+5$—the polynomial resulting from setting in (5) the condition $g_{11}=g_1=1$. In the context of this paper, the type of questions to be explored is how one can find the roots of $P_3\left(x\right)$ among the roots of $P_8\left(x\right).$ That is, to find the ranks of the roots of $P_3\left(x\right)$ on the ordered list of the roots of $P_8\left(x\right).$ Similarly, in what follows, the cycles of higher periods and the corresponding explorations will be associated with the roots of the Fibonacci-like polynomials of higher degrees.

To conclude this section, one can prove that any root of a Fibonacci-like polynomial belongs to the interval (−4, 0). Indeed, because all coefficients of a Fibonacci-like polynomial are positive numbers, the relationship $P_n\left(x_0\right)=0$ implies $x_0<0.$ The last equality implies that there exists a pair of parameters (a₀, b₀) such that $a_0{}^2+4b_0<0$ whence $b_0<0$. Therefore, $\frac{a_0{}^2}{b_0}+4>0$ or $\frac{a_0{}^2}{b_0}>-4$. Noting that $\frac{a_0{}^2}{b_0}=x_0$ completes the proof.

3. Ordinality Assignments of the Roots of Fibonacci-like Polynomials

In what follows, the location of a root of a Fibonacci-lime polynomial among its other roots will be referred to as an ordinality assignment of the root, distinguishing between the left ordinality assignment (LOA) and the right ordinality assignment (ROA). For example, on the list $x_1, x_2, x_3, x_4, x_5, x_6$ we have LOA($x_3$) = 3 and ROA($x_3$) = 4. In general, on the ordered list ${\left\{x_i\right\}}_{i=1}^n$ we have LOA($x_i$) = i and ROA($x_i$) = n − i + 1, so that LOA($x_i$) + ROA($x_i$) = n + 1. The statements about ordinality assignments will be formulated in the form of technology-motivated conjectures. The development of their formal proof may be seen as a possible avenue in experimental mathematics research.

By analogy with the pole assignment problem that ref. [7] associated with the stability of a linear control system, when with the help of a matrix of linear control the eigenvalues of the full matrix can be made to coincide with a given set of eigenvalues, in what follows, the problem of ordinality assignments of a root of a Fibonacci-like polynomial, responsible for a proper p-cycle on the ordered list of the roots of the Fibonacci-like polynomials responsible for cycles of periods 2^kp or $kp,$ will be studied computationally. This study would allow one to recognize that if $P_k\left(x_0\right)=P_n\left(x_0\right)=0$ for certain values of k, and n, n > k, then the ordinality assignments of $x_0$ among the roots of $P_n\left(x\right)$ can be formulated in terms of n and k. The formulation would make it possible, given information about the ordinality assignment of a root responsible for a p-cycle where p is a prime number among the roots of a Fibonacci-like polynomial, to determine the polynomial.

As the cyclic behavior of the orbits of Equation (5), in which $a^2+4b<0,$ depends on the roots of the Fibonacci-like polynomials, an investigation into patterns formed by the roots is of a value. First, computing shows that just as the first three (of non-zero degree) Fibonacci-like polynomials, $P_1\left(x\right)=x+1, P_2\left(x\right)=x+2$ and $P_3\left(x\right)=x^2+3x+1$, do not have common roots, any other three consecutive Fibonacci-like polynomials do not have roots in common either. However, even without computing, one can conclude that there are Fibonacci-like polynomials which do have roots in common. Indeed, because a cycle of length p can be construed as a cycle the length of which is a multiple of p, the corresponding Fibonacci-like polynomials have roots in common. Using Maple, one can discover that when p is an odd number, the largest root of the Fibonacci-like polynomial $P_{p-2}\left(x\right)$ that generates a p-cycle coincides with the largest root of the Fibonacci-like polynomial $P_{2p-2}\left(x\right),$ which generates a 2p-cycle. However, further period-doubling and period-multiplying computational investigations result in a polynomial the largest root of which is different from that of its immediate predecessor. Nonetheless, the roots of the polynomials responsible for a p-cycle and a 2p-cycle can be found among the roots of the Fibonacci-like polynomials responsible for the cycles of periods $2^{k}p$(period-doubling) and $kp$ (period-multiplying). While this is a pretty obvious statement, it is not clear which ordinality, left or right, can be assigned to the largest/smallest or any other root of the polynomial $P_{p-2}\left(x\right)$ on the ordered list of the roots of a polynomial responsible for a 2^kp-cycle or $kp$-cycle, k ≥ 2. The cases of 2^kp-cycles and kp-cycles will be considered separately, as the patterns of ordinality assignments are different for period-doubling and period-multiplying cases. Note that a cycle of period p is called a proper p-cycle if it cannot be split in several cycles of any period smaller than p [1]. When p is a prime number, a p-cycle may only be a proper cycle.

4. Exploring the Case of 2^kp-Cycles (Period-Doubling) in Fibonacci-like Polynomials

4.1. The Case of the Largest Root of the Polynomial $P_3\left(x\right)$

Consider the number $x_1=\frac{-3+\sqrt{5}}{2}\cong -0.381966$—(an approximation to) the largest root of the Fibonacci-like polynomial $P_3\left(x\right)=x^2+3x+1$—which is responsible for a 5-cycle formed by the orbits of the recursive Equation (5). By using Maple, one can discover the following:

(1)

The largest root of a fourth degree Fibonacci-like polynomial $P_8\left(x\right)$ that forms a trivial 10-cycle from two identical 5-cycles coincides with $x_1$;

(2)

The second root from the right on the ordered list of the roots of a ninth degree Fibonacci-like polynomial $P_{18}\left(x\right)$ that forms a trivial 20-cycle from four identical 5-cycles coincides with $x_1$;

(3)

The fourth root from the right on the ordered list of the roots of a 19th degree Fibonacci-like polynomial $P_{38}\left(x\right)$ that forms a trivial 40-cycle from eight identical 5-cycles coincides with $x_1$ (Figure 5);

Figure 5. The roots of the equation $P_{38}\left(x\right)=0$.

(4)

The eighth root from the right on the ordered list of the roots of a 39th degree Fibonacci-like polynomial $P_{78}\left(x\right)$ that forms a trivial 80-cycle from 16 identical 5-cycles coincides with $x_1$, and so on.

Noting that $8=5·2^1-2, 18=5·2^2-2, 38=5·2^3-2, 78=5·2^4-2 ,$ the following inductive generalization can be made:

The ROA of the largest root of a second degree Fibonacci-like polynomial $P_3\left(x\right)$is the$2^{n-1}$position from the right on the ordered list of$5·2^{n-1}-1$roots of the Fibonacci-like polynomial$P_{5·2^n-2}\left(x\right)$, n = 1, 2, 3, ….

In other words,

$$\mathrm{ROA}[\frac{-3+\sqrt{5}}{2}, P_{5·2^n-2}\left(x\right)]=2^{n-1}.$$

At the same time,

$$\mathrm{LOA}[\frac{-3+\sqrt{5}}{2}, P_{5·2^n-2}\left(x\right)]=5·2^{n-1}-1-2^{n-1}+1=2^{n-1}\left(5-1\right)=2^{n+1}.$$

For example, when n = 3, we have ROA[$\frac{-3+\sqrt{5}}{2}, P_{38}\left(x\right)$] =$4$ (in Figure 5, $P_{38}\left(x\right)={\displaystyle \sum }_{i=0}^{19}{C}_{2·19+1-i}^i{x}^{19-i}$ and $\frac{-3+\sqrt{5}}{2}\cong -0.3819660113)$ and LOA[$\frac{-3+\sqrt{5}}{2}, P_{38}\left(x\right)$] = 16.

4.2. The Case of the Largest Root of the Polynomial $P_5\left(x\right)$

The same pattern can be observed in the case of the Fibonacci-like polynomials, the roots of which are responsible for the cycles of periods $3·2^n, 7·2^n, 9·2^n, n=0, 1, 2. \dots .$ For example, the number $-0.1980622642,$ being (an approximation to) the largest root of a third degree Fibonacci-like polynomial $P_5\left(x\right)=x^3+5x^2+6x+1,$ responsible for the cycles of period seven formed by the orbits of recursive Equation (5), can be given the following ROAs on the ordered lists of the roots of the Fibonacci-like polynomials responsible for the cycles of periods 14, 28, 56, 112, and so on:

(1)

It is the first root from the right on the ordered list of the roots of a 6th degree Fibonacci-like polynomial $P_{12}\left(x\right)$ that is responsible for a trivial cycle of period 14;

(2)

It is the second root from the right on the ordered list of the roots of a 13th degree Fibonacci-like polynomial $P_{26}\left(x\right)$ that is responsible for a trivial cycle of period 28;

(3)

It is the fourth root from the right on the ordered list of the roots of a 27th degree Fibonacci-like polynomial $P_{54}\left(x\right)$ that is responsible for a trivial cycle of period 56 (see Figure 6);

Figure 6. The roots of the equation $P_{54}\left(x\right)=0$.

(4)

It is the eighth root from the right on the ordered list of the roots of a 55th degree Fibonacci-like polynomial $P_{110}\left(x\right)$ that is responsible for a trivial cycle of period 112, and so on. Noting that $12=7·2^1-2, 26=7·2^2-2, 54=7·2^3-2,$ the following inductive generalization can be made.

The ROA of the largest root of a third degree Fibonacci-like polynomial$P_5\left(x\right)$is the$2^{n-1}$position from the right on the ordered list of$7·2^{n-1}-1$roots of the Fibonacci-like polynomial$P_{7·2^n-2}\left(x\right),$n = 1, 2, 3, ….

Put another way,

$$\mathrm{ROA}[-0.1980622642, P_{7·2^n-2}\left(x\right)]=2^{n-1}.$$

At the same time,

$$\mathrm{LOA}[-0.1980622642, P_{7·2^n-2}\left(x\right)]=7·2^{n-1}-1-2^{n-1}+1=6·2^{n-1}.$$

For example, when n = 3 we have

$$\mathrm{ROA}\left[-0.1980622642, P_{54}\left(x\right)\right]=4 \mathrm{and} \mathrm{LOA}[-0.1980622642, P_{54}\left(x\right)]=24$$

(as shown in Figure 6, $P_{54}\left(x\right)={\displaystyle \sum }_{i=0}^{27}{C}_{2·27+1-i}^i{x}^{27-i}$).

However, for the cycles of period $4·2^n$ (note: four is the smallest even number period with which the generalized golden ratios can oscillate) the situation is different: the ROAs of the root of the polynomial $P_2\left(x\right)=x+2$ responsible for a 4-cycle are as follows (see Figure 7):

Figure 7. ROAs and LOAs of the root of $P_2\left(x\right)=x+2$.

(1)

It is the second root both from the right and the left on the ordered list of the roots of a third degree Fibonacci-like $P_6\left(x\right)$ that is responsible for a trivial 8-cycle;

(2)

It is the fourth root both from the right and the left on the ordered list of the roots of a seventh degree polynomial $P_{14}\left(x\right)$ that is responsible for a trivial 16-cycle;

(3)

It is the eighth root both from the right and the left on the ordered list of the roots a 15th degree polynomial $P_{30}\left(x\right)$ that is responsible for a trivial 32-cycle, and so on.

The situation just described is consistent with the phenomenon observed for the roots of the Fibonacci-like polynomials responsible for the cycles of periods $6·2^n, n=0, 1, 2, \dots$ already discussed in the context of cycles of periods $3·2^n, n=0, 1, 2, \dots .$

4.3. The Case of the Smallest Root of the Polynomial $P_3\left(x\right)$

In much the same way, one can find the LOAs for the smallest root of a second degree Fibonacci-like polynomial $P_3\left(x\right)=x^2+3x+1,$ which is also responsible for a 5-cycle, on the ordered list of the roots of the Fibonacci-like polynomials responsible for the cycles of periods 10, 20, 40, 80, and so on. This root, $\frac{-3-\sqrt{5}}{2}\approx -2.618034$, coincides with:

(1)

The second root from the left on the ordered list of the roots of a fourth degree Fibonacci-like polynomial $P_8\left(x\right)$ that forms a trivial 10-cycle from two identical 5-cycles;

(2)

The fourth root from the left on the ordered list of the roots of a ninth degree Fibonacci-like polynomial $P_{18}\left(x\right)$ that forms a trivial 20-cycle from four identical 5-cycles;

(3)

The eighth root from the left on the ordered list of the roots of a 19th degree Fibonacci-like polynomial $P_{38}\left(x\right)$ that forms a trivial 40-cycle from eight identical 5-cycles (see Figure 5);

(4)

The 16th root from the left on the ordered list of the roots of a 39th degree Fibonacci-like polynomial $P_{78}\left(x\right)$ that forms a trivial 80-cycle from 16 identical 5-cycles, and so on.

From the above four statements the following inductive generalization can be made:

The LOA of the smallest root of a second degree Fibonacci-like polynomial$P_3\left(x\right)$is the$2^n$position from the left on the ordered list of$5·2^{n-1}-1$roots of the Fibonacci-like polynomial$P_{5·2^n-2}\left(x\right)$, n = 1, 2, 3, ….

The same pattern can be observed in the case of the Fibonacci-like polynomials, the roots of which are responsible for the cycles of periods $3·2^n, 7·2^n, 9·2^n, n=0, 1, 2. \dots .$ For example, the number $-3.2469796,$ being (an approximation to) the smallest root of a third degree Fibonacci-like polynomial $P_5\left(x\right)$, the roots of which are responsible for the cycles of period seven, coincides with:

(1)

The second root from the left on the ordered list of the roots of a sixth degree Fibonacci-like polynomial $P_{12}\left(x\right)$ responsible for a trivial cycle of period 14 constructed out of two 7-cycles;

(2)

The fourth root from the left on the ordered list of the roots of a 13th degree Fibonacci-like polynomial $P_{26}\left(x\right)$ responsible for a trivial cycle of period 28 constructed out of four 7-cycles;

(3)

The eighth root from the left on the ordered list of the roots of a 27th degree Fibonacci-like polynomial $P_{54}\left(x\right)$ responsible for a trivial cycle of period 56 constructed out of eight 7-cycles (see Figure 6);

(4)

The 16th root from the left on the ordered list of the roots of a 55th degree Fibonacci-like polynomial $P_{110}\left(x\right)$ responsible for a trivial cycle of period 112 constructed out of 16 7-cycles, and so on.

Remark 1.

In the case of the cycle of period$3·2^0=3$ generated by $x=-1,$ the single root of the Fibonacci-like polynomial $P_1\left(x\right)=x+1$, the LOAs of this root are defined by doubling, respectively, its corresponding ROAs.

5. Generalization in the Case of Period Doubling Cycles

In general, the following technology-motivated conjecture can be made.

Conjecture 1.

The ROA of the largest root of the Fibonacci-like polynomial$P_{k-2}\left(x\right)$of degree$\frac{k-1}{2}$, where k is an odd number greater than one, is the$2^{n-1}$position from the right on the ordered list of$k·2^{n-1}-1$roots$x_1<x_2<\dots <x_{k·2^{n-1}-1 }$of the Fibonacci-like polynomial$P_{k·2^n-2}\left(x\right)$. At the same time, its LOA is equal to$k·2^{n-1}-1-2^{n-1}+1=2^{n-1}\left(k-1\right).$

For example, when k = 7 and n = 3 we have (see Figure 8) for the largest root of the polynomial $P_5\left(x\right)=x^3+5x^2+6x+1$, and we have:

ROA(−0.1980622642) = 4 and LOA(−0.1980622642) = 24

on the ordered list of 27 roots $x_1<x_2<x_3<x_4<\dots <x_{27}$ of the polynomial $P_{54}\left(x\right).$ This is consistent with the relation ROA($x_i$) + LOA($x_i$) = 27 + 1, i = 1, 2, 3, …, 27.

Figure 8. Illustrating Conjectures 1 and 2 when k = 7 and n = 3.

Conjecture 2.

The LOA of the smallest root of the Fibonacci-like polynomial$P_{k-2}\left(x\right)$of degree$\frac{k-1}{2}$, where k is an odd number greater than one, is the$2^n$position from the left on the ordered list of$k·2^{n-1}-1$roots$x_1<x_2<\dots <x_{k·2^{n-1}-1 }$of the Fibonacci-like polynomial$P_{k·2^n-2}\left(x\right)$. At the same time, its ROA is equal to$k·2^{n-1}-1-2^{n-1}+1=2^{n-1}\left(k-1\right).$

For example, when k = 7 and n = 3 (Figure 8) for the smallest root of the Fibonacci-like polynomial $P_5\left(x\right)=x^3+5x^2+6x+1$, we have:

ROA(−3.24697964) = 8 and LOA(−3.24697964) = 20

on the ordered list of 27 roots $x_1<x_2<x_3<x_4<\dots <x_{27}$ of the polynomial $P_{54}\left(x\right)$.

Remark 2.

One can use Conjecture 1 to determine a Fibonacci-like polynomial $P_m\left(x\right)$from information about the $\mathrm{ROA}\left(\widehat{x}\right)$and $\mathrm{LOA}\left(\widehat{x}\right)$ among the roots of this polynomial, where $\widehat{x}$ is a root of a Fibonacci-like polynomial $P_l\left(x\right), l<m,$responsible for a non-trivial (i.e., a proper) cycle of period $l+2$. Indeed, let $\widehat{x}$ be the largest root of the Fibonacci-like polynomial $P_{k-2}\left(x\right)$ of degree $\frac{k-1}{2}$ responsible for a proper k-cycle, where k is an odd number greater than one. If $\mathrm{ROA}\left(\widehat{x}\right)=2^{n-1}$and$\mathrm{LOA}\left(\widehat{x}\right)=2^{n-1}\left(k-1\right)$among the roots of a Fibonacci-like polynomial $P_m\left(x\right)$, then $m=k·2^n-2$ and $\widehat{x}$ is responsible for the cycle of period $k·2^n$.

Remark 3.

A different pattern can be observed for the ordinality assignments of the roots of the Fibonacci-like polynomial $P_{22}\left(x\right)=x^{11}+22x^{10}+210x^9+\dots +12$ that occupy the first position, both from the left and from the right, thereby generating proper 24-cycles. The roots are (approximately) −3.931851653 and −0.06814834742. Their ROAs and LOAs stay the same as the cycle’s length doubles: the second positions for a 48-cycle, the fourth positions for a 96-cycle, the eighth position for a 192-cycle, and so on.

6. The Case of kp-Cycles (Period-Multiplying) in Fibonacci-like Polynomials

As one moves from a 3-cycle defined by the polynomial $P_1\left(x\right)=x+1$ to a 6-cycle defined by the polynomial $P_4\left(x\right)=x^2+4x+1$, then to a 9-cycle defined by the polynomial $P_7\left(x\right)=x^4+7x^3+15x^2+10x+1$, then to a 12-cycle defined by the polynomial $P_{10}\left(x\right)=x^5+10x^4+36x^3+56x^2+35x+6$, and so on, the following ordinality assignments of the root x = −1 on the ordered lists of the roots of the polynomials $P_{3n+1}\left(x\right), n=0, 1, 2, \dots ,$ can be observed (Figure 9):

Figure 9. Exploring OAs among the roots of $P_{3n+1}\left(x\right)$ for x = −1.

(1)

When n = 0, the number −1 is the first from the right and the first from the left;

(2)

When n = 1, the number −1 is the first from the right and the second from the left;

(3)

When n = 2, the number −1 is the second from the right and the third from the left;

(4)

When n = 3, the number −1 is the second from the right and the fourth from the left;

(5)

When n = 4, the number −1 is the third from the right and the fifth from the left;

(6)

When n = 5, the number −1 is the third from the right and the sixth from the left.

In other words, the LOAs and ROAs of the root of the polynomial $P_1\left(x\right)=x+1$ on the ordered list of $2n+1-\lceil \frac{n}{2}\rceil$ roots of the polynomial $P_{3n+1}\left(x\right)$ are equal, respectively, to n + 1 and $\lfloor \frac{n}{2}\rfloor +1$. Here $\lceil x\rceil$ is the smallest integer greater than or equal to x and $\lfloor x\rfloor$ is the largest integer smaller than or equal to x. Note that $n+1+\lfloor \frac{n}{2}\rfloor +1=2n-\lceil \frac{n}{2}\rceil +2$ from where it follows that $\lfloor \frac{n}{2}\rfloor +\lceil \frac{n}{2}\rceil =n.$

Consider the Fibonacci-like polynomial $P_3\left(x\right)=x^2+3x+1$, the roots of which are responsible for the cycles of period five. The polynomial $P_3\left(x\right)$ has two real roots, the smaller one is $\widehat{x}\approx -2.618033989.$ Using Maple (Figure 10), the following $\mathrm{LOA}\left(\widehat{x}\right)$ and $\mathrm{ROA}\left(\widehat{x}\right)$ can be computed for the roots of the polynomials responsible for the cycles of period 5k, k ≥ 1. These assignments are presented in Table 1.

Figure 10. Using Maple to determine OAs of the root of $P_3\left(x\right)$.

Table 1. The LOAs and ROAs for the smallest root of $P_3\left(x\right)$.

F-L pol.	${\mathit{P}}_3\left(\mathit{x}\right)$	${\mathit{P}}_8\left(\mathit{x}\right)$	${\mathit{P}}_{13}\left(\mathit{x}\right)$	${\mathit{P}}_{18}\left(\mathit{x}\right)$	${\mathit{P}}_{23}\left(\mathit{x}\right)$	${\mathit{P}}_{28}\left(\mathit{x}\right)$	${\mathit{P}}_{33}\left(\mathit{x}\right)$	${\mathit{P}}_{38}\left(\mathit{x}\right)$	${\mathit{P}}_{43}\left(\mathit{x}\right)$
Pol. deg.	2	4	7	9	12	14	17	19	22
$\mathrm{LOA}\left(\widehat{x}\right)$	1	2	3	4	5	6	7	8	9
$\mathrm{ROA}\left(\widehat{x}\right)$	2	3	5	6	8	9	11	12	14

Conjecture 3.

Let$\widehat{x}$be the largest root of the Fibonacci-like polynomial$P_{k-2}\left(x\right)$of degree$\frac{k-1}{2}$where k > 1 is an odd number. If$ROA\left(\widehat{x}\right)=2^{n-1}$and$LOA\left(\widehat{x}\right)=2^n\left(k-1\right)$among the roots of a Fibonacci-like polynomial$P_m\left(x\right)$, then$m=k·2^n-2$and$\widehat{x}$forms a cycle of period$k·2^n$.

7. Conclusions

This paper introduced the notion of the left and right ordinality assignments of the roots of a Fibonacci-like polynomial responsible for the cycle of period p among the roots of the Fibonacci-like polynomials of periods $2^{k}p$ (period-doubling) and $kp$ (period-multiplying). The results regarding the bi-lateral ordinality assignments were purely computational. The ordinality assignments of the largest and the smallest roots of the Fibonacci-like polynomials of degrees two and three on the ordered lists of the Fibonacci-like polynomials of higher degrees were considered. All computations have been carried out in the contexts of Maple and Wolfram Alpha. It was suggested that the computational character of the results of this paper can be the first step towards exploring the concept of the bi-lateral ordinality assignments of the roots of the Fibonacci-like polynomials using the methods of experimental mathematics, where computational experiments open a window to the formal presentation of the results.