Abstract
A T-spherical fuzzy set is a more powerful mathematical tool to handle uncertain and vague information than several fuzzy sets, such as fuzzy set, intuitionistic fuzzy set, Pythagorean fuzzy set, q-rung orthopair fuzzy set, and picture fuzzy set. The Aczel–Alsina t-norm and s-norm are significant mathematical operations with a high premium on affectability with parameter activity, which are extremely conducive to handling imprecise and undetermined data. On the other hand, the Hamy mean operator is able to catch the interconnection among multiple input data and achieve great results in the fusion process of evaluation information. Based on the above advantages, the purpose of this study is to propose some novel aggregation operators (AOs) integrated by the Hamy mean and Aczel–Alsina operations to settle T-spherical fuzzy multi-criteria decision-making (MCDM) issues. First, a series of T-spherical fuzzy Aczel–Alsina Hamy mean AOs are advanced, including the T-spherical fuzzy Aczel–Alsina Hamy mean (TSFAAHM) operator, T-spherical fuzzy Aczel–Alsina dual Hamy mean (TSFAADHM) operator, and their weighted forms, i.e., the T-spherical fuzzy Aczel–Alsina-weighted Hamy mean (TSFAAWHM) and T-spherical fuzzy Aczel–Alsina-weighted dual Hamy mean (TSFAAWDHM) operators. Moreover, some related properties are discussed. Then, a MCDM model based on the proposed AOs is built. Lastly, a numerical example is provided to show the applicability and feasibility of the developed AOs, and the effectiveness of this study is verified by the implementation of a parameters influence test and comparison with available methods.
MSC:
03B52; 03E72; 47S40; 94D05
1. Introduction
As one of the principal branches of decision science, the topics related to MCDM have been extensively focused on in different disciplines, such as engineering, management, and economics. In general, MCDM is utilized to ascertain the optimum solution based on criteria and weights, and the evaluation information is often represented as real numbers and used as decision inputs. However, the complexity of the practical decision system makes it difficult for decision makers to make optimal and effective choices due to the fact that the evaluation values are often ambiguous and uncertain during the decision. While considering the vagueness, uncertainty, and incompleteness of evaluation information, Atanassov [] extended an intuitionistic fuzzy set (IFS) with the degree of membership (MD) (τ) and the degree of non-membership (ND) (ϑ), based on the classical fuzzy set (FS) []. The Pythagorean fuzzy set (PyFS) was proposed by Yager and Abbasov [] to make up for the deficiency when τ + ϑ > 1. Subsequently, Yager [] introduced a more flexible q-rung orthopair fuzzy set (q-ROFS) concept, namely, flexibly adjusting the decision range expressed by MD and ND through the parameter q, and meeting the condition: τq +ϑq ≤ 1, τ, ϑ ∈ [0,1]. However, the evaluation object cannot be fully described by relying only on MD and ND in the above various fuzzy sets. Thus, a picture fuzzy set (PFS) was developed by Cuong [], containing MD, abstinence degree (AD) (η ∈ [0,1]), and ND, as another form of generalized FS that can describe more information. Although PFS has the ability to describe AD information that IFS, PyFS, and q-ROFS cannot, it still has the limitation that it fails if the total value of 3 degrees is more than 1. In this regard, the concept of the spherical fuzzy set (SFS) was extended by Mahmood et al. [], then they promoted it to the generalized form, i.e., T-spherical fuzzy set (TSFS), to remove the restriction of decision-makers (DMs) in the allocation of MD, AD, and ND with a larger decision space, enabling them to express DMs’ preferences and opinions more freely. Obviously, the above extended fuzzy sets are all special cases of TSFS, which has been widely studied by numerous scholars because of the generalized form of TSFS with no limitations.
As one of the significant processing tools for fusing evaluation data, the study of AOs in the TSFS environment has also been actively followed by many scholars. The algorithms of TSFNs are important bases for AOs, and currently, t-norm and s-norm operations have emerged, such as Algebraic [], Hamacher [], Einstein [], interaction [,,], Frank [], Dombi [], Schweizer–Sklar [], Aczel–Alsina (AA) [], etc. Among the above operations, there are no decision-adjustable parameters contained in Algebraic, Hamacher, and Einstein t-norm operations, and interactive operations emphasize the interaction relationship between MD, AD, and ND in any two TSFNs to avoid counterintuitive phenomena caused when the value of the membership function is zero. In addition, Frank, Dombi, Schweizer–Sklar, AA, etc. are the t-norms operations containing decision-tunable parameters, which increase the decision flexibility of the aggregation operator, as well as a limited extent of generalization. In contrast, the AA t-norm and s-norm are more flexible to make decisions []. Apart from the arithmetic average and geometric operators, there are various novel AOs developed by integrating them with the Power, Bonferroni mean (BM), Heronian mean (HeM), Maclaurin symmetric mean (MSM), Muirhead mean (MM), etc. For example, some weighted algebraic AOs integrated with Power are advanced by Garg et al. [] in the TSFS environment, and Wang and Zhang [] proposed novel T-spherical fuzzy interaction power Heronian mean (TSFIPHeM)aggregation operators that integrated Power and HeM operators and considered the interaction of TSFNs. Liu et al. [] extended the generalized Maclaurin symmetric mean (GMSM) operator to TSFS and proposed the T-spherical fuzzy GMSM operator (TSFGMSM) and the T-spherical fuzzy weighted GMSM operator (TSFWGMSM). Liu et al. [] developed some T-spherical fuzzy power Muirhead mean (TSFPMM) and T-spherical fuzzy power dual Muirhead mean (TSFPDMM)aggregation operators based on the advantages of Power integrated with the Muirhead mean. Yang and Pang [] developed a series of interaction BM (TSFIBM), interaction geometric BM (TSFIGBM), Dombi BM (TSFDBM), and geometric Dombi BM (TSFGDBM) aggregation operators in the TSFS context.
Aczel and Alsina [] proposed two operations, i.e., AA t-norm and s-norm, emphasizing the significance of adjustable parameters. Currently, some scholars have extended AA operations to different decision environments, such as hesitant fuzzy set [], IFS [,,,,], PyFS [,], q-ROFS [], PFS [,], SFS [,], TSFS [], Neutrosophic set [,,], complex q-ROFS [], bipolar complex fuzzy set [], and cubic Fermatean fuzzy set []. Therefore, a variety of aggregation operators have been developed to solve decision challenges indifferent environments. From the above works, we find that some AA operation laws were extended in different decision-making environments, and in many, the weighted averaging and geometric AOs were developed according to AA operation rules. For instance, Senapati et al. [,] advanced some weighted average AOs in IFS and interval-valued IFS successively. Meanwhile, Senapati et al. [,] developed some weighted geometric AOs in IFS and interval-valued IFS. Further, Senapati et al. [,,] proposed some weighted average AOs in PyFS, q-ROFS, and PFS. Naeem et al. [] raised weighted geometric AOs in PFS. Several weighted average and geometric AOs were developed by Hussain et al. [] in the TSFS environment. Senapati et al. [] designed a hesitant fuzzy AA weighted BM (HFAAWBM) operator, in addition to developing weighted average and geometric AOs.
From the above review, we grasp that various AOs can be utilized to handle practical MCDM issues. To obtain the optimal option effectively by using the MCDM method, the evaluation information should be handled more expediently and availably. The TSFS, as a generalized shape of IFS, PyFS, q-ROFS, PFS, and SFS, is one of the most effective means to cope with the ambiguity and uncertainty in assessing data. The Hamy mean (HM) is an aggregation function. Like MSM and MM, HM can reflect the interrelationship among multiple attributes, but its calculation process is not as complex as MSM and MM. However, the HM operator has not been extended in the TSFS context. In addition, AA operation is more generalized and flexible than the existing operations, such as Hamcher, Einstein, Frank, and Dombi []. At present, it can be combined with various aggregation functions, but unfortunately, the research on the new AOs, based on AA operations with the capacity to capture the interrelationship among multiple variables, has not yet appeared. In order to fill the above two research gaps, it is necessary to develop a series of TSFAAHM AOs, based on the advantages of HM and AA, and to design some aggregation function-based MCDM methods in the T-spherical fuzzy environment.
The contributions of this paper are outlined below:
- (1)
- We proposed some new AOs for TSFS, which include the TSFAAHM, TSFAADHM, TSFAAWHM, and TSFAAWDHM operators, and some related properties are discussed.
- (2)
- We designed a novel T-spherical fuzzy MCDM method based on the TSFAAWHM or TSFAAWDHM operator.
- (3)
- We tested the applicability of our proposed aggregation function-based MCDM method by solving investment decision issues.
- (4)
- The proposed method is performed by parameter analysis and comparison analysis, with existing methods to show its reliability and effectiveness.
Therefore, the article is structured as follows. Some ideas of TSFS and AA operations of T-spherical fuzzy numbers are briefly reviewed in Section 2. We define a series of TSFAAHM AOs and analyze their relative properties in Section 3. In Section 4, we construct a MCDM model of applying TSFAAWHM and TSFAAWDHM operators. In Section 5, the validity of the method is verified by solving the investment firm decision problem in a numerical example, and the superiorities of the developed model are depicted by sensitivity and comparative study. Finally, we present the final conclusion in Section 6.
2. Preliminaries
Some basic ideas for TSFSs to make the manuscript self-contained are given in this section.
Definition 1 ([]).
Suppose X is a universe set, then the TSFS can be defined as
where are respectively the MD, AD, and ND of element x ∈ ℑ in X, i.e.,, and satisfying , q ≥ 1 for ∀x ∈ X. is called the degree of refusal. In order to facilitate, δ = (τ, η, ϑ) denoted the T-spherical fuzzy number (TSFN).
Definition 2 ([]).
Suppose δ = (τ, η, ϑ) is a TSFN, then the score function sc(δ) is defined as
and the accuracy function ac(δ) is described as
Let δ1 = (τ1, η1, ϑ1) and δ2 = (τ2, η2, ϑ2) be two TSFNs, the laws of comparing the two TSFNs are as below:
- (1)
- If sc(δ1) is greater than sc(δ2), then δ1 is superior to δ2, i.e., δ1 > δ2;
- (2)
- If sc(δ1) is equal to sc(δ2), then (i) if ac(δ1) is larger than ac(δ2), then δ1 is superior to δ2, i.e., δ1 > δ2; (ii) if ac(δ1) is the same as ac(δ2), then δ1 is equal to δ2, namely, δ1 = δ2.
Definition 3 ([]).
Suppose δ = (τ, η,ϑ), δ1 = (τ1, η1, ϑ1), and δ2 = (τ2, η2, ϑ2) are three arbitrary TSFNs, their basic operations are depicted as follows (λ > 0):
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- .
Definition 4 ([]).
Suppose x and y are two arbitrary, non-negative real numbers (x, y > 0), then the t-norm and s-norm of Aczel–Alsina can be described as follows:
Hussain et al. [] proposed the Aczel–Alsina operation laws for TSFNs based on the TSFS concept and Definition 4.
Definition 5 ([]).
Let δ1 = (τ1, η1, ϑ1) and δ2 = (τ2, η2, ϑ2) be any two TSFNs, q ≥ 1, λ, φ ≥ 0, and then their AA operation laws are defined as:
- (1)
- (2)
- (3)
- (4)
Theorem 1 ([]).
Let δ1 = (τ1, η1,ϑ1) and δ2 = (τ2, η2, ϑ2) be any two TSFNs, λ is a real number, λ1, λ2 ≥ 0, and then the following operation properties are satisfied:
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- ;
- (5)
- ;
- (6)
- .
3. Some TSFAAHM Operators
We propose a series of TSFAAHM AOs involving some AA operations of TSFNs, including the TSFAAHM, TSFAADHM, TSFAAWHM, and TSFAAWDHM operators. Then, we analyze their properties and discuss their special cases.
3.1. HM and DHM Operators
Hara [] introduced an AO for non-negative real numbers in 1998, i.e., HM, which has the capacity to concern the interconnection among multiple input arguments. The specific definition of HM is described as below.
Definition 6 ([]).
Suppose ai(i = 1, 2, 3, …, n) is a set of non-negative real numbers, γ = 1, 2, …, n. If
Then, HM(γ) is named as the Hamy mean, where (i1, i2, …, iγ) traverses all the γ-tuple combinations of (1, 2, …, n), and Cnγ is the binomial coefficient.
Furthermore, a dual form of HM, i.e., dual Hamy mean (DHM), was developed by We et al. [].
Definition 7 ([]).
Suppose ai(i = 1, 2, 3, …, n) is a set of non-negative real numbers, γ = 1, 2, …, n. If
Then, DHM(γ) is named as the dual Hamy mean.
3.2. TSFAAHM and TSFAAWHM Operators
Definition 8.
Let δi = (τi, ηi, ϑi) (i = 1, 2, 3, …, n) be a family of TSFNs, the form of the TSFAAHM operator can be portrayed as:
where γ (γ = 1, 2, …, n) is the parameter of this operator, andis the binomial coefficient with the constraint of 1 ≤ i1 < i2 <…< iγ ≤ n.
According to the AA operation laws of TSFNs, the aggregation results of Equation (8) are as follows.
Theorem 2.
Suppose δi = (τi, ηi, ϑi) (i = 1, 2, …, n) is a family of TSFNs, the outcome of the TSFAAHM operator is still TSFN based on the Definition 5, i.e.,
Proof of Theorem 2.
On the basis of the AA operation laws of TSFNs, there are:
and
Then,
Therefore,
Therefore, Theorem 2 is proved completely. □
Example 1.
Suppose δ1= (0.6, 0.7, 0.5), δ2= (0.9, 0.1, 0.4), δ3= (0.7, 0.6, 0.6), and δ4= (0.2, 0.8, 0.3) are four TSFNs, then the values of the parameters are shown as: q = 3, γ = 2, φ = 3. Then, we can obtain the following calculation results by utilizing Equation (9):
The MDs of δ1, δ2, δ3, and δ4 are aggregated as:
The ADs of δ1, δ2, δ3, and δ4are aggregated as:
Similarly, the NDs of δ1, δ2, δ3, and δ4 are aggregated as:
Therefore,.
Further, we should analyze the relative properties of the TSFAAHM operator.
Theorem 3.
Suppose δi = (τi, ηi, ϑi) (i = 1, 2, …, n) are a group of TSFNs, the TSFAAHM operator can meet the below properties:
- (1)
- (Idempotency) If the values of all TSFNs are equal, i.e., δi = δ = (τ, η, ϑ), then
- (2)
- (Boundness) Let and , then
- (3)
- (Monotonicity) Let (i = 1, 2, …, n) be another group of TSFNs, if all isatisfy , i.e., , and , then
The above properties can be proved as follows.
Proof of Theorem 3.
(1) (Idempotency) According to Theorem 2, the following can be obtained from the TSFAAHM operator, i.e.,:
Similarly,
Therefore, .
So, the idempotency of the operator is proved.
(2) (Boundness) Due to , on the basis of the above idempotency of the TSFAAHM operator, then:
Similarly, .
Therefore, , the boundness of this operator is validated.
(3) (Monotonicity) Due to , , , , then
Similarly,
On the basis of Theorem 2, is obtained. Thus, the monotonicity of the operator is certified.
Therefore, the proof of the properties of the TSFAAHM operator is completed. □
Although the TSFAAHM operator is able to consider the interrelationship between various criteria, it neglects the degree of importance of each criterion, for which we develop the TSFAAWHM operator, as below.
Definition 9.
Suppose δi = (τi, ηi, ϑi) (i = 1, 2, …, n) is a group of TSFNs, w = (w1, w2, …, wn)T is denoted the weight vector of δi(i = 1, 2, …, n), meeting wi ∈ [0,1] and . If
Then, the operator is named as the TSFAAWHM operator.
On the basis of the AA operation laws of TSFNs, the aggregation result of Equation (13) is as follows.
Theorem 4.
Suppose δi = (τi, ηi, ϑi) (i = 1, 2, …, n) is a family of TSFNs, the aggregation result of the TSFAAWHM operator is still TSFN, i.e.,
The aggregation result of the TSFAAWHM operator is still TSFN, and its proof is identical to Theorem 2. Hence, we ellipsis it here.
The TSFAAWHM operator still satisfies monotonicity and boundness, but not idempotency. So, we omit the proof here.
3.3. TSFAADHM and TSFAAWDHM Operators
Definition 10.
Let δi = (τi, ηi, ϑi) (i = 1, 2, …, n) be a family of TSFNs, the TSFAADHM operator is described as
According to the AA operation laws of TSFNs, the aggregation result of Equation (15) is as below.
Theorem 5.
Suppose δi (i = 1, 2, 3, …, n) is a group of TSFNs. Based on the AA operation laws for TSFNs of Definition 5, then the result of the TSFAADHM operator is still TSFN, i.e.,
Proof of Theorem 5.
According to the AA operation rules of TSFNs, we have
and
Then,
Thus,
Therefore, the proof of theorem 5 is completed. □
Example 2.
Suppose δ1= (0.6, 0.7, 0.5), δ2= (0.9, 0.1, 0.4), δ3= (0.7, 0.6, 0.6), and δ4= (0.2, 0.8, 0.3) are four TSFNs, and the values of the parameters are shown as q = 3, γ = 2, φ = 3. Then, we can obtain the following calculation results by utilizing Equation (16).
The MDs of δ1, δ2, δ3, and δ4 are aggregated as:
The ADs of δ1, δ2, δ3, and δ4 are aggregated as:
Similarly, The NDs of δ1, δ2, δ3, and δ4 are aggregated as:
Therefore, .
The TSFAADHM operator satisfies monotonicity, boundness, and idempotency. The proof of these properties resembles Theorem 3.
In order to address the condition that the TSFAADHM operator neglects the importance degree of each criterion, we can define the TSFAAWDHM operator.
Definition 11.
Suppose δi (i = 1, 2, …, n) is a group of TSFNs, w = (w1, w2, …, wn)T is denoted as the weight vector of δi (i = 1, 2, …, n), meeting wi ∈ [0,1] and . If
Then, the operator is named as the TSFAAWDHM operator.
According to the AA operation laws for TSFNs, the aggregation result of Equation (17) is as below.
Theorem 6.
Suppose δi (i = 1, 2, …, n) is a group of TSFNs. The integration result of the TSFAAWDHM operator is still TSFN, i.e.,
The TSFAAWDHM operator still satisfies monotonicity and boundness, but not idempotency. The proof process is omitted here.
4. MCDM Based on the TSFAAHM Aggregation Operators
The T-spherical fuzzy (TSF) MCDM problems can be described as: H = {h1, h2, …, hm} is denoted as a family of alternatives, C = {c1, c2, …, cn} is denoted as a family of criteria, and its weight vector is named as w = (w1, w2, …, wn)T, meeting 0 ≤ wi ≤ 1, . The criteria weight vector is determined by the comprehensive evaluation of the expert group for assignment. D = [dij]m×n is denoted as the initial TSF evaluation matrix given by experts, where is denoted as the expert’s evaluation value of alternative hi with respect to criterion cj and is expressed in terms of TSFN and satisfies 0 ≤ τij, ηij, ϑij ≤ 1 and 0 ≤ (τij)q + (ηij)q + (ϑij)q ≤ 1 (i = 1, 2, 3, …, m; j = 1, 2, 3, …, n; q ≥ 1).
Based on the above depiction of the TSFMCDM problem, we should apply the developed TSFAAWHM and TSFAAWDHM operators to handle the MCDM problem and obtain the best alternative. The specific steps are depicted as below.
Step 1. The initial T-spherical fuzzy evaluation matrix should be normalized. Generally, the criteria in the MCDM problem can be classified into cost- and benefit-type criteria. The former needs to be transformed into a benefit-type criterion, and the transformation process can be implemented by Equation (19). Therefore, the standardized T-spherical fuzzy decision-making matrix R = [rij]m×n is obtained.
where (dij)C is the complement of dij, J1 and J2 express, respectively, the criteria of the benefit- and cost-type.
Step 2. The comprehensive value for each alternative with regard to all criteria evaluation data can be computed by the TSFAAWHM (Equation (20)) or the TSFAAWDHM operator (Equation (21)).
or
Step 3. The results of the score function sc(fi) (Equation (2)) and accuracy function ac(fi) (Equation (3)) are calculated for each alternative. Then, the best option is determined after the descending ranking of alternatives, the bigger the better.
Step 4. End.
5. Numerical Example
The applicability and effectiveness of the developed aggregation operator in a TSF context can be proved by discussing the application of the developed model to evaluate and select the optimal investment strategy (revised from Ullah et al. []) in this section.
5.1. Application for Investment
Suppose that an investment company plans to choose the most desirable one to select and invest among four companies (alternatives): (1) a car company (h1); (2) a food company (h2); (3) a computer company (h3); and (4) an arms company (h4). Through preliminary research and study, the experts selected five factors as evaluation criteria: c1 (risk of loss of investment capital); c2 (probability of return on capital investment); c3 (prospects for market development); c4 (total capital subject to inflation); and c5 (industry growth potential). All of the five criteria had a great impact on the success of the investment strategy, and the experts provided their evaluations with all five criteria in mind. Let w = (0.15, 0.2, 0.3, 0.2, 0.15)T be the weight vector of the criteria. The expert panel expressed the evaluation information for each alternative with each criterion by using TSFN. Therefore, the initial TSF evaluation matrix D was given by the expert panel and is shown in Table 1.

Table 1.
The initial TSF evaluation matrix D.
5.2. Decision Analysis
5.2.1. The Method by the Proposed TSFAAWHM Operator
Step 1. Since c1 is a cost-type criterion and the rest of the criteria are all benefit-type, then the normalized TSF decision matrix R can be obtained from Equation (19), and the results can be listed in Table 2.

Table 2.
The normalized TSF decision matrix R.
Step 2. The comprehensive TSF values fi (i = 1, 2, 3, 4) for each solution with regard to all criteria are calculated by the TSFAAWHM operator (Equation (20)). Suppose the parameters q = 3, γ = 2, φ = 2.
The DM of aggregation result in the comprehensive value of alternative f1 is τ1, that is
The AD of aggregation result in the comprehensive value of alternative f1 is η1, that is
The ND of aggregation result in the comprehensive value of alternative f1 is ϑ1, that is
So, we can get the comprehensive value f1 of alternative h1, that is f1 = (0.913, 0.214, 0.497).
Similarly, we can get the comprehensive values of the other three alternatives, namely, f2 = (0.885, 0.219, 0.450), f3 = (0.892, 0.276, 0.464), and f4 = (0.931, 0.312, 0.455).
Step 3. Equation (2) is applied to compute each alternative (i = 1, 2, 3, 4). Since the values of the score functions for each alternative can be easily distinguished, it is not necessary to calculate the accuracy function of each alternative here. Therefore, we obtain
Step 4. Then, the alternatives are ranked as h4 > h1 > h2 > h3. Therefore, the optimal solution is h4.
5.2.2. The Method by the Proposed TSFAAWDHM Operator
Step 1. Since c1 is a cost-type criterion and the rest of the criteria are all benefit-type, then the normalized TSF decision-making matrix R can be obtained from Equation (19), and the calculation results are listed in Table 2.
Step 2. The comprehensive values fi (i = 1, 2, 3, 4) for each solution with regard to all criteria are calculated by the TSFAAWDHM operator (Equation (21)). Suppose the parameters q = 3, γ = 2, φ = 2.
The DM of aggregation result in the comprehensive value of alternative f1 is τ1, that is
The AD of aggregation result in the comprehensive value of alternative f1 is η1, that is
The ND of aggregation result in the comprehensive value of alternative f1 is ϑ1, that is
So, we can get the comprehensive value f1 of alternative h1, that is f1 = (0.582, 0.682, 0.875).
Similarly, we can get the comprehensive values of the other three alternatives, namely, f2 = (0.505, 0.681, 0.851), f3 = (0.533, 0.729, 0.859), and f4 = (0.614, 0.740, 0.832).
Step 3. Equation (2) is applied to calculate each alternative (i = 1, 2, 3, 4). Since the values of the score functions for each alternative can be easily distinguished, it is not necessary to calculate the accuracy function of each alternative here. Therefore, we obtain
Step 4. Then, the alternatives are ranked as h4 > h1 > h2 > h3. Therefore, the optimal solution is h4.
5.3. Parameter Analysis
In this sub-section, the sensitivity analysis on the q, γ, and φ is performed. Firstly, in the case of γ = 2 and φ = 2, we analyze the variation of the solution ranking results when the proposed AOs take diverse values of the parameter q in the range [,], as shown in Figure 1, (a) the variation of the TSFAAWHM operator results with q and (b) the variation of the TSFAAWDHM operator results with q.
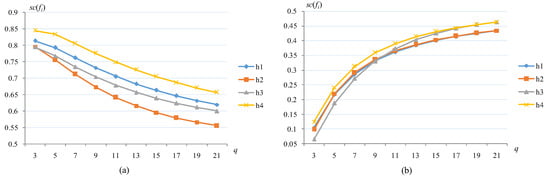
Figure 1.
The variations of (a) TSFAAWHM and (b) TSFAAWDHM with parameter q.
From Figure 1a,b, the results of the TSFAAWHM operator decrease when the q increases, while the results of the TSFAAWDHM operator are the opposite. In terms of alternative ranking, the ranking of the TSFAAWHM operator is h4 > h1 > h2 > h3 when q = 3, while the alternatives h2 and h3 are ranked slightly differently when q ≥ 4, i.e., h4 > h1 > h3 > h2, and the ranking result is relatively stable with the variety of q. However, the outcomes achieved by the TSFAAWDHM operator fluctuate considerably as the value of q changes. For example, the solution h3 changes from the last rank to the top rank when the change of parameter q is in [,]. When the change of q is in the range of [,], the alternative h4 is the best one, but when q = 21, the alternative h4 is second. In comparison, the TSFAAWHM operator is more stable and reliable than the TSFAAWDHM operator with respect to the parameter q.
Then, we check the effect of the variation of γ and φ on the ranking condition of the alternatives. Different values of the parameters γ ∈ [,] and φ ∈ [,] are taken to examine the effect on the outcomes of the alternatives in the case of q = 3. The results of the TSFAAWHM operator with respect to the parameters γ, φ are shown in Figure 2, and the results of the TSFAAWDHM operator with respect to the parameters γ, φ are shown in Figure 3.
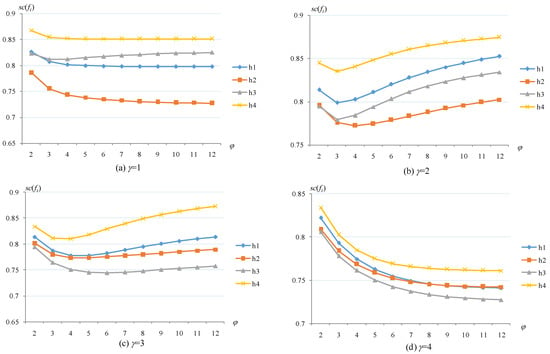
Figure 2.
The results of TSFAAWHM operator with respect to parameters γ and φ.
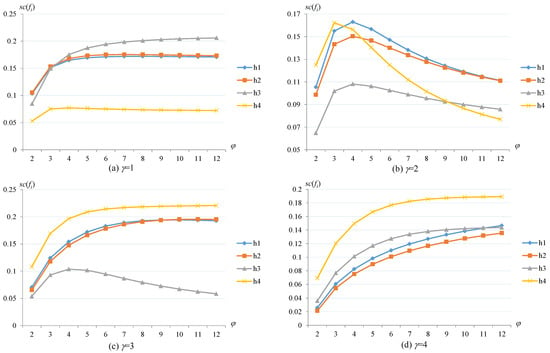
Figure 3.
The results of TSFAAWDHM operator with respect to parameters γ and φ.
When the parameter γ takes values 1, 2, 3, or 4, the parameter φ varies in the range of [,], and the results of the TSFAAWHM operator in Figure 2 also change, especially the ranking of the alternatives h1, h2, and h3, but h4 is always the optimal solution. From Figure 3, h4 is the worst one when γ = 1; h4 changes from the first one to the last ranking when γ = 2; however, 4 is always the optimal alternative when γ = 3 and 4. In addition, the rankings of the alternatives h1, h2 and h3 change in various ways. From the comparison of Figure 2 and Figure 3, the results of the TSFAAWDHM operator are more significantly influenced by the parameters γ and φ.
5.4. Comparison Analysis
The developed AOs are compared with the available AOs and alternative ranking techniques in this sub-section. Firstly, we use the existing TSF weighted average (TSFWA) [], TSF weighted geometric (TSFWG) [], TSF AA weighted average (TSFAAWA) [], TSF AA weighted geometric (TSFAAWG) [], and TSF weighted generalized MSM (TSFWGMSM) [] operators to solve the problem of the investment selection in Section 5.1. It should be noted that the values of the parameters in these AOs are q = 3, φ = 2 in the AA operator, and γ = 2 in the MSM operator. Thus, we can obtain the calculated results, and they are listed in Table 3.

Table 3.
The comparisons with different AOs.
From Table 3, the best solution for all the AOs is h4, except for the TSFAAWG operator, and the other alternatives are ranked slightly differently. It can be validated that the developed operator is feasible and effective. The detailed analysis of comparing the new method to the existing AOs is as follows:
(1) The existing TSFWA and TSFWG operators neither consider the correlation relationship between the criteria nor include the flexibility parameter, thus these two AOs do not have the advantages of the proposed TSFAAWHM and TSFAAWDHM operators in the practical decision process.
(2) The TSFAAWA and TSFAAWG operators also contain AA t-norms with the flexibility parameter, but they still do not reach the extent of decision flexibility of the proposed operators. Moreover, these two AOs not only advocate the independence of criterion, but also ignore the interrelationship among multiple criteria. The results of these two AOs are similar to the proposed AOs from Table 4 when γ = 1, and the optimal alternative is h4 or h1.

Table 4.
The comparisons with different ranking techniques.
(3) In the TSFWGMSM operator, which contains multiple parameters, its extent of decision flexibility is comparable to that of the proposed AOs, and it also can capture the correlation relationship between multiple criteria, so the results of the alternatives ranking are similar to the developed AOs in this article.
Next, it can be seen that the optimum alternative obtained by the methods in this paper and the existing ranking techniques are all h4, and the other alternatives are ranked slightly differently from Table 4. Specifically, the distance-based TOPSIS (Technique for order preference by similarity to an ideal solution) [] and TODIM (Portuguese acronym meaning interactive multi-criteria decision making) [] methods yield alternatives ranked as h4 > h1 > h3 > h2, which is consistent with the results of the TSFAAWHM operator and slightly different from the results of the TSFAAWDHM operator in terms of the alternatives h2 and h3. However, compared to the utility-based CoCoSo (Combined compromise solution) [] and MULTIMOORA (multi-objective optimization based on the ratio analysis with the full multiplicative form) [] methods, the results of the alternatives ranking consist of a larger difference, except for the optimal solution is h4. In addition, the steps in the presented method are more succinct than the existing ranking techniques in selecting the best solution and can overcome the drawback that these ranking techniques ignore the correlation relationship between criteria. In summary, the developed method in this paper has a certain effectiveness and operability in solving the TSF MCDM problem.
6. Conclusions
The MCDM problem with uncertainty and complexity is prevalent in real-life, and the evaluation information representation and aggregation in solving the decision problem has been one of the challenging tasks. In this article, the integrating Hamy mean operator and AA t-norms were investigated to deal with the MCDM issues in the TSF setting. We developed a series of TSFAAHM AOs, named TSFAAHM, TSFAADHM, TSFAAWHM and TSFAAWDHM operators, and then analyzed the different properties of these AOs. We also applied the TSFAAWHM and TSFAAWDHM operators to construct the MCDM method. We showed the practicability and effectiveness of the raised decision method by means of numerical example, and then verified the superiority of the developed approach by parameter tests and contrastive study. The proposed AOs and methods in this paper not only improve the decision-making theory and method system, but also provide industry managers with decision analysis tools, and the results can be used as the basis for decisions.
Although the AOs proposed in this article can flexibly adjust the decision parameters according to the practical decision conditions in the TSF MCDM problems, and it can consider the interrelationship among multiple decision criteria, there are still some limitations for the decision method based on the developed AOs. (1) The criterion weight information may be completely or partially unknown in practical MCDM problems, but the criterion weights are given in the numerical example for the TSFMCDM problem in this paper. (2) If the MCDM problem has a lot of criteria, then it will cause a more complicated calculation process in the TSFAAWHM or TSFAAWDHM operator. (3) For the results of utilizing the proposed AOs, the score function or the accuracy function of TSFN (see Definition 2) are often used for defuzzification, but they ignore the role of the refusal degree in TSFN during the defuzzification process, which may lead to partial loss of information and make the final value imprecise.
In order to eliminate these above-mentioned drawbacks, in the future, we will construct new distance measure-based, criterion weight determination methods, such as Lance distance in the TSF MCDM problem. We attempt to design a hierarchical aggregation model for evaluation information to reduce the computational complexity of the AO involving correlations among multiple criteria, i.e., partitioned BM [], HeM [], and MM [], while eliminating computational difficulties, with the help of computational software tools. We will combine the proposed AOs with ranking techniques, such as ARAS (Additive Ratio ASsessment) [], MARCOS (Measurement Alternatives and Ranking based on the COmpromise Solution) [], EDAS (Evaluation based on Distance from Average Solution) [], DNMA (Double Normalization-based Multi-Aggregation) [], etc., to achieve precision by distance measures, thus replacing the use of the score or accuracy function of TSFN. Further, we will develop these methods to construct group decision models to solve realistic decision-making issues, such as green supplier selection, site selection decision, and technology selection in real enterprises.
Author Contributions
Conceptualization, H.W. and T.X.; methodology, H.W. and T.X.; formal analysis, L.F.; investigation, H.W. and T.M.; resources, L.F.; writing—original draft preparation, H.W. and T.X.; writing—review and editing, H.W., K.U. and T.M.; visualization, T.X.; supervision, L.F.; project administration, H.W. and L.F.; funding acquisition, H.W. and L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 71862025), the Humanities and Social Sciences Foundation of Ministry of Education of the People’s Republic of China (No. 19YJC630164), and the Postdoctoral Science Foundation of Jiangxi Province (No. 2019KY14).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Notations
| ac(δ) | Accuracy function of TSFN δ |
| ai | The i-th non-negative real number |
| αi, χi, βi | The assessment values of the i-th alternative obtained by TSFMULTIMOORA |
| C | Criteria set |
| Cnγ | The binomial coefficient |
| cj | The j-th criterion |
| cci | The closeness coefficient of the i-th alternative obtained by TSF TOPSIS |
| γ | The number of combinations in the Hamy mean |
| D | The initial TSF evaluation matrix |
| dij | The initial TSF evaluation value of the alternative hi w.r.t. criterion cj |
| δ | TSFN of ℑ |
| δ−, δ+ | The minimum and maximum values of TSFN |
| fi | The comprehensive value of the i-th alternative |
| H | Alternative set |
| hi | The i-th alternative |
| i,j | Index of number |
| J1, J2 | Benefit and cost criterion type |
| n,m | Number of evaluation objects |
| q | Power of MD, AD, and ND of TSFN |
| R | The standardized TSF evaluation matrix |
| rij | The standardized TSF evaluation value of the alternative hi w.r.t. criterion cj |
| ℑ | T-spherical fuzzy set |
| SAφ | The s-norm of the Aczel–Alsina operator |
| sc(δ) | Score function of TSFN δ |
| TAφ | The t-norm of Aczel–Alsina |
| τ, η, ϑ | MD, AD, ND of TSFN |
| w | The weight vector of criteria |
| wj | Weight of the j-th criterion |
| φ | Modulation parameter in the Aczel–Alsina operator |
| X | A universe set |
| x, y, λ | Non-negative real numbers |
| Zi | The assessment value of the i-th alternative obtained by TSF CoCoSo |
References
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Cuong, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409–420. [Google Scholar]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, l31, 7041–7053. [Google Scholar] [CrossRef]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide for Practitioners; Springer: Heidelberg/Berlin, Germany, 2007. [Google Scholar]
- Zhou, S.H.; Chang, W.B. Approach to multiple attribute decision making based on the Hamacher operation with fuzzy number intuitionistic fuzzy information and their application. J. Intell. Fuzzy Syst. 2014, 27, 1087–1094. [Google Scholar] [CrossRef]
- Zhao, X.F.; Wei, G.W. Some intuitionistic fuzzy Einstein hybrid aggregation operators and their application to multiple attribute decision making. Knowl.-Based Syst. 2013, 37, 472–479. [Google Scholar] [CrossRef]
- Wei, G.W. Pythagorean fuzzy interaction aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 2119–2132. [Google Scholar] [CrossRef]
- Ju, Y.B.; Liang, Y.Y.; Luo, C.; Dong, P.W.; Gonzalez, E.D.R.S.; Wang, A.H. T-spherical fuzzy TODIM method for multi-criteria group decision-making problem with incomplete weight information. Soft Comput. 2021, 25, 2981–3001. [Google Scholar] [CrossRef]
- Wang, H.L.; Zhang, F.M. Interaction power Heronian mean aggregation operators for multiple attribute decision making with T-spherical fuzzy information. J. Intell. Fuzzy Syst. 2022, 42, 5712–5739. [Google Scholar] [CrossRef]
- Mahnaz, S.; Ali, J.; Malik, M.G.A.; Bashir, Z. T-spherical fuzzy Frank aggregation operators and their application to decision making with unknown weight information. IEEE Access 2022, 10, 7408–7438. [Google Scholar] [CrossRef]
- Jana, C.; Senapati, T.; Pal, M. Pythagorean fuzzy Dombi aggregation operators and its applications in multiple attribute decision-making. Int. J. Intell. Syst. 2019, 34, 2019–2038. [Google Scholar] [CrossRef]
- Khan, Q.; Gwak, J.; Shahzad, M.; Alam, M.K. A novel approached based on T-spherical fuzzy Schweizer-Sklar power Heronian mean operator for evaluating water reuse applications under uncertainty. Sustainability 2021, 13, 7108. [Google Scholar] [CrossRef]
- Hussain, A.; Ullah, K.; Yang, M.S.; Pamucar, D. Aczel-Alsina aggregation operator on T-spherical fuzzy (TSF) information with application to TSF Multi-attribute decision making. IEEE Access 2022, 10, 26011–26023. [Google Scholar] [CrossRef]
- Garg, H.; Ullah, K.; Mahmood, T.; Hassan, N.; Jan, N. T-spherical fuzzy power aggregation operators and their applications in multi-attribute decision making. J. Ambient Intell. Humaniz. Comput. 2021, 12, 9076–9080. [Google Scholar] [CrossRef]
- Liu, P.D.; Zhu, B.Y.; Wang, P. A multi-attribute decision-making approach based on spherical fuzzy sets for Yunnan Baiyao’s R & D project selection. Int. J. Fuzzy Syst. 2019, 21, 2168–2191. [Google Scholar]
- Liu, P.D.; Khan, Q.; Mahmood, T.; Hassan, N. T-spherical fuzzy power Muirhead mean operator based on novel operational laws and their application in multi-attribute group decision making. IEEE Access 2019, 7, 22613–22632. [Google Scholar] [CrossRef]
- Yang, W.; Pang, Y.F. T-spherical fuzzy Bonferroni mean operators and their application in multiple attribute decision making. Mathematics 2022, 10, 988. [Google Scholar] [CrossRef]
- Aczel, J.; Alsina, C. Characterization of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgments. Aequ. Math. 1982, 25, 313–315. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.Y.; Mesiar, R.; Yager, R.R.; Saha, A. Novel Aczel-Alsina operations-based hesitant fuzzy aggregation operators and their applications in cyclone disaster assessment. Int. J. Gen. Syst. 2022, 51, 511–546. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.Y.; Yager, R.R. Aczel-Alsina aggregation operators and their application to intuitionistic fuzzy multiple attribute decision making. Int. J. Intell. Syst. 2022, 37, 1529–1551. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.Y.; Mesiar, R.; Yager, R.R. Intuitionistic fuzzy geometric aggregation operators in the framework of Aczel-Alsina triangular norms and their application to multiple attribute decision making. Expert Syst. Appl. 2023, 212, 118832. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.Y.; Mesiar, R.; Yager, R.R. Novel Aczel-Alsina operations-based interval-valued intuitionistic fuzzy aggregation operators and their applications in multiple attribute decision-making process. Int. J. Intell. Syst. 2022, 37, 5059–5081. [Google Scholar] [CrossRef]
- Senapati, T.; Mesiar, R.; Simic, V.; Iampan, A.; Chinram, R.; Ali, R. Analysis of interval-value intuitionistic fuzzy Aczel-Alsina geometric aggregation operators and their application to multiple attribute decision-making. Axioms 2022, 11, 258. [Google Scholar] [CrossRef]
- Senapati, T.; Simic, V.; Saha, A.; Dobrodolac, M.; Rong, Y.; Tirkolaee, E.B. Intuitionistic fuzzy power Aczel-Alsina model for prioritization of sustainable transportation sharing practices. Eng. Appl. Artif. Intell. 2023, 119, 105716. [Google Scholar] [CrossRef]
- Senapati, T.; Mishra, A.R.; Saha, A.; Simic, V.; Rani, P.; Ali, R. Construction of interval-valued Pythagorean fuzzy Aczel-Alsina aggregation operators for decision making: A case study in emerging IT software company selection. Sādhanā 2022, 47, 255. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.Y.; Mesiar, R.; Saha, A. Multiple attribute decision making based on Pythagorean fuzzy Aczel-Alsina average aggregation operators. J. Ambient Intell. Humaniz. Comput. 2022. [Google Scholar] [CrossRef]
- Senapati, T.; Martinez, L.; Chen, G.Y. Selection of appropriate global partner for companies using q-rung orthopair fuzzy Aczel-Alsina average aggregation operators. Int. J. Fuzzy Syst. 2022. [Google Scholar] [CrossRef]
- Senapati, T. Approaches to multi-attribute decision-making based on picture fuzzy Aczel-Alsina average aggregation operators. Comput. Appl. Math. 2022, 41, 40. [Google Scholar] [CrossRef]
- Naeem, M.; Khan, Y.; Ashraf, S.; Weera, W.; Batool, B. A novel picture fuzzy Aczel-Alsina geometric aggregation information: Application to determining the factors affecting mango crops. AIMS Math. 2022, 7, 12264–12288. [Google Scholar] [CrossRef]
- Naeem, M.; Ali, J.A. novel multi-criteria group decision-making method based on Aczel-Alsina spherical fuzzy aggregation operators: Application to evaluation of solar energy cells. Phys. Scr. 2022, 97, 085203. [Google Scholar] [CrossRef]
- Riaz, M.; Farid, H.M.A.; Pamucar, D.; Tanveer, S. Spherical fuzzy information aggregation based on Aczel-Alsina operations and data analysis for supply chain. Math. Probl. Eng. 2022, 2022, 9657703. [Google Scholar] [CrossRef]
- Ye, J.; Du, S.G.; Yong, R. Aczel-Alsina weighted aggregation operators of Neutrosophic Z-numbers and their multiple attribute decision-making method. Int. J. Fuzzy Syst. 2022, 24, 2397–2410. [Google Scholar] [CrossRef]
- Ashraf, S.; Ahmad, S.; Naeem, M.; Riza, M.; Alam, M.A. Novel EDAS methodology based on single-valued neutrosophicAczel-Alsina aggregation information and their application in complex decision-making. Complexity 2022, 2022, 2394472. [Google Scholar] [CrossRef]
- Yong, R.; Ye, J.; Du, S.G.; Zhu, A.Q.; Zhang, Y.Y. Aczel-Alsina weighted aggregation operators of simplified Neutrosophic numbers and its application in multiple attributedecision making. CMES-Comp. Model. Eng. 2022, 132, 569–584. [Google Scholar]
- Ali, J.; Naeem, M. Complex q-rung orthopair fuzzy Aczel-Alsina aggregation operators and its application to multiple criteria decision-making with unknown weight information. IEEE Access 2022, 10, 85315–85342. [Google Scholar] [CrossRef]
- Mahmood, T.; Rehman, U.; Ali, Z. Analysis and application of Aczel-Alsina aggregation operators based on bipolar complex fuzzy information in multiple attribute decision making. Inf. Sci. 2023, 169, 817–833. [Google Scholar] [CrossRef]
- Rong, Y.; Yu, L.Y.; Niu, W.Y.; Liu, Y.; Senapati, T.; Mishra, A.R. MARCOS approach based upon cubic Fermatean fuzzy set and its application in evaluation and selecting cold chain logistics distribution center. Eng. Appl. Artif. Intell. 2022, 116, 105401. [Google Scholar] [CrossRef]
- Hara, Y.; Uchiyama, M.; Takahasi, S.E. A refinement of various mean inequalities. J. Inequalities Appl. 1998, 2, 387–395. [Google Scholar] [CrossRef]
- Wu, S.J.; Wang, J.; Wei, G.W.; Wei, Y. Research on construction engineering project risk assessment with some 2-tuple linguistic neutrosophicHamy mean operators. Sustainability 2018, 10, 1536. [Google Scholar] [CrossRef]
- Ullah, K.; Hassan, N.; Mahmood, T.; Jan, N.; Hassan, M. Evaluation of investment policy based on multi-attribute decision-making using interval-valued T-spherical fuzzy aggregation operators. Symmetry 2019, 11, 357. [Google Scholar] [CrossRef]
- Ullah, K.; Ali, Z.; Mahmood, T.; Garg, H.; Chinram, R. Method for multi-attribute decision making, pattern recognition and clustering based on T-spherical fuzzy information measures. J. Intell. Fuzzy Syst. 2022, 42, 2957–2977. [Google Scholar] [CrossRef]
- Huang, G.Q.; Xiao, L.M.; Pedrycz, W.; Zhang, G.H.; Martinez, L. Failure mode and effect analysis using T-spherical fuzzy maximizing deviation and combined comparison solution methods. IEEE Trans. Reliab. 2022. [Google Scholar] [CrossRef]
- Mahmood, T.; Warraich, M.S.; Ali, Z.; Pamucar, D. Generalized MULTIMOORA method and Dombi prioritized weighted aggregation operators based on T-spherical fuzzy sets and their applications. Int. J. Intell. Syst. 2021, 36, 4659–4692. [Google Scholar] [CrossRef]
- Banerjee, D.; Guha, D.; Mesiar, R.; Mondol, J.K. Development of the generalized multi-dimensional extended partitioned Bonferroni mean operator and its application in hierarchical MCDM. Axioms 2022, 11, 600. [Google Scholar] [CrossRef]
- Selvaraj, J.; Gatiyala, P.; Zolfani, S.H. Trapezoidal intuitionistic fuzzy power Heronian aggregation operator and its applications to multiple-attribute group decision-making. Axioms 2022, 11, 588. [Google Scholar] [CrossRef]
- Zavadskas, E.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Stevic, Z.; Pamucar, D.; Puska, A.; Chatterjee, P. Sustainable supplier selection in healthcare industries using a new MCDM method: Measurement of alternatives and ranking according to compromise solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Keshavarz, G.M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Liao, H.C.; Wu, X.L. DNMA: A double normalization-based multiple aggregation method for multi-expert multi-criteria decision making. Omega 2020, 94, 102058. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).