Viability Analysis of Tidal Turbine Installation Using Fuzzy Logic: Case Study and Design Considerations

Abstract

Tidal energy represents a clean and sustainable source of energy generation that can address renewable energy challenges, especially the global challenge of optimizing alternatives for stable supply. Although tidal stream energy extraction technology is in the early stages of development, it shows great potential compared to other renewable energy sources. The main objective of this research is to provide a digital tool for the optimization of the installation of turbines through fuzzy logic. The methodology in this study includes the design and development of a fuzzy-logic-based tool for this purpose. Design criteria included parameters such as salinity, temperature, currents, depth, and water viscosity, which affect the performance of tidal turbines. These parameters are obtained from the geographic location of the installation. A decision-making system is provided to support the tool. The designed fuzzy logic system evaluates the suitability of different turbine locations and presents the results through graphics and probability of success percentages. The results indicate that currents and temperatures are the most limiting factors in terms of potential turbine locations. The program provides a practical and efficient tool for optimizing the selection of tidal turbines and generating energy from ocean currents. This tool is evaluated and validated through different cases. With this approach, the aim is to encourage the development of tidal energy and its adoption worldwide.

1. Introduction

The availability of energy is an essential requirement for the economic and technical development of all countries. However, the current energy and environmental issues, both those derived from the depletion of resources and the temporary ones, are becoming increasingly serious. Resources such as oil, natural gas, etc., are being gradually depleted, and their availability depends on third parties. Therefore, both industries and individuals must start looking for alternative energy sources and give more attention to renewable energy sources [1,2].

The energy derived from the tides represents a clean and sustainable source that can be explored in greater depth and rigor to face the current energy issues [3]. Tidal energy has benefits such as security of supply and reduction in CO₂ emissions. For these reasons, it is necessary to support this technology and give it due attention to increase its adoption [4].

Tidal current and offshore wind energy production techniques together account for about 0.75% of global energy production [5]. Tidal current energy has more potential for regular, daily use compared to wave energy or offshore wind energy, which is more subject to variations and greater dispersion [6]. However, very few areas are suitable for extracting energy from tidal currents. The technology related to the extraction of energy from tidal currents has been historically used for centuries in coastal areas, e.g., for the production of flour (as in tidal mills); however, it is still in an incipient stage of development for electrical use. Some of the places with the greatest potential include the United Kingdom, Canada, France, Norway, Spain, Indonesia, Taiwan, and New Zealand, among others, due to the properties of the marine currents in these geographical areas [7,8,9,10,11].

The selection of a specific location for tidal turbines is often based on large amounts of information, and is sometimes complex. These problems are often complex, both in structure and management. To formally structure the process of making complex decisions on the location of tidal turbines, some theoretical tools have been proposed [12,13,14]. However, they lack automated support to facilitate this decision making. Therefore, the aim of this work was to propose accessible, scalable, digital-based tools to promote the implementation of this type of technology.

One way to approach this type of decision is to apply a branch of mathematics known as fuzzy logic. Fuzzy logic has been applied to decision-making problems in a wide spectrum of applications in the field of operations management [15]. Due to the strong similarities between the different applications in this field, fuzzy logic could also be considered a feasible method to redirect decision making.

Fuzzy logic has gained great relevance due to the variety of its applications, which range from the control of complex industrial processes to the design of artificial devices for automatic deduction, through to the construction of electronic devices for home use and entertainment, as well as diagnostic systems [16].

Similar solutions to the one proposed in this study have been developed for traditional wind turbine applications [17,18]. Fuzzy logic has been used in the health sector in the development of a decision support system for the diagnosis of diabetes mellitus [19]. There are also studies that have used fuzzy logic to optimize the location of onshore wind turbines [20]. Xue et al. proposed a fuzzy model for offshore wind turbines in China, while Abdelmassih et al. proposed a fuzzy logic solution for wind farm applications in the USA. Smith et al. optimized wind turbine placement using fuzzy logic. However, in this research context, there is a gap in digital tools for decision making, and although there are existing proposals, they do not have the same application. This work thus focused on providing a solution for this specific application, within a scalable context.

The use of the fuzzy methodology based on the theory of fuzzy sets allows the management of uncertainty and imprecision in the data. By employing fuzzy logic, one can model and analyze variables that are not easily quantifiable, or assignment ranges that have a subjective nature [21,22,23,24]. The fuzzy logic models used in the article, present advantages such as uncertainty management, flexibility, intuitive interpretation, and the integration of expert knowledge. However, there are other models and approaches that could also be considered, such as multicriteria analysis, traditional statistical methods, mathematical programming models, and approaches based on machine learning and artificial intelligence.

Therefore, in this work, a set of fuzzy rules and membership functions that describe the relationships between the variables and their linguistic values are required. These rules and functions allow us to evaluate the quality of the location of marine turbines in a more precise and adaptable way to tailor to the specific conditions of the environment [25,26,27]. There are also programs that aim to help in the selection of turbines to take advantage of the energy not used in hydraulic networks. Fuzzy logic also provides a practical and efficient tool to optimize energy recovery in this type of system [28].

The objective of this study was to design and develop a fuzzy-logic-based computer program to support the selection of tidal turbines locations to take advantage of the energy that can be obtained from the movements of ocean and sea currents. This design provides an applied and efficient way to optimize installation selection for tidal turbines and power generation from ocean currents. In addition, it was validated and evaluated through different case studies, which supports its usefulness and precision in decision-making. The novelty of this study lies in the development of a digital tool based on fuzzy logic for the selection and evaluation of tidal turbine locations. This digital tool provides a scalable application environment. The input variables of this application are the hydrodynamic parameters and conditions of the study area (current speed, depth of the water sheet, water temperature, and salinity). From these, it is possible to estimate the corresponding performance that different types of turbines will present [29,30]. The result obtained from the developed program is the level of feasibility of a given location based on its intrinsic characteristics for the installation of this type of power generation system.

The next section details the design of the fuzzy logic system, including the criteria on which it has been based, as well as the design and implementation of the digital tool itself. Then, in the Results section, the interface of this fuzzy logic tool is shown, together with the application to specific practical cases, analyzing them with respect to the key parameters. Finally, the discussions and conclusions about the work are presented.

2. Fuzzy Logic System Design and Methodology

2.1. System Design Criteria

In this study, a digital tool was designed for the evaluation of the location of tidal turbines. The most important parameters for optimizing the placement of a tidal turbine include the placement depth, velocity of the sea current, salinity, temperature, density, and viscosity of the water. The proper placement depth is an important factor affecting the performance of the turbine because this allows sufficient water flow for the turbine to generate power. The sea depth affects the time of its maintenance. The speed of the sea current is a critical factor that affects the performance of the turbine. A constant and strong current of water is necessary to generate a sufficient amount of energy. The salinity, temperature, and density of the water are also important in the design. Reducing the viscosity of the water can reduce the efficiency of the turbine and must be considered in the selection of the turbine design [31,32,33].

The design criteria for the digital tool presented are as follows:

-

Evaluation of the installation of a turbine based on its location;

-

Parameters of salinity, temperature, currents and depth obtained by selecting the location on an interactive map;

-

Viscosity parameter depending on the temperature and salinity of the selected location;

-

Density parameter depending on the temperature and salinity of the selected location;

-

Turbine depth parameter entered by the user in a variable data field;

-

Evaluation of the possible cases of success of the installation through fuzzy logic;

-

Presentation of the possible cases in graphs by probability ranges;

-

Presentation of the probability of success of the installation;

The scheme of the designed digital system, based on the previous criteria, is presented in Figure 1. By selecting a location for the placement of the turbine on a world map, data on salinity, temperature, currents and depth are obtained from different sources [34,35,36,37]. Therefore, it is not necessary for the user to indicate to the designed system the parameters corresponding to the area where the turbine is going to be installed, since these can be obtained with the geographic location as the only input parameter. From these parameters, through interpolation, the values of the viscosity and the density of water for the selected location are obtained directly from the geographical location. All these parameters, together with the selection of the turbine depth, are the input parameters into the designed fuzzy logic system. The output of the fuzzy logic system provides the graphs by ranges of memberships, as well as the percent probability of success of the installation.

2.2. Fuzzy Logic Design

The fuzzy logic design was based on the membership of the key parameters within typical ranges, where the probability of success, based on the operation of the turbine, can be optimized. A table (

Table 1. Parameter range for the fuzzy logic system.

Range Value	Temperature (C°)	Salinity (g/L)	Currents (cm/s)	Density (kg/m3)	Viscosity (cp)	Depth (m)	Turbine Placement Depth (m)
Very high	40–25	45–39	500–300	2–1.2	2–1.6	300–8000	300–8000
High	25–20	39–38	300–200	1.2–1.04	1.6–1,5	150–300	150–300
Mid	20–10	38–37	200–100	1.04–1.03	1.5–1.35	80–150	70–150
Low	10–5	37–34	100–50	1.03–1.02	1.35–1.2	30–80	20–70
Very low	5–(−10)	34–31	50–0	1.02–1	1.2–1	0–30	0–20

) was established with membership ranges, classifying the value of the parameters as very low, low, medium, high, or very high. Likewise, a color code is established for these ranges, depending on their suitability. Green is the best range for turbine installation, followed by yellow and orange, with red being the worst. The values in this table, and their corresponding sources, are given in detail for each parameter.

Tidal turbines are designed to operate in a wide range of seawater temperatures, from near-freezing cold water to near-surface warm water. However, the temperature of the water can affect the performance and efficiency of the turbine, so the specific environmental conditions at the installation site must be taken into account. If the water temperature is too low, the density of the water will increase and this can affect the flow of the water and reduce the efficiency of the turbine. On the other hand, if the water temperature is too high, this can affect the stability and life of the turbine components. In general, tidal turbines are designed to operate in waters with typical seawater temperatures, which can range from 10 °C to 30 °C. It is important to carry out a detailed study of the environmental conditions and the turbine in question to determine the optimum level of water temperature for its installation. As observed in Table 1, temperatures below 10 °C are considered to be negative for the placement of turbines, ruling out temperatures below 5 °C.

The typical salinity of seawater is around 35 g/L, so tidal turbines are usually designed to operate in water with a salinity of at least 30 g/L. Salinity above 37 g/L begins to be detrimental to the turbine, and water with salinity above 39 g/L rules out the possibility of turbines, as can be seen in Table 1.

The density of seawater can vary depending on salinity, temperature, and water pressure. The typical density of seawater is around 1025 kg/m³, but it can vary from around 1020 kg/m³ in areas with low salinity to more than 1030 kg/m³ in areas with high salinity. In the case of a density above 1.2 kg/m³, the turbine would be discarded as it would be at a very low temperatures, and very low temperatures would cause a very low water density.

Regarding the viscosity of seawater, it can also vary depending on the temperature and salinity of the water. Seawater viscosity typically increases with salinity and decreases with temperature. Viscosity above 1.6 hundredth of a poise (cp) is ruled out, since salinity is very high at these levels [38].

There are two main types of tidal turbines: tidal stream turbines and water current turbines. Tidal stream turbines are installed in areas of high tidal current energy, which are often in relatively shallow water, while water current turbines can be installed at a variety of depths, from shallow water to deep water. To determine the optimal placement of the turbine, the current has to be above 200 cm/s, and it will be ruled out if it is below 50 cm/s, as can be seen in Table 1.

Tidal stream turbines are installed in areas of high energy tidal currents, which are often in relatively shallow water, although this can vary depending on the project and the technology used. Some tidal stream turbine projects have been installed in water depths of less than 20 m, while other projects have been installed in deeper water, up to 50 or 60 m. As can be seen in Table 1, the optimal placement of the turbine is considered to be between 20 and 70 m deep. In general, tidal stream turbines can be installed in shallow water, as tidal currents tend to be strongest near the surface of the water. Also, installing turbines in shallow water can be easier and less expensive than installing them in deeper water. This study focused mainly on this type of turbine [39,40,41,42].

Considering the ranges of the design parameters, defined in Table 1, the flowchart that defines the fuzzy logic programming was specifically designed. Figure 2 shows how, based on the design parameters, and in which design range (classified in Table 1 by colors) the case is found, turbine installation is considered optimal, very good, good, not recommended, or discarded. The ranges in Table 1 are parameterized in such a way that the ranges cross each other and the same specific value of a parameter can give rise to different cases of probability of success in the installation.

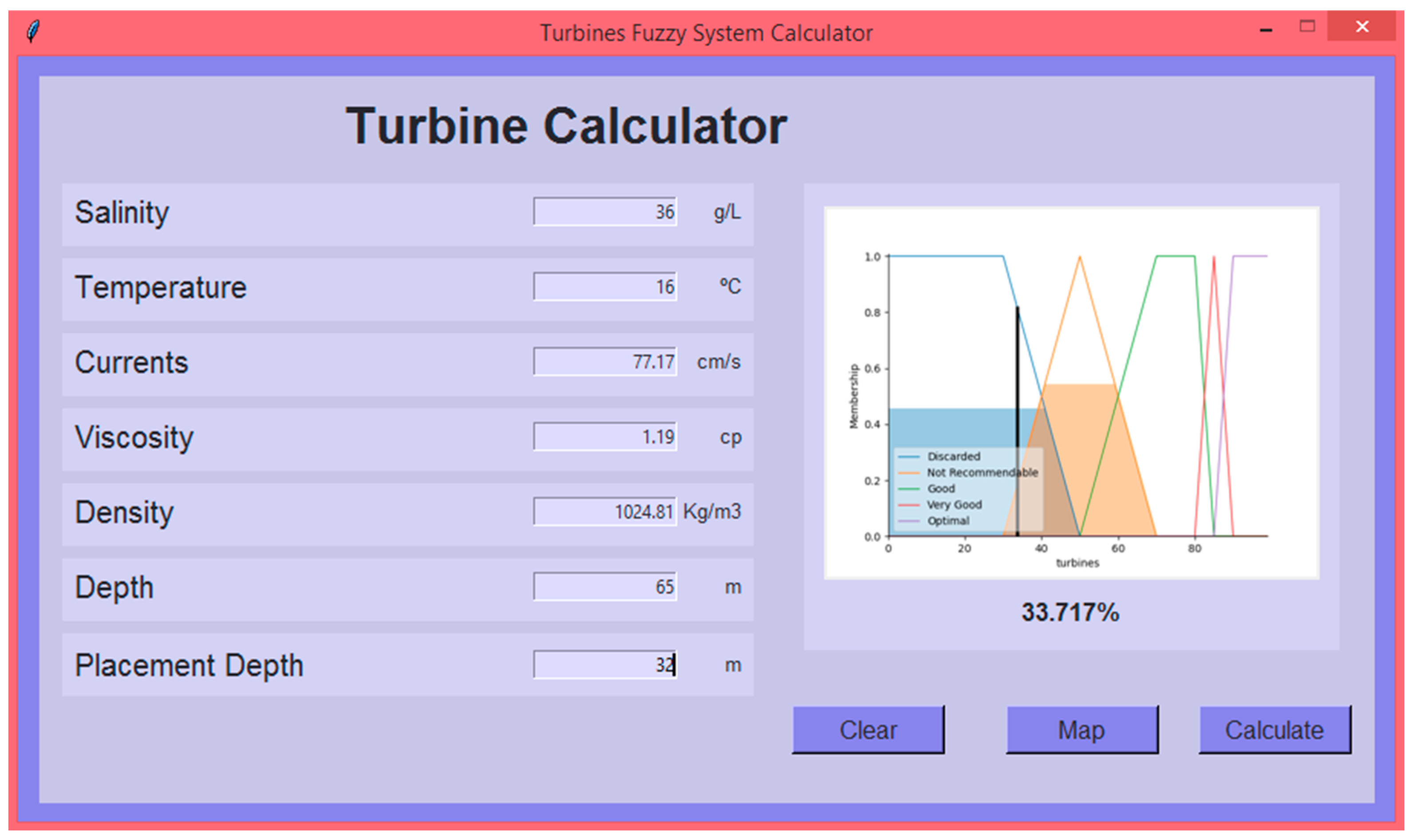
3. Results

Based on the design criteria and the fuzzy logic system, a digital platform was implemented for the simulation of specific cases of turbine installation based on the location and design parameters. This tool was based on Python and its interface is shown in Figure 3. The initial window of the program is shown, in which the values of the different parameters are observed depending on the selected location, as well as three buttons at the bottom right to clear the current data, return to the selection map or calculate. The box on the right is intended to display the simulation results.

When the map button is selected, the map shown in Figure 4 is accessed, where you can manually select the location at which to install the turbine. In the case of selecting a non-viable location, for example, on land, the system launches a warning message, as shown in Figure 4.

To validate the designed fuzzy logic digital tool, the following cases are presented below (Figure 5):

• Case A: Turbine in the English Channel;
• Case B: Turbine in the south of Portugal;
• Case C: Turbine in the Cantabrian Sea;
• Case D: Turbine in Iceland.

The first case involves a turbine to be installed in the English Channel. Based on the location, there are large currents that identified an optimal location for the installation of the turbine, with a probability of success of 93.2%, as shown in Figure 6.

The second case involves a turbine to be installed in the Algarve, in the south of Portugal. This location provides moderate currents; the tool estimated locations ranging from optimal to not recommended, with a probability of success of 65.319%, as shown in Figure 7.

The third case involves a turbine to be installed in the north of Spain, in the Cantabrian Sea. Although this location has stable design parameters, the currents in this area are quite low; the tool estimated locations ranging from not recommendable to discarded, with a probability of success of 33,717%, as shown in Figure 8.

Finally, the case of a turbine to be installed in the southeast of Iceland was simulated. This location, in addition to reduced currents, has very low temperatures, which is why mainly discarded cases were estimated, with a probability of success of 21.188%, as shown in Figure 9.

Based on the results of the simulations, and analyzing the known cases of turbines in said locations, it was verified that the estimates corresponded to the operation or real turbines, thus validating the proposed design.

The probability of success indicates the estimated viability for the installation of turbines in each case. Based on these results, we can see that case A in the English Channel has the highest probability of success (93.2%), followed by case B in the south of Portugal (65.319%). Cases C and D have lower probabilities of success (33.717% and 21.188%, respectively). In general terms, case A in the English Channel seems to be the most favorable for the installation of tidal turbines, since it has large currents and moderate temperatures, which contribute to a higher probability of success.

A graph with the design parameters from the cases analyzed is shown in Figure 10. The graph verifies that the salinity and depth parameters were within the preferred values, so they did not critically affect the results. The temperatures were also at preferential values, except in the case where the low temperature affects the decrease in the probability of success. It is clear that the current was the most restrictive parameter and critically affected the probability of success of the turbine installation.

4. Discussion

This research focused on the design and development of a fuzzy-logic-based digital tool for the selection of tidal turbines and the evaluation of their feasibility in different locations. Based on the results presented in the tidal turbine installation simulation cases, relevant discussions arise about the importance of the location, limitations of the design parameters, validation of the fuzzy logic approach, and other key considerations. There are several discussion points:

• Importance of location: The results show that the choice of location is crucial to determining the feasibility of installing tidal turbines. Currents and temperatures are key factors influencing the probability of success. Case A in the English Channel, with large currents and moderate temperatures, had the highest probability of success, while Case D in Iceland, with low currents and very low temperatures, showed the least probability of success;
• Limitations of currents and temperatures: The results reveal that currents and temperatures are significant parameters for evaluating the suitability of a location for the installation of tidal turbines. In cases B, C, and D, where the currents are moderate or low, the probability of success decreased considerably, even if the temperatures remained stable. This indicates that currents have a significant impact on the efficiency and profitability of tidal turbines;
• Validation of the fuzzy logic approach: This study used fuzzy logic to process the data and obtain estimates of the probability of success. The results obtained from this approach were compared with cases of existing tidal turbines in the same locations, which validated the effectiveness of the proposed design, as results were consistent with the cases analyzed. This demonstrates that fuzzy logic can be a useful decision-making tool for the location of tidal turbines, providing accurate and scalable results.

Additional considerations: Although the simulation results are important, it is essential to take other considerations into account when making decisions about the installation of tidal turbines. Aspects such as environmental impact, legal and regulatory aspects, the existing infrastructure, and the availability of resources and technology must also be evaluated in order to make informed and holistic decisions. In summary, the choice of location is a crucial factor in the feasibility of installing tidal turbines. Currents and temperatures play a key role, and the fuzzy logic approach used in the study provides accurate estimates. However, other relevant factors must be considered before making a final decision on the installation of tidal turbines.

5. Conclusions

A fuzzy-logic-based computer program has been designed and developed, the use of which facilitates decision-making regarding the location of tidal turbines. This is useful in the incipient phases of the development of tidal turbine implementation projects. The results obtained through the simulation of case studies validated the usefulness and precision of the proposed approach. This approach can be a valuable tool for the tidal power industry in making informed decisions about turbine installation and fostering the development and adoption of this sustainable energy source. The location is a crucial factor in the feasibility of installing tidal turbines. The parameters of currents and temperatures play a fundamental role in the probability of success. The analyzed case studies showed that locations with favorable currents and moderate temperatures have higher chances of success in the installation of tidal turbines. In cases where currents are moderate or low, the probability of success is greatly decreased, even if temperatures remain stable. This highlights the critical importance of having adequate currents to maximize the efficiency and profitability of tidal turbines.

The use of fuzzy logic allows us to, from relatively generic data such as temperature, salinity, or depth, carry out an inference process through which sufficiently precise results are obtained to make pertinent decisions in the incipient phases of facility design processes. The fuzzy logic approach used in this study has proven to be effective and accurate in the selection of tidal turbine locations. The results obtained through the simulation of study cases were compared with real cases of turbines in the same locations, thus validating the usefulness and validity of the proposed approach. Fuzzy logic provides a flexible way of dealing with uncertainty and imprecision in decision making, and has shown to be a practical tool for assessing the feasibility of installing tidal turbines. However, it is important to take into account its limitations in terms of the static ranges provided in the model and the ranges of probabilities within the results obtained.

Although the simulation results are important, it is essential to consider other factors before making final decisions about the installation of tidal turbines. Aspects such as environmental impact, legal and regulatory considerations, existing infrastructure, and the availability of resources and technology must also be comprehensively assessed in order to make informed decisions.

Importantly, while this study has provided promising results, there are opportunities for future research. Fermatean fuzzy sets offer additional flexibility in handling uncertainty and imprecision by incorporating a Fermatean metric, which allows for a more nuanced representation of membership degrees [43]. By applying Fermatean fuzzy sets to the design and evaluation of tidal turbine locations, it may be possible to achieve even more precise and adaptable results, while considering the inherent uncertainties and complexities of the marine environment. Additional approaches can be explored to improve the accuracy of site assessment, consider other relevant parameters and factors, and perform a more thorough analysis of the economic and environmental aspects associated with tidal turbine installation. Additionally, this can be scaled and adapted to specific regions with a greater degree of precision. These advances can contribute to a more efficient and effective implementation of tidal energy production around the world.