The Stability Analysis of Linear Systems with Cauchy—Polynomial-Vandermonde Matrices

Abstract

The numerical approximation of both eigenvalues and singular values corresponding to a class of totally positive Bernstein–Vandermonde matrices, Bernstein–Bezoutian structured matrices, Cauchy—polynomial-Vandermonde structured matrices, and quasi-rational Bernstein–Vandermonde structured matrices are well studied and investigated in the literature. We aim to present some new results for the numerical approximation of the largest singular values corresponding to Bernstein–Vandermonde, Bernstein–Bezoutian, Cauchy—polynomial-Vandermonde and quasi-rational Bernstein–Vandermonde structured matrices. The numerical approximation for the reciprocal of the largest singular values returns the structured singular values. The new results for the numerical approximation of bounds from below for structured singular values are accomplished by computing the largest singular values of totally positive Bernstein–Vandermonde structured matrices, Bernstein–Bezoutian structured matrices, Cauchy—polynomial-Vandermonde structured matrices, and quasi-rational Bernstein–Vandermonde structured matrices. Furthermore, we present the spectral properties of totally positive Bernstein–Vandermonde structured matrices, Bernstein–Bezoutian structured matrices, Cauchy—polynomial-Vandermonde structured matrices, and structured quasi-rational Bernstein–Vandermonde matrices by computing the eigenvalues, singular values, structured singular values and its lower and upper bounds and condition numbers.

1. Introduction

In numerical linear algebra, the design of some accurate as well as efficient numerical algorithms for a class of structured matrices remains an interesting topic in research in recent years. Among these structured matrices, an interesting class of matrices is totally positive matrices. The several classes of very structured matrices are studied in [1,2,3,4]. The important and interesting literature in the listed articles covers many aspects of both theory and application but does not contain topics such as accuracy and efficient numerical computations with such kinds of structured matrices. For more details on the computational aspects of structured totally positive matrices can be found in the work [5,6,7].

We consider a special class of totally positive structured matrices that are deeply studied and analyzed in [8] for solving a system of linear equations: Bernstein–Vandermonde matrices. Such a class of matrices has been used to solve and analyze least squares fitting problems while considering the Bernstein basis [9]. The Bernstein–Vandermonde structured matrices are the straightforward generalization of the Vandermonde structured matrices when the most suitable choice of Bernstein basis is considered rather than monomial basis corresponding to a space spanned by algebraic polynomials with degree bounded above by n. The Bernstein polynomials were originally discovered about a hundred years ago by Sergi Natanovich Bernstein in order to facilitate the most famous proof of the Weierstrass approximation theorem. The work by Bezier and de Casteljau introduces the Bernstein polynomials in computer-aided geometric design; see [10] for more details.

The numerical methods based upon Bezier curves are more popular in computer-aided geometric design (CAGD), see [11,12,13,14,15]. The Bernstein polynomials parameterize the Bezier curves reduce to Bernstein polynomial basis.

The theoretical basis to design fast and accurate algorithms in order to compute the greatest $p\left(a\right)$ common divisor for the real type of polynomials and $q\left(a\right)$ with degree of at most n and which are expressible in Bernstein polynomial basis $\{{\alpha }_0^{\left(n\right)},\cdots ,{\alpha }_n^{\left(n\right)}\}$, where ${\alpha }_0^{\left(n\right)}\left(a\right)=\left(\genfrac{}{}{0pt}{}{n}{i}\right){(1-a)}^{n-i}{a}^i,0\le i\le a$, are studied in [16]. The fast $O\left(n^2\right)$ algorithms to determine the required power form of the polynomials $p\left(a\right)$ and $q\left(a\right)$ are studied in [17,18] or its matrix counterparts [19] for the evaluation of GCD.

In [16], the Bezout form $B=\left(b_{i,j}\right)\in {\mathbb{R}}^{n\times n}$ for polynomials $p\left(a\right)$ and $q\left(a\right)$ is defined by the expression of the form

$$p\left(a\right)q\left(w\right)-p\left(w\right)q\left(a\right)=(a-w)\sum _{i,j=1}^n{b}_{i,j}{\alpha }_{i-1}^{(n-1)}\left(a\right){\alpha }_{j-1}^{(n-1)}\left(w\right).$$

Furthermore, the Bezoution matrices, while considering different polynomial bases, are studied by various authors, see [20,21,22,23,24].

The structured matrices, particularly both Vandermonde matrices and Cauchy matrices, appear in the vast areas of computation, see [25,26]. The Cauchy–Vandermonde structured matrices act as useful tools to study the numerical approximation of solution corresponding to singular integral equations; for more detail, we refer [27]. Such a type of structured matrices does occur in connection with numerical approximation of solutions of problems related to study quadrature [28]. In fact, Cauchy–Vandermonde matrices are ill-conditional matrices. The high accuracy of numerical approximation has been achieved for such a class of structured matrices while very carefully studying their specific structure properties [1,29,30,31,32,33,34,35,36].

The Vandermonde matrices appear during the study of interpolation problems in order to exploit the monomial basis [25]. The polynomial-Vandermonde matrices appear when the polynomial basis is considered rather than the monomial basis, and such matrices help to study many applications. A few included in the list are approximation, interpolation, and Gaussian quadrature [37,38,39,40,41,42].

An extensive amount of research has been done in order to analyze the high accuracy of numerical approximations for many classes of matrices having specific structures. This does includes a class of structured matrices includes: totally positive and totally negative matrices [6,43], totally non-positive matrices [44,45], matrices having rank-revealing decomposition [46,47], rank structured matrices [48,49], the diagonally dominant structured M-matrices [50,51] and the structured sign regular matrices [7,52]. The numerical approximation of eigenvalues for structured quasi-rational Bernstein–Vandermonde matrices up to high accuracy (relative) are studied in much greater detail in [53,54].

An extensive amount of work has been done in the direction of discussing both necessary and sufficient criteria for swarm stability asymptotically. The system under consideration achieves the asymptotically if and only if there exists Hermitian matrices satisfying complex Lyapunov inequality for all of the system vertex matrices [55].

The symmetry and asymmetry properties of orthogonal polynomials play a key role in solving system of differential equations that appear in mathematical modeling corresponding to real-world problems. The classical orthogonal polynomials, for instance, Hermit, Legendre, Laguerre, and Discrete, including Krawtchouk and Chebyshev, have numerous widespread applications across many very important branches of science and engineering. In [56], Chebyshev polynomials are used to discuss the simulation of a two-dimensional mass transfer equation subject to Robin and Neumann boundary conditions.

The Boolean complexity for the multiplication of structured matrices by a vector and the solution of nonsingular linear systems of equations with a class of such matrices is studied in [57]. The main focus is to study four basic and most popular classes, that is, Toeplitz, Hankel, Cauchy, and Vandermonde matrices, for which the cited computational problems are equivalent to the task of polynomial multiplication and division and polynomial and rational multipoint evaluation and interpolation.

In this article, we present the spectral properties of a class of structured matrices. We study the behavior of eigenvalues, singular values, and structured singular values for a class of structured matrices, that is, totally positive Bernstein–Vandermonde matrices, Bernstein–Bezoutian structured matrices, Cauchy—polynomial-Vandermonde structured matrices and quasi-rational Bernstein–Vandermonde structured matrices. Furthermore, we also present the numerical approximation of conditioned numbers for structured matrices considered in the current study. Our proposed approach in a recent study differs from the methodology [58] where a low-rank ODE-based technique was developed to study the stability and instability analysis of linear time-invariant system appearing in control and was mainly based on a two level-algorithm, that is, inner-outer algorithm.

The key contribution of this paper is to study and investigate the spectral properties (particularly the computation of structured singular) of totally positive Bernstein–Vandermonde matrices, Bernstein–Bezoutian matrices, Cauchy—polynomial-Vandermonde matrices, and structured quasi-rational Bernstein–Vandermonde matrices and this act as the novel contribution to this paper.

In Section 2 of this article, we aim to present the definitions of structured totally positive Bernstein–Vandermonde matrices, Bernstein–Bezoutian matrices, Cauchy—polynomial-Vandermonde matrices and quasi-rational Bernstein–Vandermonde matrices.

We give a brief and concise introduction to the numerical approximation of the structured singular values in Section 3. Section 4 contains the main results on the numerical computation of the largest and the smallest singular values. Furthermore, the exact behavior of the largest and smallest singular values is also discussed. In Section 5, we present numerical experimentation for Bernstein–Vandermonde and Bernstein–Bezoutian matrices. The numerical approximation of eigenvalues and both singular values and structured singular values are also analyzed and presented. The numerical experimentation for spectral quantities of Cauchy-polynomial-Vandermonde structured matrices and quasi-rational Bernstein–Vandermonde structured matrices are presented in Section 6 and Section 7, respectively. Section 8 contains the numerical testing for the comparison between the approximated lower bounds of structured singular values for a class of higher dimensional structured Bernstein–Vandermonde matrices. Finally, in Section, we present concluding remarks.

2. Preliminaries

Definition 1

([59]). The Bernstein basis on the closed interval $[0,1]$ for the space $S_n\left(x\right)$ of polynomials of degree less than or equal to n is defined as

$${\mathbb{B}}_n=\{{\widehat{b}}_i^{\left(n\right)}\left(x\right)=\left(\genfrac{}{}{0pt}{}{n}{i}\right){(1-x)}^{n-i}{x}^i,i=0:n\}.$$

(1)

Definition 2

([59]). The $(m+1)\times (n+1)$ Bernstein–Vandermonde structured matrix for ${\mathbb{B}}_n$ and nodes ${\left\{x_i\right\}}_{1\le i\le m+1}$ is defined as

$$B=\left[\begin{array}{cccc}\left(\genfrac{}{}{0pt}{}{n}{0}\right){(1-x_1)}^n& \left(\genfrac{}{}{0pt}{}{n}{1}\right)x_1{(1-x_1)}^{n-1}& \cdots & \left(\genfrac{}{}{0pt}{}{n}{n}\right)x_1^n\\ \left(\genfrac{}{}{0pt}{}{n}{0}\right){(1-x_2)}^n& \left(\genfrac{}{}{0pt}{}{n}{1}\right)x_2{(1-x_2)}^{n-1}& \cdots & \left(\genfrac{}{}{0pt}{}{n}{n}\right)x_2^n\\ ⋮& & & ⋮\\ \left(\genfrac{}{}{0pt}{}{n}{0}\right){(1-x_{m+1})}^n& \left(\genfrac{}{}{0pt}{}{n}{1}\right)x_{m+1}{(1-x_{m+1})}^{n-1}& \cdots & \left(\genfrac{}{}{0pt}{}{n}{n}\right)x_{m+1}^n\end{array}\right].$$

(2)

Definition 3

([16]). The transformation matrix between Bernstein and power basis is defined as

$$T_n\left[\begin{array}{c}{\alpha }_0^{\left(n\right)}\left(a\right)\\ ⋮\\ {\alpha }_n^{\left(n\right)}\left(a\right)\end{array}\right]=\left[\begin{array}{c}1\\ ⋮\\ a^n\end{array}\right],$$

(3)

where

$$t_{i,j}^{\left(n\right)}=\left\{\begin{array}{cc}0,\hfill & ifi>j\hfill \\ \left(\begin{array}{c}j-1\\ i-1\end{array}\right){\left(\begin{array}{c}n\\ i-1\end{array}\right)}^{-1},\hfill & ifi\le j.\hfill \end{array}\right.$$

Definition 4

([16]). The Bezoutian matrix $B\in {\mathbb{R}}^{n\times n}$ for polynomials having at most the degree k, that is, $p\left(a\right)={\sum }_{i=0}^n{p}_i{\alpha }_i^{\left(n\right)}\left(a\right)$, $q\left(a\right)={\sum }_{i=0}^n{q}_i{\alpha }_i^{\left(n\right)}\left(a\right)$ in the Bernstein basis $\{{\alpha }_0^{(n-1)}\left(a\right),\cdots ,{\alpha }_n^{(n-1)}\left(a\right)\}$ is defined as

$$\frac{p\left(a\right)q\left(w\right)-p\left(w\right)q\left(a\right)}{a-w}=\sum _{i,j=1}^n{b}_{i,j}{\alpha }_{i-1}^{(n-1)}\left(a\right){\alpha }_{j-1}^{(n-1)}\left(w\right).$$

(4)

Definition 5

([60]). The coefficient matrix (associated with an interpolation problem) of the form

$$M=\left[\begin{array}{cccccc}\frac{1}{x_1+y_1}& \cdots & \frac{1}{x_2+y_l}{a}_0& a_0+a_1{x}_1& \cdots & \sum _{k=0}^{n-l-1}{a}_k{x}_1^k\\ \frac{1}{x_2+y_1}& \cdots & \frac{1}{x_2+y_l}{a}_0& a_0+a_1{x}_2& \cdots & \sum _{k=0}^{n-l-1}{a}_k{x}_2^k\\ ⋮& & & & & ⋮\\ \frac{1}{x_n+y_1}& \cdots & \frac{1}{x_n+y_l}{a}_0& a_0+a_1{x}_n& \cdots & \sum _{k=0}^{n-l-1}{a}_k{x}_n^k\end{array}\right]$$

(5)

is known to be a Polynomial-Vandermonde structured matrix if $l=0$ and a Cauchy matrix if $l=n$. Otherwise, it is a Cauchy—polynomial-Vandermonde structured matrix.

Definition 6

([60]). For a sequence of positive integers (in strict sense) ${\left\{w_i\right\}}_{0\le i\le n-1}$ and the Bernstein basis of the space $S_{n-1}\left(n\right)$ of polynomials on the closed interval $[0,1]$ having the degree less than or equal to $(n-1)$, the rational Bernstein basis are defined as

$${\mathbb{B}}_n^r=\left\{r_i^{(n-1)}\left(x\right)=\frac{w_i{b}_i^{(n-1)}\left(x\right)}{W\left(x\right)},i\in \{0,\cdots ,n-1\}\right\}$$

(6)

with $b_i^{(n-1)}\left(x\right)=\left(\genfrac{}{}{0pt}{}{n-1}{i}\right)x^i{(1-x)}^{n-i-1}$ and $W\left(x\right)={\sum }_{i=0}^{n-1}{w}_i{b}_i^{n-1}\left(x\right).$

Definition 7

([60]). For rational Bernstein basis ${\mathbb{B}}_n^r$, the rational Bernstein–Vandermonde matrix is defined as

$$B=\left[\begin{array}{ccc}\frac{w_0\left(\genfrac{}{}{0pt}{}{n-1}{0}\right){(1-x_1)}^{n-1}}{W\left(x_1\right)}& \cdots & \frac{w_{n-1}\left(\genfrac{}{}{0pt}{}{n-1}{n-1}\right){\left(x_1\right)}^{n-1}}{W\left(x_1\right)}\\ ⋮& & ⋮\\ \frac{w_0\left(\genfrac{}{}{0pt}{}{n-1}{0}\right){(1-x_n)}^{n-1}}{W\left(x_n\right)}& \cdots & \frac{w_{n-1}\left(\genfrac{}{}{0pt}{}{n-1}{n-1}\right){\left(x_n\right)}^{n-1}}{W\left(x_n\right)}\end{array}\right].$$

(7)

Definition 8

([60]). The quasi-rational Bernstein–Vandermonde structured matrix $B_{qr}=\left(r_{ij}\right)\in {\mathbb{R}}^{n\times n}$ is defined as

$$r_{ij}=\left\{\begin{array}{cc}\frac{w_{j-1}\left(\genfrac{}{}{0pt}{}{n-1}{j-1}\right)x_i^{j-1}{(1-x_i)}^{n-j}}{W\left(x_i\right)},\hfill & if1\le i,j\le n,(i,j)\ne (n,n)\hfill \\ \frac{w_{n-1}\left(\genfrac{}{}{0pt}{}{n-1}{n-1}\right)x_n^{n-1}}{W\left(x_n\right)}-\widehat{w},\hfill & if(i,j)=(n,n).\hfill \end{array}\right.$$

(8)

where perturbation parameter $\widehat{w}$ satisfies

$$\left\{\begin{array}{c}0<x_1<x_2<\cdots <x_n<1\hfill \\ \frac{x_n-x_1}{1-x_1}\gamma <\widehat{w}\le x_n\gamma with\gamma =\frac{w_{n-1}}{W\left(x_n\right)}\prod _{k=2}^{n-1}\frac{(x_n-x_k)}{(1-x_k)}.\hfill \end{array}\right.$$

3. Structured Singular Values

In this section, we introduce a mathematical quantity appearing in control theory known as structured singular value, that is, $\mu$-values. Let $A\in {\mathbb{R}}^{n\times n}$ and $\Delta \in {\mathbb{R}}^{n\times n}$. The matrix $\Delta$ represents the admissible uncertainty from the set of block diagonal matrices (or set of uncertainties), that is,

$$\mathbb{B}:=\{diag\left({\Delta }_i\right),{\Delta }_i\in {\mathbb{R}}^{n\times n},i=1:n\}.$$

(9)

Definition 9.

For a given A, the structured singular value dented with $\mu \left(·\right)$ is defined as

$${\mu }_{\Delta }\left(A\right):=\frac{1}{min\{{\sigma }_{max}(\Delta ):\Delta \in \mathbb{B},det\left(I-A\Delta \right)=0\}}.$$

(10)

If there exist no such uncertainty $\Delta \in \mathbb{B}$ such that $det(I-A\Delta )$ becomes zero, then ${\mu }_{\Delta }\left(A\right)=0.$

By definition, the mathematical quantities 9, $det\left(·\right)$ denotes the determinant of some structured matrix under consideration. The exact computation of structured singular value or $\mu$-value for a class of very large-scale structured matrices is NP-hard [61]. Because of this, one needs to numerically approximate the tighter bounds of structured singular values. The numerical computation of the tighter lower bounds of structured singular values or $\mu$-values ensures enough information to study and discuss the instability of the dynamical system. On the other hand, the numerical approximation of an upper bound of structured singular value or $\mu$-value helps in a great manner to study and discuss the stability analysis of systems.

4. Main Results

In this section, we aim to present our new and main results concerning the numerical approximation of the largest singular value ${\sigma }_{max}$ of $A\in {\mathbb{R}}^{n\times n}$. Furthermore, we also discuss the increasing behavior of ${\sigma }_{max}$ and the decreasing behavior of ${\sigma }_{min}$. The following Theorem 1 allows the computation of ${\sigma }_{max}$.

Definition 10.

For a given matrix $A\in {\mathbb{R}}^{n\times n}$, the scalars ${\lambda }_i$ are called the eigenvalues of A such that $det(A-{\lambda }_{i}I)=0,$ where I denotes an identity matrix possessing the same dimension as of the matrix A.

Definition 11.

For a given matrix $A\in {\mathbb{R}}^{n\times n}$, the non-negative numbers ${\sigma }_i$ are known as the singular values of A if A can be decomposed as $A=U\Sigma V^t$, where the matrices U and V are the orthogonal and Σ is a diagonal matrix having ${\sigma }_i$ on its main diagonal.

Lemma 1.

Let $A:\mathbb{R}\to {\mathbb{C}}^{n\times n}$ be matrix family (smooth). Let $\lambda \left(t\right)$ denotes the eigenvalue of $A\left(t\right)$, $t\in \mathbb{R}$ that converges to an eigenvalue (simple) ${\lambda }_0$ of $A_0$ as $t\to 0$. Then, the continuous branch of eigenvalues $\lambda \left(t\right)$ is analytic nearby $t=0$ having

$$\frac{d}{dt}\left(\lambda \left(0\right)\right)=\frac{y_0^{\ast }{A}_1{x}_0}{y_0^{\ast }{x}_0}.$$

(11)

Here, $A_1=\dot{A}\left(0\right)$ and $x_0$ and $y_0$ denotes left and right hands singular vectors of $A_0$ corresponding to ${\lambda }_0.$

Theorem 1.

For a given $A\in {\mathbb{R}}^{n\times n}$, ${\sigma }_{max}\left(A\right)$, the largest singular value is obtained as

$${\sigma }_{max}\left(A\right)=\alpha \beta ,$$

where

$$\alpha =\frac{{\prod }_i{\lambda }_i^{\frac{1}{2-n}}\left(D\right){\left(\frac{1}{2}\right)}^{\frac{n-1}{(n-2)}}{\left(\frac{1}{n-1}\right)}^{\frac{n-1}{2(n-2)}}{\sum }_i{\left({\sigma }_i^2\right)}^{\frac{n-1}{n-2}}\left(D\right)}{n^{-\frac{1}{2}}{\sum }_i{\sigma }_i^2\left(D\right)},$$

and

$$\beta =\frac{{\prod }_i{\lambda }_i^{\frac{1}{n^2-4n+4}}\left(E\right){\left(\frac{1}{2}\right)}^{\frac{n^2-2n+1}{n^2-4n+4}}{\left(\frac{1}{n-1}\right)}^{\frac{n^2-2n+1}{2n^2-8n+8}}{\sum }_i{\left({\sigma }_i^2\right)}^{\frac{n^2-2n+1}{n^2-4n+4}}\left(E\right)}{n^{-1}{\sum }_i\left({\sigma }_i^4\right)\left(E\right)}.$$

Proof. 

First, we show that the above-given expressions for $\alpha$ and $\beta$ are valid. We consider the following factorization of A. For the following factorization of A, we refer interested readers to see [62].

$$A=D^{-1}E{\left(E^t{D}^{-1}E\right)}^{-1}{E}^t.$$

Here, D denotes a diagonal non-negative matrix while E is of the full-rank.

For the quantity ${\prod }_i{\lambda }_i^{\frac{1}{2-n}}\left(D\right){\left(\frac{1}{2}\right)}^{\frac{n-1}{(n-2)}}{\left(\frac{1}{n-1}\right)}^{\frac{n-1}{2(n-2)}}{\sum }_i{\left({\sigma }_i^2\right)}^{\frac{n-1}{n-2}}\left(D\right)$, which is the numerator of $\alpha$, we make use of arithmetic-geometric-mean inequality that allows us to write the following inequality for singular values of D.

$${\sigma }_1^2\left(D\right)\left[{\sigma }_2^2\left(D\right)+{\sigma }_3^2\left(D\right)+\cdots +{\sigma }_n^2\left(D\right)\right]\le \frac{{({\sigma }_1^2\left(D\right)+{\sigma }_2^2\left(D\right)+\cdots +{\sigma }_n^2\left(D\right))}^2}{4}.$$

(12)

Next, we make use of arithmetic-geometric-mean inequality on the quantity ${\sigma }_1^{2n-4}\left(D\right){\prod }_i{\sigma }_i\left(D\right)$, which yields

$$\begin{array}{cc}\hfill {\sigma }_1^{2n-4}\left(D\right)\prod _i{\sigma }_i^2\left(D\right)& ={\sigma }_1^{2n-4}\left(D\right){\sigma }_1^2\left(D\right)\cdots {\sigma }_n^2\left(D\right),\hfill \\ \hfill & ={\sigma }_1^{2n-2}\left(D\right){\sigma }_2^2\left(D\right)\cdots {\sigma }_n^2\left(D\right),\hfill \\ \hfill & <\frac{{\sigma }_1^2\left(D\right){\left[{\sigma }_2^2\left(D\right)+\cdots +{\sigma }_n^2\left(D\right)\right]}^{n-1}}{{(n-1)}^{n-1}}.\hfill \end{array}$$

(13)

Equations (12) and (13) allows us to write

$${\sigma }_1^{2n-4}\left(D\right)\prod _i{\sigma }_i^2\left(D\right)\le \frac{{\left[{\sum }_i{\left({\sigma }_i^2\right)}^2\left(D\right)\right]}^{n-1}}{{(4n-4)}^{n-1}}.$$

(14)

Finally, from Equation (14), we have

$${\sigma }_1\left(D\right)={\sigma }_{max}\left(D\right)\le \prod _i{\lambda }_i^{\frac{1}{2-n}}\left(D\right){\left(\frac{1}{4n-4}\right)}^{\frac{n-1}{2(n-2)}}\sum _i{\left({\sigma }_i^2\right)}^{\frac{n-1}{n-2}}\left(D\right).$$

For the quantity $n^{-\frac{1}{2}}{\sum }_i{\sigma }_i^2\left(D\right)$ which is the denominator of $\alpha$, we make use of arithmetic-geometric-mean inequality for the singular values of D as,

$$\prod _i{\left({\sigma }_i^2\left(D\right)\right)}^{\frac{1}{n}}\le \frac{1}{n}\sum _i{\sigma }_i^2\left(D\right).$$

(15)

In addition,

$$n\prod _i{\left(\frac{1}{{\sigma }_i^2\left(D\right)}\right)}^{\frac{1}{n}}\le \sum _i\frac{1}{{\sigma }_i^2\left(D\right)}.$$

(16)

The inequalities in Equations (15) and (16) yields

$$n^2\le \sum _i{\sigma }_i^2\left(D\right)\sum _i\frac{1}{{\sigma }_i^2\left(D\right)}.$$

(17)

Because we know that the matrix 2-norm of matrix D can be written as

$${\parallel D\parallel }_2^2={\sigma }_i^2\left(D\right).$$

(18)

Therefore, Equations (17) and (18) implies that

$$n^2\le \sum _i{\sigma }_i^2\left(D\right)\sum _i\frac{1}{{\sigma }_i^2\left(D\right)}.$$

or

$${\sigma }_n\left(D\right)={\sigma }_{min}\left(D\right)=n^{\frac{-1}{2}}\sum _i{\sigma }_i^2\left(D\right).$$

In a similar way, we can obtain the expressions for the numerator and denominator of $\beta$. Now, we aim to prove that ${\sigma }_{max}\left(A\right)=\alpha \beta$.

Since, $D=D^t$ and ${\lambda }_i\left(D\right)\ge 0,\forall i$. Thus, the matrix D takes the form of $D={\left(D^{\frac{1}{2}}\right)}^2$ and $D^{-\frac{1}{2}}={\left(D^{\frac{1}{2}}\right)}^{-1}$. We obtain the following expression while making use of the singular value decomposition of $D^{-\frac{1}{2}}E$ yields

$$\begin{array}{cc}\hfill D^{-\frac{1}{2}}E& =\left[\begin{array}{cccccc}{u}_1& \cdots & u_n& u_{n+1}& \cdots & u_N\end{array}\right]\left[\begin{array}{ccccc}{\sigma }_1& 0& \cdots & \cdots & 0\\ 0& {\sigma }_2& 0& \cdots & 0\\ ⋮& ⋮& & & ⋮\\ 0& 0& \cdots & \cdots & {\sigma }_n\\ 0& 0& \cdots & \cdots & 0\\ ⋮& ⋮& \cdots & \cdots & ⋮\\ 0& 0& \cdots & \cdots & 0\end{array}\right]\begin{array}{cccccc}[v_1& \cdots & v_n& v_{n+1}& \cdots & v_N{]}^t\end{array},\hfill \\ \hfill & =\left[\begin{array}{cccccc}{u}_1& \cdots & u_n& u_{n+1}& \cdots & u_N\end{array}\right]\left[\begin{array}{c}\sum _1\\ 0\end{array}\right]{\left[\begin{array}{cccccc}{v}_1& \cdots & v_n& v_{n+1}& \cdots & v_N\end{array}\right]}^t.\hfill \end{array}$$

From [63], the ${\sigma }_{max}\left(D^{-\frac{1}{2}}E\right)$ can be written as

$$\begin{array}{cc}\hfill {\sigma }_{max}\left(D^{-\frac{1}{2}}E\right)& \le {\sigma }_{max}\left(D^{-\frac{1}{2}}\right){\sigma }_{max}\left(E\right),\hfill \\ \hfill & =\frac{{\sigma }_{max}\left(E\right)}{{\sigma }_{max}\left(D^{\frac{1}{2}}\right)},\hfill \\ \hfill & =\frac{{\prod }_i{\lambda }_i^{\frac{1}{n^2-4n+4}}\left(E\right){\left(\frac{1}{2}\right)}^{\frac{n^2-2n+1}{n^2-4n+4}}{\left(\frac{1}{n-1}\right)}^{\frac{n^2-2n+1}{2n^2-8n+8}}{\sum }_i{\left({\sigma }_i^2\right)}^{\frac{n^2-2n+1}{n^2-4n+4}}\left(E\right)}{n^{-1}{\sum }_i{\sigma }_i^4\left(D\right)}\hfill \end{array}$$

with ${\sigma }_{min\left(D\right)}=n^{-\frac{1}{2}}{\sum }_i{\sigma }_i^2\left(D\right)\ne 0.$

In a similar way from [63], ${\sigma }_{min}\left(D^{-\frac{1}{2}}E\right)$ takes the following form as, that is,

$$\begin{array}{cc}\hfill {\sigma }_{min}\left(D\right)& \ge {\sigma }_{min}\left(D^{-\frac{1}{2}}\right){\sigma }_{min}\left(E\right)=\frac{{\sigma }_{min}\left(E\right)}{{\left({\sigma }_{max}\left(D\right)\right)}^{\frac{1}{2}}}.\hfill \\ \hfill & =\frac{n^{-1}{\sum }_i{\sigma }_i^4\left(E\right)}{{\prod }_i{\lambda }_i^{\frac{1}{{(2-n)}^2}}\left(D\right){\left(\frac{1}{2}\right)}^{{\left(\frac{n-1}{2(n-2)}\right)}^2}{\left(\frac{1}{n-1}\right)}^{{\left(\frac{n-1}{2(n-2)}\right)}^2}{\sum }_i{\left({\sigma }_i^2\right)}^{{\left(\frac{n-1}{n-2}\right)}^2}\left(D\right)}\hfill \end{array}$$

with ${\sigma }_{max}\left(D\right)={\prod }_i{\lambda }_i^{\frac{1}{2-n}}\left(D\right){\left(\frac{1}{2}\right)}^{\frac{n-1}{2(n-2)}}{\left(\frac{1}{n-1}\right)}^{\frac{n-1}{2(n-2)}}{\sum }_i{\left({\sigma }_i^2\right)}^{\frac{n-1}{n-2}}\left(D\right)\ne 0$.

The singular value decomposition of ${\left(E^t{D}^{-1}E\right)}^{-1}$ yields ${\left(E^t{D}^{-1}E\right)}^{-1}=V{\Sigma }_1^{-2}{V}^t$ where ${\Sigma }_1=\left[\begin{array}{cccc}{\sigma }_1& 0& \cdots & 0\\ 0& {\sigma }_2& \cdots & 0\\ ⋮& & & ⋮\\ 0& 0& \cdots & {\sigma }_n\end{array}\right].$ As,

$$\begin{array}{cc}\hfill A& =D^{-1}E{\left(E{D}^{-1}E\right)}^{-1}{E}^t,\hfill \\ \hfill & \stackrel{\mathrm{svd}}{=}{D}^{-1}E{V}^t{\Sigma }_1^{-2}V{E}^t.\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\sigma }_{max}\left(A\right)& \le {\sigma }_{max}\left(D^{-1}\right){\sigma }_{max}^2\left(E\right){\sigma }_{max}\left({\Sigma }_1^{-2}\right),\hfill \\ \hfill & \le \frac{{\sigma }_{max}^2\left(E\right)}{{\sigma }_{min}\left(D\right){\sigma }_{min}\left({\sum }_1^2\right)}\le \frac{{\sigma }_{max}^2\left(E\right)}{{\sigma }_{min}\left(D\right){\left[\frac{{\sigma }_{min}\left(E\right)}{{\left({\sigma }_{max}\left(D\right)\right)}^{\frac{1}{2}}}\right]}^2},\hfill \\ \hfill & =\frac{{\sigma }_{max}\left(D\right)}{{\sigma }_{min}\left(D\right)}\frac{{\sigma }_{max}^2\left(E\right)}{{\sigma }_{min}^2\left(E\right)},\hfill \\ \hfill & =\frac{{\prod }_i{\lambda }_i^{\frac{1}{2-n}}\left(D\right){\left(\frac{1}{2}\right)}^{\frac{n-1}{2(n-2)}}{\left(\frac{1}{n-1}\right)}^{\frac{n-1}{2(n-2)}}{\sum }_i{\left({\sigma }_i^2\right)}^{\frac{n-1}{n-2}}\left(D\right)}{n^{-\frac{1}{2}}{\sum }_i{\sigma }_i^2\left(D\right)},\hfill \\ \hfill & =\frac{{\prod }_i{\lambda }_i^{\frac{1}{n^2-4n+4}}\left(E\right){\left(\frac{1}{2}\right)}^{\frac{n^2-2n+1}{n^2-4n+4}}{\left(\frac{1}{n-1}\right)}^{\frac{n^2-2n+1}{2n^2-8n+8}}{\sum }_i{\left({\sigma }_i^2\right)}^{\frac{n^2-2n+1}{n^2-4n+4}}\left(E\right)}{n^{-1}{\sum }_i\left({\sigma }_i^4\right)\left(E\right)},\hfill \\ \hfill & =\alpha \beta .\hfill \end{array}$$

   □

The increasing behavior of ${\sigma }_{max}$ for $A\in {\mathbb{R}}^{n\times n}$ is given in Theorem 2. Furthermore, $A_i=A_i\left(t\right)$ and ${\sigma }_i={\sigma }_i\left(t\right)$. For simplicity, we omit the dependency of $A_i$ and ${\sigma }_i$ on t in Theorem 2.

Theorem 2.

Let $A_i\in {\mathbb{R}}^{n_i\times n_i},\forall i\le j$ are submatrices of $A_{j+1}\in {\mathbb{R}}^{n_{j+1}\times n_{j+1}}\forall j$, and let ${\sigma }_i\left(A_i\right)$ be the largest singular values of $A_i$ and ${\sigma }_{j+1}\left(A_{j+1}\right)$ denotes the largest singular values of $A_{j+1}$. The largest singular values of ${\sigma }_{j+1}\left(A_{j+1}\right)$ satisfies the inequality

$$\frac{d}{dt}\left({\sigma }_{j+1}\left(A_{j+1}^{\ast }{A}_{j+1}\right)\right)\ge \frac{d}{dt}\left({\sigma }_i\left(A_i^{\ast }{A}_i\right)\right).$$

Proof. 

For $i\le j$, the submatrices $A_i$ and matrices $A_{j+1}$ can be written as

$$A_i^{\ast }{A}_i=\sum _{k=1}^i{a}_k{a}_k^{\ast },$$

(19)

and

$$A_{j+1}^{\ast }{A}_{j+1}=A_i^{\ast }{A}_i+r_{j+1}{r}_{j+1}^{\ast }.$$

(20)

In Equations (19) and (20), $a_k$ denotes all the k components of sub-matrix $A_i$ and $r_{j+1}$ denotes all components of $A_{j+1}$ for $j\ge i$. Let $u_i$ and $v_i$ denotes the left and right hand sides singular vectors of $A_i^{\ast }{A}_i$, then

$$\frac{d}{dt}\left({\sigma }_i\left(A_i^{\ast }{A}_i\right)\right)=\frac{d}{dt}\left({\sigma }_i\left(\sum _{k=1}^i{a}_k{a}_k^{\ast }\right)\right)=\frac{u_i^{\ast }\frac{d}{dt}\left({\sum }_{k=1}^i{a}_k{a}_k^{\ast }\right)v_i}{u_i^{\ast }{v}_i}=u_i^{\ast }\frac{d}{dt}\left(\sum _{k=1}^i{a}_k{a}_k^{\ast }\right)v_i,$$

(21)

From Equation (21), we have

$$\frac{d}{dt}\left({\sigma }_{j+1}\left(A_{j+1}^{\ast }{A}_{j+1}\right)\right)=\frac{d}{dt}\left({\sigma }_i\left(A_i^{\ast }\right)A_i\right)+\frac{d}{dt}\left({\sigma }_{j+1}\left(r_{j+1}{r}_{j+1}^{\ast }\right)\right)=\frac{d}{dt}\left({\sigma }_i\left(A_i^{\ast }{A}_i\right)\right)+{\widehat{u}}_{j+1}\frac{d}{dt}\left(r_{j+1}{r}_{j+1}^{\ast }\right){\widehat{v}}_{j+1}.$$

(22)

In Equation (22), ${\widehat{u}}_{j+1}$, and ${\widehat{v}}_{j+1}$ denote the right and left-hand sides singular vectors corresponding to a family of matrices $A_{j+1}^{\ast }{A}_{j+1}$, respectively. From Equations (21) and (22), we have

$$\frac{d}{dt}\left({\sigma }_{j+1}\left(A_{j+1}^{\ast }{A}_{j+1}\right)\right)\ge \frac{d}{dt}\left({\sigma }_i\left(A_i^{\ast }{A}_i\right)\right).$$

   □

The decreasing behavior of ${\sigma }_{min}$ for $A\in {\mathbb{R}}^{n\times n}$ is given in Theorem 3.

Theorem 3.

Let $A_i\in {\mathbb{R}}^{n_i\times n_i},\forall i\le j$ are sub-matrices of $A_{j+1}\in {\mathbb{R}}^{n_{j+1}\times n_{j+1}}\forall j$, and let ${\widehat{\sigma }}_i\left(A_i\right)$ be the smallest singular values of $A_i$ and ${\sigma }_{j+1}^{^}\left(A_{j+1}\right)$ are the smallest singular values of $A_{j+1}$. The smallest singular vales ${\widehat{\sigma }}_{j+1}\left(A_{j+1}\right)$ satisfies the inequality

$$\frac{d}{dt}\left({\widehat{\sigma }}_{j+1}\left(A_{j+1}^{\ast }{A}_{j+1}\right)\right)\le \frac{d}{dt}\left({\widehat{\sigma }}_i\left(A_i^{\ast }{A}_i\right)\right).$$

Proof. 

For $i\le j$, the matrices $A_i$ and $A_{j+1}$ can be written as

$$A_i^{\ast }{A}_i=\sum _{k=1}^i{a}_k{a}_k^{\ast },$$

and

$$A_{j+1}^{\ast }{A}_{j+1}=A_i^{\ast }{A}_i+b_{j+1}{b}_{j+1}^{\ast }.$$

(23)

Let ${\widehat{u}}_i$ and ${\widehat{v}}_i$ be left hand and right hand singular vectors of $A_i^{\ast }{A}_i$, then

$$\frac{d}{dt}\left({\widehat{\sigma }}_i\left(A_i^{\ast }{A}_i\right)\right)=\frac{d}{dt}\left({\widehat{\sigma }}_i\left(\sum _{k=1}^i{a}_k{a}_k^{\ast }\right)\right)={\widehat{u}}_i^{\ast }\frac{d}{dt}\left(\sum _{k=1}^i{a}_k{a}_k^{\ast }\right)v_i^{\ast }.$$

(24)

Now,

$$\frac{d}{dt}\left({\widehat{\sigma }}_{j+1}\left(A_{j+1}^{\ast }{A}_{j+1}\right)\right)=\frac{d}{dt}\left({\widehat{\sigma }}_i\left(A_i^{\ast }{A}_i\right)\right)+{\widehat{u}}_{j+1}\left(b_{j+1}{b}_{j+1}^{\ast }\right){\widehat{v}}_{j+1}.$$

(25)

Since, ${\widehat{\sigma }}_i$ and ${\widehat{\sigma }}_{j+1}$ are the smallest singular values of $\left(A_i^{\ast }{A}_i\right)$ and $\left(A_{j+1}^{\ast }{A}_{j+1}\right)$ for $i\le j$, thus Equations (24) and (25) yields

$$\frac{d}{dt}\left({\widehat{\sigma }}_{j+1}\left(A_{j+1}^{\ast }{A}_{j+1}\right)\right)\le \frac{d}{dt}\left({\widehat{\sigma }}_i\left(A_i^{\ast }{A}_i\right)\right).$$

   □

Next, we aim to fix the largest singular value ${\sigma }_{max}\left(A\right)$ for $A\in {\mathbb{R}}^{n\times n}$ such that ${\sigma }_{max}=1$. For this purpose, we make use of an inner-outer algorithm. The main objective is to develop and then solve an optimization problem. In turn, this optimization problem yields a system of ordinary differential equations (ODEs). On the other hand, for the case of the outer algorithm, our main aim is to modify the perturbation level $ϵ$ via fast Newton’s iteration. For more details, we refer [58].

5. Total Positive Bernstein–Vandermonde and Bernstein–Bezoutian Matrices

The following theorem guarantees us that if all of the computed minors are non-negative and respectively positive, then the given original matrix appears to be a totally positive (respectively, strictly totally positive) matrix.

Theorem 4

([59]). A structured matrix is strictly totally positive if its Neville elimination [21, 22] is performed without making any changes in the row and column. For A and $A^t$, multipliers of Neville elimination are positive, and A has positive diagonal pivots for its Neville elimination.

Proof. 

For proof, see [59].    □

The Bernstein–Vandermonde matrix appears to be a strictly totally positive structured matrix for given nodes $0<x_1<x_2<\cdots <x_{k+1}<1$. The obtained result is the consequence of the following theorem.

Theorem 5

([59]). Let $M={\left(m_{ij}\right)}_{k\le i,j\le k+1}$ be a Bernstein–Vandermonde structured matrix. The existing nodes of M satisfies $0<x_1<x_2<\cdots <x_{k+1}<1$, then $M^{-1}$ satisfies the matrix factorization possessing the form

$$M^{-1}=A_1{A}_2\cdots A_n{D}^{-1}{B}_n{B}_{n-1}\cdots B_1,$$

where $B_i,\forall i\le i\le n$ are $(n+1)\times (n+1)$ bi-diagonal structured matrices of the form

$$B_i=\left[\begin{array}{cccccccc}1& & & & & & & \\ 0& 1& & & & & & \\ & 0& \ddots & & & & & \\ & & \ddots & 1& & & & \\ & & & -r_{i+1,i}& 1& & & \\ & & & & -r_{i+2,i}& 1& & \\ & & & & & \ddots & \ddots & \\ & & & & & & -r_{n+1,i}& 1\end{array}\right],$$

$B_i^t\forall 1\le i\le n$ are $(n+1)\times (n+1)$ bi-diagonal structured matrices of the form

$$B_i^t=\left[\begin{array}{cccccccc}1& & & & & & & \\ 0& 1& & & & & & \\ & 0& \ddots & & & & & \\ & & \ddots & 1& & & & \\ & & & -{\widehat{r}}_{i+1,i}& 1& & & \\ & & & & -{\widehat{r}}_{i+2,i}& 1& & \\ & & & & & \ddots & \ddots & \\ & & & & & & -{\widehat{r}}_{n+1,i}& 1\end{array}\right],$$

and the matrix D is diagonal having order $(n+1)$ such that

$$D=diag\{d_{1,1},d_{2,2},\cdots ,d_{n+1,n+1}\}.$$

For the given matrix M, $r_{ij}$ are the possible multipliers of Neville elimination and are obtained as

$$m_{i,j}=\frac{{(1-x_i)}^{n-j+1}(1-x_{i-j}{\prod }_{l=1}^{j-1}(x_i-x_{i-l}))}{{(1-x_{i-1})}^{n-j-2}{\prod }_{l=2}^j(x_{i-1}-x_{i-l})},j=1:n,i=j+1:n+1.$$

For $M^t$, the possible quantities ${\widehat{m}}_{i,j}$ are the multiplies of Neville elimination and are obtained as

$${\widehat{m}}_{i,j}=\frac{(n-i+2)x_j}{(i-1)(1-x_j)},j=1:n,i=j+1:n+1.$$

Finally, the $i^{th}$-diagonal element of D is the diagonal pivot of Neville elimination of M and is expressed as

$$d_{i,i}=\frac{\left(\genfrac{}{}{0pt}{}{n}{i-1}\right){(1-x_i)}^{n-i+1}{\prod }_{l<i}(x_i-x_k)}{{\prod }_{l=1}^{i-1}(1-x_k)},i=1:n.$$

Proof. 

It can be seen in [59].    □

Spectral Properties of Total Positive Bernstein–Vandermonde and Bernstein–Bezoutian Matrices

In this subsection, we aim to present the spectral properties of Bernstein–Vandermonde structured matrices and Bernstein–Bezoutian structured matrices. These structured matrices are taken from the paper by [59] for the numerical approximations of structured singular values.

In our numerical experimentation, we make use of MATLAB functions $eig(·)$ and $svd(·)$ for the numerical approximation of both eigenvalues and singular values. The main aim is to numerically approximate the lower bounds of structured singular or $\mu$-value, which is nothing but the straightforward generalization of singular values for a class of structured matrices. Furthermore, the use of MATLAB functions mussv is considered for the numerical approximation of both lower and upper bounds corresponding to structured singular values.

Example 1.

We consider a $3\times 3$ Bernstein–Vandermonde structured matrix

$$M_1=\left[\begin{array}{ccc}\frac{9}{16}& \frac{3}{8}& \frac{1}{16}\\ \frac{1}{14}& \frac{1}{2}& \frac{1}{4}\\ \frac{1}{16}& \frac{3}{8}& \frac{9}{16}\end{array}\right].$$

The first column of Table 1 represents the numerically approximated eigenvalues of $M_1$ via MATLAB function $eig(·)$. The second column represents the singular values approximated by MATLAB function $svd(·)$. The third and fourth columns represent the numerical approximation of both upper and lower bounds of structured singular values approximated by MATLAB function mussv. The numerical approximation to the lower bounds of structured singular values or $\mu$-values approximated by methodology based on low-rank ODEs [58] is represented in the very last column of the table.

Table 1. Spectral properties of $M_1$.

Eigenvalues	Singular Values	ssv (Upper)	ssv (Lower)	ssv (Lower New)
$\left\{0.9153,0.5000,0.2097\right\}$	$\left\{0.9698,0.5113,0.1936\right\}$	$0.9698$	$0.9698$	$0.9698$

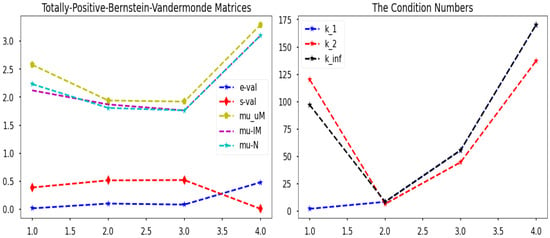
In Figure 1, the left-hand side subfigure represents the plots of eigenvalues, singular values, and the numerical approximation of both lower and upper bounds of structured singular values against the time t. In Figure 1, the blue color dotted line starting from point $\left(1.0,0.0\right)$ at the bottom of the left side figure denotes the spectrum, that is, the eigenvalues of $M_1$. Because singular values are non-negative numbers, the red color dotted line starting from point $\left(1.0,0.4\right)$ indicates that eigenvalues are bounded above by singular values. The golden color dotted line starting from point $\left(1.0,2.6\right)$ shows that all quantities, that is, eigenvalues, singular values, and numerically approximated lower bounds corresponding to structured singular values approximated by mussv function, which is represented with a purple color dotted line starting from point $\left(1.0,2.1\right)$ and the numerical approximation to the lower bounds of structured singular values approximated with [58] represented with turquoise color dotted line starting from point $\left(1.0,2.3\right)$ are strictly bounded by the numerical approximation of the upper bounds of structured singular values or $\mu$-values with the help of MATLAB function mussv.

Figure 1. Behaviour of eigenvalues, singular values, structured singular values and condition numbers.

In Figure 1, the right-hand side subfigure represents the plots of condition numbers vs. time. Furthermore, the behaviour of spectral condition numbers $k_1\left(M_1\right)$ starting from point $\left(1.0,0.0\right)$, $k_2\left(M_1\right)$ starting from point $\left(1.0,124\right)$ and $K_{\infty }\left(M_1\right)$ starting from point $\left(1.0,100\right)$ is shown in right hand side figure of Figure 1.

In Figure 1, the behavior of the continuous branch of the eigenvalues (in terms of absolute values) of the three-dimensional Bernstein–Vandermonde matrix is shown with a dotted blue line in the left subfigure. This continuous branch of eigenvalues is dominated by a continuous branch of singular values (denoted with a red dotted line) for the values of $t\le 3.5.$ This is because of the fact that the computation of the singular values is the generalization of eigenvalues. However, surprisingly, after $t\ge 3.5$, the behavior of both eigenvalues and singular values abruptly changes. The dotted line with the light olive color (the topmost line) represents how the numerical approximation of upper bounds corresponding to the structured singular values computed with MATLAB function mussv acts and behaves. All continuous branches of eigenvalues, singular values, and numerically approximated lower bounds of structured singular values are bounded above by the numerical approximation of the upper bounds of structured singular values or $\mu$-values (light olive color). This is possible because of the fact that the numerical approximation of structured singular value or $\mu$-value is the generalization of both eigenvalues and singular values.

Example 2.

The following Bernstein–Bezoutian matrix is taken from [16]. The polynomials

$$p\left(a\right)=4-s{a}^2+a^4=4{\alpha }_0^{\left(4\right)}\left(a\right)+4{\alpha }_1^{\left(4\right)}\left(a\right)+\frac{19}{6}{\alpha }_2^{\left(4\right)}\left(a\right)+\frac{3}{2}{\alpha }_3^{\left(4\right)}\left(a\right),$$

and

$$q\left(a\right)=\frac{1}{2}-\frac{1}{4}a-2a^2+a^3=\frac{1}{2}{\alpha }_0^{\left(4\right)}\left(a\right)+\frac{7}{16}{\alpha }_1^{\left(4\right)}\left(a\right)+\frac{1}{24}{\alpha }_2^{\left(4\right)}\left(a\right)-\frac{7}{16}{\alpha }_3^{\left(4\right)}\left(a\right)-\frac{3}{4}{\alpha }_4^{\left(4\right)}\left(a\right),$$

gives the matrix

$$M_2=\left[\begin{array}{cccc}1& \frac{17}{6}& \frac{10}{3}& 3\\ \frac{17}{6}& \frac{157}{36}& \frac{83}{18}& 4\\ \frac{10}{3}& \frac{83}{18}& \frac{187}{36}& \frac{19}{4}\\ 3& 4& \frac{19}{4}& \frac{9}{2}\end{array}\right].$$

The first column appearing in Table 2 denotes the eigenvalues of $M_2$ computed by MATLAB function $eig(·)$. The second column represents the singular values approximated with MATLAB function $svd(·)$. The third and fourth columns represent the approximation (numerically) of both upper and lower bounds of structured singular values or $\mu$-values approximated by MATLAB function mussv. The numerically computed lower bounds of structured singular values or $\mu$-values via [58] are represented in the very last column.

Table 2. Spectral properties of $M_2$.

Eigenvalues	Singular Values	ssv (Upper)	ssv (Lower)	ssv (Lower New)
$\left\{-0.9403,0,0.4361,15.5597\right\}$	$\left\{15.5597,0.9403,0.4361,0\right\}$	$0.0643$	$0.0621$	$0.0634$

The behaviour of spectral condition numbers $k_2\left(M_i\right)$ for all $i=2,3,4$, the condition numbers $k_1\left(M_i\right)$ and $K_{\infty }$ for all $i=2,3,4$ are shown in Table 3.

Table 3. The condition number of $M_2$.

${\mathit{K}}_1\left({\mathit{M}}_2\right)$	${\mathit{K}}_2\left({\mathit{M}}_2\right)$	${\mathit{K}}_{\mathit{\infty }}\left({\mathit{M}}_2\right)$
$8.4464\times {10}^{16}$	$3.3158\times {10}^{16}$	$8.4464\times {10}^{16}$

6. Cauchy—Polynomial-Vandermonde Matrices (CPV Matrices)

The following lemma by Zhao Yang [60] provides results for the determinant of CPV-matrices.

Lemma 2

([60]). Let $A\in {\mathbb{R}}^{n\times n}$ be a Cauchy—polynomial-Vandermonde matrix, then the expression for the determinant $d\left(A\right)$ is given as

$$d\left(A\right)=\prod _{i=0}^{n-k-1}{a}_i\frac{{\prod }_{1\le t\le s\le n}(x_s-x_t){\prod }_{1\le t\le s\le n}(y_s-y_t)}{{\prod }_{1\le s\le n,1\le t\le k}(x_s+y_t)}.$$

Proof. 

For proof, see [60].    □

The minors of Cauchy—polynomial-Vandermonde matrices are computed with the help of the following result.

Theorem 6

([60]). Let $A\in {\mathbb{R}}^{n\times n}$ be a Cauchy—polynomial-Vandermonde matrix, then

$$d\left(A(i-j+1:i,1:j)\right)=\left\{\begin{array}{cc}\frac{{\prod }_{i-j+1\le t<s\le i}(x_s-x_t){\prod }_{1\le t<s\le j}(y_s-y_t)}{{\prod }_{i-j+1\le s\le i,1\le t\le j}(x_s+y_t)},\hfill & \forall j\le 1\hfill \\ \frac{{\prod }_{r=0}^{j-k-1}{a}_r{\prod }_{i-j+1\le s\le i,1\le t\le k}(x_s+x_t){\prod }_{1\le t<s\le k}(y_s-y_t)}{{\prod }_{i-j+1\le s\le i,1\le t\le k}(x_s+y_t)},\hfill & \forall j\ge k,\hfill \end{array}\right.$$

which holds true for all $i\ge j$.

Furthermore, we have that

$$d\left(A(1:i,j-i+1:j)\right)=\left\{\begin{array}{ll}\frac{{\prod }_{1\le t<s\le i}(x_s-x_t){\prod }_{j-i+1\le t<s\le j}(y_s-y_t)}{{\prod }_{1\le s\le i,j-i+1\le t\le j}(x_s+y_t)},& \forall j\le k\hfill \\ \frac{{\prod }_{r=0}^{j-k-1}{a}_r{\prod }_{1\le t<s\le i}(x_s-x_t){\prod }_{j-i+1\le t<s\le k}(y_s-y_t)}{{\prod }_{1\le s\le i,j-i+1\le t\le k}(x_s+y_t)},& \forall j-i+1\le k,j\ge k+1\\ \prod _{r=0}^{j-k-1}{a}_r\prod _{1\le t<s\le i}(x_s-x_t),& \forall j-i+1=k+1\\ \prod _{r=j-i-k+1}^{j-k-1}{a}_r\prod _{1\le t<s\le i}(x_s-x_t)g(i,j,k),& \forall j-i+1\ge k+2.\end{array}\right.$$

where

$$g(i,j,k)=\sum _{r=0}^{j-i-k}\left(a_r{s}_{\lambda }(j-i-k,r)\left(x_{1:i}\right)\right),\forall j-i-k\ge 1.$$

with

$$\lambda (j-i-k,r)=(j-i-k,\cdots ,j-i-k,r)\in {\mathbb{R}}^i$$

Proof. 

For proof, see [60].    □

Spectral Properties of Cauchy—Polynomial-Vandermonde Matrices

In this subsection, we aim to present and discuss the meaningful spectral properties of Cauchy—polynomial-Vandermonde structured matrices. For the numerical approximations of desired structured singular values or $\mu$-values, we let a class of test matrices from the paper by [60].

We make use of built-in MATLAB functions $eig(·)$ and $svd(·)$ to numerically approximate both the eigenvalues and singular values. Thus, our main aim is to approximate numerically the obtained lower bounds of structured singular values, a simple and straightforward generalization of singular values for structured matrices. Furthermore, we make use of the built-in MATLAB functions mussv to approximate numerically both the lower and upper bounds of structured singular values or or $\mu$-values for the structured matrices.

Example 3.

Consider a $2\times 2$ Cauchy—polynomial-Vandermonde matrix

$$M_3=\left[\begin{array}{cc}\frac{-6}{5}& \frac{-6}{7}\\ \frac{-6}{11}& \frac{-6}{13}\end{array}\right]$$

The matrix $M_3$ is obtained with ${\left\{a_i\right\}}_{0\le i\le n-k-1},{\left\{x_i\right\}}_{1\le i\le n}$ and ${\left\{y_i\right\}}_{1\le j\le k}$ which are given as

$$\left\{\begin{array}{cc}{a}_r={\left(\frac{-1}{2}\right)}^{r+1},\hfill & 1r=0,1,2,\cdots ,n-k+1\hfill \\ x_i=-i+\frac{1}{2},\hfill & i=1,2,3,\cdots ,n\hfill \\ y_i=\frac{-j}{3},\hfill & j=1,2,3,\cdots ,k.\hfill \end{array}\right.$$

(26)

For $M_3$, we consider

$$\left\{\begin{array}{c}{a}_0=-\frac{1}{2}\hfill \\ a_1=\frac{1}{4}\hfill \end{array}\right.,\left\{\begin{array}{c}{x}_1=-\frac{1}{2}\hfill \\ x_2=-\frac{3}{2}\hfill \\ x_3=-\frac{5}{2}\hfill \end{array}\right.\mathrm{and}\left\{\begin{array}{c}{y}_1=-\frac{1}{3}\hfill \\ y_2=-\frac{2}{3}\hfill \\ y_3=-1\hfill \end{array}\right.$$

in Equ (4.1).

The first column of Table 4 denotes the approximated eigenvalues of $M_3$ computed by MATLAB function $eig(·)$. The second column represents the singular values computed with MATLAB function $svd(·)$. The third and fourth columns represent the approximation (numerically) of both upper and lower bounds of structured singular values, which are approximated by MATLAB function mussv. The numerical approximations of the lower bounds of structured singular values or the or $\mu$-values with the help of algorithm [58] is represented in the very last column.

Table 4. Spectral properties of $M_3$.

Eigenvalues	Singular Values	ssv (Upper)	ssv (Lower)	ssv (Lower New)
$\left\{-1.6079,-0.0537\right\}$	$\left\{1.6378,0.0527\right\}$	$1.7415$	$1.7415$	$1.7415$

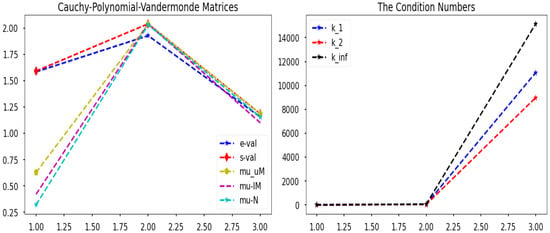
In Figure 2, the left-hand side subfigure represents the plots of eigenvalues, singular values, and numerical approximation to both lower and upper bounds of structured singular values or $\mu$-values against the time t. In Figure 2, the blue color dotted line identified with point $\left(2.0,1.75\right)$ denotes the spectrum, that is, the eigenvalues of $M_3$. Because singular values are non-negative numbers, the red color dotted line starting from point $\left(1.0,1.60\right)$ indicates that all eigenvalues are bounded above by singular values. The golden color dotted line starting from point $\left(1.0,0.60\right)$ shows that all quantities, that is, positive eigenvalues, singular values, and numerically approximated bounds from below for structured singular values or $\mu$-values via mussv function which is represented with purple color dotted line starting from point $\left(1.0,0.40\right)$ and the numerically approximated lower bounds of structured singular values with [58] represented with turquoise color dotted line starting from point $\left(1.0,0.26\right)$ are strictly bounded by upper bounds (numerically approximated) of structured singular values with MATLAB function mussv.

Figure 2. Behavior of eigenvalues, singular values, structured singular values, and condition numbers.

In Figure 2, the right-hand side subfigure represents the plots of condition numbers vs. time. Furthermore, the behaviour of spectral condition numbers $k_1\left(M_3\right)$ containing end point $\left(3.0,11,000\right)$, $k_2\left(M_3\right)$ containing end point $\left(3.0,8000\right)$ and $K_{\infty }\left(M_3\right)$ containing end point $\left(3.0,15,000\right)$ is shown in right hand side figure of Figure 2.

7. Quasi-Rational Bernstein–Vandermonde Matrices

The following result in [60] is the computation of the determinant of quasi-rational Bernstein–Vandermonde structured matrices.

Theorem 7

([60]). Let $M_b=\left(m_{ij}\right)\in {\mathbb{R}}^{n\times n}$ be a quasi-rational Bernstein–Vandermonde matrix. Then, the determinant $d(·)$ is computed as

$d\left(M_b(i-j+1:i|i:j)\right)=\frac{\left(\genfrac{}{}{0pt}{}{n-1}{0}\right)\cdots \left(\genfrac{}{}{0pt}{}{n-1}{j-1}\right)}{{\prod }_{k=i-j+1}^{i}W\left(x_k\right)}{\prod }_{k=0}^{j-1}{w}_k{\prod }_{k=i-j+1}{(1-x_k)}^{n-j}{\prod }_{i-j+1\le t<s\le i}(x_s-x_t),\forall i\ge j\ne n.$

In addition,

$d\left(M_b(1:i|j-i+1:j)\right)=\frac{\left(\genfrac{}{}{0pt}{}{n-1}{j-1}\right)\cdots \left(\genfrac{}{}{0pt}{}{n-1}{j-1}\right)}{\prod {\prod }_{k=1}^{i}W\left(x_k\right)}{\prod }_{k=1}^i{x}_k^{j-i}{\prod }_{k=j-i}^{j-1}{w}_k{\prod }_{k=1}^i{(1-x_k)}^{n-j}{\prod }_{1\le t<s\le i}(x_s-x_t),\forall i<j$

and

$\left\{\begin{array}{c}det\left(M_b\right)=(\frac{w_{n-1}}{W\left(x_n\right)}{\prod }_{k=1}^{n-1}(x_n-x_k)-w{\prod }_{k=1}^{n-1}(1-x_k))\frac{\left(\genfrac{}{}{0pt}{}{n-1}{0}\right)\cdots \left(\genfrac{}{}{0pt}{}{n-1}{n-2}\right)}{{\prod }_{k=1}^{n-1}W\left(x_k\right)}{\prod }_{k=0}^{n-2}{w}_k{\prod }_{1\le t<s\le n-1}(x_s-x_t),\hfill \\ det\left(M_b(2:n)\right)=(\frac{w_{n-1}{x}_n}{W\left(x_n\right)}{\prod }_{k=2}^{n-1}(x_n-x_k)-w{\prod }_{k=2}^{n-1}(1-x_k))\frac{\left(\genfrac{}{}{0pt}{}{n-1}{1}\right)\cdots \left(\genfrac{}{}{0pt}{}{n-1}{n-2}\right)}{{\prod }_{k=2}^{n-1}W\left(x_k\right)}{\prod }_{k=1}^{n-2}{w}_k{\prod }_{k=2}^{n-1}{x}_k{\prod }_{2\le t<s\le (n-1)}(x_S-x_t).\hfill \end{array}\right.$

Proof. 

For proof, see [60].    □

The parametric matrix $P_{r}M\left(M_b\right)$ for a quasi-rational Bernstein–Vandermonde matrix is given by the following theorem.

Theorem 8.

Let $M_b=\left(m_{ij}\right)\in {\mathbb{R}}^{n\times n}$ is a non-singular quasi-rational Bernstein–Vandermonde matrix. The parametric matrix $P_{r}M\left(M_b\right)\in {\mathbb{R}}^{n\times n}$ is the following matrix

$P_{r}M\left(M_b\right)=\left\{\begin{array}{cc}{d}_{ii}=\frac{\left(\genfrac{}{}{0pt}{}{n-1}{i-1}\right)w_{i-1}{(1-x_i)}^{n-i}}{W\left(x_i\right)}{\prod }_{k=1}^i\frac{(x_i-x_k)}{(1-x_k)},\hfill & 1\le i\le n-2\hfill \\ d_{n-1,n-1}=\frac{\left(\genfrac{}{}{0pt}{}{n-1}{n-2}\right)w_{n-2}(1-x_n)}{W\left(x_n\right)}{\prod }_{k=2}^{n-1}\frac{(x_n-x_k)}{(1-x_k)},\hfill & i=n-1\hfill \\ d_{n,n}=(w{\prod }_{k=1}^{n-1}(1-x_k)-\frac{w_{n-1}}{W\left(x_n\right)}{\prod }_{k=1}^{n-1}(x_n-x_k))\hfill \\ \phantom{Beta}\frac{W\left(x_n\right)(1-x_{n-1})}{W\left(x_{n-1}\right)(1-x_1)(1-x_n){\prod }_{k=2}^{n-1}(x_n-x_k)}{\prod }_{k=1}^{n-2}\frac{(x_{n-1}-x_k)}{(1-x_k)},\hfill & i=n,\forall 1\le i\le n.\hfill \end{array}\right.$,

$P_{r}M{\left(m_b\right)}_{ij}=\left\{\begin{array}{cc}{x}_{ij}=\frac{w\left(x_{i-1}\right){(1-x_i)}^{n-j}(1-x_{i-j})(x_i-x_{i-1})}{W\left(x_i\right){(1-x_{i-1})}^{n-j+1}(x_{i-1}-x_{i-j})}{\prod }_{k=i-j+1}^{i-2}\frac{x_i-x_k}{x_{i-1}-x_k},\hfill & (i,j)\ne (n,n-1)\hfill \\ x_{n,n-1}=\frac{w\left(x_n\right){(1-x_n)}^2(x_{n-1}-x_1)}{W\left(x_{n-1}\right)(1-x_n)(1-x_1)(x_n-x_{n-1})}{\prod }_{k=2}^{n-2}\frac{x_{n-1}-x_k}{x_n-x_k},\hfill & (i,j)=(n,n-1),\forall 1\le j\le i\le n.\hfill \end{array}\right.$ and

$P_{r}M{\left(m_b\right)}_{ij}=\left\{\begin{array}{cc}{B}_{ij}=\frac{(n-j+1)w_{j-1}{x}_i}{(j-1)w_{j-2}(1-x_i)},\hfill & 1\le i\le n-2\hfill \\ \delta =(\frac{w_{n-1}{x}_n}{W\left(x_n\right)}{\prod }_{k=2}^{n-1}(x_n-x_k)-w{\prod }_{k=2}^{n-1}(1-x_k))\hfill \\ \phantom{Beta}\frac{\left(\genfrac{}{}{0pt}{}{n-1}{1}\right)...\left(\genfrac{}{}{0pt}{}{n-1}{n-2}\right){\prod }_{k=1}^{n-2}{w}_k{\prod }_{k=2}^{n-1}{x}_k{\prod }_{2\le t<s\le n-1}^{k=2}(x_s-x_t)}{d_{n-1,n-1}{\prod }_{t=3}^n{d}_{t-2,t-2}{\beta }_{t-2,t-1}{\gamma }_{t-1,t-2}{\prod }_{k=2}^{n-1}W\left(x_k\right)},\hfill & \forall 1\le i\le i\le n.\hfill \end{array}\right.$

Spectral Properties of Quasi-Rational Bernstein–Vandermonde Matrices

In this subsection, we aim to present important and meaningful spectral properties of quasi-rational Bernstein–Vandermonde matrices. These matrices are taken from the paper [60] for the numerical approximations of structured singular values.

We make use of the well-known MATLAB functions $eig(·)$ and $svd(·)$ to approximate numerically both eigenvalues and singular values. Our main objective is to approximate numerically the lower bounds of structured singular value or $\mu$-value, which is a straightforward generalization of singular values for constant structured matrices. Furthermore, we make use of MATLAB functions mussv to compute both lower and upper bounds of structured singular values or $\mu$-values for constant structured matrices numerically.

Example 4.

Consider a $6\times 6$ quasi-rational Bernstein–Vandermonde matrix

$$M_4=\left[\begin{array}{cccccc}2.9091\times {10}^5& 2.1818\times {10}^5& 3.6364\times {10}^4& 2.5455\times {10}^3& 8.1818\times {10}^1& 1.0000\\ 7.0344\times {10}^3& 1.1107\times {10}^4& 3.8972\times {10}^3& 5.7432\times {10}^2& 3.8864\times {10}^1& 1.0000\\ 7.0691\times {10}^2& 1.7673\times {10}^3& 9.8182\times {10}^2& 2.2909\times {10}^2& 2.4545\times {10}^1& 1.0000\\ 1.2605\times {10}^2& 4.4489\times {10}^2& 3.4893\times {10}^2& 1.1494\times {10}^2& 1.7386\times {10}^1& 1.0000\\ 3.0504\times {10}^1& 1.4299\times {10}^2& 1.4895\times {10}^2& 6.5164\times {10}^1& 1.3091\times {10}^1& 9.9999\times {10}^{-1}\\ 8.8778& 5.3267\times {10}^1& 7.1023\times {10}^1& 3.9772\times {10}^1& 1.0227\times {10}^1& 9.6161\times {10}^{-1}\end{array}\right].$$

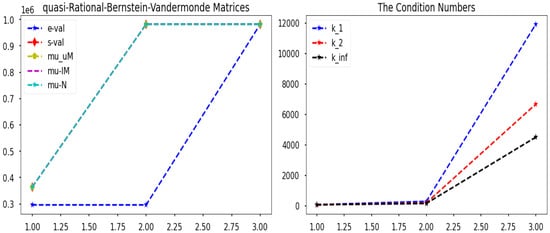
The computation of both eigenvalues and singular values are obtained as $1.0\times {10}^5\times \left\{2.9639,0.0642,0.0030,0.0002,0,0\right\}$ and $1.0\times {10}^5\times \left\{3.6568,0.0555,0.0030,0.0002,0,0\right\},$ respectively. The first and second columns represent numerically approximated upper and lower bounds of structured singular values or $\mu$-values via MATLAB function mussv. The approximation (numerical) lower bounds of structured singular values or $\mu$-values with algorithm [58] are represented in the very last column of Table 5.

Table 5. Spectral properties of $M_4$.

ssv (Upper)	ssv (Lower)	ssv (Lower New)
$1.0\times {10}^{0.5\times 3.6568}$	$1.0\times {10}^{0.5\times 3.6568}$	$3.6568\times {10}^5$

In Figure 3, the left-hand side subfigure represents the plots of eigenvalues, singular values, and numerically approximated bounds (from below and above) of structured singular values or $\mu$-values against the time t. In Figure 3, the blue color dotted line starting from point $\left(1.0,0.3\right)$ at the bottom of the left side figure denotes the spectrum, that is, the eigenvalues of $M_4$. Because singular values are non-negative numbers, the red color dotted line starting from point $\left(1.0,0.37\right)$ indicates that numerically approximated eigenvalues are bounded from above by means of singular values. The golden color dotted line starting from point $\left(1.0,0.37\right)$ shows that all quantities, that is, eigenvalues, singular values, and lower bounds of structured singular values or $\mu$-values approximated by MATLAB mussv function, which is represented with the purple color dotted line starting from point $\left(1.0,0.37\right)$ and the numerically approximated lower bounds of structured singular values or $\mu$-values via algorithm [58] represented with a turquoise color dotted line starting from point $\left(1.0,0.37\right)$ are strictly bounded by upper bounds (computed numerically) of structured singular values with MATLAB function mussv.

Figure 3. Behavior of eigenvalues, singular values, structured singular values, and condition numbers.

In Figure 3, the right-hand side subfigure represents the plots of condition numbers vs. time. Furthermore, the behaviour of spectral condition numbers $k_1\left(M_4\right)$ having end point $\left(3.0,12,000\right)$, $k_2\left(M_4\right)$ having end point $\left(3.0,6000\right)$ and $K_{\infty }\left(M_4\right)$ having end point $\left(3.0,4000\right)$ is shown in right hand side figure of Figure 3.

8. Numerical Testing for Matrices in Higher Dimensions

In this section, we aim to present the comparison of the numerically approximated bounds of structured singular values for Bernstein-Vandermonde structured matrices in higher dimensions. For numerical testing, we choose the Bernstein-Vandermonde matrices having sizes $10,15,20,25,30$, respectively.

The very first column in Table 6 denoted the size of square Bernstein–Vandermonde structured matrices, which are under consideration in this article. Both the second and third columns indicate the numerical approximation to both upper and lower bounds of structured singular values or $\mu$-values with the help of MATLAB function mussv, respectively. The last and fourth column of Table 6 shows the numerical approximation of the bounds (from below) of structured singular value or $\mu$-value computed via algorithm [58]. For the size 10, the lower bound of structured singular value approximated numerically via MATLAB mussv function is much better. However, for the sizes $15,20,25,30$, the lower bounds approximated by [58] are significantly better than the lower bounds approximated by MATLAB function mussv.

Algorithm 1 Approximate perturbation level.

procedure Given A, $\mathbb{B}$,THE TOLERANCE $tol>0$, ${ϵ}^{\left(0\right)}$(BOUND FROM BELOW), ${ϵ}_l$(BOUND FROM ABOVE), ${ϵ}_u$(GIVEN UPPER BOUND), $i_{max}$(INITIAL OF EIGENVALUES) $\mathit{for}i\leftarrow 1\mathit{to}$ imax $do$ Determine solution to system of ODEs (4.10) in [58] for all cases that begin with the initial choice of the value of ${\Delta }_i\left(0\right)$. The quantity ${\Delta }_i$ denotes solution (of stationary nature) and let ${\xi }_i$ denotes smallest eigenvalue corresponding to modified perturbed structured matrix $I-{ϵ}^{\left(0\right)}A{\Delta }_i$ Take $i_{\ast }=argmin\left|{\xi }_i\right|$ Take ${\Delta }^{\left(0\right)}={\Delta }_{i_{\ast }}$, ${\xi }^{\left(0\right)}={\xi }_i$, $x^{\left(0\right)}$, $y^{\left(0\right)}$ the computed eigenvectors Determine ${ϵ}^{\left(1\right)}$ via a single step fast Newton iteration Set $k=1$ While $|{ϵ}^{\left(k\right)}-{ϵ}^{(k-1)}|>tolthen,do$ Determine solution to ODEs (4.10) in [58] with $ϵ={ϵ}^{\left(k\right)}$ begins from $\Delta \left(0\right)={\Delta }^{(k-1)}$ Consider ${\Delta }^{\left(k\right)}$, solution (stationary) of (4.10) in [58] Consider ${\xi }^{\left(k\right)}$, the smallest eigenvalue of modified structured matrix $I-{ϵ}^{\left(0\right)}A{\Delta }^{\left(k\right)}$ if $|{\xi }^{\left(k\right)}|>tolthen,do$ Set perturbation level ${ϵ}_l={ϵ}^{\left(k\right)}$ Determine suitable value of ${ϵ}^{(k+1)}$ with one step fast Newton iteration. end procedure

Table 6. Comparison of bounds of structured singular values for Bernstein–Vandermonde matrices in higher dimensions.

n	ssv (Upper)	ssv (Lower)	ssv (Lower New)
10	$4.5711\times {10}^4$	$4.5711\times {10}^4$	$4.4640\times {10}^4$
15	$2.3241\times {10}^8$	$2.2732\times {10}^8$	$2.2878\times {10}^8$
20	$3.3512\times {10}^{12}$	$3.30011\times {10}^{12}$	$3.30035\times {10}^{12}$
25	$7.9028\times {10}^{16}$	$7.7121\times {10}^{16}$	$7.7987\times {10}^{16}$
30	$6.2264\times {10}^{24}$	$0.0005\times {10}^{21}$	$0.0005\times {10}^{24}$

9. Conclusions

In this article, we have presented and analyzed the numerical approximation of a mathematical tool commonly known as structured singular value for a class of totally positive Bernstein–Vandermonde structured matrices, Bernstein–Bezoutian structured matrices, Cauchy—polynomial-Vandermonde structured matrices, and quasi-rational Bernstein–Vandermonde structured matrices. The numerical computation of both eigenvalues and singular values for such a class of structured matrices is presented and investigated with MATLAB functions $eig(·)$ and $ssv(·)$. The new contribution in this article is to make a comparison for the numerical approximation of lower bounds of structured singular value compared with MATLAB function $mussv$ available in MATLAB Control Toolbox.