Analytic Solutions for Hilfer Type Fractional Langevin Equations with Variable Coefficients in a Weighted Space

Abstract

In this work, analytic solutions of initial value problems for fractional Langevin equations involving Hilfer fractional derivatives and variable coefficients are studied. Firstly, the equivalence of an initial value problem to an integral equation is proved. Secondly, the existence and uniqueness of solutions for the above initial value problem are obtained without a contractive assumption. Finally, a formula of explicit solutions for the proposed problem is derived. By using similar arguments, corresponding conclusions for the case involving Riemann–Liouville fractional derivatives and variable coefficients are obtained. Moreover, the nonlinear case is discussed. Two examples are provided to illustrate theoretical results.

1. Introduction

In 1908, Langevin introduced an integer-order equation

$$\begin{array}{c}\hfill m{x}^{″}\left(t\right)=-\lambda x^{\prime }\left(t\right)+F\left(t\right),\end{array}$$

where m is the mass of a Brownian particle, $x\left(t\right)$ is the particle’s position, $-\lambda x^{\prime }\left(t\right)$ is the viscous force with coefficient $\lambda$ and $F\left(t\right)$ is the fluctuating force. It is regarded as an effective tool to describe the evolution of physical phenomena in fluctuating environments [1].

Fractional differential equations are important tools for investigating many practical problems in physics, chemistry, biology, etc. Many scholars have conducted extensive research on equations involving Riemann–Liouville or Caputo fractional derivatives—for details, see [2,3,4,5].

For more complex physical phenomena, some researchers have generalized Langevin equations from integer order to fractional order. In 1996, the above classical Langevin equation was generalized by Mainardi and Pironi [6] to the fractional Langevin equation (FLE)

$$x^{″}\left(t\right)+\frac{1}{\sigma }\sqrt{\frac{a^2}{\nu }}{D}_0^{\frac{1}{2}}{x}^{\prime }\left(t\right)=F(t,x\left(t\right)),$$

where a is the particle’s radius, $\nu$ is the fluid’s viscosity, $\frac{1}{\sigma }$ is the friction coefficient for unit mass, $F(t,x\left(t\right))=-\frac{1}{\sigma }{x}^{\prime }\left(t\right)+\frac{1}{m}R\left(t\right)$ and $R\left(t\right)$ is a random force.

FLEs have attracted many scholars to study properties of solutions for FLEs—for instance, the existence and uniqueness of solutions for FLEs with Caputo or Riemann–Liouville fractional derivatives [7,8], boundary value problems for FLEs [9,10,11,12], etc. Baghani and Nieto [13] studied the following Langevin differential equation with two different fractional orders:

$${\hspace{0.17em}}^c{D}^{\xi }{(}^c{D}^{\nu }+\lambda )x\left(t\right)=h(t,x\left(t\right)).$$

In 2000, a fractional derivative operator ${\hspace{0.17em}}^H{D}_{a^{+}}^{\alpha ,\beta }$ ($\alpha \in (n-1,n)$, $\beta \in [0,1]$) was introduced by Hilfer, which can be applied to characterize many complicated phenomena in various engineering and scientific disciplines; for instance, it has applications in regular variation in thermodynamics, physics and materials (see, e.g., [14]). More applications can be found in [15,16] and the references therein. When $\beta =0$ or $\beta =1$, ${\hspace{0.17em}}^H{D}_{a^{+}}^{\alpha ,\beta }$ reduces to ${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{\alpha }$(Riemann–Liouville fractional derivative operator) or ${\hspace{0.17em}}^c{D}_{a^{+}}^{\alpha }$(Caputo fractional derivative operator), respectively.

Moreover, we refer to some recent works [17,18] that deal with a qualitative analysis of FLEs with Hilfer fractional derivatives.

In [17], the authors studied a nonlinear fractional Langevin dynamical system with impulse as follows:

$$\left\{\begin{array}{c}{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,\beta }[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,\beta }+A]x\left(t\right)=Ku\left(t\right)+H(t,x\left(t\right)),t\in [0,b],\hfill \\ \Delta I_{0^{+}}^{1-\gamma }{x(·)|}_{t=t_k}=g_k\left(x\left(t_k^{-}\right)\right),k=1,2,\cdots ,m,\hfill \\ I_{0^{+}}^{1-\gamma }x\left(0\right)=x_0,{\hspace{0.17em}}^H{D}^{{\alpha }_2,\beta }x\left(0\right)=0,\gamma =(1-\beta )({\alpha }_1+{\alpha }_2)+\beta ,t\in [0,b].\hfill \end{array}\right.$$

In [18], the authors investigated the existence and uniqueness of solutions to the following system of Hilfer FLEs:

$$\left\{\begin{array}{c}{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,{\beta }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}+{\lambda }_1]x\left(t\right)=f(t,x\left(t\right),y\left(t\right)),t\in [a,b],\hfill \\ {\hspace{0.17em}}^H{D}_{a^{+}}^{p_2,q_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{p_1,q_1}+{\lambda }_2]y\left(t\right)=g(t,x\left(t\right),y\left(t\right)),t\in [a,b],\hfill \\ x\left(a\right)=0,x\left(b\right)={\displaystyle \sum _{i=1}^n}{\mu }_i\left(I^{{\nu }_i}y\right)\left({\eta }_i\right),\hfill \\ y\left(a\right)=0,y\left(b\right)={\displaystyle \sum _{j=1}^m}{\omega }_j\left(I^{{\sigma }_j}x\right)\left({\xi }_j\right).\hfill \end{array}\right.$$

Due to the complexity of variable-coefficient functions, it is very hard to obtain representations of solutions of FLEs with variable coefficients. Recently, some methods have been presented to deal with linear fractional differential equations with continuous coefficients, such as power series methods [19,20] and the Banach fixed point theorem [21]. However, to the best of our knowledge, there are very few studies on FLEs with Hilfer derivatives and negative power function coefficients.

Motivated by previous research, in this article, we study the initial value problem (IVP) for FLEs with Hilfer derivatives and variable coefficients:

$$\begin{array}{c}\{\begin{array}{}\mathrm{(1)}& {\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,{\beta }_2}({\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}+\lambda \left(t\right))x\left(t\right)+\delta \left(t\right)x\left(t\right)=f\left(t\right),t\in (a,T],\hfill \mathrm{(2)}& \left(I_{a^{+}}^{1-{\gamma }_1}x\right)\left(a^{+}\right)=x_0,\hfill \end{array}\end{array}$$

where $0<{\alpha }_2<{\gamma }_2<{\alpha }_1<{\gamma }_1$, ${\alpha }_2+{\gamma }_1>1$, ${\gamma }_i={\alpha }_i+{\beta }_i(1-{\alpha }_i)(i=1,2)$ and $\lambda \left(t\right)$ is a continuous function. More details about $\delta \left(t\right)$ and $f\left(t\right)$ are given later.

The main contribution in this article is presented as follows:

• Using new techniques, we present an explicit representation of solutions to Problems (1) and (2).
• We obtain the existence and uniqueness of solutions for Problems (1) and (2) without a contractive assumption.
• We present a nonlinear mixed Fredholm–Volterra integral solution for nonlinear initial value Problem (22)–(23).

This paper is split into six sections. Some definitions and properties of fractional derivatives are provided in Section 2. We study the existence and uniqueness of solutions for the linear case and the nonlinear case in Section 3 and Section 4, respectively. In Section 5, we present two examples to illustrate our results and provide an approximate result. Finally, in Section 6, we present the conclusions.

2. Preliminaries

Firstly, we recall the basic definitions and properties of fractional derivatives and weighted spaces.

Definition 1

([5]). Let $\alpha \in (0,1)$. The Riemann–Liouville fractional integral $I_{a^{+}}^{\alpha }f$ and derivative ${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{\alpha }f$ are defined by

$$\begin{array}{ccc}\hfill \left(I_{a^{+}}^{\alpha }f\right)\left(t\right)& =& \frac{1}{\Gamma \left(\alpha \right)}{\int }_a^t{(t-s)}^{\alpha -1}f\left(s\right)ds,t>a,f\in L^1(a,b),\hfill \\ \hfill \left({\hspace{0.17em}}^{RL}{D}_{a^{+}}^{\alpha }f\right)\left(t\right)& =& \frac{d}{dt}\left(I_{a^{+}}^{1-\alpha }f\right)\left(t\right)=\frac{1}{\Gamma (1-\alpha )}\frac{d}{dt}{\int }_a^t{(t-s)}^{-\alpha }f\left(s\right)ds,t>a,\hfill \end{array}$$

(3)

where $\Gamma (·)$ is the Gamma function, provided that the right-hand side of (3) exists.

Definition 2

([14]). The left-sided Hilfer fractional derivative of order $\alpha \in (0,1)$ and type $\beta \in [0,1]$ of $f\left(t\right)$ is defined by

$${\hspace{0.17em}}^H{D}_{a^{+}}^{\alpha ,\beta }f\left(t\right)=I_{a^{+}}^{\gamma -\alpha }\frac{d}{dt}{I}_{a^{+}}^{1-\gamma }f\left(t\right)=I_{a^{+}}^{\gamma -\alpha }{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{\gamma }f\left(t\right),$$

(4)

where $\gamma =\alpha +\beta (1-\alpha )$, provided that the expression on the right-hand side exists.

A modified Hilfer derivative was presented in [20].

Definition 3

([20]). The left-sided Hilfer fractional derivative of order $\alpha \in (0,1)$ and type $\beta \in [0,1]$ of $f\left(t\right)$ is defined by

$${\hspace{0.17em}}^H{D}_{a^{+}}^{\alpha ,\beta }f\left(t\right)={\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-\gamma +\alpha }[\left(I_{a^{+}}^{1-\gamma }f\right)\left(t\right)-\left(I_{a^{+}}^{1-\gamma }f\right)\left(a^{+}\right)],$$

(5)

where $\gamma =\alpha +\beta (1-\alpha )$, provided that the right-hand side exists.

It is not difficult to see that the conditions to guarantee the existence of the Riemann–Liouville derivative in (5) are weaker than those needed for the Hilfer fractional derivative in (4) [20].

Definition 4

([5,22]). Let $\sigma \in [0,1)$, $\omega \in (0,1)$ and $\xi \in [0,1)$.

(i)

$C[a,b]$ is the space of functions x, which are continuous on $[a,b]$ and ${\parallel x\parallel }_C=\underset{t\in [a,b]}{max}\left|x\left(t\right)\right|$.

(ii)

The weighted space $C_{\sigma }[a,b]$ is defined by

$$C_{\sigma }[a,b]:=\{x:(a,b]\to \mathbb{R};{(t-a)}^{\sigma }x\left(t\right)\in C[a,b]\}\mathit{and}{\parallel x\parallel }_{C_{\sigma }}=\underset{t\in [a,b]}{max}\left|{(t-a)}^{\sigma }x\left(t\right)\right|.$$

(iii)

$C_{\sigma }^n[a,b]$ is the weighted space of functions x, which are continuously differentiable on $[a,b]$ up to order $n-1$ and have the derivative of order n on $(a,b]$ such that $x^{\left(n\right)}\in C_{\sigma }[a,b]$:

$$C_{\sigma }^n[a,b]:=\{x\in C^{n-1}[a,b];x^{\left(n\right)}\in C_{\sigma }[a,b],n\in \mathbb{N}\},$$

with the norm ${\parallel x\parallel }_{C_{\sigma }^n}={\displaystyle \sum _{k=0}^{n-1}}\parallel x^{\left(k\right)}{\parallel }_C+{\parallel x^{\left(n\right)}\parallel }_{C_{\sigma }}$.

(iv)

We denote the weighted space

$$C_{\sigma ,\xi }^{\omega ,RL}[a,b]=\{x\in C_{\sigma }[a,b];{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{\omega }x\in C_{\xi }[a,b]\},$$

with the norm ${\parallel x\parallel }_{C_{\sigma ,\xi }^{\omega ,RL}}={\parallel x\parallel }_{C_{\sigma }}+{{\parallel }^{RL}{D}_{a^{+}}^{\omega }x\parallel }_{C_{\xi }}$. When $\xi =\sigma$, $C_{\sigma ,\sigma }^{\omega ,RL}[a,b]$ is denoted by $C_{\sigma }^{\omega ,RL}[a,b]$.

(v)

We denote the weighted space

$$C_{\sigma ,\xi }^{\alpha ,\beta }[a,b]=\{x\in C_{\sigma }[a,b];{\hspace{0.17em}}^H{D}_{a^{+}}^{\alpha ,\beta }x\in C_{\xi }[a,b]\},$$

with the norm ${\parallel x\parallel }_{C_{\sigma ,\xi }^{\alpha ,\beta }}={\parallel x\parallel }_{C_{\sigma }}+{{\parallel }^H{D}_{a^{+}}^{\alpha ,\beta }x\parallel }_{C_{\xi }}$. When $\xi =\sigma$, $C_{\sigma ,\sigma }^{\alpha ,\beta }[a,b]$ is denoted by $C_{\sigma }^{\alpha ,\beta }[a,b]$.

Clearly, $C_0[a,b]=C[a,b]$. We abbreviate $C[a,b]$, $C_{\sigma }[a,b]$, $C_{\sigma }^n[a,b]$, $C_{\sigma }^{\omega ,RL}[a,b]$, $C_{\sigma ,\xi }^{\omega ,RL}[a,b]$, $C_{\sigma }^{\alpha ,\beta }[a,b]$ and $C_{\sigma ,\xi }^{\alpha ,\beta }[a,b]$ to $\mathcal{C}$, $C_{\sigma }$, $C_{\sigma }^n$, $C_{\sigma }^{\omega ,RL}$, $C_{\sigma ,\xi }^{\omega ,RL}$, $C_{\sigma }^{\alpha ,\beta }$ and $C_{\sigma ,\xi }^{\alpha ,\beta }$ respectively.

Lemma 1

([5]). If $\omega \in (0,1)$ and $\sigma \in [0,1)$, then $I_{a^{+}}^{\omega }$ is bounded from $C_{\sigma }$ into $C_{\sigma }$.

Lemma 2

([5]). Let $0<\omega <\sigma <1$ and $y\in C_{\sigma }$; then, $\left(I_{a^{+}}^{\omega }y\right)\left(t\right)\in C_{\sigma -\omega }$.

Lemma 3

([5]). Let $\sigma \in [0,1)$, $\sigma \le \omega$ and $y\in C_{\sigma }$; then, $\left(I_{a^{+}}^{\omega }y\right)\left(t\right)\in \mathcal{C}$.

Lemma 4.

Let $0\le \sigma <\omega <1$ and $y\in C_{\sigma }$; then, ${\displaystyle \left(I_{a^{+}}^{\omega }y\right)(a+)=\underset{t\to a^{+}}{lim}\left(I_{a^{+}}^{\omega }y\right)\left(t\right)=0}$.

Lemma 5

([5]). Let ${\omega }_1,{\omega }_2>0$, $0\le \sigma <1$. Then, for $\phi \in C_{\sigma }$, the following assertions are valid.

$$\begin{array}{ccc}\hfill \left(I_{a^{+}}^{{\omega }_1}{I}_{a^{+}}^{{\omega }_2}\phi \right)\left(t\right)& =& \left(I_{a^{+}}^{{\omega }_1+{\omega }_2}\phi \right)\left(t\right),\hfill \\ \hfill \left({\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\omega }_1}{I}_{a^{+}}^{{\omega }_1}\phi \right)\left(t\right)& =& \phi \left(t\right),\hfill \\ \hfill \left({\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\omega }_2}{I}_{a^{+}}^{{\omega }_1}\phi \right)\left(t\right)& =& \left(I_{a^{+}}^{{\omega }_1-{\omega }_2}\phi \right)\left(t\right),\mathit{for}{\omega }_1>{\omega }_2.\hfill \end{array}$$

Lemma 6

([5]). Let $\sigma \in [0,1)$ and $\omega \in (0,1)$. If $y\in C_{\sigma }$ and $I_{a^{+}}^{1-\omega }y\in C_{\sigma }^1$, then

$$\left(I_{a^{+}}^{\omega }{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{\omega }y\right)\left(t\right)=y\left(t\right)-\frac{\left(I_{a^{+}}^{1-\omega }y\right)\left(a^{+}\right)}{\Gamma \left(\omega \right)}{(t-a)}^{\omega -1}.$$

(6)

Lemma 7

([5]). Let $0\le \sigma <1$. The space $C_{\sigma }^1[a,b]$ consists of those and only those functions g, which are represented in the form

$$\begin{array}{c}\hfill g\left(t\right)={\int }_a^t\phi \left(s\right)ds+c,\end{array}$$

where $\phi \in C_{\sigma }$ and $c=g\left(a\right)$.

Theorem 1.

Let $\omega ,\sigma ,\xi \in (0,1)$. If $y\in C_{\sigma }$ and $I_{a^{+}}^{1-\omega }y\in C_{\xi }^1$, then

$$\left(I_{a^{+}}^{\omega }{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{\omega }y\right)\left(t\right)=y\left(t\right)-\frac{\left(I_{a^{+}}^{1-\omega }y\right)\left(a^{+}\right)}{\Gamma \left(\omega \right)}{(t-a)}^{\omega -1}.$$

Proof. 

Since $I_{a^{+}}^{1-\omega }y\in C_{\xi }^1$, from Lemma 7, there exists $\phi \in C_{\xi }$ such that

$$\left(I_{a^{+}}^{1-\omega }y\right)\left(t\right)={\int }_a^t\phi \left(s\right)ds+c,$$

where $c=\left(I_{a^{+}}^{1-\omega }y\right)\left(a^{+}\right)$. Thus,

$$I_{a^{+}}^{1-\omega }[y\left(t\right)-\left(I_{a^{+}}^{\omega }\phi \right)\left(t\right)-\frac{c{(t-a)}^{\omega -1}}{\Gamma \left(\omega \right)}]=0,$$

then

$$y\left(t\right)=\left(I_{a^{+}}^{\omega }\phi \right)\left(t\right)+\frac{c{(t-a)}^{\omega -1}}{\Gamma \left(\omega \right)}.$$

(7)

Moreover, note that

$$\left(I_{a^{+}}^{\omega }{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{\omega }y\right)\left(t\right)=I_{a^{+}}^{\omega }(\frac{d}{dt}{I}_{a^{+}}^{1-\omega }y)\left(t\right)=\left(I_{a^{+}}^{\omega }\phi \right)\left(t\right)$$

and, combining with (7), we obtain the result. □

Theorem 2.

Let $y\in C_{1-\gamma }^{\alpha ,\beta }(\beta \ne 0)$; then,

$$\left(I_{a^{+}}^{\alpha }{\hspace{0.17em}}^H{D}_{a^{+}}^{\alpha ,\beta }y\right)\left(t\right)=y\left(t\right)-\frac{\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right)}{\Gamma \left(\gamma \right)}{(t-a)}^{\gamma -1}.$$

Proof. 

Since $y\in C_{1-\gamma }^{\alpha ,\beta }$, we can see that $y\in C_{1-\gamma }$ and ${\hspace{0.17em}}^H{D}_{a^{+}}^{\alpha ,\beta }y\left(t\right)\in C_{1-\gamma }$, then

$$I_{a^{+}}^{\gamma -\alpha }[\left(I_{a^{+}}^{1-\gamma }y\right)\left(t\right)-\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right)]\in C_{1-\gamma }^1$$

and

$$\begin{array}{c}\hfill \left\{I_{a^{+}}^{\gamma -\alpha }[\left(I_{a^{+}}^{1-\gamma }y\right)\left(t\right)-\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right)]\right\}\left(a^{+}\right)=0.\end{array}$$

(8)

From Lemma 6, it follows that

$$I_{a^{+}}^{1-\gamma +\alpha }{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-\gamma +\alpha }[\left(I_{a^{+}}^{1-\gamma }y\right)\left(t\right)-\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right)]=\left(I_{a^{+}}^{1-\gamma }y\right)\left(t\right)-\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right),$$

thus,

$$\begin{array}{ccc}\hfill \left(I_{a^{+}}^{\alpha }{\hspace{0.17em}}^H{D}_{a^{+}}^{\alpha ,\beta }y\right)\left(t\right)& =& I_{a^{+}}^{\alpha }{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-\gamma +\alpha }[\left(I_{a^{+}}^{1-\gamma }y\right)\left(t\right)-\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right)]\hfill \\ & =& {\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-\gamma }{I}_{a^{+}}^{1-\gamma +\alpha }{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-\gamma +\alpha }[\left(I_{a^{+}}^{1-\gamma }y\right)\left(t\right)-\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right)]\hfill \\ & =& {\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-\gamma }[\left(I_{a^{+}}^{1-\gamma }y\right)\left(t\right)-\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right)]\hfill \\ & =& y\left(t\right)-\frac{\left(I_{a^{+}}^{1-\gamma }y\right)\left(a^{+}\right)}{\Gamma \left(\gamma \right)}{(t-a)}^{\gamma -1}.\hfill \end{array}$$

□

3. Equivalence with an Integral Equation

We consider the following IVP for FLEs with Hilfer derivatives and variable coefficients:

$$\begin{array}{c}\left\{\begin{array}{}\mathrm{(9)}& {\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,{\beta }_2}({\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}+\lambda \left(t\right))x\left(t\right)+\delta \left(t\right)x\left(t\right)=f\left(t\right),t\in (a,T],\hfill \mathrm{(10)}& \left(I_{a^{+}}^{1-{\gamma }_1}x\right)\left(a^{+}\right)=x_0.\hfill \end{array}\right.\end{array}$$

We define the following constants $\nu ,\mu >0$ such that

$$\begin{array}{c}\hfill {\alpha }_2<\mu <1-{\gamma }_1+{\alpha }_2;0<\nu <\mu +{\gamma }_1-1.\end{array}$$

(11)

Theorem 3.

Let $\delta \left(t\right)\in C_{\nu }$ and $f\left(t\right)\in C_{\mu }$; then, $x\in C_{1-{\gamma }_1}^{{\alpha }_1,{\beta }_1}$ satisfies (9) and (10) if and only if x satisfies the following equation

$$x\left(t\right)=-I_{a^{+}}^{{\alpha }_1}[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right)+\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0.$$

(12)

Proof. 

Let $x\in C_{1-{\gamma }_1}^{{\alpha }_1,{\beta }_1}$ satisfy (9) and (10); then, ${\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)\in C_{1-{\gamma }_1,\mu }^{{\alpha }_2,{\beta }_2}$, from Lemma 4,

$$\left\{I_{a^{+}}^{1-{\gamma }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]\right\}\left(a^{+}\right)=0.$$

Thus,

$$\begin{array}{ccc}\hfill {\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,{\beta }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]& =& {\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-{\gamma }_2+{\alpha }_2}{I}_{a^{+}}^{1-{\gamma }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]\hfill \\ & =& \frac{d}{dt}{I}_{a^{+}}^{1-{\alpha }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]\in C_{\mu }.\hfill \end{array}$$

By Theorem 1,

$$\begin{array}{ccc}\hfill I_{a^{+}}^{{\alpha }_2}{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,{\beta }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]& =& I_{a^{+}}^{{\alpha }_2}{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]\hfill \\ & =& {\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right).\hfill \end{array}$$

(13)

Applying $I_{a^{+}}^{{\alpha }_2}$ to (9) and in view of (13), one obtains

$${\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)=I_{a^{+}}^{{\alpha }_2}f\left(t\right).$$

(14)

By Theorem 2, we obtain

$$\begin{array}{ccc}\hfill I_{a^{+}}^{{\alpha }_1}{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)& =& x\left(t\right)-\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0.\hfill \end{array}$$

Applying $I_{a^{+}}^{{\alpha }_1}$ to (14), one obtains

$$\begin{array}{c}\hfill x\left(t\right)=-I_{a^{+}}^{{\alpha }_1}[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right)+\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0,\end{array}$$

which means that $x\left(t\right)$ satisfies (12).

If $x\left(t\right)$ satisfies (12), then

$$I_{a^{+}}^{1-{\gamma }_1}x\left(t\right)-x_0=I_{a^{+}}^{1-{\gamma }_1+{\alpha }_1}\left[-\lambda \left(t\right)x\left(t\right)-I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)+I_{a^{+}}^{{\alpha }_2}f\left(t\right)\right].$$

Clearly, $\left(I_{a^{+}}^{1-{\gamma }_1}x\right)\left(a^{+}\right)=x_0$ and

$${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-{\gamma }_1+{\alpha }_1}[I_{a^{+}}^{1-{\gamma }_1}x\left(t\right)-x_0]=-[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_2}f\left(t\right)\in C_{1-{\gamma }_1}.$$

Hence, ${\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)$ exists and belongs to $C_{1-{\gamma }_1}$. Then,

$$\begin{array}{c}\hfill {\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)=I_{a^{+}}^{{\alpha }_2}\left[-\delta \left(t\right)x\left(t\right)+f\left(t\right)\right]\in C_{1-{\gamma }_1},\end{array}$$

which implies

$${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-{\gamma }_2+{\alpha }_2}{I}_{a^{+}}^{1-{\gamma }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]={\hspace{0.17em}}^{RL}{D}_{a^{+}}^{1-{\gamma }_2+{\alpha }_2}{I}_{a^{+}}^{1-{\gamma }_2+{\alpha }_2}\left[-\delta \left(t\right)x\left(t\right)+f\left(t\right)\right]=-\delta \left(t\right)x\left(t\right)+f\left(t\right).$$

Taking into account the fact that $I_{a^{+}}^{1-{\gamma }_2}{I}_{a^{+}}^{{\alpha }_2}\left[-\delta \left(t\right)x\left(t\right)+f\left(t\right)\right]\left(a^{+}\right)=0$ and Definition 2, we obtain

$${\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,{\beta }_2}[{\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]=-\delta \left(t\right)x\left(t\right)+f\left(t\right),$$

this yields (9). The results are proved completely. □

Theorem 4.

Let $\delta \left(t\right)\in C_{\nu }$ and $f\left(t\right)\in C_{\mu }$. Then, there exists a unique solution $x\left(t\right)\in C_{1-{\gamma }_1}^{{\alpha }_1,{\beta }_1}$ to Problems (9) and (10) given by

$$x\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k({\mathcal{T}}^k\Phi )\left(t\right),$$

where

$$\begin{array}{ccc}\hfill \left(\mathcal{T}z\right)\left(t\right)& :=& \left\{\left[I_{a^{+}}^{{\alpha }_1}\lambda (·)+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}\delta (·)\right]z\right\}\left(t\right),\mathit{for}z\in C_{1-{\gamma }_1},\hfill \\ \hfill \Phi \left(t\right)& :=& \frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right).\hfill \end{array}$$

Proof. 

We define an operator $\mathcal{F}:C_{1-{\gamma }_1}\to C_{1-{\gamma }_1}$ as follows:

$$\begin{array}{c}\hfill \left(\mathcal{F}x\right)\left(t\right)=-I_{a^{+}}^{{\alpha }_1}[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right)+\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0.\end{array}$$

It is easy to see that $\mathcal{F}$ is a well-defined operator whose fixed point determines the solution of Equation (12). Since

$$\begin{array}{c}{\int }_a^t{(t-s)}^{{\theta }_1-1}{(s-a)}^{{\theta }_2-1}ds={(t-a)}^{{\theta }_1+{\theta }_2-1}·\frac{\Gamma \left({\theta }_1\right)\Gamma \left({\theta }_2\right)}{\Gamma ({\theta }_1+{\theta }_2)},0<{\theta }_1,{\theta }_2<1,\hfill \end{array}$$

for $x,\tilde{x}\in C_{1-{\gamma }_1}$, we have

$$\begin{array}{cc}& {(t-a)}^{1-{\gamma }_1}|\left(\mathcal{F}x\right)\left(t\right)-\left(\mathcal{F}\tilde{x}\right)\left(t\right)|\hfill \\ \le & {(t-a)}^{1-{\gamma }_1}\left[\frac{{(T-a)}^{\nu }{\parallel \lambda \parallel }_{\mathcal{C}}}{\Gamma \left({\alpha }_1\right)}+\frac{{(T-a)}^{{\alpha }_2}{\parallel \delta \parallel }_{C_{\nu }}}{\Gamma ({\alpha }_1+{\alpha }_2)}\right]{\int }_a^t{(t-s)}^{{\alpha }_1-1}{(s-a)}^{{\gamma }_1-\nu -1}ds·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}}\hfill \\ =& {(t-a)}^{{\alpha }_1-\nu }\frac{\Lambda \Gamma ({\gamma }_1-\nu )}{\Gamma ({\alpha }_1+{\gamma }_1-\nu )}·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}},\hfill \end{array}$$

(15)

where $\Lambda :={(T-a)}^{\nu }{\parallel \lambda \parallel }_{\mathcal{C}}+\frac{\Gamma \left({\alpha }_1\right){(T-a)}^{{\alpha }_2}}{\Gamma ({\alpha }_1+{\alpha }_2)}{\parallel \delta \parallel }_{C_{\nu }}$. Furthermore, we find

$$\begin{array}{cc}& {(t-a)}^{1-{\gamma }_1}|\left({\mathcal{F}}^{2}x\right)\left(t\right)-\left({\mathcal{F}}^2\tilde{x}\right)\left(t\right)|\hfill \\ \le & {(t-a)}^{1-{\gamma }_1}\left[\frac{{(T-a)}^{\nu }{\parallel \lambda \parallel }_{\mathcal{C}}}{\Gamma \left({\alpha }_1\right)}+\frac{{(T-a)}^{{\alpha }_2}{\parallel \delta \parallel }_{C_{\nu }}}{\Gamma ({\alpha }_1+{\alpha }_2)}\right]{\int }_a^t{(t-s)}^{{\alpha }_1-1}{(s-a)}^{-\nu }|\left(\mathcal{F}x\right)\left(s\right)-\left(\mathcal{F}\tilde{x}\right)\left(s\right)|ds\hfill \\ \le & \frac{\Lambda \Gamma ({\gamma }_1-\nu ){(t-a)}^{1-{\gamma }_1}}{\Gamma ({\alpha }_1+{\gamma }_1-\nu )}\left[\frac{{(T-a)}^{\nu }{\parallel \lambda \parallel }_{\mathcal{C}}}{\Gamma \left({\alpha }_1\right)}+\frac{{(T-a)}^{{\alpha }_2}{\parallel \delta \parallel }_{C_{\nu }}}{\Gamma ({\alpha }_1+{\alpha }_2)}\right]\hfill \\ & ·{\int }_a^t{(t-s)}^{{\alpha }_1-1}{(s-a)}^{{\gamma }_1+{\alpha }_1-2\nu -1}ds·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}}\hfill \\ =& {\Lambda }^2\prod _{i=0}^1\frac{\Gamma (i({\alpha }_1-\nu )+{\gamma }_1-\nu )}{\Gamma (i({\alpha }_1-\nu )+{\alpha }_1+{\gamma }_1-\nu )}{(t-a)}^{2({\alpha }_1-\nu )}·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}}.\hfill \end{array}$$

(16)

By induction, we deduce that

$$\begin{array}{c}\hfill {(t-a)}^{1-{\gamma }_1}|\left({\mathcal{F}}^{k}x\right)\left(t\right)-\left({\mathcal{F}}^k\tilde{x}\right)\left(t\right)|\le {\Lambda }^k{(T-a)}^{k({\alpha }_1-\nu )}\prod _{i=0}^{k-1}\frac{\Gamma (i({\alpha }_1-\nu )+{\gamma }_1-\nu )}{\Gamma (i({\alpha }_1-\nu )+{\alpha }_1+{\gamma }_1-\nu )}·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}}.\end{array}$$

We write

$$d_k=\prod _{i=0}^{k-1}\frac{\Gamma (i({\alpha }_1-\nu )+{\gamma }_1-\nu )}{\Gamma (i({\alpha }_1-\nu )+{\alpha }_1+{\gamma }_1-\nu )},k=1,2,\cdots ,$$

and from [23] (5.2.13), it follows that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\frac{klnk}{ln\left(\frac{1}{d_k}\right)}=\frac{1}{{\alpha }_1}.\end{array}$$

When k is sufficiently large, the right-hand side of (16) is less than $L\parallel x-\tilde{x}{\parallel }_{C_{1-{\gamma }_1}}(L\in (0,1))$. By the generalized Banach fixed point theorem, $\mathcal{F}$ has a unique fixed point $x\in C_{1-{\gamma }_1}$ satisfying (12). Then, the following sequence $\left\{x_n\right\}$ is convergent in $C_{1-{\gamma }_1}$:

$$\left\{\begin{array}{c}{x}_0\left(t\right)=\Phi \left(t\right),\hfill \\ x_n\left(t\right)=x_0\left(t\right)-\left(\mathcal{T}{x}_{n-1}\right)\left(t\right),n=1,2,\cdots .\hfill \end{array}\right.$$

Furthermore, we find

$$\begin{array}{ccc}\hfill x_1\left(t\right)& =& x_0\left(t\right)-\left(\mathcal{T}{x}_0\right)\left(t\right),\hfill \\ \hfill x_2\left(t\right)& =& x_0\left(t\right)+{\displaystyle \sum _{k=1}^2}{(-1)}^k\left({\mathcal{T}}^k{x}_0\right)\left(t\right),\hfill \\ \hfill \cdots \\ \hfill x_n\left(t\right)& =& x_0\left(t\right)+{\displaystyle \sum _{k=1}^n}{(-1)}^k\left({\mathcal{T}}^k{x}_0\right)\left(t\right).\hfill \end{array}$$

Taking the limit as $n\to \infty$ in the last identity, we arrive at

$$x\left(t\right)=\underset{n\to \infty }{lim}{\displaystyle \sum _{k=0}^n}{(-1)}^k({\mathcal{T}}^k\Phi )\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k({\mathcal{T}}^k\Phi )\left(t\right)$$

and $x\left(t\right)$ is the unique solution of (9) and (10). □

Next, we consider the following IVP for FLEs with Riemann–Liouville derivatives.

$$\begin{array}{c}\left\{\begin{array}{}\mathrm{(17)}& {\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_2}[{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}+\lambda \left(t\right)]x\left(t\right)+\delta \left(t\right)x\left(t\right)=f\left(t\right),t\in (a,T],\hfill \mathrm{(18)}& \left(I_{a^{+}}^{1-{\alpha }_1}x\right)\left(a^{+}\right)=x_0.\hfill \end{array}\right.\end{array}$$

In this case, the constants $\mu ,\nu$ satisfy ${\alpha }_2<\mu <1-{\alpha }_1+{\alpha }_2$ and $0<\nu <\mu +{\alpha }_1-1$.

Theorem 5.

Let $\delta \left(t\right)\in C_{\nu }$ and $f\left(t\right)\in C_{\mu }$; then, $x\in C_{1-{\alpha }_1}^{{\alpha }_1,RL}$ satisfies (22) and (23) if and only if x satisfies the following equation:

$$x\left(t\right)=-I_{a^{+}}^{{\alpha }_1}[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right)+\frac{{(t-a)}^{{\alpha }_1-1}}{\Gamma \left({\alpha }_1\right)}{x}_0.$$

(19)

Proof. 

Let $x\in C_{1-{\alpha }_1}^{{\alpha }_1,RL}$ satisfy (17) and (18); then, ${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)\in C_{1-{\alpha }_1,\mu }^{{\alpha }_2,RL}$. From Lemma 4, one has

$$\left\{I_{a^{+}}^{1-{\alpha }_2}[{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]\right\}\left(a^{+}\right)=0,$$

and

$$\begin{array}{ccc}\hfill {\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_2}[{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]& =& \frac{d}{dt}{I}_{a^{+}}^{1-{\alpha }_2}[{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]\in C_{\mu }.\hfill \end{array}$$

By Theorem 1, we have

$$\begin{array}{c}\hfill I_{a^{+}}^{{\alpha }_2}{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_2}[{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]={\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right).\end{array}$$

(20)

Applying $I_{a^{+}}^{{\alpha }_2}$ to (17) and taking (20) into account, one obtains

$${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)=I_{a^{+}}^{{\alpha }_2}f\left(t\right).$$

(21)

Applying $I_{a^{+}}^{{\alpha }_1}$ to (21) and in view of Lemma 6, one obtains

$$\begin{array}{c}\hfill x\left(t\right)=-I_{a^{+}}^{{\alpha }_1}[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right)+\frac{{(t-a)}^{{\alpha }_1-1}}{\Gamma \left({\alpha }_1\right)}{x}_0,\end{array}$$

which means that $x\left(t\right)$ satisfies (19).

If $x\left(t\right)$ satisfies (19), then

$$I_{a^{+}}^{1-{\alpha }_1}x\left(t\right)=I_{a^{+}}^1\left[-\lambda \left(t\right)x\left(t\right)-I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)+I_{a^{+}}^{{\alpha }_2}f\left(t\right)\right]+x_0.$$

Obviously, $\left(I_{a^{+}}^{1-{\alpha }_1}x\right)\left(a^{+}\right)=x_0$ and

$$\frac{d}{dt}{I}_{a^{+}}^{1-{\alpha }_1}x\left(t\right)=\left[-\lambda \left(t\right)x\left(t\right)-I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)+I_{a^{+}}^{{\alpha }_2}f\left(t\right)\right]\in C_{1-{\alpha }_1},$$

which means that ${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)$ exists and belongs to $C_{1-{\alpha }_1}$. Hence,

$${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)=-I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)+I_{a^{+}}^{{\alpha }_2}f\left(t\right),$$

then

$${\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_2}{[}^{RL}{D}_{a^{+}}^{{\alpha }_1}x\left(t\right)+\lambda \left(t\right)x\left(t\right)]=-\delta \left(t\right)x\left(t\right)+f\left(t\right),$$

which yields (17). The proof is complete. □

Similar to the arguments of Theorem 4, we have the following conclusion.

Theorem 6.

For ${\alpha }_2<\mu <1-{\alpha }_1+{\alpha }_2$ and $0<\nu <\mu +{\alpha }_1-1$, if $\delta \left(t\right)\in C_{\nu }$ and $f\left(t\right)\in C_{\mu }$, then there exists a unique solution $x\left(t\right)\in C_{1-{\alpha }_1}^{{\alpha }_1,RL}$ to the following IVP

$$\left\{\begin{array}{c}{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_2}[{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}+\lambda \left(t\right)]x\left(t\right)+\delta \left(t\right)x\left(t\right)=f\left(t\right),t\in (a,T],\hfill \\ \left(I_{a^{+}}^{1-{\alpha }_1}x\right)\left(a^{+}\right)=x_0,\hfill \end{array}\right.$$

and this solution has the form

$$x\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k({\mathcal{T}}^k\Psi )\left(t\right),$$

where

$$\begin{array}{c}\hfill \Psi \left(t\right):=\frac{{(t-a)}^{{\alpha }_1-1}}{\Gamma \left({\alpha }_1\right)}{x}_0+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right).\end{array}$$

4. Nonlinear Case

We consider the following IVP for nonlinear FLEs with Hilfer derivatives and variable coefficients:

$$\begin{array}{c}\left\{\begin{array}{}\mathrm{(22)}& {\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,{\beta }_2}({\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}+\lambda \left(t\right))x\left(t\right)+\delta \left(t\right)x\left(t\right)=f(t,\left(I_{a^{+}}^{\eta }x\right)\left(t\right)),t\in (a,T],\hfill \mathrm{(23)}& \left(I_{a^{+}}^{1-{\gamma }_1}x\right)\left(a^{+}\right)=x_0,\hfill \end{array}\right.\end{array}$$

where $\mu <\eta <1$.

We define the constants $\nu ,\mu >0$ as (11) and let $\delta \left(t\right)\in C_{\nu }$. Similar to the arguments of Theorem 3, we have the following result.

Theorem 7.

Let $f(t,y\left(t\right))\in C_{\mu }$ for any $y\in C_{\mu }$; then, $x\in C_{1-{\gamma }_1}^{{\alpha }_1,{\beta }_1}$ satisfies (22) and (23) if and only if x satisfies the following equation:

$$x\left(t\right)=-I_{a^{+}}^{{\alpha }_1}[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f(t,\left(I_{a^{+}}^{\eta }x\right)\left(t\right))+\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0.$$

(24)

Set the operator $G:C_{1-{\gamma }_1}\to C_{1-{\gamma }_1}$ as follows:

$$\left(Gx\right)\left(t\right)=-I_{a^{+}}^{{\alpha }_1}[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f(t,\left(I_{a^{+}}^{\eta }x\right)\left(t\right))+\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0,$$

clearly, G is a well-defined operator, whose fixed point is the solution of Equation (24).

Theorem 8.

Let $f(t,y\left(t\right))\in C_{\mu }$ for any $y\in C_{\mu }$. If there exists a non-negative function $l\left(t\right)\in C_{\mu }$ such that

$$|f(t,y\left(t\right))-f(t,\tilde{y}\left(t\right))|\le l\left(t\right)|y\left(t\right)-\tilde{y}\left(t\right)|,$$

then problem (22)–(23) have a unique solution $x\left(t\right)\in C_{1-{\gamma }_1}^{{\alpha }_1,{\beta }_1}$ given by (24).

Proof. 

For $x,\tilde{x}\in C_{1-{\gamma }_1}$, note that

$$\begin{array}{cc}& |f(t,\left(I_{a^{+}}^{\eta }x\right)\left(t\right))-f(t,\left(I_{a^{+}}^{\eta }\tilde{x}\right)\left(t\right))|\hfill \\ \le & \frac{{(t-a)}^{-\mu }{\parallel l\parallel }_{C_{\mu }}}{\Gamma \left(\eta \right)}{\int }_a^t{(t-s)}^{\eta -1}{(s-a)}^{{\gamma }_1-1}ds·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}}\hfill \\ =& \frac{{(t-a)}^{\eta +{\gamma }_1-\mu -1}\Gamma \left({\gamma }_1\right){\parallel l\parallel }_{C_{\mu }}}{\Gamma ({\gamma }_1+\eta )}·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}},\hfill \end{array}$$

We have

$$\begin{array}{cc}& {(t-a)}^{1-{\gamma }_1}|I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f(t,\left(I_{a^{+}}^{\eta }x\right)\left(t\right))-I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f(t,\left(I_{a^{+}}^{\eta }\tilde{x}\right)\left(t\right))|\hfill \\ \le & \frac{{(t-a)}^{1-{\gamma }_1}{\parallel l\parallel }_{C_{\mu }}\Gamma \left({\gamma }_1\right){(T-a)}^{{\alpha }_2+\eta -\mu +\nu }}{\Gamma ({\alpha }_1+{\alpha }_2)\Gamma ({\gamma }_1+\eta )}{\int }_a^t{(t-s)}^{{\alpha }_1-1}{(s-a)}^{{\gamma }_1-\nu -1}ds·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}}\hfill \\ =& \frac{\tilde{\Lambda }{(t-a)}^{{\alpha }_1-\nu }\Gamma ({\gamma }_1-\nu )}{\Gamma ({\alpha }_1+{\gamma }_1-\nu )}·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}},\hfill \end{array}$$

where $\tilde{\Lambda }=\frac{{\parallel l\parallel }_{C_{\mu }}\Gamma \left({\alpha }_1\right)\Gamma \left({\gamma }_1\right){(T-a)}^{{\alpha }_2+\eta -\mu +\nu }}{\Gamma ({\alpha }_1+{\alpha }_2)\Gamma ({\gamma }_1+\eta )}$. Combining with (15), we obtain

$$\begin{array}{c}\hfill {(t-a)}^{1-{\gamma }_1}|\left(Gx\right)\left(t\right)-\left(G\tilde{x}\right)\left(t\right)|\le \frac{M{(t-a)}^{{\alpha }_1-\nu }\Gamma ({\gamma }_1-\nu )}{\Gamma ({\alpha }_1+{\gamma }_1-\nu )}·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}},\end{array}$$

where $M:=\Lambda +\tilde{\Lambda }$. By similar arguments of Theorem 4 and induction, we deduce that

$$\begin{array}{c}\hfill {(t-a)}^{1-{\gamma }_1}|\left(G^{k}x\right)\left(t\right)-\left(G^k\tilde{x}\right)\left(t\right)|\le M^k{(T-a)}^{k({\alpha }_1-\nu )}\prod _{i=0}^{k-1}\frac{\Gamma (i({\alpha }_1-\nu )+{\gamma }_1-\nu )}{\Gamma (i({\alpha }_1-\nu )+{\alpha }_1+{\gamma }_1-\nu )}·{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}},\end{array}$$

and for sufficiently large k, the right side of the above inequality is smaller than $\tilde{L}{\parallel x-\tilde{x}\parallel }_{C_{1-{\gamma }_1}}(\tilde{L}\in (0,1))$. With the help of the generalized Banach fixed point theorem, $x\in C_{1-{\gamma }_1}$ satisfying (24) is the unique fixed point of G. □

In particular, we take the following IVP for Hilfer-type fractional Langevin integro-differential equations with variable coefficients into account:

$$\begin{array}{c}\left\{\begin{array}{}\mathrm{(25)}& {\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_2,{\beta }_2}({\hspace{0.17em}}^H{D}_{a^{+}}^{{\alpha }_1,{\beta }_1}+\lambda \left(t\right))x\left(t\right)+l\left(t\right)\left(I_{a^{+}}^{\eta }x\right)\left(t\right)=f\left(t\right),t\in (a,T],\hfill \mathrm{(26)}& \left(I_{a^{+}}^{1-{\gamma }_1}x\right)\left(a^{+}\right)=x_0,\hfill \end{array}\right.\end{array}$$

where $\mu <\eta <1$.

Theorem 9.

Let $l\left(t\right)\in C_{\mu }$ and $f\left(t\right)\in C_{\mu }$. Then, there exists a unique solution $x\left(t\right)\in C_{1-{\gamma }_1}^{{\alpha }_1,{\beta }_1}$ to problem (25)–(26) given by

$$x\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k{\left[I_{a^{+}}^{{\alpha }_1}\lambda (·)+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}l(·)I_{a^{+}}^{\eta }\right]}^k\left[\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right)\right].$$

Proof. 

It follows from Theorem 8 that (25) and (26) have a unique solution

$$\begin{array}{ccc}\hfill x\left(t\right)& =& -\left[I_{a^{+}}^{{\alpha }_1}\left(\lambda \left(t\right)x\left(t\right)\right)+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}\left(l\left(t\right)I_{a^{+}}^{\eta }x\left(t\right)\right)\right]+\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right).\hfill \end{array}$$

Similar to the arguments of Theorem 4, one has

$$x\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k{\left[I_{a^{+}}^{{\alpha }_1}\lambda (·)+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}l(·)I_{a^{+}}^{\eta }\right]}^k\left[\frac{{(t-a)}^{{\gamma }_1-1}}{\Gamma \left({\gamma }_1\right)}{x}_0+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f\left(t\right)\right].$$

□

Similar to the arguments of Theorem 4, we can deduce the corresponding conclusions of the IVP for Riemann–Liouville-type FLEs. We set ${\alpha }_2<\mu <1-{\alpha }_1+{\alpha }_2$ and $0<\nu <\mu +{\alpha }_1-1$.

Theorem 10.

Let $f(t,y\left(t\right))\in C_{\mu }$ for any $y\in C_{\mu }$. If there exists a non-negative function $l\left(t\right)\in C_{\mu }$ such that

$$|f(t,y\left(t\right))-f(t,\tilde{y}\left(t\right))|\le l\left(t\right)|y\left(t\right)-\tilde{y}\left(t\right)|,$$

then $x\left(t\right)\in C_{1-{\alpha }_1}^{{\alpha }_1,RL}$ given by

$$x\left(t\right)=-I_{a^{+}}^{{\alpha }_1}[\lambda \left(t\right)x\left(t\right)+I_{a^{+}}^{{\alpha }_2}\left(\delta \left(t\right)x\left(t\right)\right)]+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}f(t,\left(I_{a^{+}}^{\eta }x\right)\left(t\right))+\frac{{(t-a)}^{{\alpha }_1-1}}{\Gamma \left({\alpha }_1\right)}{x}_0,$$

is the unique solution to the following IVP

$$\left\{\begin{array}{c}{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_2}[{\hspace{0.17em}}^{RL}{D}_{a^{+}}^{{\alpha }_1}+\lambda \left(t\right)]x\left(t\right)+\delta \left(t\right)x\left(t\right)=f(t,\left(I_{a^{+}}^{\eta }x\right)\left(t\right)),t\in (a,T],\hfill \\ \left(I_{a^{+}}^{1-{\alpha }_1}x\right)\left(a^{+}\right)=x_0.\hfill \end{array}\right.$$

In particular, if $\delta \left(t\right)=0$ and $f(t,\left(I_{a^{+}}^{\eta }x\right)\left(t\right))=g\left(t\right)-l\left(t\right)\left(I_{a^{+}}^{\eta }x\right)\left(t\right)$, then the explicit solution $x\left(t\right)$ is given by

$$x\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k{\left[I_{a^{+}}^{{\alpha }_1}\lambda (·)+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}l(·)I_{a^{+}}^{\eta }\right]}^k\left[\frac{{(t-a)}^{{\alpha }_1-1}}{\Gamma \left({\alpha }_1\right)}{x}_0+I_{a^{+}}^{{\alpha }_1+{\alpha }_2}g\left(t\right)\right].$$

5. Applications

Example 1.

Consider the following IVP for a Hilfer-type fractional Langevin differential equation with variable coefficients:

$$\begin{array}{c}\left\{\begin{array}{}\mathrm{(27)}& {\hspace{0.17em}}^H{D}_{0^{+}}^{\frac{1}{4},\frac{1}{5}}({\hspace{0.17em}}^H{D}_{0^{+}}^{\frac{1}{2},\frac{3}{5}}+t^2)x\left(t\right)+t^{-\frac{1}{18}}x\left(t\right)=t^{-\frac{3}{10}},t\in (0,T],\hfill \mathrm{(28)}& (I_{0^{+}}^{\frac{1}{5}}x)\left(0^{+}\right)=1.\hfill \end{array}\right.\end{array}$$

Taking ${\alpha }_1=\frac{1}{2},{\alpha }_2=\frac{1}{4},{\beta }_1=\frac{3}{5},{\beta }_2=\frac{1}{5},\lambda \left(t\right)=t^2,\delta \left(t\right)=t^{-\frac{1}{18}},f\left(t\right)=t^{-\frac{3}{10}},x_0=1$, $\mu =\frac{3}{10}$ and $\nu =\frac{1}{18}$ from Theorem 4, it follows that $x\left(t\right)\in C_{\frac{1}{5}}^{\frac{1}{2},\frac{3}{5}}$ in the form

$$x\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k{\left[I_{0^{+}}^{\frac{1}{2}}{t}^2+I_{0^{+}}^{\frac{3}{4}}{t}^{-\frac{1}{18}}\right]}^k\left[\frac{t^{-\frac{1}{5}}}{\Gamma \left(\frac{4}{5}\right)}+I_{0^{+}}^{\frac{3}{4}}{t}^{-\frac{3}{10}}\right]$$

is the unique solution to problem (27)–(28).

Example 2.

Consider the following IVP for a Riemann–Liouville-type fractional Langevin integro-differential equation with variable coefficients:

$$\begin{array}{c}\left\{\begin{array}{}\mathrm{(29)}& {\hspace{0.17em}}^{RL}{D}_{0^{+}}^{\frac{1}{3}}({\hspace{0.17em}}^{RL}{D}_{0^{+}}^{\frac{4}{5}}+t)x\left(t\right)+t^{-\frac{1}{5}}{I}_{0^{+}}^{\frac{1}{2}}x\left(t\right)=t^{-\frac{2}{5}},t\in (0,1],\hfill \mathrm{(30)}& (I_{0^{+}}^{\frac{1}{5}}x)\left(0^{+}\right)=1.\hfill \end{array}\right.\end{array}$$

(I150+x)(0+)=1.

Taking ${\alpha }_1=\frac{4}{5},{\alpha }_2=\frac{1}{3},\eta =\frac{1}{2},\lambda \left(t\right)=t,\delta \left(t\right)=0,l\left(t\right)=t^{-\frac{1}{5}},f\left(t\right)=t^{-\frac{2}{5}},x_0=1$ and $\mu =\frac{2}{5}$, from Theorem 10 it follows that $x\left(t\right)\in C_{\frac{1}{5}}^{\frac{4}{5},RL}$ in the form

$$x\left(t\right)={\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k{\left[I_{0^{+}}^{\frac{4}{5}}t+I_{0^{+}}^{\frac{17}{15}}{t}^{-\frac{1}{5}}{I}_{0^{+}}^{\frac{1}{2}}\right]}^k\left[\frac{t^{-\frac{1}{5}}}{\Gamma \left(\frac{4}{5}\right)}+I_{0^{+}}^{\frac{17}{15}}{t}^{-\frac{2}{5}}\right]$$

is the unique solution to problem (29)–(30).

Clearly, the approximate solution $x_n\left(t\right)$ of problem (27)–(28) can be given by

$$x_n\left(t\right)={\displaystyle \sum _{k=0}^n}{(-1)}^k{\left[I_{0^{+}}^{\frac{1}{2}}{t}^2+I_{0^{+}}^{\frac{3}{4}}{t}^{-\frac{1}{18}}\right]}^k\left[\frac{t^{-\frac{1}{5}}}{\Gamma \left(\frac{4}{5}\right)}+I_{0^{+}}^{\frac{3}{4}}{t}^{-\frac{3}{10}}\right].$$

Approximate solutions of Problems (27) and (28) evaluated at some points $t\in (0,1]$ with the step $\Delta t=0.01$ using different values of $n(=5,10,20,40)$ are shown in Figure 1.

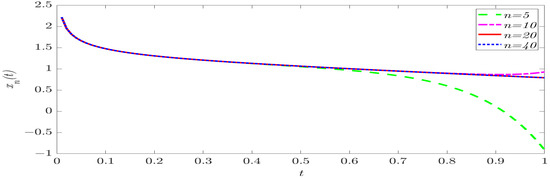
Figure 1. Approximate solutions for (27) and (28).

6. Conclusions

In this paper, the existence and uniqueness results of solutions of IVPs for FLEs with Hilfer derivatives and variable coefficients are obtained in weighted spaces. The variable-coefficient function $\delta \left(t\right)(\in C_{\nu })$ is not necessarily continuous on a closed interval. Our technique is also useful to solve more general equations. Moreover, the boundary value problem for corresponding equations can be studied.