Estimation of Random Coefficient Autoregressive Model with Error in Covariates
Abstract
:1. Introduction
2. The Model and Estimation Methods
2.1. The RCA Model with Errors in Covariates
- In order to derive the limit distribution of estimators, we consider the following assumptions:
2.2. The Corrected Least Squares Procedure
2.3. The Corrected Weighted Least Squares Procedure
2.4. Estimated Error Variance
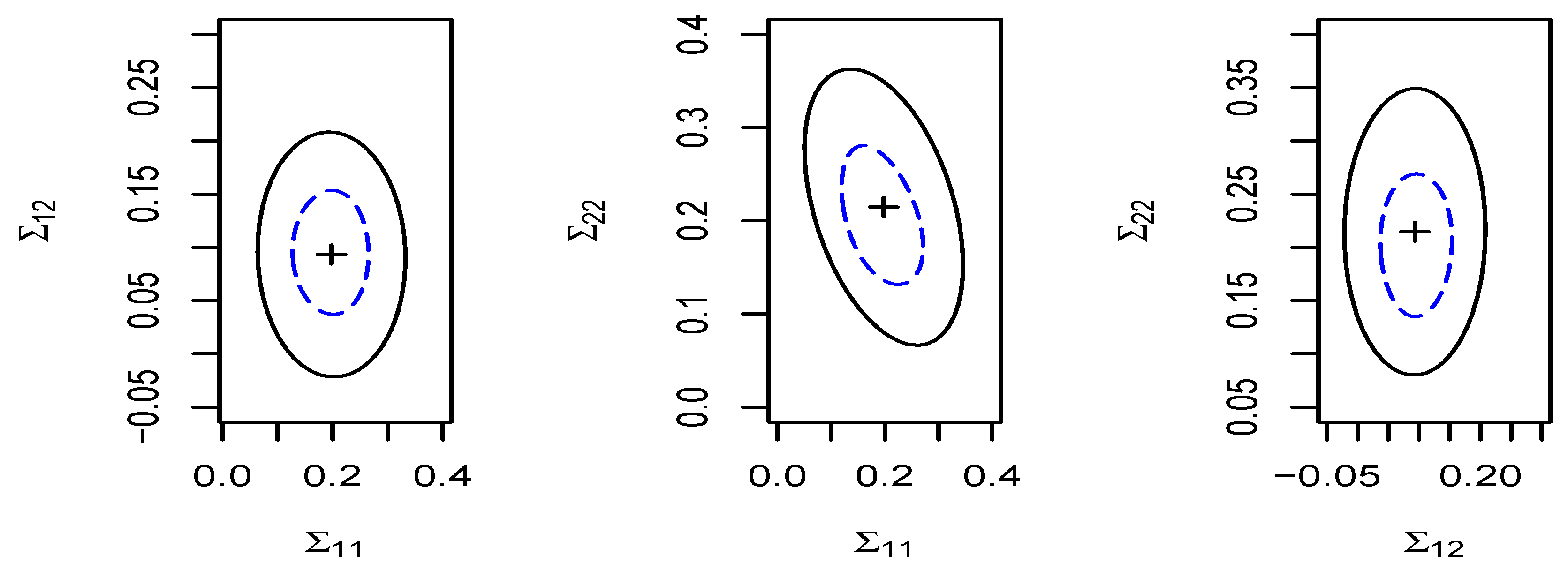
3. The Empirical Likelihood Ratio and the Confidence Region
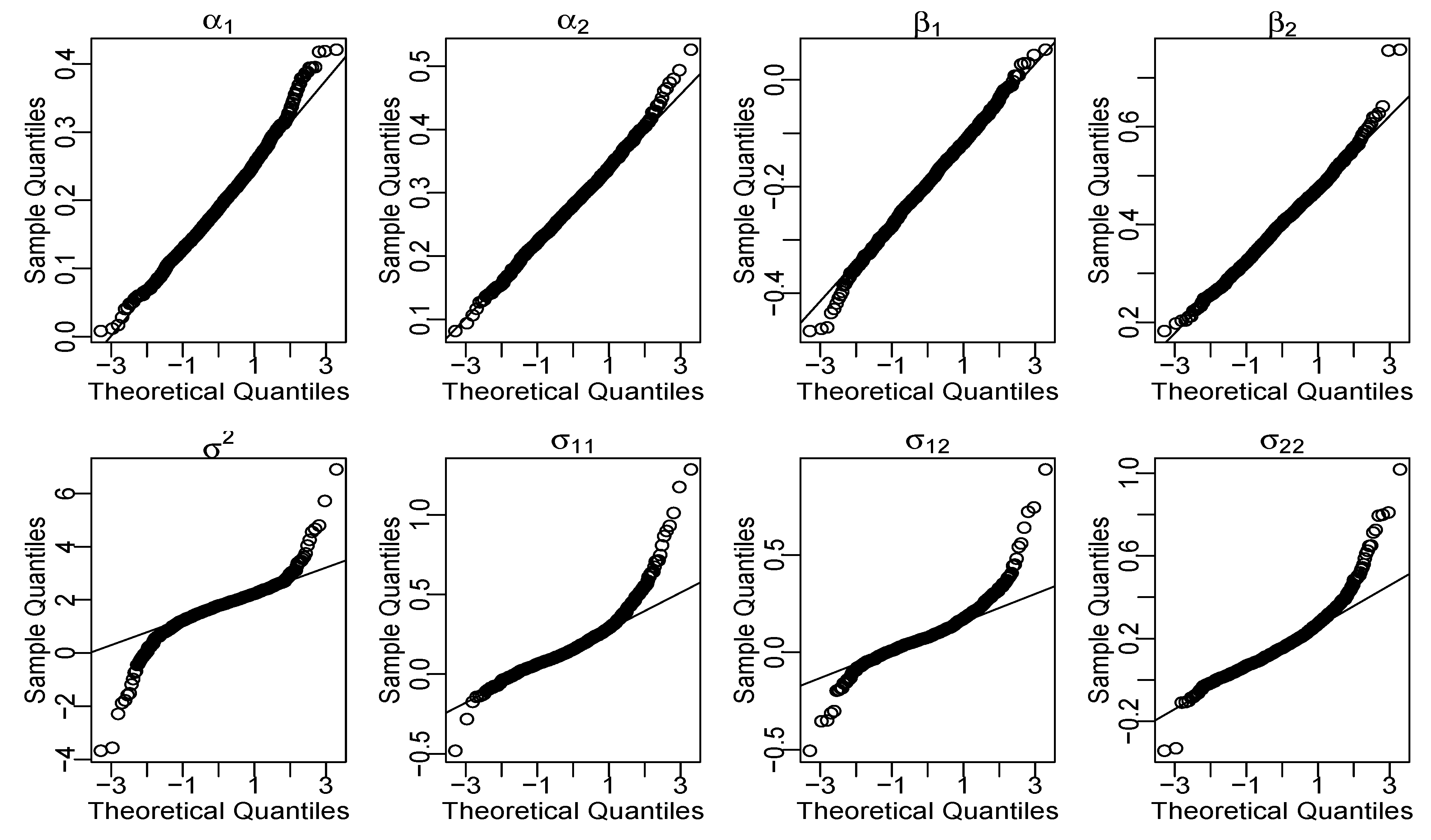
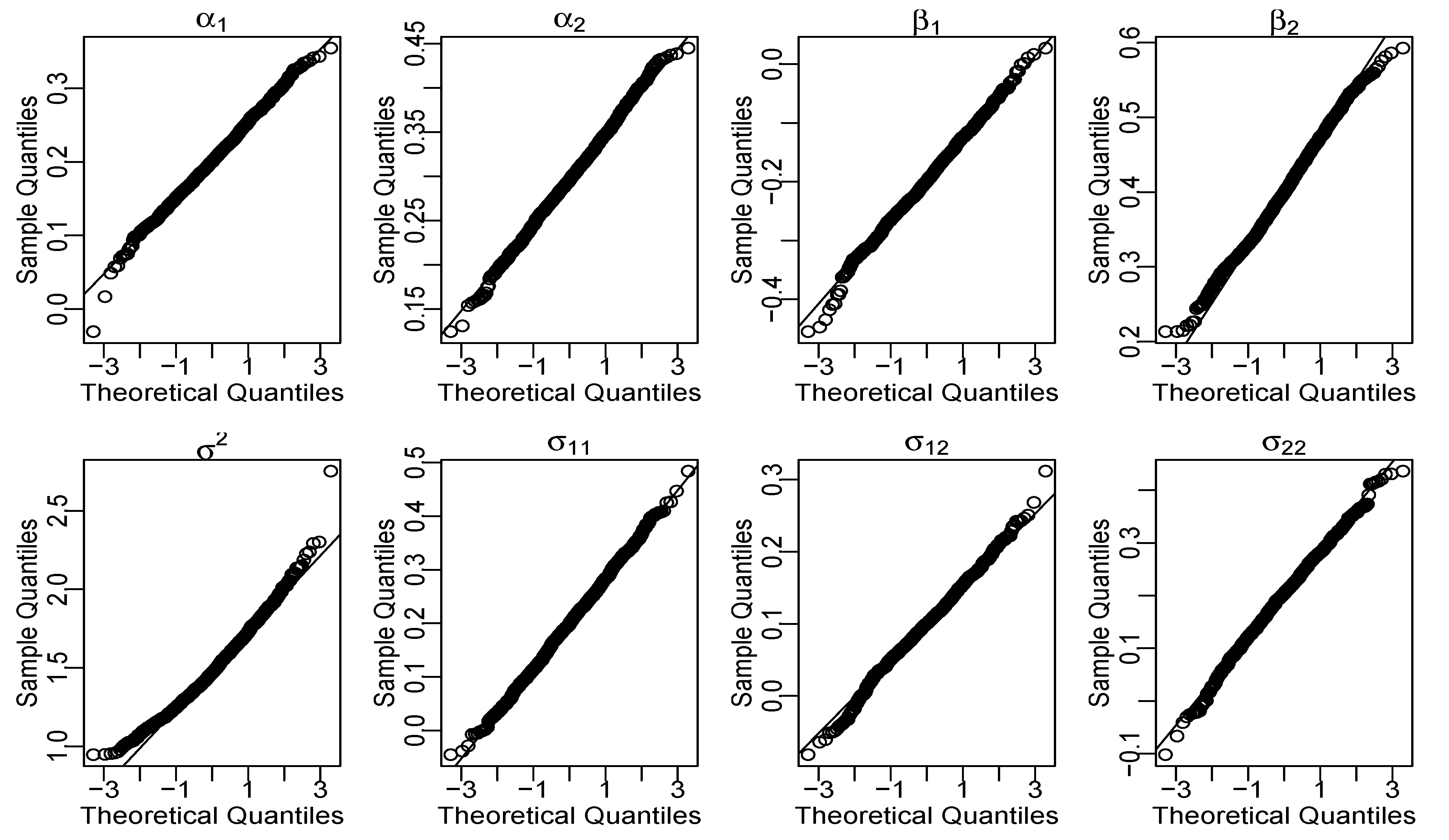
4. Simulation Study
- Model A: .
- Model B: .
- Note that assumption (C.1) is fulfilled, because matrix has eigenvalues 0.8, −0.5, −0.3 and 0.2, which are less than one, in the modulus. All the calculations are performed by using 1000 replications.
4.1. Point Estimation of Parameters
4.2. Confidence Regions of Parameters
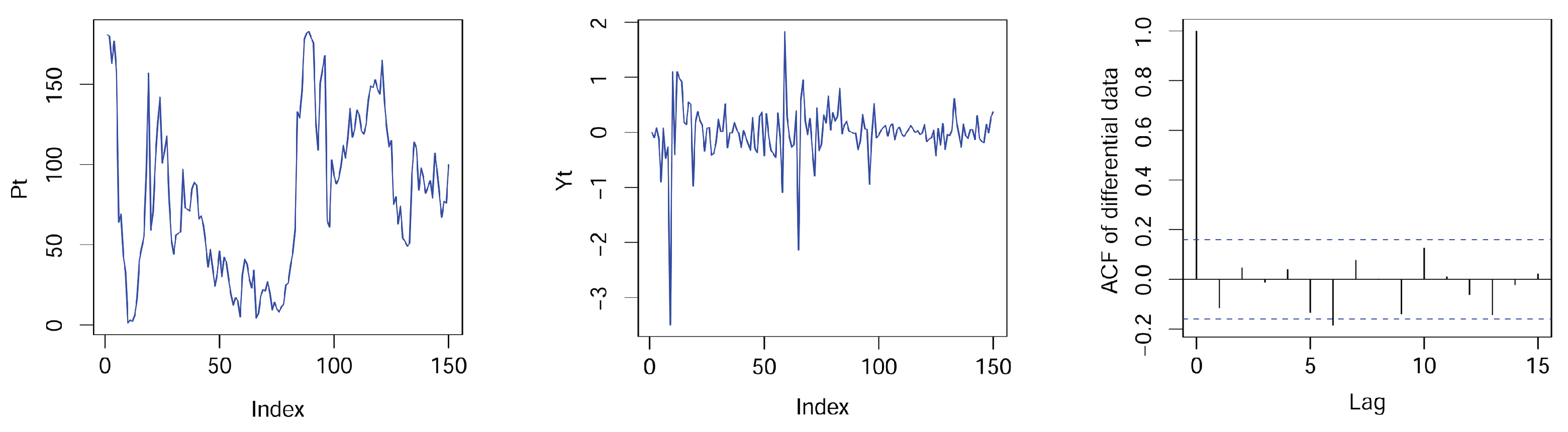
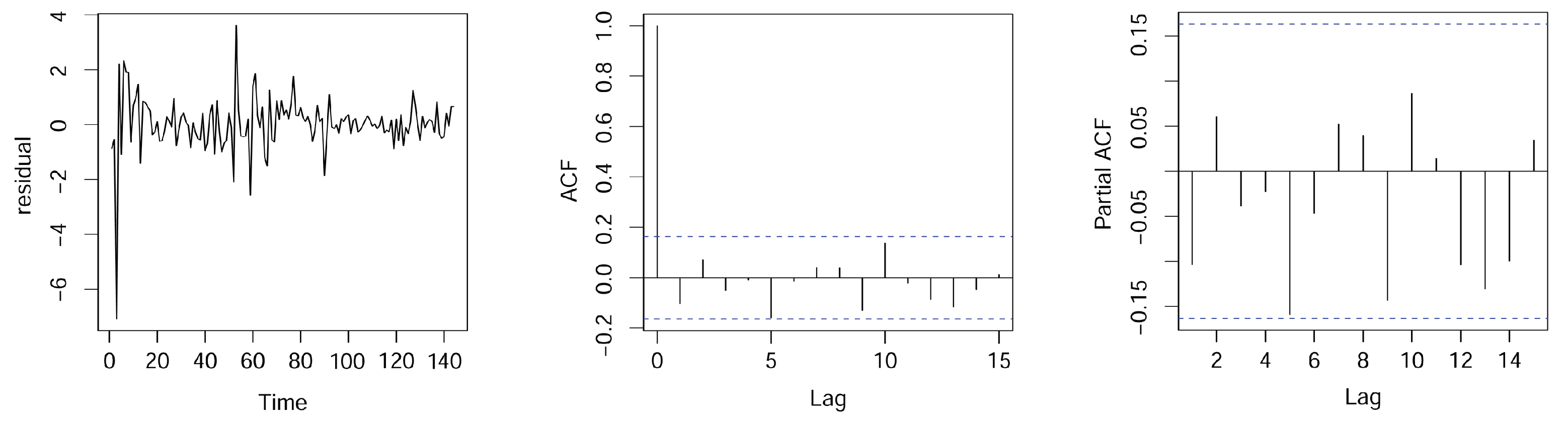
5. Real Data Example
- Model 1 (AR-X):
- Model 2 (RCAR-X):
- Model 3 (RCAR-X-EV):
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hwang, S.Y.; Basawa, I.V. Parameter estimation for generalized random coefficient autoregressive processes. J. Stat. Plan. Inference 1998, 68, 323–337. [Google Scholar] [CrossRef]
- Hill, J.; Peng, L. Unified interval estimation for random coefficient autoregressive models. J. Time Ser. Anal. 2014, 35, 282–297. [Google Scholar] [CrossRef]
- Regis, M.; Serra, P.; Heuvel, E. Random autoregressive models: A structured Overview. Econom. Rev. 2022, 41, 207–230. [Google Scholar] [CrossRef]
- Anderson, T.W.; Rubin, H. The asymptotic propertics of estimates of the parameters of a single equation in a complete system of stochastic equations. Ann. Math. Stat. 1950, 21, 570–582. [Google Scholar] [CrossRef]
- Koopmans, T. Statistical Inference in Dynamic Economic Models; Wiley: New York, NY, USA, 1950. [Google Scholar]
- Yang, K.; Wang, D.H. Bayesian estimation for first-order autoregressive model with explanatory variables. Commun. Stat.-Theory Methods 2017, 46, 11214–11227. [Google Scholar] [CrossRef]
- Peng, B.; Yang, K.; Dong, X.G. Variable selection for quantile autoregressive model: Bayesian methods versus classical methods. J. Appl. Stat. 2023, 51, 1098–1130. [Google Scholar] [CrossRef] [PubMed]
- Fuller, W.A. Measurement Error Models; John Wiley and Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Carroll, R.J.; Ruppert, D.; Stefanski, L. Measurement Error in Nonlinear Models; Chapman and Hall/CRC: London, UK, 1995. [Google Scholar]
- Ding, H.; Zhang, R.; Zhu, H. New estimation for heteroscedastic single-index measurement error models. J. Nonparametric Stat. 2022, 34, 95–112. [Google Scholar] [CrossRef]
- Sinha, S.; Ma, Y. Semiparametric analysis of linear transformation models with covariate measurement errors. Biometrics 2014, 70, 21–32. [Google Scholar] [CrossRef] [PubMed]
- Owen, A. Empirical likelihood ratio confidence intervals for a single functional. Biometrika 1988, 75, 237–249. [Google Scholar] [CrossRef]
- Owen, A. Empirical likelihood ratio confidence regions. Ann. Stat. 1990, 18, 90–120. [Google Scholar] [CrossRef]
- Qin, J.; Lawless, J. Empirical likelihood and general estimating equations. Ann. Stat. 1994, 22, 300–325. [Google Scholar] [CrossRef]
- Yang, K.; Ding, X.; Yuan, X.H. Bayesian empirical likelihood inference and order shrinkage for autoregressive models. Stat. Pap. 2022, 63, 97–121. [Google Scholar] [CrossRef]
- Liu, P.P.; Zhao, Y.C. A review of recent advances in empirical likelihood. Wiley Interdiscip. Rev.-Comput. Stat. 2022, 15, e1599. [Google Scholar] [CrossRef]
- Nicholls, D.F.; Quinn, B.G. Random Coefficient Autoregressive Models: An Introduction; Springer: New York, NY, USA, 1982. [Google Scholar]
- Feigin, P.D.; Tweedie, R.L. Random coefficient autoregressive processes: A markov chain analysis of stationarity and finiteness of moments. J. Time Ser. Anal. 1985, 6, 1–14. [Google Scholar] [CrossRef]
- Liang, H.; Härdle, W.; Carroll, R.J. Estimation in a semiparametric partially linear errors-in-variables model. Ann. Stat. 1999, 27, 1519–1535. [Google Scholar] [CrossRef]
- Horváth, L.; Trapani, L. Testing for randomness in a random coefficient autoregression model. J. Econom. 2019, 209, 338–352. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Wang, D.H. Statistical inference for generalized random coefficient autoregressive model. Math. Comput. Model. 2012, 52, 152–166. [Google Scholar] [CrossRef]
- Cheang, W.K.; Reinsel, G.C. Bias reduction of autoregressive estimates in time series regression model through restricted maximum likelihood. J. Am. Stat. Assoc. 2000, 95, 1173–1184. [Google Scholar] [CrossRef]
- Pei, G. Estimation of functional-coefficient autoregressive models with measurement error. J. Multivar. Anal. 2022, 192, 105077. [Google Scholar]
- Hall, P.; Heyde, C.C. Martingale Limit Theory and Its Application; Academic Press: New York, NY, USA, 1980. [Google Scholar]


| Para. | Known | Unknown | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | RB | SD | MSE | Mean | RB | SD | MSE | ||
| 0.1871 | −0.0640 | 0.1209 | 0.0147 | 0.1803 | −0.0985 | 0.1253 | 0.0161 | ||
| 0.2579 | −0.1400 | 0.1181 | 0.0157 | 0.2702 | −0.0993 | 0.1242 | 0.0163 | ||
| −0.2028 | 0.0135 | 0.1572 | 0.0247 | −0.2040 | 0.0200 | 0.1557 | 0.0242 | ||
| 0.4011 | 0.0028 | 0.1605 | 0.0257 | 0.4115 | 0.0290 | 0.1572 | 0.0248 | ||
| 1.1667 | 0.1667 | 0.6308 | 0.4254 | 1.1207 | 0.1207 | 0.7228 | 0.5365 | ||
| 0.1587 | −0.2065 | 0.2016 | 0.0423 | 0.1566 | −0.2170 | 0.1964 | 0.0404 | ||
| 0.0854 | −0.1460 | 0.1259 | 0.0160 | 0.0879 | −0.1210 | 0.1488 | 0.0222 | ||
| 0.1483 | −0.2585 | 0.1586 | 0.0278 | 0.1675 | −0.1620 | 0.1828 | 0.0344 | ||
| 0.1728 | −0.1360 | 0.1177 | 0.0145 | 0.1732 | −0.1340 | 0.1184 | 0.0147 | ||
| 0.2669 | −0.1103 | 0.1172 | 0.0148 | 0.2622 | −0.1260 | 0.1183 | 0.0154 | ||
| −0.1948 | −0.0260 | 0.1800 | 0.0324 | −0.2063 | 0.0315 | 0.1904 | 0.0362 | ||
| 0.4017 | 0.0043 | 0.1879 | 0.0352 | 0.4009 | 0.0023 | 0.1786 | 0.0318 | ||
| 1.7238 | 0.1492 | 1.0813 | 1.2183 | 1.6653 | 0.1102 | 1.1464 | 1.3404 | ||
| 0.1550 | −0.2250 | 0.1914 | 0.0386 | 0.1702 | −0.1490 | 0.2066 | 0.0435 | ||
| 0.0847 | −0.1520 | 0.1444 | 0.0210 | 0.0899 | −0.1010 | 0.1481 | 0.0220 | ||
| 0.1559 | −0.2205 | 0.1724 | 0.0316 | 0.1489 | −0.2555 | 0.1704 | 0.0316 | ||
| 0.1749 | −0.1255 | 0.1258 | 0.0164 | 0.1750 | −0.1250 | 0.1205 | 0.0151 | ||
| 0.2589 | −0.1370 | 0.1179 | 0.0155 | 0.2628 | −0.1240 | 0.1209 | 0.0160 | ||
| −0.2059 | 0.0295 | 0.1930 | 0.0372 | −0.2159 | 0.0795 | 0.1902 | 0.0364 | ||
| 0.3937 | −0.0158 | 0.1906 | 0.0363 | 0.3971 | −0.0073 | 0.1886 | 0.0355 | ||
| 1.6838 | 0.1225 | 0.9930 | 1.0190 | 1.7219 | 0.1479 | 0.9557 | 0.9617 | ||
| 0.1727 | −0.1365 | 0.2019 | 0.0414 | 0.1670 | −0.1650 | 0.2066 | 0.0437 | ||
| 0.0828 | −0.1720 | 0.1477 | 0.0221 | 0.0735 | −0.2650 | 0.1585 | 0.0258 | ||
| 0.1510 | −0.2450 | 0.1702 | 0.0313 | 0.1612 | −0.1940 | 0.1736 | 0.0316 | ||
| 0.1719 | −0.1405 | 0.1218 | 0.0156 | 0.1789 | −0.1050 | 0.1201 | 0.0148 | ||
| 0.2663 | −0.1123 | 0.1167 | 0.0147 | 0.2582 | −0.1390 | 0.1166 | 0.0153 | ||
| −0.1988 | −0.0055 | 0.1742 | 0.0303 | −0.2008 | 0.0040 | 0.1737 | 0.0301 | ||
| 0.3946 | −0.0133 | 0.1714 | 0.0293 | 0.4068 | 0.0170 | 0.1720 | 0.0296 | ||
| 1.3948 | 0.1158 | 0.7364 | 0.5627 | 1.4419 | 0.1535 | 0.7231 | 0.5593 | ||
| 0.1617 | −0.1910 | 0.1921 | 0.0383 | 0.1634 | −0.1825 | 0.1874 | 0.0364 | ||
| 0.0790 | −0.2097 | 0.1322 | 0.0179 | 0.0888 | −0.1117 | 0.1428 | 0.0205 | ||
| 0.1595 | −0.2021 | 0.1640 | 0.0285 | 0.1613 | −0.1931 | 0.1704 | 0.0305 | ||
| Model | n | Para. | LS | WLS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | RB | SD | MSE | Mean | RB | SD | MSE | |||
| A | 100 | 0.1871 | −0.0640 | 0.1209 | 0.0147 | 0.2067 | 0.0335 | 0.1143 | 0.0130 | |
| 0.2579 | −0.1400 | 0.1181 | 0.0157 | 0.2840 | −0.0533 | 0.1107 | 0.0125 | |||
| −0.2028 | −0.0135 | 0.1572 | 0.0247 | −0.2044 | 0.0220 | 0.1457 | 0.0212 | |||
| 0.4011 | 0.0028 | 0.1605 | 0.0257 | 0.4088 | 0.0220 | 0.1471 | 0.0217 | |||
| 1.1667 | 0.1667 | 0.6308 | 0.4254 | 0.9765 | −0.0235 | 0.3104 | 0.0968 | |||
| 0.1587 | −0.2065 | 0.2016 | 0.0423 | 0.1856 | −0.0720 | 0.1587 | 0.0253 | |||
| 0.0854 | −0.1460 | 0.1259 | 0.0160 | 0.0937 | −0.0630 | 0.1093 | 0.0119 | |||
| 0.1483 | −0.2585 | 0.1586 | 0.0278 | 0.1911 | −0.0445 | 0.1509 | 0.0228 | |||
| 200 | 0.1800 | −0.1000 | 0.0883 | 0.0081 | 0.1951 | −0.0245 | 0.0781 | 0.0061 | ||
| 0.2742 | −0.0860 | 0.0884 | 0.0084 | 0.2946 | −0.0180 | 0.0805 | 0.0065 | |||
| −0.1982 | −0.0090 | 0.1109 | 0.0123 | −0.2010 | 0.0050 | 0.1002 | 0.0100 | |||
| 0.4000 | −0.0000 | 0.1045 | 0.0109 | 0.4001 | −0.0003 | 0.0943 | 0.0088 | |||
| 1.1769 | 0.1769 | 0.5509 | 0.3345 | 0.9735 | −0.0265 | 0.2191 | 0.0486 | |||
| 0.1679 | −0.1605 | 0.1615 | 0.0270 | 0.2005 | 0.0029 | 0.1159 | 0.0134 | |||
| 0.0872 | −0.1278 | 0.1122 | 0.0127 | 0.1028 | 0.0284 | 0.0750 | 0.0056 | |||
| 0.1591 | −0.2045 | 0.1327 | 0.0192 | 0.1985 | −0.0077 | 0.1096 | 0.0120 | |||
| 500 | 0.1916 | −0.0421 | 0.0677 | 0.0046 | 0.1965 | −0.0175 | 0.0490 | 0.0024 | ||
| 0.2871 | −0.0427 | 0.0648 | 0.0043 | 0.2997 | −0.0010 | 0.0508 | 0.0025 | |||
| −0.1967 | −0.0165 | 0.0721 | 0.0052 | −0.1994 | −0.0030 | 0.0624 | 0.0038 | |||
| 0.3966 | −0.0085 | 0.0690 | 0.0047 | 0.3991 | −0.0023 | 0.0652 | 0.0042 | |||
| 1.1258 | 0.1258 | 0.5348 | 0.3015 | 0.9878 | −0.0122 | 0.1412 | 0.0200 | |||
| 0.1826 | −0.0870 | 0.1499 | 0.0227 | 0.2043 | 0.0215 | 0.0698 | 0.0048 | |||
| 0.0873 | −0.1270 | 0.1047 | 0.0111 | 0.1005 | 0.0053 | 0.0458 | 0.0020 | |||
| 0.1791 | −0.1043 | 0.1291 | 0.0170 | 0.1984 | −0.0080 | 0.0713 | 0.0050 | |||
| B | 100 | 0.1748 | −0.1260 | 0.1177 | 0.0144 | 0.1942 | −0.0290 | 0.1108 | 0.0123 | |
| 0.2619 | −0.1267 | 0.1150 | 0.0146 | 0.2867 | −0.0443 | 0.1098 | 0.0122 | |||
| 0.4000 | 0.0000 | 0.1633 | 0.0266 | 0.3973 | −0.0068 | 0.1431 | 0.0204 | |||
| −0.5999 | −0.0002 | 0.1649 | 0.0271 | −0.6128 | 0.0213 | 0.1509 | 0.0229 | |||
| 1.1936 | 0.1936 | 0.8545 | 0.7670 | 0.9526 | −0.0474 | 0.3312 | 0.1118 | |||
| 0.1487 | −0.2565 | 0.1876 | 0.0378 | 0.2024 | 0.0120 | 0.1408 | 0.0198 | |||
| 0.0830 | −0.1698 | 0.1458 | 0.0215 | 0.0923 | −0.0774 | 0.0981 | 0.0096 | |||
| 0.1641 | −0.1795 | 0.1829 | 0.0347 | 0.1962 | −0.0190 | 0.1438 | 0.0206 | |||
| 200 | 0.1827 | −0.0865 | 0.0887 | 0.0081 | 0.1987 | −0.0065 | 0.0747 | 0.0055 | ||
| 0.2782 | −0.0727 | 0.0859 | 0.0078 | 0.2956 | −0.0147 | 0.0755 | 0.0057 | |||
| 0.4040 | 0.0100 | 0.1188 | 0.0141 | 0.4043 | 0.0108 | 0.1035 | 0.0107 | |||
| −0.6012 | 0.0020 | 0.1165 | 0.0135 | −0.5998 | −0.0003 | 0.0969 | 0.0093 | |||
| 1.2056 | 0.2056 | 0.6565 | 0.4729 | 0.9842 | −0.0158 | 0.2411 | 0.0583 | |||
| 0.1702 | −0.1490 | 0.1786 | 0.0327 | 0.1975 | −0.0125 | 0.1046 | 0.0109 | |||
| 0.0816 | −0.1840 | 0.1239 | 0.0156 | 0.0948 | −0.0515 | 0.0692 | 0.0048 | |||
| 0.1613 | −0.1930 | 0.1336 | 0.0193 | 0.1926 | −0.0370 | 0.1010 | 0.0102 | |||
| 500 | 0.1940 | −0.0300 | 0.0613 | 0.0037 | 0.2004 | 0.0020 | 0.0467 | 0.0021 | ||
| 0.2858 | −0.0473 | 0.0610 | 0.0039 | 0.2998 | −0.0007 | 0.0472 | 0.0022 | |||
| 0.3975 | −0.0063 | 0.0852 | 0.0072 | 0.3981 | −0.0048 | 0.0651 | 0.0042 | |||
| −0.5973 | −0.0045 | 0.0774 | 0.0060 | −0.6004 | 0.0007 | 0.0659 | 0.0043 | |||
| 1.1874 | 0.1874 | 0.6513 | 0.4589 | 0.9858 | −0.0142 | 0.1466 | 0.0216 | |||
| 0.1756 | −0.1220 | 0.1617 | 0.0267 | 0.2026 | 0.0130 | 0.0644 | 0.0041 | |||
| 0.0875 | −0.1250 | 0.1147 | 0.0133 | 0.1006 | 0.0060 | 0.0422 | 0.0017 | |||
| 0.1732 | −0.1340 | 0.1268 | 0.0167 | 0.1975 | −0.0125 | 0.0633 | 0.0040 | |||
| Para. | n = 100 | n = 200 | n = 500 | |||||
|---|---|---|---|---|---|---|---|---|
| vech | EL | WLS | EL | WLS | EL | WLS | ||
| (0.2, 0.3, 0.4, −0.6)’ | (0, 0, 0)’ | 0.884 | 0.894 | 0.910 | 0.910 | 0.930 | 0.932 | |
| (0.1, 0.05, 0.1)’ | 0.898 | 0.888 | 0.936 | 0.932 | 0.948 | 0.946 | ||
| (0.2, 0.1, 0.2)’ | 0.902 | 0.882 | 0.926 | 0.920 | 0.956 | 0.956 | ||
| (0.3, 0.15, 0.3)’ | 0.900 | 0.890 | 0.932 | 0.930 | 0.958 | 0.952 | ||
| (0.2, 0.3, −0.2, 0.4)’ | (0, 0, 0)’ | 0.908 | 0.906 | 0.944 | 0.938 | 0.946 | 0.946 | |
| (0.1, 0.05, 0.1)’ | 0.890 | 0.888 | 0.942 | 0.940 | 0.950 | 0.944 | ||
| (0.2, 0.1, 0.2)’ | 0.918 | 0.920 | 0.934 | 0.924 | 0.942 | 0.938 | ||
| (0.3, 0.15, 0.3)’ | 0.894 | 0.890 | 0.928 | 0.926 | 0.958 | 0.956 | ||
| (0.2, 0.3, 0.4, −0.6)’ | (0, 0, 0)’ | 0.912 | 0.898 | 0.918 | 0.912 | 0.936 | 0.928 | |
| (0.1, 0.05, 0.1)’ | 0.868 | 0.872 | 0.922 | 0.916 | 0.926 | 0.922 | ||
| (0.2, 0.1, 0.2)’ | 0.912 | 0.886 | 0.926 | 0.926 | 0.942 | 0.944 | ||
| (0.3, 0.15, 0.3)’ | 0.906 | 0.890 | 0.944 | 0.942 | 0.944 | 0.940 | ||
| (0.2, 0.3, −0.2, 0.4)’ | (0, 0, 0)’ | 0.880 | 0.874 | 0.922 | 0.918 | 0.928 | 0.926 | |
| (0.1, 0.05, 0.1)’ | 0.910 | 0.914 | 0.930 | 0.940 | 0.946 | 0.940 | ||
| (0.2, 0.1, 0.2)’ | 0.888 | 0.886 | 0.942 | 0.940 | 0.954 | 0.954 | ||
| (0.3, 0.15, 0.3)’ | 0.882 | 0.878 | 0.918 | 0.910 | 0.934 | 0.938 | ||
| (0.2, 0.3, 0.4, −0.6)’ | (0, 0, 0)’ | 0.884 | 0.910 | 0.918 | 0.934 | 0.928 | 0.934 | |
| (0.1, 0.05, 0.1)’ | 0.884 | 0.908 | 0.914 | 0.930 | 0.924 | 0.926 | ||
| (0.2, 0.1, 0.2)’ | 0.896 | 0.908 | 0.918 | 0.914 | 0.930 | 0.934 | ||
| (0.3, 0.15, 0.3)’ | 0.862 | 0.874 | 0.898 | 0.900 | 0.940 | 0.948 | ||
| (0.2, 0.3, −0.2, 0.4)’ | (0, 0, 0)’ | 0.888 | 0.918 | 0.904 | 0.920 | 0.936 | 0.938 | |
| (0.1, 0.05, 0.1)’ | 0.888 | 0.916 | 0.918 | 0.930 | 0.942 | 0.948 | ||
| (0.2, 0.1, 0.2)’ | 0.876 | 0.900 | 0.912 | 0.918 | 0.936 | 0.944 | ||
| (0.3, 0.15, 0.3)’ | 0.898 | 0.920 | 0.916 | 0.930 | 0.940 | 0.938 | ||
| (0.2, 0.3, 0.4, −0.6)’ | (0, 0, 0)’ | 0.876 | 0.892 | 0.902 | 0.918 | 0.950 | 0.948 | |
| (0.1, 0.05, 0.1)’ | 0.884 | 0.888 | 0.924 | 0.926 | 0.940 | 0.930 | ||
| (0.2, 0.1, 0.2)’ | 0.894 | 0.908 | 0.932 | 0.934 | 0.938 | 0.936 | ||
| (0.3, 0.15, 0.3)’ | 0.898 | 0.882 | 0.922 | 0.916 | 0.932 | 0.930 | ||
| (0.2, 0.3, −0.2, 0.4)’ | (0, 0, 0)’ | 0.896 | 0.904 | 0.934 | 0.940 | 0.954 | 0.950 | |
| (0.1, 0.05, 0.1)’ | 0.878 | 0.888 | 0.914 | 0.926 | 0.928 | 0.930 | ||
| (0.2, 0.1, 0.2)’ | 0.892 | 0.894 | 0.928 | 0.936 | 0.940 | 0.938 | ||
| (0.3, 0.15, 0.3)’ | 0.906 | 0.904 | 0.924 | 0.920 | 0.952 | 0.954 | ||
| Para. | n = 200 | n = 500 | n = 1000 | n = 2000 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| vech | EL | WLS | EL | WLS | EL | WLS | EL | WLS | ||
| ’ | (0.1, 0.05, 0.1)’ | 0.858 | 0.844 | 0.920 | 0.898 | 0.946 | 0.926 | 0.942 | 0.934 | |
| (0.2, 0.1, 0.2)’ | 0.872 | 0.832 | 0.956 | 0.938 | 0.956 | 0.924 | 0.952 | 0.944 | ||
| (0.3, 0.15, 0.3)’ | 0.872 | 0.816 | 0.926 | 0.910 | 0.946 | 0.932 | 0.956 | 0.940 | ||
| (0.1, 0.05, 0.1)’ | 0.852 | 0.836 | 0.920 | 0.908 | 0.932 | 0.922 | 0.928 | 0.910 | ||
| (0.2, 0.1, 0.2)’ | 0.868 | 0.826 | 0.940 | 0.910 | 0.942 | 0.924 | 0.934 | 0.922 | ||
| (0.3, 0.15, 0.3)’ | 0.872 | 0.808 | 0.924 | 0.888 | 0.950 | 0.920 | 0.942 | 0.936 | ||
| (0.1, 0.05, 0.1)’ | 0.774 | 0.714 | 0.868 | 0.800 | 0.886 | 0.862 | 0.920 | 0.892 | ||
| (0.2, 0.1, 0.2)’ | 0.806 | 0.756 | 0.876 | 0.820 | 0.888 | 0.876 | 0.944 | 0.926 | ||
| (0.3, 0.15, 0.3)’ | 0.798 | 0.740 | 0.876 | 0.842 | 0.906 | 0.876 | 0.934 | 0.904 | ||
| (0.1, 0.05, 0.1)’ | 0.826 | 0.772 | 0.904 | 0.856 | 0.920 | 0.916 | 0.926 | 0.914 | ||
| (0.2, 0.1, 0.2)’ | 0.868 | 0.834 | 0.900 | 0.878 | 0.928 | 0.906 | 0.934 | 0.914 | ||
| (0.3, 0.15, 0.3)’ | 0.866 | 0.802 | 0.890 | 0.854 | 0.916 | 0.888 | 0.938 | 0.918 | ||
| ’ | (0.1, 0.05, 0.1)’ | 0.890 | 0.840 | 0.940 | 0.930 | 0.946 | 0.930 | 0.944 | 0.954 | |
| (0.2, 0.1, 0.2)’ | 0.892 | 0.836 | 0.936 | 0.910 | 0.940 | 0.918 | 0.952 | 0.942 | ||
| (0.3, 0.15, 0.3)’ | 0.876 | 0.818 | 0.918 | 0.898 | 0.940 | 0.916 | 0.956 | 0.938 | ||
| (0.1, 0.05, 0.1)’ | 0.874 | 0.850 | 0.928 | 0.886 | 0.934 | 0.932 | 0.946 | 0.946 | ||
| (0.2, 0.1, 0.2)’ | 0.886 | 0.854 | 0.924 | 0.910 | 0.932 | 0.914 | 0.940 | 0.928 | ||
| (0.3, 0.15, 0.3)’ | 0.892 | 0.846 | 0.918 | 0.904 | 0.920 | 0.904 | 0.960 | 0.958 | ||
| (0.1, 0.05, 0.1)’ | 0.778 | 0.708 | 0.854 | 0.822 | 0.904 | 0.886 | 0.936 | 0.910 | ||
| (0.2, 0.1, 0.2)’ | 0.810 | 0.748 | 0.862 | 0.830 | 0.898 | 0.868 | 0.928 | 0.922 | ||
| (0.3, 0.15, 0.3)’ | 0.822 | 0.766 | 0.846 | 0.808 | 0.900 | 0.860 | 0.920 | 0.904 | ||
| (0.1, 0.05, 0.1)’ | 0.840 | 0.794 | 0.886 | 0.882 | 0.922 | 0.908 | 0.948 | 0.924 | ||
| (0.2, 0.1, 0.2)’ | 0.868 | 0.830 | 0.906 | 0.872 | 0.910 | 0.886 | 0.944 | 0.922 | ||
| (0.3, 0.15, 0.3)’ | 0.854 | 0.816 | 0.910 | 0.894 | 0.922 | 0.908 | 0.940 | 0.918 | ||
| Model | Estimator | MSE |
|---|---|---|
| AR-X | 0.9445 | |
| RCAR-X | 0.8951 | |
| RCAR-X-EV | 0.7074 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, J.; Li, Q. Estimation of Random Coefficient Autoregressive Model with Error in Covariates. Axioms 2024, 13, 303. https://doi.org/10.3390/axioms13050303
Zhang X, Chen J, Li Q. Estimation of Random Coefficient Autoregressive Model with Error in Covariates. Axioms. 2024; 13(5):303. https://doi.org/10.3390/axioms13050303
Chicago/Turabian StyleZhang, Xiaolei, Jin Chen, and Qi Li. 2024. "Estimation of Random Coefficient Autoregressive Model with Error in Covariates" Axioms 13, no. 5: 303. https://doi.org/10.3390/axioms13050303
APA StyleZhang, X., Chen, J., & Li, Q. (2024). Estimation of Random Coefficient Autoregressive Model with Error in Covariates. Axioms, 13(5), 303. https://doi.org/10.3390/axioms13050303




