From the Crossing Numbers of K₅ + P_n and K₅ + C_n to the Crossing Numbers of W_m + S_n and W_m + W_n

Abstract

The crossing number of a graph is a significant measure that indicates the complexity of the graph and the difficulty of visualizing it. In this paper, we examine the crossing numbers of join products involving the complete graph $K_5$ with discrete graphs, paths, and cycles. We analyze optimal drawings of $K_5$, identify all five non-isomorphic drawings, and address previously hypothesized crossing numbers for $K_5+P_n$, and $K_5+C_n$. Through a simplified approach, we first establish $\mathrm{cr}(K_5+D_n)$ and then extend our method to prove the crossing numbers $\mathrm{cr}(K_5+P_n)$ and $\mathrm{cr}(K_5+C_n)$. These results also lead to new hypotheses for $\mathrm{cr}(W_m+S_n)$ and $\mathrm{cr}(W_m+W_n)$ involving wheels and stars. Our findings correct previous inaccuracies in the literature and provide a foundation for future research.

1. Introduction

Graph theory serves as a foundational framework for modeling and analyzing complex systems across various disciplines, ranging from computer science to social networks to biology. One fundamental aspect of graph theory is the concept of crossing numbers, which quantifies the minimum number of crossings required in a drawing of a graph [1]. The understanding and minimization of the crossing number of a graph have significant implications in numerous areas, encompassing both theoretical and practical domains. In computer science, minimizing the crossing number of a graph is essential for optimizing layout algorithms in circuit design, VLSI layout, and graph drawing applications. Moreover, in network design, reducing the crossing number enhances the efficiency and reliability of communication networks by minimizing signal interference and congestion. Furthermore, the crossing number has implications in spatial visualization and cartography, where minimizing crossings leads to clearer and more interpretable representations of geographic networks and transportation systems. In social network analysis, understanding the crossing number sheds light on the underlying structure and dynamics of social interactions, facilitating the identification of cohesive communities and influential nodes. Overall, reducing the number of crossings on graph edges can help in visualizing and understanding complex data, improving system performance, and optimizing graph algorithms [2,3].

In the paper, we will focus on the crossing number $\mathrm{cr}\left(G\right)$ of a composite graph G obtained by combining two graphs $G_i$ and $G_j$, known as their join product $G=G_i+G_j$. It is constructed by incorporating separate copies of $G_i$ and $G_j$ with no shared vertices and by adding all possible edges between the vertex sets $V\left(G_i\right)$ and $V\left(G_j\right)$. In the case where $\left|V\right(G_i\left)\right|=m$ and $\left|V\right(G_j\left)\right|=n$, the edge set of G is composed of the disjoint sets of edges $E\left(G_i\right)$, $E\left(G_j\right)$ and the complete bipartite graph $K_{m,n}$. Therefore, some parts of proofs will be based on Kleitman’s result [4] on the crossing numbers for some $K_{m,n}$. He showed that

$$\mathrm{cr}\left(K_{m,n}\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋,\mathrm{if}m\le 6.$$

(1)

The graph terminology used is taken from the book [5].

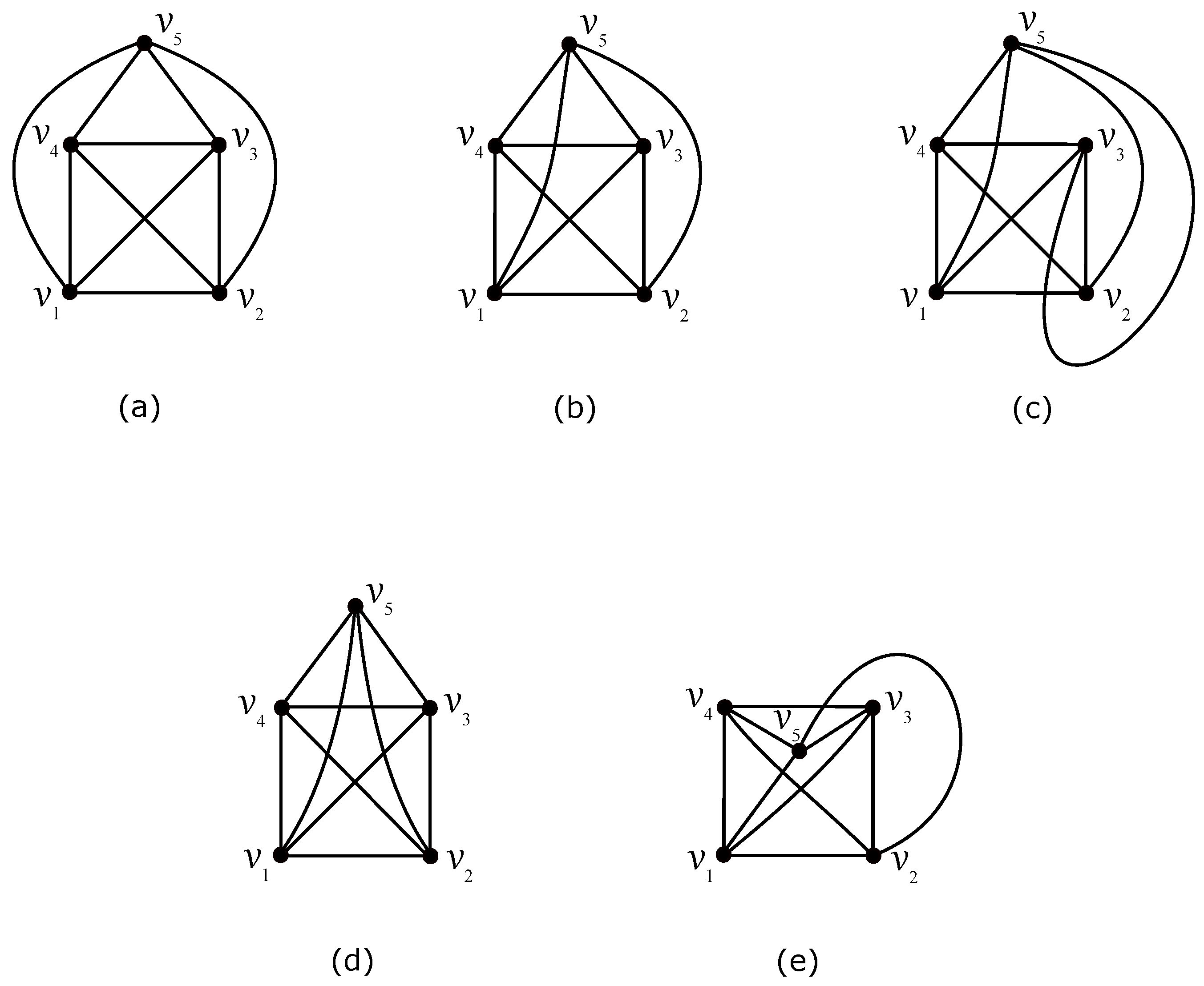
One graph of our considered join product G will be a complete graph with five vertices $K_5$, which is specific for its symmetries. As the crossing number $\mathrm{cr}\left(K_5\right)=1$, there is at least one crossing over all optimal drawings of $K_5$ with the vertex set $V\left(K_5\right)=\{v_1,\dots ,v_5\}$. In the rest of the paper, let the edges $v_1{v}_3$ and $v_2{v}_4$ be crossed. The edges $v_1{v}_2$, $v_2{v}_3$, $v_3{v}_4$, and $v_4{v}_1$ cannot cross each other because we are only interested in optimal subdrawings. Finally, all considered drawings of $K_5$ can be achieved from the nonplanar drawing of $K_4$ by adding one vertex $v_5$ with the four corresponding edges $v_1{v}_5$, $v_2{v}_5$, $v_3{v}_5$, and $v_4{v}_5$. As a result, there are only five mutually non-isomorphic drawings of $K_5$, which are depicted in Figure 1.

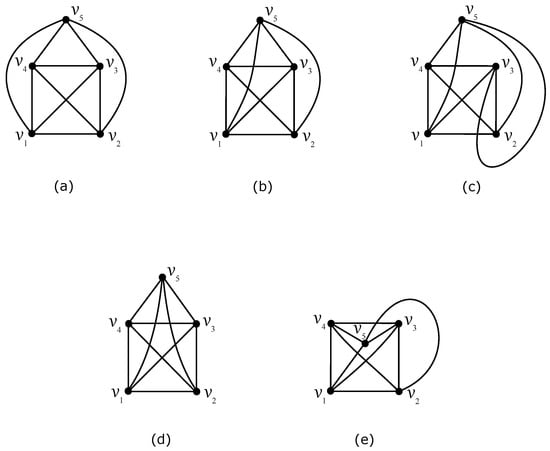
Figure 1. Five mutually non-isomorphic drawings of $K_5$: (a) only one crossing; (b) additional crossing on the edge $v_1{v}_5$; (c) additional crossings on the edges $v_1{v}_5$ and $v_3{v}_5$; (d) additional crossings on the edges $v_1{v}_5$ and $v_2{v}_5$; (e) additional crossings on the edges $v_1{v}_5$ and $v_2{v}_5$ with the vertex $v_5$ located inside the inner region of $K_4$.

Currently, the crossing numbers of the graphs $K_5+P_n$ and $K_5+C_n$, where $P_n$ and $C_n$ are paths and cycles on n vertices, are given only as hypotheses. The crossing number of $K_5+P_n$ graphs for $n\ge 2$ was previously investigated in Su’s paper [6], but with several errors in the main proof caused by an inconsistent discussion of possible subcases (e.g., wrong drawings or not considering all the drawings with respect to a given subcase). To prove it correctly, we will first build the necessary mathematical apparatus for the case $\mathrm{cr}(K_5+D_n)$, where $D_n$ denotes a discrete graph on n vertices. Lü and Huang [7] already proved it, albeit in a rather complicated way. We offer an alternative proof that is simpler, and its same main idea can be used later for determining $\mathrm{cr}(K_5+P_n)$. The intended idea lies in the use of the existence of different cycles of $C_3$ as subgraphs of $K_5$ that can perform the function of separation concerning the remaining two vertices of $K_5$. By gradually adding edges, we will also determine the crossing number for the $K_5+C_n$, which was an open problem until now. Additionally, the obtained values $\mathrm{cr}(K_5+P_n)$ and $\mathrm{cr}(K_5+C_n)$ will help us establish completely new hypotheses for $\mathrm{cr}(W_m+S_n)$ and $\mathrm{cr}(W_m+W_n)$, where $W_n$ and $S_n$ are wheels and stars on $n+1$ vertices, respectively [8].

Regarding the practical importance of the problem, it can be mentioned that some algorithms constructing the graph drawings with a minimal number of crossings have already been created [9,10,11]. For example, the algorithm located on the website [12] can find the crossing numbers of small sparse graphs using an integer linear programming (ILP) formulation based on Kuratowski subgraphs. The system also generates verifiable formal proofs, as described by Chimani and Wiedera [11]. However, for our research, the capacity of the system is insufficient, because the join products considered in this paper belong to dense graphs. This confirms that examining the number of crossings of simple graphs is a classic but still challenging problem. Garey and Johnson [13] even proved that it belongs between NP-complete problems.

2. The Crossing Number of ${\mathit{K}}_{\mathbf{5}}+{\mathit{D}}_{\mathit{n}}$

The considered join product $K_5+D_n$ is formed by combining a copy of the graph $K_5$ with n additional vertices labeled as $t_1,\dots ,t_n$. Each of these newly added vertices $t_i$ is connected to every vertex in the original graph $K_5$. We define the subgraph $T^i$ as the collection of five edges incident to the fixed vertex $t_i$. In the drawing D of $K_5+D_n$, it is advantageous to categorize the n subgraphs $T^i$ into three distinct subsets based on the number of times they intersect the edges of $K_5$. Let $R_D$ represent the set of subgraphs where ${\mathrm{cr}}_D(K_5,T^i)=0$ (indicating zero crossings), and let $S_D$ represent the set of subgraphs where ${\mathrm{cr}}_D(K_5,T^i)=1$ (indicating one crossing). All remaining subgraphs $T^i$, which cross edges of $K_5$ at least twice in D, fall into the third subset. We note that the same categorization will also be used later in the drawing of $K_5+P_n$ and $K_5+C_n$ too.

It is evident that a drawing characterized by a minimal number of crossings, known as an optimal drawing, inherently possesses the desirable qualities of a good drawing. In such a drawing, the edges do not intersect themselves, no two edges cross multiple times, and there are no instances where two edges connected to the same vertex intersect [14]. In a good drawing D of some graph G, we say that a cycle C separates two different vertices of the subgraph $G\setminus C$ if they are contained in different components of ${\mathbb{R}}^2\setminus C$, where ${\mathbb{R}}^2$ means a two-dimensional space. This considered cycle C is said to be a separating cycle of graph G in D.

To determine the value of the crossing number for the composite graph $K_5+D_n$, we will divide five possible mutually non-isomorphic drawings of $K_5$ into two groups. First, we will look at those in which it is possible to find the separating cycle $C_3$. In fact, there is such an option in all but one of the drawings in Figure 1. Their crossing numbers will be proved in Lemma 1 using the already known crossing number of the complete tripartite graph $K_{1,1,3}$ in combination with $D_n$, which is summarized in Theorem 1:

Theorem 1

([15]). $\mathrm{cr}(K_{1,1,3}+D_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$ for $n\ge 1$.

Subsequently, in Lemma 2, we will deal with $\mathrm{cr}(K_5+D_n)$ for the two smallest possible n values. After that, we are ready to state the final Theorem 2, and in its proof, we take advantage of the previous two lemmas and discuss in more detail the last case when it is not possible to find a separating cycle $C_3$ in $D\left(K_5\right)$. As part of it, we will also use a concept of the rotation, ${\mathrm{rot}}_D\left(t_i\right)$, of a vertex $t_i$ in D of $K_5+D_n$. It is defined as the cyclic permutation that documents the counterclockwise order, in which the edges departing from $t_i$ appear. This rotation, introduced by Hernández-Vélez et al. [16] or Woodall [17], employs a notation $\left(12345\right)$ to represent the counter-clockwise order of edges incident to the vertex $t_i$, such as $t_i{v}_1$, $t_i{v}_2$, $t_i{v}_3$, $t_i{v}_4$ and $t_i{v}_5$. It is important to note that the rotation signifies a cyclic permutation.

Lemma 1.

For $n\ge 2$, let D be a good drawing of $K_5+D_n$. If there is a separating cycle $C_3$ of $K_5$ in the subdrawing $D\left(K_5\right)$, then there are at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+1$ crossings in D.

Proof. 

By assumption, let us consider a separating cycle $C_3=c_1{c}_2{c}_3{c}_1$ of $K_5$ in the subdrawing $D\left(K_5\right)$. Since the two remaining vertices of $K_5$ lie in different regions of $D\left(C_3\right)$, there is no subgraph $T^i$ for which the edges of $C_3$ are not crossed. Hence, each subgraph $T^i$ crosses the edges of $C_3$ at least once, which yields that ${\mathrm{cr}}_D(C_3,{\bigcup }_{i=1}^n{T}^i)\ge n$. Let G be the graph difference of graphs $K_5$ and $C_3$; i.e., G is isomorphic to the complete tripartite graph $K_{1,1,3}$. The exact value for the crossing number of $G+D_n$ is given by Theorem 1; that is, ${\mathrm{cr}}_D(G+D_n)\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$. This enforces at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋+n+1$ crossings in D because some edge of the cycle $C_3$ is also crossed in $D\left(K_5\right)$. □

Lemma 2.

$\mathrm{cr}(K_5+D_1)=3$ and $\mathrm{cr}(K_5+D_2)=6$.

Proof. 

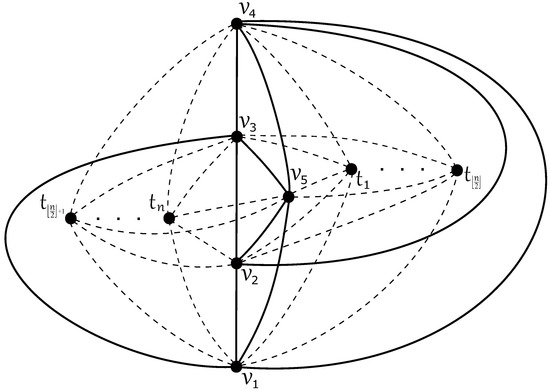
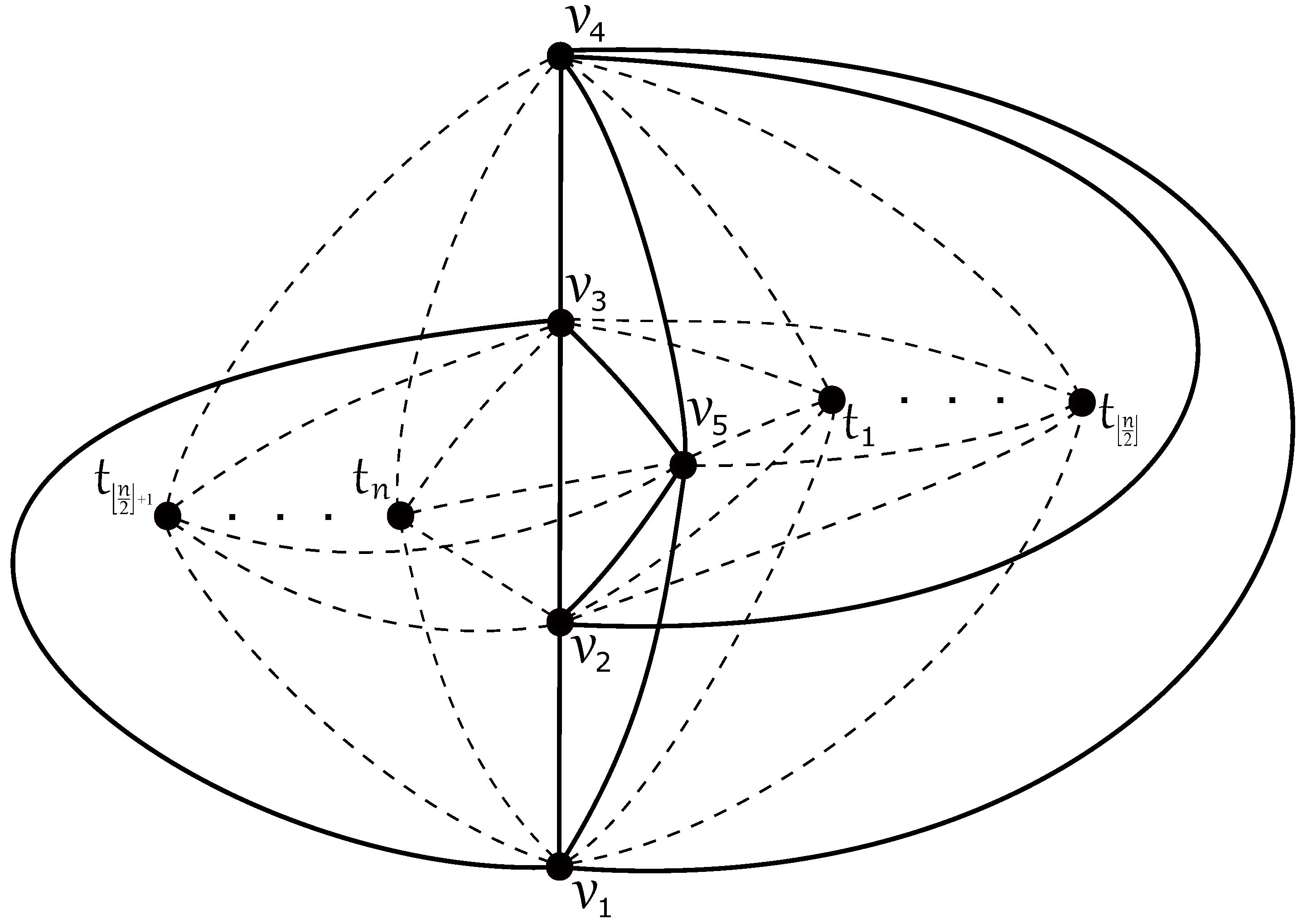
Notice that the graphs $K_5+D_1$ and $K_5+D_2$ are isomorphic to the join product of the complete graph $K_4$ with the paths $P_2$ and $P_3$, respectively (Figure 2). Since it was proved in [18] that $\mathrm{cr}(K_4+P_2)=3$ and $\mathrm{cr}(K_4+P_3)=6$, due to isomorphism, we can directly state that $\mathrm{cr}(K_5+D_1)=3$ and $\mathrm{cr}(K_5+D_2)=6$. □

Figure 2. The good drawing of $K_5+D_n$ with $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+1$ crossings.

Theorem 2.

$\mathrm{cr}(K_5+D_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+1$ for $n\ge 1$.

Proof. 

By Lemma 2, the result is true for $n=1$ and $n=2$. In Figure 2, the edges of $K_{5,n}$ cross each other $4\lfloor \frac{n}{2}\rfloor \lfloor \frac{n-1}{2}\rfloor$ times, each subgraph $T^i$, $i=1,\dots ,\lfloor \frac{n}{2}\rfloor$ on the right side crosses edges of the complete graph $K_5$ three times, and each subgraph $T^i$, $i=\lfloor \frac{n}{2}\rfloor +1,\dots ,n$ on the left side crosses edges of $K_5$ exactly twice. As there is one crossing among edges of $K_5$, we obtain $\mathrm{cr}(K_5+D_n)\le 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+1$. To prove the reverse inequality by induction on n, suppose now that there is an optimal drawing D of $K_5+D_n$ with

$${\mathrm{cr}}_D(K_5+D_n)\le 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋\mathrm{for}\mathrm{some}n\ge 3,$$

(2)

and also let

$$\mathrm{cr}(K_5+D_m)=4⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+2m+⌊\frac{m}{2}⌋+1\mathrm{for}\mathrm{any}\mathrm{positive}\mathrm{integer}m<n.$$

(3)

According to Lemma 1, we can suppose only the drawing of $K_5$ induced by D in such a way as shown in Figure 1d because there is a possibility of obtaining a separating cycle $C_3$ for all four remaining subdrawings $D\left(K_5\right)$. Note that such a single possible induced drawing of $K_5$ does not allow the addition of a subgraph $T^k$ with $1\le {\mathrm{cr}}_D(K_5,T^k)\le 2$. Moreover, if $r=\left|R_D\right|$, the assumption (2), together with the well-known fact ${\mathrm{cr}}_D\left(K_{5,n}\right)\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$, thanks to (1), implies that in D,

$$5+0r+3(n-r)\le 2n+⌊\frac{n}{2}⌋.$$

(4)

The obtained inequality (4) forces $3r\ge ⌈\frac{n}{2}⌉+5$, that is, $r\ge 2$ for n at least 3. For all subgraphs $T^i\in R_D$, there is only one subdrawing of $K_5\cup T^i$ represented by the rotation $\left(14532\right)$ (for our purposes, it does not matter which of the regions is unbounded). If there is a subgraph $T^k$ such that ${\mathrm{cr}}_D(T^i,T^k)=0$, then the edges of $K_5$ are crossed at least five times by edges of $T^i\cup T^k$ based on the discussion of inserting the vertex $t_k$ with corresponding edges over eleven considered regions of $D(K_5\cup T^i)$. As a result, the number of crossings in D, we have

$${\mathrm{cr}}_D(K_5+D_n)={\mathrm{cr}}_D(K_5+D_{n-2})+{\mathrm{cr}}_D(T^i\cup T^k)+{\mathrm{cr}}_D(K_{5,n-2},T^i\cup T^k)+{\mathrm{cr}}_D(K_5,T^i\cup T^k)$$

$$\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+2(n-2)+⌊\frac{n-2}{2}⌋+1+4(n-2)+5$$

$$=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+1,$$

where each of $n-2$ subgraphs $T^l$, $l\ne i,k$, crosses the edges of $T^i\cup T^k$ at least four times due to ${\mathrm{cr}}_D\left(K_{5,3}\right)\ge 4$ again by (1). This contradiction with the assumption (2) confirms that the edges of all $T^i\in R_D$ must be crossed at least once by any other subgraph $T^k$. For two different subgraphs $T^i,T^j\in R_D$, ${\mathrm{cr}}_D(T^i\cup T^j,T^k)\ge 4+4=8$ holds for any $T^k\in R_D$, $k\ne i,j,$ provided by ${\mathrm{rot}}_D\left(t_i\right)={\mathrm{rot}}_D\left(t_j\right)={\mathrm{rot}}_D\left(t_k\right)$. Moreover, the edges of $K_5\cup T^i\cup T^j$ are crossed at least seven times by any subgraph $T^k\notin R_D$, because ${\mathrm{cr}}_D(K_5\cup T^i,T^k)\ge 6$ is fulfilled using the discussion over all possible regions of $D(K_5\cup T^i)$. As ${\mathrm{cr}}_D(K_5\cup T^i\cup T^j)\ge 5+4=9$, by fixing the subgraph $K_5\cup T^i\cup T^j$, we have

$${\mathrm{cr}}_D(K_5+D_n)\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+8(r-2)+7(n-r)+9=4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋$$

$$+7n+r-7\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+7n+2-7\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+1.$$

We have shown, in all cases, that there are at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+1$ crossings in each good drawing D of the graph $K_5+D_n$. The proof of Theorem 2 is complete. □

3. The Crossing Number of ${\mathit{K}}_{\mathbf{5}}+{\mathit{P}}_{\mathit{n}}$

In the drawing of $K_5+D_n$ depicted in Figure 2, it is possible to add $n-1$ new edges $t_i{t}_{i+1}$ for $i=1,\dots ,n-1$ forming the path $P_n^{*}$ on vertices of $D_n$ with exactly three additional crossings. Thus, $\mathrm{cr}(K_5+P_n)\le 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+4$. Our goal is to show that the crossing number of $K_5+P_n$ is equal to this upper bound. Note that this result was already predicted by Su [6], but we have found several mistakes in his proofs. Our Lemma 3 will confirm this result for $n=2$ and $n=3$, whereas its proof will be strongly based on isomorphisms. Then, we will focus in Lemma 4 on the case when a separating cycle $C_3$ of $K_5$ exists in the subdrawing $D\left(K_5\right)$. The crossing numbers of the join products of $K_{1,1,3}$ with paths $P_n$ (summarized in Theorem 3), which have already been determined by Staš and Timková in [19], concludes the main idea of the proof.

Theorem 3

([19], Theorem 3.5). $\mathrm{cr}(K_{1,1,3}+P_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋+2$ for $n\ge 2$.

Subsequently, Lemma 4 will result in Corollary 1, which discusses the subdrawing of $K_5$ induced by D given in Figure 1a. This drawing of $K_5$ has only one crossing on the edges of $C_3$ in $D(K_5\cup P_n^{*})$, and therefore, the condition of Lemma 4 is not fulfilled. After that, the statement of the main Theorem 4 about $\mathrm{cr}(K_5+P_n)$, in the proof of which we take advantage of the pre-prepared Lemma 3, Lemma 4, and Corollary 1, can be established.

Lemma 3.

$\mathrm{cr}(K_5+P_2)=9$ and $\mathrm{cr}(K_5+P_3)=15$.

Proof. 

Notice that the graphs $K_5+P_2$ and $K_5+P_3$ are isomorphic to the complete graph $K_7$ and $K_8\setminus e$ obtained by removing one edge from $K_8$, respectively. Guy [20] and Zheng et al. [21] proved that $\mathrm{cr}\left(K_7\right)=9$ and $\mathrm{cr}(K_8\setminus e)=15$. Therefore, $\mathrm{cr}(K_5+P_2)=\mathrm{cr}\left(K_7\right)=9$ and $\mathrm{cr}(K_5+P_3)=\mathrm{cr}(K_8\setminus e)=15$, and the proof of Lemma 3 is complete. □

Lemma 4.

For $n\ge 2$, let D be a good drawing of $K_5+P_n$. If there is a separating cycle $C_3$ of $K_5$ in the subdrawing $D\left(K_5\right)$ with at least two crossings on the edges of $C_3$ in $D(K_5\cup P_n^{*})$, then there are at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+4$ crossings in D.

Proof. 

Using arguments similar to the proof of Lemma 1, the edges of any separating cycle $C_3$ in $D\left(K_5\right)$ are crossed at least n times by ${\bigcup }_{i=1}^n{T}^i$. If G is the graph difference of graphs $K_5$ and $C_3$, then ${\mathrm{cr}}_D(G+P_n)\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋+2$ by Theorem 3 enforces at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋+n+4$ crossings in D. □

Corollary 1.

For $n\ge 4$, if D is a good drawing of $K_5+P_n$ with the subdrawing of $K_5$ induced by D given in Figure 1a, then there are at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+4$ crossings in D.

Proof. 

In Figure 1a, there are two separate cycles $C_3$ of $K_5$, but both have only one crossing on their edges in the subdrawing $D\left(K_5\right)$. If some edge of the path $P_n^{*}$ crosses any edge of these separating cycles, we obtain the desired result in D using Lemma 4. Of course, we also obtain at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+4$ crossings in D if the edges of some separating cycle $C_3$ are crossed more than once by edges of some subgraph $T^i$ (see the proof of Lemma 1).

Now, we assume that there are exactly n crossings on the edges of each separating 3-cycle; that is, each subgraph $T^i$ crosses the edges of any separating 3-cycle exactly once, and also, the edges of path $P_n^{*}$ do not produce any crossing on the edges of both separating 3-cycles. In the rest of the proof, let all vertices $t_i$ of $P_n^{*}$ be placed in the outer region of $D\left(K_5\right)$ with three vertices $v_1$, $v_2$, and $v_5$ or in the inner triangular region with two vertices $v_1$ and $v_2$ of $K_5$ on its boundary. Our assumption enforces no crossing on two edges $v_3{v}_5$ and $v_4{v}_5$ in D, which yields the fact that there are exactly $2n+1$ crossings on four edges $v_1{v}_3$, $v_1{v}_5$, $v_2{v}_4$, and $v_2{v}_5$ in D. Let us denote by H the subgraph of $K_5$ with the vertex set $V\left(K_5\right)$ and the edge set $\{v_1{v}_4,v_2{v}_3,v_3{v}_4,v_3{v}_5,v_4{v}_5\}$. By Klešč and Staš [22], it was proved that $\mathrm{cr}(H+P_n)=4\lfloor \frac{n}{2}\rfloor \lfloor \frac{n-1}{2}\rfloor +\lfloor \frac{n}{2}\rfloor$, and thus, we receive the desired result if there are at least three crossings on the edge $v_1{v}_2$ in D.

Finally, let us turn to the possibility that there are at most two crossings on the edge $v_1{v}_2$ in D. For $n\ge 4$, we obtain at least one subgraph $T^j$ (but there are definitely at least two) whose edges do not cross this edge $v_1{v}_2$ of the graph $K_5$. This enforces the fact that no edge of $K_5$ is crossed by the edge $t_j{v}_5$ and ${\mathrm{cr}}_D(K_5,T^j)=2$ only for $T^j$ with ${\mathrm{rot}}_D\left(t_j\right)=\left(14532\right)$. It is easy to verify over six possible regions of $D(K_5\cup T^j)$ that each of the $n-1$ remaining subgraphs $T^k$ crosses the edges of $K_5\cup T^j$ at least five times. As ${\mathrm{cr}}_D(K_5\cup T^j)=3$, by fixing the subgraph $K_5\cup T^j$, we have

$${\mathrm{cr}}_D(K_5+P_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+5(n-1)+3+1\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+4.$$

We could add $+1$ in the previous estimate because the number of crossings on edges of $K_5\cup T^j$ can be increased up to 6 for each subgraph $T^k$, $k\ne j$ if both vertices $t_j$ and $t_k$ are placed in the same outer region of $D\left(K_5\right)$. The proof of Corollary 1 is done. □

Theorem 4.

$\mathrm{cr}(K_5+P_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+4$ for $n\ge 2$.

Proof. 

The proof proceeds similarly to the graph $K_5+D_n$ in Theorem 2. Using Lemma 3, we suppose that there is an optimal drawing D of $K_5+P_n$ with

$${\mathrm{cr}}_D(K_5+P_n)\le 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+3\mathrm{for}\mathrm{some}n\ge 4,$$

(5)

and that

$$\mathrm{cr}(K_5+P_m)=4⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+2m+⌊\frac{m}{2}⌋+4\mathrm{for}\mathrm{any}\mathrm{positive}\mathrm{integer}m<n.$$

(6)

By Lemma 4 and Corollary 1, we consider only the subdrawing of the graph $K_5$ induced by D with ${\mathrm{cr}}_D\left(K_5\right)=5$ presented in Figure 1d. For $r=\left|R_D\right|$, the relation with respect to edge crossings of the subgraph $K_5$ in D produces

$$5+0r+3(n-r)\le 2n+⌊\frac{n}{2}⌋+3,$$

(7)

which again yields $r\ge 2$ for an n of at least four. Since $4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+7n-5$ is at least as much as $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+4$, the proof of Theorem 4 is complete. □

4. The Crossing Number of ${\mathit{K}}_{\mathbf{5}}+{\mathit{C}}_{\mathit{n}}$

To date, the crossing numbers of the join product $K_5+C_n$ were not claimed in any hypothesis. The upper bound of $\mathrm{cr}(K_5+C_n)$ can be easily estimated from Figure 2 by the addition of n new edges $t_n{t}_1$ and $t_i{t}_{i+1}$, $i=1,\dots ,n-1$ forming the cycle $C_n^{*}$ on vertices of $D_n$ with just six additional crossings. In such a way, we obtain

$$\mathrm{cr}(K_5+C_n)\le 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+7$$

(8)

and we will show that the upper bound in (8) holds with equality for all n at least three in the following statements. Lemma 5 will confirm this result for $n=3$, because $K_5+C_3$ is isomorphic to the complete graph $K_8$ and it is shown by Guy [20] that $\mathrm{cr}\left(K_8\right)=18$. Similar to the previous two sections, we will focus first on Lemma 6 in the case when there is a separating cycle $C_3$ of $K_5$ in the subdrawing $D\left(K_5\right)$. As the crossing numbers of the join products of $K_{1,1,3}$ with the cycles $C_n$ have been determined by Staš and Timková [19], they can be safely used in the last part of the proof of Lemma 6.

Theorem 5

([19], Theorem 4.9). $\mathrm{cr}(K_{1,1,3}+C_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋+4$ for $n\ge 3$.

The condition of Lemma 6 for at least three crossings on edges of $C_3$ in $D(K_5\cup C_n^{*})$ is not fulfilled for the subdrawing of $K_5$ induced by D given in Figure 1a and Figure 1b, respectively. Therefore, these special cases will be discussed separately in Corollary 2 and Corollary 3. After that, we will turn our attention to the subdrawing of $K_5$ induced by D given in Figure 1d. It represents the only subdrawing of $K_5$ without the existence of a separating cycle $C_3$ and is addressed in Lemma 7 for $n=4$; i.e., $\mathrm{cr}(K_5+C_4)$ is pre-prepared for the final statement. That will be introduced in Theorem 6 and will establish $\mathrm{cr}(K_5+C_n)$ for arbitrary $n\ge 3$.

Lemma 5.

$\mathrm{cr}(K_5+C_3)=18$.

Lemma 6.

For $n\ge 3$, let D be a good drawing of $K_5+C_n$. If there is a separating cycle $C_3$ of $K_5$ in the subdrawing $D\left(K_5\right)$ with at least three crossings on edges of $C_3$ in $D(K_5\cup C_n^{*})$, then there are at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+7$ crossings in D.

Proof. 

Using arguments similar to the proof of Lemma 1, the edges of any separating cycle $C_3$ in $D\left(K_5\right)$ are crossed at least n times by ${\bigcup }_{i=1}^n{T}^i$. If G is the graph difference of graphs $K_5$ and $C_3$, then ${\mathrm{cr}}_D(G+C_n)\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋+4$ by Theorem 5 enforces at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋+n+7$ crossings in D. □

Corollary 2.

For $n\ge 4$, if D is a good drawing of $K_5+C_n$ with the subdrawing of $K_5$ induced by D given in Figure 1a, then there are at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+7$ crossings in D.

Proof. 

In Figure 1a, there are two separate cycles $C_3$ of $K_5$, namely 3-cycles $v_1{v}_3{v}_5{v}_1$ and $v_2{v}_5{v}_4{v}_2$. Both have only one crossing on their edges in the subdrawing $D\left(K_5\right)$. If some edge of the cycle $C_n^{*}$ crosses any edge of one separating 3-cycle, we obtain the desired result in D using Lemma 6. Clearly, we also obtain at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+7$ crossings in D if there are at least $n+2$ crossings between ${\bigcup }_{i=1}^n{T}^i$ and one separating cycle (see the proof of Lemma 1). In the following, suppose that a separating cycle $C_3$ can be crossed at most twice by only one subgraph $T^i$.

Now, we assume that the edges of cycle $C_n^{*}$ do not produce any crossing on the edges of separating 3-cycles. In the rest of the paper, let all vertices $t_i$ of $C_n^{*}$ be placed in the outer region of $D\left(K_5\right)$ with three vertices $v_1$, $v_2$, and $v_5$ or in the inner triangular region with two vertices $v_1$ and $v_2$ of $K_5$ on its boundary. We discuss two subcases:

• ${\mathrm{cr}}_D(K_5,T^i)\ge 3$ for each subgraph $T^i$, $i=1,\dots ,n$. If all vertices $t_i$ of $C_n^{*}$ are placed in the outer region of $D\left(K_5\right)$ with three vertices $v_1$, $v_2$, and $v_5$ of $K_5$ on its boundary, then we obtain at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋+4+2n$ crossings in D, which is caused by at least $2n$ crossings on the edges of the 3-cycle $v_1{v}_2{v}_5{v}_1$ and also due to Theorem 5. Below, suppose that they are not placed only in the outer region of $D\left(K_5\right)$. Let us denote by H the subgraph of $K_5$ with the vertex set $V\left(K_5\right)$, and the edge set $\{v_1{v}_4,v_2{v}_3,v_3{v}_4,v_3{v}_5,v_4{v}_5\}$. Klešč and Staš [22] proved that $\mathrm{cr}(H+C_n)=4\lfloor \frac{n}{2}\rfloor \lfloor \frac{n-1}{2}\rfloor +\lfloor \frac{n}{2}\rfloor +2$. It is easy to verify that edges of the subgraph $K_5-H$ are crossed at least twice by any subgraph $T^i$ and just two crossings can be achieved only for at most two possible different subgraphs given our assumptions. This implies ${\mathrm{cr}}_D(K_5-H,{\bigcup }_{i=1}^n{T}^i)\ge 3n-\alpha$, where $\alpha$ is the number of such subgraphs forcing two crossings on edges of $K_5-H$. Thus, we obtain at least

  $$4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋+2+3n-\alpha +{\mathrm{cr}}_D(K_5-H)+{\mathrm{cr}}_D(v_1{v}_2,C_n^{*})$$

  (9)

  crossings in D. As ${\mathrm{cr}}_D(K_5-H)=1$ and ${\mathrm{cr}}_D(v_1{v}_2,C_n^{*})-\alpha \ge 0$, we are done.
• There is a subgraph $T^i$ such that ${\mathrm{cr}}_D(K_5,T^i)<3$. Without loss of generality, let $T^n$ be a subgraph by which the edges of $K_5$ are crossed just twice, that is, ${\mathrm{rot}}_D\left(t_n\right)=\left(14532\right)$. It is not difficult to verify over six possible regions of $D(K_5\cup T^n)$ that the edges of $K_5\cup T^n$ are crossed at least five times by each other subgraph $T^j$, $j\ne n$ and just five crossings can be achieved for several possible different subgraphs given our assumptions. This implies ${\mathrm{cr}}_D(K_5\cup T^n,{\bigcup }_{j=1}^{n-1}{T}^j)\ge 6(n-1)-\beta$, where $\beta$ is the number of such subgraphs forcing five crossings on the edges of $K_5\cup T^n$. For $\beta \le 2$, by fixing the subgraph $K_5\cup T^n$, we have at least

  $$4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+6(n-1)-\beta +{\mathrm{cr}}_D(K_5\cup T^n)+{\mathrm{cr}}_D(v_1{v}_2,C_n^{*})$$

  (10)

  crossings in D. As ${\mathrm{cr}}_D(K_5\cup T^n)=3$ and ${\mathrm{cr}}_D(v_1{v}_2,C_n^{*})-\beta \ge 0$, we are again done.
  Finally, for $\beta \ge 3$, let H be the subgraph of $K_5$ defined in the same way as in the previous subcase. This implies ${\mathrm{cr}}_D(K_5-H,{\bigcup }_{j=1}^n{T}^j)\ge 2n+\beta$, which yields at least

  $$4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋+2+2n+\beta +{\mathrm{cr}}_D(v_1{v}_2,C_n^{*})$$

  (11)

  crossings in D. As $\beta +{\mathrm{cr}}_D(v_1{v}_2,C_n^{*})\ge 5$, we achieve the desired result in D.

□

Corollary 3.

For $n\ge 4$, if D is a good drawing of $K_5+C_n$ with the subdrawing of $K_5$ induced by D given in Figure 1b, then there are at least $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+7$ crossings in D.

Proof. 

In Figure 1b, there are two separate cycles $C_3$ of $K_5$ but both have only two crossings on their edges in the subdrawing $D\left(K_5\right)$. Let us denote by H the subgraph of $K_5$ with the vertex set $V\left(K_5\right)$ and the edge set $\{v_1{v}_3,v_1{v}_4,v_2{v}_3,v_3{v}_4,v_3{v}_5\}$. If some edge of the cycle $C_n^{*}$ crosses any edge of these separating cycles, we obtain the desired result in D using Lemma 6. Now, we assume that no edge of $C_n^{*}$ crosses any edge of these separating cycles, that is, all vertices $t_i$ of $C_n^{*}$ are placed in some common region of $D(K_5-H)$. The crossing numbers of the join product of the graph H with cycles are already known by Staš [23], i.e., $\mathrm{cr}(H+C_n)=4\lfloor \frac{n}{2}\rfloor \lfloor \frac{n-1}{2}\rfloor +2\lfloor \frac{n}{2}\rfloor +2$. Since the edges of the subgraph $K_5-H$ (edges of both separating cycles together) are crossed at least $2n+3$ times in D, we obtain at least $4\lfloor \frac{n}{2}\rfloor \lfloor \frac{n-1}{2}\rfloor +2\lfloor \frac{n}{2}\rfloor +2+2n+3$ crossings, and this completes the proof of Corollary 3. □

Lemma 7.

If D is a good drawing of $K_5+C_4$ with the subdrawing of $K_5$ induced by D given in Figure 1d with the nonempty set $R_D$, then there are at least 25 crossings in D.

Proof. 

For easier reading, let $r=\left|R_D\right|$. By the assumption of Lemma 7, ${\mathrm{cr}}_D\left(K_5\right)=5$ and $r\ge 1$. We remember that there is only one subdrawing of $F^i=K_5\cup T^i$ represented by the rotation $\left(14532\right)$ for all subgraphs $T^i\in R_D$. If $n=r=4$, we obtain at least $\left(\genfrac{}{}{0pt}{}{4}{2}\right)4+5=29$ crossings in D because every two different subgraphs from $R_D$ with the same rotations produce at least four crossings on their edges. Below, let $T^1\in R_D$ and let r be at most three. We discuss two possibilities:

• Assume there exists a subgraph $T^j$, say $T^4$, by which the edges of $T^1$ are not crossed. The edges of $K_5$ must be crossed at least nine times by the edges of $T^4\cup C_n^{*}$ due to the location of the vertex $t_4$ in $D(K_5\cup T^1)$. For $r=3$, we obtain at least

  $${\mathrm{cr}}_D\left(\bigcup _{i=1}^3{T}^i\right)+{\mathrm{cr}}_D\left(K_5\right)+{\mathrm{cr}}_D(K_5,T^4\cup C_n^{*})\ge \left(\genfrac{}{}{0pt}{}{3}{2}\right)4+5+9=26$$

  crossings in D. For $1\le r\le 2$, we obtain at least

  $${\mathrm{cr}}_D(T^1\cup T^4,T^2\cup T^3)+{\mathrm{cr}}_D\left(K_5\right)+{\mathrm{cr}}_D(K_5,T^4\cup C_n^{*})+{\mathrm{cr}}_D(K_5,T^2\cup T^3)$$

  $$\ge 8+5+9+3=25$$

  crossings in D because ${\mathrm{cr}}_D(T^1\cup T^4,T^2\cup T^3)\ge 4+4$ thanks to (1), and at least one of the subgraphs $T^2$, $T^3$ crosses the edges of $K_5$ at least three times.
• ${\mathrm{cr}}_D(T^1,T^j)\ne 0$ for any $j=2,3,4$. In the rest of the proof, let $T^4\notin R_D$ in the case of $r=3$. If ${\mathrm{cr}}_D(T^i,T^4)=0$ for some $i\in \{2,3\}$, the proof can proceed in the same way as in the previous case. Taking into account the assumption that ${\mathrm{cr}}_D(T^2\cup T^3,T^4)\ge 2$, we obtain at least

  $${\mathrm{cr}}_D\left(\bigcup _{i=1}^3{T}^i\right)+{\mathrm{cr}}_D\left(K_5\right)+{\mathrm{cr}}_D(K_5\cup T^1,T^4)+{\mathrm{cr}}_D(T^2\cup T^3,T^4)\ge \left(\genfrac{}{}{0pt}{}{3}{2}\right)4+5+6+2=25$$

  crossings in D because the edges of $K_5\cup T^1$ are crossed at least six times by any subgraph $T^i\notin R_D$. For $1\le r\le 2$, we obtain at least

  $${\mathrm{cr}}_D\left(K_5\cup T^1,\bigcup _{i=2}^4{T}^i\right)+{\mathrm{cr}}_D\left(K_5\right)+{\mathrm{cr}}_D\left(\bigcup _{i=2}^4{T}^i\right)\ge (6+6+4)+5+4=25$$

  crossings in D, where ${\mathrm{cr}}_D(T^2\cup T^3\cup T^4)\ge 4$, again thanks to (1).

□

Theorem 6.

$\mathrm{cr}(K_5+C_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+7$ for $n\ge 3$.

Proof. 

Using Lemma 5, we suppose that there is an optimal drawing D of $K_5+C_n$ with

$${\mathrm{cr}}_D(K_5+C_n)\le 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+6\mathrm{for}\mathrm{some}n\ge 4,$$

(12)

and that

$$\mathrm{cr}(K_5+C_m)=4⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+2m+⌊\frac{m}{2}⌋+7\mathrm{for}\mathrm{any}\mathrm{positive}\mathrm{integer}m<n.$$

(13)

By Lemma 6 and Corollaries 2, 3, we only consider the drawing of $K_5$ induced by D presented in Figure 1d. For $r=\left|R_D\right|$, the relation with respect to edge crossings of the complete graph $K_5$ in D produces

$$5+0r+3(n-r)\le 2n+⌊\frac{n}{2}⌋+6,$$

(14)

which yields $r\ge 1$ for an n value of at least four. As the set $R_D$ is nonempty, Lemma 7 enforces $n\ge 5$. Similarly as in the proof of Theorem 2 for a subgraph $T^i\in R_D$, if there is a $T^k$ such that ${\mathrm{cr}}_D(T^i,T^k)=0$, then we can obtain a contradiction with the assumption (12) in D by fixing $T^i\cup T^k$. In the following, the edges of all $T^i\in R_D$ must be crossed at least once by each other subgraph $T^k$, and we will discuss two possibilities:

• Assume $1\le r\le ⌊\frac{3n-6}{4}⌋$. By fixing the subgraph $K_5\cup T^i$, we have

  $${\mathrm{cr}}_D(K_5+C_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4(r-1)+6(n-r)+5$$

  $$=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+6n-2r+1\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+6n-2⌊\frac{3n-6}{4}⌋+1$$

  $$\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+7.$$
• Assume $⌊\frac{3n-6}{4}⌋<r\le n$. By fixing the subgraph $K_5\cup T^i\cup T^j$, we have

  $${\mathrm{cr}}_D(K_5+C_n)\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+8(r-2)+7(n-r)+9$$

  $$=4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+7n+r-7\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+7n+⌊\frac{3n-6}{4}⌋+1-7$$

  $$\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+⌊\frac{n}{2}⌋+7.$$

The obtained contradictions in both subcases complete the proof of Theorem 6. □

5. The Crossing Number of ${\mathit{W}}_{\mathit{m}}+{\mathit{S}}_{\mathit{n}}$ and ${\mathit{W}}_{\mathit{m}}+{\mathit{W}}_{\mathit{n}}$

Let $W_n$ and $S_n$ denote the wheel and the star on $n+1$ vertices, respectively. In general, the graphs $W_m+D_n$ and $W_m+C_n$ are isomorphic to $C_m+S_n$ and $C_m+W_n$ for all integers $m,n\ge 3$, respectively. Three conjectures about the crossing numbers of $W_m$ in the join product with $D_n$, $P_n$, and $C_n$ have already been established, for more see [24,25,26]. Now, we can postulate that for all $m,n\ge 3$,

$$\mathrm{cr}(W_m+S_n)=[Z\left(m\right)+m][Z\left(n\right)+n]-mn+n+⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+1,$$

(15)

where $Z\left(m\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋$ denotes Zarankiewicz’s number [17,27].

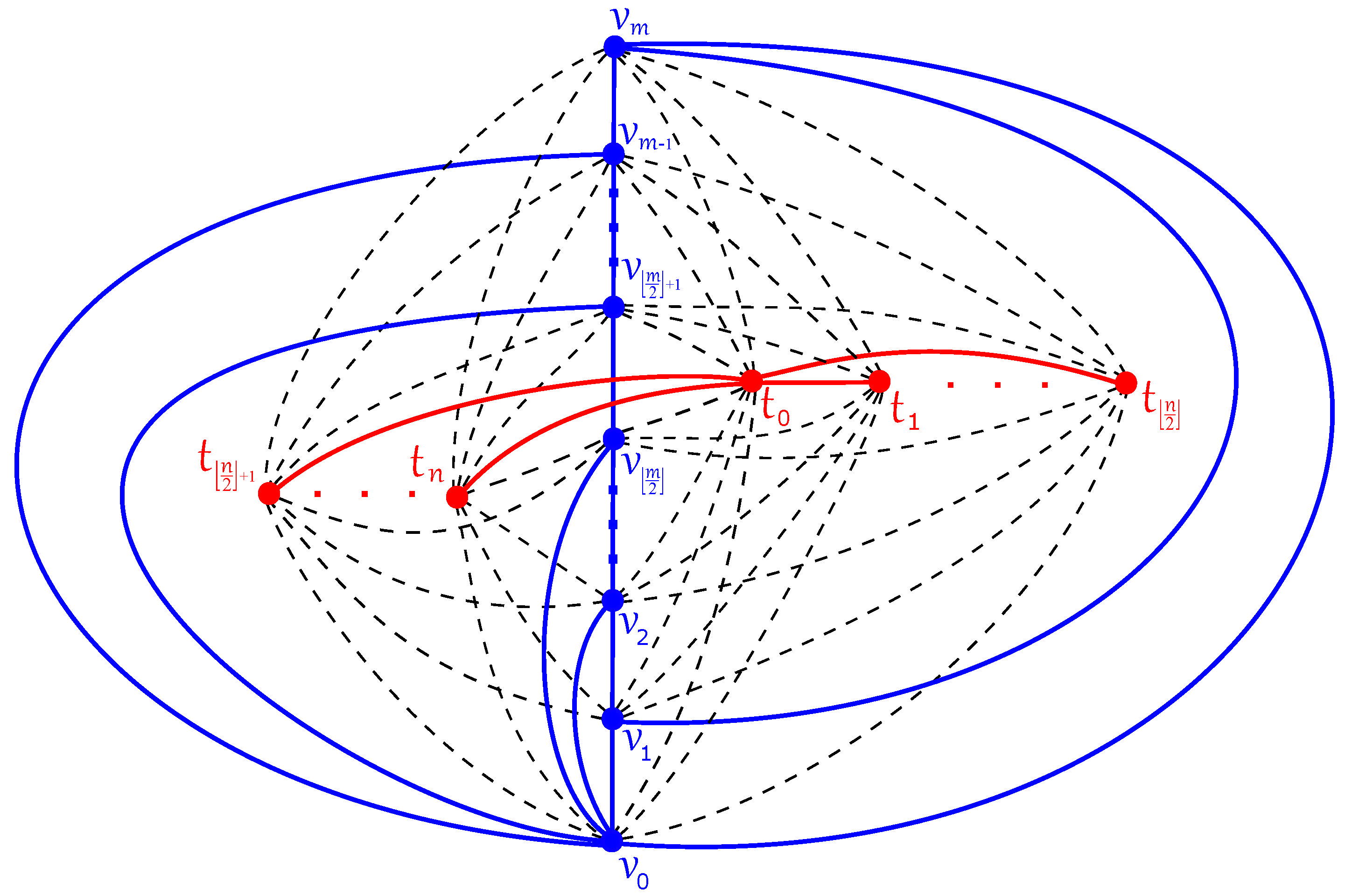
In Figure 3, the edges of $K_{m+1,n}$ cross each other

$$⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋\left(\genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}\right)+⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋\left(\genfrac{}{}{0pt}{}{\lfloor \frac{n}{2}\rfloor }{2}\right)=⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$$

times, each subgraph $T^i$, $i=1,\dots ,⌊\frac{n}{2}⌋$ on the right side crosses the edges of $W_m$ exactly once, and each subgraph $T^i$, $i=⌊\frac{n}{2}⌋+1,\dots ,n$ on the left side crosses the edges of $W_m$ exactly $⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋$ times. The other $⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+⌈\frac{n}{2}⌉+⌈\frac{m}{2}⌉⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+1$ crossings are contained on the edges of the subgraph $T^0$. Thus,

$$⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋+⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌈\frac{n}{2}⌉+⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+$$

$$+⌈\frac{n}{2}⌉+⌈\frac{m}{2}⌉⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+1=⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌈\frac{n}{2}⌉+$$

$$+n+1+⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+⌈\frac{m}{2}⌉⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋=⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+$$

$$+⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋\left(n-⌊\frac{n}{2}⌋\right)+n+1+⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+\left(m-⌊\frac{m}{2}⌋\right)⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋=$$

$$=⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋n-⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋+n+1+$$

$$+⌊\frac{m+1}{2}⌋⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+m⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋-⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋=$$

$$=⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋\left(⌊\frac{m+1}{2}⌋-1\right)+nZ\left(m\right)+⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋\left(⌊\frac{m+1}{2}⌋-⌊\frac{m-1}{2}⌋\right)+$$

$$+n+1+mZ\left(n\right)=Z\left(m\right)Z\left(n\right)+nZ\left(m\right)+⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+n+1+mZ\left(n\right)=$$

$$=[Z\left(m\right)+m][Z\left(n\right)+n]-mn+n+⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+1$$

crossings appear among the edges of the graph $W_m+S_n$ in this drawing.

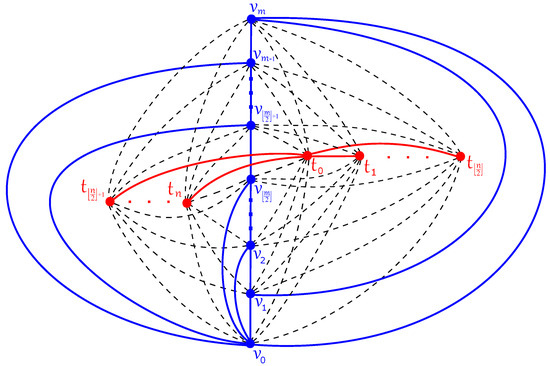
Figure 3. The good drawing of $W_m+S_n$ with $[Z\left(m\right)+m][Z\left(n\right)+n]-mn+n+⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+1$ crossings.

Usually, the star $S_n$ is defined for an n of at least three, but the conjecture (15) can also be generalized for $n=1$ and $n=2$. In this case, the stars $S_1$ and $S_2$ are isomorphic to the paths $P_2$ and $P_3$, respectively. The crossing numbers of the join products of $W_m$ with $P_2$ and $P_3$ were determined by Staš and Valiska [25].

Theorem 7

([25], Theorem 5.1). $\mathrm{cr}(W_m+P_2)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+2$ for $m\ge 3$.

Theorem 8

([25], Theorem 5.2). $\mathrm{cr}(W_m+P_3)=2⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+⌊\frac{m}{2}⌋+3$ for $m\ge 3$.

Using the aforementioned isomorphisms, our conjecture holds for $n=1$ and $n=2$ thanks to Theorems 7 and 8. As the graph $W_m+S_3$ is isomorphic to $K_{1,1,3}+C_m$, Theorem 5 also confirms the validity of this conjecture for $n=3$. Similarly, the graph $W_m+S_4$ is isomorphic to $K_{1,1,4}+C_m$, but only the crossing number of $K_{1,1,4}+D_m$ has been shown by Su and Klešč [28]. On the other hand, Theorem 2 again confirms the validity of our conjecture for $W_3+S_n$ because the graph $K_5+D_n$ is isomorphic to $W_3+S_n$. We add that Wang and Huang [29] also dealt with establishing hypotheses for crossing numbers of connected graphs involving stars, specifically for $S_m+P_n$ and $S_m+C_n$. Our conjecture complements this knowledge for $S_m+W_n$.

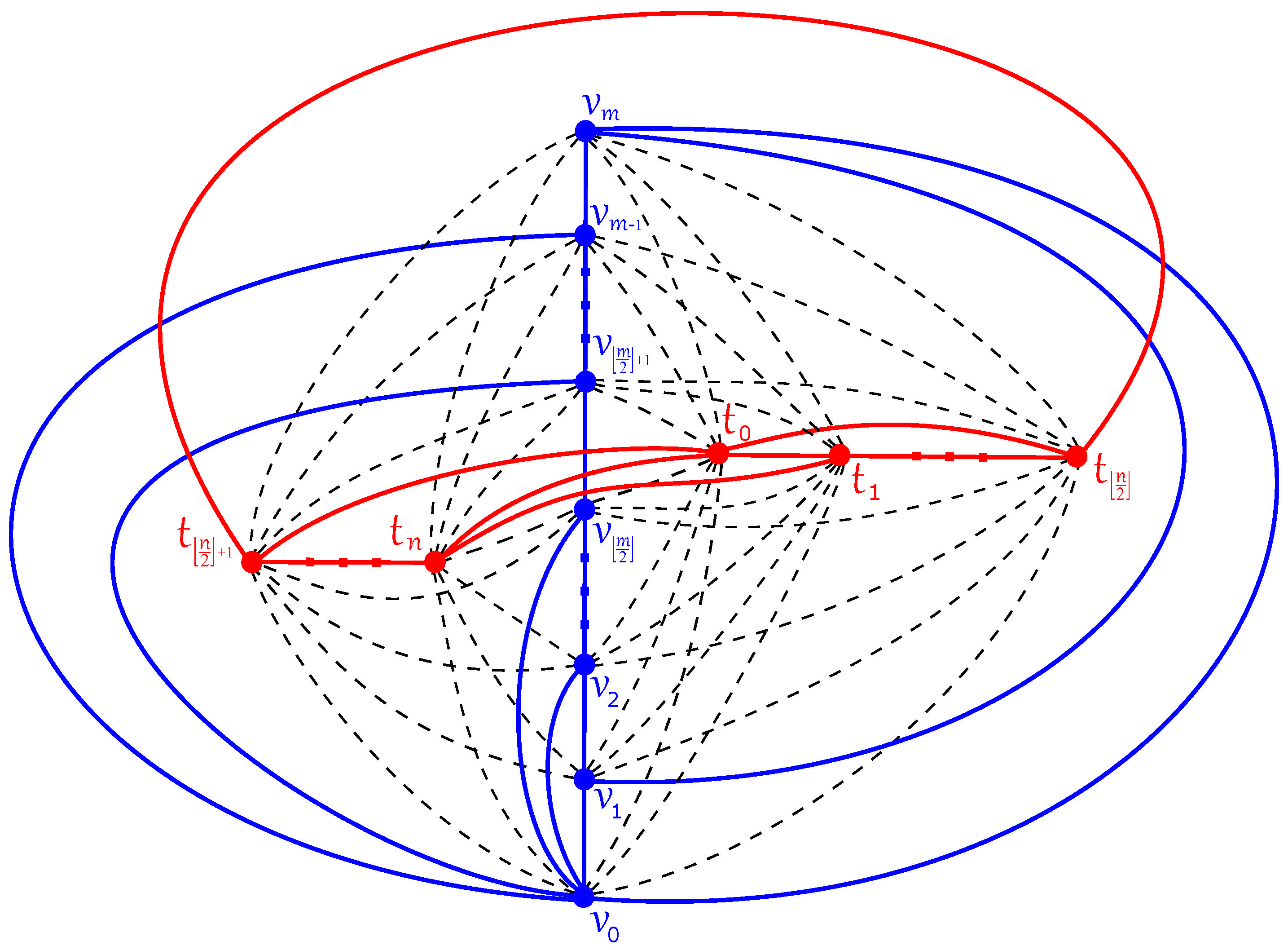
Now, let us turn to postulate that for all $m,n\ge 3$

$$\mathrm{cr}(W_m+W_n)=[Z\left(m\right)+m][Z\left(n\right)+n]-mn+m+n+⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+4.$$

(16)

This makes it possible to add n new edges $t_i{t}_{i+1}$ and $t_n{t}_1$ for $i=1,\dots ,n-1$ into the drawing D of $W_m+S_n$ in Figure 3, which form the rim edge set of $W_n$ with $m+3$ additional crossings. In Figure 4, the edges $t_{\lfloor \frac{n}{2}\rfloor }{t}_{\lfloor \frac{n}{2}\rfloor +1}$ and $t_n{t}_1$ force $2+⌈\frac{m}{2}⌉-1$ and $1+⌊\frac{m}{2}⌋+1$ crossings on edges of $W_m+S_n$, respectively. In such a way, we obtain a good drawing of $W_m+W_n$ with exactly ${\mathrm{cr}}_D(W_m+S_n)+m+3=[Z\left(m\right)+m][Z\left(n\right)+n]-mn+m+n+⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+4$ crossings.

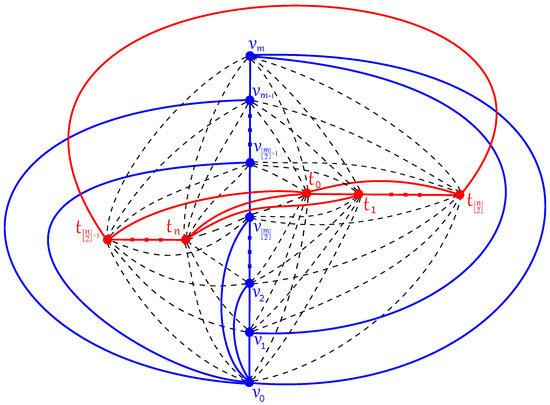
Figure 4. The good drawing of $W_m+W_n$ with $[Z\left(m\right)+m][Z\left(n\right)+n]-mn+m+n+⌊\frac{m}{2}⌋⌊\frac{n}{2}⌋+4$ crossings.

As the graph $W_m+W_3$ is isomorphic to $K_5+C_m$, Theorem 6 confirms the validity of the conjecture (16) for $n=3$. Due to the symmetry, the same holds for $m=3$. The graph $W_m+W_4$ is isomorphic to $K_{1,1,2,2}+C_m$, but at the moment we do not even know the crossing number of the join product of $K_{1,1,2,2}$ with discrete graphs $D_m$, i.e., whether $\mathrm{cr}\left(K_{1,1,2,2,m}\right)\le 6⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+3m+2⌊\frac{m}{2}⌋+1$ holds with equality.

6. Conclusions

In this article, we focused on proving the crossing numbers for three connected graphs that include a complete graph on five vertices $K_5$. We began by explaining why $K_5$ has only five non-isomorphic drawings. Then, we used a similar procedure, involving the existence of different separating cycles $C_3$, the concept of rotation, and the known crossing numbers of related graphs, to prove the crossing numbers $\mathrm{cr}(K_5+D_n)$, $\mathrm{cr}(K_5+P_n)$, and $\mathrm{cr}(K_5+C_n)$. With these results, we have resolved all open problems concerning connected graphs on five vertices because the last hypotheses regarding $\mathrm{cr}(K_5\setminus e+P_n)$ and $\mathrm{cr}(K_5\setminus e+C_n)$ were just recently proven in [30]. Regarding disconnected graphs on five vertices, there is only one graph left for which the crossing numbers in combination with $D_n$, $P_n$, and $C_n$ are not exactly proven, namely the graph $2K_1\cup K_3$. Since we obtain this graph by removing one edge from the graph $K_2\cup K_3$, it is assumed that their crossing numbers in the respective join products will be the same. However, precise proof represents a challenge. If it is mastered, all graphs on five vertices in combination with discrete graphs, paths, and cycles will have exactly known crossing numbers, similar to the case of all graphs on four vertices [31,32].

Additionally, we proposed new hypotheses for $\mathrm{cr}(W_m+S_n)$ and $\mathrm{cr}(W_m+W_n)$, which we verified for the smallest possible values, $m=3$ and $n=3$, due to their isomorphisms with $K_5+D_n$ and $K_5+C_n$, respectively. Figure 3 and Figure 4 provide upper bounds for these conjectures for all $m,n\ge 3$. However, the lower bounds still need to be proven, presenting an interesting topic for future research in this area.