Abstract
A new form of the mathematical expression for the co-moving volume element of a flat universe with cosmological constant, cold matter, and stiff matter is presented. It is used to determine the constraints from the Planck measurements of the Hubble parameter on the amount of stiff matter in the universe. These constraints are used to investigate whether the presence of stiff matter can solve the Hubble tension. It is found that the Planck measurements lead to an upper bound on the present value of the density parameter of stiff matter , and that this is too small to solve the Hubble tension. Report. The main objective of this article is to introduce a novel mathematical expression for the co-moving volume element in a flat universe that includes a cosmological constant, cold matter, and stiff matter. This expression is utilized to derive constraints on the amount of stiff matter in the universe based on the Planck measurements of the Hubble parameter. These constraints are then examined to assess whether stiff matter could potentially resolve the Hubble tension. The findings indicate that the Planck measurements impose an upper limit on the current value of the density parameter of stiff matter, , which is insufficient to resolve the Hubble tension.
Keywords:
Hubble parameter; stiff matter; cosmology; co-moving volume element; Planck measurements; Hubble tension MSC:
83-08; 83B05
1. Introduction
Recently, there has been some focus on universe models with relativistically stiff matter, i.e., matter in which the velocity of sound is equal to the velocity of light in empty space. Such stiff matter obeys an equation of state , where p is the density and the energy density.
In 1962, Zel’dovich [1] considered interactions of baryons through a vector field with the intention of deducing the equation of the state of a fluid dominated by particles participating in such interactions. He showed (both by considering the interaction of pairs of baryons and using the stress tensor of the field) how, in this case, the equation of state is realized.
Ten years later, he proposed the existence of a very early era in the universe dominated by a fluid composed of cold baryons acting gravitationally like stiff matter [2]. He showed that during the expansion in a universe model with scale factor , normalized with a present value , the density of stiff matter decreases as , where V is the co-moving volume . Hence, if stiff matter exists, the density of stiff matter may have been very large in the early universe when the co-moving volume was very small. Thus, there may have existed an early era dominated by stiff matter, even if its present density is negligible.
In 1990, M. Kamionkowski and M. S. Turner [3] studied how the relic abundances of dark-matter particles changed in the early universe with stiff matter. M. Joyce [4] investigated how the production of baryon-asymmetry is affected by the inclusion of stiff matter in a model of the early universe.
As noted by G. Oliveira-Neto and co-workers [5] a stiff fluid can also be described by a massless free scalar field, and this has been utilized in studies of the early universe.
Universe models from an early time era dominated by stiff matter have been investigated from the point of view of modified gravity by S. D. Odintsov and V.K. Oikonomou [6]. They constructed a model for the inflationary and stiff era, with the latter commencing after the end of the inflationary era. Furthermore, they assumed that baryogenesis occurred during the stiff era and calculated the baryon-to-entropy ratio, which constrains the theory of gravity.
S. Dutta and R. J. Scherrer [7] have used the influence of stiff matter on cosmic nucleosynthesis to constrain the amount of stiff matter in the universe. They found that current estimates of primordial helium-abundance give the constraint on a stiff fluid energy density ρS10/ρR10 < 30, where ρS10 and ρR10 are the stiff fluid energy density and density of radiation and relativistic particles, respectively, at = 10 MeV = 1.2·1011 K, which was the temperature of the cosmic plasma around tE = 10 s after the Big Bang, at the beginning of the cosmic nucleosynthesis. This corresponds to an extremely small present ( years) density of the stiff matter. Using that and , we obtain . Since the temperature, T, of the radiation varies inversely with the scale factor we have . The temperature was given in terms of the photon energy by Dutta and Scherrer. Expressed in this way, the present temperature of the CMB-radiation is eV, giving . Dividing by the present critical density, i.e., by the total density of the contents of a flat universe, this may be written in terms of the density parameters, . Since , this means that the present value of the density parameter of the stiff matter is .
Furthermore, Dutta and Scherrer [7] mentioned four classes of universe models with stiff matter that have been discussed during the last 20 years:
- (a)
- Kination: A “kination field” is a scalar field whose energy density is dominated by kinetic energy. A period dominated by a kination fluid can follow a period of inflation. This was first studied in the context of electroweak baryogenesis [4]. Its impact on reheating and the freeze-out of dark-matter particles was studied by Kamionkowski and Turner [3].
- (b)
- Interacting dark matter: For models with a warm self-interacting dark-matter component, the elastic self-interactions between the dark-matter particles can be characterized by the exchange of vector mesons via minimal coupling. For these models, the self-interaction energy can be shown to behave like a stiff fluid [8].
- (c)
- Hořava-Lifshitz cosmologies: Cosmological models based on Hořava–Lifshitz gravity have been studied, and observational constraints on such models, including stiff fluid, were considered.
- (d)
- Non-singular cosmological models: Stiff fluids have also been found to show up in non-singular inhomogeneous cosmological models.
Due to the interesting properties of the early era during and before the cosmic nucleosynthesis of universe models, including stiff matter, it is useful to derive supplementary limits on the density of a stiff fluid in the early universe. We shall, therefore, present a new form of the mathematical expression for the co-moving volume of a flat universe, generalizing the ΛCDM-universe to include stiff matter and use it to consider the constraints put on the amount of stiff matter coming from the Planck observations that determined the value of the Hubble constant with high precision, by measuring the temperature fluctuations in the cosmic microwave background radiation 380,000 years after the Big Bang.
2. Universe Models with Stiff Matter, Dust, and Dark Energy
T. K. Mathew, M. B. Ashwathy, and M. Manoj [8] have investigated cosmological models with vanishing cosmological constant dominated by dust and a stiff fluid with a constant bulk viscosity. They found that the viscosity of the stiff matter could induce a late era with accelerated expansion and considered a flat Lemaître–Friedmann–Robertson–Walker universe model. Mathew et al. [8] assumed for illustrating purposes that the present density of the stiff fluid is equal to the critical density, which makes the model very unrealistic. For example, with this universe model, a transition to an accelerated era due to the viscosity of the stiff fluid would not happen in our universe since the stiff matter has nearly vanishing density and hence is totally insignificant for the late evolution of the universe.
P. H. Chavanis [9] presented nice analytical solutions of the Friedmann equations for a universe containing stiff matter and different combinations of dust, Lorentz Invariant Dark Energy (LIVE) with constant density, represented by the cosmological constant, and radiation. He noted that a stiff matter era is present in the cosmological model of Zel’dovich [2], where the primordial universe is assumed to be made of a cold gas of baryons. For different signs of the energy density of the stiff matter and of the dark energy, he obtained singular and non-singular expanding or cyclic universes. He wrote that he had chosen a relatively large value of the density of stiff matter for a better illustration of his results. In this connection, it should be noted that Dutta and Scherrer [7] obtained the constraint from an analysis of cosmic nucleosynthesis.
M. Dariescu and co-workers [10] analyzed a universe model with stiff, non-viscous matter, dust, and a non-vanishing cosmological constant and investigated the thermodynamic properties of such a universe model. They deduced several nice mathematical expressions for the description of their model.
They also deduced a relationship between the present values of the density parameters of the stiff matter, , and the dust, , by deducing an expression for the age of the universe in a flat universe model with LIVE (Lorentz Invariant Vacuum Energy), dust, and stiff matter. Please note that LIVE has a constant density during the expansion, which is represented by the cosmological constant. The authors inserted the age obtained from the standard ΛCDM universe model, in combination with measurements of the Hubble constant, and obtained the relationship shown in Equation (1) and Figure 1,
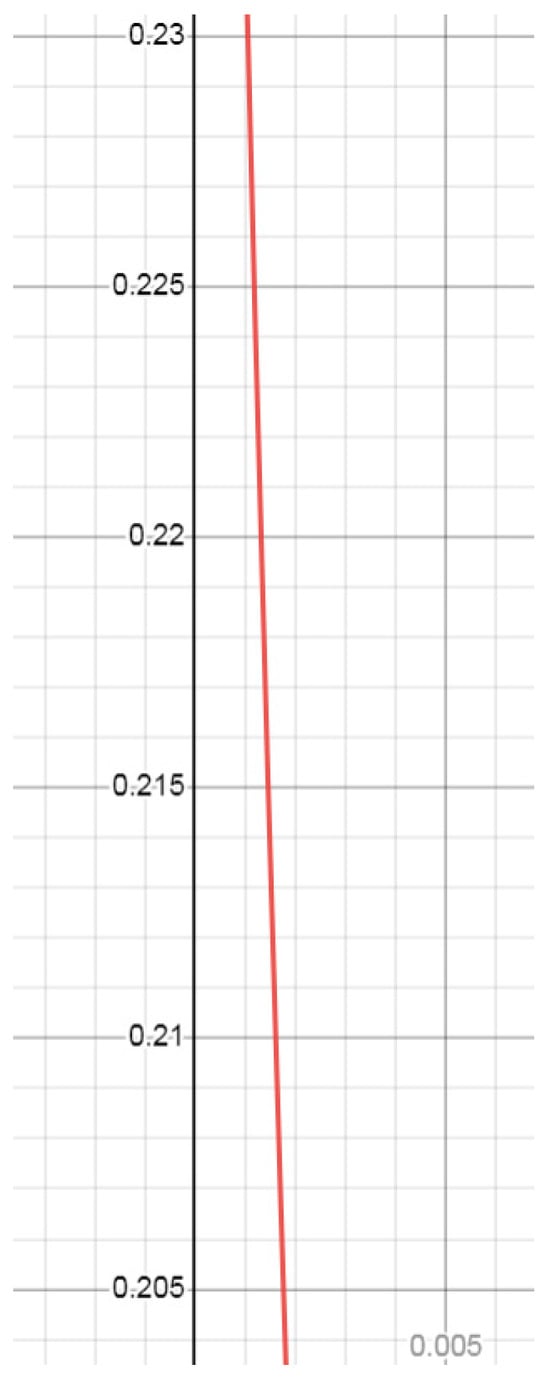
Figure 1.
Relationship between the density parameter, , of stiff matter (horizontal axis) and the density parameter, , of dust plus dark matter (vertical axis) in the universe model of Dariescu et al. [10]. The graph shows that for which was an example mentioned in ref. [9]. Prolonging the graph upwards one finds that to have the density parameter of the stiff matter must be as small as . Furthermore, for , which are the values favored by the constraints of Dutta and Scherrer [7].
In the figure we have chosen to show the part of the curve close to the example mentioned in ref. [10], , . However, the physically relevant part of the curve is far upwards for the part of the curve shown in Figure 1, near , .
3. The Co-Moving Volume of a Flat Universe with Stiff Matter, Dust, and LIVE
We shall here deduce a new form of the mathematical expression for the co-moving volume of a flat universe with stiff matter, dust and LIVE. Since this universe model generalizes the ΛCDM-universe by including stiff matter, it will be called the SΛCDM-universe. Fortunately, it turns out that the co-moving volume can be written in a form such that the contributions from LIVE and cold matter are separated from the contribution of stiff matter. This is useful for (a) investigating whether stiff matter can solve the Hubble tension and (b) restricting the density of the stiff matter by means of the Planck measurements of the Hubble parameter at the point of time = 380,000 years when the universe became transparent for the CMB-radiation.
The line element of the flat Lemaître–Friedmann–Robertson–Walker universe model has the form
For such a universe containing stiff matter, dust, and LIVE, and with the standard normalization of the scale factor, there represents the present age of the universe, the expression of the Hubble parameter takes the form
where we write for and for , i.e., for the present value of the Hubble parameter in the SΛCDM-universe—the Hubble constant, and is the present value of the density parameter of LIVE. Hence, the Friedmann equation can be written as
For this may be written
Introducing a new variable
Equation (5) takes the form
Integrationgives
Defining the dimensionless cosmic time
and using that , Equation (9) leads to the following expression for the co-moving volume
where
It may be noted that with the Dutta–Sherrer restriction, the constant has a value . Using the equality sign for together with and gives the values of the constants, . Furthermore, the dimensionless cosmic time can be written , where years. Hence, at the present time . The cosmological constant is , where (including the velocity of light just here) is Einstein’s gravitational constant. Equation (11) shows that for , i.e., far in the future, this universe goes into an era with eternal exponential expansion. Using that
and , Equations (10) and (11) lead to
This form of the expression for the co-moving volume of a flat universe with LIVE, dust and stiff matter is new. It separates the contributions of LIVE and dust from that of the stiff matter in two terms. The first term is the expression for the co-moving volume in the universe model. Hence, the expression (12) shows how the present universe model generalizes the model by including stiff matter.
In the following, we shall need the derivative of the co-moving volume,
Calculating the Hubble parameter either from , or by inserting the expression (12) into the right-hand expression of Equation (3) and using that
one finds
This can be written as
which expresses the Hubble parameter at an arbitrary point of time in terms of the Hubble constant and the present values of the density parameters. The corresponding formula for the Hubble parameter in the universe is the first term
4. Evolution of the SΛCDM-Universe
The deceleration parameter is defined by
Inserting the expression (10) and its derivatives gives
This may be written in factorized form as
There is a transition from decelerated to accelerated expansion when . To decide whether this happens at a time determined by or we consider the special case when the model reduces to the standard universe model. Then and , also and . In this case, the expression for the deceleration parameter reduces to
and the transition from decelerated to accelerated expansion happens at a point in time given by
corresponding to . Hence, for the model with stiff matter, this transition happens at a point in time given by
Equation (22) gives years. Since we can with good accuracy linearize the expression for , which leads to . Since is extremely small, the stiff matter does not have a noticeable effect on the transition time from deceleration to acceleration. The late time behavior of the universe model, including stiff matter, is very similar to that of the ΛCDM-universe, with decelerated expansion before years and accelerated expansion afterward.
The age of the ΛCDM-universe is given by inserting in Equation (15), giving
where we have used that . The first term gives the age of the ΛCDM-universe, which may be written
A series expansion of the expression (22) to first order in gives
It follows from Equations (25) and (26) that to 1. order in the contribution to the age of the universe from the stiff matter is
Neglecting the last term in the denominator and using the approximation, , valid for we have good accuracy
Inserting the values and years gives years. Hence the stiff matter gives a very small contribution to the age of the universe.
We shall now find the evolution with time of the density parameters of the dust and the stiff matter. The critical density at an arbitrary point in time is
Using the expressions (12), (29) and that the density of the dust decreases inversely proportional to the co-moving volume, , we find that the density parameter of the dust varies as
The density parameter of the stiff matter is
Hence, the point of time when the densities of the stiff matter and the dust were equal is given by
The solution of this equation is
Since we have with good accuracy
Compared to Equation (28) we obtain
which gives years. Before this time, the density of the stiff matter was greater than that of the dust. The cosmic nucleosynthesis lasted for about 15 minutes. Hence if the universe contains stiff matter with a present density parameter , then the stiff matter dominated over cold matter at the time of the cosmic nucleosynthesis. However, at the time of cosmic nucleosynthesis, the density of the cosmic background radiation was much larger than that of the dust. So, we should rather compare the densities of stiff matter and radiation at the point of time tE = 10 s after the Big Bang. The ratio of the densities of stiff matter and radiation at this point in time was
The point of time s corresponds to . Hence, at this point in time, the expression (12) for the co-moving volume can, with good accuracy, be approximated by
With , it follows from Equation (31) that at this time, the term representing stiff matter dominates over the term representing cold matter. Hence, we have, with good accuracy
which gives . Inserting this into Equation (35) and using that gives . Hence, the density of stiff matter was less than the radiation energy density during the period of cosmic nucleosynthesis.
5. Application to the Hubble Tension
The value of the Hubble constant, as determined from measurements of the temperature fluctuations in the microwave background radiation by the Planck team, is H0 = (67.4 ± 0.5) km s−1 Mpc−1 = 1/1.45·1010 years.
We shall now use the expression (16) for the Hubble parameter to investigate whether the expansion isotropy is large enough to solve the Hubble tension. We define the difference between the Hubble constant in a universe with and without stiff matter as . To solve the Hubble tension, the present value of must be positive and at least as large as the difference between the late time and early time measurements of the Hubble constant, (km/s)Mpc−1.
The method takes as a point of departure that the value of the Hubble parameter determined from the temperature fluctuations at 380,000 years, i.e., at , is one and the same whether the universe is assumed to contain stiff matter or not. It is a model-independent quantity determined directly from observations. Hence, putting in Equations (15) and (16), we obtain
This is the relationship between the Hubble constant in the universe with stiff matter and the -universe as determined from the Planck measurements. Thus, the difference between the Hubble constant in a universe with stiff matter and the universe can be expressed (exactly) as,
which is positive. Hence, the Hubble constant is larger with stiff matter than without. This goes in the right direction since the point of departure for this calculation is the value of the Hubble constant as determined by the Planck measurements, and this value is lower than the late universe measurements.
Here , and . This means that the expression for can with good accuracy be approximated by
This is too small to solve the Hubble tension.
6. Constraining Stiff Matter from the Planck Determination of the Hubble Parameter
Since the contribution of the stiff matter to the value of the Hubble parameter at the point of time can, according to Equation (16), be approximated by
Hence,
The Planck measurements determined the Hubble constant with around 1% accuracy. I will therefore use . Inserting , and then gives . This agrees with the Dutta–Scherrer restriction.
7. Conclusions
The research presented here is in the tradition of investigating consequences of the theory of relativity by means of exact and physically interesting solutions of Einstein’s field equations with nice mathematical properties. Such solutions are expected to tell us something about the properties of our universe.
In 1962 and 1972, Zel’dovich published two papers [1,2], where he showed that there may have existed an early era in the history of the universe where the evolution of the cosmic expansion was dominated by a maximally stiff fluid. He deduced the equation of state of this fluid and showed that its density was inversely proportional to the square of the co-moving volume. So, if it exists, it had a large density in the early universe.
Dutta and Sherrer [8] investigated the influence of stiff matter on cosmic nucleosynthesis. From current estimates of the primordial helium abundance, they deduced that the stiff fluid energy density at the beginning of the cosmic nucleosynthesis must have obeyed ρS10/ρR10 < 30 corresponding to a present value of the density parameter .
By means of a new form of the expression for the co-moving volume of a flat universe with LIVE, cold matter, and stiff matter, I have here shown that the Planck measurements lead to a similar result, , and that this upper bound is so small that the eventual presence of stiff matter in the universe does not have any consequence for the Hubble tension.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
I would like to thank the referee for useful suggestions that contributed to improvements to the paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Zel’dovich, Y.B. The Equation of State at Ultrahigh densities and its relativistic limitations. Sov. Phys. JETP 1962, 14, 1143. [Google Scholar]
- Zel’dovich, Y.B. A Hypothesis Unifying the Structure and the Entropy of the Universe. Mon. Not. R. Astron. Soc. 1972, 160, 1P–3P. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Turner, M.S. Thermal relics: Do we know their abundances? Phys. Rev. D 1990, 42, 3310. [Google Scholar] [CrossRef] [PubMed]
- Joyce, M. Electroweak Baryogenesis and the Expansion Rate of the Universe. Phys. Rev. D 1997, 55, 1875. [Google Scholar] [CrossRef]
- Oliveira-Neto, G.; Monerat, G.A.; Silva, E.V.C.; Neves, C.; Filho, L.G.F. An Early Universe Model with Stiff Matter and a Cosmological Constant. Int. J. Mod. Phys. 2011, 3, 254–265. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. The Early-time Cosmology with Stiff Era from Modified Gravity. Phys. Rev. D 2017, 96, 104059. [Google Scholar] [CrossRef]
- Dutta, S.; Scherrer, R.J. Big Bang nucleosynthesis with a stiff fluid. Phys. Rev. D 2010, 82, 083501. [Google Scholar] [CrossRef]
- Mathew, T.K.; Ashwathy, M.B.; Manoj, M. Cosmology and thermodynamics of FRW universe with bulk viscosity. Eur. Phys. J. C 2014, 74, 3188. [Google Scholar] [CrossRef]
- Chavanis, P.H. Cosmology with a stiff matter era. Phys. Rev. D 2015, 92, 103004. [Google Scholar] [CrossRef]
- Dariescu, M.; Mihu, D.; Dariescu, C. Spatially-flat Robertson-Walker models with combined ΛCDM and stiff matter sources and corresponding thermodynamics. Rom. J. Phys. 2017, 62, 101. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).