An Extension of Left Radau Type Inequalities to Fractal Spaces and Applications

Abstract

In this study, we introduce a novel local fractional integral identity related to the Gaussian two-point left Radau rule. Based on this identity, we establish some new fractal inequalities for functions whose first-order local fractional derivatives are generalized convex and concave. The obtained results not only represent an extension of certain previously established findings to fractal sets but also a refinement of these when the fractal dimension $\mu$ is equal to one. Finally, to support our findings, we present a practical application to demonstrate the effectiveness of our results.

1. Introduction

Convexity, a central concept in mathematical analysis, holds pivotal significance in both pure and applied mathematics. A function $ð:I\to \mathbb{R}$ defined on an interval I is considered convex if, for any ${\varkappa }_1,{\varkappa }_2\in I$ and $t\in [0,1]$, the following condition holds [1]:

$$ð(t{\varkappa }_1+(1-t){\varkappa }_2)\le tð\left({\varkappa }_1\right)+(1-t)ð\left({\varkappa }_2\right).$$

This geometric and analytical property offers a profound understanding of the behavior of mathematical functions; see [2].

Convex functions play a fundamental role in various mathematical disciplines, with far-reaching implications in optimization, economics, and approximation theory. In the realm of approximation, the study of convexity becomes particularly compelling. It provides a robust framework for understanding the approximation quality of integrals, and one of the key results in this context is the Hermite–Hadamard inequality which can be expressed as follows: for a convex function $ð:I\to \mathbb{R}$ defined on a closed interval $[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2]$, we have:

$$ð\left({\displaystyle \frac{{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{2}}\right)\le {\displaystyle \frac{1}{{\mathsf{\ell }}_2-{\mathsf{\ell }}_1}}{\int }_{{\mathsf{\ell }}_1}^{{\mathsf{\ell }}_2}ð\left(\varkappa \right)d\varkappa \le {\displaystyle \frac{ð\left({\mathsf{\ell }}_1\right)+ð\left({\mathsf{\ell }}_2\right)}{2}}.$$

This inequality establishes a profound relationship between the average of a real-valued function over an interval and its endpoint values. It serves as a powerful tool in analyzing the behavior of convex functions and has wide-ranging applications in diverse mathematical and scientific fields.

Several results regarding error estimates of Newton–Cotes formulas via convexity have been established; see [3,4,5,6,7] and the references therein. However, the literature suffers from a significant gap concerning error estimates for Gauss quadrature rules, primarily due to their non-symmetric nature, which complicates the task. Among the limited existing results, the authors in [8] have established the following result concerning the two-point left Radau rule.

Theorem 1.

Let $ð:\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]\to \mathbb{R}$ be a differentiable function on $\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$ such that $ð\in L^1\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$. If $\left|{ð}^{\prime }\right|$ is convex on $\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$, then

$$\left|\frac{ð\left({\mathsf{\ell }}_1\right)+3ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)}{4}-\frac{1}{{\mathsf{\ell }}_2-{\mathsf{\ell }}_1}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}ð\left(\varkappa \right)d\varkappa \right|\le \frac{25\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}{72}\left(\frac{157\left|{ð}^{\prime }\left({\mathsf{\ell }}_1\right)\right|+379\left|{ð}^{\prime }\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|+64\left|{ð}^{\prime }\left({\mathsf{\ell }}_2\right)\right|}{600}\right).$$

A fractal set is a mathematical construct that exhibits self-similarity at various scales. Unlike traditional geometric shapes with integer dimensions (such as squares or circles), fractals often have non-integer or fractional dimensions. The defining characteristic of a fractal is the repetition of similar patterns at different levels of magnification. This property makes fractals particularly fascinating in the realms of mathematics, art, and nature.

The Mandelbrot set [9], Sierpinski triangle [10], and Koch snowflake [11] are well-known examples of fractal sets. Fractals find applications in diverse fields, including computer graphics, image compression, and the modeling of natural phenomena like coastlines and mountain landscapes.

Local fractional calculus is an extension of classical calculus that deals with derivatives and integrals in the context of functions with a fractal or non-integer dimension. Unlike traditional calculus, which operates on functions with integer dimensions, local fractional calculus allows for the analysis of functions defined on fractal sets [12,13,14].

Yang introduced the concept of generalized convexity applied to fractal sets in [15]. This concept is defined as follows:

Definition 1.

Consider $ð:I\subseteq \mathbb{R}\to {\mathbb{R}}^{\mu }$, where $\mu \in (0,1]$ is the fractal dimension. If for any ${\varkappa }_1,{\varkappa }_2\in I$ and $t\in [0,1]$, the inequality

$$ð\left(t{\varkappa }_1+\left(1-t\right){\varkappa }_2\right)\le t^{\mu }ð\left({\varkappa }_1\right)+{\left(1-t\right)}^{\mu }ð\left({\varkappa }_2\right)$$

holds, then ð is termed generalized convex on I. If the inequality holds in the reverse direction, then ð is termed generalized concave.

Since the inception of this concept, numerous research efforts have aimed to extend classical findings regarding integral inequalities to the realm of fractals. Notably, Xu et al. made a significant contribution by presenting a series of fractal dual Simpson-like inequalities in [16]. Du and Yuan, in [17], conducted a parameterized study where they established several interesting fractal inequalities related to three-point Newton–Cotes formulas. Li et al. focused on four-point formulas and derived some local fractional inequalities using generalized $(s,P)$-convexity in [18]. A more noteworthy study was carried out by Xu et al. in [19], where the authors established a fractal Hermite–Hadamard inequality for generalized $\alpha$-convex functions. They further conducted an extensive investigation, establishing numerous inequalities for different types of one, two, three, and four-point Newton–Cotes rules using the same form of convexity. For additional works on this subject, the readers are referred to [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34].

In this article, we extend the two-point left Radau inequality to the framework of local fractional integrals. To achieve this, we begin by introducing a new local fractional integral identity from which we establish our results. The study is concluded with several applications.

2. Preliminaries

Definition 2

([15]). A non-differentiable function $ð:\mathbb{R}\to {\mathbb{R}}^{\mu }$ is local fractional continuous at ${\varkappa }_0$, if

$$\forall ϵ>0,\exists \delta >0:\left|ð\left(\varkappa \right)-ð\left({\varkappa }_0\right)\right|<{ϵ}^{\mu }$$

holds for $\left|\varkappa -{\varkappa }_0\right|<\delta$. We denote the set of all local fractional continuous functions on $\left({\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right)$ by $C_{\mu }\left({\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right)$.

Definition 3

([15]). The local fractional derivative of $ð\left(\varkappa \right)$ of order μ at $\varkappa ={\varkappa }_0$ is defined as:

$${ð}^{\left(\mu \right)}\left({\varkappa }_0\right)={\left.\frac{d^{\mu }ð\left(\varkappa \right)}{d{\varkappa }^{\mu }}\right|}_{\varkappa ={\varkappa }_0}=\underset{\varkappa \to {\varkappa }_0}{lim}\frac{{\Delta }^{\mu }\left(ð\left(\varkappa \right)-ð\left({\varkappa }_0\right)\right)}{{\left(\varkappa -{\varkappa }_0\right)}^{\mu }},$$

where ${\Delta }^{\mu }\left(ð\left(\varkappa \right)-ð\left({\varkappa }_0\right)\right)\cong \mathsf{\Gamma }\left(\mu +1\right)\left(ð\left(\varkappa \right)-ð\left({\varkappa }_0\right)\right)$.

We denote the set of all local fractional differentiable functions on $\left({\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right)$ by $D_{\mu }\left({\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right)$.

Definition 4

([15]). Let $ð\left(\varkappa \right)\in C_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$. Then, the local fractional integral is defined by,

$${}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)=\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}ð\left(t\right){\left(dt\right)}^{\mu }=\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{\Delta t\to 0}{lim}\stackrel{N-1}{\sum _{j=0}}ð\left({\varkappa }_j\right){\left(\Delta {\varkappa }_j\right)}^{\mu }$$

with $\Delta {\varkappa }_j={\varkappa }_{j+1}-{\varkappa }_j$ and $\Delta t=max\left\{\Delta {\varkappa }_1,\Delta {\varkappa }_2,\dots ,\Delta {\varkappa }_{N-1}\right\}$, where $\left[{\varkappa }_j,{\varkappa }_{j+1}\right],j=0,1,\dots , N-1$ and ${\mathsf{\ell }}_1={\varkappa }_0<{\varkappa }_1<\dots <{\varkappa }_N={\mathsf{\ell }}_2$ is a partition of interval $\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$.

Here, it follows that ${}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)=0$ if ${\mathsf{\ell }}_1={\mathsf{\ell }}_2$ and ${}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)={-}_{{\mathsf{\ell }}_2}{I}_{{\mathsf{\ell }}_1}^{\mu }ð\left(\varkappa \right)$ if ${\mathsf{\ell }}_1<{\mathsf{\ell }}_2$. If for any $\varkappa \in [{\mathsf{\ell }}_1,{\mathsf{\ell }}_2]$, there exists ${}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)$, then we denote it by $ð\left(\varkappa \right)\in I_u^{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$.

Lemma 1

([15]).

1. 

(Local fractional integration is anti-differentiation) Suppose that $ð\left(\varkappa \right)={\hslash }^{\left(\mu \right)}\left(\varkappa \right)\in C_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$; then, we have

$${}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)=\hslash \left({\mathsf{\ell }}_2\right)-\hslash \left({\mathsf{\ell }}_1\right).$$

2. 

(Local fractional integration by parts) Suppose that $ð,\hslash \in D_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$ and ${ð}^{\left(\mu \right)}\left(\varkappa \right),{\hslash }^{\left(\mu \right)}\left(\varkappa \right)\in C_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$; then, we have

$${}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right){\hslash }^{\left(\mu \right)}\left(\varkappa \right)={\left.ð\left(\varkappa \right)\hslash \left(\varkappa \right)\right|}_{{\mathsf{\ell }}_1}^{{\mathsf{\ell }}_2}-{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }{ð}^{\left(\mu \right)}\left(\varkappa \right)\hslash \left(\varkappa \right).$$

Lemma 2

([15]). For $s\in \mathbb{R}$, the following identities hold

$$\begin{array}{cc}\hfill \frac{d^{\mu }{\varkappa }^{s\mu }}{d{\varkappa }^{\mu }}=& \frac{\mathsf{\Gamma }\left(1+s\mu \right)}{\mathsf{\Gamma }\left(1+\left(s-1\right)\mu \right)}{\varkappa }^{\left(s-1\right)\mu },\hfill \\ \hfill \frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}{\varkappa }^{s\mu }{\left(d\varkappa \right)}^{\mu }=& \frac{\mathsf{\Gamma }\left(1+s\mu \right)}{\mathsf{\Gamma }\left(1+\left(s+1\right)\mu \right)}\left({\mathsf{\ell }}_2^{\left(s+1\right)\mu }-{\mathsf{\ell }}_1^{\left(s+1\right)\mu }\right).\hfill \end{array}$$

Lemma 3

(Generalized Hölder’s inequality [35]).

Let $ð,\hslash \in C_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$ and ${\left|ð\left(\varkappa \right)\right|}^p,{\left|\hslash \left(\varkappa \right)\right|}^q$ where $p,q>1$ with ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$, be both integrable under the frame of the fractal spaces; then, we have

$$\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}\left|ð\left(\varkappa \right)\hslash \left(\varkappa \right)\right|{\left(d\varkappa \right)}^{\mu }\le {\left(\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}{\left|ð\left(\varkappa \right)\right|}^p{\left(d\varkappa \right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}{\left|\hslash \left(\varkappa \right)\right|}^q{\left(d\varkappa \right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}.$$

Lemma 4

(Generalized power mean inequality [35]).

Let $ð,\hslash \in C_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$ and $\left|ð\left(\varkappa \right)\right|,\left|ð\left(\varkappa \right)\right|{\left|\hslash \left(\varkappa \right)\right|}^q$ where $q>1$ be both integrable under the frame of the fractal spaces; then, we have

$$\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}\left|ð\left(\varkappa \right)\hslash \left(\varkappa \right)\right|{\left(d\varkappa \right)}^{\mu }\le {\left(\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}\left|ð\left(\varkappa \right)\right|{\left(d\varkappa \right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}\left|ð\left(\varkappa \right)\right|{\left|\hslash \left(\varkappa \right)\right|}^q{\left(d\varkappa \right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}.$$

Lemma 5

(Improved generalized power mean inequality [36]).

Let $ð,\hslash \in C_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$ and $\left|ð\left(\varkappa \right)\right|,\left|ð\left(\varkappa \right)\right|{\left|\hslash \left(\varkappa \right)\right|}^q$ where $q>1$ be both integrable under the frame of the fractal spaces; then, we have

$$\begin{array}{cc}\hfill & \frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}\left|ð\left(\varkappa \right)\hslash \left(\varkappa \right)\right|{\left(d\varkappa \right)}^{\mu }\hfill \\ \hfill \le & {\left(\frac{1}{{\mathsf{\ell }}_2-{\mathsf{\ell }}_1}\right)}^{\mu }\left({\left(\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}{\left({\mathsf{\ell }}_2-\varkappa \right)}^{\mu }\left|ð\left(\varkappa \right)\right|{\left(d\varkappa \right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.{\left(\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}{\left({\mathsf{\ell }}_2-\varkappa \right)}^{\mu }\left|ð\left(\varkappa \right)\right|{\left|\hslash \left(\varkappa \right)\right|}^q{\left(d\varkappa \right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}{\left(\varkappa -{\mathsf{\ell }}_1\right)}^{\mu }\left|ð\left(\varkappa \right)\right|{\left(d\varkappa \right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\left.{\left(\frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}{\left(\varkappa -{\mathsf{\ell }}_1\right)}^{\mu }\left|ð\left(\varkappa \right)\right|{\left|\hslash \left(\varkappa \right)\right|}^q{\left(d\varkappa \right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

3. Main Results

The following lemma functions as the crucial and principal instrument for establishing the outcomes of our research.

Lemma 6

Let $ð:I\to {\mathbb{R}}^{\mu }$ be a function such that $ð\in D_{\mu }\left(I^{\circ }\right)$, ${\mathsf{\ell }}_1,{\mathsf{\ell }}_2\in I^{\circ }$ with ${\mathsf{\ell }}_1<{\mathsf{\ell }}_2$, and ${ð}^{\left(\mu \right)}\in C_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$, then the following equality holds for $\mu >0$:

$$\begin{array}{cc}\hfill & \frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\hfill \\ \hfill =& \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(t-\frac{3}{4}\right)}^{\mu }{ð}^{\left(\mu \right)}\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right){\left(dt\right)}^{\mu }\right.\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(\frac{1}{4}+t\right)}^{\mu }{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right){\left(dt\right)}^{\mu }\hfill \\ \hfill & +\left.\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(t-1\right)}^{\mu }{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right){\left(dt\right)}^{\mu }\right),\hfill \end{array}$$

where

$${}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)=\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}ð\left(\varkappa \right){\left(d\varkappa \right)}^{\mu }.$$

Proof. 

Let

$$\mathcal{I}={\mathcal{I}}_1+{\mathcal{I}}_2+{\mathcal{I}}_3,$$

(1)

where

$$\begin{array}{cc}\hfill {\mathcal{I}}_1=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(t-\frac{3}{4}\right)}^{\mu }{ð}^{\left(\mu \right)}\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right){\left(dt\right)}^{\mu },\hfill \\ \hfill {\mathcal{I}}_2=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(\frac{1}{4}+t\right)}^{\mu }{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right){\left(dt\right)}^{\mu }\hfill \end{array}$$

and

$${\mathcal{I}}_3=\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(t-1\right)}^{\mu }{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right){\left(dt\right)}^{\mu }.$$

Using Lemma 1, ${\mathcal{I}}_1$ gives

$$\begin{array}{cc}\hfill & {\mathcal{I}}_1={\left.\frac{3^{\mu }}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{\left(t-\frac{3}{4}\right)}^{\mu }ð\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}_0^1\hfill \\ \hfill & -\frac{3^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}\underset{0}{\stackrel{1}{\int }}ð\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right){\left(dt\right)}^{\mu }\hfill \\ \hfill =& \frac{3^{\mu }}{4^{\mu }{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}ð\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)+\frac{9^{\mu }}{4^{\mu }{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}ð\left({\mathsf{\ell }}_1\right)\hfill \\ \hfill & -\frac{9^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{2\mu }\mathsf{\Gamma }\left(\mu +1\right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\displaystyle \frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}}}{\int }}ð\left(\varkappa \right){\left(d\varkappa \right)}^{\mu }.\hfill \end{array}$$

(2)

Similarly, we obtain

$$\begin{array}{cc}\hfill & {\mathcal{I}}_2={\left.\frac{3^{\mu }}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{\left(\frac{1}{4}+t\right)}^{\mu }ð\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}_0^1\hfill \\ \hfill & -\frac{3^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}\underset{0}{\stackrel{1}{\int }}ð\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right){\left(dt\right)}^{\mu }\hfill \\ \hfill =& \frac{{\left(15\right)}^{\mu }}{4^{\mu }{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)-\frac{3^{\mu }}{4^{\mu }{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}ð\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\hfill \\ \hfill & -\frac{9^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{2\mu }\mathsf{\Gamma }\left(\mu +1\right)}\underset{{\displaystyle \frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}}}{\stackrel{{\displaystyle \frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}}}{\int }}ð\left(\varkappa \right){\left(d\varkappa \right)}^{\mu }\hfill \end{array}$$

(3)

and

$$\begin{array}{cc}\hfill {\mathcal{I}}_3=& {\left.\frac{3^{\mu }}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{\left(t-1\right)}^{\mu }ð\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right)\right|}_0^1\hfill \\ \hfill & -\frac{3^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}\underset{0}{\stackrel{1}{\int }}ð\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right){\left(dt\right)}^{\mu }\hfill \\ \hfill =& \frac{3^{\mu }}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)-\frac{9^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{2\mu }\mathsf{\Gamma }\left(\mu +1\right)}\underset{{\displaystyle \frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}}}{\stackrel{{\mathsf{\ell }}_2}{\int }}ð\left(\varkappa \right){\left(d\varkappa \right)}^{\mu }.\hfill \end{array}$$

(4)

Using (2)–(4) in (1), then multiplying the resulting equality by $\frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}$, we obtain the desired result. □

Theorem 2.

Assume that all the assumptions of Lemma 6 are satisfied. If $\left|{ð}^{\left(\mu \right)}\right|$ is generalized convex on $\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left(\left({\left(\frac{31}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-{\left(\frac{7}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|\right.\hfill \\ \hfill & +\left({\left(\frac{43}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-{\left(\frac{27}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|\hfill \\ \hfill & +\left(2^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{1}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|\hfill \\ \hfill & +\left.\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|\right).\hfill \end{array}$$

Proof. 

From Lemma 6 and the properties of the modulus, we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|{\left(dt\right)}^{\mu }\right.\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|{\left(dt\right)}^{\mu }\hfill \\ \hfill & +\left.\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right)\right|{\left(dt\right)}^{\mu }\right).\hfill \end{array}$$

Using the generalized convexity of $\left|{ð}^{\left(\mu \right)}\right|$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }\left({\left(1-t\right)}^{\mu }\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|+t^{\mu }\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|\right){\left(dt\right)}^{\mu }\right.\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }\left({\left(1-t\right)}^{\mu }\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|+t^{\mu }\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|\right){\left(dt\right)}^{\mu }\hfill \\ \hfill & +\left.\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }\left({\left(1-t\right)}^{\mu }\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|+t^{\mu }\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|\right){\left(dt\right)}^{\mu }\right)\hfill \\ \hfill =& \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left(\left({\left(\frac{31}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-{\left(\frac{7}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|\right.\hfill \\ \hfill & +\left({\left(\frac{43}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-{\left(\frac{27}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|\hfill \\ \hfill & +\left(2^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{1}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|\hfill \\ \hfill & +\left.\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|\right),\hfill \end{array}$$

where we have used

$$\begin{array}{cc}\hfill & \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }{\left(1-t\right)}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{31}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-{\left(\frac{7}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }{t}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{5}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{3}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }{\left(1-t\right)}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{5}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }{t}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{1}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }{\left(1-t\right)}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\hfill \end{array}$$

(9)

and

$$\begin{array}{cc}\hfill & \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }{t}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}.\hfill \end{array}$$

(10)

Thus, the proof is completed. □

Corollary 1.

In Theorem 2, if $\mu \to 1$, we obtain the following result for the Riemann integral.

$$\begin{array}{cc}\hfill & \left|\frac{1}{4}\left(ð\left({\mathsf{\ell }}_1\right)+3ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{1}{{\mathsf{\ell }}_2-{\mathsf{\ell }}_1}\underset{0}{\stackrel{1}{\int }}ð\left(\varkappa \right)d\varkappa \right|\hfill \\ \hfill \le & \frac{{\mathsf{\ell }}_2-{\mathsf{\ell }}_1}{9}\left(\frac{41\left|{ð}^{\prime }\left({\mathsf{\ell }}_1\right)\right|+75\left|{ð}^{\prime }\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|+152\left|{ð}^{\prime }\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|+32\left|{ð}^{\prime }\left({\mathsf{\ell }}_2\right)\right|}{192}\right).\hfill \end{array}$$

Remark 1.

Corollary 1 constitutes a refinement of the result established in Corollary 1 from [8], as the latter can be inferred by leveraging the convexity of $\left|{ð}^{\prime }\right|$ with respect to the term $\left|{ð}^{\prime }\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|$, specifically, $\left|{ð}^{\prime }\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|\le \frac{1}{2}\left(\left|{ð}^{\prime }\left({\mathsf{\ell }}_1\right)\right|+\left|{ð}^{\prime }\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|\right)$.

Corollary 2.

In Theorem 2, using the generalized convexity of $\left|{ð}^{\left(\mu \right)}\right|$ with respect to the terms $\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|$ and $\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|$, i.e., $\left|{ð}^{\left(\mu \right)}\left(\frac{a{\mathsf{\ell }}_1+b{\mathsf{\ell }}_2}{a+b}\right)\right|\le \frac{a^{\mu }}{{(a+b)}^{\mu }}\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|+\frac{b^{\mu }}{{(a+b)}^{\mu }}\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|$, we obtain the following inequality, which involves only the endpoints.

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{{27}^{\mu }}\left(\left({\left(\frac{103}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{73}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|\right.\hfill \\ \hfill & +\left.\left({\left(\frac{155}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}+{\left(\frac{5}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|\right).\hfill \end{array}$$

Now, to validate the accuracy of the result obtained in Theorem 2, we provide a numerical example along with a graphical representation to support the results.

Example 1.

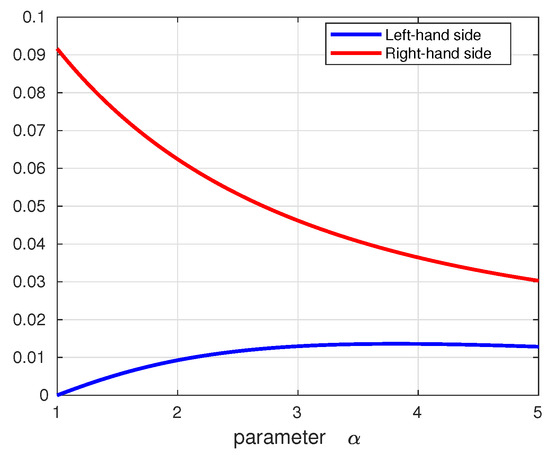
Consider the function $ð:[0,1]\to {\mathbb{R}}^{\mu }$ defined by $ð\left(\varkappa \right)={\displaystyle \frac{\mathsf{\Gamma }\left(1+\alpha \mu \right)}{\mathsf{\Gamma }\left(1+(\alpha +1)\mu \right)}}{\varkappa }^{(\alpha +1)\mu }$ with $\alpha \ge 1$. This function satisfies the conditions of our study, as its local fractional derivative, given by $\left|{ð}^{\left(\mu \right)}\left(\varkappa \right)\right|={\varkappa }^{\alpha \mu }$, is convex on the interval $[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2]=[0,1]$.

Let us note that for the function considered, Corollary 1 gives:

$$\left|\frac{1}{\alpha +1}\left(\frac{3}{4}{\left(\frac{2}{3}\right)}^{\alpha +1}-\frac{1}{\alpha +2}\right)\right|\le \frac{1}{1728}\left[75{\left(\frac{1}{3}\right)}^{\alpha }+152{\left(\frac{2}{3}\right)}^{\alpha }+32\right].$$

The result above is graphically represented in Figure 1, where the red curve corresponds to the left-hand side, and the blue curve represents the right-hand side.

Figure 1. Graphical representation of Corollary 1.

The representation shown in Figure 1 confirms the accuracy and precision of the result obtained in Theorem 2.

Theorem 3.

Assume that all the assumptions of Lemma 6 are satisfied. If ${\left|{ð}^{\left(\mu \right)}\right|}^q$ is generalized convex, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}{\left(\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times \left({\left(\frac{1+3^{p+1}}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}{\left({\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left(\frac{5^{p+1}-1}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}{\left({\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left({\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right),\hfill \end{array}$$

where $p,q>1$ with ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$.

Proof. 

From Lemma 6 and the properties of the modulus along with the generalized Hölder inequality, we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}\right.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}\left.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

Using the generalized convexity of ${\left|{ð}^{\left(\mu \right)}\right|}^q$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}\right.\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}\hfill \\ \hfill & \times \left.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill =& \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}{\left(\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times \left({\left(\frac{1+3^{p+1}}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}{\left({\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left(\frac{5^{p+1}-1}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}{\left({\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left({\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right),\hfill \end{array}$$

where we have used

$$\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{p\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}{\left({\left(\frac{3}{4}\right)}^{p+1}+{\left(\frac{1}{4}\right)}^{p+1}\right)}^{\mu },$$

(11)

$$\begin{array}{c}\hfill \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{p\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}{\left({\left(\frac{5}{4}\right)}^{p+1}-{\left(\frac{1}{4}\right)}^{p+1}\right)}^{\mu }\end{array}$$

(12)

and

$$\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{p\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}.$$

(13)

The proof is completed. □

Corollary 3.

In Theorem 3, using the generalized convexity of ${\left|{ð}^{\left(\mu \right)}\right|}^q$ with respect to the terms ${\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q$ and ${\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}{\left(\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{2^{\mu }\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)}^{{\displaystyle \frac{1}{q}}}\left({\left(\frac{1+3^{p+1}}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}{\left(\frac{5^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q}{6^{\mu }}\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left(\frac{5^{p+1}-1}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}{\left(\frac{{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q}{2^{\mu }}\right)}^{{\displaystyle \frac{1}{q}}}+\left.{\left(\frac{{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+2^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q}{3^{\mu }}\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

Theorem 4.

Assume that all the assumptions of Lemma 6 are satisfied. If ${\left|{ð}^{\left(\mu \right)}\right|}^q$ is generalized convex for $q>1$, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}{\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)}^{1-{\displaystyle \frac{1}{q}}}\left({\left(\frac{5}{8}\right)}^{\mu \left(1-{\displaystyle \frac{1}{q}}\right)}\left(\left({\left(\frac{31}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-{\left(\frac{7}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q\right.\right.\hfill \\ \hfill & +{\left.\left({\left(\frac{3}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}+{\left(\frac{5}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{3}{2}\right)}^{\mu \left(1-{\displaystyle \frac{1}{q}}\right)}\left(\left({\left(\frac{5}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right.\hfill \\ \hfill & +{\left.\left(\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{1}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left(\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

Proof. 

From Lemma 6 and the properties of the modulus along with the generalized power mean inequality, we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\left.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

Using the generalized convexity of ${\left|{ð}^{\left(\mu \right)}\right|}^q$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times \left.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill =& \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}{\left(\frac{5}{8}\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \times {\left(\frac{{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }{\left(1-t\right)}^{\mu }{\left(dt\right)}^{\mu }+\frac{{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{\mu }{t}^{\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{3}{2}\right)}^{\mu \left(1-{\displaystyle \frac{1}{q}}\right)}{\left(\frac{{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }{\left(1-t\right)}^{\mu }{\left(dt\right)}^{\mu }+\frac{{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{\mu }{t}^{\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)}^{1-{\displaystyle \frac{1}{q}}}\left.{\left(\frac{{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }{\left(1-t\right)}^{\mu }{\left(dt\right)}^{\mu }+\frac{{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{\mu }{t}^{\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill =& \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}{\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)}^{1-{\displaystyle \frac{1}{q}}}\left({\left(\frac{5}{8}\right)}^{\mu \left(1-{\displaystyle \frac{1}{q}}\right)}\left(\left({\left(\frac{31}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-{\left(\frac{7}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q\right.\right.\hfill \\ \hfill & +{\left.\left({\left(\frac{3}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}+{\left(\frac{5}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{3}{2}\right)}^{\mu \left(1-{\displaystyle \frac{1}{q}}\right)}\left(\left({\left(\frac{5}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right.\hfill \\ \hfill & +{\left.\left(\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{1}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left(\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right),\hfill \end{array}$$

where we have used (5)–(13).

This completes the proof. □

Corollary 4.

In Theorem 4, using the generalized convexity of ${\left|{ð}^{\left(\mu \right)}\right|}^q$ with respect to the terms ${\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q$ and ${\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }{\left(\lambda \right)}^{\mu }}\left({\lambda }^{\mu }ð\left({\mathsf{\ell }}_1\right)+3^{\mu }{\lambda }^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}{\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)}^{1-{\displaystyle \frac{1}{q}}}\left({\left(\frac{5}{8}\right)}^{\mu \left(1-{\displaystyle \frac{1}{q}}\right)}\left(\left({\left(\frac{103}{96}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-{\left(\frac{15}{96}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q\right.\right.\hfill \\ \hfill & +{\left.\left({\left(\frac{5}{96}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{1}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{3}{2}\right)}^{\mu \left(1-{\displaystyle \frac{1}{q}}\right)}\left(\left({\left(\frac{11}{12}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-{\left(\frac{1}{3}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q\right.\hfill \\ \hfill & +{\left.\left({\left(\frac{1}{3}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{7}{12}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left({\left(\frac{1}{3}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+\left(\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-{\left(\frac{1}{3}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

In [36], Yu et al. presented an improved version of the power mean inequality given in Lemma 5. In the following theorem, we apply this new inequality to derive a more refined result than the one obtained in Theorem 4.

Theorem 5.

Assume that all the assumptions of Lemma 6 are satisfied. If ${\left|{ð}^{\left(\mu \right)}\right|}^q$ is generalized convex for $q>1$, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left({\mathcal{A}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{A}}_2\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+{\mathcal{A}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left({\mathcal{A}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{A}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+{\mathcal{A}}_5\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{B}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{B}}_2\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\mathcal{B}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{B}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{B}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\mathcal{B}}_5\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{C}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{C}}_2\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\mathcal{C}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left({\mathcal{C}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{C}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\mathcal{C}}_5\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right),\hfill \end{array}$$

where ${\mathcal{A}}_i,{\mathcal{B}}_i$, and ${\mathcal{C}}_i$ are defined for $i=1,2,\dots ,5$ by (14)–(28), respectively.

Proof. 

From Lemma 6 and the improved generalized power mean inequality along with the generalized convexity of ${\left|{ð}^{\left(\mu \right)}\right|}^q$, we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-1\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times \left.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-1\right|}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times {\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-1\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }\right)}^{1-{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & \times \left.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-1\right|}^{\mu }\left({\left(1-t\right)}^{\mu }{\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+t^{\mu }{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right){\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill =& \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left({\mathcal{A}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{A}}_2\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+{\mathcal{A}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left({\mathcal{A}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{A}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+{\mathcal{A}}_5\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{B}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{B}}_2\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\mathcal{B}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{B}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{B}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\mathcal{B}}_5\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{C}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{C}}_2\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\mathcal{C}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left({\mathcal{C}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left({\mathcal{C}}_3\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q+{\mathcal{C}}_5\left(\mu \right){\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right),\hfill \end{array}$$

where we have used

$$\begin{array}{cc}\hfill {\mathcal{A}}_1\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{31}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-{\left(\frac{7}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\mathcal{A}}_2\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{2\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{127}{128}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)}-{\left(\frac{31}{128}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)},\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\mathcal{A}}_3\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{t}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }\hfill \\ \hfill =& -{\left(\frac{47}{128}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)}+{\left(\frac{35}{128}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{3}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\mathcal{A}}_4\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{3}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}+{\left(\frac{5}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\mathcal{A}}_5\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{2\mu }{\left|t-\frac{3}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{47}{128}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)}-{\left(\frac{15}{128}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\mathcal{B}}_1\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{5}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\mathcal{B}}_2\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{2\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{5}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)},\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\mathcal{B}}_3\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left(1-t\right)}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }={\left(\frac{1}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}+{\left(\frac{3}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\mathcal{B}}_4\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t+\frac{1}{4}\right|}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{1}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\mathcal{B}}_5\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{2\mu }{\left|-\frac{1}{4}-t\right|}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)}+{\left(\frac{1}{4}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\mathcal{C}}_1\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)},\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\mathcal{C}}_2\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left(1-t\right)}^{2\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\mathcal{C}}_3\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left(1-t\right)}^{\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\mathcal{C}}_4\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}-\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)},\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\mathcal{C}}_5\left(\mu \right)=& \frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{t}^{2\mu }{\left|t-1\right|}^{\mu }{\left(dt\right)}^{\mu }=\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}-\frac{\mathsf{\Gamma }\left(1+3\mu \right)}{\mathsf{\Gamma }\left(1+4\mu \right)}.\hfill \end{array}$$

(28)

The proof is completed. □

Corollary 5.

In Theorem 5, using the generalized convexity of ${\left|{ð}^{\left(\mu \right)}\right|}^q$ with respect to the terms ${\left|{ð}^{\left(\mu \right)}\left(\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q$ and ${\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left({\mathcal{A}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{3^{\mu }{\mathcal{A}}_2\left(\mu \right)+2^{\mu }{\mathcal{A}}_3\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+\frac{{\mathcal{A}}_3\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right.\hfill \\ \hfill & +{\left({\mathcal{A}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{3^{\mu }{\mathcal{A}}_3\left(\mu \right)+2^{\mu }{\mathcal{A}}_5\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+\frac{{\mathcal{A}}_5\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{B}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{2^{\mu }{\mathcal{B}}_2\left(\mu \right)+{\mathcal{B}}_3\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+\frac{{\mathcal{B}}_2\left(\mu \right)+2^{\mu }{\mathcal{B}}_3\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{B}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{2^{\mu }{\mathcal{B}}_3\left(\mu ,\lambda \right)+{\mathcal{B}}_5\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+\frac{{\mathcal{B}}_3\left(\mu \right)+2^{\mu }{\mathcal{B}}_5\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left({\mathcal{C}}_1\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{{\mathcal{C}}_2\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+\frac{2^{\mu }{\mathcal{C}}_2\left(\mu \right)+3^{\mu }{\mathcal{C}}_3\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +\left.{\left({\mathcal{C}}_4\left(\mu \right)\right)}^{1-{\displaystyle \frac{1}{q}}}{\left(\frac{{\mathcal{C}}_3\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_1\right)\right|}^q+\frac{2^{\mu }{\mathcal{C}}_3\left(\mu \right)+3^{\mu }{\mathcal{C}}_5\left(\mu \right)}{3^{\mu }}{\left|{ð}^{\left(\mu \right)}\left({\mathsf{\ell }}_2\right)\right|}^q\right)}^{{\displaystyle \frac{1}{q}}}\right).\hfill \end{array}$$

Theorem 6.

Assume that all the assumptions of Lemma 6 are satisfied. If ${\left|{ð}^{\left(\mu \right)}\right|}^q$ is generalized concave, then we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}{\left(\frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{3^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}\right)}^{{\displaystyle \frac{1}{q}}}{\left(\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}\right)}^{{\displaystyle \frac{1}{p}}}\left({\left(\frac{5^{p+1}-1}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{2}\right)\right|\right.\hfill \\ \hfill & +\left.{\left(\frac{1+3^{p+1}}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}\left|{ð}^{\left(\mu \right)}\left(\frac{5{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{6}\right)\right|+\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+5{\mathsf{\ell }}_2}{6}\right)\right|\right),\hfill \end{array}$$

where $p,q>1$ with ${\displaystyle \frac{1}{p}}+{\displaystyle \frac{1}{q}}=1$.

Proof. 

From Lemma 6, the properties of the modulus, the generalized Hölder inequality, and the generalized concavity of ${\left|{ð}^{\left(\mu \right)}\right|}^q$, we have

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\mathsf{\ell }}_1\right)+3^{\mu }ð\left(\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{}_{{\mathsf{\ell }}_1}I_{{\mathsf{\ell }}_2}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-\frac{3}{4}\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}\right.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right){\mathsf{\ell }}_1+t\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|\frac{1}{4}+t\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{2{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{3}+t\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\hfill \\ \hfill & +{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|t-1\right|}^{p\mu }{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}\left.{\left(\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{0}{\stackrel{1}{\int }}{\left|{ð}^{\left(\mu \right)}\left(\left(1-t\right)\frac{{\mathsf{\ell }}_1+2{\mathsf{\ell }}_2}{3}+t{\mathsf{\ell }}_2\right)\right|}^q{\left(dt\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{q}}}\right)\hfill \\ \hfill \le & \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}\left({\left(\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}{\left({\left(\frac{3}{4}\right)}^{p+1}+{\left(\frac{1}{4}\right)}^{p+1}\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}\right.{\left(\frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{3^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}\right)}^{{\displaystyle \frac{1}{q}}}\left|{ð}^{\left(\mu \right)}\left(\frac{5{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{6}\right)\right|\hfill \\ \hfill & +{\left(\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}{\left(\frac{5^{p+1}-1}{4^{p+1}}\right)}^{\mu }\right)}^{{\displaystyle \frac{1}{p}}}{\left(\frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{3^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}\right)}^{{\displaystyle \frac{1}{q}}}\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{2}\right)\right|\hfill \\ \hfill & +{\left(\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}\right)}^{{\displaystyle \frac{1}{p}}}\left.{\left(\frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{3^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}\right)}^{{\displaystyle \frac{1}{q}}}\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+5{\mathsf{\ell }}_2}{6}\right)\right|\right)\hfill \\ \hfill =& \frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{9^{\mu }}{\left(\frac{{\left({\mathsf{\ell }}_2-{\mathsf{\ell }}_1\right)}^{\mu }}{3^{\mu }\mathsf{\Gamma }\left(\mu +1\right)}\right)}^{{\displaystyle \frac{1}{q}}}{\left(\frac{\mathsf{\Gamma }\left(1+p\mu \right)}{\mathsf{\Gamma }\left(1+\left(p+1\right)\mu \right)}\right)}^{{\displaystyle \frac{1}{p}}}\left({\left(\frac{5^{p+1}-1}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{2}\right)\right|\right.\hfill \\ \hfill & +\left.{\left(\frac{3^{p+1}+1}{4^{p+1}}\right)}^{{\displaystyle \frac{\mu }{p}}}\left|{ð}^{\left(\mu \right)}\left(\frac{5{\mathsf{\ell }}_1+{\mathsf{\ell }}_2}{6}\right)\right|+\left|{ð}^{\left(\mu \right)}\left(\frac{{\mathsf{\ell }}_1+5{\mathsf{\ell }}_2}{6}\right)\right|\right),\hfill \end{array}$$

where we have used (11)–(13). The proof is completed. □

4. Application to Quadrature Formula

Let $\mathsf{\Theta }$ be the partition of the points ${\mathsf{\ell }}_1={\varkappa }_0<{\varkappa }_1<\dots <{\varkappa }_n={\mathsf{\ell }}_2$ of the interval $\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$, and consider the quadrature formula

$$\frac{1}{\mathsf{\Gamma }\left(\mu +1\right)}\underset{{\mathsf{\ell }}_1}{\stackrel{{\mathsf{\ell }}_2}{\int }}ð\left(\varkappa \right){\left(d\varkappa \right)}^{\mu }=\mathsf{\Omega }\left(ð,\mathsf{\Theta }\right)+R\left(ð,\mathsf{\Theta }\right),$$

where

$$\mathsf{\Omega }\left(ð,\mathsf{\Theta }\right)=\underset{i=0}{\sum ^{n-1}}\frac{{\left({\varkappa }_{i+1}-{\varkappa }_i\right)}^{\mu }}{\mathsf{\Gamma }\left(\mu +1\right)}\frac{1}{4^{\mu }}\left(ð\left({\varkappa }_i\right)+3^{\mu }ð\left(\frac{{\varkappa }_i+2{\varkappa }_{i+1}}{3}\right)\right),$$

and $R\left(ð,\mathsf{\Theta }\right)$ denotes the associated approximation error.

Proposition 1.

Let $n\in \mathbb{N}$ and $ð:\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]\to {\mathbb{R}}^{\mu }$ be a differentiable function on $\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$ with $0\le {\mathsf{\ell }}_1<{\mathsf{\ell }}_2$ and ${ð}^{\left(\mu \right)}$$\in C_{\mu }\left[{\mathsf{\ell }}_1,{\mathsf{\ell }}_2\right]$. If $\left|{ð}^{\left(\mu \right)}\right|$ is a generalized convex function, we have

$$\begin{array}{cc}\hfill \left|R\left(ð,\mathsf{\Theta }\right)\right|\le & \underset{i=0}{\sum ^{n-1}}\frac{{\left({\varkappa }_{i+1}-{\varkappa }_i\right)}^{2\mu }}{{27}^{\mu }\mathsf{\Gamma }\left(1+\mu \right)}\left(\left({\left(\frac{103}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{73}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\varkappa }_i\right)\right|\right.\hfill \\ \hfill & +\left.\left({\left(\frac{155}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}+{\left(\frac{5}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\varkappa }_{i+1}\right)\right|\right).\hfill \end{array}$$

Proof. 

Applying Corollary 2 on the subintervals $\left[{\varkappa }_i,{\varkappa }_{i+1}\right]$$\left(i=0,1,\dots ,n-1\right)$ of the partition $\mathsf{\Theta }$, we obtain

$$\begin{array}{cc}\hfill & \left|\frac{1}{4^{\mu }}\left(ð\left({\varkappa }_i\right)+3^{\mu }ð\left(\frac{{\varkappa }_i+2{\varkappa }_{i+1}}{3}\right)\right)-\frac{\mathsf{\Gamma }\left(\mu +1\right)}{{\left({\varkappa }_{i+1}-{\varkappa }_i\right)}^{\mu }}{}_{{\varkappa }_i}I_{{\varkappa }_{i+1}}^{\mu }ð\left(\varkappa \right)\right|\hfill \\ \hfill \le & \frac{{\left({\varkappa }_{i+1}-{\varkappa }_i\right)}^{\mu }}{{27}^{\mu }}\left(\left({\left(\frac{103}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}+{\left(\frac{73}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\varkappa }_i\right)\right|\right.\hfill \\ \hfill & +\left.\left({\left(\frac{155}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+\mu \right)}{\mathsf{\Gamma }\left(1+2\mu \right)}+{\left(\frac{5}{32}\right)}^{\mu }\frac{\mathsf{\Gamma }\left(1+2\mu \right)}{\mathsf{\Gamma }\left(1+3\mu \right)}\right)\left|{ð}^{\left(\mu \right)}\left({\varkappa }_{i+1}\right)\right|\right).\hfill \end{array}$$

Multiplying both sides of the above inequality by ${\displaystyle \frac{1}{\mathsf{\Gamma }\left(1+\mu \right)}}{\left({\varkappa }_{i+1}-{\varkappa }_i\right)}^{\mu }$, and then summing the obtained inequalities for all $i=0,1,\dots ,n-1$ and using the triangular inequality, we obtain the desired result. □

5. Conclusions

In conclusion, our study introduced a novel local fractional integral identity tied to the Gaussian two-point left Radau rule. Using this identity, we established some new fractal inequalities applicable to functions with generalized convex and concave first-order local fractional derivatives. Our practical applications further demonstrated the effectiveness of these results, highlighting their potential impact and relevance in various contexts.