Superconvergence of a Nonconforming Interface Penalty Finite Element Method for Elliptic Interface Problems

Abstract

In our previous works, we developed the superconvergence of a nonconforming finite element method based on unfitted meshes for an elliptic interface problem and elliptic problem, respectively. In this paper, a nonconforming interface penalty finite element method (NIPFEM) based on body-fitted meshes is explored for elliptic interface problems, which allows us to use different meshes in different sub-domains separated by the interface. A nonconforming finite element method based on rectangular meshes is studied and the supercloseness property between the gradient of the numerical solution and the gradient of the interpolation of the exact solution is proven for both symmetric NIPFEM and nonsymmetric NIPFEM. Then, the global superconvergence rate $O(h_i^{{\displaystyle \frac{3}{2}}})$ between the postprocessed numerical solution of NIPFEM and the exact solution is derived by using an interpolation postprocessing technique. Numerical examples are carried out to demonstrate the theoretical results.

1. Introduction

We consider the following elliptic interface problem:

$$\left\{\begin{array}{ccc}\hfill & -\nabla ·\left(a\left(x\right)\nabla u\right)=f\hfill & \hfill \mathrm{in}{\Omega }_1\cup {\Omega }_2,\\ \hfill & \left[u\right]=g_D,\left[\left(a\left(x\right)\nabla u\right)·\mathbf{n}\right]=g_N\hfill & \hfill \mathrm{on}\Gamma ,\\ \hfill & u=0\hfill & \hfill \mathrm{on}\partial \Omega ,\end{array}\right.$$

(1)

where $\Omega ={\Omega }_1\cup \Gamma \cup {\Omega }_2$ is a bounded and convex domain in ${\mathbb{R}}^2$, ${\Omega }_1$ and ${\Omega }_2$ are two subdomains of $\Omega$ and $\Gamma =\partial {\Omega }_1\cap \partial {\Omega }_2$, $\left[v\right]=v{{|}_{{\Omega }_1}-v|}_{{\Omega }_2}$ denotes the jump of v across the interface $\Gamma$, and $\mathbf{n}$ is the unit normal vector to $\Gamma$ pointing from ${\Omega }_1$ to ${\Omega }_2$. We assume that $a\left(x\right)=a_i$ for $x\in {\Omega }_i$ with constants $a_i>0,i=1,2$.

Interface problems frequently arise in many applications in fluid dynamics, material science, and so on. Over the past several decades, the literature on numerical methods and simulation for interface problems has grown extensively. This includes body-fitted grid methods ([1,2,3,4], etc.), where the mesh is aligned with the interface, and unfitted grid methods ([5,6,7,8,9,10,11,12], etc.), where the mesh does not fit the interface. These fitted and unfitted methods are mainly concentrated on the convergence analysis in the energy and $L^2$ norms. We note that an interface penalty finite element method (IPFEM) has been proposed based on body-fitted and piecewise meshes for elliptic interface problems in [4].

Meanwhile, superconvergence is a phenomenon that numerical solutions and/or their derivatives are more accurate at some special points than the best global rate. Since the 1970s, superconvergence analysis has been an active research topic and has been considered in the finite element community. The theory of superconvergence for finite element methods has been well developed to solve smooth problems ([13,14,15,16,17,18,19,20,21,22], etc.). And some works are focused on superconvergence of the interface problems based on conforming finite element methods [23,24,25,26,27,28]. Note that, in [23], a body-fitted triangular mesh was generated by combining the adaptive mesh refinement and the B$\ddot{o}$rgers’ algorithm, and then, a superconvergence analysis was developed. A new gradient recovery method by applying polynomial preserving recovery (PPR) [14] was introduced and superconvergence has been proved for triangular body-fitted mesh [24]. Then, superconvergence results of immersed finite element methods [9] and partially penalized immersed finite element methods [10] by using PPR based on unfitted meshes have been established in [25,26], respectively. However, there are few works using the nonconforming elements to study the superconvergence for interface problems. Recently, the superconvergence of the nonconforming Rannacher–Turek finite element method based on a unfitted square mesh has been developed [29], where a new postprocessing interpolation operator was introduced.

We are interested in the nonconforming finite element methods with a body-fitted and rectangular mesh. In this study, we shall combine the nonconforming element [16] and IPFEM [4] to research the supercloseness and superconvergence analysis of the nonconforming interface penalty finite element method (NIPFEM) based on rectangular and piecewise meshes. We first obtain the supercloseness estimate between the numerical solution and the nonconforming finite element interpolant. Furthermore, by applying the interpolation postprocessing technique, the corresponding global superconvergence estimate is derived. Finally, numerical examples are provided to confirm the theoretical analysis.

Throughout the paper, C is used to denote a generic positive constant which is independent of the mesh sizes, the penalty parameters, and the jump of the coefficient $a\left(x\right)$. We also use the shorthand notation $A\lesssim B$ and $B\gtrsim A$ for the inequality $A\le CB$ and $B\ge CA$. The space, norm, and inner product notation used in this paper are all standard, we refer to [30] for their precise definitions. Moreover, denote by $W^{s,p}({\Omega }_1\cup {\Omega }_2):=\left\{{v:v|}_{{\Omega }_i}\in W^{s,p}\left({\Omega }_i\right),i=1,2\right\}$ the piecewise $W^{s,p}$ space on ${\Omega }_1\cup {\Omega }_2$ and by ${∥v∥}_{s,p,{\Omega }_1\cup {\Omega }_2}$ and ${\left|v\right|}_{s,p,{\Omega }_1\cup {\Omega }_2}$ its norm and semi-norm.

2. NIPFEM for the Elliptic Interface Problem

We introduce partition of $\Omega$. Let $\left\{{\mathcal{T}}_{h,i}\right\}$ be two families of conforming, quasi-uniform, and regular rectangles of the subdomains ${\Omega }_i$ ($i=1,2$), respectively. For any $K\in {\mathcal{T}}_{h,i}$, we define $h_K:=diam\left(K\right)$. Let $h_i:={max}_{K\in {\mathcal{T}}_{h,i}}{h}_K,i=1,2$. Then, $h_K\eqsim h_i$ for $K\in {\mathcal{T}}_{h,i}$. Note that any element $K\in {\mathcal{T}}_{h,i}$ is considered closed. Obviously, ${\mathcal{T}}_h:={\mathcal{T}}_{h,1}\cup {\mathcal{T}}_{h,2}$ forms a rectangles of the whole domain $\Omega$. Here, we allow the mesh sizes $h_1$ and $h_2$ to be quite different in this paper; then, ${\mathcal{T}}_h$ may have many hanging nodes on the interface $\Gamma$. Clearly, each partition ${\mathcal{T}}_{h,i}$ induces a partition, denoted by ${\Gamma }_{h,i}(i=1,2)$ of the interface $\Gamma$, as follows:

$${\Gamma }_{h,i}=\left\{E:E=K\cap \Gamma ,\left|E\right|\ne 0,K\in {\mathcal{T}}_{h,i}\right\}.$$

(2)

Let $E_{h,i},E_{h,i}^0$ and $E_{h,i}^{\partial }$ denote the set of edges, interior edges, and boundary edges of ${\mathcal{T}}_{h,i}$, respectively.

Define a weak space as follows:

$$V:=\left\{v:{v|}_{{\Omega }_i}\in H^1\left({\Omega }_i\right){,v|}_K\in H^2\left(K\right),\forall K\in {\mathcal{T}}_{h,i},i=1,2,{\mathrm{and}v|}_{\partial \Omega }=0\right\}.$$

Let $V_{h,i}$ be the nonconforming finite element space on ${\mathcal{T}}_{h,i}(i=1,2)$, that is,

$$V_{h,i}:=\left\{v_{h,i}\in L^2\left({\Omega }_i\right):v_{h,i}{|}_K\in {\tilde{Q}}_1\left(K\right),\forall K\in {\mathcal{T}}_{h,i};{\int }_E\left[v_{h,i}\right]=0,\forall E\in E_{h,i}^0\right\},$$

(3)

where

$${\tilde{Q}}_1\left(K\right):=span\{1,x,y,x^2,y^2\}.$$

Then, the nonconforming interface penalty finite element approximation space is defined by the following:

$$V_h:=\left\{v_h:v_h{|}_{{\Omega }_i}\in V_{h,i},i=1,2,{\int }_{E\cap \partial \Omega }{v}_h=0,\forall E\in E_{h,i}^{\partial }\right\}.$$

(4)

Clearly, $V_h\not\subset V$.

For any $v\in V+V_h$ and weights $w_i,i=1,2$, let $v_i{=v|}_{{\Omega }_i},i=1,2$ and define the jump $\left[v\right]$ and averages ${\left\{v\right\}}_w,{\left\{v\right\}}^w$ of v on the interface $\Gamma$ as

$$\left[v\right]:=v_1{{|}_{\Gamma }-v_2|}_{\Gamma },{\left\{v\right\}}_w:=w_1{v}_1+w_2{v}_2,{\left\{v\right\}}^w:=w_2{v}_1+w_1{v}_2,$$

(5)

with

$$\begin{array}{c}\hfill w_1={\displaystyle \frac{a_2{h}_1}{a_1{h}_2+a_2{h}_1}},\mathrm{and}{w}_2={\displaystyle \frac{a_1{h}_2}{a_1{h}_2+a_2{h}_1}}.\end{array}$$

(6)

It is clear that

$$\begin{array}{c}\hfill {\left\{{\displaystyle \frac{a}{h}}\right\}}_w=2{\displaystyle \frac{a_i}{h_i}}{w}_i={\displaystyle \frac{2a_1{a}_2}{a_1{h}_2+a_2{h}_1}}={\displaystyle \frac{2}{\frac{h_1}{a_1}+\frac{h_2}{a_2}}}.\end{array}$$

(7)

Note that ${\left\{{\displaystyle \frac{a}{h}}\right\}}_w$ is the harmonic average of ${\displaystyle \frac{a_1}{h_1}}$ and ${\displaystyle \frac{a_2}{h_2}}$. Remark that we obtain a quasi-uniform mesh and piecewise mesh by $h_1=h_2$ and $h_1\ne h_2$, respectively. And for the case of a quasi-uniform mesh, the harmonic weights are used for discontinuous Galerkin (DG) methods in [31,32,33,34].

Let $a_h(·,·)$ be the bilinear form on $(V+V_h)\times (V+V_h)$ and $F_h(·)$ be the linear form on $V+V_h$ defined by

$$\begin{array}{cc}\hfill a_h(u,v):=& \sum _{i=1}^2\sum _{K\in {\mathcal{T}}_{h,i}}{\int }_K{a}_i\nabla u·\nabla v-{\int }_{\Gamma }\left({\left\{a\nabla u·\mathbf{n}\right\}}_w\left[v\right]+\beta \left[u\right]{\left\{a\nabla v·\mathbf{n}\right\}}_w\right)\hfill \\ \hfill & +\gamma {\int }_{\Gamma }{\left\{{\displaystyle \frac{a}{h}}\right\}}_w\left[u\right]\left[v\right],\hfill \end{array}$$

(8)

and

$$\begin{array}{cc}\hfill F_h\left(v\right):=& {\int }_{\Omega }fv+{\int }_{\Gamma }{g}_N{\left\{v\right\}}^w-{\int }_{\Gamma }\beta g_D{\left\{a\nabla v·\mathbf{n}\right\}}_w+\gamma {\int }_{\Gamma }{\left\{{\displaystyle \frac{a}{h}}\right\}}_w{g}_D\left[v\right],\hfill \end{array}$$

(9)

where $\beta$ is a real number, $\gamma$ is a positive number.

The nonconforming interface penalty finite element approximation of (1) is as follows: find $u_h\in V_h$ such that

$$a_h(u_h,v_h)=F_h\left(v_h\right)\forall v_h\in V_h.$$

(10)

Remark 1.

In the above bilinear form $a_h$, when $\beta =1$, the method is called the symmetric nonconforming interface penalty finite element method (SNIPFEM). On the other hand, when $\beta =-1$, the method is termed the nonsymmetric nonconforming interface penalty finite element method (NNIPFEM).

We introduce the following discrete energy-norm on the space $V+V_h$ as follows:

$$\begin{array}{cc}\hfill {∥\left|v\right|∥}_h:=({\parallel a^{{\displaystyle \frac{1}{2}}}\nabla v\parallel }_{L^2({\Omega }_1\cup {\Omega }_2)}^2& +\gamma {\left\{{\displaystyle \frac{a}{h}}\right\}}_w{∥\left[v\right]∥}_{L^2(\Gamma )}^2\hfill \\ \hfill & +{\left(\gamma {\left\{{\displaystyle \frac{a}{h}}\right\}}_w\right)}^{-1}{∥{\left\{a\nabla v·\mathbf{n}\right\}}_w∥}_{L^2(\Gamma )}^2{)}^{{\displaystyle \frac{1}{2}}}.\hfill \end{array}$$

(11)

It is easy to check that, if the problem (1) attains a classical solution satisfying ${u|}_{{\Omega }_i}\in H^2\left({\Omega }_i\right),i=1,2$, then the following inconsistency holds:

$$a_h(u-u_h,v_h)=\sum _{i=1}^2\sum _{E\in E_{h,i}\setminus {\Gamma }_{h,i}}{\int }_E{a}_i\nabla u·\mathbf{n}\left[v_h\right]\forall v_h\in V_h.$$

(12)

It can be proven similarly to Lemma 3.1 and Lemma 4.1 of [4] that the continuity and coercivity of $a_h(·,·)$ for both SNIPFEM and NNIPFEM hold. By the coercivity and the inconsistency, a priori error estimate for SNIPFEM with sufficiently large penalty parameter $\gamma$ and NNIPFEM with $\gamma \gtrsim 1$ hold as follows:

$${∥\left|u-u_h\right|∥}_h\lesssim {\gamma }^{{\displaystyle \frac{1}{2}}}{\left(\sum _{i=1}^2{a}_i{h}_i^2{∥u∥}_{H^2\left({\Omega }_i\right)}^2\right)}^{{\displaystyle \frac{1}{2}}}.$$

3. Supercloseness and Superconvergence

In this section, an interpolation is first introduced and the postprocessing operator introduced in [15,16] is shown. Furthermore, the nonconforming finite element solution is proved to be superclose to the interpolation and it is proved that the postprocessed gradient is superconvergent to the exact gradient.

3.1. Preliminaries

Let ${\Pi }_{h,i}:H^1\left({\Omega }_i\right)\to V_{h,i}(i=1,2)$ by ${\Pi }_{h,i}{v|}_K={\Pi }_{K}v$, where ${\Pi }_{K}v$ is defined by ${\int }_e{\Pi }_{K}v={\int }_{e}v$ and ${\int }_K{\Pi }_{K}v={\int }_{K}v$ for any rectangular element $K\in {\mathcal{T}}_{h,i}$ and $e\subset \partial K$. Denote the interpolation operator ${\Pi }_h:H^1\left({\Omega }_i\right)\to V_h$ by $\left({\Pi }_{h}v\right){|}_{{\Omega }_i}={\Pi }_{h,i}\left(v{|}_{{\Omega }_i}\right),i=1,2$. From the interpolation theory in [35], we have the following approximation estimate:

$${\left(\sum _{K\in {\mathcal{T}}_{h,i}}{|v-{\Pi }_{h}v|}_{W^{l,p}\left(K\right)}^2\right)}^{{\displaystyle \frac{1}{2}}}\lesssim h_i^{2-l}{\left|v\right|}_{W^{2,p}\left({\Omega }_i\right)},$$

(13)

where $l=0,1$, $1\le p\le \infty$ and $i=1,2$.

Now, we will apply the postprocessing operator defined in [15,16], which shows that the gradient of the postprocessed NIPFEM solution is superconvergent to the exact gradient. For each partition ${\mathcal{T}}_{h,i}$ of subdomain ${\Omega }_i(i=1,2)$, we assume that ${\mathcal{T}}_{h,i}$ is obtained from ${\mathcal{T}}_{2h,i}$ by dividing each element M of ${\mathcal{T}}_{2h,i}$ into $2\times 2$ elements $K_j\in {\mathcal{T}}_{h,i},j=1,\dots ,4$, namely, $M={\cup }_{j=1}^4{K}_j$. Denote an operator ${\mathcal{I}}_{2h,i}$ on ${\mathcal{T}}_{2h,i}$ by ${\mathcal{I}}_{2h,i}{v|}_M={\mathcal{I}}_{M}v$, where ${\mathcal{I}}_M:L^1\left(M\right)\to P_2\left(M\right)$ is defined by

$${\int }_{e_j}({\mathcal{I}}_{M}v-v)=0,(j=1,\dots ,4);{\int }_{K_1\cup K_3}({\mathcal{I}}_{M}v-v)=0;{\int }_{K_2\cup K_4}({\mathcal{I}}_{M}v-v)=0,$$

where $e_j(j=1,\dots ,4)$ are four edges of M.

Then, a postprocessing operator ${\mathcal{I}}_{2h}$ defined by

$${\mathcal{I}}_{2h}{v|}_{{\Omega }_i}={\mathcal{I}}_{2h,i}\left(v{|}_{{\Omega }_i}\right).$$

Set

$${∥·∥}_{h,{\Omega }_i}={\left(\sum _{K\in {\mathcal{T}}_{h,i}}{|·|}_{1,K}^2\right)}^{{\displaystyle \frac{1}{2}}},and{∥·∥}_{h,\Omega }={\left(\sum _{i=1}^2{∥·∥}_{h,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}.$$

Now we present the following Lemma, which shows the properties of operator ${\mathcal{I}}_{2h}$ by using Lemma 3.2 of [16].

Lemma 1.

For each subdomain ${\Omega }_i,(i=1,2)$, the postprocessing operator ${\mathcal{I}}_{2h}$ satisfies

$${\mathcal{I}}_{2h}{\Pi }_{h}v{{|}_{{\Omega }_i}={\mathcal{I}}_{2h}v|}_{{\Omega }_i},{∥v-{\mathcal{I}}_{2h}v∥}_{h,{\Omega }_i}\lesssim h_i^2{∥v∥}_{3,{\Omega }_i},{∥{\mathcal{I}}_{2h}{v}_h∥}_{h,{\Omega }_i}\lesssim {∥v_h∥}_{h,{\Omega }_i}.$$

3.2. Main Results

In this subsection, we will apply the interpolation and the postprocessing operator defined in the Preliminaries and show the supercloseness and superconvergence results.

Theorem 1.

Let u be the exact solution of (1) and ${\Pi }_{h}u$ be the interpolation of u defined as above. Assume $u\in W^{2,\infty }({\Omega }_1\cup {\Omega }_2)$ and for all $v_h\in V_h$, then

$$a_h(u-{\Pi }_{h}u,v_h)\lesssim \left({\gamma }^{{\displaystyle \frac{1}{2}}}+{\gamma }^{-{\displaystyle \frac{1}{2}}}\right){\left(\sum _{i=1}^2{a}_i{h}_i^3{∥u∥}_{2,\infty ,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|v_h\right|∥}_h.$$

Proof. 

By the definition of $a_h(·,·)$, we have

$$\begin{array}{cc}\hfill a_h(u-{\Pi }_{h}u,v_h)& =\sum _{i=1}^2\sum _{K\in {\mathcal{T}}_{h,i}}{\int }_K{a}_i\nabla (u-{\Pi }_{h}u)·\nabla v_h\hfill \\ \hfill & -{\int }_{\Gamma }\left({\left\{a\nabla (u-{\Pi }_{h}u)·\mathbf{n}\right\}}_w\left[v_h\right]+\beta \left[u-{\Pi }_{h}u\right]{\left\{a\nabla v_h·\mathbf{n}\right\}}_w\right)\hfill \\ \hfill & +\gamma {\int }_{\Gamma }{\left\{{\displaystyle \frac{a}{h}}\right\}}_w[u-{\Pi }_{h}u]\left[v_h\right]\hfill \\ \hfill & =I_1+I_2+I_3+I_4.\hfill \end{array}$$

(14)

For any rectangular element $K\in {\mathcal{T}}_{h,i}(i=1,2)$ and $v_h\in V_h$, noticing that $\nabla ·(\nabla v_h)$ and $(\nabla v_h·{\mathbf{n}}_{\partial K}){|}_{\partial K}$ are constants, then by Green’s formula and the definition of ${\Pi }_h$, it holds that

$${\int }_K{a}_i\nabla (u-{\Pi }_{h}u)·\nabla v_h=-{\int }_K{a}_i(u-{\Pi }_{h}u)\nabla ·(\nabla v_h)+{\int }_{\partial K}{a}_i(u-{\Pi }_{h}u)\nabla v_h·{\mathbf{n}}_{\partial K}=0;$$

therefore,

$$I_1=0.$$

(15)

Note that ${\left({\left\{{\displaystyle \frac{a}{h}}\right\}}_w\right)}^{-1}{a}_i{w}_i={\displaystyle \frac{h_i}{2}},i=1,2$; then, the Cauchy–Schwartz inequality implies that

$$\begin{array}{cc}\hfill I_2& \lesssim {\left(\sum _{i=1}^2\sum _{E\in {\Gamma }_{h,i}}{\left(\gamma {\left\{{\displaystyle \frac{a}{h}}\right\}}_w\right)}^{-1}{a}_i^2{w}_i^2{∥\nabla (u-{\Pi }_{h}u)∥}_{L^2\left(E\right)}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|v_h\right|∥}_h\hfill \\ \hfill & \lesssim {\gamma }^{-{\displaystyle \frac{1}{2}}}{\left(\sum _{i=1}^2\sum _{E\in {\Gamma }_{h,i}}{a}_i{w}_i{h}_i^2{∥\nabla (u-{\Pi }_{h}u)∥}_{L^{\infty }\left(K_E\right)}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|v_h\right|∥}_h\hfill \\ \hfill & \lesssim {\gamma }^{-{\displaystyle \frac{1}{2}}}{\left(\sum _{i=1}^2{a}_i{h}_i^4\left(\sum _{E\in {\Gamma }_{h,i}}1\right){∥u∥}_{2,\infty ,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|v_h\right|∥}_h\hfill \\ \hfill & \lesssim {\gamma }^{-{\displaystyle \frac{1}{2}}}{\left(\sum _{i=1}^2{a}_i{h}_i^3{∥u∥}_{2,\infty ,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|v_h\right|∥}_h,\hfill \end{array}$$

(16)

where $E\subset K_E,K_E\in {\mathcal{T}}_{h,i}$ and we have used the approximation estimate (13) and ${\sum }_{E\in {\Gamma }_{h,i}}1\approx O\left(h_i^{-1}\right)$.

To bound $I_3$, we use the standard trace inequality and obtain

$$\begin{array}{cc}\hfill \sum _{E\in {\Gamma }_{h,i}}& {\left\{{\displaystyle \frac{a}{h}}\right\}}_w{∥u-{\Pi }_{h}u∥}_{L^2\left(E\right)}^2\hfill \\ \hfill & \lesssim \sum _{E\in {\Gamma }_{h,i}}{\displaystyle \frac{a_i{w}_i}{h_i}}\left(h_i^{-1}{∥u-{\Pi }_{h}u∥}_{L^2\left(K_E\right)}^2+h_i{∥\nabla (u-{\Pi }_{h}u)∥}_{L^2\left(K_E\right)}^2\right)\hfill \\ \hfill & \lesssim \sum _{E\in {\Gamma }_{h,i}}{a}_i\left({∥u-{\Pi }_{h}u∥}_{L^{\infty }\left(K_E\right)}^2+h_i^2{∥\nabla (u-{\Pi }_{h}u)∥}_{L^{\infty }\left(K_E\right)}^2\right)\hfill \\ \hfill & \lesssim a_i{h}_i^4\left(\sum _{E\in {\Gamma }_{h,i}}1\right){∥u∥}_{2,\infty ,{\Omega }_i}^2,\hfill \end{array}$$

(17)

and

$$\begin{array}{cc}\hfill \sum _{E\in {\Gamma }_{h,i}}& {\left({\left\{{\displaystyle \frac{a}{h}}\right\}}_w\right)}^{-1}{a}_i^2{w}_i^2{∥\nabla v_h·n∥}_{L^2\left(E\right)}^2\hfill \\ \hfill & \lesssim \sum _{E\in {\Gamma }_{h,i}}{a}_i{w}_i{h}_i{h}_i^{-1}{∥\nabla v_h∥}_{L^2\left(K_E\right)}^2\lesssim {∥\left|v_h\right|∥}_h.\hfill \end{array}$$

(18)

Then, $I_3$ is estimated by

$$I_3\lesssim {\left(\sum _{i=1}^2{a}_i{h}_i^3{∥u∥}_{2,\infty ,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|v_h\right|∥}_h,$$

(19)

where we have used the Cauchy–Schwartz inequality, (17), (18) and the fact that ${\sum }_{E\in {\Gamma }_{h,i}}1\approx O\left(h_i^{-1}\right)$. A similar argument follows for $I_4$, and we obtain

$$I_4\lesssim {\gamma }^{{\displaystyle \frac{1}{2}}}{\left(\sum _{i=1}^2{a}_i{h}_i^3{∥u∥}_{2,\infty ,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|v_h\right|∥}_h.$$

(20)

Thus, we complete the proof. □

Based on Theorem 1 and the consistency error estimate for (12) (see Lemma 3.1 of [15]), it is easy to prove the following supercloseness theorem, which is similar to the proof of Theorem 1 of [36].

Theorem 2.

Let $u_h$ be the nonconforming finite element solution and ${\Pi }_{h}u$ be the interpolation of u, $u\in H^3({\Omega }_1\cup {\Omega }_2)\cap W^{2,\infty }({\Omega }_1\cup {\Omega }_2)$; then, for SNIPFEM with a sufficiently large penalty parameter γ and NNIPFEM with $\gamma \gtrsim 1$, there holds the following supercloseness result

$${∥\left|u_h-{\Pi }_{h}u\right|∥}_h\lesssim {\gamma }^{{\displaystyle \frac{1}{2}}}{\left(\sum _{i=1}^2{a}_i\left(h_i^3{∥u∥}_{2,\infty ,{\Omega }_i}^2+h_i^4{∥u∥}_{3,{\Omega }_i}^2\right)\right)}^{{\displaystyle \frac{1}{2}}}.$$

Proof. 

Using the coercivity of $a_h(·,·)$, we have

$$\begin{array}{cc}\hfill {∥\left|u_h-{\Pi }_{h}u\right|∥}_h^2& \lesssim a_h(u_h-{\Pi }_{h}u,u_h-{\Pi }_{h}u)\hfill \\ \hfill & =a_h(u-{\Pi }_{h}u,u_h-{\Pi }_{h}u)-a_h(u-u_h,u_h-{\Pi }_{h}u).\hfill \end{array}$$

(21)

From Theorem 1, the first term on the right hand can be estimated via

$$a_h(u-{\Pi }_{h}u,u_h-{\Pi }_{h}u)\lesssim \left({\gamma }^{{\displaystyle \frac{1}{2}}}+{\gamma }^{-{\displaystyle \frac{1}{2}}}\right){\left(\sum _{i=1}^2{a}_i{h}_i^3{∥u∥}_{2,\infty ,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|u_h-{\Pi }_{h}u\right|∥}_h.$$

(22)

From Lemma 3.1 of [15], the following consistency error estimate holds:

$$a_h(u-u_h,u_h-{\Pi }_{h}u)\lesssim {\left(\sum _{i=1}^2{a}_i{h}_i^4{∥u∥}_{3,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}{∥\left|u_h-{\Pi }_{h}u\right|∥}_h.$$

(23)

Combining (22) with (23), we complete the proof. □

Theorem 3.

Let u and $u_h$ be the solution of (1) and (10), respectively, and let ${\mathcal{I}}_{2h}$ be the postprocessing operator defined above. Assume that $u\in H^3({\Omega }_1\cup {\Omega }_2)\cap W^{2,\infty }({\Omega }_1\cup {\Omega }_2)$; then, for a SNIPFEM with a sufficiently large penalty parameter γ and NNIPFEM with $\gamma \gtrsim 1$,

$${∥a^{{\displaystyle \frac{1}{2}}}(u-{\mathcal{I}}_{2h}{u}_h)∥}_{h,\Omega }\lesssim {\gamma }^{{\displaystyle \frac{1}{2}}}{\left(\sum _{i=1}^2{a}_i\left(h_i^3{∥u∥}_{2,\infty ,{\Omega }_i}^2+h_i^4{∥u∥}_{3,{\Omega }_i}^2\right)\right)}^{{\displaystyle \frac{1}{2}}}.$$

Proof. 

We decompose $u-{\mathcal{I}}_{2h}{u}_h$ as $u-{\mathcal{I}}_{2h}{\Pi }_{h}u$ and ${\mathcal{I}}_{2h}{\Pi }_{h}u-{\mathcal{I}}_{2h}{u}_h$. Then, the triangle inequality implies that

$${∥a^{{\displaystyle \frac{1}{2}}}(u-{\mathcal{I}}_{2h}{u}_h)∥}_{h,\Omega }\le {∥a^{{\displaystyle \frac{1}{2}}}(u-{\mathcal{I}}_{2h}{\Pi }_{h}u)∥}_{h,\Omega }+{∥a^{{\displaystyle \frac{1}{2}}}({\mathcal{I}}_{2h}{\Pi }_{h}u-{\mathcal{I}}_{2h}{u}_h)∥}_{h,\Omega }.$$

Noticing that ${\mathcal{I}}_{2h}{\Pi }_{h}u{{|}_{{\Omega }_i}={\mathcal{I}}_{2h}u|}_{{\Omega }_i}$, and by Lemma 1, we have

$${∥u-{\mathcal{I}}_{2h}{\Pi }_{h}u∥}_{h,{\Omega }_i}\lesssim h_i^2{∥u∥}_{3,{\Omega }_i},$$

and

$${∥{\mathcal{I}}_{2h}{\Pi }_{h}u-{\mathcal{I}}_{2h}{u}_h∥}_{h,{\Omega }_i}\lesssim {∥{\Pi }_{h}u-u_h∥}_{h,{\Omega }_i}.$$

Thus, we have

$${∥a^{{\displaystyle \frac{1}{2}}}(u-{\mathcal{I}}_{2h}{\Pi }_{h}u)∥}_{h,\Omega }\lesssim {\left(\sum _{i=1}^2{a}_i{h}_i^4{∥u∥}_{3,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}},$$

(24)

and

$$\begin{array}{cc}\hfill {∥a^{{\displaystyle \frac{1}{2}}}({\mathcal{I}}_{2h}{\Pi }_{h}u-{\mathcal{I}}_{2h}{u}_h)∥}_{h,\Omega }& \lesssim {\left(\sum _{i=1}^2{∥a_i^{{\displaystyle \frac{1}{2}}}({\Pi }_{h}u-u_h)∥}_{h,{\Omega }_i}^2\right)}^{{\displaystyle \frac{1}{2}}}\hfill \\ \hfill & \lesssim {\gamma }^{{\displaystyle \frac{1}{2}}}{\left(\sum _{i=1}^2{a}_i\left(h_i^3{∥u∥}_{2,\infty ,{\Omega }_i}^2+h_i^4{∥u∥}_{3,{\Omega }_i}^2\right)\right)}^{{\displaystyle \frac{1}{2}}},\hfill \end{array}$$

(25)

where we have used the definition of ${∥\left|·\right|∥}_h$ and Theorem 2. Finally, combing (24) and (25) completes the proof. □

4. Numerical Experiments

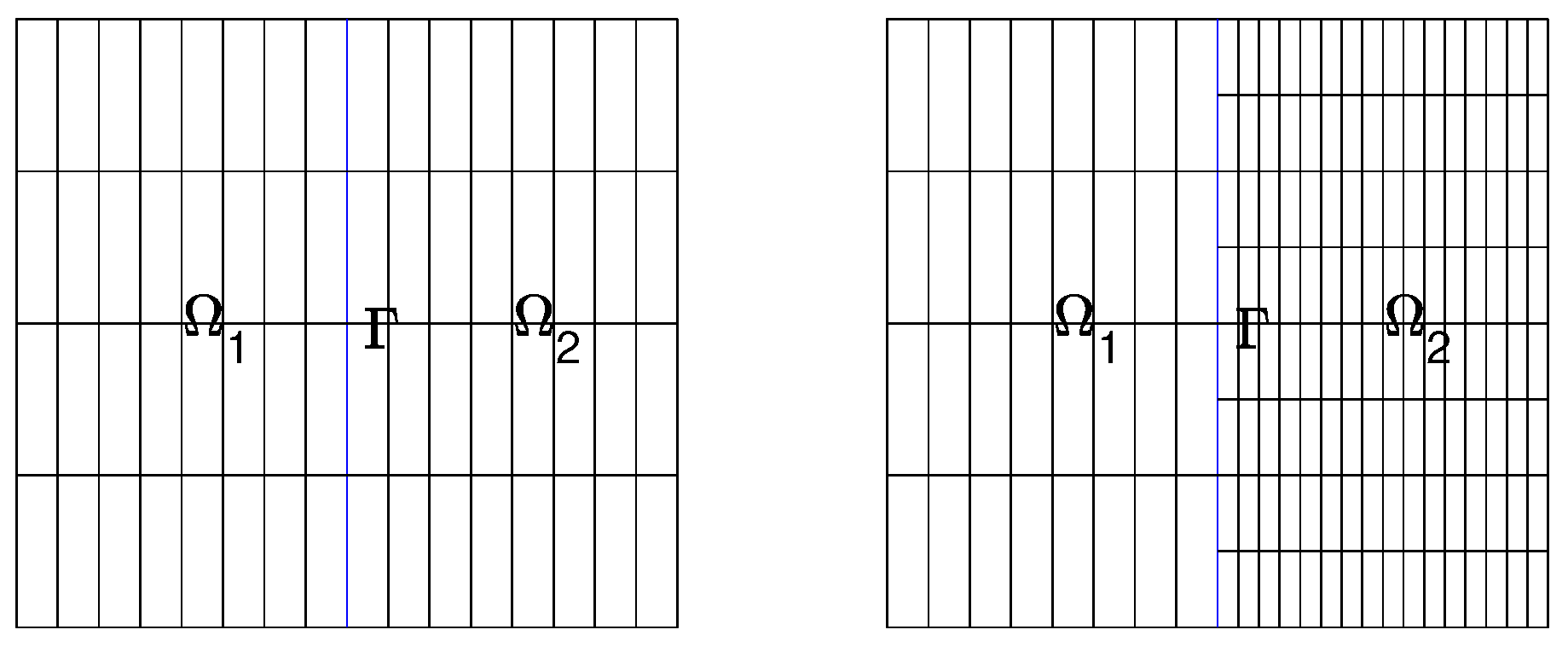
In this section, the previously developed supercloseness and superconvergence theory will be verified by two numerical examples. In these examples, the domains are chosen as $(0,2)\times (0,1)$ and ${\Omega }_1:=\{(x,y)\in \Omega :0<x<1,0<y<1\}$, ${\Omega }_2:=\{(x,y)\in \Omega :1<x<2,0<y<1\}$, and $\Gamma :=\left\{\right(x,y)\in \Omega :x=1,0<y<1\}$. We firstly test the convergence rate, supercloseness result, and superconvergence rate based on square and rectangular meshes, where the quasi-uniform (Left of Figure 1) and piecewise meshes (Right of Figure 1) are considered. We test these examples using two different NIPFEM methods as follows: SNIPFEM and NNIPFEM. Moreover, we explore the influence of the jump of the coefficients on the errors. All the following results are obtained by choosing the penalty parameter $\gamma =10$ for SNIPFEM and NNIPFEM. For convenience, we summarize our experimental results in tables, adopting the following errors: $De:={\parallel a^{{\displaystyle \frac{1}{2}}}(u-u_h)\parallel }_{h,\Omega },D^{\Pi }e:={\parallel a^{{\displaystyle \frac{1}{2}}}(u_h-{\Pi }_{h}u)\parallel }_{h,\Omega }$ and $D^{\mathcal{I}}e:={\parallel a^{{\displaystyle \frac{1}{2}}}(u-{\mathcal{I}}_{2h}{u}_h)\parallel }_{h,\Omega }$.

Figure 1. (Left): quasi-uniform meshes. (Right): piecewise meshes.

4.1. Example 1

In this example, we consider the exact solution as follows:

$$u(x,y)=\left\{\begin{array}{cc}{\displaystyle \frac{e^{xy}(x^2+y^2-1/4)}{a_1}}\hfill & \mathrm{in}{\Omega }_1,\\ {\displaystyle \frac{e^{xy}(x^2+y^2-1/4)}{a_2}}\hfill & \mathrm{in}{\Omega }_2.\end{array}\right.$$

(26)

Note that the elliptic interface problem has $g_D\ne 0$ and $g_N=0$. Firstly, the performance for errors $De$, $D^{\Pi }e$, and $D^{\mathcal{I}}e$ on the square quasi-uniform $(h_1=h_2)$ and piecewise $(h_1\ne h_2)$ meshes for SNIPFEM and NNIPFEM are shown in Table 1 and Table 2, respectively. Also we test the rates of errors $De$, $D^{\Pi }e$, and $D^{\mathcal{I}}e$ on rectangular quasi-uniform and piecewise meshes for SNIPFEM and NNIPFEM in Table 3 and Table 4, respectively. In all different cases, it shows that the NIPFEM converges with the optimal rate $O\left(h_i\right)$ for $De$ and with $O\left(h_i^{1.6}\right)$ and $O\left(h_i^2\right)$ orders of convergence for $D^{\Pi }e$ and $D^{\mathcal{I}}e$, respectively, which is better than our Theorems 2 and 3.

Table 1. Rates of errors for Example 1 based on square quasi-uniform and piecewise meshes with $a_1=1$ and $a_2=1000$ for SNIPFEM.

$({\mathit{h}}_{1,\mathit{x}},{\mathit{h}}_{1,\mathit{y}})$	$({\mathit{h}}_{2,\mathit{x}},{\mathit{h}}_{2,\mathit{y}})$	$\mathit{D}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathbf{\Pi }}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathcal{I}}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$
(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{4}}$)	(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{4}}$)	4.6196 $\times {10}^{-1}$		7.8364 $\times {10}^{-2}$		3.3026 $\times {10}^{-1}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	2.3164 $\times {10}^{-1}$	0.9958	2.2308 $\times {10}^{-2}$	1.8126	9.0132 $\times {10}^{-2}$	1.8734
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	1.1580 $\times {10}^{-1}$	1.0003	5.2043 $\times {10}^{-3}$	2.0998	2.3018 $\times {10}^{-2}$	1.9692
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	5.7900 $\times {10}^{-2}$	0.9999	1.1042 $\times {10}^{-3}$	2.2366	5.7681 $\times {10}^{-3}$	1.9966
(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{4}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	4.5010 $\times {10}^{-1}$		7.9155 $\times {10}^{-2}$		3.2036 $\times {10}^{-1}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	2.2559 $\times {10}^{-1}$	0.9965	2.3180 $\times {10}^{-2}$	1.7717	8.7343 $\times {10}^{-2}$	1.8749
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	1.1274 $\times {10}^{-1}$	1.0007	5.8135 $\times {10}^{-3}$	1.9954	2.2310 $\times {10}^{-2}$	1.9689
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{64}}$)	5.6363 $\times {10}^{-2}$	1.0001	1.4727 $\times {10}^{-3}$	1.9808	5.5966 $\times {10}^{-3}$	1.9951

Table 2. Rates of errors for Example 1 based on square quasi-uniform and piecewise meshes with $\gamma =10$ and $a_1=1$ and $a_2=1000$ for NNIPFEM.

$({\mathit{h}}_{1,\mathit{x}},{\mathit{h}}_{1,\mathit{y}})$	$({\mathit{h}}_{2,\mathit{x}},{\mathit{h}}_{2,\mathit{y}})$	$\mathit{D}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathbf{\Pi }}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathcal{I}}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$
(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{4}}$)	(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{4}}$)	4.6394 $\times {10}^{-1}$		9.1992 $\times {10}^{-2}$		3.3182 $\times {10}^{-1}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	2.3191 $\times {10}^{-1}$	1.0003	2.5519 $\times {10}^{-2}$	1.8499	9.0549 $\times {10}^{-2}$	1.8736
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	1.1582 $\times {10}^{-1}$	1.0016	5.8662 $\times {10}^{-3}$	2.1210	2.3102 $\times {10}^{-2}$	1.9706
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	5.7902 $\times {10}^{-2}$	1.0002	1.2288 $\times {10}^{-3}$	2.2551	5.7821 $\times {10}^{-3}$	1.9984
(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{4}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	4.5246 $\times {10}^{-1}$		9.4562 $\times {10}^{-2}$		3.2196 $\times {10}^{-1}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	2.2597 $\times {10}^{-1}$	1.0016	2.7429 $\times {10}^{-2}$	1.7855	8.7770 $\times {10}^{-2}$	1.8751
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	1.1280 $\times {10}^{-1}$	1.0024	7.0802 $\times {10}^{-3}$	1.9538	2.2396 $\times {10}^{-2}$	1.9704
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{64}}$)	5.6374 $\times {10}^{-2}$	1.0006	1.9158 $\times {10}^{-3}$	1.8858	5.6108 $\times {10}^{-3}$	1.9969

Table 3. Rates of errors for Example 1 based on rectangular quasi-uniform and piecewise meshes with $\gamma =10$ and $a_1=1,a_2=1000$ for SNIPFEM.

$({\mathit{h}}_{1,\mathit{x}},{\mathit{h}}_{1,\mathit{y}})$	$({\mathit{h}}_{2,\mathit{x}},{\mathit{h}}_{2,\mathit{y}})$	$\mathit{D}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathbf{\Pi }}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathcal{I}}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$
(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{8}}$)	3.6234 $\times {10}^{-1}$		2.3571 $\times {10}^{-2}$		1.9231 $\times {10}^{-1}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	1.8263 $\times {10}^{-1}$	0.9884	6.3468 $\times {10}^{-3}$	1.8929	5.0804 $\times {10}^{-2}$	1.9204
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	9.1496 $\times {10}^{-2}$	0.9971	1.5595 $\times {10}^{-3}$	2.0249	1.2884 $\times {10}^{-2}$	1.9792
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	4.5770 $\times {10}^{-2}$	0.9992	3.6774 $\times {10}^{-4}$	2.0843	3.2320 $\times {10}^{-3}$	1.9951
(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	3.5277 $\times {10}^{-1}$		2.4795 $\times {10}^{-2}$		1.8719 $\times {10}^{-1}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	1.7779 $\times {10}^{-1}$	0.9884	7.4105 $\times {10}^{-3}$	1.7424	4.9452 $\times {10}^{-2}$	1.9204
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	8.9066 $\times {10}^{-2}$	0.9972	2.1790 $\times {10}^{-3}$	1.7658	1.2544 $\times {10}^{-2}$	1.9789
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{128}}$)	4.4552 $\times {10}^{-2}$	0.9993	6.7520 $\times {10}^{-4}$	1.6902	3.1480 $\times {10}^{-3}$	1.9945

Table 4. Rates of errors for Example 1 based on rectangular quasi-uniform and piecewise meshes with $\gamma =10$ and $a_1=1,a_2=1000$ for NNIPFEM.

$({\mathit{h}}_{1,\mathit{x}},{\mathit{h}}_{1,\mathit{y}})$	$({\mathit{h}}_{2,\mathit{x}},{\mathit{h}}_{2,\mathit{y}})$	$\mathit{D}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathbf{\Pi }}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathcal{I}}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$
(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{8}}$)	3.6307 $\times {10}^{-1}$		3.5022 $\times {10}^{-2}$		1.9292 $\times {10}^{-1}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	1.8271 $\times {10}^{-1}$	0.9906	8.8727 $\times {10}^{-3}$	1.9808	5.0970 $\times {10}^{-2}$	1.9203
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	9.1503 $\times {10}^{-2}$	0.9976	2.0360 $\times {10}^{-3}$	2.1236	1.2917 $\times {10}^{-2}$	1.9803
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	4.5771 $\times {10}^{-2}$	0.9993	4.4831 $\times {10}^{-4}$	2.1831	3.2374 $\times {10}^{-3}$	1.9964
(${\displaystyle \frac{1}{4}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	3.5367 $\times {10}^{-1}$		3.7686 $\times {10}^{-2}$		1.8781 $\times {10}^{-1}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	1.7793 $\times {10}^{-1}$	0.9910	1.0722 $\times {10}^{-2}$	1.8134	4.9621 $\times {10}^{-2}$	1.9202
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	8.9087 $\times {10}^{-2}$	0.9980	3.0838 $\times {10}^{-3}$	1.7978	1.2578 $\times {10}^{-2}$	1.9800
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{128}}$)	4.4556 $\times {10}^{-2}$	0.9995	9.6200 $\times {10}^{-4}$	1.6805	3.1535 $\times {10}^{-3}$	1.9958

We also test the influence of errors on the jump of coefficients. The results for errors $De$, $D^{\Pi }e$, and $D^{\mathcal{I}}e$ based on SNIPFEM and NNIPFEM are listed in Table 5 with $(a_1,a_2)=(1,10)$, $(1,{10}^2)$, $\dots (1,{10}^6)$, and the fixed $(h_{1,x},h_{1,y})=(1/16,1/32)$ and $(h_{2,x},h_{2,y})=(1/32,1/64)$. We can observe that as $a_2/a_1$ becomes larger, the change of the errors is very small, which means that the errors are all independent of the jump of the coefficients.

Table 5. Study of the dependence of the errors for Example 1 on the jump of coefficients with $(a_1,a_2)=(1,10)$,$(1,{10}^2)$,$\dots (1,{10}^6)$, $(h_{1,x},h_{1,y})=(1/16,1/32)$, and $(h_{2,x},h_{2,y})=(1/32,1/64)$ for SNIPFEM and NNIPFEM, respectively.

$({\mathit{a}}_1,{\mathit{a}}_2)$	$(1,10)$	$(1,{10}^2)$	$(1,{10}^3)$	$(1,{10}^4)$	$(1,{10}^5)$	$(1,{10}^6)$
$De$	1.5041 $\times {10}^{-1}$	9.6301 $\times {10}^{-2}$	8.9066 $\times {10}^{-2}$	8.8309 $\times {10}^{-2}$	8.8233 $\times {10}^{-2}$	8.8226 $\times {10}^{-2}$
$D^{\Pi }e$	1.2868 $\times {10}^{-2}$	5.1235 $\times {10}^{-3}$	2.1790 $\times {10}^{-3}$	1.5790 $\times {10}^{-3}$	1.5056 $\times {10}^{-3}$	1.4981 $\times {10}^{-3}$
$D^{\mathcal{I}}e$	1.4935 $\times {10}^{-2}$	1.2793 $\times {10}^{-2}$	1.2544 $\times {10}^{-2}$	1.2519 $\times {10}^{-2}$	1.2516 $\times {10}^{-2}$	1.2516 $\times {10}^{-2}$
$De$	1.5081 $\times {10}^{-1}$	9.6426 $\times {10}^{-2}$	8.9087 $\times {10}^{-2}$	8.8319 $\times {10}^{-2}$	8.8241 $\times {10}^{-2}$	8.8234 $\times {10}^{-2}$
$D^{\Pi }e$	1.7818 $\times {10}^{-2}$	7.5053 $\times {10}^{-3}$	3.0838 $\times {10}^{-3}$	2.1238 $\times {10}^{-3}$	2.0018 $\times {10}^{-3}$	1.9892 $\times {10}^{-3}$
$D^{\mathcal{I}}e$	1.4922 $\times {10}^{-2}$	1.2824 $\times {10}^{-2}$	1.2578 $\times {10}^{-2}$	1.2552 $\times {10}^{-2}$	1.2550 $\times {10}^{-2}$	1.2550 $\times {10}^{-2}$

4.2. Example 2

In this example, we choose suitable $f,g_D$, and $g_N$ values such that the exact solution is as follows:

$$u(x,y)=\left\{\begin{array}{cc}{\displaystyle \frac{sin\left(2\pi x\right)sin\left(2\pi y\right)+2xy}{a_1}}\hfill & \mathrm{in}{\Omega }_1,\\ {\displaystyle \frac{sin\left(2\pi x\right)sin\left(2\pi y\right)}{a_2}}\hfill & \mathrm{in}{\Omega }_2.\end{array}\right.$$

(27)

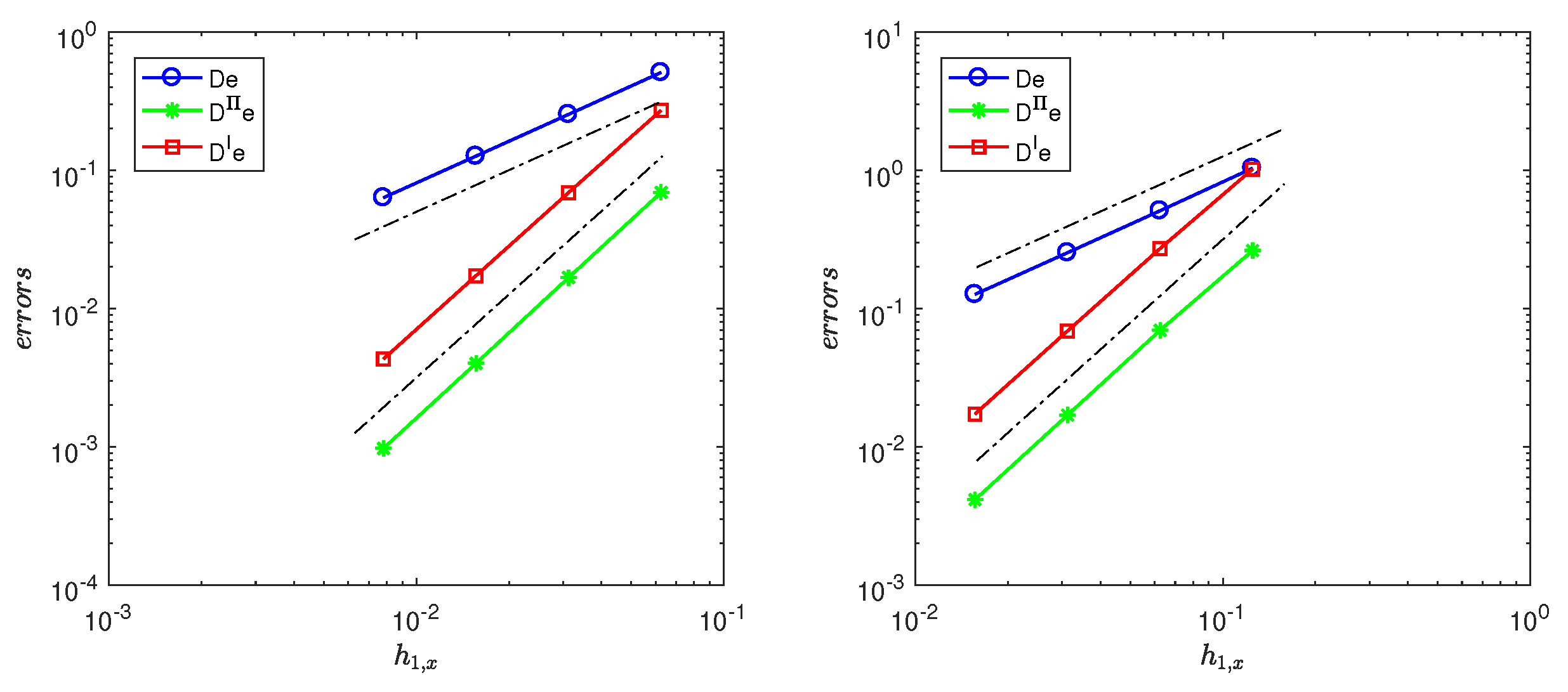
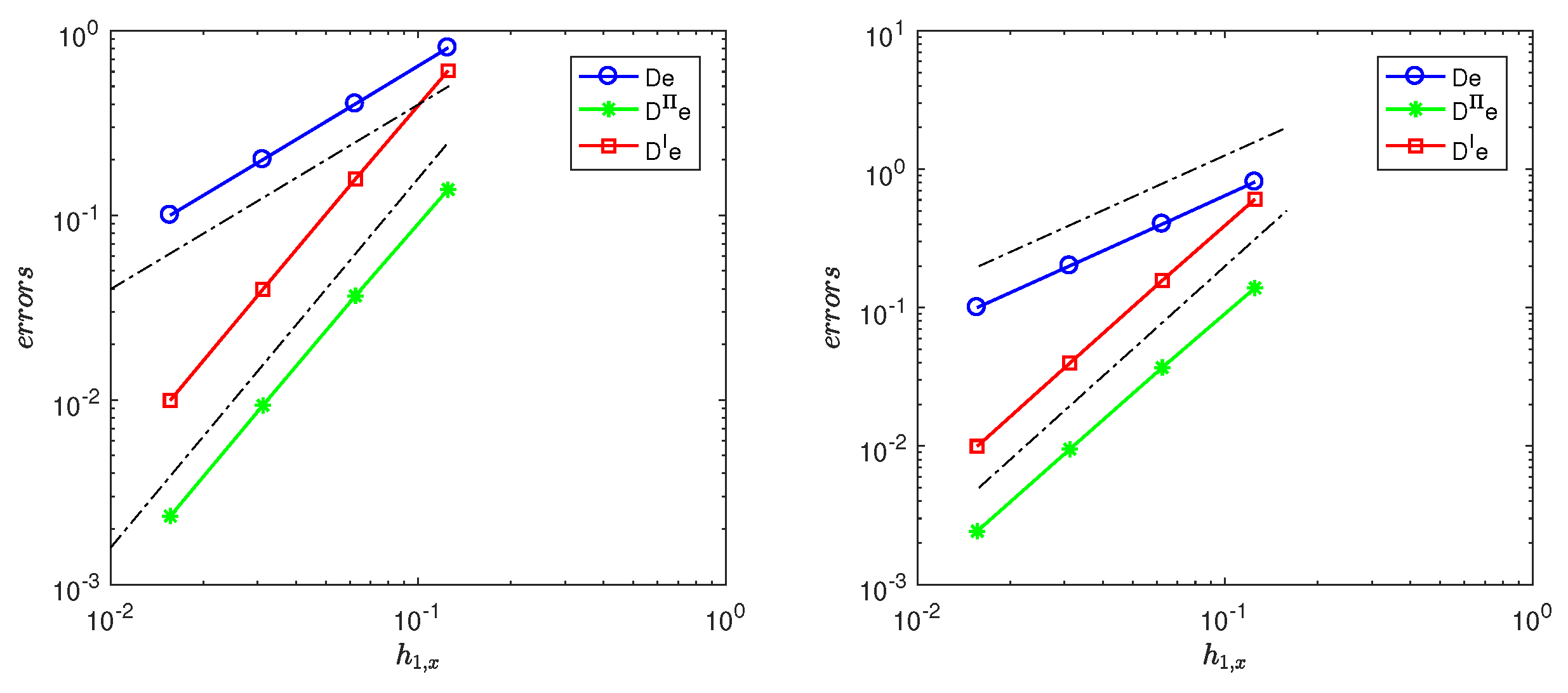
Note that elliptic interface problems have nonhomogeneous jump conditions, namely, $g_D\ne 0$ and $g_N\ne 0$. Figure 2 and Figure 3 and Table 6 and Table 7 report the convergence rates of errors for our NIPFEM based on square and rectangular meshes. For $De$, all two methods (SNIPFEM and NNIPFEM) converge with the optimal rate $O\left(h_i\right)$ for square and rectangular meshes. As for $D^{\Pi }e$ and $D^{\mathcal{I}}e$, $O\left(h_i^2\right)$, the order of convergence can be observed for all cases, and it is superior to the $O\left(h_i^{3/2}\right)$ presented in Theorems 2 and 3 we developed. Table 8 displays the influence of errors on the jump of coefficients with a rectangular piecewise mesh $(h_{1,x},h_{1,y})=(1/16,1/32)$ and $(h_{2,x},h_{2,y})=(1/32,1/64)$ for our NIPFEM. It is shown that the errors are not sensitive to the jump of the coefficients.

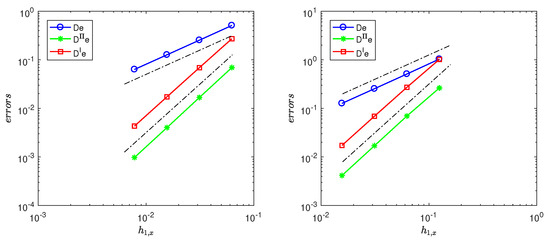
Figure 2. (Left): Log–log plot of errors $De$, $D^{\Pi }e$, and $D^{\mathcal{I}}e$ versus $h_{1,x}$ with $h_{1,x}={\displaystyle \frac{1}{16}},{\displaystyle \frac{1}{32}},{\displaystyle \frac{1}{64}},{\displaystyle \frac{1}{128}}$ based on square quasi-uniform meshes $h_{1,x}=h_{1,y}=h_{2,x}=h_{2,y}$ for $(a_2,a_1)=(1000,1)$ and $\gamma =10$ for SNIPFEM. The dotted line gives the reference lines of slope 1 and 2. (Right): Log–log plot of errors $De$, $D^{\Pi }e$, and $D^{\mathcal{I}}e$ versus $h_{1,x}$ with $h_{1,x}={\displaystyle \frac{1}{8}},{\displaystyle \frac{1}{16}},{\displaystyle \frac{1}{32}},{\displaystyle \frac{1}{64}}$ based on square piecewise meshes $h_{1,x}=h_{1,y}$ and $h_{2,x}=h_{2,y}={\displaystyle \frac{h_{1,x}}{2}}$ for $(a_2,a_1)=(1000,1)$ and $\gamma =10$ for SNIPFEM. The dotted line gives the reference lines of slope 1 and 2.

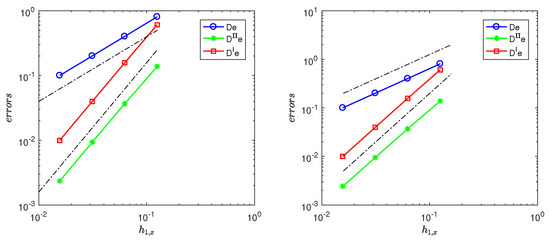
Figure 3. (Left): Log–log plot of errors $De$, $D^{\Pi }e$, and $D^{\mathcal{I}}e$ versus $h_{1,x}$ with $h_{1,x}={\displaystyle \frac{1}{8}},{\displaystyle \frac{1}{16}},{\displaystyle \frac{1}{32}},{\displaystyle \frac{1}{64}}$ based on rectangular quasi-uniform meshes $h_{1,x}=h_{2,x}$, $h_{1,y}=h_{2,y}={\displaystyle \frac{h_{1,x}}{2}}$ for $(a_2,a_1)=(1000,1)$ and $\gamma =10$ for SNIPFEM. The dotted line gives the reference lines of slope 1 and 2. (Right): Log–log plot of errors $De$, $D^{\Pi }e$, and $D^{\mathcal{I}}e$ versus $h_{1,x}$ with $h_{1,x}={\displaystyle \frac{1}{8}},{\displaystyle \frac{1}{16}},{\displaystyle \frac{1}{32}},{\displaystyle \frac{1}{64}}$ based on rectangular piecewise meshes $h_{1,y}={\displaystyle \frac{h_{1,x}}{2}}$ and $h_{2,x}={\displaystyle \frac{h_{1,x}}{2}}$, $h_{2,y}={\displaystyle \frac{h_{1,y}}{2}}$ for $(a_2,a_1)=(1000,1)$ and $\gamma =10$ for SNIPFEM. The dotted line gives the reference lines of slope 1 and 2.

Table 6. Rates of errors for Example 2 based on square quasi-uniform and piecewise meshes with $\gamma =10$ and $a_1=1,a_2=1000$ for NNIPFEM.

$({\mathit{h}}_{1,\mathit{x}},{\mathit{h}}_{1,\mathit{y}})$	$({\mathit{h}}_{2,\mathit{x}},{\mathit{h}}_{2,\mathit{y}})$	$\mathit{D}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathbf{\Pi }}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathcal{I}}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	5.1043 $\times {10}^{-1}$		7.3770 $\times {10}^{-2}$		2.7228 $\times {10}^{-1}$
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	2.5368 $\times {10}^{-1}$	1.0086	1.7462 $\times {10}^{-2}$	2.0787	6.9024 $\times {10}^{-2}$	1.9799
(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{64}}$)	(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{64}}$)	1.2667 $\times {10}^{-1}$	1.0019	4.1175 $\times {10}^{-3}$	2.0844	1.7292 $\times {10}^{-2}$	1.9969
(${\displaystyle \frac{1}{128}}$,${\displaystyle \frac{1}{128}}$)	(${\displaystyle \frac{1}{128}}$,${\displaystyle \frac{1}{128}}$)	6.3316 $\times {10}^{-2}$	1.0004	9.8873 $\times {10}^{-4}$	2.0581	4.3221 $\times {10}^{-3}$	2.0002
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{8}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	1.0409 $\times {10}^{-0}$		2.8618 $\times {10}^{-1}$		1.0224 $\times {10}^{-0}$
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	5.1034 $\times {10}^{-1}$	1.0284	7.4612 $\times {10}^{-2}$	1.9394	2.7217 $\times {10}^{-1}$	1.9094
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{64}}$)	2.5362 $\times {10}^{-1}$	1.0087	1.7989 $\times {10}^{-2}$	2.0522	6.9001 $\times {10}^{-2}$	1.9798
(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{64}}$)	(${\displaystyle \frac{1}{128}}$,${\displaystyle \frac{1}{128}}$)	1.2663 $\times {10}^{-1}$	1.0020	4.4065 $\times {10}^{-3}$	2.0294	1.7289 $\times {10}^{-2}$	1.9967

Table 7. Rates of errors for Example 2 based on rectangular quasi-uniform and piecewise meshes with $\gamma =10$ and $a_1=1,a_2=1000$ for NNIPFEM.

$({\mathit{h}}_{1,\mathit{x}},{\mathit{h}}_{1,\mathit{y}})$	$({\mathit{h}}_{2,\mathit{x}},{\mathit{h}}_{2,\mathit{y}})$	$\mathit{D}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathbf{\Pi }}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$	${\mathit{D}}^{\mathcal{I}}\mathit{e}$	$\mathit{R}\mathit{a}\mathit{t}\mathit{e}$
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	8.0920 $\times {10}^{-1}$		1.4805 $\times {10}^{-1}$		6.0783 $\times {10}^{-1}$
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	4.0160 $\times {10}^{-1}$	1.0107	3.8413 $\times {10}^{-2}$	1.9464	1.5756 $\times {10}^{-1}$	1.9476
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	2.0035 $\times {10}^{-1}$	1.0031	9.5984 $\times {10}^{-3}$	2.0007	3.9752 $\times {10}^{-2}$	1.9868
(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{128}}$)	(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{128}}$)	1.0012 $\times {10}^{-1}$	1.0008	2.3824 $\times {10}^{-3}$	2.0103	9.9597 $\times {10}^{-3}$	1.9968
(${\displaystyle \frac{1}{8}}$,${\displaystyle \frac{1}{16}}$)	(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	8.0907 $\times {10}^{-1}$		1.4914 $\times {10}^{-1}$		6.0755 $\times {10}^{-1}$
(${\displaystyle \frac{1}{16}}$,${\displaystyle \frac{1}{32}}$)	(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	4.0150 $\times {10}^{-1}$	1.0108	3.9040 $\times {10}^{-2}$	1.9336	1.5749 $\times {10}^{-1}$	1.9476
(${\displaystyle \frac{1}{32}}$,${\displaystyle \frac{1}{64}}$)	(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{128}}$)	2.0029 $\times {10}^{-1}$	1.0032	9.9301 $\times {10}^{-3}$	1.9750	3.9735 $\times {10}^{-2}$	1.9868
(${\displaystyle \frac{1}{64}}$,${\displaystyle \frac{1}{128}}$)	(${\displaystyle \frac{1}{128}}$,${\displaystyle \frac{1}{256}}$)	1.0008 $\times {10}^{-1}$	1.0008	2.5501 $\times {10}^{-3}$	1.9612	9.9560 $\times {10}^{-3}$	1.9967

Table 8. Study of the dependence of the errors on the jump of coefficients with $(a_1,a_2)=(1,10)$, $(1,{10}^2)$, $\dots (1,{10}^6)$, $(h_{1,x},h_{1,y})=(1/16,1/32)$, and $(h_{2,x},h_{2,y})=(1/32,1/64)$ for SNIPFEM and NNIPFEM, respectively.

$({\mathit{a}}_1,{\mathit{a}}_2)$	$(1,10)$	$(1,{10}^2)$	$(1,{10}^3)$	$(1,{10}^4)$	$(1,{10}^5)$	$(1,{10}^6)$
$De$	4.0771 $\times {10}^{-1}$	4.0199 $\times {10}^{-1}$	4.0134 $\times {10}^{-1}$	4.0128 $\times {10}^{-1}$	4.0127 $\times {10}^{-1}$	4.0127 $\times {10}^{-1}$
$D^{\Pi }e$	5.3341 $\times {10}^{-2}$	3.9508 $\times {10}^{-2}$	3.6929 $\times {10}^{-2}$	3.6648 $\times {10}^{-2}$	3.6620 $\times {10}^{-2}$	3.6617 $\times {10}^{-2}$
$D^{\mathcal{I}}e$	1.5806 $\times {10}^{-1}$	1.5739 $\times {10}^{-1}$	1.5732 $\times {10}^{-1}$	1.5731 $\times {10}^{-1}$	1.5731 $\times {10}^{-1}$	1.5731 $\times {10}^{-1}$
$De$	4.0913 $\times {10}^{-1}$	4.0237 $\times {10}^{-1}$	4.0150 $\times {10}^{-1}$	4.0141 $\times {10}^{-1}$	4.0140 $\times {10}^{-1}$	4.0140 $\times {10}^{-1}$
$D^{\Pi }e$	6.5611 $\times {10}^{-2}$	4.4112 $\times {10}^{-2}$	3.9040 $\times {10}^{-2}$	3.8459 $\times {10}^{-2}$	3.8400 $\times {10}^{-2}$	3.8394 $\times {10}^{-2}$
$D^{\mathcal{I}}e$	1.5814 $\times {10}^{-1}$	1.5756 $\times {10}^{-1}$	1.5749 $\times {10}^{-1}$	1.5749 $\times {10}^{-1}$	1.5748 $\times {10}^{-1}$	1.5748 $\times {10}^{-1}$

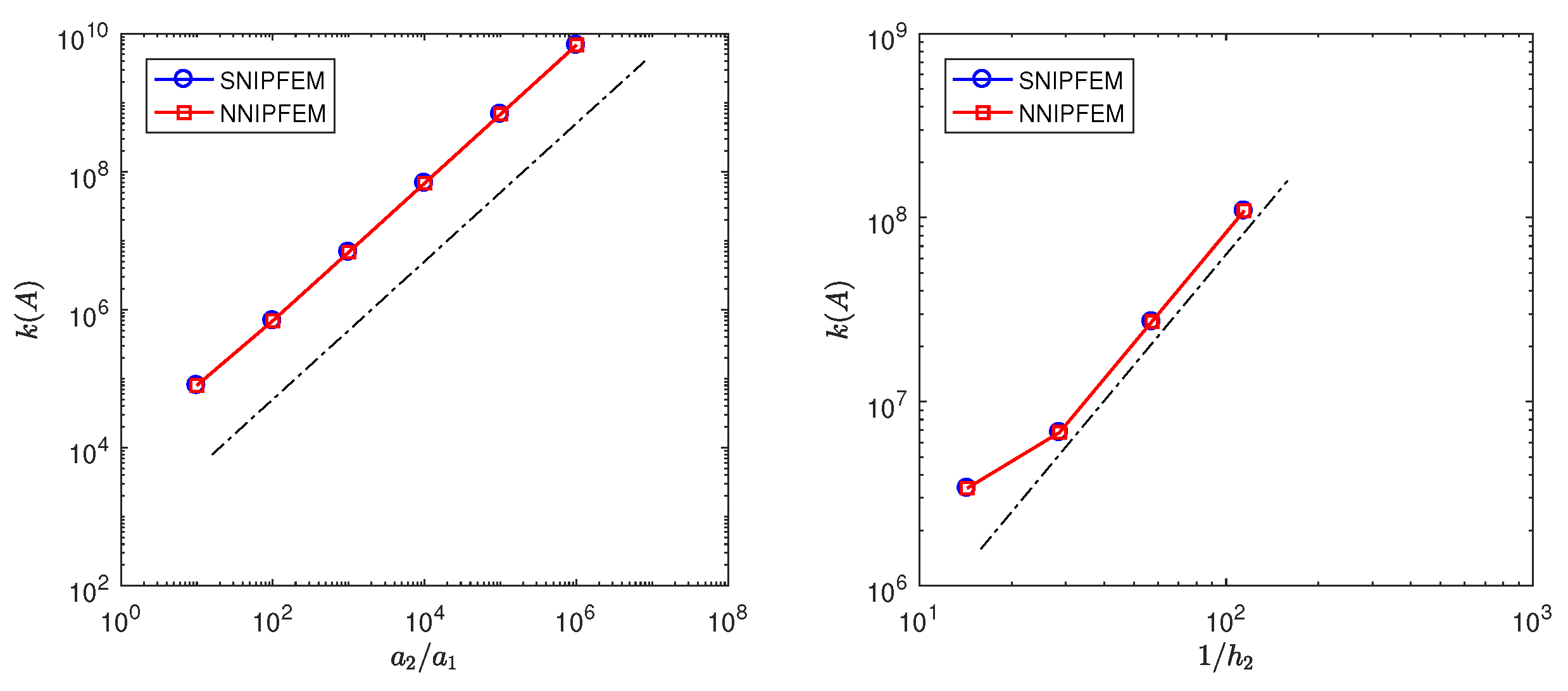
Finally, we provide two tests to report the condition number of the stiffness matrix. First, we fix the mesh size $h_{1,x}={\displaystyle \frac{1}{16}},h_{1,y}={\displaystyle \frac{1}{32}},h_{2,x}={\displaystyle \frac{1}{32}},h_{2,y}={\displaystyle \frac{1}{64}}$ and test the influence of the ratio of the coefficients on the condition number. Left of Figure 4 shows the log–log plot of condition number $\mathit{K}\left(\mathit{A}\right)$ versus $a_2/a_1$ with $(a_2,a_1)=(10,1)$, $({10}^2,1)$, $\dots ,({10}^6,1)$ for SNIPFEM and NNIPFEM. It shows that the condition number $\mathit{K}\left(\mathit{A}\right)$ depends on ${\displaystyle \frac{a_{max}}{a_{min}}}$ linearly, where $a_{max}=max\{a_1,a_2\}$ and $a_{min}=min\{a_1,a_2\}$. Second, we fix $a_1=1,a_2=1000$ and ${\displaystyle \frac{h_1}{h_2}}=2$ and change the value $h_2$ to test the influence of the mesh size on the condition number. Right of Figure 4 reports the log–log plot of condition number $\mathit{K}\left(\mathit{A}\right)$ versus $1/h_2$ with $(h_{2,x},h_{2,y})=({\displaystyle \frac{1}{8}},{\displaystyle \frac{1}{16}}),({\displaystyle \frac{1}{16}},{\displaystyle \frac{1}{32}}),({\displaystyle \frac{1}{32}},{\displaystyle \frac{1}{64}}),({\displaystyle \frac{1}{64}},{\displaystyle \frac{1}{128}})$ for SNIPFEM and NNIPFEM. We observe that $\mathit{K}\left(\mathit{A}\right)=O\left(h_{min}^{-2}\right)$, where $h_{min}=min\{h_1,h_2\}$.

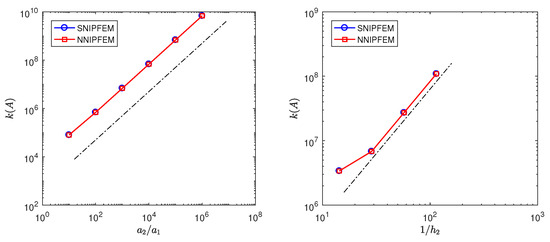
Figure 4. (Left): Log–log plot of condition number $\mathit{K}\left(\mathit{A}\right)$ versus $a_2/a_1$ with $(a_2,a_1)=(10,1)$, $({10}^2,1)$, $\dots ,({10}^6,1)$, fixed $h_{1,x}={\displaystyle \frac{1}{16}},h_{1,y}={\displaystyle \frac{1}{32}},h_{2,x}={\displaystyle \frac{1}{32}},h_{2,y}={\displaystyle \frac{1}{64}}$, and $\gamma =10$ for SNIPFEM and NNIPFEM, respectively. The dotted line gives the reference line of slope 1. (Right): Log–log plot of condition number $\mathit{K}\left(\mathit{A}\right)$ versus $1/h_2$ with $(h_{2,x},h_{2,y})=({\displaystyle \frac{1}{8}},{\displaystyle \frac{1}{16}}),({\displaystyle \frac{1}{16}},{\displaystyle \frac{1}{32}}),({\displaystyle \frac{1}{32}},{\displaystyle \frac{1}{64}}),({\displaystyle \frac{1}{64}},{\displaystyle \frac{1}{128}})$, and fixed $(a_2,a_1)=(1000,1)$, ${\displaystyle \frac{h_1}{h_2}}=2$ and $\gamma =10$ for SNIPFEM and NNIPFEM, respectively. The dotted line gives the reference line of slope 2.

5. Conclusions

In this article, we study the superconvergence theory of the nonconforming interface penalty finite element method to solve elliptic interface problems based on body-fitted and rectangular piecewise meshes. We have obtained the supercloseness result between the numerical solution and the interpolation of the exact solution. Moreover, we have applied a postprocessing operator and have proved the superconvergence result between the postprocessed gradient and the exact gradient. Two numerical examples have been presented to support our theoretical results, and it is shown that the supercloseness and superconvergence results based on quasi-uniform and piecewise meshes for both SNIPFEM and NNIPFEM are better than the theoretical results, especially as $D^{\mathcal{I}}e$ superconverges at the order of $O\left(h_i^2\right)$. It is well known that the triangular meshes are efficiently solving the interface problems with complicated interface. Hence, studying the superconvergence of the nonconforming element based on a triangular mesh for interface problems is a future direction for our research.