A Dynamic Pole Motion Approach for Control of Nonlinear Hybrid Soft Legs: A Preliminary Study
Abstract
:1. Introduction
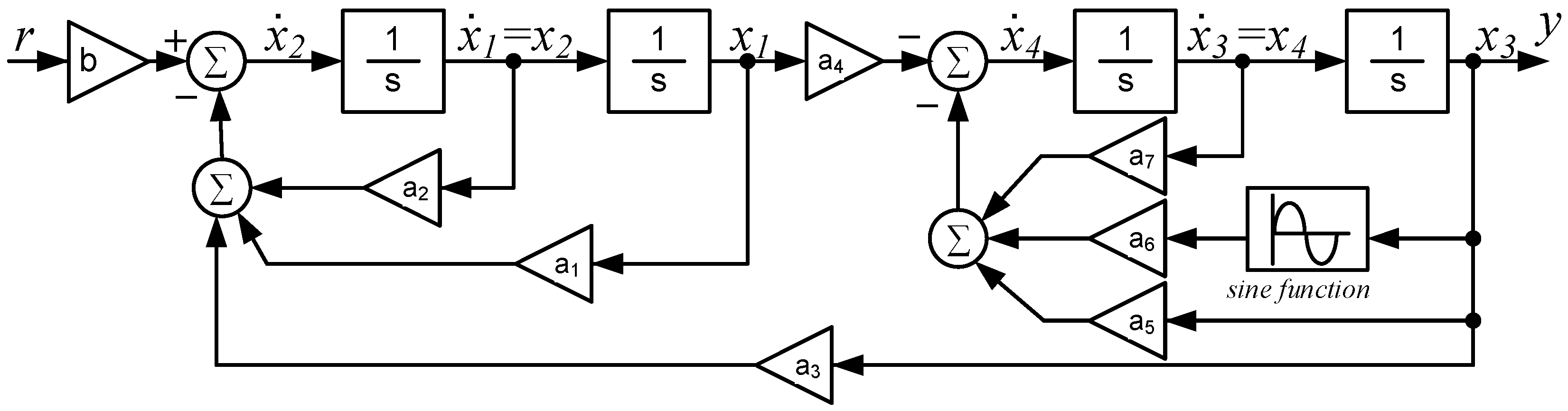
2. Analysis of a Motorized Hybrid Soft Leg: Dynamic Routh’s Stability Criterion for Nonlinear Systems
- (a)
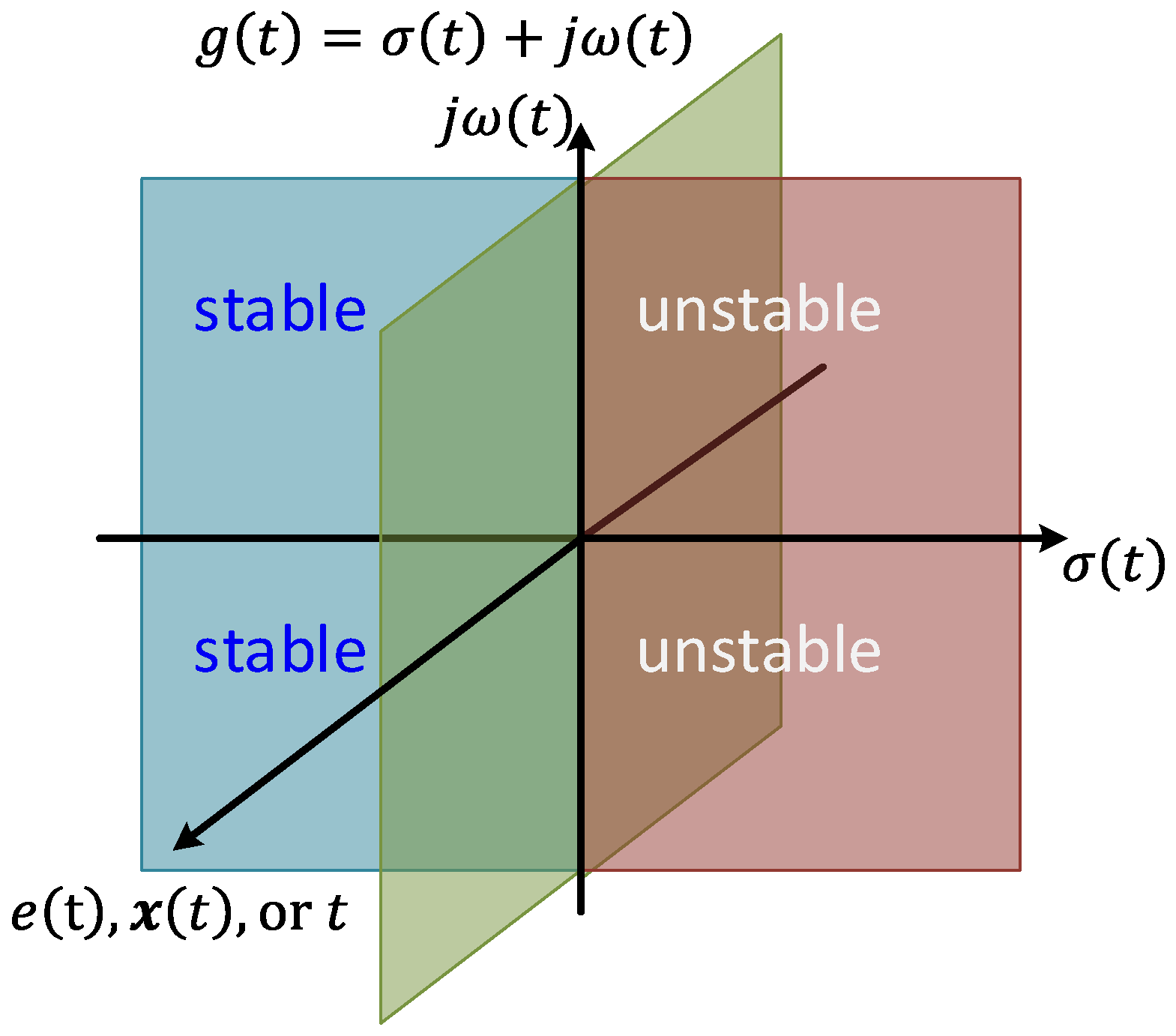
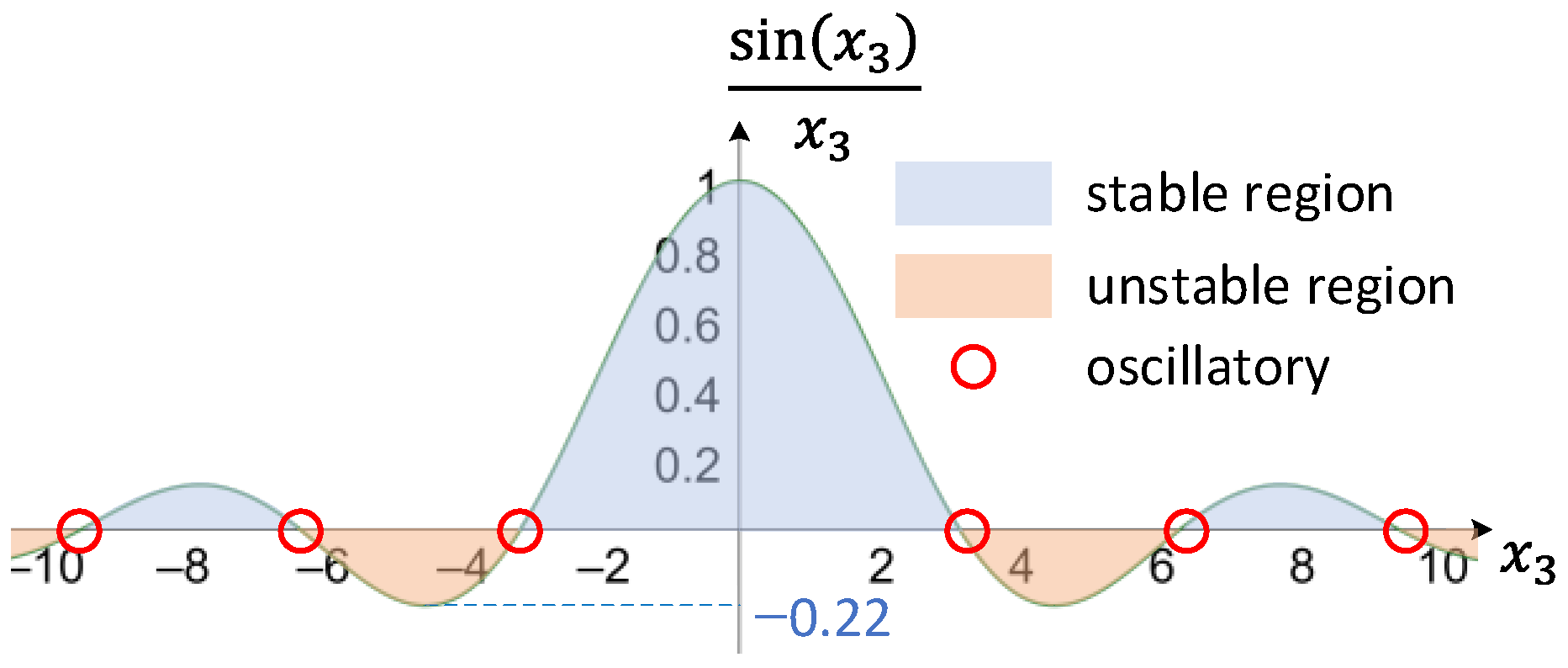
- For stability of the system, all the elements in the first column of the dynamic Routh’s array must be positive non-zero values. Thus, we find that from all the conditions of , , and from each row, which means the condition of should be met to make the system stable. The stability region of is graphically represented in Figure 5.
- (b)
- Zero value at any rows in the first column of the dynamic Routh’s array represents that oscillatory dynamic poles are located on the imaginary axis of the g-plane, which indicates instability of the system. Zero value exists only if , which occurs periodically.
- (c)
- As the conventional Routh’s stability criterion, the dynamic Routh’s stability criterion can indicate the number of dynamic poles on the right-hand plane (RHP) of the g-plane by the number of sign (+ or −) changes in the first column of the dynamic Routh’s array. From the array, it can be found that one sign change could occur, which represents that one dynamic pole could be located in RHP of the g-plane when the system is not stable. Without a sign change, no dynamic poles are located in RHP of the g-plane, and the system is stable.
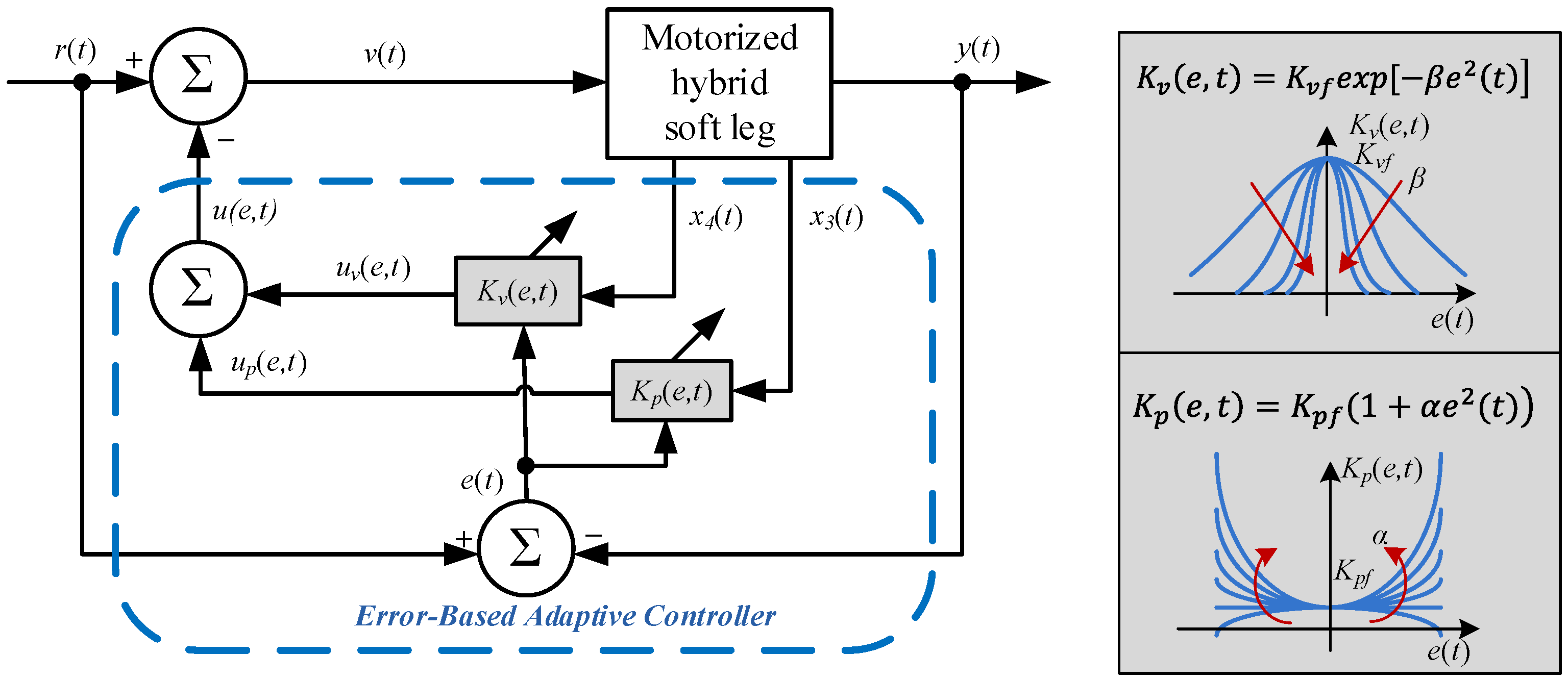
3. Error-Based Adaptive Controller (E-BAC) for the Motorized Hybrid Soft Leg
‘As error decreases from a large value to a small value, is continuously decreased from a very large value to a small value, and simultaneously, is increased from a small value to a large value’.
- (a)
- For the stability of the hybrid soft leg system, the dynamic poles should be always located on LHP on the g-plane for all values of .
- (b)
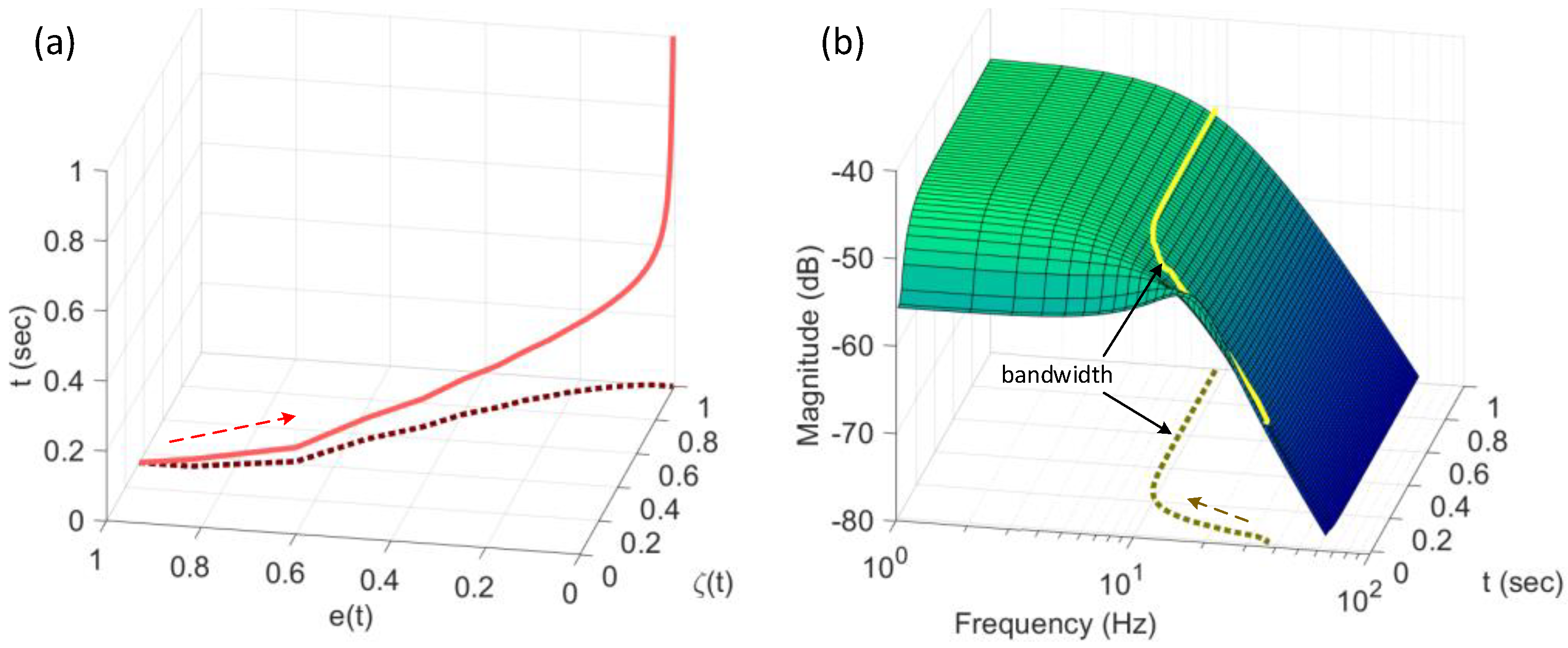
- For achieving the fast response time, the system must have a large bandwidth for large errors and small bandwidth for small errors. Thus, the position feedback as the bandwidth parameter must be a function of the system error .
- (c)
- For no overshoot in the system response, damping should be adjusted continuously as a function of . and are designed such that they yield a small damping ratio with a large bandwidth for large errors, and a large damping ratio with small bandwidth for small errors.
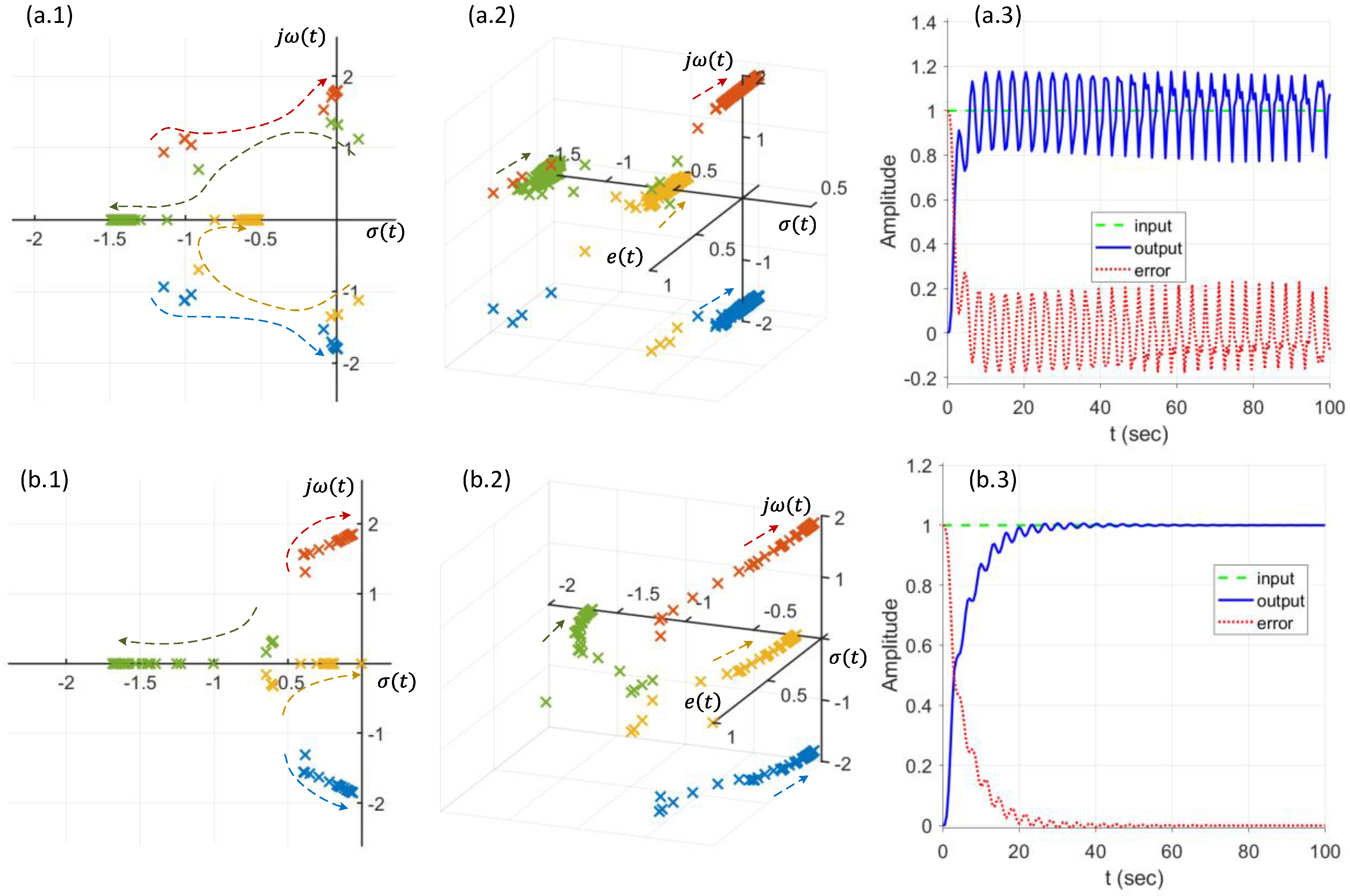
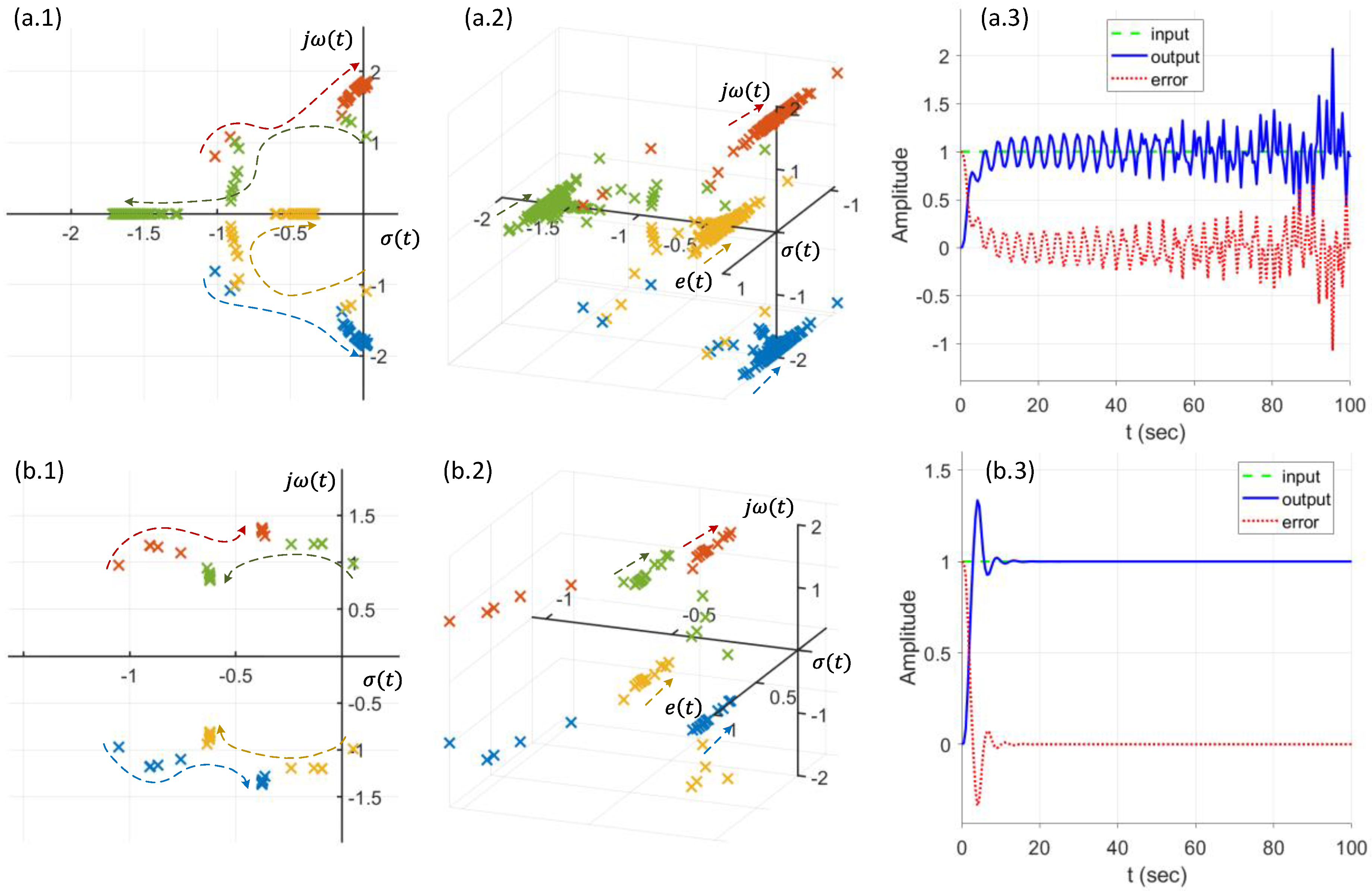
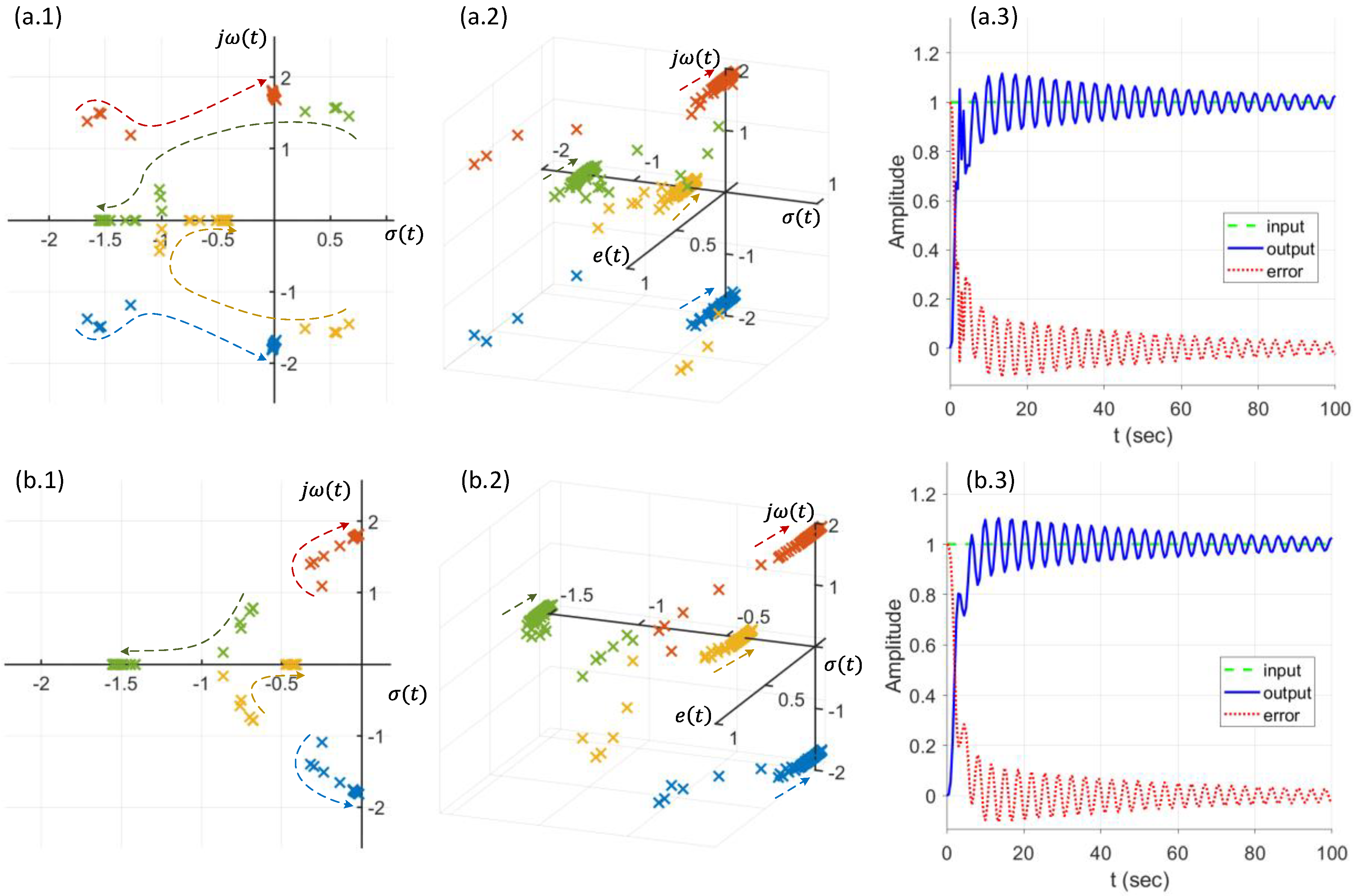
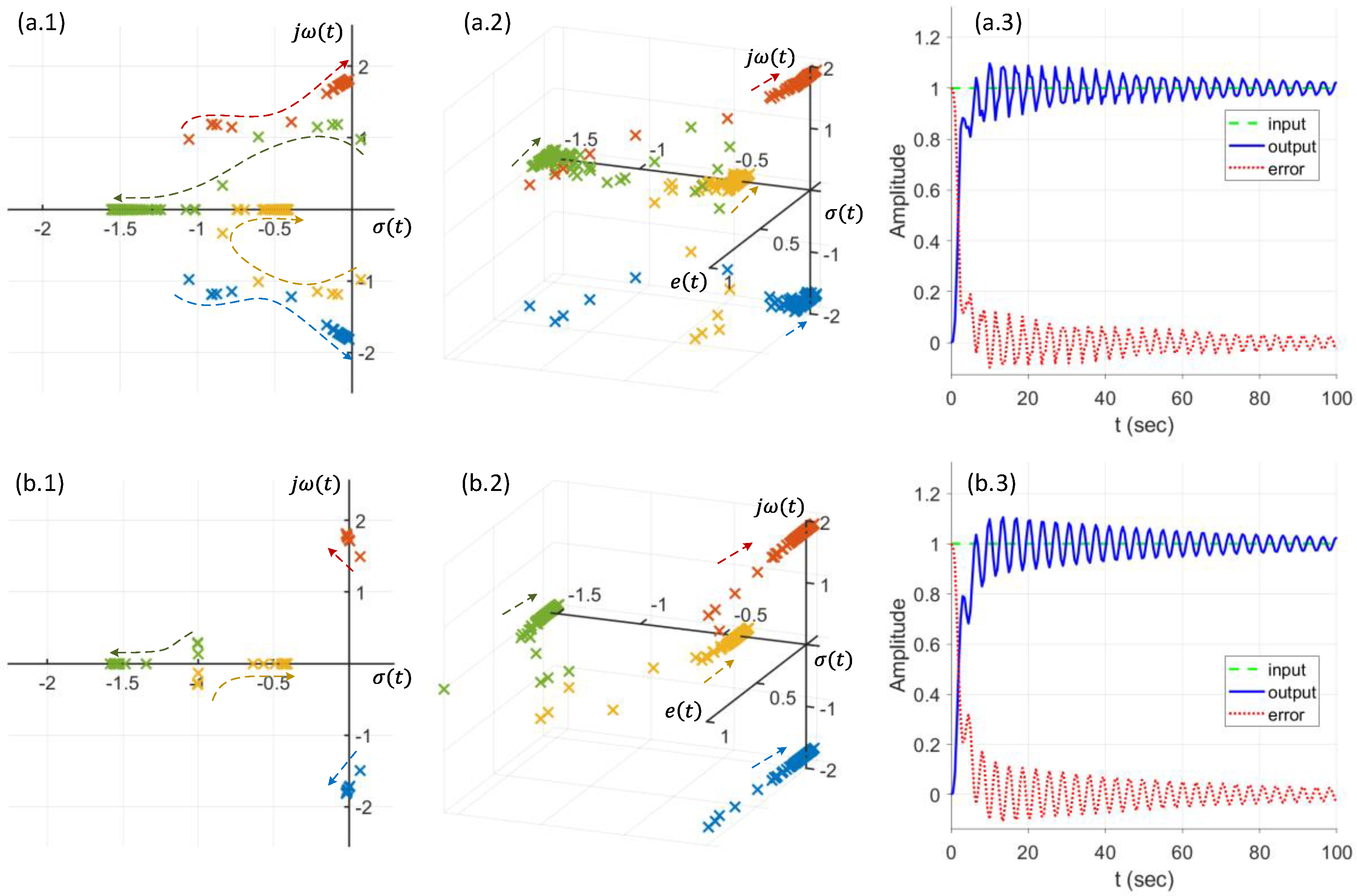
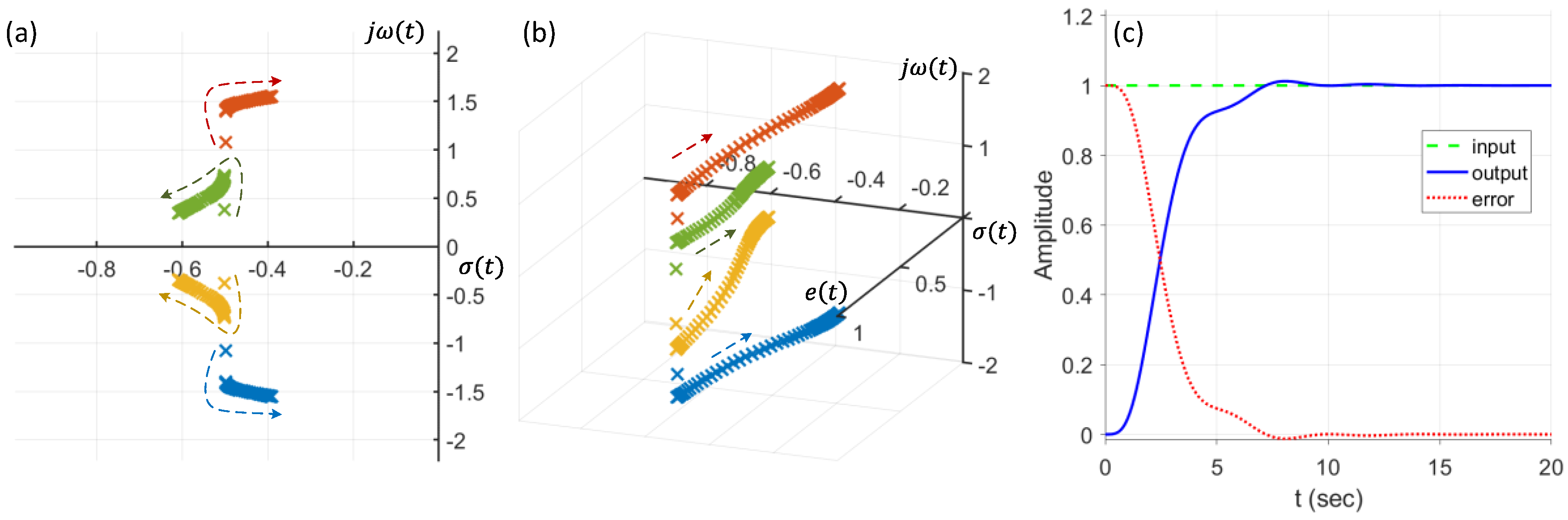
4. Simulation Study and Results
5. Discussion and Conclusions
- ○
- The dynamic pole motion approach based on the g-plane is effective to control the NLTV hybrid soft leg systems.
- ○
- The dynamic Routh’s stability criteria can quickly confirm the instability of the NLTV hybrid soft leg system.
- ○
- The E-BAC can control an unstable state of the NLTV hybrid soft leg system to quickly get back to a stable state of the system without any overshoot.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, Q.; Mahtab, B.; Zhao, F.; Song, K.Y.; Feng, Y. Bioinspiration to Robot Locomotion implementing 3D printed Foxtail Grass. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 27–31 December 2021; pp. 69–73. [Google Scholar]
- Kim, D.; Jorgensen, S.J.; Lee, J.; Ahn, J.; Luo, J.; Sentis, L. Dynamic locomotion for passive-ankle biped robots and humanoids using whole-body locomotion control. Int. J. Robot. Res. 2020, 39, 936–956. [Google Scholar] [CrossRef]
- Wu, Q.; Yang, X.; Wu, Y.; Zhou, Z.; Wang, J.; Zhang, B.; Luo, Y.; Chepinskiy, S.A.; Zhilenkov, A.A. A novel underwater bipedal walking soft robot bio-inspired by the coconut octopus. Bioinspiration Biomim. 2021, 16, 046007. [Google Scholar] [CrossRef] [PubMed]
- Hyun, D.J.; Seok, S.O.; Lee, J.; Kim, S. High speed trot-running: Implementation of a hierarchical controller using proprioceptive impedance control on the MIT Cheetah. Int. J. Robot. Res. 2014, 33, 1417–1445. [Google Scholar] [CrossRef]
- Tanaka, H.; Chen, T.-Y.; Hosoda, K. Dynamic Turning of a Soft Quadruped Robot by Changing Phase Difference. Front. Robot. AI 2021, 8, 629523. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Gao, H.; Ding, L.; Li, M.; Deng, Z.; Liu, G. Gait Generation with Smooth Transition Using CPG-Based Locomotion Control for Hexapod Walking Robot. IEEE Trans. Ind. Electron. 2016, 63, 5488–5500. [Google Scholar] [CrossRef]
- Fu, J.; Zhang, J.; She, Z.; Ovur, S.E.; Li, W.; Qi, W.; Su, H.; Ferrigno, G.; De Momi, E. Whole-body Spatial Teleoperation Control of a Hexapod Robot in Unstructured Environment. In Proceedings of the 2021 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021; pp. 93–98. [Google Scholar]
- Grzelczyk, D.; Szymanowska, O.; Awrejcewicz, J. Kinematic and dynamic simulation of an octopod robot controlled by different central pattern generators. Proc. Inst. Mech. Eng. Part I: J. Syst. Control. Eng. 2019, 233, 400–417. [Google Scholar] [CrossRef]
- Kumar, V.A.; Meenakshipriya, B.; Bijoy Antony, P.T.; Adithya, B.; Vikinesh, M.H. Design and Fabrication of Octopod for Survey and Rescue Operation. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1055, 012021. [Google Scholar] [CrossRef]
- Wang, F.; Qian, Z.; Yan, Z.; Yuan, C.; Zhang, W. A Novel Resilient Robot: Kinematic Analysis and Experimentation. IEEE Access 2020, 8, 2885–2892. [Google Scholar] [CrossRef]
- Wang, Z.; Qian, Z.; Song, Z.; Liu, H.; Zhang, W.; Bi, Z. Instrumentation and self-repairing control for resilient multi-rotor aircrafts. Ind. Robot. Int. J. Robot. Res. Appl. 2019, 45, 647–656. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, W.; Gupta, M.M. Resilient Robots: Concept, Review, and Future Directions. Robotics 2017, 6, 22. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.H.; Yang, G.S.; Zhang, B.; Zhang, W.J. On the concept of the resilient machine. In Proceedings of the 2011 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 357–360. [Google Scholar]
- Manoonpong, P.; Patanè, L.; Xiong, X.; Brodoline, I.; Dupeyroux, J.; Viollet, S.; Arena, P.; Serres, J.R. Insect-Inspired Robots: Bridging Biological and Artificial Systems. Sensors 2021, 21, 7609. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liang, Z.; Zhu, Y.; Zhao, J. Improving Kinematic Flexibility and Walking Performance of a Six-legged Robot by Rationally Designing Leg Morphology. J. Bionic Eng. 2019, 16, 608–620. [Google Scholar] [CrossRef]
- Weihmann, T. Survey of biomechanical aspects of arthropod terrestrialisation—Substrate bound legged locomotion. Arthropod Struct. Dev. 2020, 59, 100983. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Xu, M.; Li, W.; Zhang, S. Design and Implementation of a Soft Robotic Arm Driven by SMA Coils. IEEE Trans. Ind. Electron. 2018, 66, 6108–6116. [Google Scholar] [CrossRef]
- Zhou, D.; Zuo, W.; Tang, X.; Deng, J.; Liu, Y. A multi-motion bionic soft hexapod robot driven by self-sensing controlled twisted artificial muscles. Bioinspiration Biomim. 2021, 16, 045003. [Google Scholar] [CrossRef]
- Chen, A.; Yin, R.; Cao, L.; Yuan, C.; Ding, H.K.; Zhang, W.J. Soft robotics: Definition and research issues. In Proceedings of the 2017 24th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 21–23 November 2017; pp. 366–370. [Google Scholar]
- Tony, A.; Rasouli, A.; Farahinia, A.; Wells, G.; Zhang, H.; Achenbach, S.; Yang, S.M.; Sun, W.; Zhang, W. Toward a Soft Microfluidic System: Concept and Preliminary Developments. In Proceedings of the 2021 27th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Shanghai, China, 26–28 November 2021; pp. 755–759. [Google Scholar]
- Cao, L.; Dolovich, A.T.; Chen, A.; Zhang, W. Topology optimization of efficient and strong hybrid compliant mechanisms using a mixed mesh of beams and flexure hinges with strength control. Mech. Mach. Theory 2018, 121, 213–227. [Google Scholar] [CrossRef]
- Cheng, L.; Lin, Y.; Hou, Z.-G.; Tan, M.; Huang, J.; Zhang, W.J. Adaptive Tracking Control of Hybrid Machines: A Closed-Chain Five-Bar Mechanism Case. IEEE/ASME Trans. Mechatron. 2011, 16, 1155–1163. [Google Scholar] [CrossRef]
- Zhang, W.J.; Ouyang, P.R.; Sun, Z.H. A novel hybridization design principle for intelligent mechatronics systems. In Proceedings of the Abstracts of the International Conference on Advanced Mechatronics: Toward Evolutionary Fusion of IT and Mechatronics: ICAM 2010.5, Toyonaka, Japan, 4–6 October 2010; pp. 67–74. [Google Scholar]
- Wang, K.; Yin, R.; Lu, Y.; Qiao, H.; Zhu, Q.; He, J.; Zhou, W.; Zhang, H.; Tang, T.; Zhang, W. Soft-hard hybrid covalent-network polymer sponges with super resilience, recoverable energy dissipation and fatigue resistance under large deformation. Mater. Sci. Eng. C 2021, 126, 112185. [Google Scholar] [CrossRef]
- Stokes, A.; Shepherd, R.; Morin, S.A.; Ilievski, F.; Whitesides, G.M. A Hybrid Combining Hard and Soft Robots. Soft Robot. 2014, 1, 70–74. [Google Scholar] [CrossRef]
- Stano, G.; Percoco, G. Additive manufacturing aimed to soft robots fabrication: A review. Extreme Mech. Lett. 2020, 42, 101079. [Google Scholar] [CrossRef]
- Sachyani Keneth, E.; Kamyshny, A.; Totaro, M.; Beccai, L.; Magdassi, S. 3D Printing Materials for Soft Robotics. Adv. Mater. 2021, 33, 2003387. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Zhou, Z.; Gravish, N. Flexoskeleton Printing Enables Versatile Fabrication of Hybrid Soft and Rigid Robots. Soft Robot. 2020, 7, 770–778. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chortos, A. Control Strategies for Soft Robot Systems. Adv. Intell. Syst. 2022, 4, 2100165. [Google Scholar] [CrossRef]
- Tolley, M.T.; Shepherd, R.F.; Mosadegh, B.; Galloway, K.C.; Wehner, M.; Karpelson, M.; Wood, R.J.; Whitesides, G.M. A Resilient, Untethered Soft Robot. Soft Robot. 2014, 1, 213–223. [Google Scholar] [CrossRef]
- Martinez, R.V.; Branch, J.L.; Fish, C.R.; Jin, L.; Shepherd, R.F.; Nunes, R.M.; Suo, Z.; Whitesides, G.M. Robotic Tentacles with Three-Dimensional Mobility Based on Flexible Elastomers. Adv. Mater. 2013, 25, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Marchese, A.D.; Komorowski, K.; Onal, C.D.; Rus, D. Design and control of a soft and continuously deformable 2D robotic manipulation system. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2189–2196. [Google Scholar]
- Sepulchre, R.; Jankovic, M.; Kokotovic, P.V. Integrator forwarding: A new recursive nonlinear robust design. Automatica 1997, 33, 979–984. [Google Scholar] [CrossRef]
- Kalman, R.E. When Is a Linear Control System Optimal? J. Basic Eng. 1964, 86, 51–60. [Google Scholar] [CrossRef]
- Skorina, E.H.; Luo, M.; Tao, W.; Chen, F.; Fu, J.; Onal, C.D. Adapting to Flexibility: Model Reference Adaptive Control of Soft Bending Actuators. IEEE Robot. Autom. Lett. 2017, 2, 964–970. [Google Scholar] [CrossRef]
- Cao, G.; Liu, Y.; Zhu, Z. Observer-based Adaptive Robust Control of Soft Pneumatic Network Actuators. Int. J. Control. Autom. Syst. 2022, 20, 1695–1705. [Google Scholar] [CrossRef]
- Gerboni, G.; Diodato, A.; Ciuti, G.; Cianchetti, M.; Menciassi, A. Feedback Control of Soft Robot Actuators via Commercial Flex Bend Sensors. IEEE/ASME Trans. Mechatron. 2017, 22, 1881–1888. [Google Scholar] [CrossRef]
- Li, D.; Dornadula, V.; Lin, K.; Wehner, M. Position Control for Soft Actuators, Next Steps toward Inherently Safe Interaction. Electronics 2021, 10, 1116. [Google Scholar] [CrossRef]
- Khan, A.H.; Shao, Z.; Li, S.; Wang, Q.; Guan, N. Which is the best PID variant for pneumatic soft robots an experimental study. IEEE/CAA J. Autom. Sin. 2020, 7, 451–460. [Google Scholar] [CrossRef]
- Katzschmann, R.K.; Thieffry, M.; Goury, O.; Kruszewski, A.; Guerra, T.-M.; Duriez, C.; Rus, D. Dynamically Closed-Loop Controlled Soft Robotic Arm using a Reduced Order Finite Element Model with State Observer. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Korea, 14–18 April 2019; pp. 717–724. [Google Scholar] [CrossRef]
- Zhang, Z.; Dequidt, J.; Kruszewski, A.; Largilliere, F.; Duriez, C. Kinematic modeling and observer based control of soft robot using real-time Finite Element Method. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 5509–5514. [Google Scholar] [CrossRef]
- Marchese, A.D.; Tedrake, R.; Rus, D. Dynamics and trajectory optimization for a soft spatial fluidic elastomer manipulator. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2528–2535. [Google Scholar]
- Van Meerbeek, I.M.; De Sa, C.M.; Shepherd, R.F. Soft optoelectronic sensory foams with proprioception. Sci. Robot. 2018, 3, eaau2489. [Google Scholar] [CrossRef] [PubMed]
- Homberg, B.S.; Katzschmann, R.K.; Dogar, M.R.; Rus, D. Robust proprioceptive grasping with a soft robot hand. Auton. Robot. 2019, 43, 681–696. [Google Scholar] [CrossRef]
- Truby, R.L.; Della Santina, C.; Rus, D. Distributed Proprioception of 3D Configuration in Soft, Sensorized Robots via Deep Learning. IEEE Robot. Autom. Lett. 2020, 5, 3299–3306. [Google Scholar] [CrossRef]
- Kang, B.B.; Kim, D.; Choi, H.; Jeong, U.; Kim, K.B.; Jo, S.; Cho, K.-J. Learning-Based Fingertip Force Estimation for Soft Wearable Hand Robot With Tendon-Sheath Mechanism. IEEE Robot. Autom. Lett. 2020, 5, 946–953. [Google Scholar] [CrossRef]
- Glauser, O.; Wu, S.; Panozzo, D.; Hilliges, O.; Sorkine-Hornung, O. Interactive hand pose estimation using a stretch-sensing soft glove. ACM Trans. Graph. 2019, 38, 1–15. [Google Scholar] [CrossRef]
- Roberge, J.P.; Rispal, S.; Wong, T.; Duchaine, V. Unsupervised feature learning for classifying dynamic tactile events using sparse coding. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 2675–2681. [Google Scholar]
- Kim, D.; Kim, S.H.; Kim, T.; Kang, B.B.; Lee, M.; Park, W.; Ku, S.; Kim, D.; Kwon, J.; Lee, H.; et al. Review of machine learning methods in soft robotics. PLoS ONE 2021, 16, e0246102. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.J.; Triblehorn, J.D. Mechanical properties of the cuticles of three cockroach species that differ in their wind-evoked escape behavior. PeerJ 2014, 2, e501. [Google Scholar] [CrossRef]
- Sahu, B.K.; Gupta, M.M.; Subudhi, B. Stability analysis of nonlinear systems using dynamic-Routh’s stability criterion: A new approach. In Proceedings of the 2013 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Mysore, India, 22–25 August 2013; pp. 1765–1769. [Google Scholar]
- Song, K.; Gupta, M.M.; Jena, D.; Subudhi, B. Design of a robust neuro-controller for complex dynamic systems. In Proceedings of the NAFIPS 2009—2009 Annual Meeting of the North American Fuzzy Information Processing Society, Cincinnati, OH, USA, 14–17 June 2009; pp. 1–5. [Google Scholar]
- Song, K.-Y.; Gupta, M.M.; Jena, D. Design of an error-based robust adaptive controller. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 2386–2390. [Google Scholar] [CrossRef]
- Song, K.-Y.; Gupta, M.M.; Homma, N. Design of an Error-Based Adaptive Controller for a Flexible Robot Arm Using Dynamic Pole Motion Approach. J. Robot. 2011, 2011, 726807. [Google Scholar] [CrossRef]
- Laschi, C.; Cianchetti, M.; Mazzolai, B.; Margheri, L.; Follador, M.; Dario, P. Soft Robot Arm Inspired by the Octopus. Adv. Robot. 2012, 26, 709–727. [Google Scholar] [CrossRef]
- Soomro, A.M.; Memon, F.H.; Lee, J.-W.; Ahmed, F.; Kim, K.H.; Kim, Y.S.; Choi, K.H. Fully 3D printed multi-material soft bio-inspired frog for underwater synchronous swimming. Int. J. Mech. Sci. 2021, 210, 106725. [Google Scholar] [CrossRef]
- Almubarak, Y.; Punnoose, M.; Maly, N.X.; Hamidi, A.; Tadesse, Y. KryptoJelly: A jellyfish robot with confined, adjust pre-stress, and easily replaceable shape memory alloy NiTi actuators. Smart Mater. Struct. 2020, 29, 075011. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, K.-Y.; Behzadfar, M.; Zhang, W.-J. A Dynamic Pole Motion Approach for Control of Nonlinear Hybrid Soft Legs: A Preliminary Study. Machines 2022, 10, 875. https://doi.org/10.3390/machines10100875
Song K-Y, Behzadfar M, Zhang W-J. A Dynamic Pole Motion Approach for Control of Nonlinear Hybrid Soft Legs: A Preliminary Study. Machines. 2022; 10(10):875. https://doi.org/10.3390/machines10100875
Chicago/Turabian StyleSong, Ki-Young, Mahtab Behzadfar, and Wen-Jun Zhang. 2022. "A Dynamic Pole Motion Approach for Control of Nonlinear Hybrid Soft Legs: A Preliminary Study" Machines 10, no. 10: 875. https://doi.org/10.3390/machines10100875
APA StyleSong, K.-Y., Behzadfar, M., & Zhang, W.-J. (2022). A Dynamic Pole Motion Approach for Control of Nonlinear Hybrid Soft Legs: A Preliminary Study. Machines, 10(10), 875. https://doi.org/10.3390/machines10100875






