Solution of Spatial Transformation Relationship of Similar Ruled Surfaces Based on Registration of Divided Regions
Abstract
:1. Introduction
2. Description of Spatial Transformation Relationship
3. Solving the Spatial Transformation Relation
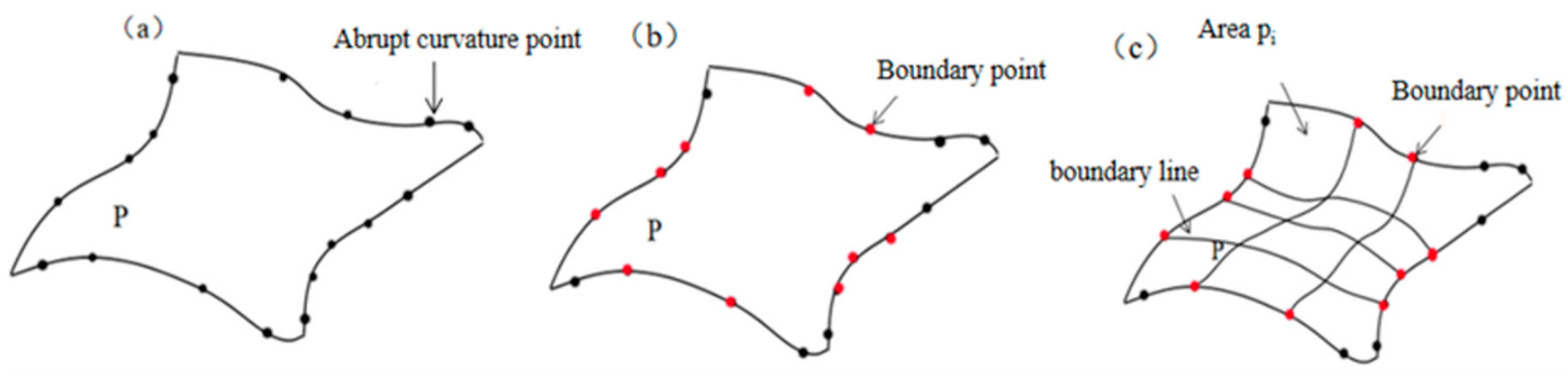
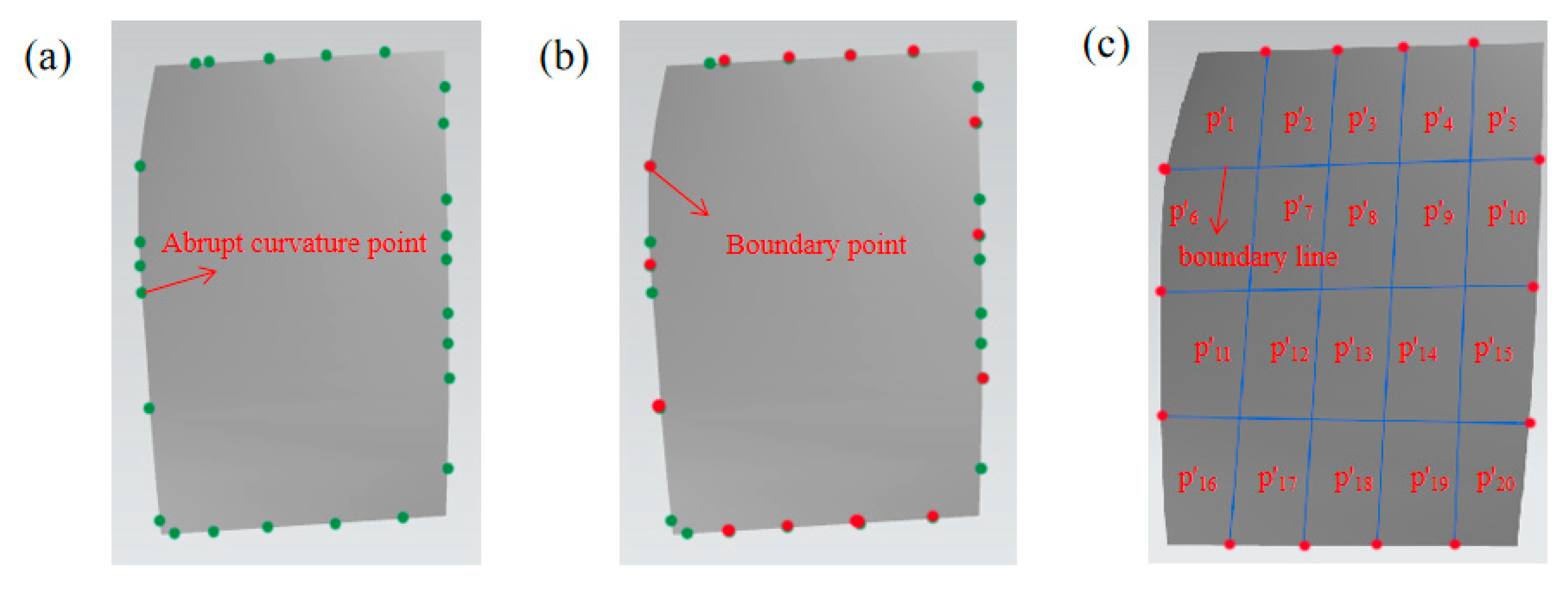
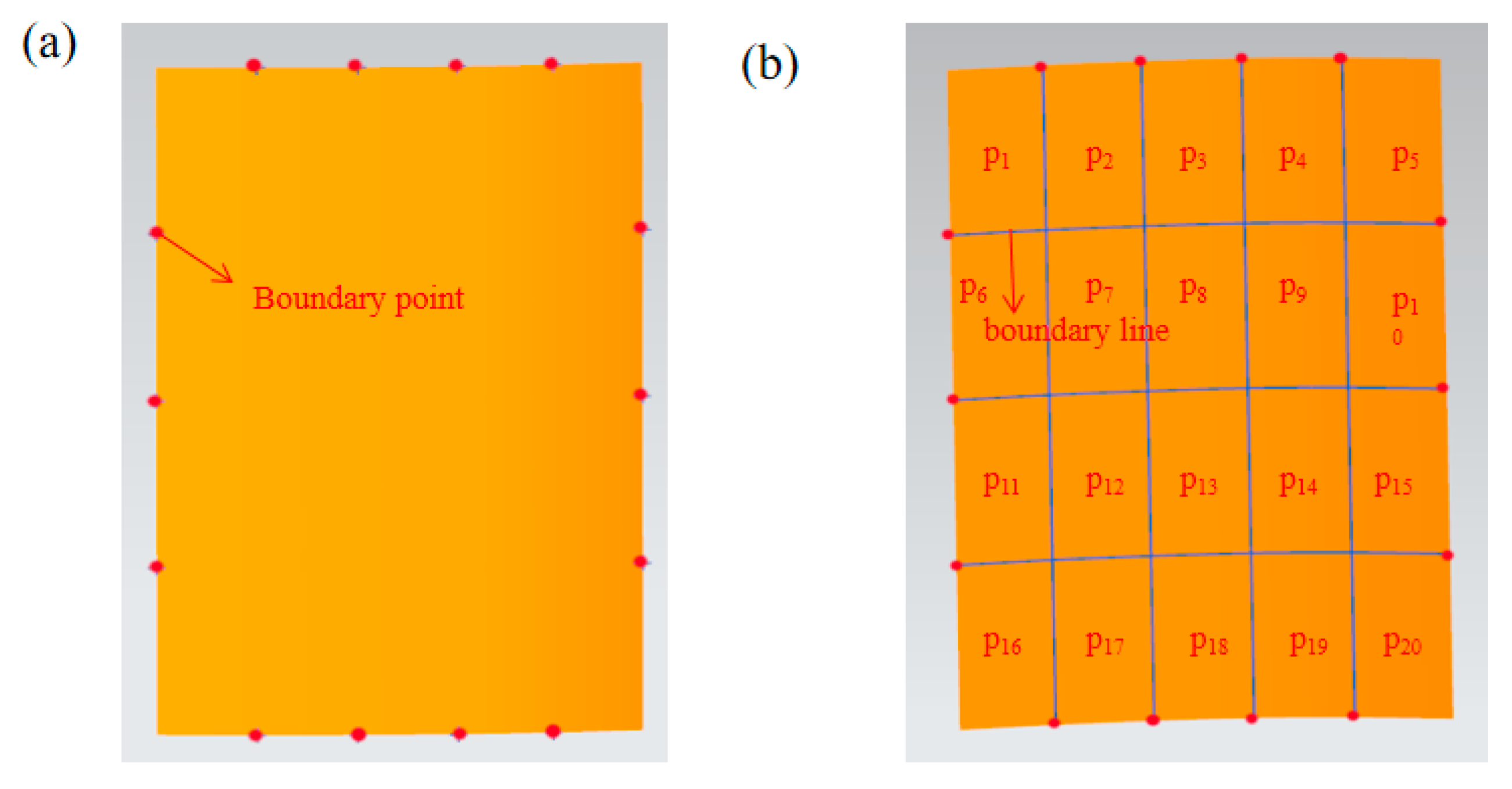
3.1. Adaptive Region Division Algorithm for Similar Surfaces
3.2. Similarity Judgment of Differential Geometric Properties
3.2.1. Curvature Property Constraints
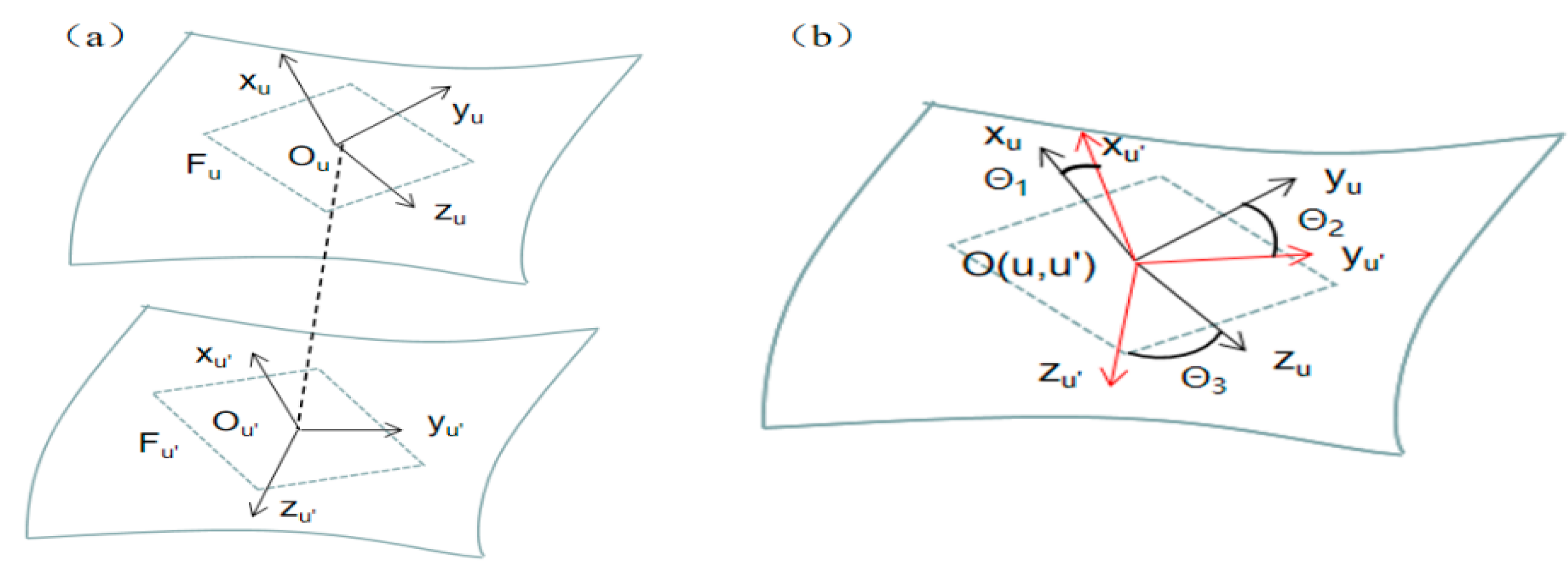
3.2.2. Local Coordinate System Property Constraints
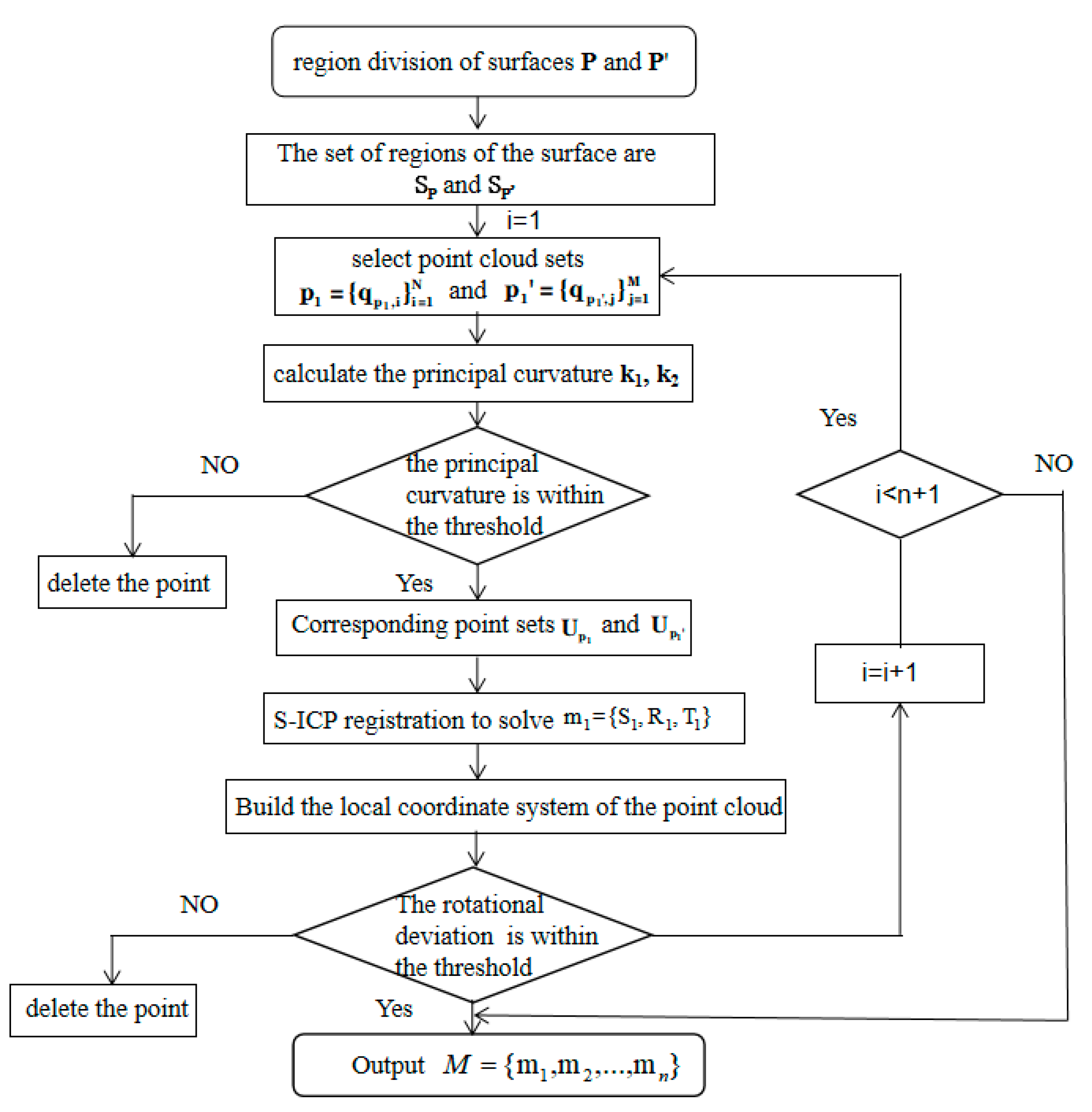
3.3. Region Registration Algorithm for Similar Surfaces
4. Experimental Design and Results
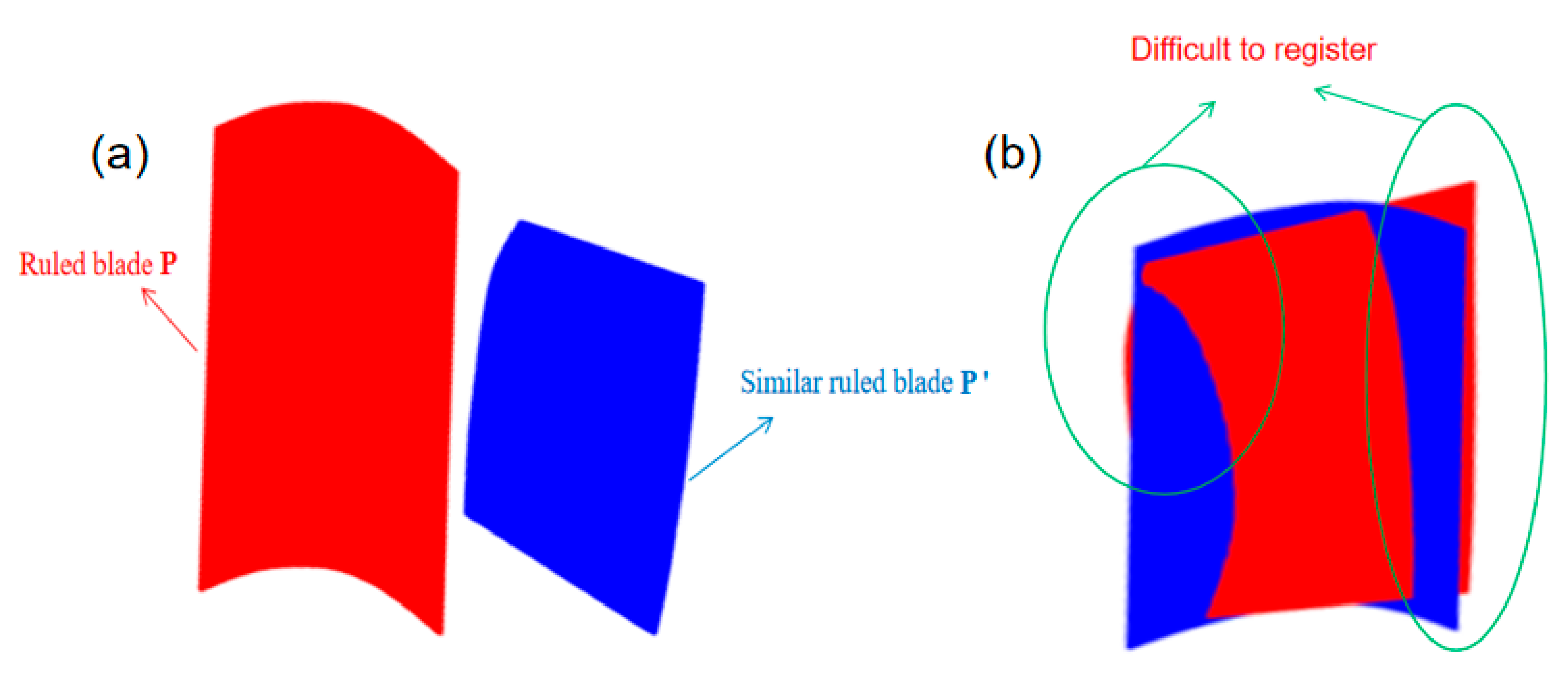
4.1. Similar Surface Region Division
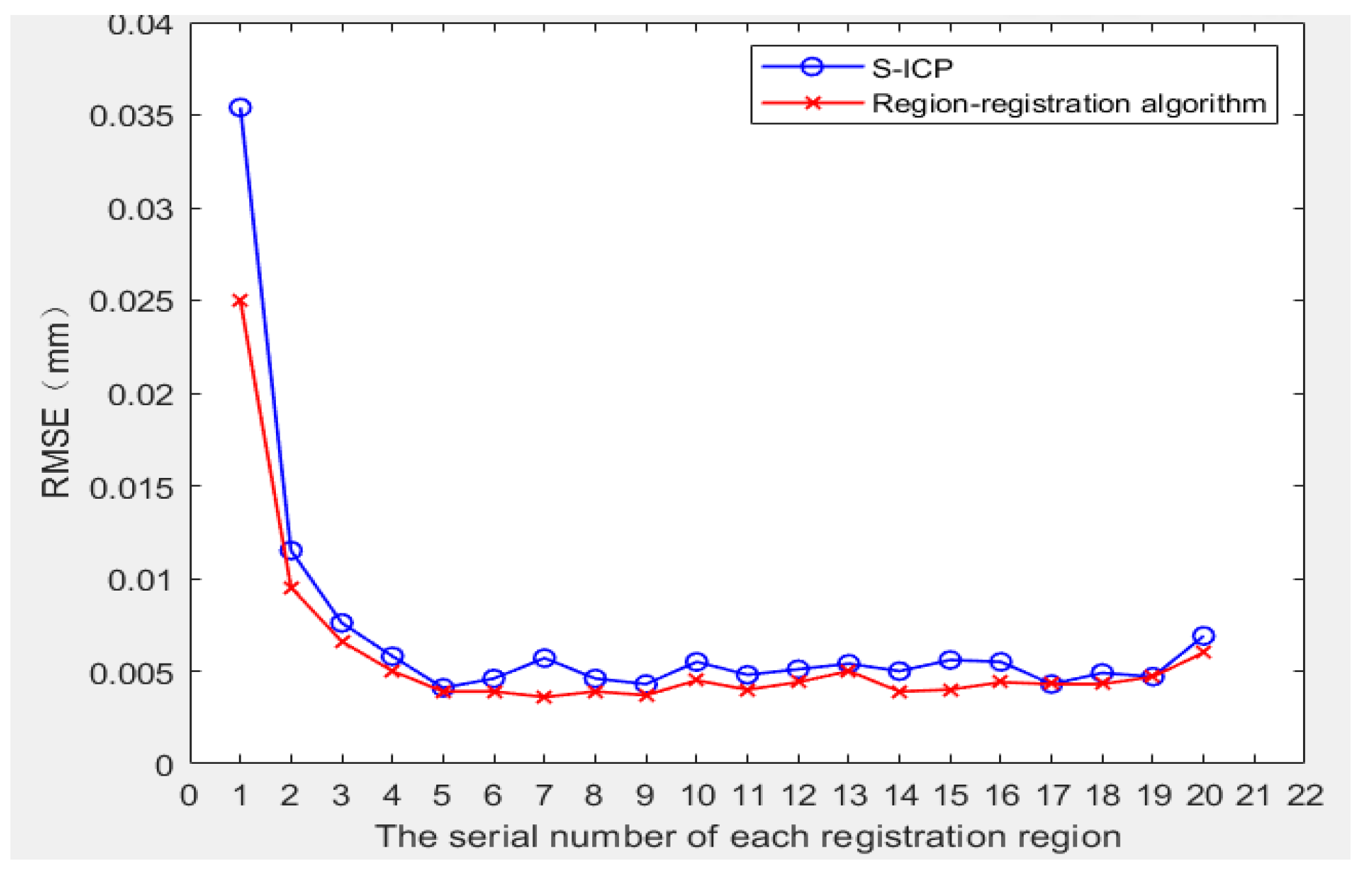
4.2. Point Cloud Registration for Each Sub-Region
5. Conclusions
- An adaptive region division algorithm is proposed to accurately divide the complex surfaces by finding curvature mutation points on the surface boundary. This region division algorithm can ensure that the corresponding regions between similar surfaces are similar in shape, and have the same number, which provides the possibility for the subsequent point cloud registration of each sub-region.
- The traditional S-ICP algorithm is improved by introducing the similarity judgment of curvature characteristics and differential geometry properties, and the registration efficiency and accuracy are improved. Moreover, the improved S-ICP algorithm can ensure that the differential geometric properties between corresponding points are similar after registration, which provides a basis for mapping and reuse of process knowledge between corresponding points on similar surfaces.
- The calculation results show that the method proposed in this paper can effectively complete the registration of each sub-region and solve the spatial transformation relationship. Compared with the traditional S-ICP algorithm, the registration accuracy of the proposed method is improved, and the registration time of each sub-region is reduced by about 20%. In addition, the simulation results show that the registration effect of the overall surface which is formed by each sub-region after registration is also very good, it can achieve a better fit even in the area of local deformation or curvature changes. It is proven that the proposed method in this paper is suitable for the situation that it is difficult to solve the spatial geometric transformation relationship of similar surfaces with complex transformation through global registration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, R.; Zhang, S.; Xu, C.; Zhang, X.; Zhang, C. A flexible and effective NC machining process reuse approach for similar subparts. Comput. -Aided Des. 2015, 62, 64–77. [Google Scholar] [CrossRef]
- Huang, B.; Zhang, S.; Huang, R.; Li, X.; Zhang, Y. An effective retrieval approach of 3D CAD models for macro process reuse. Int. J. Adv. Manuf. Technol. 2019, 102, 1067–1089. [Google Scholar] [CrossRef]
- Sun, Y.; Jia, J.; Xu, J.; Chen, M.; Niu, J.P. feedrate and trajectory planning for free-form surface machining: A state-of-the-art review. Chin. J. Aeronaut. 2022, 35, 12–29. [Google Scholar] [CrossRef]
- Yan, S.; Sun, Y. Early chatter detection in thin-walled workpiece milling process based on multi-synchro squeezing transform and feature selection. Mech. Syst. Signal Process 2022, 169, 108622. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, S. Predictive modeling of chatter stability considering force-induced deformation effect in milling thin-walled parts. Int. J. Mach. Tools Manuf. 2018, 135, 38–52. [Google Scholar] [CrossRef]
- Huang, R.; Jing, J.F.; He, K.; Chen, Z. An effective free form surface retrieval approach for potential machining process reuse. Int. J. Adv. Manuf. Technol. 2017, 91, 4341–4358. [Google Scholar] [CrossRef]
- Thompson, E.H. An exact linear solution of the problem of absolute orientation. Photogrammetria 1958, 15, 163–179. [Google Scholar] [CrossRef]
- Horn, B.K.P. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. A 1987, 4, 629–642. [Google Scholar] [CrossRef]
- Besl, P.J.; Mckay, H.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef] [Green Version]
- Yao, Z.; Zhao, Q.; Li, X.; Bi, Q. Point cloud registration algorithm based on curvature feature similarity. Measurement 2021, 177, 109274. [Google Scholar] [CrossRef]
- Xu, G.; Pang, Y.; Bai, Z.; Wang, Y.; Lu, Z. A Fast Point Clouds Registration Algorithm for Laser Scanners. Appl. Sci. 2021, 11, 3426. [Google Scholar] [CrossRef]
- Žagar, B.L.; Yurtsever, E.; Peters, A.; Knoll, A.C. Point Cloud Registration With Object-Centric Alignment. IEEE Access 2022, 10, 76586–76595. [Google Scholar] [CrossRef]
- Geng, N.; Ma, F.; Yang, H.; Li, B.; Zhang, Z. Neighboring constraint-based pairwise point cloud registration algorithm. Multimed. Tools Appl. 2016, 75, 16763–16780. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Z.; Hua, B.; Chen, K. Automatic point cloud registration algorithm based on the feature histogram of local surface. PLoS ONE 2020, 15, e0238802. [Google Scholar] [CrossRef]
- Li, J.; Huang, S.; Cui, H.; Ma, Y.; Chen, X. Automatic Point Cloud Registration for Large Outdoor Scenes Using a Priori Semantic Information. Remote Sens. 2021, 13, 3474. [Google Scholar] [CrossRef]
- Du, S.Y.; Zheng, N.; Lei, X.; Ying, S.H.; Xue, J. Scaling iterative closest point algorithm for registration of m-D point sets. J. Vis. Commun. ImageRepresentation 2010, 21, 442–452. [Google Scholar] [CrossRef]
- Wang, C.; Shu, Q.; Yang, Y.; Deng, S. Point cloud registration in multidirectional affine transformation with variance compensation. Acta Opt. Sin. 2019, 39, 0215002. [Google Scholar] [CrossRef]
- Shu, Q.; He, X.; Wang, C.; Yang, Y.; Cui, Z. Fast point cloud registration in multidirectional affine transformation. Opt. —Int. J. Light Electron Opt. 2021, 229, 165884. [Google Scholar] [CrossRef]
- Netto, G.M.; Oliveira, M.M. Robust point-cloud registration based on dense point matching and probabilistic modeling. Vis Comput. 2022, 38, 3217–3230. [Google Scholar] [CrossRef]
- Han, F.Y.; Zhang, C.W.; Guo, W.; Peng, X.L.; Zhang, W. A high-efficiency generation method of integral impeller channel tool path based on parametric domain template trajectory mapping. Int. J. Adv. Manuf. Technol. 2019, 100, 75–85. [Google Scholar] [CrossRef]
- Ying, S.H.; Peng, J.G.; Du, S.Y.; Qiao, H. A Scale Stretch Method Based on ICP for 3D Data Registration. IEEE Trans. Autom. Sci. Eng. 2009, 6, 559–565. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, J.; Xiao, J. Blending Surface Segmentation and Editing for 3D Models. IEEE Trans. Vis. Comput. Graph. 2020, 28, 2879–2894. [Google Scholar] [CrossRef] [PubMed]
- Wan, J.; Li, X. Analysis of a superconvergent recursive moving least squares approximation. Appl. Math. Lett. 2022, 133, 108223. [Google Scholar] [CrossRef]
- Wang, C.; Shu, Q.; Yang, Y.; Deng, S. Point Cloud Registration in Multidirectional Affine Transformation. IEEE Photonics J. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Barequet, G.; Sharir, M. Partial Surface and Volume Matching in Three Dimensions. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 19, 929–948. [Google Scholar] [CrossRef]
- Li, L.; Cao, X.; Sun, J. Three-Dimensional Point Cloud Registration Based on Normal Vector Angle. J. Indian Soc. Remote Sens. 2019, 47, 585–593. [Google Scholar] [CrossRef]





| Method | Scale | Rotation | Translation | Time/s | RMES/mm |
|---|---|---|---|---|---|
| S-ICP algorithm | diag(0.753,0.766,0.754) | (29.22,20.86,92.10) | 40.7 | 0.0564 | |
| Region-registration algorithm | diag(0.752,0.762,0.751) | (29.67,20.63,92.22) | 30.5 | 0.0354 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, F.; Hu, Z.; He, L.; Peng, X.; Yang, M.; Zhang, C. Solution of Spatial Transformation Relationship of Similar Ruled Surfaces Based on Registration of Divided Regions. Machines 2022, 10, 956. https://doi.org/10.3390/machines10100956
Han F, Hu Z, He L, Peng X, Yang M, Zhang C. Solution of Spatial Transformation Relationship of Similar Ruled Surfaces Based on Registration of Divided Regions. Machines. 2022; 10(10):956. https://doi.org/10.3390/machines10100956
Chicago/Turabian StyleHan, Feiyan, Zhitao Hu, Longlong He, Xianlong Peng, Manzhi Yang, and Chuanwei Zhang. 2022. "Solution of Spatial Transformation Relationship of Similar Ruled Surfaces Based on Registration of Divided Regions" Machines 10, no. 10: 956. https://doi.org/10.3390/machines10100956
APA StyleHan, F., Hu, Z., He, L., Peng, X., Yang, M., & Zhang, C. (2022). Solution of Spatial Transformation Relationship of Similar Ruled Surfaces Based on Registration of Divided Regions. Machines, 10(10), 956. https://doi.org/10.3390/machines10100956





