Influence of Different Reflux Groove Structures on the Flow Characteristics of the Roots Pump
Abstract
1. Introduction
2. Governing Equations of Gas Flow
3. Flow Field Calculation of the Roots Pump
3.1. Fluid Domain Modeling and Meshing
3.2. The Setting of the CFD
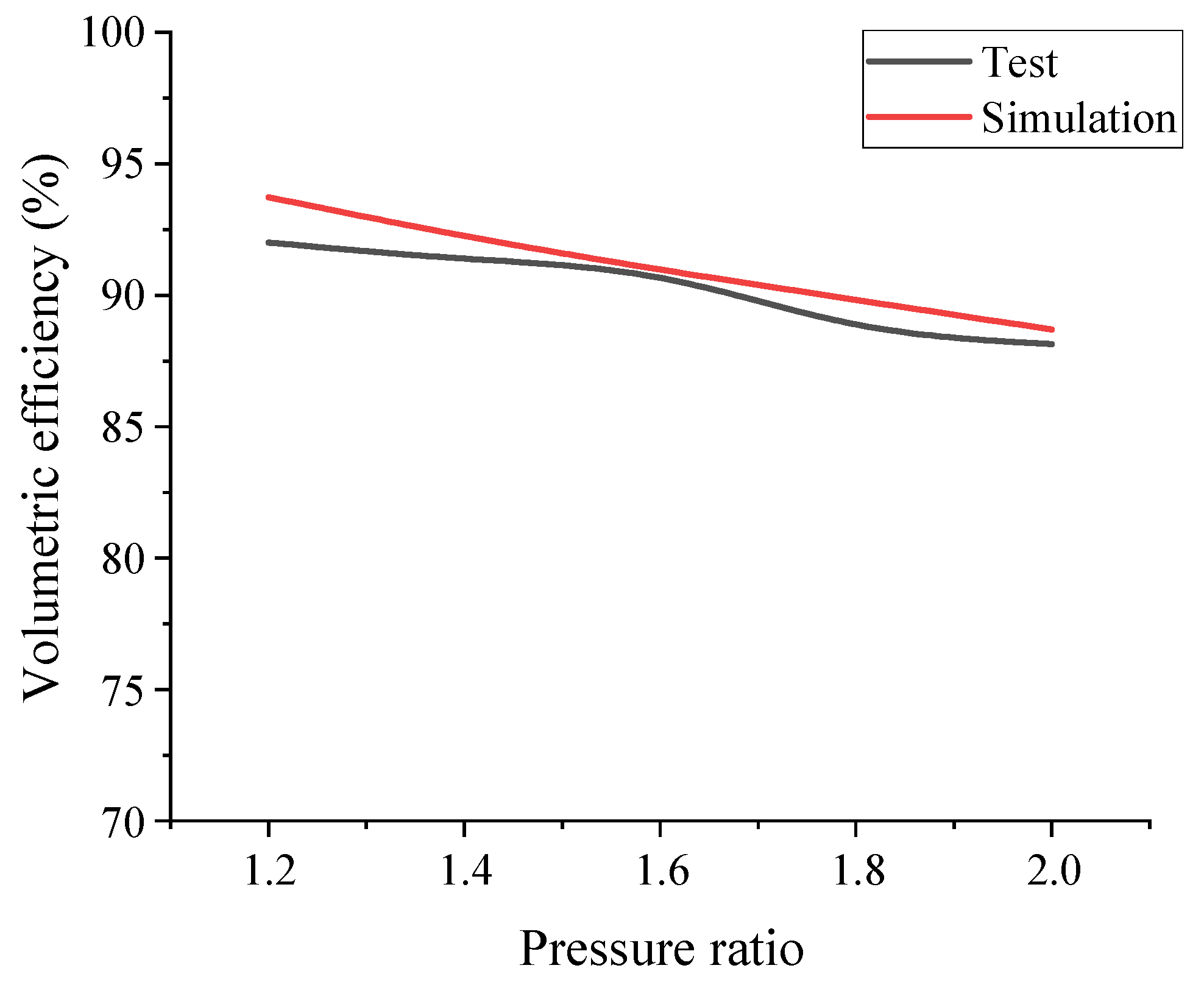
3.3. Comparison between the Experimental and Simulation Results
4. Analysis of the External Characteristics
4.1. Influence of the Reflux Groove Structure on the Inlet Flow Measurement
4.2. Influence of the Reflux Groove Structure on the Exhaust Flow Measurement
5. Analysis of the Internal Characteristics
5.1. Vortex Distribution in the Roots Pump
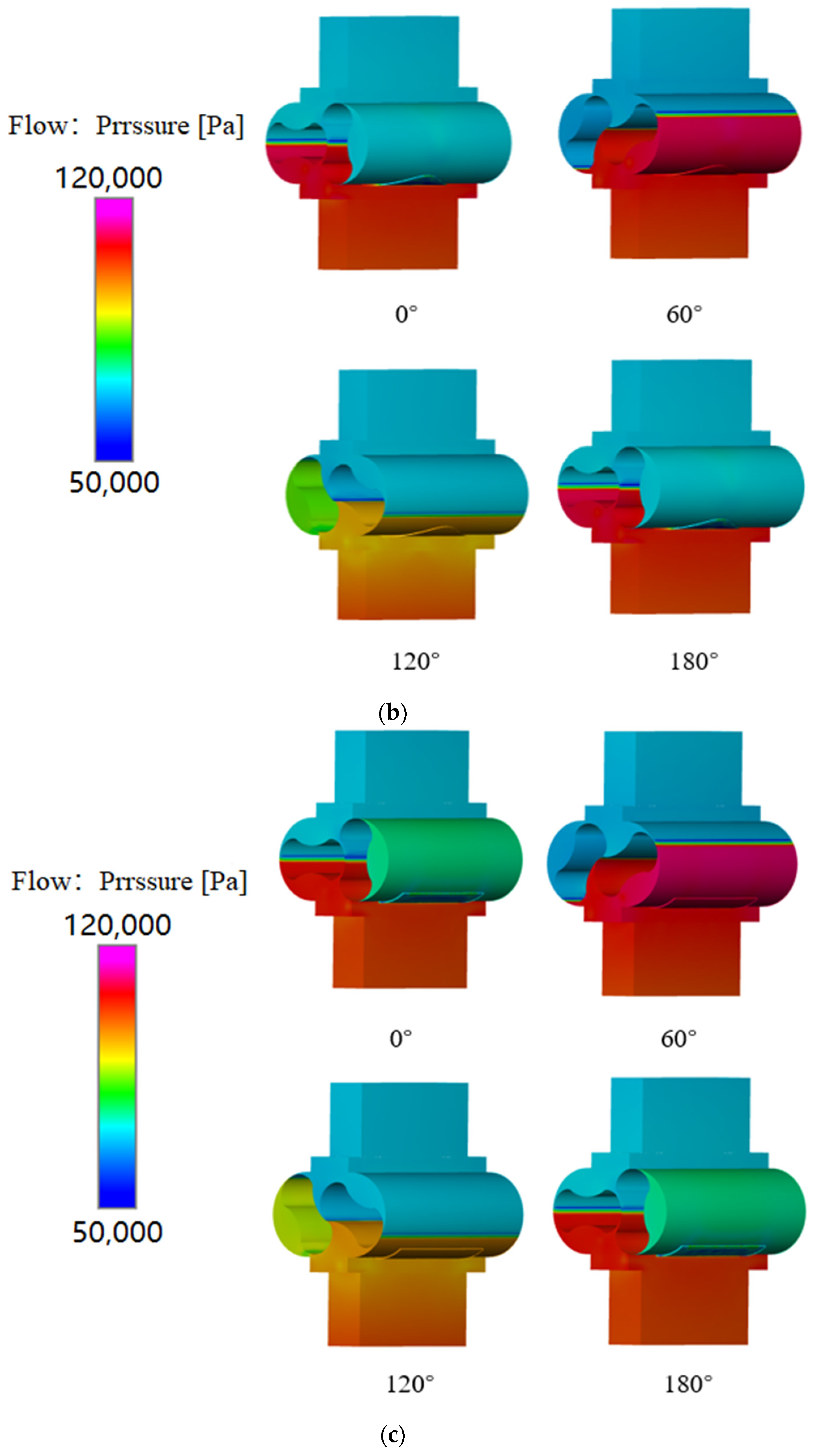
5.2. The Pressure Distribution in the Roots Pump
6. Conclusions
- (1)
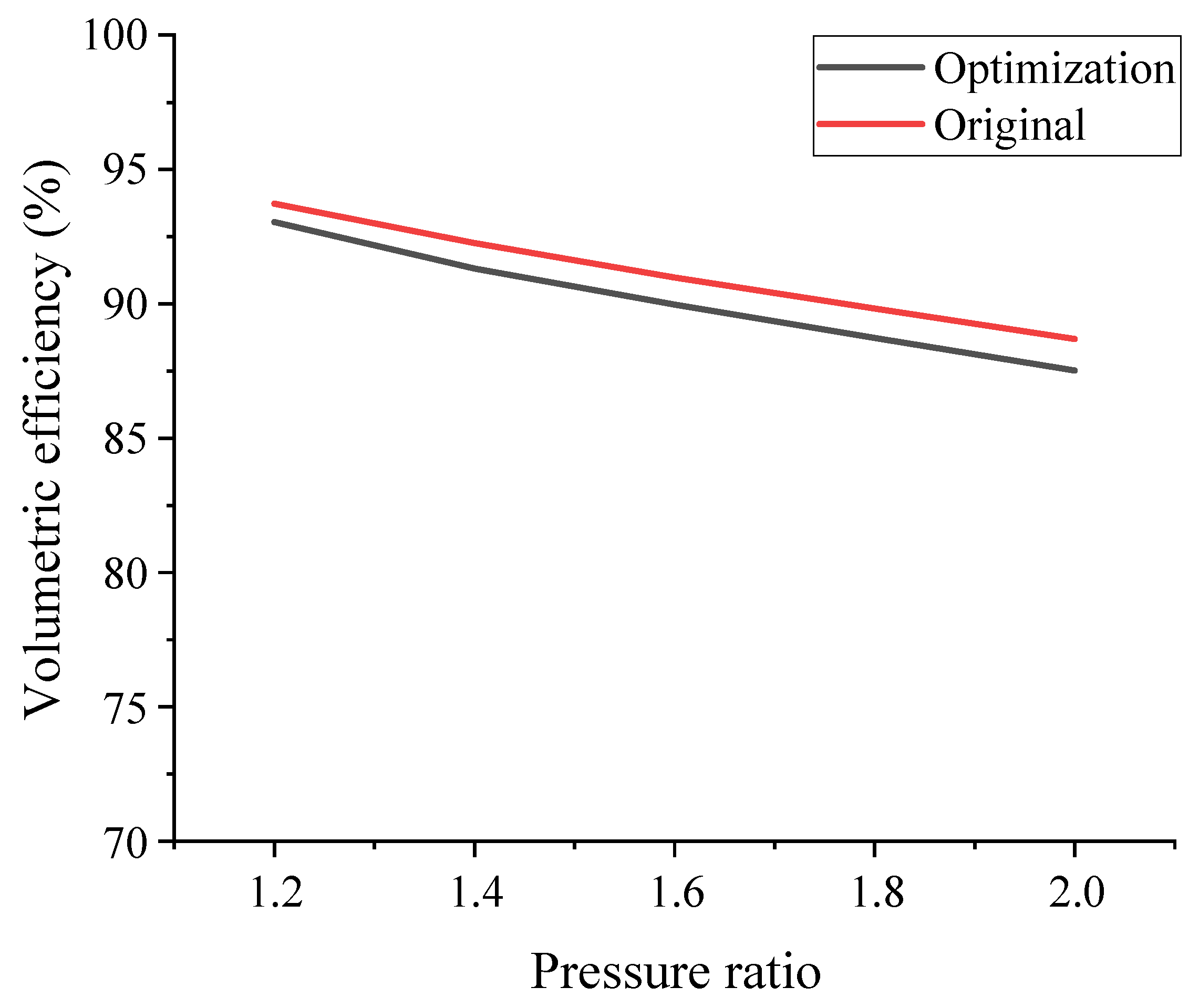
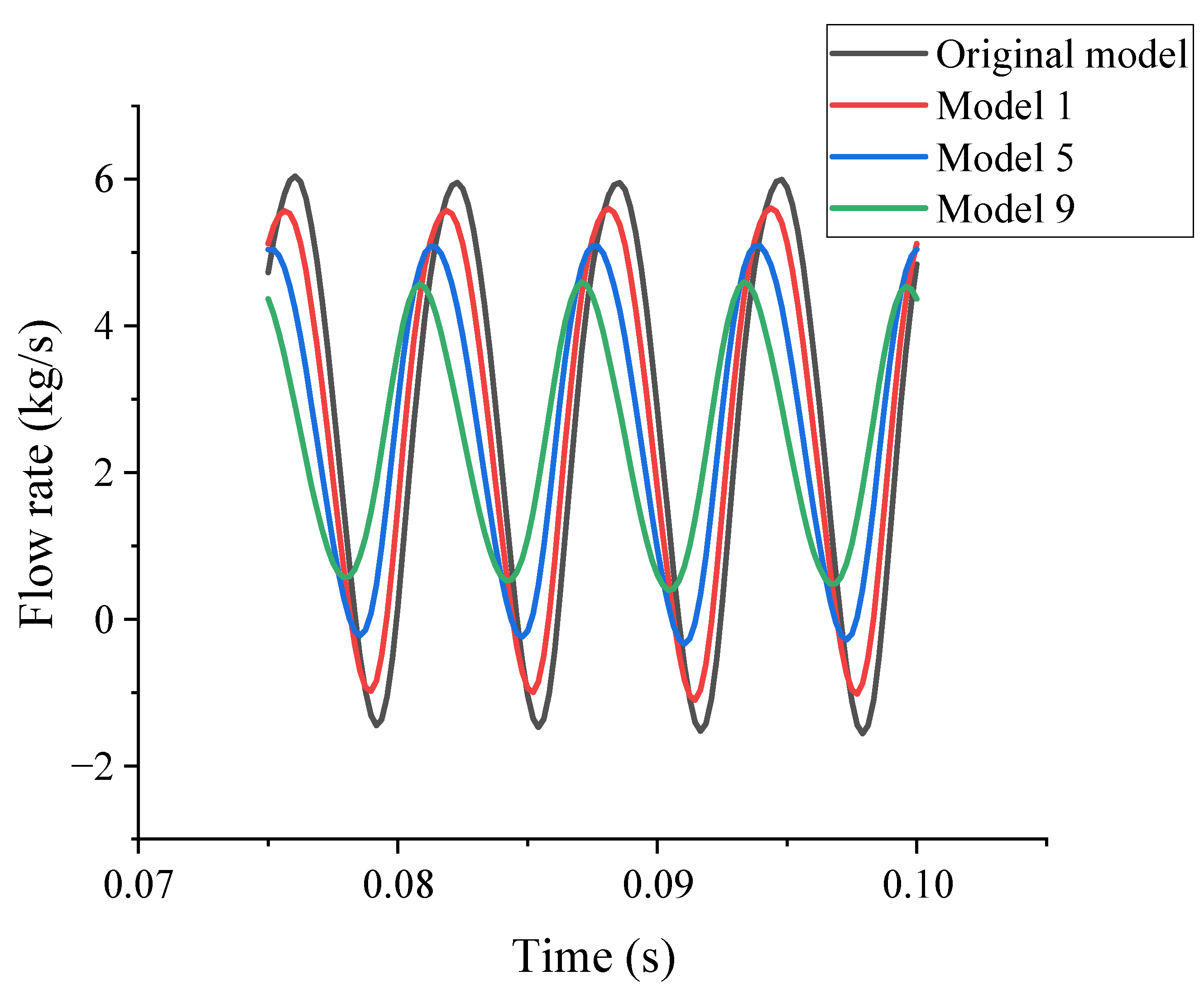
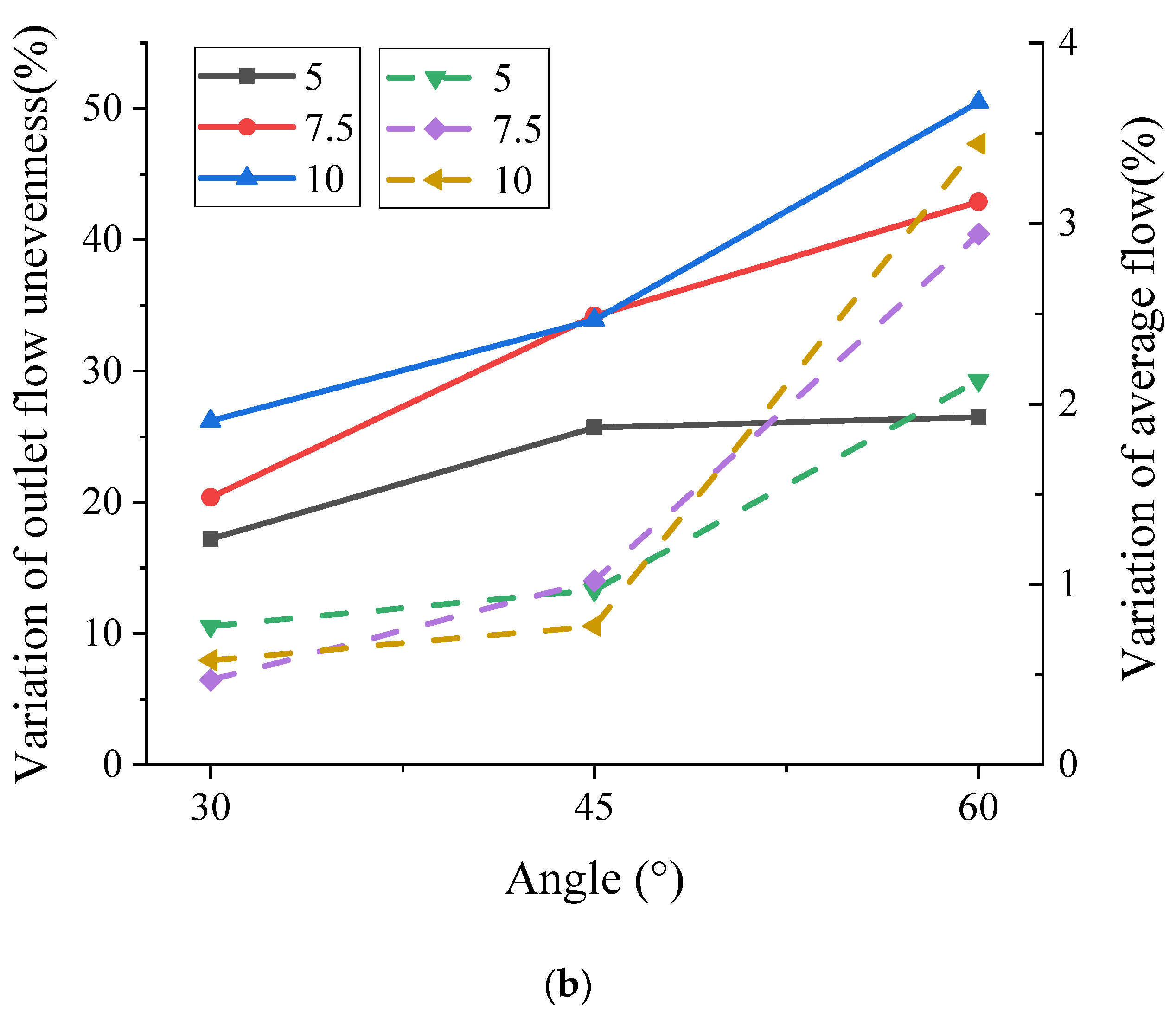
- The reflux groove structure only had a better optimization effect on the outlet flow pulsation of the Roots pump; nevertheless, it had a subtle effect on the inlet flow field, which was within the range of 5%. The effect of the rectangular reflux groove on reducing the pulsation amplitude was comparatively better compared to the curved reflux groove. In addition, the flow loss of the rectangular reflux groove was quite substantial than that of the curved reflux groove.
- (2)
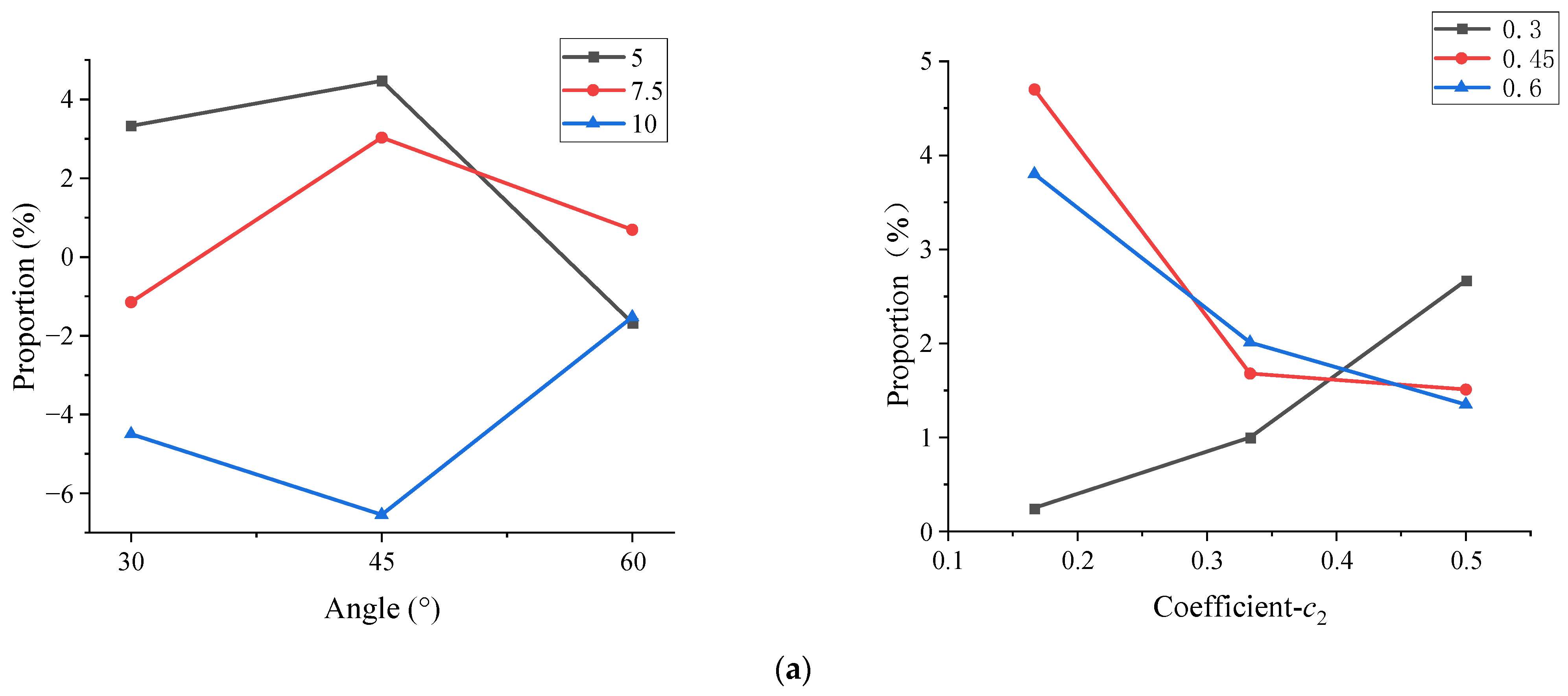
- With regards to the rectangular groove, the outlet flow pulsation unevenness and the exhaust pressure pulsation coefficient gradually decreased with the increase in the thickness and angle of the reflux groove, meanwhile increasing the flow rate. Taking the flow rate and outlet pulsation into consideration, the effect was more pronounced when the reflux groove angle was approximately 45° and the thickness was approximately 7.5 mm. Without considering the other optimized structures, the size of the reflux groove could avert the negative flow when the angle was 45–60° and the thickness was 7.5–10 mm.
- (3)
- When the Bezier curve of the arc-type reflux groove was constructed to determine the starting point, middle point and the end point, it was realized that the increase in the coefficient and coefficient , the decreased proportion of the flow inhomogeneity was higher. However, the change in had minimal impact on the inhomogeneity when was less than 0.45, and the optimization effect increased only modestly as increased. When both and were more than 0.45, the change in had a disproportionately large impact on the Roots pump’s pressure pulsation.
- (4)
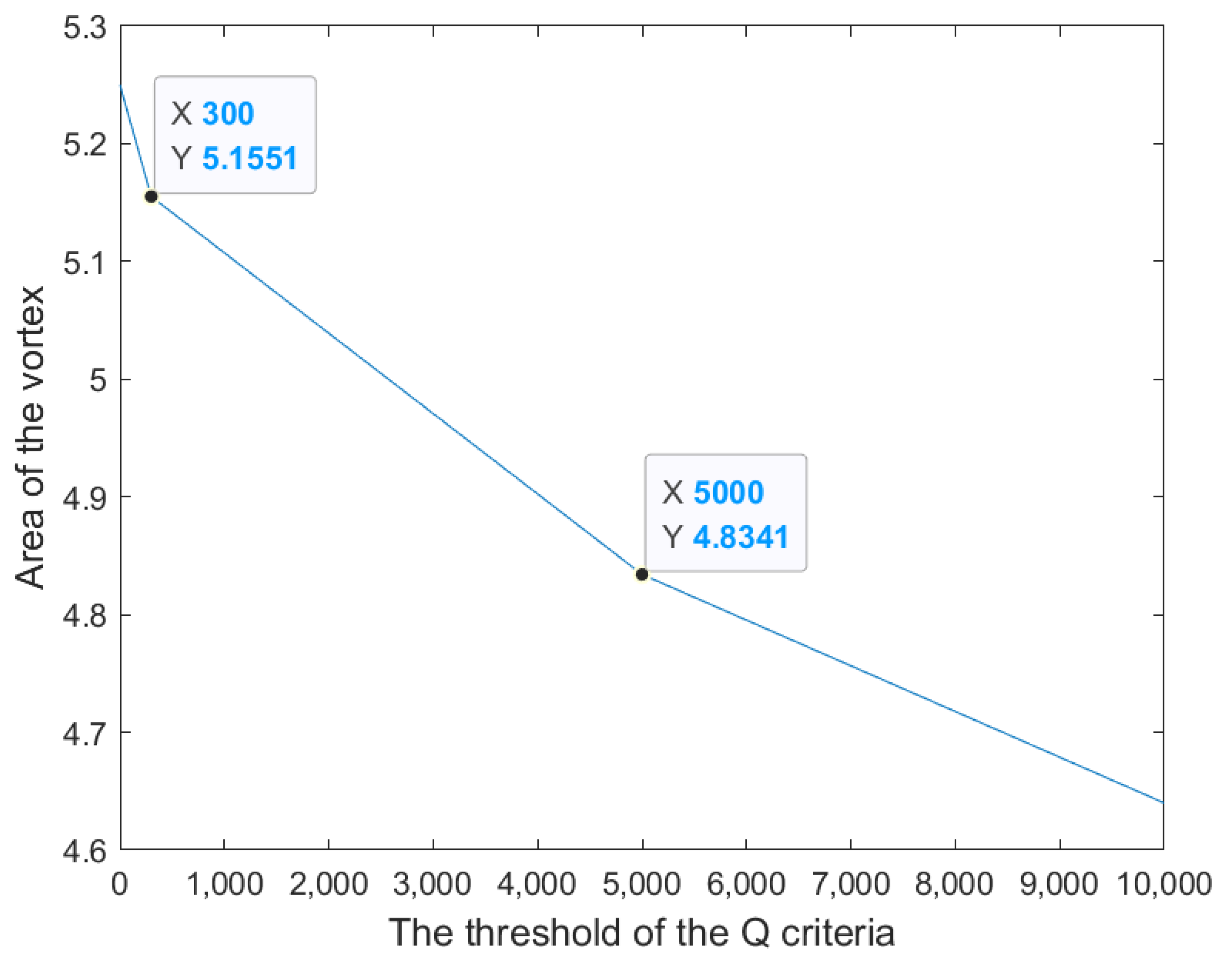
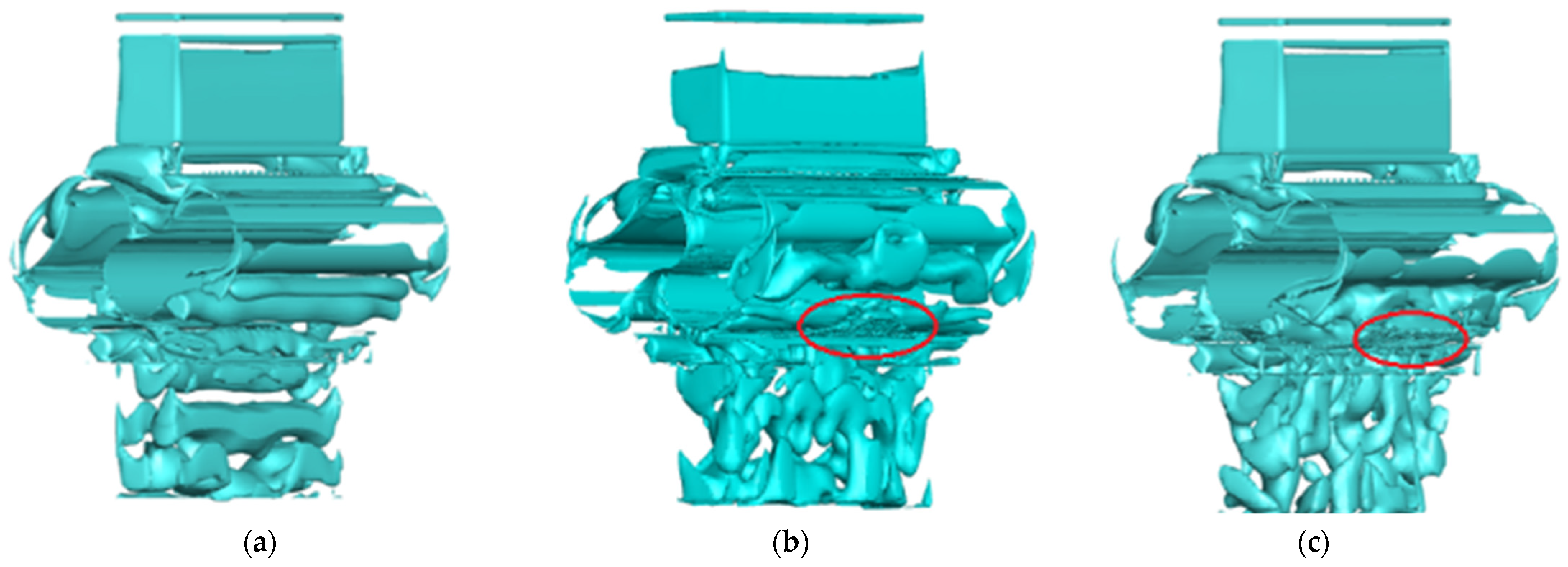
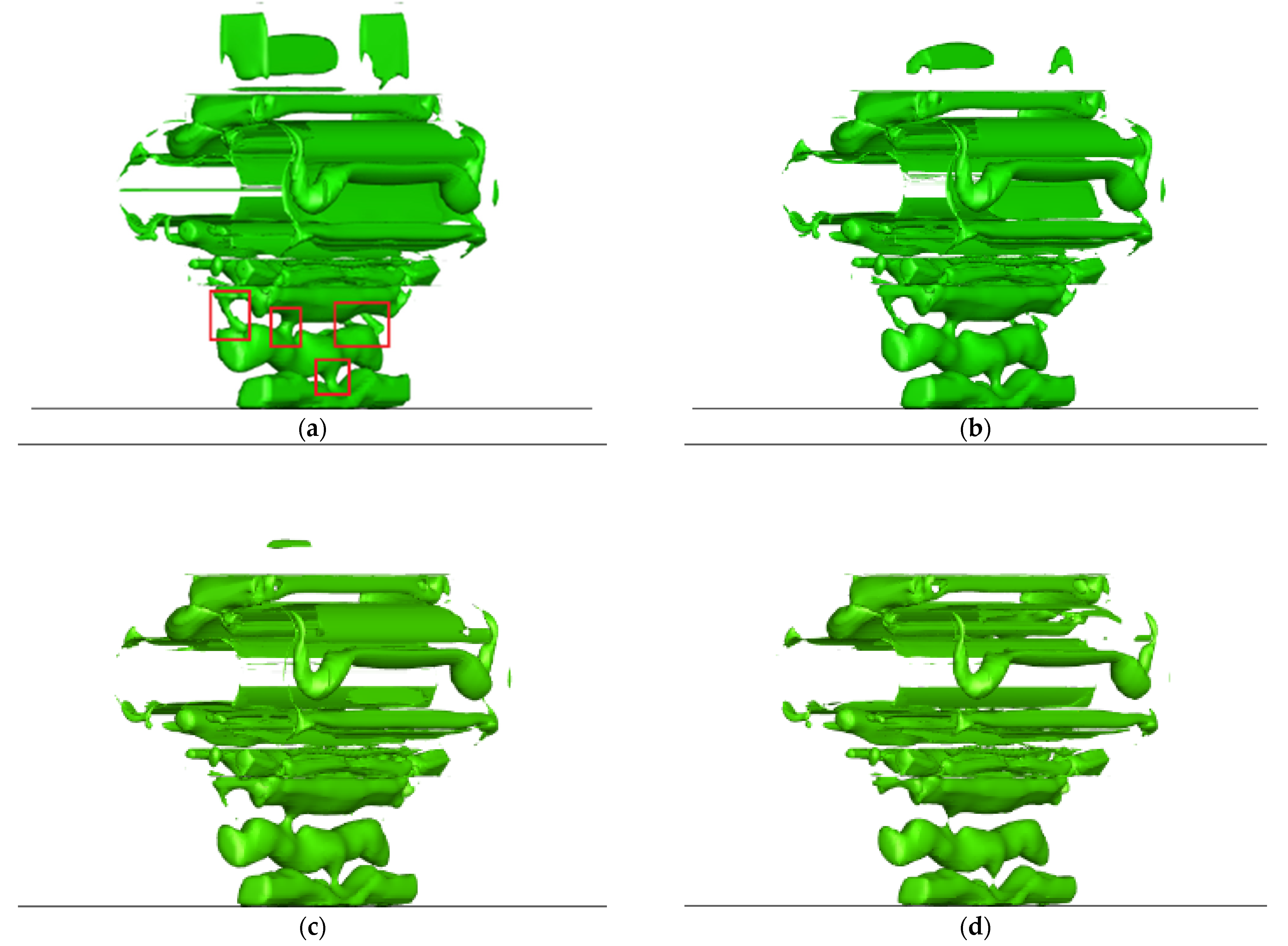
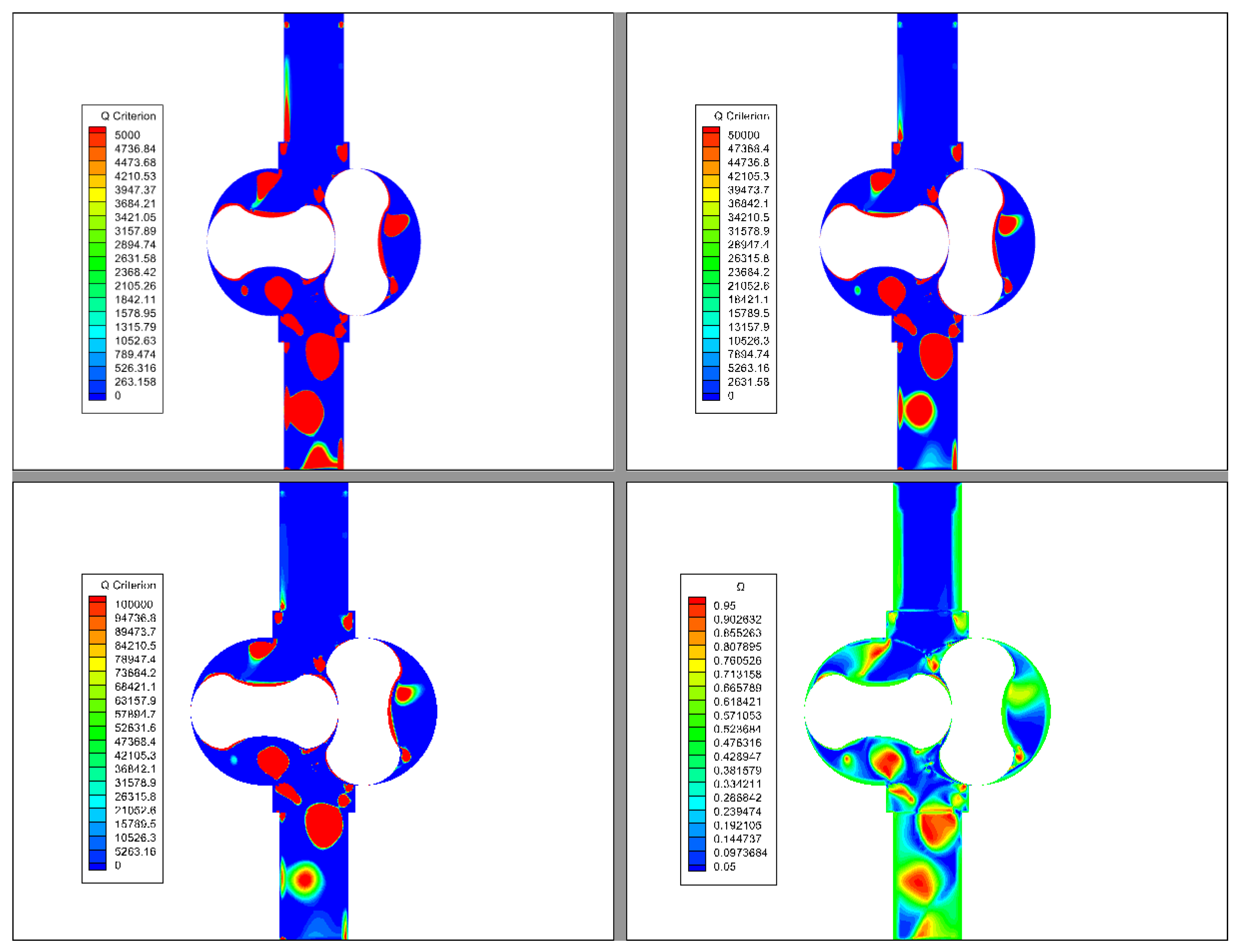
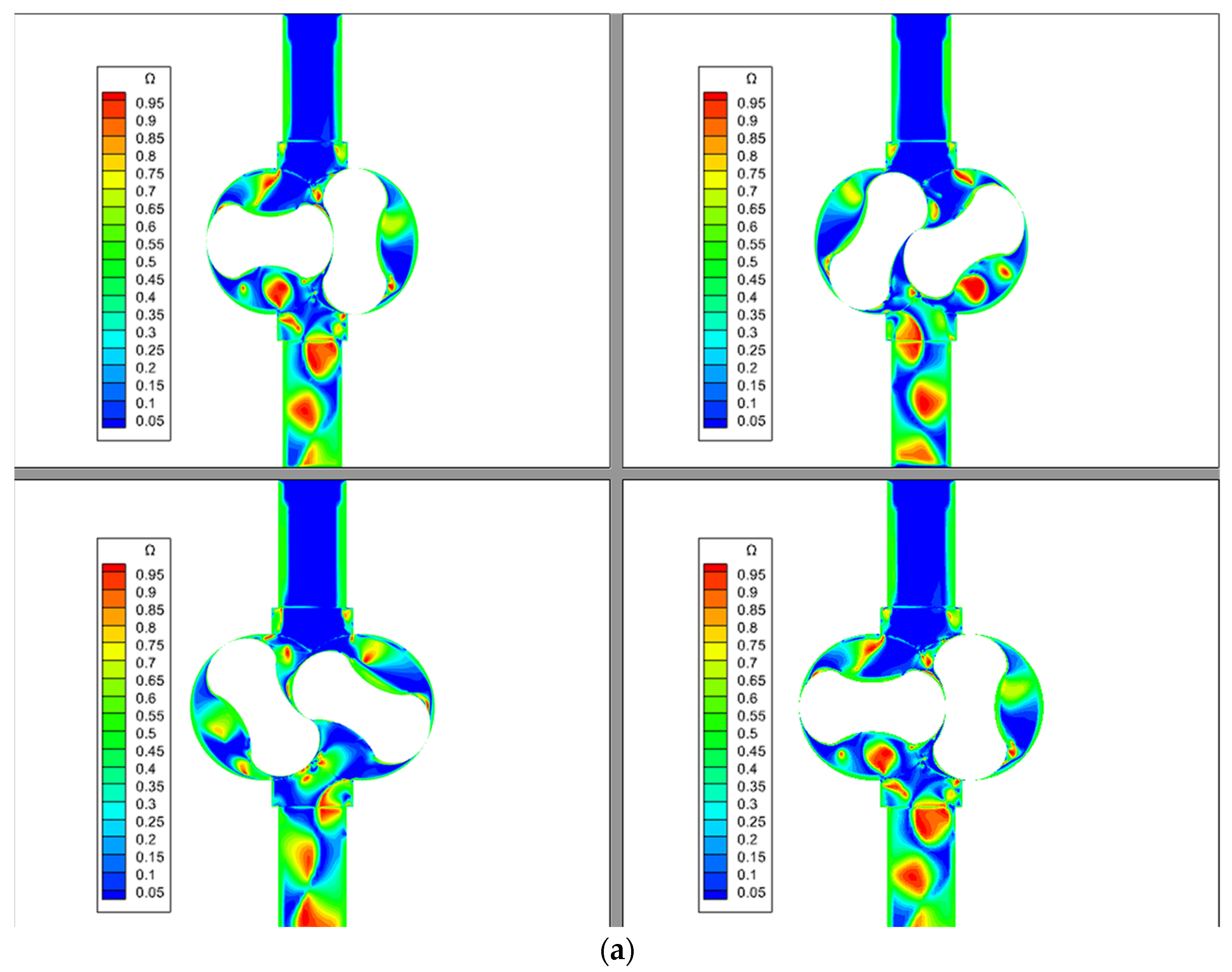
- Although the Q criterion could be analyzed quickly, it had a poor capacity to capture both strong and weak vortices, and this capability was significantly influenced by the threshold. The Q criterion is therefore proposed for qualitative analysis. In comparison to the Q criterion, the vortex structure captured by the omega criterion was more distinct, continuous and less sensitive to the threshold. In the Roots pump, when ε was 0.001, the effect of obtaining the vortex was better, and the vortex production site of the Roots pump was mainly located in the rotor edge and outlet sections. At the same time, the reflux groove structure had a good effect on reducing the vortex structures at the outlet section.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kovacevic, A.; Stosic, N.; Mujic, E.; Smith, I.K. CFD Integrated Design of Screw Compressors. Eng. Appl. Comput. Fluid Mech. 2007, 1, 96–108. [Google Scholar] [CrossRef][Green Version]
- Borisova, K.; Ivanova, T.; Latypov, R. Study of Screw Pump Stator and Rotor Working Capacity to Increase the Output. Procedia Eng. 2017, 206, 688–691. [Google Scholar] [CrossRef]
- Petrovic, R.; Pezdirnik, J.; Banaszek, A.; Duricic, L. Influence of compressibility of working fluid on hydrodynamic processes in the axial piston pump with combined distribution/flow of working fluid. In Proceedings of the 2011 International Conference on Fluid Power and Mechatronics, Beijing, China, 17–20 August 2011; pp. 335–339. [Google Scholar] [CrossRef]
- Todić, N.; Savić, S.; Gordić, D.; Petrović, R. Experimental Research of the Hydrodynamic Processes of an Axial Piston Water Hydraulic Pump. Machines 2022, 10, 728. [Google Scholar] [CrossRef]
- Petrovic, R.; Andjelkovic, M.; Radosavljevic, M.; Todić, N. Experimental Research and Optimization of Characteristic Parameters of the Valve Plate of the Axial Piston Pump/Motor. In The Latest Methods of Construction Design; Dynybyl, V., Berka, O., Petr, K., Lopot, F., Dub, M., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 173–183. [Google Scholar] [CrossRef]
- Riemslagh, K.; Vierendeels, J.; Dick, E. Two-dimensional incompressible Navier-Stokes calculations in complex-shaped moving domains. In Floating, Flowing, Flying; Dijkstra, D., Geurts, B.J., Kuerten, J.G.M., Kuiken, H.K., Eds.; Springer: Dordrecht, The Netherlands, 1998; pp. 57–73. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Tong, S.-H. The specific flowrate of deviation function based lobe pumps—Derivation and analysis q. Mech. Mach. Theory 2002, 18, 1025–1042. [Google Scholar] [CrossRef]
- Voss, G. An analytical model to describe the compression in turbomolecular pumps and roots blowers. J. Phys. Conf. Ser. 2008, 114, 012018. [Google Scholar] [CrossRef]
- Sun, S.H.; Kovacevic, A.; Bruecker, C.; Leto, A.; Singh, G.; Ghavami, M. Numerical and Experimental Analysis of Transient Flow in Roots Blower. IOP Conf. Ser. Mater. Sci. Eng. 2018, 425, 012024. [Google Scholar] [CrossRef]
- Singh, G.; Sun, S.; Kovacevic, A.; Li, Q.; Bruecker, C. Transient flow analysis in a Roots blower: Experimental and numerical investigations. Mech. Syst. Signal Process. 2019, 134, 106305. [Google Scholar] [CrossRef]
- Hsieh, C.-F.; Deng, Y.-C. A design method for improving the flow characteristics of a multistage Roots pumps. Vacuum 2015, 121, 217–222. [Google Scholar] [CrossRef]
- Wu, Y.-R.; Tran, V.-T. Generation method for a novel Roots rotor profile to improve performance of dry multi-stage vacuum pumps. Mech. Mach. Theory 2018, 128, 475–491. [Google Scholar] [CrossRef]
- Li, Y.B.; Jia, K.; Meng, Q.W.; Shen, H.; Sang, X.H. Flow simulation of the effects of pressure angle to lobe pump rotor meshing characteristics. IOP Conf. Ser. Mater. Sci. Eng. 2013, 52, 032022. [Google Scholar] [CrossRef]
- Hsieh, C.-F. A new curve for application to the rotor profile of rotary lobe pumps. Mech. Mach. Theory 2015, 87, 70–81. [Google Scholar] [CrossRef]
- Wang, J.; Liu, R.; Yang, S.; Li, H.; Wang, Z.; Li, Q. Geometric study and simulation of an elliptical rotor profile for Roots vacuum pumps. Vacuum 2018, 153, 168–175. [Google Scholar] [CrossRef]
- Xing, L.; Feng, J.; Chen, W.; Xing, Z.; Peng, X. Development and Testing of a Roots Pump for Hydrogen Recirculation in Fuel Cell System. Appl. Sci. 2020, 10, 8091. [Google Scholar] [CrossRef]
- Hsieh, C.-F.; Zhou, Q.-J. Fluid analysis of cylindrical and screw type Roots vacuum pumps. Vacuum 2015, 121, 274–282. [Google Scholar] [CrossRef]
- Li, Y.B.; Sang, X.H.; Meng, Q.W.; Shen, H.; Jia, K. Transient simulation in interior flow field of lobe pump. IOP Conf. Series: Mater. Sci. Eng. 2013, 52, 032019. [Google Scholar] [CrossRef]
- Vizgalov, S.V.; Chekushkin, G.N.; Volkov, M.V. Investigation of three lobes roots blower with special ejector. IOP Conf. Series: Mater. Sci. Eng. 2015, 90, 012082. [Google Scholar] [CrossRef]
- Sun, S.K.; Zhou, Q.; Wen, J.; Peng, X.Y. Three-dimensional numerical simulation and experimental validation of flows in working chambers of roots blowers with backflow design. IOP Conf. Ser. Mater. Sci. Eng. 2017, 232, 012079. [Google Scholar] [CrossRef]
- Sun, S.-K.; Jia, X.-H.; Xing, L.-F.; Peng, X.-Y. Numerical study and experimental validation of a Roots blower with backflow design. Eng. Appl. Comput. Fluid Mech. 2018, 12, 282–292. [Google Scholar] [CrossRef]
- Li, Y.-B.; Guo, D.-S.; Li, X.-B. Mitigation of radial exciting force of rotary lobe pump by gradually varied gap. Eng. Appl. Comput. Fluid Mech. 2018, 12, 711–723. [Google Scholar] [CrossRef]
- Li, Y.-B.; Du, J.; Guo, D.-S. Numerical research on viscous oil flow characteristics inside the rotor cavity of rotary lobe pump. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 274. [Google Scholar] [CrossRef]
- Liu, H.; Wu, Y.; Li, Z. Simulation research on Reducing Airflow Pulsation method of Roots Mechanical Supercharger Based on CFD. Intern. Combust. Engine Accessories 2015, 4, 8–12. (In Chinese) [Google Scholar]
- Li, Y.B.; Guo, D.S. Transient Mechanism of CAM Pump Rotor Cavity; Jiangsu University Press: Zhenjiang, China, 2019. [Google Scholar]
- Kang, Y.-H.; Vu, H.-H. A newly developed rotor profile for lobe pumps: Generation and numerical performance assessment. J. Mech. Sci. Technol. 2014, 28, 915–926. [Google Scholar] [CrossRef]
- Zhou, S.; Jia, X.; Yan, H.; Peng, X. A novel profile with high efficiency for hydrogen-circulating Roots pumps used in FCVs. Int. J. Hydrogen Energy 2021, 46, 22122–22133. [Google Scholar] [CrossRef]
- Guo, Q.; Qin, K.; Li, D.; Huang, C.; Luo, K. Numerical investigation and performance enhancement of roots pumps operating with gas-liquid mixtures. Vacuum 2020, 176, 109303. [Google Scholar] [CrossRef]
- Li, Y.; Guo, D.; Li, X. The effect of startup modes on a vacuum cam pump. Vacuum 2019, 166, 170–177. [Google Scholar] [CrossRef]
- Sun, S.-K.; Zhao, B.; Jia, X.-H.; Peng, X.-Y. Three-dimensional numerical simulation and experimental validation of flows in working chambers and inlet/outlet pockets of Roots pump. Vacuum 2017, 137, 195–204. [Google Scholar] [CrossRef]
- Bhuyan, P.; Ghosh, S. Influence of rotor speed, discharge pressure, and clearance size on the unsteady flow dynamics and heat interaction of roots blower. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 48. [Google Scholar] [CrossRef]
- Su, C.M. Roots Blower and Its Use; Central South University Press: Changsha, China, 2000. [Google Scholar]
- Gao, Y.; Liu, C. Rortex and comparison with eigenvalue-based vortex identification criteria. Phys. Fluids 2018, 30, 085107. [Google Scholar] [CrossRef]
- Zhang, F.; Appiah, D.; Chen, K.; Yuan, S.; Adu-Poku, K.A.; Zhu, L. Investigation on the Flow Behavior of Side Channel Pumps Based on Vortex Identification. Chin. J. Mech. Eng. 2021, 34, 120. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Yang, Y.; Duan, Z. New omega vortex identification method. Sci. China Ser. G Phys. Mech. Astron. 2016, 59, 684711. [Google Scholar] [CrossRef]
- Dong, X.; Wang, Y.; Chen, X.; Dong, Y.; Zhang, Y.; Liu, C. Determination of epsilon for Omega vortex identification method. J. Hydrodyn. 2018, 30, 541–548. [Google Scholar] [CrossRef]



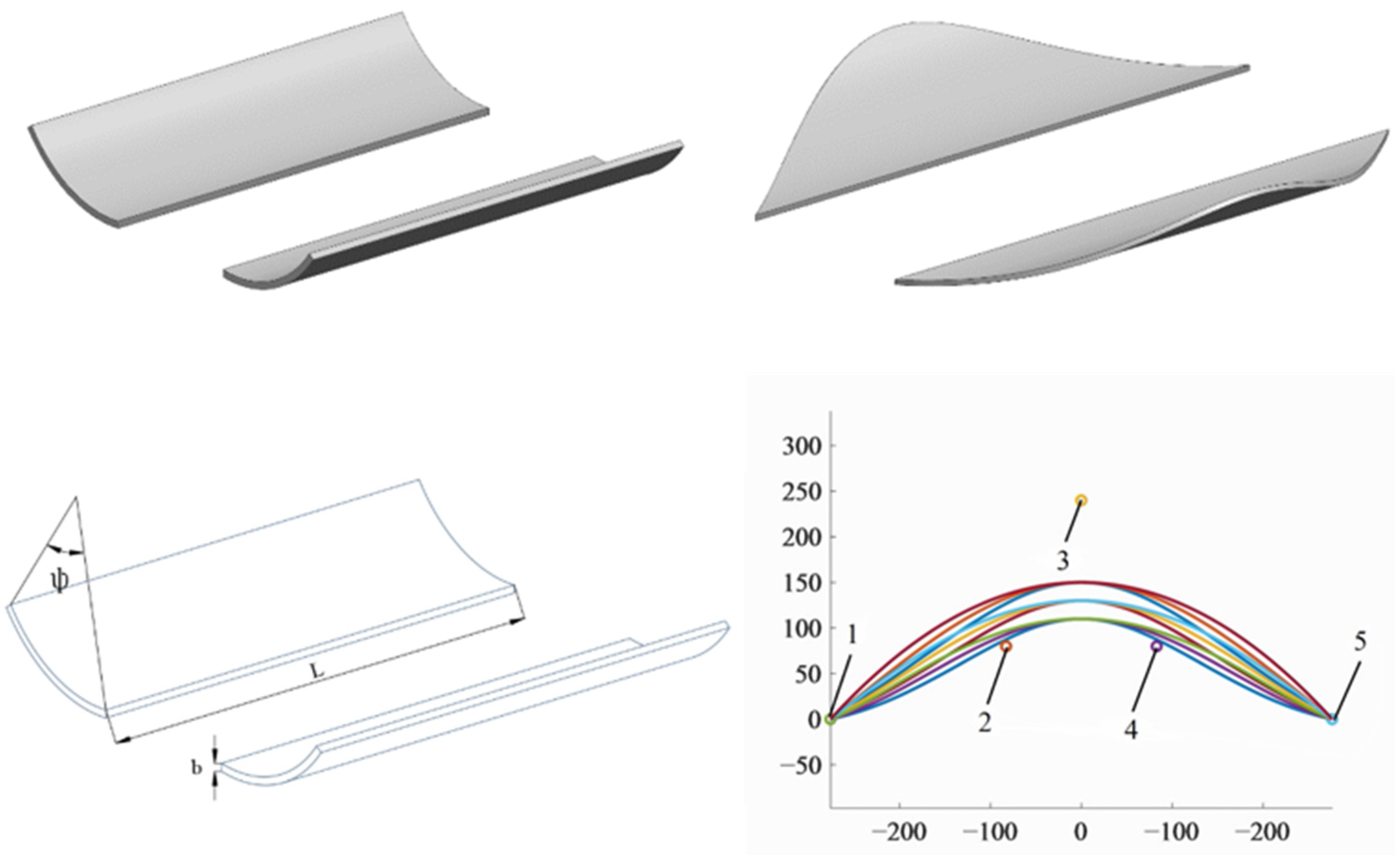







| Model | Angle (°) | Thickness (mm) |
|---|---|---|
| Model 1 | 30 | 5 |
| Model 2 | 30 | 7.5 |
| Model 3 | 30 | 10 |
| Model 4 | 45 | 5 |
| Model 5 | 45 | 7.5 |
| Model 6 | 45 | 10 |
| Model 7 | 60 | 5 |
| Model 8 | 60 | 7.5 |
| Model 9 | 60 | 10 |
| Model | Coefficient c1 | Coefficient c2 |
|---|---|---|
| Model 10 | 0.3 | 1/6 |
| Model 11 | 0.3 | 1/3 |
| Model 12 | 0.3 | 1/2 |
| Model 13 | 0.45 | 1/6 |
| Model 14 | 0.45 | 1/3 |
| Model 15 | 0.45 | 1/2 |
| Model 16 | 0.6 | 1/6 |
| Model 17 | 0.6 | 1/3 |
| Model 18 | 0.6 | 1/2 |
| Parameter | Value |
|---|---|
| Unevenness of inlet flow | −0.33396 |
| Unevenness of outlet flow | 3.390946 |
| Inlet pressure pulsation coefficient | 0.027563 |
| Outlet pressure pulsation coefficient | 0.184533 |
| Average outlet flow | 2.561141 |
| Model | Model | ||||||
|---|---|---|---|---|---|---|---|
| Model 1 | 6.04 | −1.55 | 2.97 | Model 10 | 5.65 | −1.13 | 3.00 |
| Model 2 | 5.60 | −1.10 | 2.98 | Model 11 | 5.60 | −1.07 | 2.95 |
| Model 3 | 5.66 | −0.62 | 2.49 | Model 12 | 5.58 | −1.05 | 2.93 |
| Model 4 | 5.28 | −0.74 | 2.65 | Model 13 | 5.45 | −0.89 | 2.78 |
| Model 5 | 5.09 | −0.33 | 2.28 | Model 14 | 5.46 | −0.89 | 2.78 |
| Model 6 | 5.26 | −0.11 | 2.09 | Model 15 | 5.44 | −0.87 | 2.76 |
| Model 7 | 5.18 | −0.72 | 2.65 | Model 16 | 5.30 | −0.80 | 2.71 |
| Model 8 | 4.65 | 0.45 | 1.96 | Model 17 | 5.30 | −0.79 | 2.70 |
| Model 9 | 4.60 | 0.40 | 1.68 | Model 18 | 5.23 | −0.67 | 2.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, W.; Zhang, F.; Zhao, F.; Song, J.; Zhu, X.; Tang, X. Influence of Different Reflux Groove Structures on the Flow Characteristics of the Roots Pump. Machines 2022, 10, 1087. https://doi.org/10.3390/machines10111087
Xing W, Zhang F, Zhao F, Song J, Zhu X, Tang X. Influence of Different Reflux Groove Structures on the Flow Characteristics of the Roots Pump. Machines. 2022; 10(11):1087. https://doi.org/10.3390/machines10111087
Chicago/Turabian StyleXing, Wenshuai, Fan Zhang, Feifei Zhao, Jialong Song, Xiumei Zhu, and Xingpeng Tang. 2022. "Influence of Different Reflux Groove Structures on the Flow Characteristics of the Roots Pump" Machines 10, no. 11: 1087. https://doi.org/10.3390/machines10111087
APA StyleXing, W., Zhang, F., Zhao, F., Song, J., Zhu, X., & Tang, X. (2022). Influence of Different Reflux Groove Structures on the Flow Characteristics of the Roots Pump. Machines, 10(11), 1087. https://doi.org/10.3390/machines10111087






