Hydrodynamics Simulations and Analyses of a Fluid Lubricated Screw-Nut Pair
Abstract
:1. Introduction
2. Materials and Methods
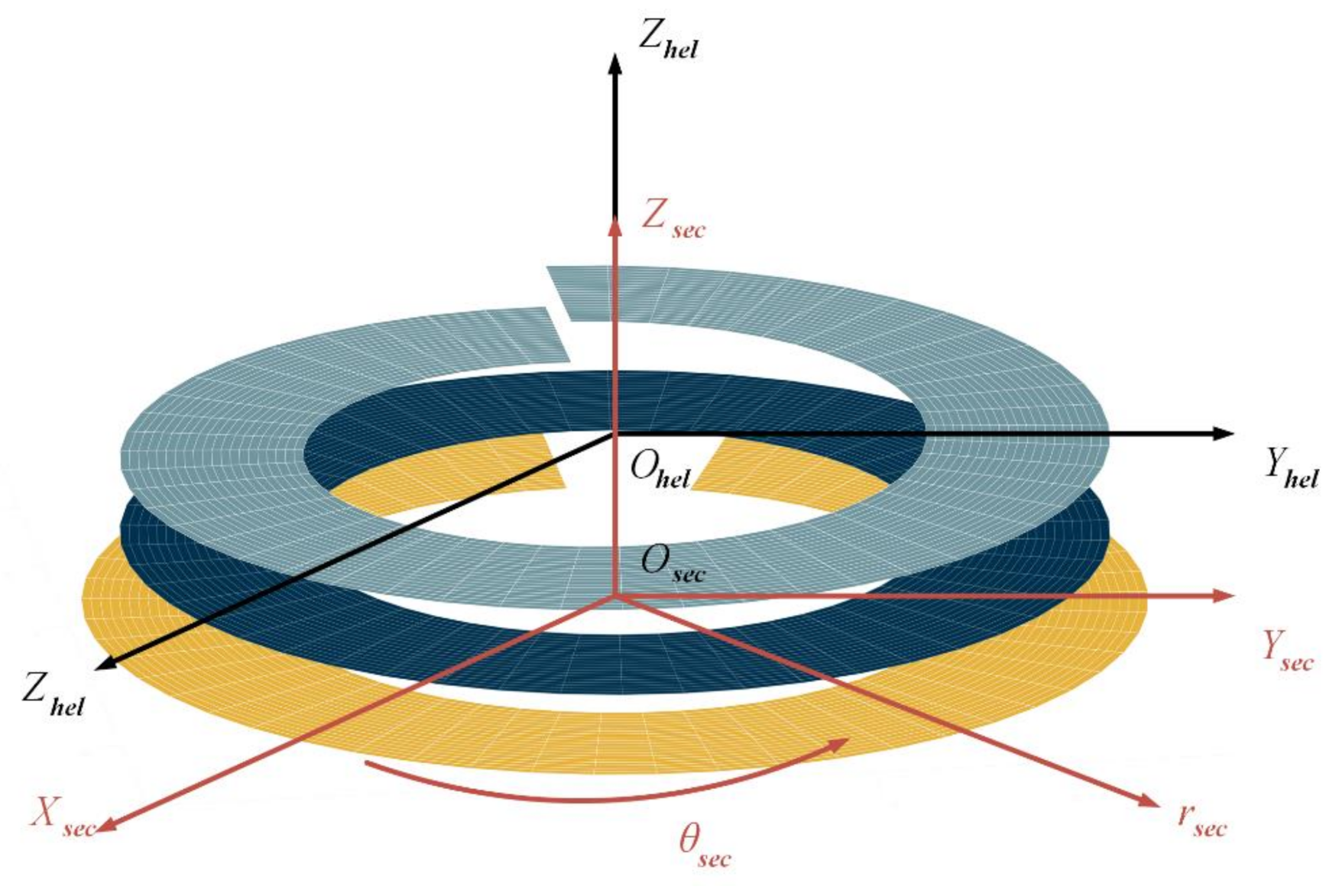
2.1. CFD Modelling for the Gap Flow Field of a Fluid Lubricated Screw-Nut Pair
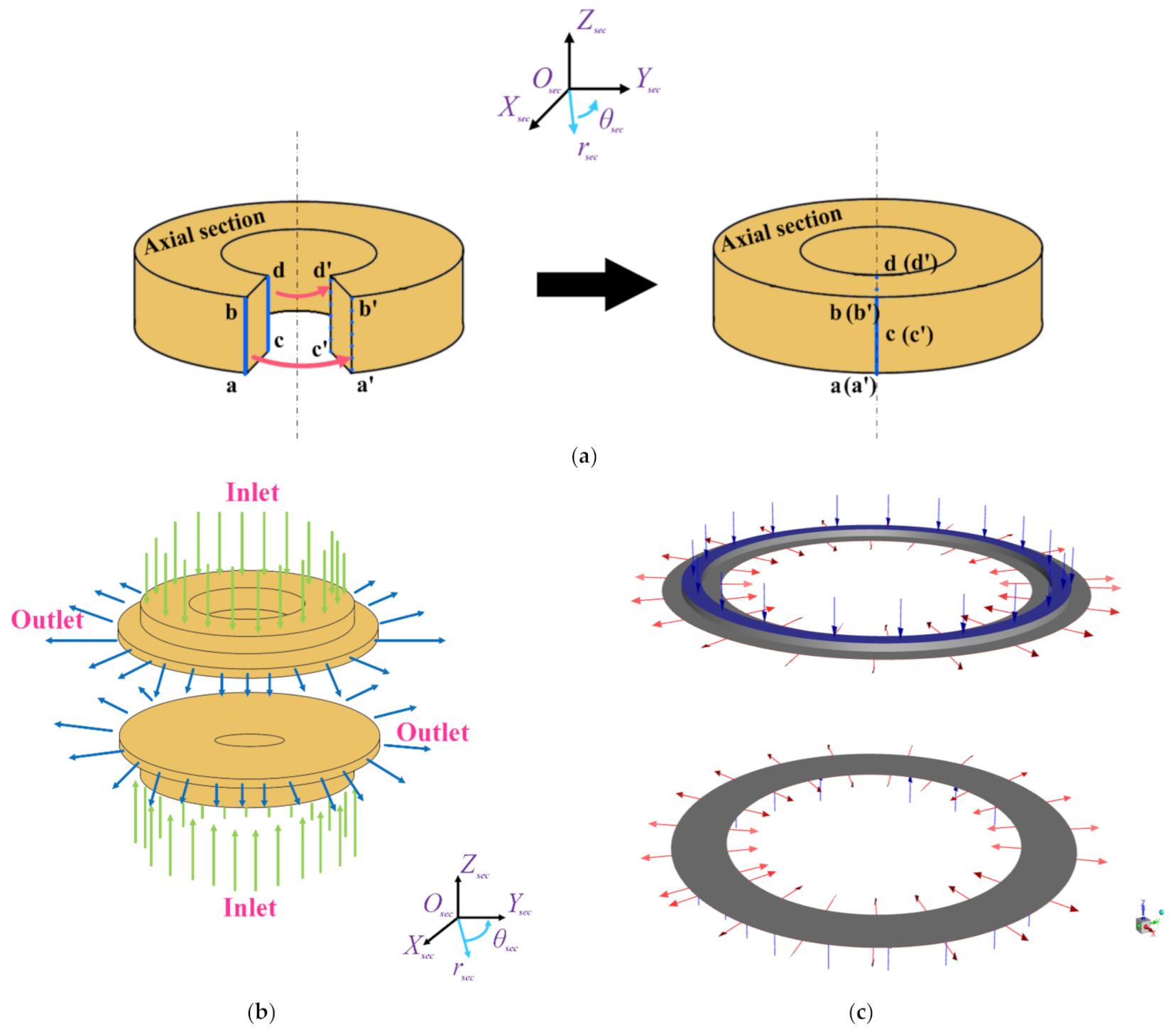
2.1.1. Simplification for the Fluid Domain
2.1.2. Meshing
2.1.3. Governing Equations
2.1.4. Boundary Conditions
2.2. Restrictor Setting
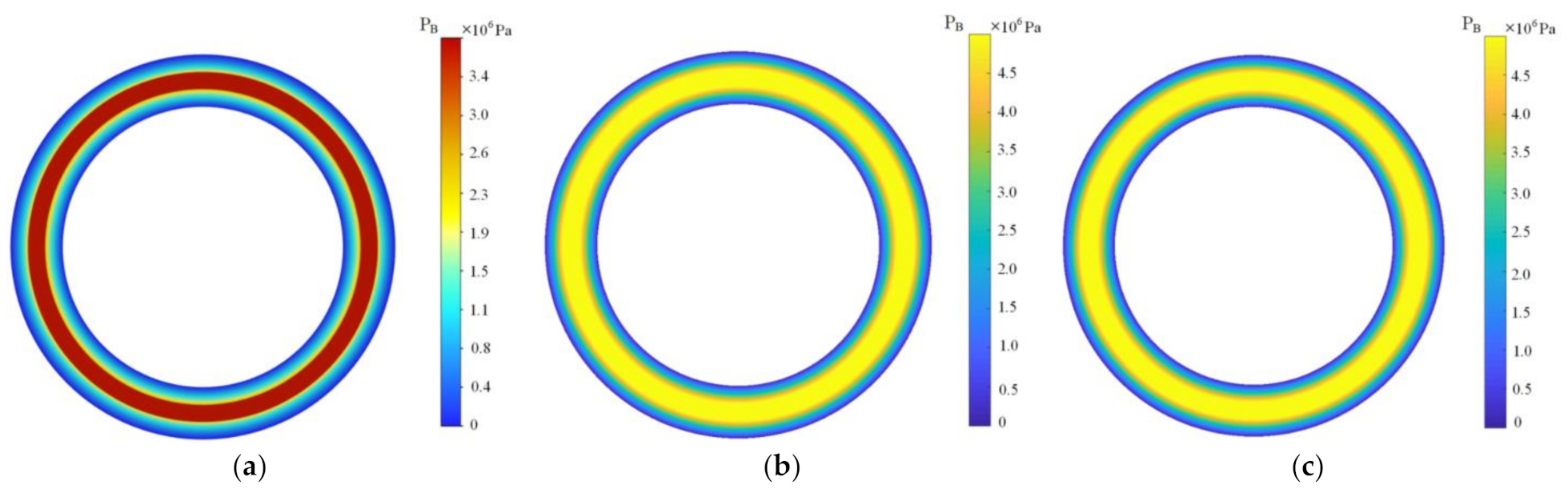
3. Results and Discussion
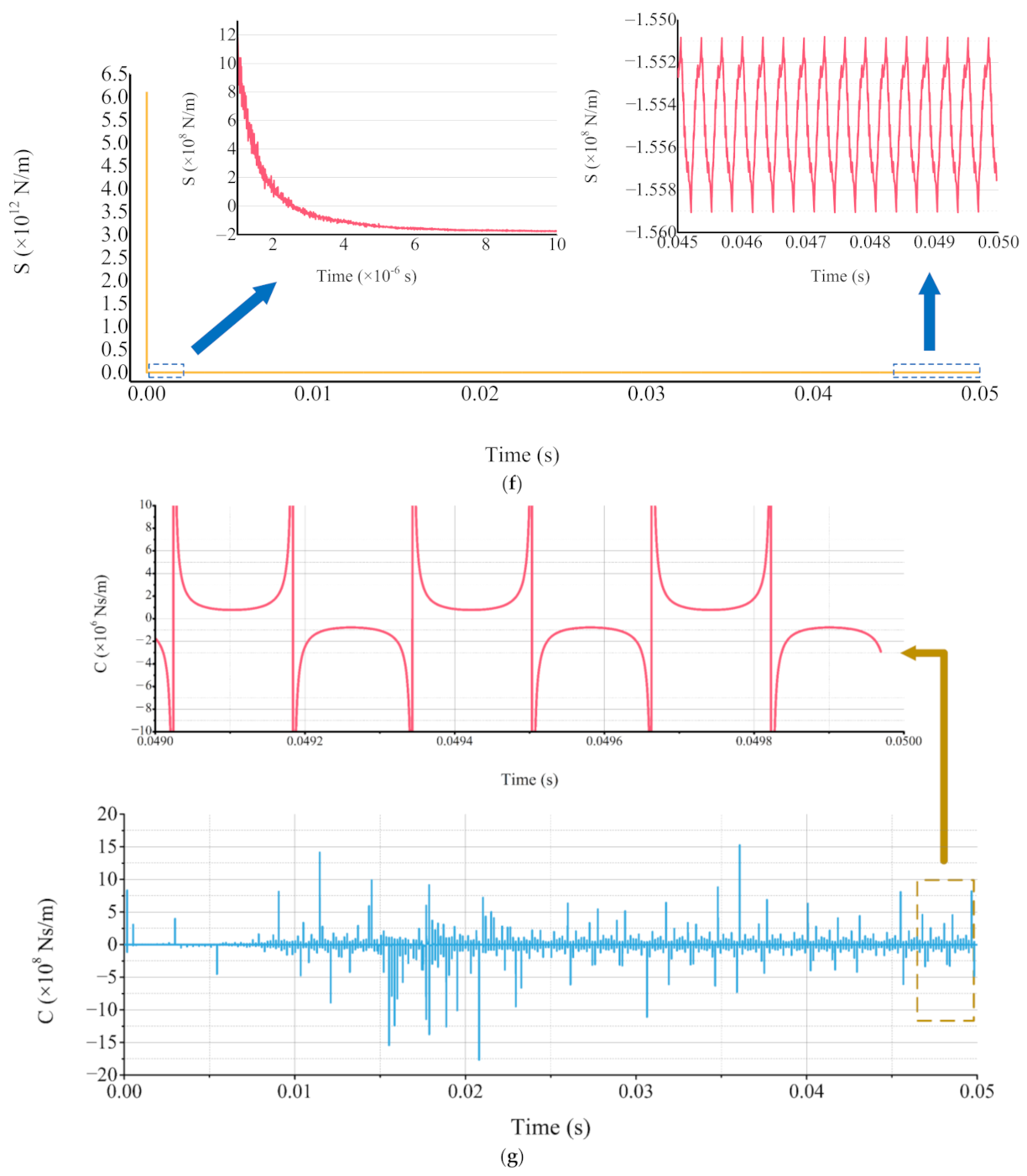
3.1. The Computation of the Stiffness and Damping Coefficients
3.1.1. Solution Method
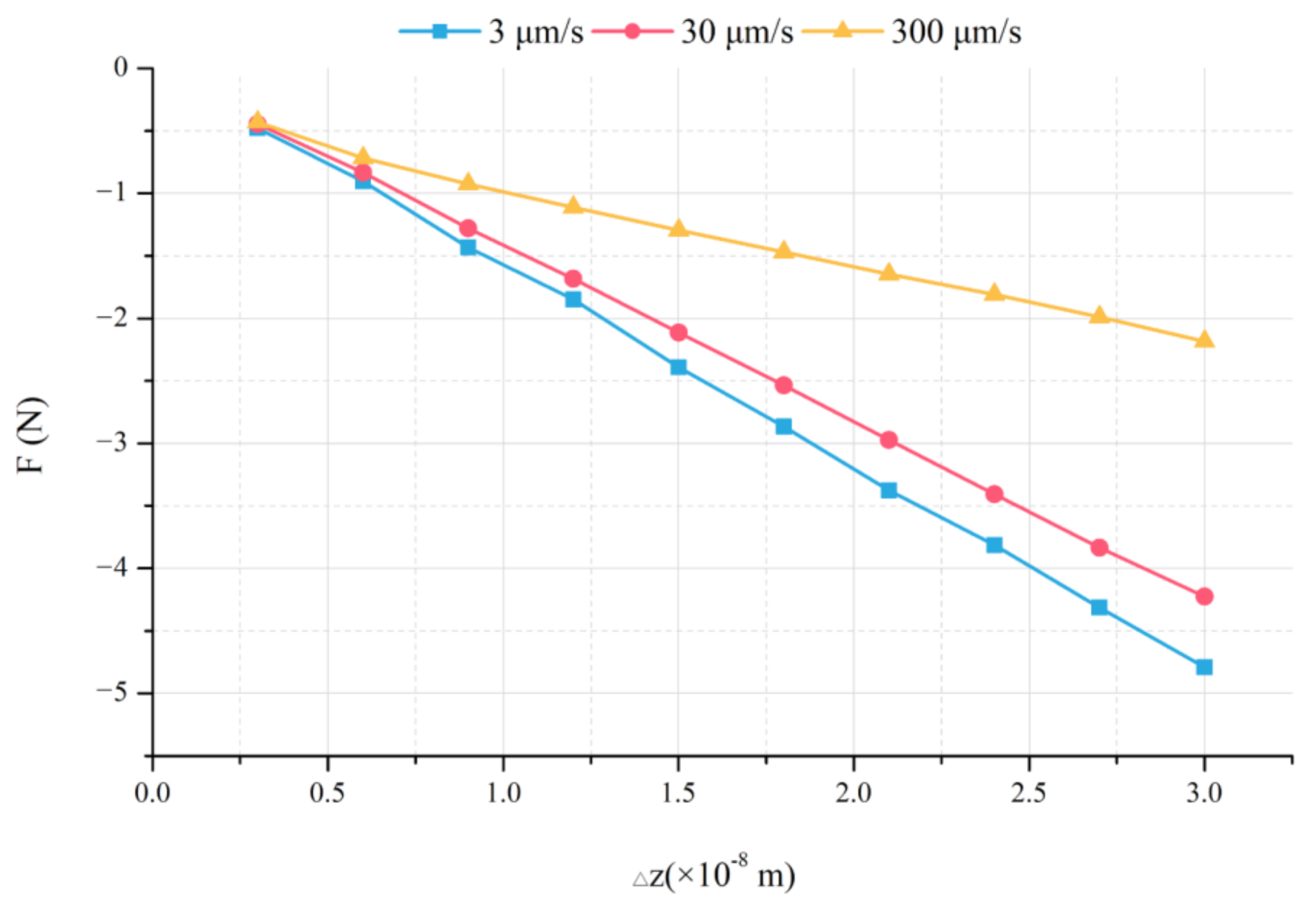
3.1.2. Calculation Case
3.2. Dynamics Analyses of a Fluid Lubricated Screw-Nut Pair Based on the Fluid–Solid Interaction
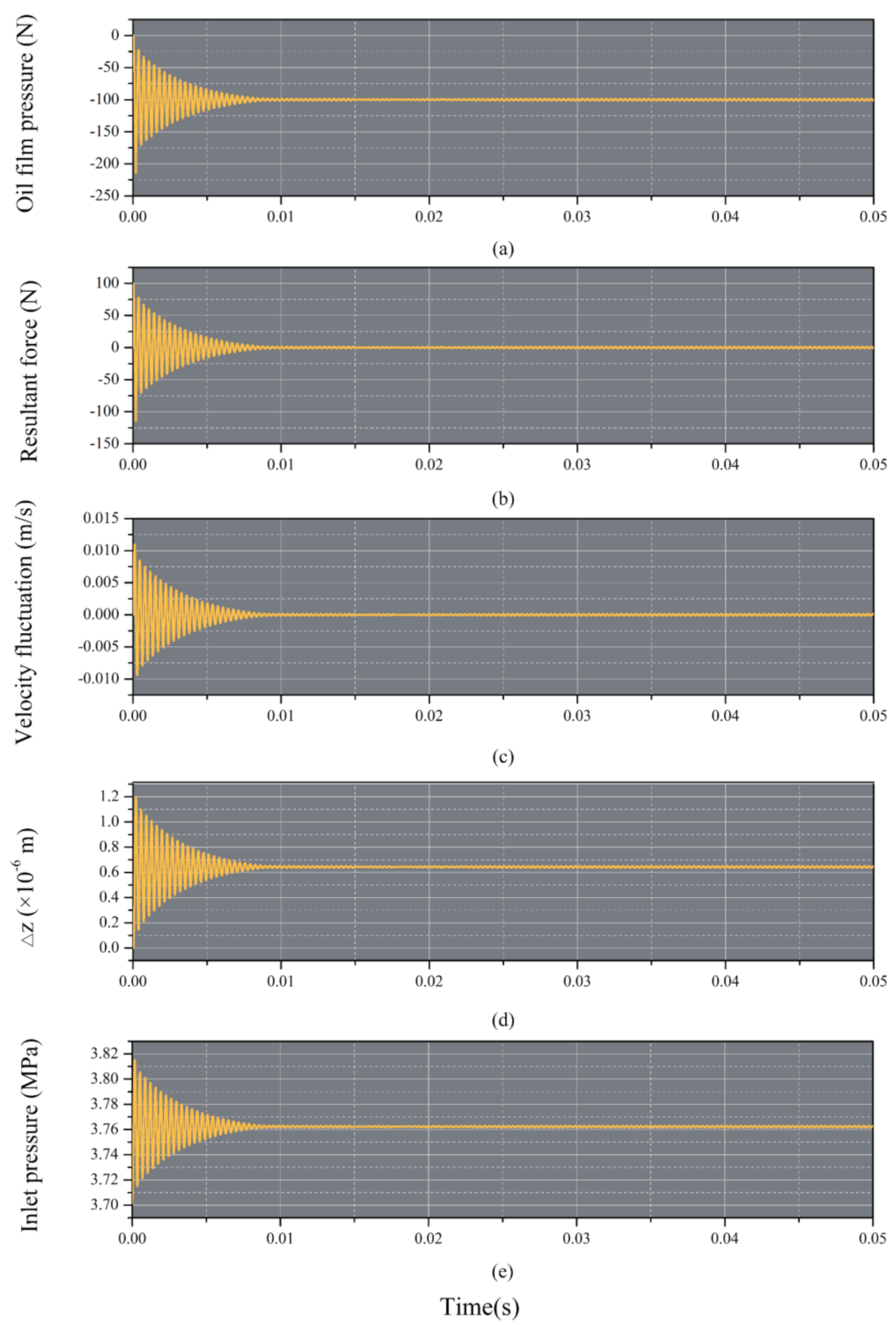
3.2.1. Translational Motion in the -Axis Direction
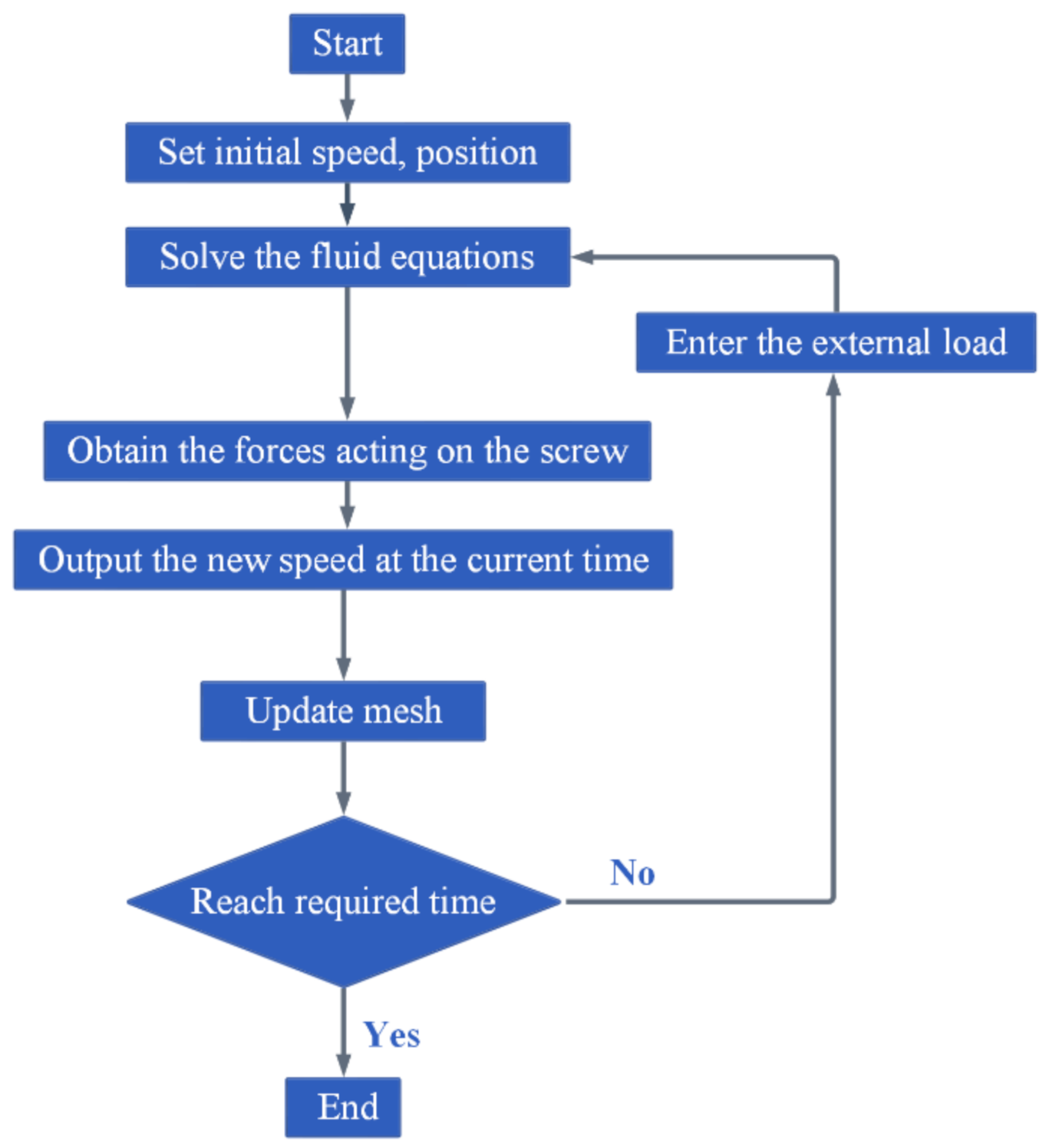
3.2.2. Fluid–Solid Interaction
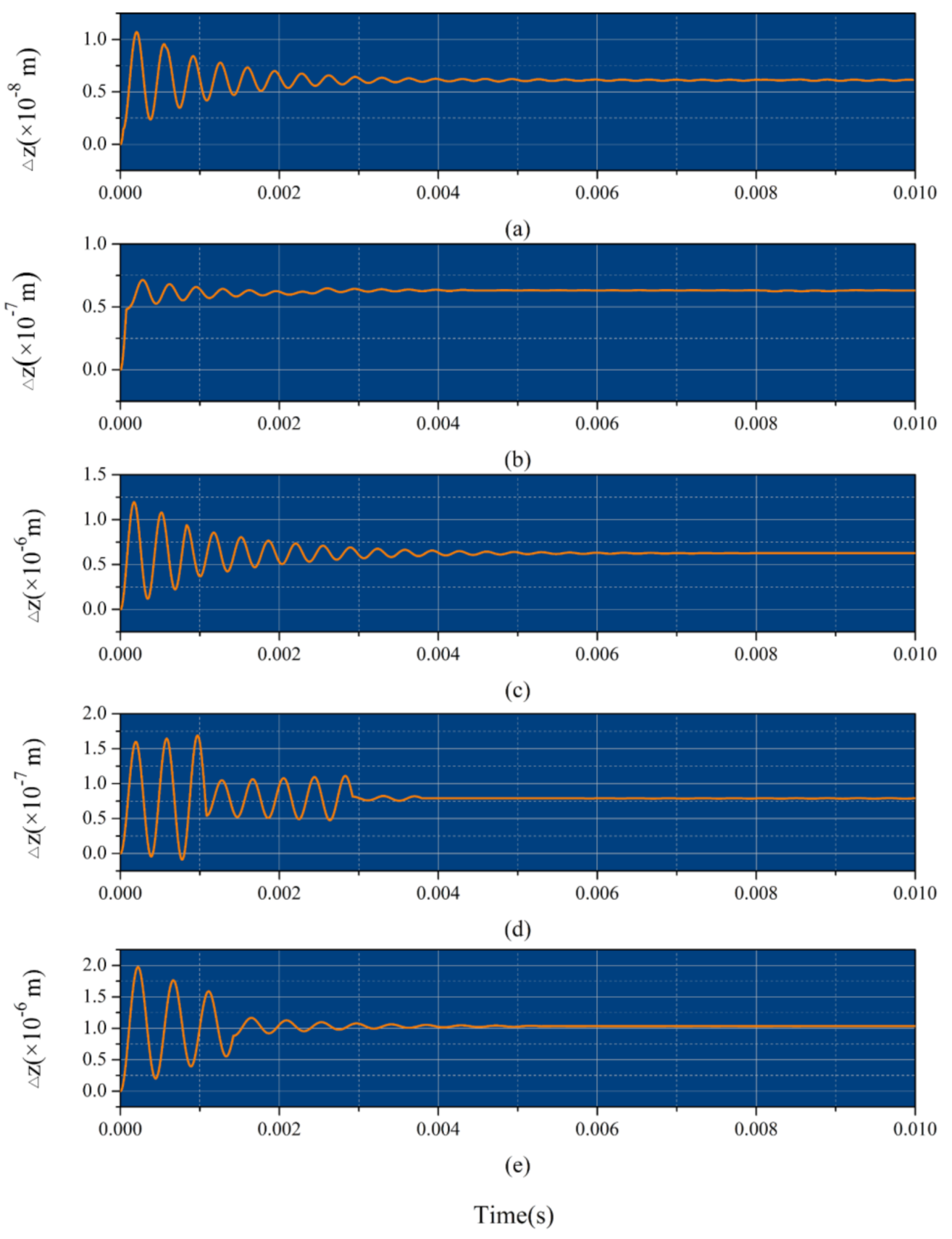
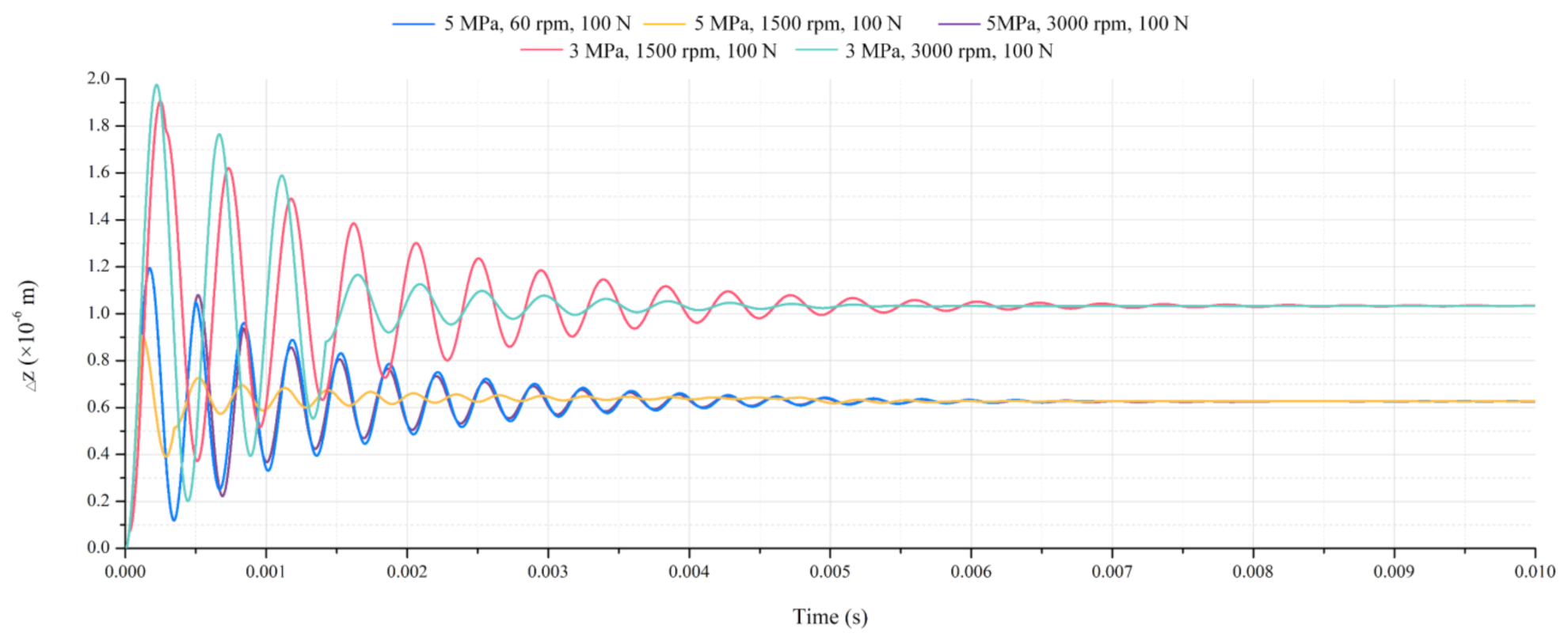
3.2.3. Dynamics Properties under an External Load
3.3. Comparison with the Previous Method
3.4. Feasibility Evaluation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Rectangular coordinate system on the screw-nut pair | |
| Rectangular coordinate system on the Computational Fluid Dynamics (CFD) model | |
| Cylindrical coordinate system corresponding to | |
| Pitch () | |
| Radius of any point on the helicoid () | |
| Inner radius of the nut () | |
| Inner radius of the recess of the screw-nut pair () | |
| Outer radius of the recess of the screw-nut pair () | |
| Outer radius of the screw () | |
| Lead angle at () | |
| Lead angle at () | |
| Half of thread angle () | |
| Angular velocity of the screw () | |
| Angular velocity of the thrust bearing transformed from the screw () | |
| // | Velocity component of any point in the / / -axis direction () |
| Angle contained by two sides of the annular-sector plane () | |
| Angular position in () | |
| Radius of any particle in the CFD model () | |
| Inner radius of the CFD model () | |
| Inner radius of the recess of the CFD model () | |
| Outer radius of the recess of the CFD model () | |
| Outer radius of the CFD model () | |
| Oil density () | |
| Oil viscosity () | |
| Oil supply pressure () | |
| Resistance of the capillary restrictor () | |
| Restrictor factor () | |
| Length and the diameter of the capillary restrictor () | |
| Diameter of the capillary restrictor () | |
| Resistance of the recess of the transformed thrust bearing () | |
| Initial clearance () | |
| Displacement of the screw from equilibrium position () | |
| / | Upper/lower recess pressure () |
| Variation of the oil film force caused by the perturbations () | |
| Stiffness coefficient () | |
| Damping coefficient () | |
| Resultant oil film force acting on the screw in the -axis direction () | |
| / | Fluid pressure applied to the upside/downside of the screw () |
| External load applied to the screw () | |
| Mass of the thrust bearing corresponding to the screw within pitch () | |
| Translational acceleration along the -axis direction () |
References
- Brecher, C.; Utsch, P.; Klar, R.; Wenzel, C. Compact design for high precision machine tools. Int. J. Mach. Tools Manuf. 2010, 50, 328–334. [Google Scholar] [CrossRef]
- Sun, T.; Wang, M.; Gao, X.; Zhao, Y. Non-hertzian elastohydrodynamic contact stress calculation of high-speed ball screws. Appl. Sci. 2021, 11, 12081. [Google Scholar] [CrossRef]
- Barewar, A.M.; Padole, A.A.; Nagpure, Y.D.; Gaupale, P.S.; Nagmote, S.B.; Ram, C.K.; Raut, R.S. Fabrication of automatic screw jack. Int. J. Adv. Res. Dev. 2018, 3, 64–67. [Google Scholar]
- Matataro, T.; Akira, Y. A study on hydrostatic lead screws (1st Report). J. Jpn. Soc. Precis. Eng. 1981, 47, 1504–1509. [Google Scholar]
- Satomi, T.; Yamamoto, A. Studies on the aerostatic lead screws (1st Report). J. Jpn. Soc. Precis. Eng. 1984, 50, 975–980. [Google Scholar] [CrossRef] [Green Version]
- Shen, T. Research on Aerostatic Leading Screw. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2008. [Google Scholar]
- Luo, S.; Zhao, S. Liquid nut for high speed transmission system. Mach. Tool Hydraul. 2008, 36, 327–328. [Google Scholar] [CrossRef]
- Zhong, W. Performance Research on Hydrostatic Lead Screws with Spool-Type Restrictors. Master’s Thesis, Shandong University, Jinan, China, 2017. [Google Scholar]
- Xin, Z. Design and Dynamic Analysis of Full Static Pressure Double Drive Screw Transmission System. Master’s Thesis, Shandong University, Jinan, China, 2020. [Google Scholar]
- Elsayed, H.R.; Khatan, H. A suggested new profile for externally pressurized power screws. Wear 1976, 30, 237–247. [Google Scholar] [CrossRef]
- Elsayed, H.R.; Khatan, H. The exact performance of externally pressurized power screws. Wear 1976, 39, 285–306. [Google Scholar] [CrossRef]
- Elsayed, H.R.; Khatan, H. The running performance of externally pressurized power screws. Wear 1975, 31, 141–156. [Google Scholar] [CrossRef]
- Susumu, O. A prototype production of aerostatic lead screw with resin molded bearing surfaces and performance evaluation. J. Jpn. Soc. Precis. Eng. 2015, 81, 570–575. [Google Scholar]
- Zhang, Y.; Lu, C.; Ma, J. Research on two methods for improving the axial static and dynamic characteristics of hydrostatic lead screws. Tribol. Int. 2017, 109, 152–164. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, S.; Lu, C.; Liu, Z. Performance analysis of capillary-compensated hydrostatic lead screws with discontinuous helical recesses including influence of pitch errors in nut. Tribol. T. 2017, 60, 974–987. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, C.; Liu, Y. Averaging effect on pitch errors in hydrostatic lead screws considering helical recess layout and nut misalignment. Proc. Inst. Mech. Eng. Part J. 2018, 232, 1181–1192. [Google Scholar] [CrossRef]
- Zhang, Y. Research on Pitch Error Mechanism and Motion Characteristics of Hydrostatic Lead Screws. Ph.D. Thesis, Shandong University, Jinan, China, 2017. [Google Scholar]
- Lu, J.; Feng, X.; Su, Z.; Liu, Y.; Wang, D. Modeling and analysis for the transmission characteristics of a proposed dual-drive hydrostatic lead screw system. J. Tribol. 2022, 144, 071202. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, X.; Li, Y.; Lu, J.; Su, Z. Research on boundary slip of hydrostatic lead screw under different driving modes. Sci. Rep. 2021, 11, 22307. [Google Scholar] [CrossRef]
- Sommerfield, A. Ein Beitrag zur hydrodynamischen Erkläerung der turbulenten Flüssigkeitsbewegüngen (A Contribution to Hydrodynamic Explanation of Turbulent Fluid Motions). In Proceedings of the 4th International Congress of Mathematicians, Roma, Italy, 6–11 April 1908; 3, pp. 116–124. [Google Scholar]
- Seshadri, K.; Williams, F.A. Laminar flow between parallel plates with injection of a reactant at high reynolds number. Int. J. Heat Mass Transfer 1978, 21, 251–253. [Google Scholar] [CrossRef]
- Streeter, V.L. Fluid Mechanics, 4th ed.; Tata McGraw-Hill Education: New York, NY, USA, 1966. [Google Scholar]
- Alfonsi, G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- Snyder, T.; Braun, M. Comparison of perturbed Reynolds equation and CFD models for the prediction of dynamic coefficients of sliding bearings. Lubricants 2018, 6, 5. [Google Scholar] [CrossRef] [Green Version]
- Sahlin, F.; Glavatskih, S.B.; Almqvist, T.R.; Larsson, R. 2D CFD-Analysis of Micro-Patterned Surfaces in Hydrodynamic Lubrication. In Proceedings of the ASME/STLE 2004 International Joint Tribology Conference, Long Beach, CA, USA, 24–27 October 2004; pp. 1657–1665. [Google Scholar]
- Mori, A.; Makino, T.; Mori, H. Entry flow and pressure jump in submerged multi-pad bearings and grooved bearings. J. Tribol. 1992, 114, 370–377. [Google Scholar] [CrossRef]
- Tucker, P.G.; Keogh, P.S. On the dynamic thermal state in a hydrodynamic bearing with a whirling journal using CFD techniques. Int. J. Multiphas. Flow. 1997, 23, 118. [Google Scholar] [CrossRef]
- Yang, S.; Ai, Z.; Zhang, C.; Dong, S.; Ouyang, X.; Liu, R.; Zhang, P. Study on optimization of tunnel ventilation flow field in long tunnel based on CFD computer simulation technology. Sustainability 2022, 14, 11486. [Google Scholar] [CrossRef]
- Ni, J.; Dong, J.; Ullah, I.; Mao, H. CFD simulation of sucrose flow field in the stem of greenhouse tomato seedling. Int. J. Agric. Biol. Eng. 2022, 15, 111–115. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Park, J.Y. Review of computational fluid dynamics modeling of iron sintering process. Int. J. Eng. Sci. Technol. 2022, 36, 4501–4508. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y. Research on Aerodynamic Characteristics of Non-Circular Cross-Section Missile Based on Fluent. In Proceedings of the IEEE International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 1224–1229. [Google Scholar]
- Zhu, Q.; Zhang, Y.; Zhu, D. Study on dynamic characteristics of the bladder fluid pulsation attenuator based on dynamic mesh technology. J. Mech. Sci. Technol. 2019, 33, 1159–1168. [Google Scholar] [CrossRef]
- Corvaglia, A.; Altare, G.; Finesso, R.; Rundo, M. Computational Fluid Dynamics Modelling of a Load Sensing Proportional Valve. In Proceedings of the ASME-JSME-KSME 2019 Joint Fluids Engineering Conference, San Francisco, CA, USA, 28 July–1 August 2019. [Google Scholar]
- Nishikawa, H. Uses of Zero and Negative Volume Elements for Node-Centered Edge-Based Discretization. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Graebel, W. Advanced Fluid Mechanics; Academic Press: Cambridge, MA, USA, 2007; pp. 11–15. [Google Scholar]
- Zhang, Y.; Yu, S.; Lu, C.; Zhao, H.; Liang, P. An improved lumped parameter method for calculating static characteristics of multi-recess hydrostatic journal bearings. Proc. Inst. Mech. Eng. Part J. 2020, 234, 301–310. [Google Scholar] [CrossRef]
- Wang, D. Lubrication Technical Manual, 1st ed.; China Machine Press: Beijing, China, 1999; pp. 28–29. [Google Scholar]
- Dhakad, R.; Pradhan, B.K.; Kumar, J.; Behera, S.K. Prediction of Stiffness and Damping of Gas Foil Journal Bearing for High-Speed Rotor. In Proceedings of the TRIBOINDIA-2018 An International Conference on Tribology, Mumbai, India, 13–15 December 2018. [Google Scholar]
- Yang, L.; Li, H.; Yu, L. Dynamic stiffness and damping coefficients of aerodynamic tilting-pad journal bearings. Tribol. Int. 2007, 40, 1399–1410. [Google Scholar]
- Peng, J.; Carpino, M. Calculation of stiffness and damping coefficients for elastically supported gas foil bearings. J. Tribol. 1993, 115, 20–27. [Google Scholar] [CrossRef]



| Parameter | Symbol | Units | Value |
|---|---|---|---|
| Inner radiance of the nut | |||
| Inner radiance of the recess | |||
| Outer radiance of the recess | |||
| Outer radiance of the screw | |||
| Thread angle | |||
| Pitch | |||
| Initial clearance | |||
| Oil density | |||
| Oil viscosity | |||
| Restrictor factor |
| Parameters | Value |
|---|---|
| () | |
| () | |
| () | |
| Method | ||||
|---|---|---|---|---|
| a | ||||
| b |
| Case | () | () | () | () | () | Method |
|---|---|---|---|---|---|---|
| 1 | a | |||||
| 2 | b | |||||
| 3 |
| Parameters | Value |
|---|---|
| () | |
| () | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z.; Feng, X.; Li, H.; Liu, Y.; Lu, Z. Hydrodynamics Simulations and Analyses of a Fluid Lubricated Screw-Nut Pair. Machines 2022, 10, 970. https://doi.org/10.3390/machines10110970
Su Z, Feng X, Li H, Liu Y, Lu Z. Hydrodynamics Simulations and Analyses of a Fluid Lubricated Screw-Nut Pair. Machines. 2022; 10(11):970. https://doi.org/10.3390/machines10110970
Chicago/Turabian StyleSu, Zhe, Xianying Feng, Hui Li, Yandong Liu, and Ziteng Lu. 2022. "Hydrodynamics Simulations and Analyses of a Fluid Lubricated Screw-Nut Pair" Machines 10, no. 11: 970. https://doi.org/10.3390/machines10110970
APA StyleSu, Z., Feng, X., Li, H., Liu, Y., & Lu, Z. (2022). Hydrodynamics Simulations and Analyses of a Fluid Lubricated Screw-Nut Pair. Machines, 10(11), 970. https://doi.org/10.3390/machines10110970





