Optimal Design of a Five-Bar Planar Manipulator and Its Controller by Using Different Algorithms for Minimum Shaking Forces and Moments for the Largest Trajectory in a Usable Workspace
Abstract
1. Introduction
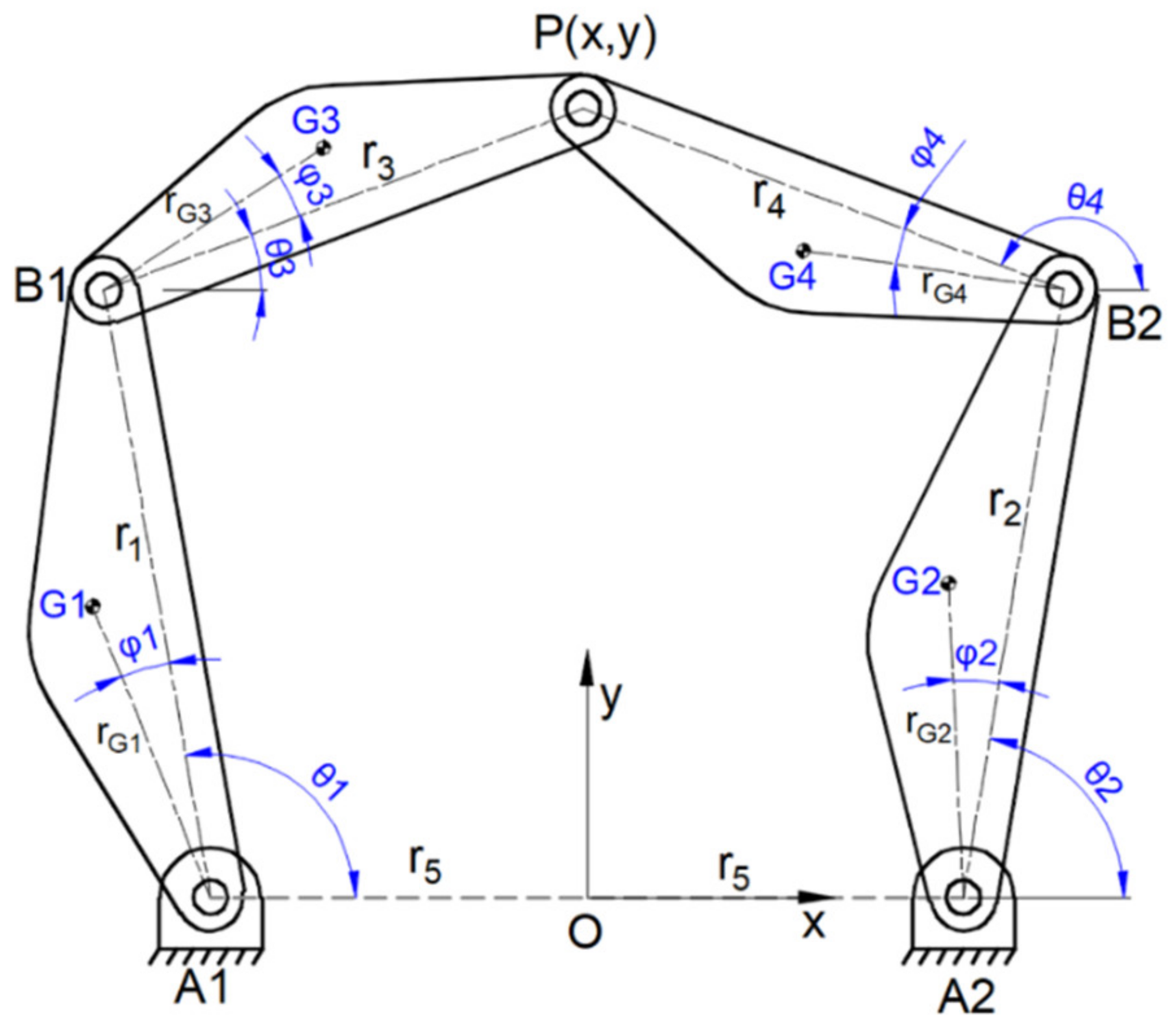
2. Modeling of the Five-Bar Planar Manipulator
2.1. Inverse Kinematics of the Five-Bar Planar Manipulator
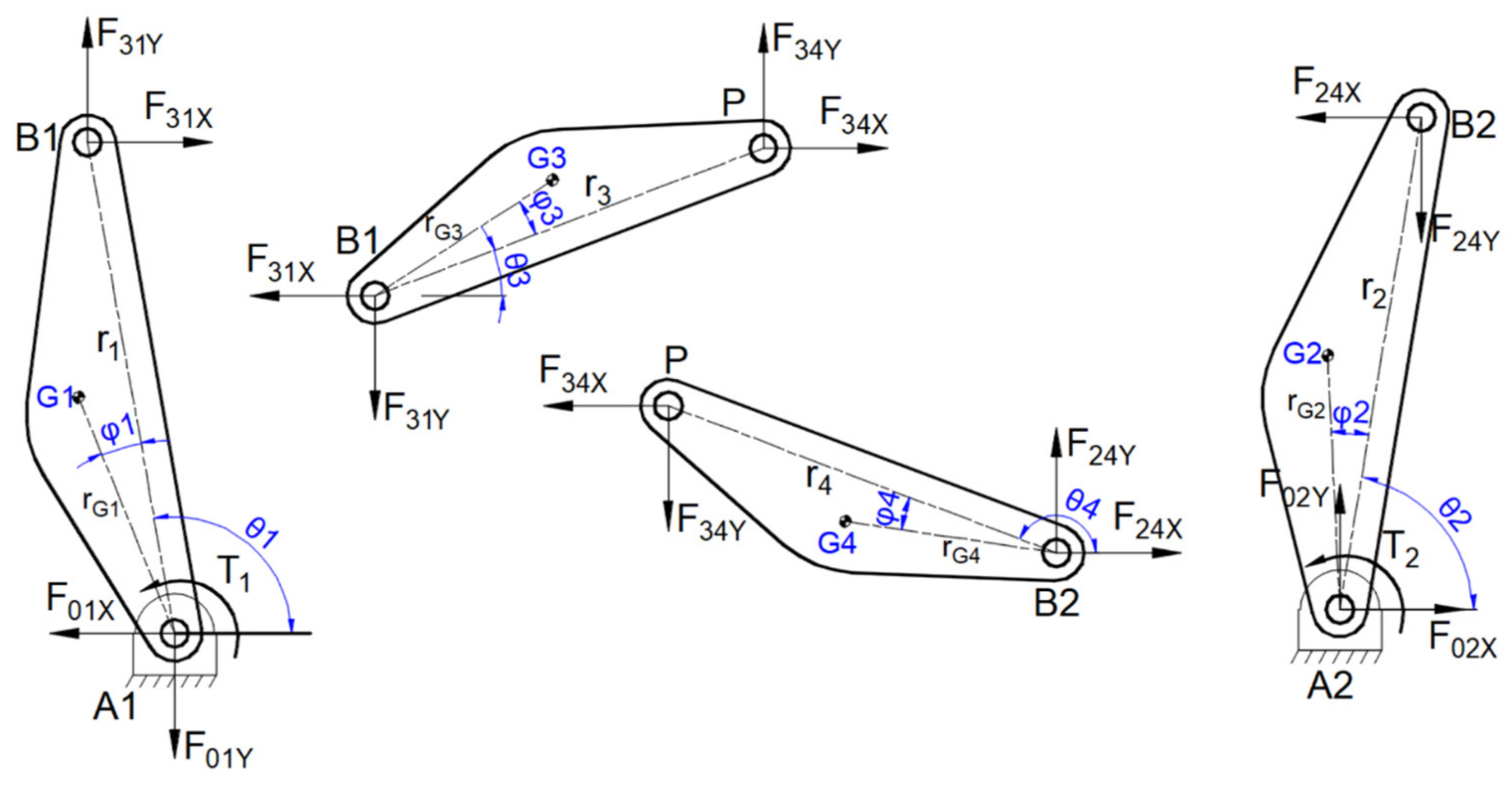
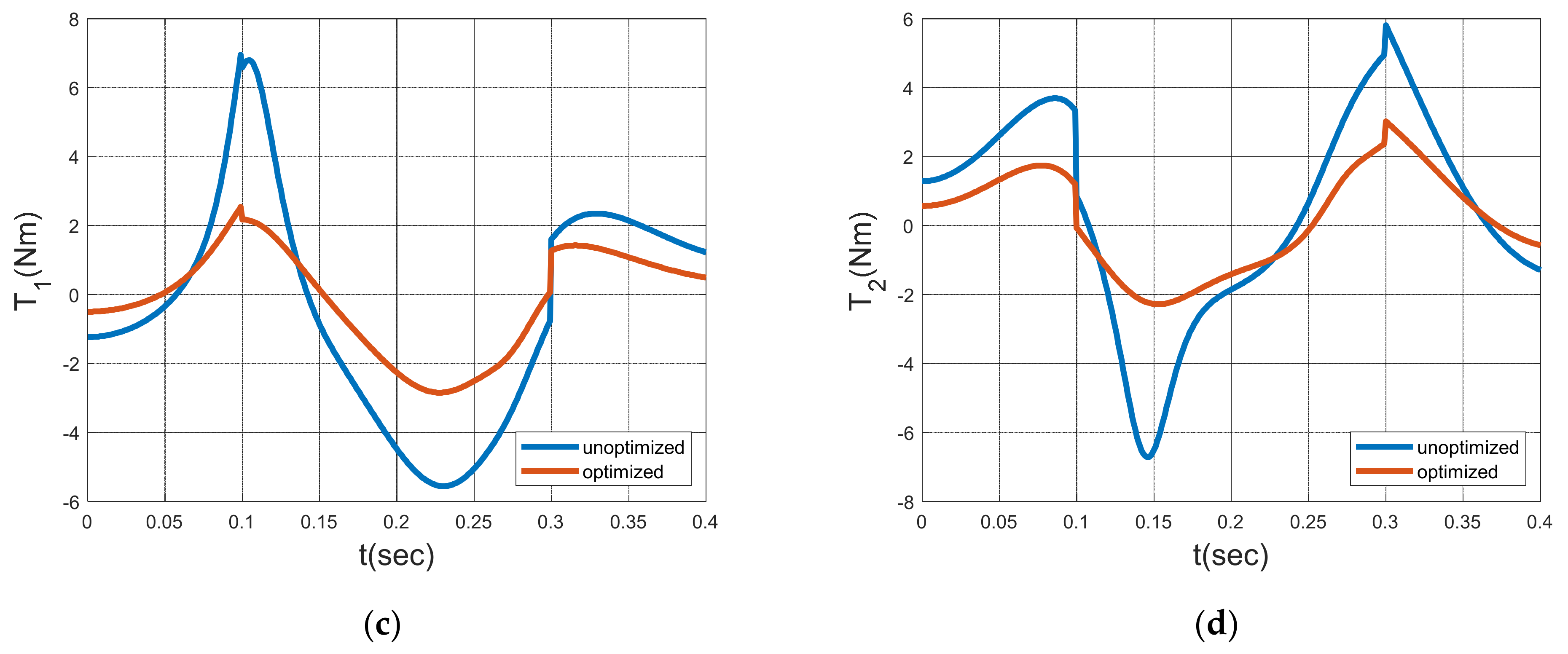
2.2. Inverse Dynamics of the Five-Bar Planar Manipulator
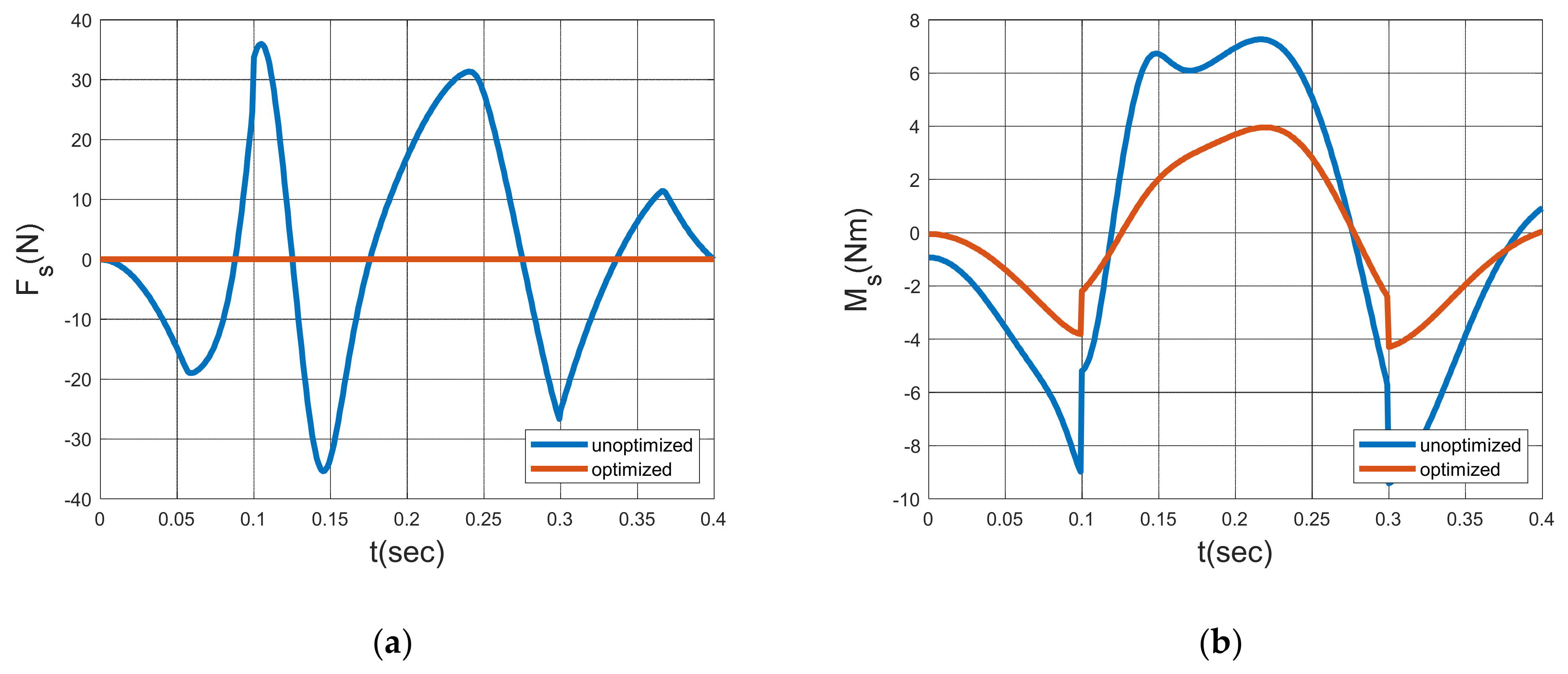
2.3. Shaking Force and Moment of the Five-Bar Planar Manipulator
3. Structural Optimization of Five-Bar Planar Manipulator
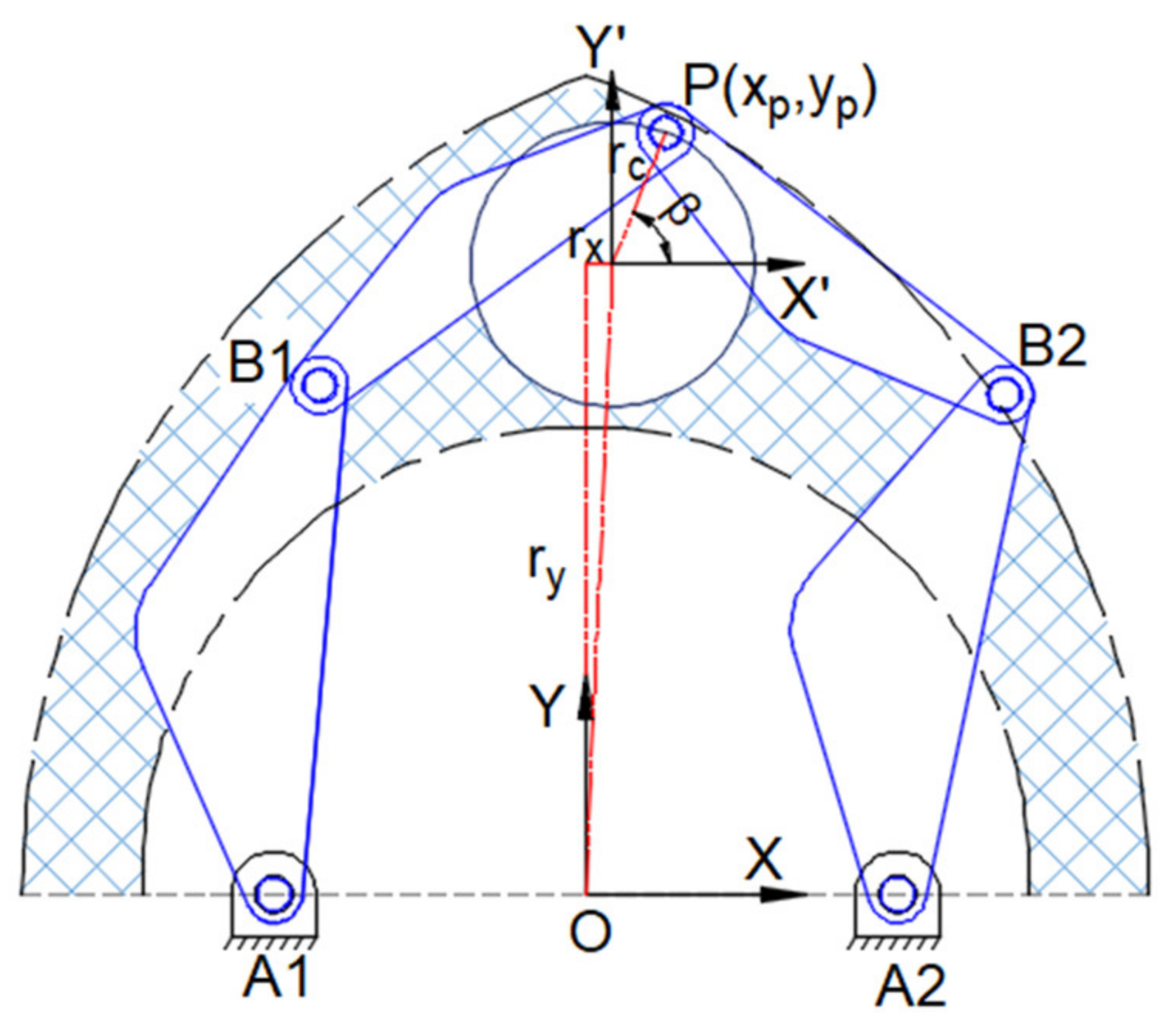
3.1. Desired Trajectory Planning
3.2. Definition of the Objective Function, Design Variables, and Constraints
3.3. Applied Optimization Methods
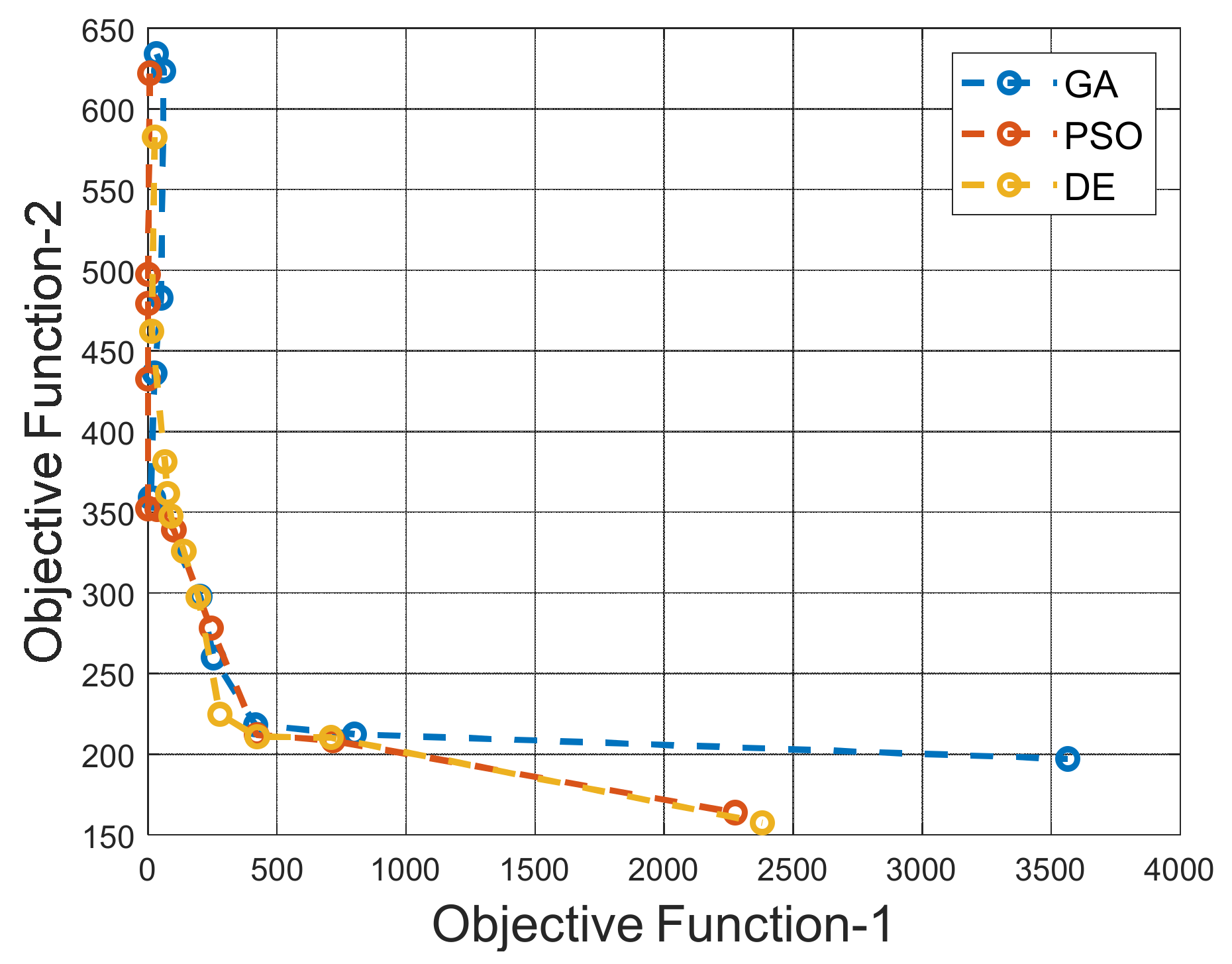
3.4. Structural Optimization Results
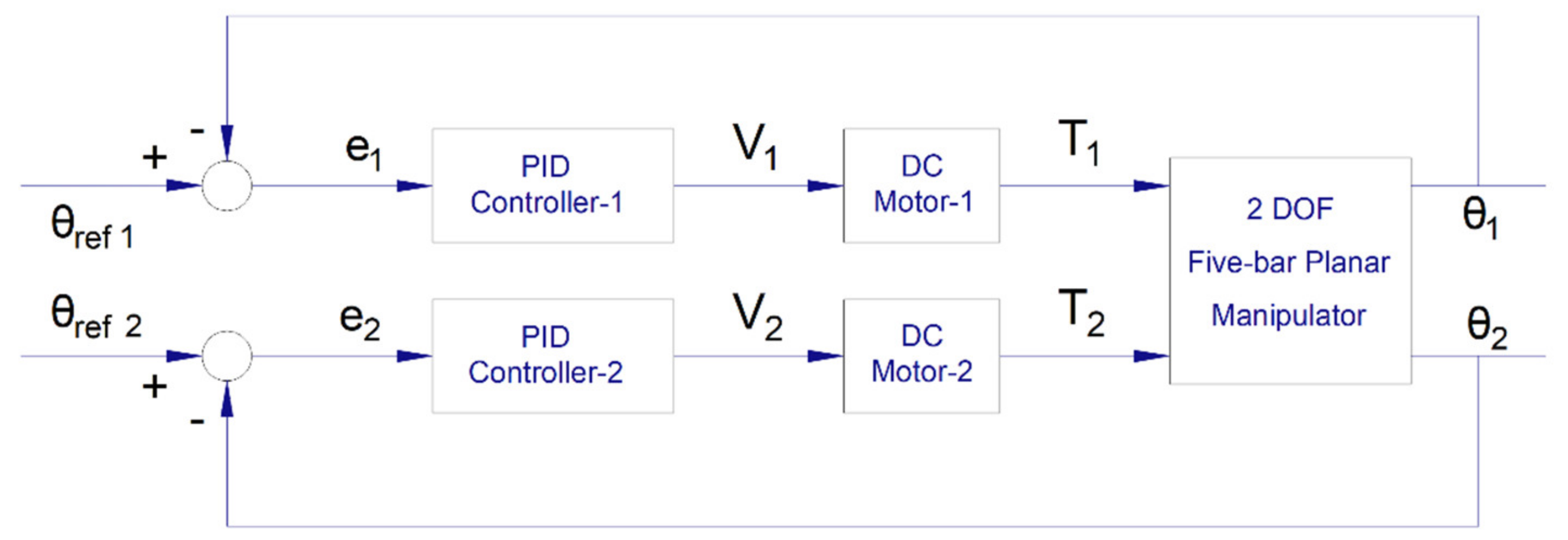
4. Controller Design
4.1. Mathematical Model of DC Motor
4.2. Tuning of PID Controller Using Optimization Methods
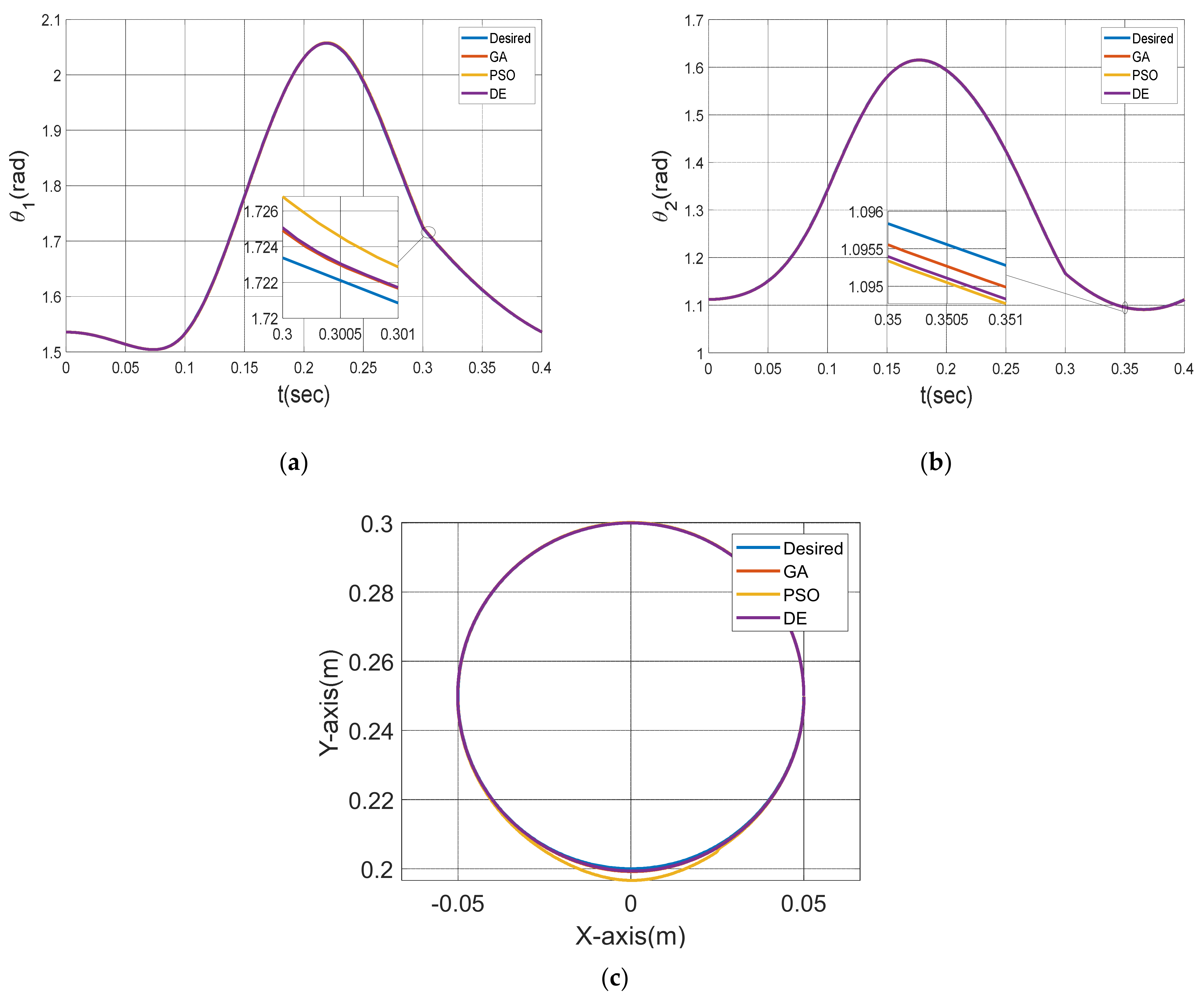
4.3. PID-Controller Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Cervantes-Sánchez, J.J.; Rendón-Sánchez, J.G. Simplified approach for obtaining the workspace of a class of 2-dof planar parallel manipulators. Mech. Mach. Theory 1999, 34, 1057–1073. [Google Scholar] [CrossRef]
- Cervantes-Sánchez, J.; Hernández-Rodríguez, J.; Rendón-Sánchez, J. On the workspace, assembly configurations and singularity curves of the RRRRR-type planar manipulator. Mech. Mach. Theory 2000, 35, 1117–1139. [Google Scholar] [CrossRef]
- Liu, X.-J.; Wang, J.; Pritschow, G. Kinematics, singularity and workspace of planar 5R symmetrical parallel mechanisms. Mech. Mach. Theory 2006, 41, 145–169. [Google Scholar] [CrossRef]
- Alıcı, G. Determination of singularity contours for five-bar planar parallel manipulators. Robotica 2000, 18, 569–575. [Google Scholar] [CrossRef]
- Liu, X.-J.; Wang, J.; Zheng, H.-J. Optimum design of the 5R symmetrical parallel manipulator with a surrounded and good-condition workspace. Robot. Auton. Syst. 2006, 54, 221–233. [Google Scholar] [CrossRef]
- Stan, S.; Lăpuşan, C. Workspace analysis of a 2 dof mini parallel robot. In Proceedings of the 8th National Symposium with International Participation COMPUTER AIDED DESIGN-PRASIC’06, Braşov, Romania, 9–10 November 2006; pp. 175–180. [Google Scholar]
- Liu, X.-J.; Wang, J.; Pritschow, G. On the optimal kinematic design of the PRRRP 2-DoF parallel mechanism. Mech. Mach. Theory 2006, 41, 1111–1130. [Google Scholar] [CrossRef]
- Campos, L.; Bourbonnais, F.; Bonev, I.A.; Bigras, P. Development of a Five-Bar Parallel Robot with Large Workspace. Proc. ASME Des. Eng. Tech. Conf. 2010, 2, 917–922. [Google Scholar] [CrossRef]
- Stan, S.-D.; Maties, V.; Bal, R. Optimal Design of Parallel Kinematics Machines with 2 Degrees of Freedom. Parallel Manip. Towar. New Appl. 2008, 14, 1–29. [Google Scholar] [CrossRef][Green Version]
- Oarcea, A.; Cobilean, V.; Stan, S.-D. Trajectory planning of a 3-RRRRR planar parallel robot. In Proceedings of the 2021 9th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 16–17 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mundo, D.; Gatti, G.; Dooner, D. Optimized five-bar linkages with non-circular gears for exact path generation. Mech. Mach. Theory 2009, 44, 751–760. [Google Scholar] [CrossRef]
- Mundo, D.; Gatti, G.; Dooner, D.B. Combined synthesis of five-bar linkages and non-circular gears for precise path generation. In Proceedings of the 12th IFToMM World Congr., Besançon, France, 17–21 June 2007. [Google Scholar]
- Uzunoglu, E.; Dede, M.; Kiper, G. Trajectory planning for a planar macro-micro manipulator of a laser-cutting machine. Ind. Robot 2016, 43, 513–523. [Google Scholar] [CrossRef]
- Berkoff, R.S. Complete force and moment balancing of inline four-bar linkages. Mech. Mach. Theory 1973, 8, 397–410. [Google Scholar] [CrossRef]
- Elliott, J.L.; Tesar, D. The theory of torque, shaking force and shaking moment balancing of four link mechanisms. Trans. ASME J. Eng. Ind. 1977, 97, 715–722. [Google Scholar] [CrossRef]
- Acevedo, M.; Orvananos, T.; Velazquez, R.; Haro, E. Optimum Balancing of the Four-Bar Linkage Using Fully Cartesian Coordinates. IEEE Lat. Am. Trans. 2019, 17, 983–990. [Google Scholar] [CrossRef]
- Alici, G.; Shirinzadeh, B. Optimum dynamic balancing of planar parallel manipulators. In Proceedings of the 2004 IEEE International Conference on Robotics & Automation, New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar] [CrossRef]
- Alici, G.; Shirinzadeh, B. Optimum dynamic balancing of planar parallel manipulators based on sensitivity analysis. Mech. Mach. Theory 2006, 41, 1520–1532. [Google Scholar] [CrossRef]
- Nehemiah, P.; Sundara Siva Rao, B.S.K.; Ramji, K. Shaking force and shaking moment balancing of planar mechanisms with high degree of complexity. Jordan J. Mech. Ind. Eng. 2012, 6, 17–24. [Google Scholar]
- Ilia, D.; Sinatra, R. A novel formulation of the dynamic balancing of five-bar linkages with applications to link optimization. Multibody Syst. Dyn. 2009, 21, 193–211. [Google Scholar] [CrossRef]
- Alici, G.; Shirinzadeh, B. Optimum force balancing with mass distribution and a single elastic element for a five-bar parallel manipulator. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 3666–3671. [Google Scholar] [CrossRef]
- Shaking Force Balancing of Planar Linkages with Force Transmission Irregularities Using Balancing Idler Loops—Science Direct. [Online]. Available online: https://www.sciencedirect.com/science/article/abs/pii/0094114X79900132 (accessed on 24 January 2021).
- Acevedo, M.; Orvañanos-Guerrero, M.T.; Velázquez, R.; Arakelian, V. An Alternative Method for Shaking Force Balancing of the 3RRR PPM through Acceleration Control of the Center of Mass. Appl. Sci. 2020, 10, 1351. [Google Scholar] [CrossRef]
- McCall, J. Genetic algorithms for modeling and optimization. J. Comput. Appl. Math. 2005, 184, 205–222. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the 6th international symposium on micro machine and human science, Nagoya, Japan, 13–16 March 1995; pp. 39–43. [Google Scholar]
- Mayer, D.; Kinghorn, B.; Archer, A. Differential evolution—An easy and efficient evolutionary algorithm for model optimisation. Agric. Syst. 2005, 83, 315–328. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. A global Performance Index for the Kinematic Optimization of Robotic Manipulators. J. Mech. Des. 1991, 113, 220–226. [Google Scholar] [CrossRef]
- Yildiz, A. Parametric synthesis of two different trunk lid mechanisms for sedan vehicles using population-based optimisation algorithms. Mech. Mach. Theory 2021, 156, 104130. [Google Scholar] [CrossRef]
- Le, T.D.; Kang, H.-J.; Doan, Q.V. A method for optimal kinematic design of five-bar planar parallel manipulators. In Proceedings of the 2013 International Conference on Control, Automation and Information Sciences (ICCAIS), Nha Trang, Vietnam, 25–28 November 2013; pp. 7–11. [Google Scholar] [CrossRef]
- Stan, S.; Vistrian, M.; Balan, R. Optimal Design of a 2 DOF Micro Parallel Robot Using Genetic Algorithms. In Proceedings of the 2007 IEEE-ICIT 2007, IEEE International Conference on Integration Technology, Shenzhen, China, 20–24 March 2007; pp. 719–724. [Google Scholar] [CrossRef]
- Ganesh, S.S.; Rao, A.K. Kinematic and Dynamic Optimization of a 2-DOF Parallel Kinematic Mechanism. Procedia Comput. Sci. 2018, 133, 576–584. [Google Scholar] [CrossRef]
- Bingul, O.; Yildiz, A. Fuzzy logic and proportional integral derivative based multi-objective optimization of active suspension system of a 4×4 in-wheel motor driven electrical vehicle. J. Vib. Control 2022, 10775463211062691. [Google Scholar] [CrossRef]
- Yildiz, A. Optimum suspension design for non-linear half vehicle model using particle swarm optimization (PSO) algorithm. In Proceedings of the 41st International JVE Conference Vibration, Leipzig, Germany, 30 September 2019. [Google Scholar]
- Yildiz, A.; Yilmaz, O.; Karabulut, H. Structural design optimization of the arc spring and dual-mass flywheel integrated with different optimization methods. Mater. Test. 2022, 64, 240–248. [Google Scholar] [CrossRef]
- Yildiz, A. A comparative study on the optimal non-linear seat and suspension design for an electric vehicle using different population-based optimisation algorithms. Int. J. Veh. Des. 2019, 80, 241–256. [Google Scholar] [CrossRef]
- Giberti, H.; Cinquemani, S.; Ambrosetti, S. 5R 2dof parallel kinematic manipulator—A multidisciplinary test case in mechatronics. Mechatronics 2013, 23, 949–959. [Google Scholar] [CrossRef]
- Tao, J.; Sadler, J. Constant speed control of a motor driven mechanism system. Mech. Mach. Theory 1995, 30, 737–748. [Google Scholar] [CrossRef]
- Feng, H.; Yin, C.-B.; Weng, W.-W.; Ma, W.; Zhou, J.-J.; Jia, W.-H.; Zhang, Z.-L. Robotic excavator trajectory control using an improved GA based PID controller. Mech. Syst. Signal Process. 2018, 105, 153–168. [Google Scholar] [CrossRef]
- Feng, H.; Ma, W.; Yin, C.; Cao, D. Trajectory control of electro-hydraulic position servo system using improved PSO-PID controller. Autom. Constr. 2021, 127, 103722. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, L.; Wu, N.; Chen, M.; Liu, D.; Zhang, Z.; Liu, J. Adaptive Neural-PID Visual Servoing Tracking Control via Extreme Learning Machine. Machines 2022, 10, 782. [Google Scholar] [CrossRef]


| Pseudo-codes | |||||
| GA | PSO | DE | |||
| START Generate the initial population Compute fitness REPEAT Selection Crossover Mutation Compute fitness UNTIL population has converged STOP | START Initialize Parameters Initialize Population For each particle Update velocity and position Evaluate Update local best Update global best UNTIL the stopping criterion is met STOP | START Generate the initial population Evaluation REPEAT Mutation Recombination Evaluation Selection UNTIL the stopping criterion is met STOP | |||
| The optimization parameters | |||||
| Population Size | 100 | ||||
| Population Size | 100 | Crossover Operator | 0.4 | ||
| Crossover Operator | 0.5 | Swarm Size | 100 | Low Bound of Scaling Factor | 0.2 |
| Mutation Operator | 0.03 | Function Tolerance | 1 × 10−5 | Upper Bound of Scaling Factor | 0.8 |
| Number of Iteration | 200 | Number of Iteration | 200 | Number of Iteration | 200 |
| Weight ing Factor | Un-optimized | GA | PSO | DE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F Obj. Fun. | F(1) | F(2) | F Obj. Fun. | F(1) | F(2) | F Obj. Fun. | F(1) | F(2) | F Obj. Fun. | |
| = 1 and = 0 | 4215.3 | 33.4 | 634.1 | 33.4 | 7.1 | 622.1 | 7.1 | 26.1 | 582.6 | 26.1 |
| = 0.9 and = 0.1 | 3895.8 | 61.1 | 623.5 | 117.2 | 0.43 | 497.4 | 50.1 | 14.8 | 462.3 | 59.5 |
| = 0.8 and = 0.2 | 3576.3 | 51.0 | 482.9 | 137.4 | 0.05 | 479.3 | 95.9 | 65.9 | 381.4 | 129.0 |
| = 0.7 and = 0.3 | 3256.9 | 25.8 | 436.1 | 148.9 | 0.10 | 432.5 | 129.8 | 75.6 | 361.6 | 161.4 |
| = 0.6 and = 0.4 | 2937.4 | 10.0 | 359.1 | 149.6 | 0.01 | 352.3 | 140.9 | 88.9 | 347.7 | 192.4 |
| = 0.5 and = 0.5 | 2617.9 | 21.4 | 358.7 | 190.1 | 36.1 | 351.8 | 193.9 | 138.8 | 325.9 | 232.4 |
| = 0.4 and = 0.6 | 2298.4 | 201.81 | 297.8 | 259.4 | 100.7 | 339.0 | 243.7 | 195.3 | 297.4 | 256.6 |
| = 0.3 and = 0.7 | 1978.9 | 254.45 | 259.9 | 258.3 | 245.0 | 278.2 | 268.2 | 278.9 | 224.7 | 214.0 |
| = 0.2 and = 0.8 | 1659.5 | 416.60 | 218.1 | 257.8 | 421.5 | 211.9 | 253.9 | 423.8 | 210.8 | 253.4 |
| = 0.1 and = 0.9 | 1340.0 | 800.40 | 212.4 | 271.2 | 717.1 | 208.4 | 259.2 | 709.5 | 210.3 | 260.2 |
| = 0 and = 1 | 1020.5 | 3564.5 | 197.1 | 244.7 | 2275.5 | 163.8 | 163.8 | 2379.8 | 157.5 | 157.5 |
| Link i | mi (kg) | ri (m) | Igi (kgm2) | rgi (m) | φi (rad) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Initial | Optimum | Initial | Optimum | Initial | Optimum | Initial | Optimum | Initial | Optimum | |
| 1 | 1.8711 | 2.1438 | 0.180 | 0.189 | 0.0093 | 0.0075 | 0.0772 | 0.0216 | 0 | 3.1387 |
| 2 | 1.8711 | 1.5887 | 0.180 | 0.196 | 0.0093 | 0.0075 | 0.0772 | 0.0346 | 0 | 3.1440 |
| 3 | 0.3269 | 0.2615 | 0.150 | 0.165 | 0.0008 | 0.0006 | 0.075 | 0.0110 | 0 | 0.0408 |
| 4 | 0.3276 | 0.2621 | 0.150 | 0.164 | 0.0008 | 0.0006 | 0.0801 | 0.0109 | 0 | 3.1826 |
| 5 | - | - | 0.110 | 0.111 | - | - | - | - | - | - |
| Motor Properties | GPX37-DCX32L |
|---|---|
| -Armature resistance (ohm) -Armature inductance (H) - Torque constant (Nm/A) -Back emf constant (Vs./rad) -Rotor Inertia (kgm2) -Viscous friction coefficient (Nms/rad) n-Reducer ratio | 0.331 0.103 × 10−3 27.3 × 10−3 2.85 × 10−3 72.8 × 10−7 1 × 10−5 26 |
| GA | PSO | DE | ||||
|---|---|---|---|---|---|---|
| Motor-1 | Motor-2 | Motor-1 | Motor-2 | Motor-1 | Motor-2 | |
| Kp | 36,282 | 49,929 | 36,347 | 40,904 | 41,771 | 47,353 |
| Kd | 49,989 | 50,000 | 22,591 | 38,205 | 46,534 | 37,040 |
| Ki | 72,884 | 99,996 | 80,320 | 100,00 | 100,00 | 62,028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kavala Sen, D.; Yildiz, A.; Kopmaz, O. Optimal Design of a Five-Bar Planar Manipulator and Its Controller by Using Different Algorithms for Minimum Shaking Forces and Moments for the Largest Trajectory in a Usable Workspace. Machines 2022, 10, 971. https://doi.org/10.3390/machines10110971
Kavala Sen D, Yildiz A, Kopmaz O. Optimal Design of a Five-Bar Planar Manipulator and Its Controller by Using Different Algorithms for Minimum Shaking Forces and Moments for the Largest Trajectory in a Usable Workspace. Machines. 2022; 10(11):971. https://doi.org/10.3390/machines10110971
Chicago/Turabian StyleKavala Sen, Deniz, Ahmet Yildiz, and Osman Kopmaz. 2022. "Optimal Design of a Five-Bar Planar Manipulator and Its Controller by Using Different Algorithms for Minimum Shaking Forces and Moments for the Largest Trajectory in a Usable Workspace" Machines 10, no. 11: 971. https://doi.org/10.3390/machines10110971
APA StyleKavala Sen, D., Yildiz, A., & Kopmaz, O. (2022). Optimal Design of a Five-Bar Planar Manipulator and Its Controller by Using Different Algorithms for Minimum Shaking Forces and Moments for the Largest Trajectory in a Usable Workspace. Machines, 10(11), 971. https://doi.org/10.3390/machines10110971







