On-Line Detection of Demagnetization for Permanent Magnet Synchronous Motor via Flux Observer
Abstract
:1. Introduction
2. Influence of Magnetic Property Degradation in PMSM
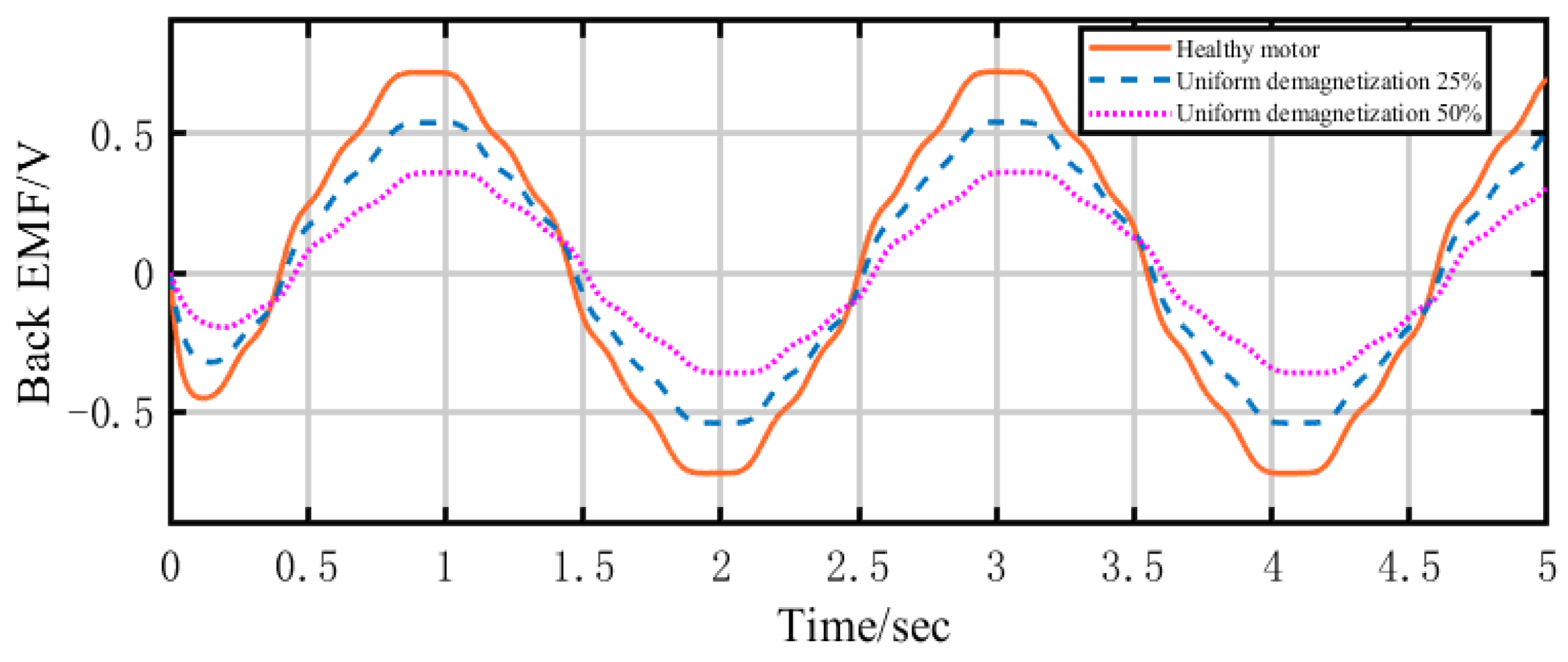
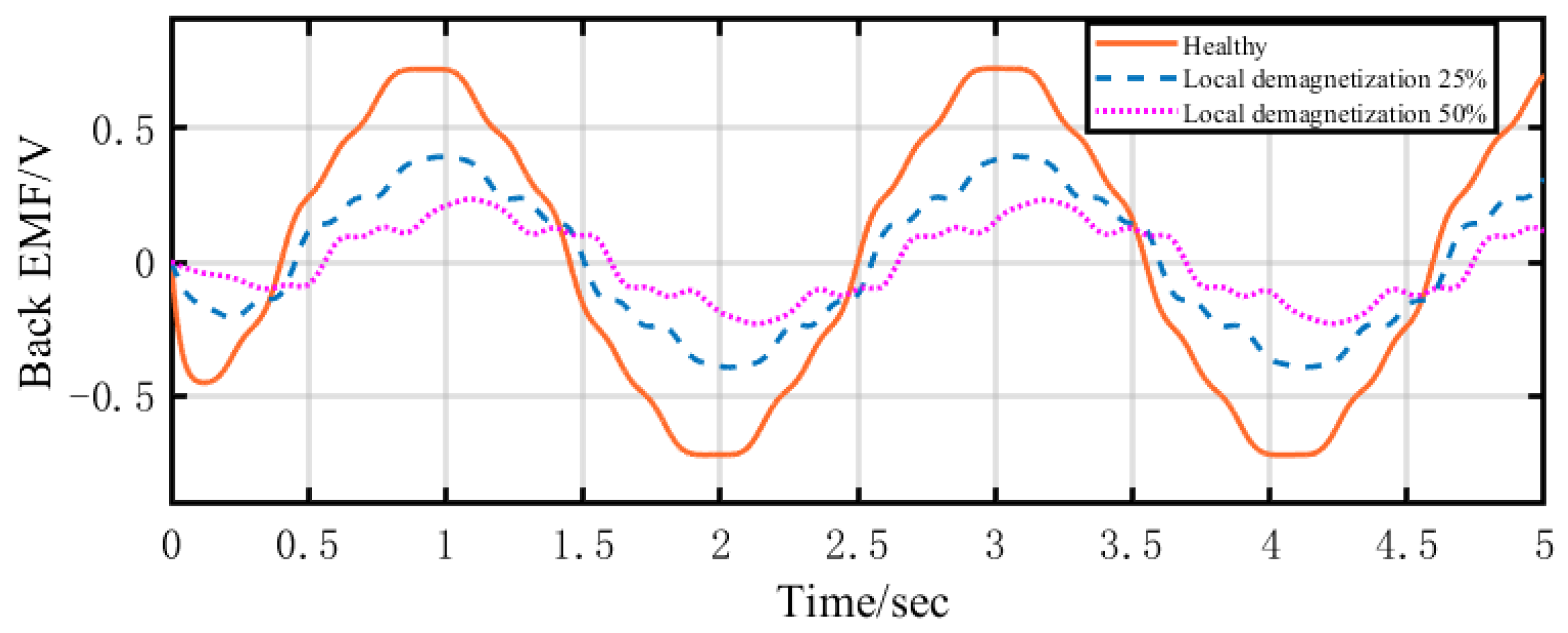
2.1. Influence on Back EMFs
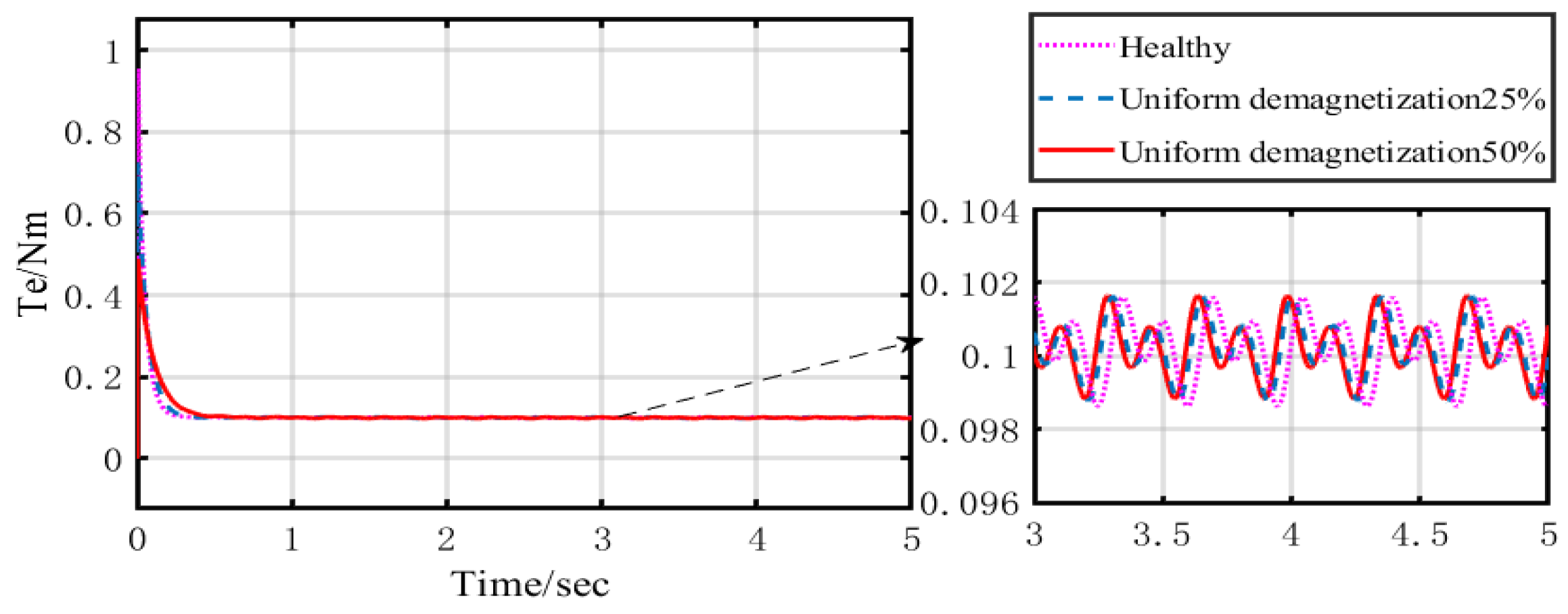
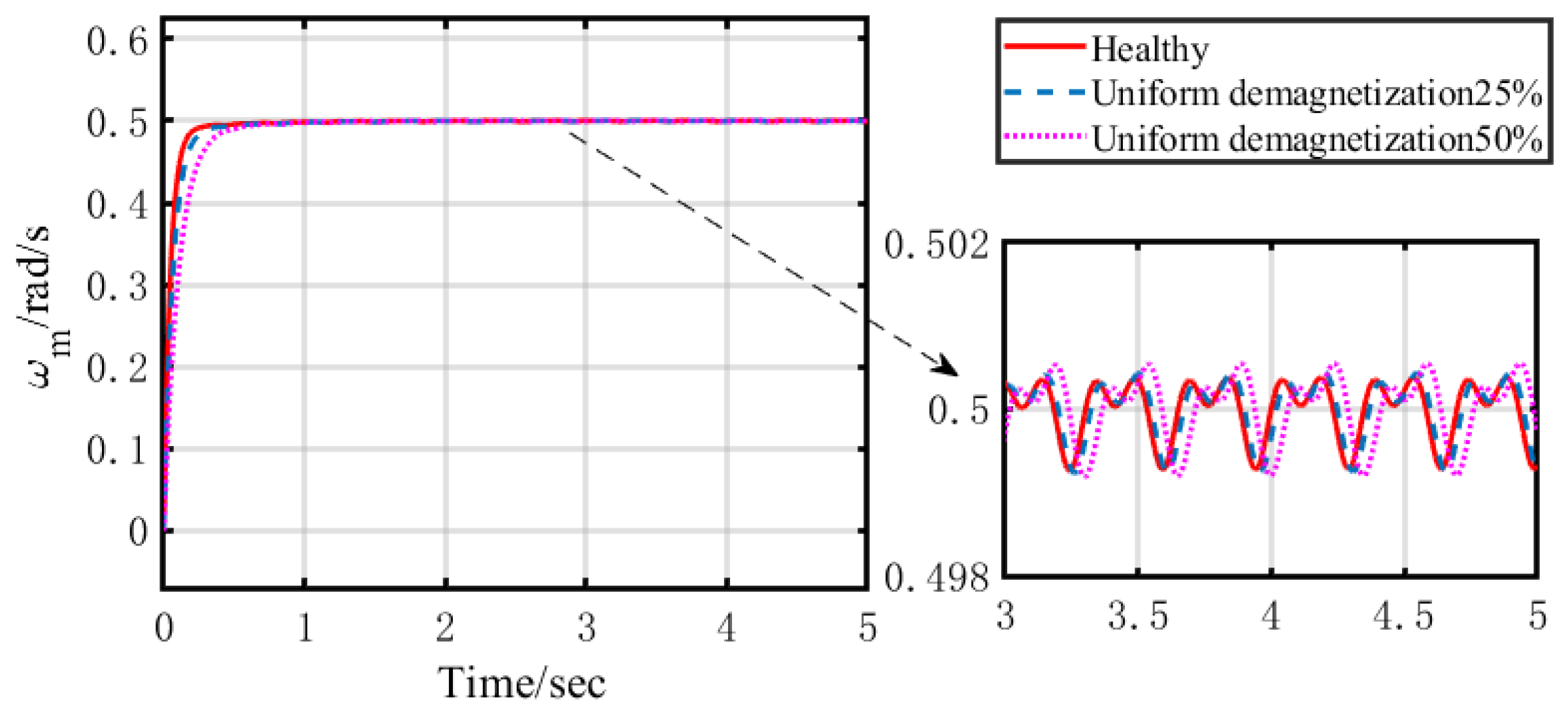
2.2. Influence on Electromagnetic Torque and Speed
3. Demagnetization Detection Method
3.1. Flux Observer
3.2. Demagnetization Index
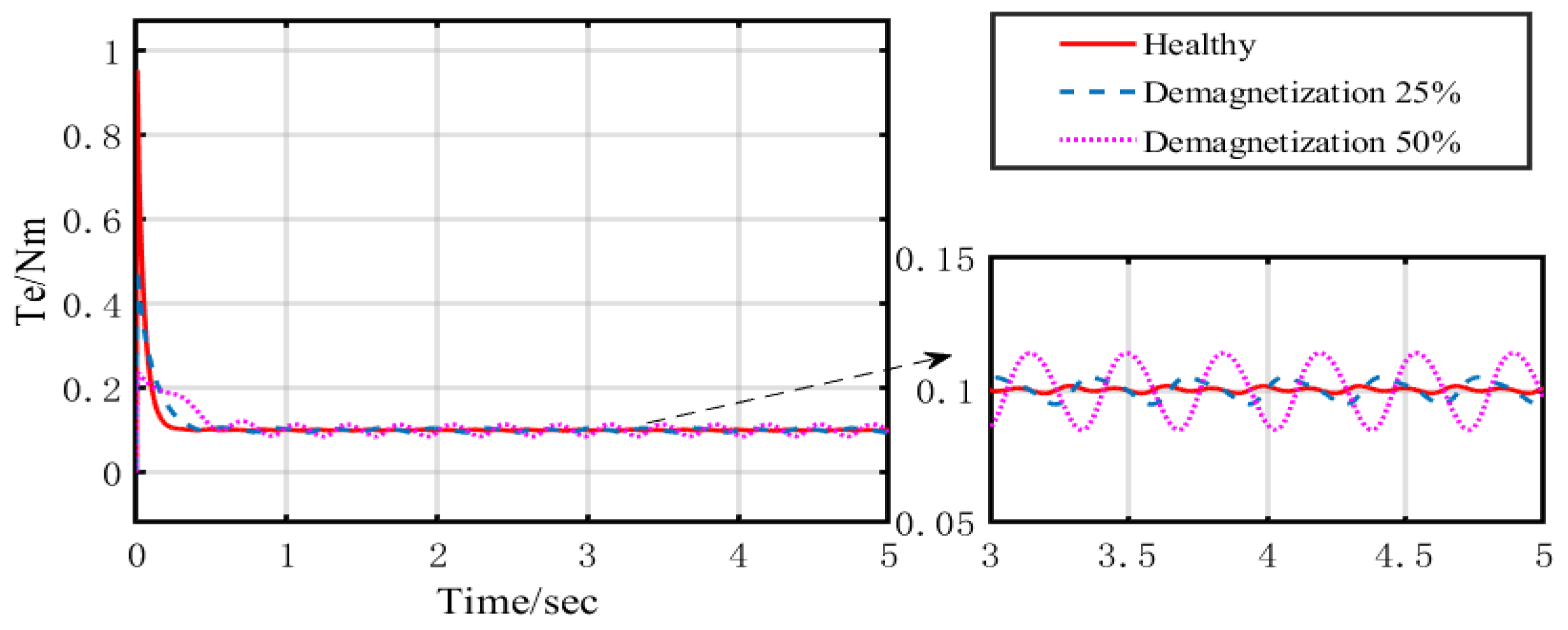
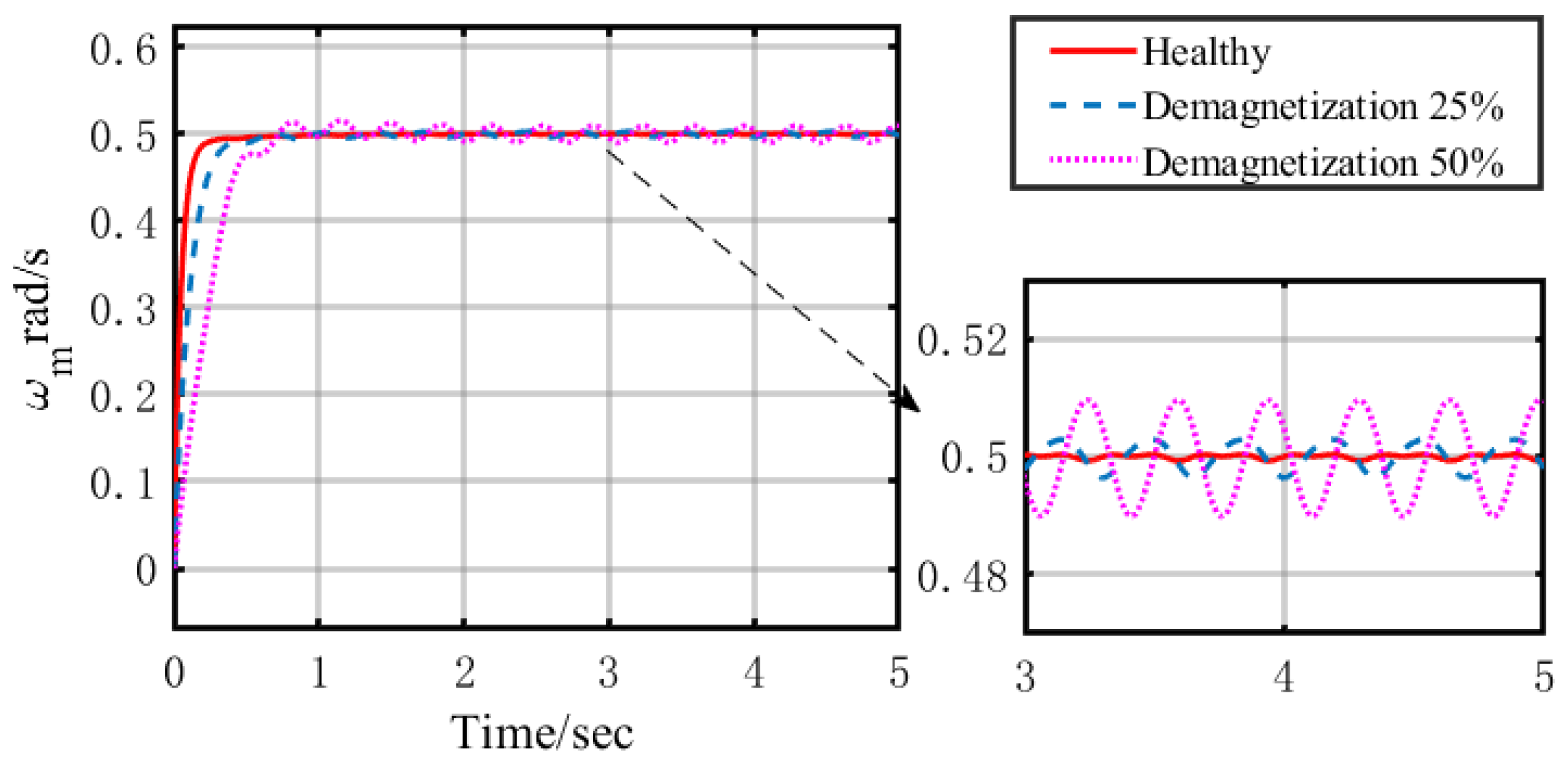
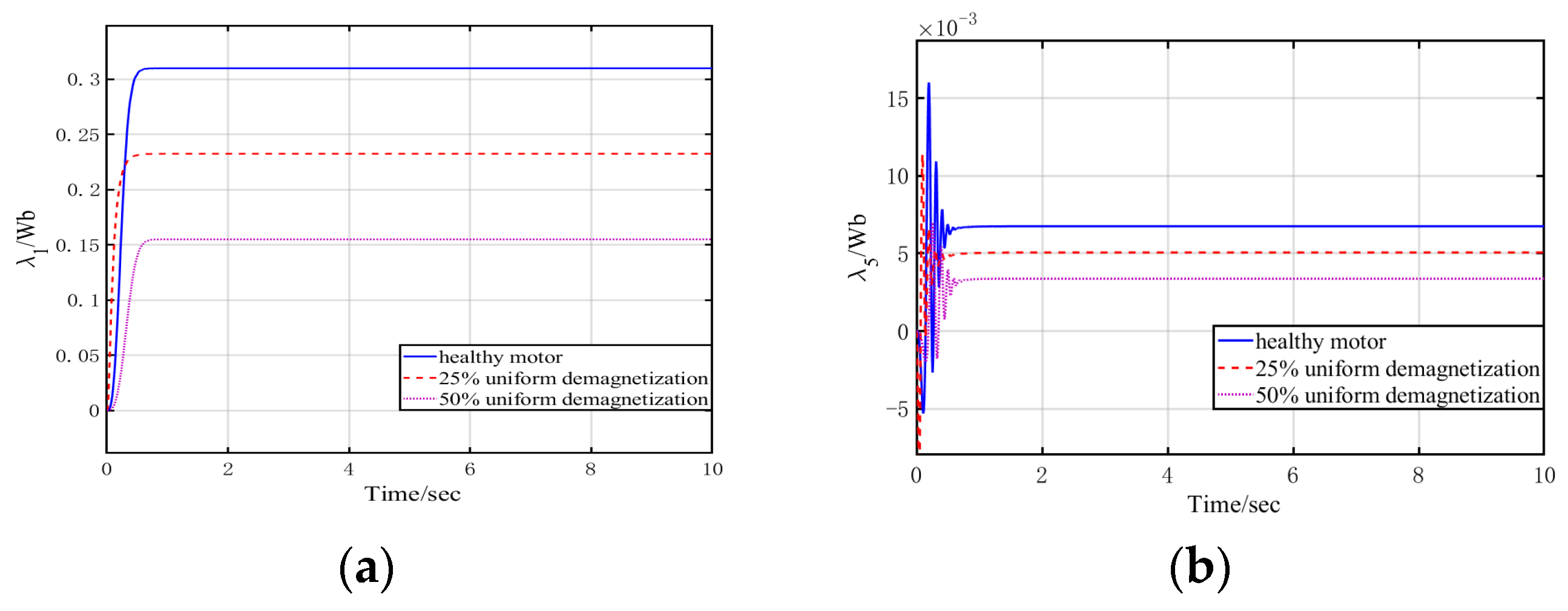
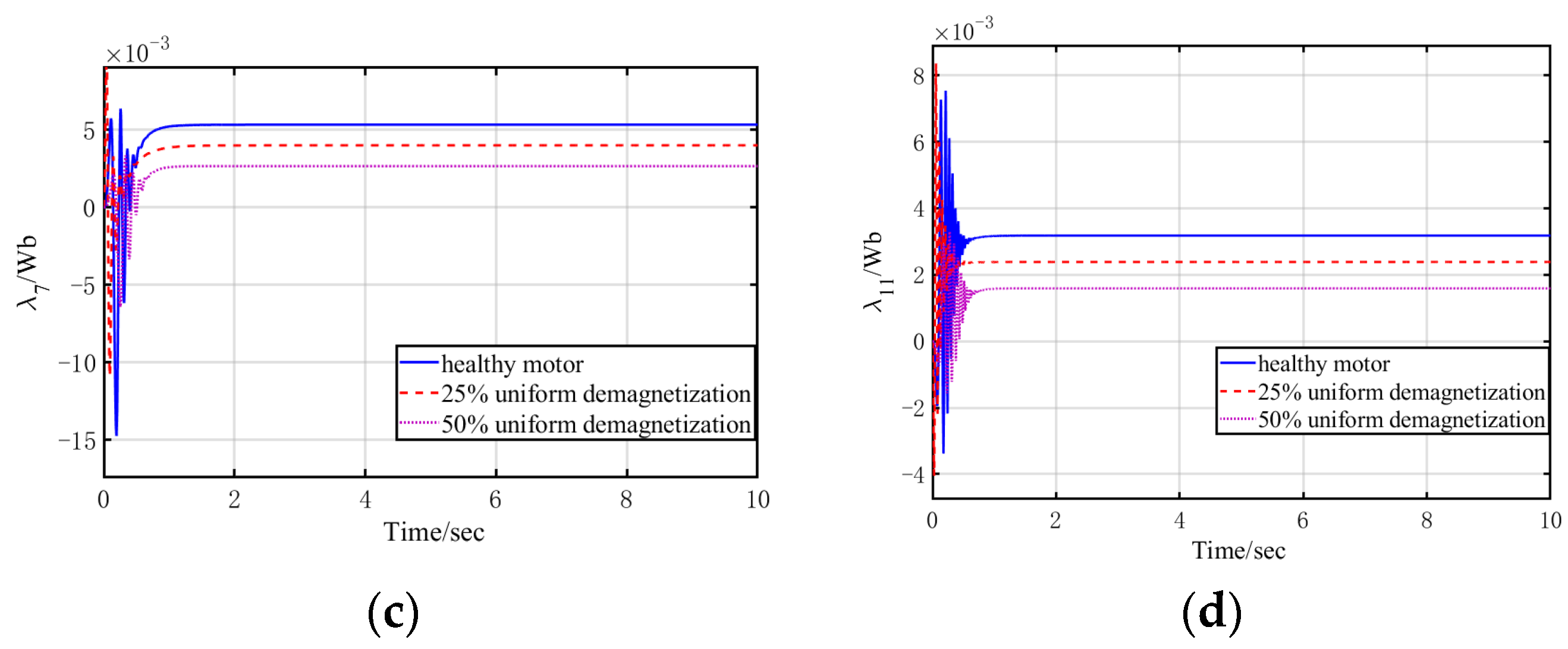
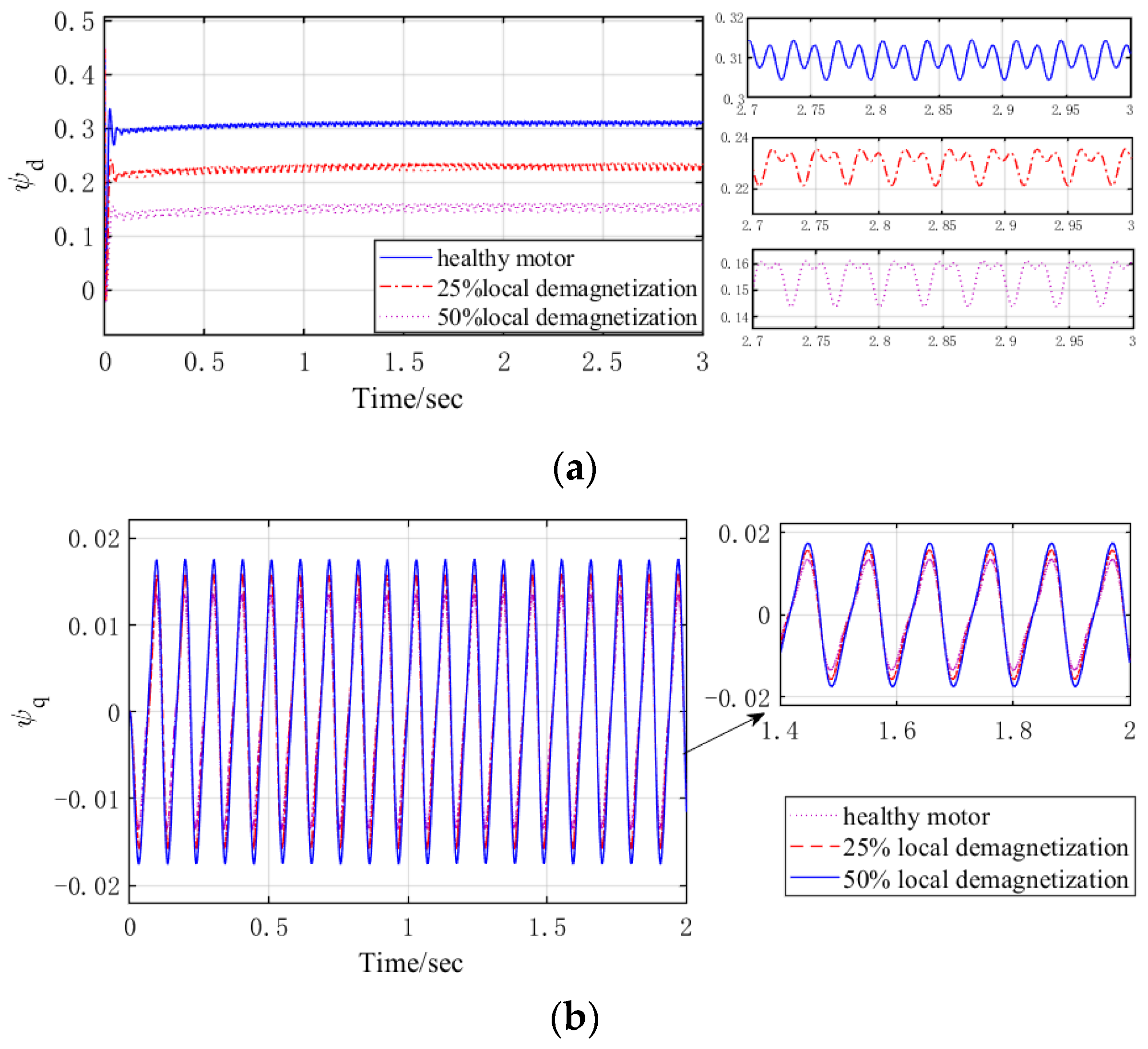
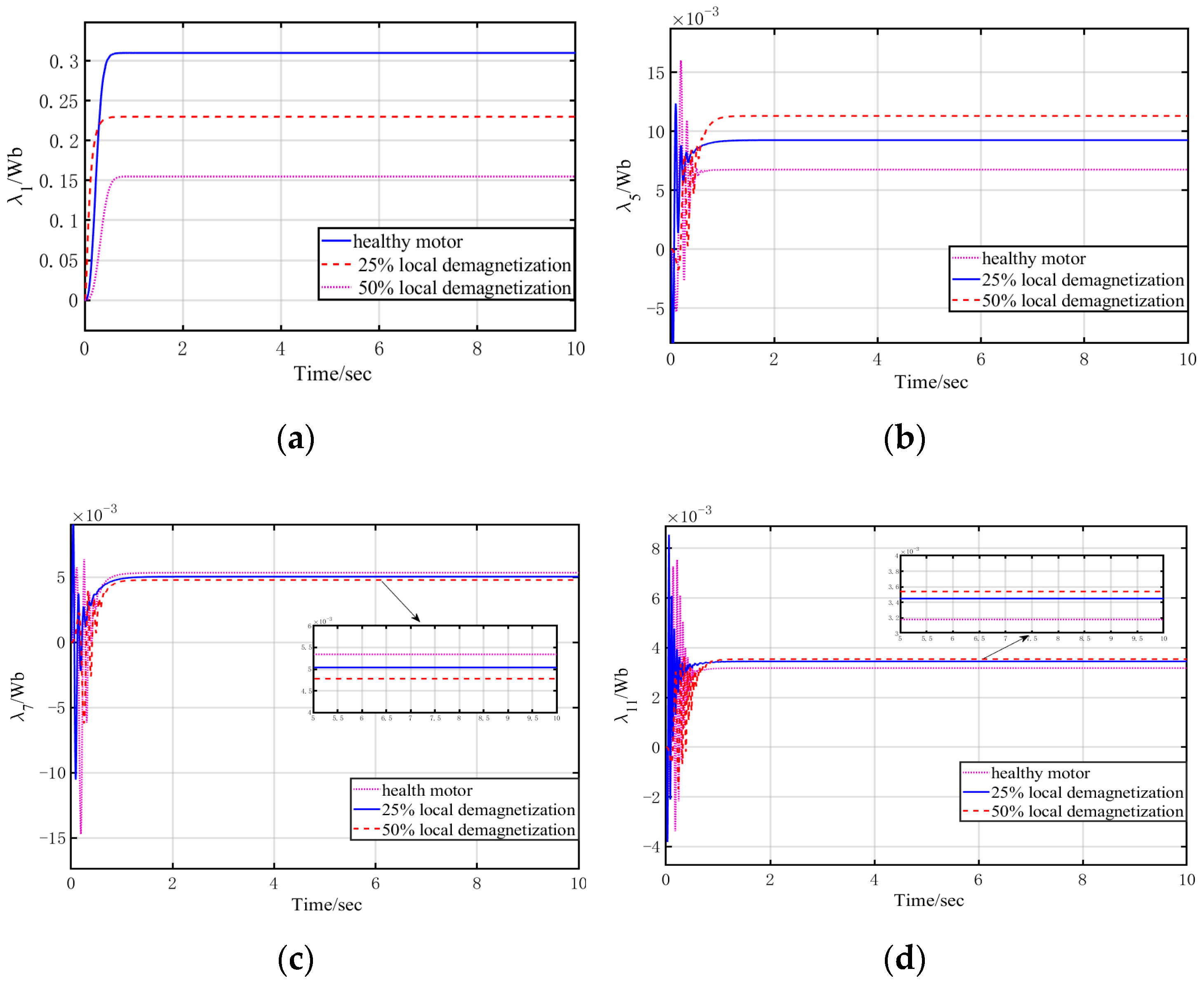
4. Simulation Results
- (1)
- Healthy motor: λ1 = 0.31 Wb, λ5 = 6.75 × 10−3 Wb, λ7 = 5.34 × 10−3 Wb, λ11 = 3.18 × 10−3 Wb;
- (2)
- Uniform demagnetization: uniform reduction of 25% and 50% of each harmonic of flux in healthy motor;
- (3)
- Twenty-five-percent local demagnetization motor: λ1 = 0.23 Wb, λ5 = 9.25 × 10−3 Wb, λ7 = 5.04 × 10−3 Wb, λ11 = 3.45 × 10−3 Wb;
- (4)
- Fifty-percent local demagnetization motor: λ1 = 0.16 Wb, λ5 = 1.13 × 10−2 Wb, λ7 = 4.78 × 10−3 Wb, λ11 = 3.56 × 10−3 Wb.
4.1. Influence Analysis of Magnetic Property Degradation
4.2. Proposed Detection Method
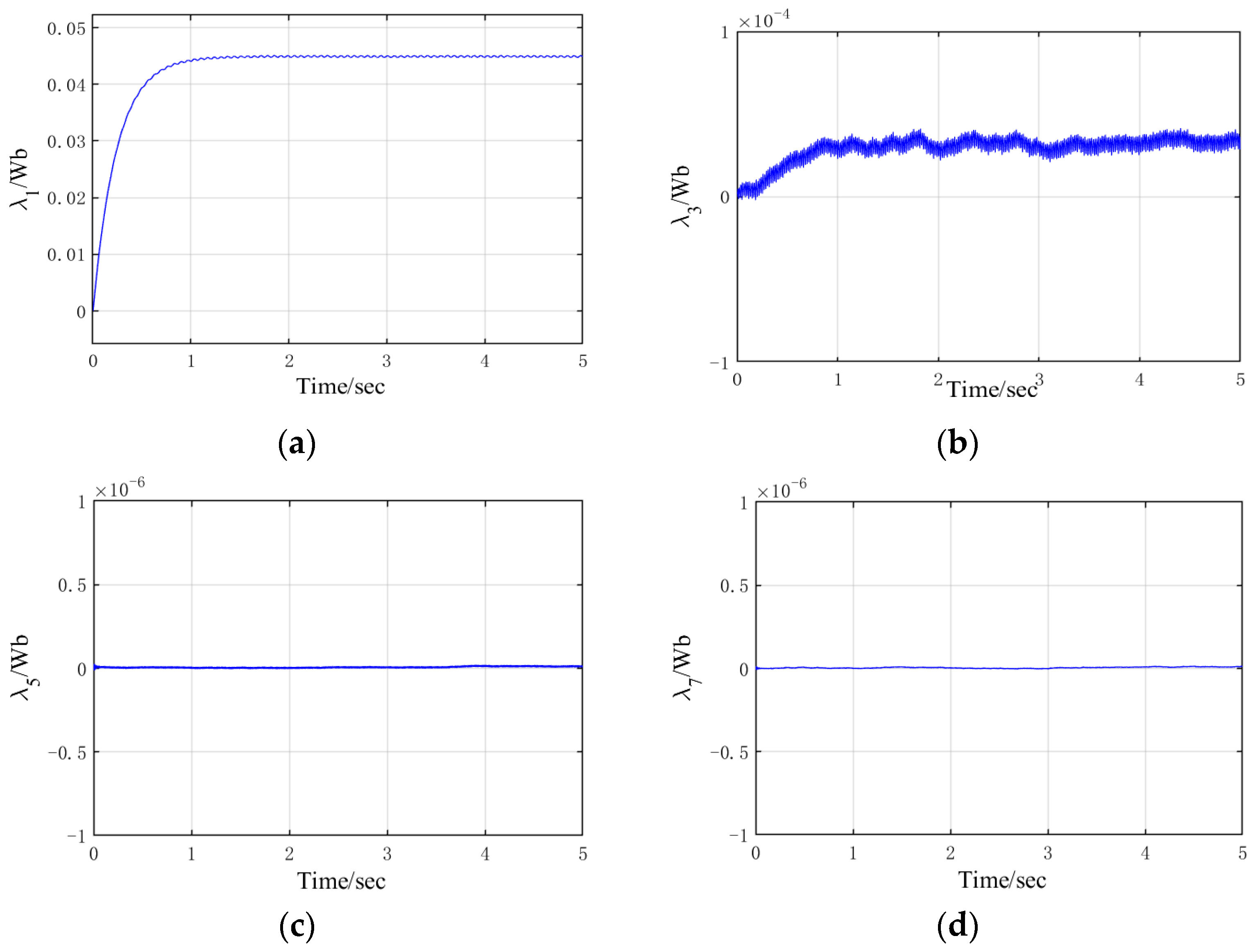
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ehsani, M.; Rahman, K.M.; Toliyat, H.A. Propulsion system design of electric and hybrid vehicles. IEEE Trans. Ind. Electron. 1997, 44, 19–27. [Google Scholar] [CrossRef]
- Lu, X.; Iyer, K.L.V.; Mukherjee, K.; Ramkumar, K.; Kar, N.C. Investigation of permanent-magnet motor drives incorporating damper bars for electrified vehicles. IEEE Trans. Ind. Electron. 2015, 62, 3234–3244. [Google Scholar] [CrossRef]
- Tianze, M.; Pinjia, Z. A review of thermal monitoring techniques for radial permanent magnet machines. Machines 2021, 10, 18. [Google Scholar]
- Reigosa, D.; Fernández, D.; Martínez, M.; Park, Y.; Lee, S.B.; Briz, F. Permanent magnet synchronous machine non-uniform demagnetization detection using zero-sequence magnetic field density. IEEE Trans. Ind. Appl. 2019, 55, 3823–3833. [Google Scholar] [CrossRef]
- Mengoni, M.; Vancini, L.; Tani, A.; Gritli, Y.; Zarri, L.; Rossi, C. On-line detection of magnet demagnetization in asymmetrical six-phase surface-mounted permanent magnet synchronous motor drives. In Proceedings of the 2019 IEEE 12th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Toulouse, France, 27–30 August 2019; pp. 188–194. [Google Scholar]
- Kim, K.C.; Lim, S.B.; Koo, D.H.; Ju, L. The shape design of permanent magnet for permanent magnet synchronous motor considering partial demagnetization. IEEE Trans. Magn. 2006, 42, 3485–3487. [Google Scholar] [CrossRef]
- Ruiz, J.; Rosero, J.A.; Espinosa, A.G.; Romeral, L. Detection of demagnetization faults in permanent-magnet synchronous motors under nonstationary conditions. IEEE Trans. Magn. 2009, 45, 2961–2969. [Google Scholar] [CrossRef]
- Le Roux, W.; Harley, R.G.; Habetler, T.G. Detecting rotor faults in low power permanent magnet synchronous machines. IEEE Trans. Power Electron. 2007, 22, 322–328. [Google Scholar] [CrossRef]
- Krichen, M.; Elbouchikhi, E.; Naourez, B.; Chaieb, M.; Neji, R. Motor current signature analysis-based permanent magnet synchronous motor demagnetization characterization and detection. Machines 2020, 8, 35. [Google Scholar] [CrossRef]
- Gritli, Y.; Rossi, C.; Casadei, D.; Zarri, L.; Filippetti, F. Demagnetization diagnosis for permanent magnet synchronous motors based on advanced wavelet analysis. In Proceedings of the 2012 International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2397–2403. [Google Scholar]
- Candelo-Zuluaga, C.; Riba, J.R.; Thangamuthu, D.V.; Garcia, A. Detection of partial demagnetization faults in five-phase permanent magnet assisted synchronous reluctance machines. Energies 2020, 13, 3496. [Google Scholar] [CrossRef]
- Urresty, J.C.; Ruiz, J.R.; Romeral, L. A back-emf based method to detect magnet failures in PMSMs. IEEE Trans. Magn. 2012, 49, 591–598. [Google Scholar] [CrossRef]
- Urresty, J.C.; Riba, J.R.; Delgado, M.; Romeral, L. Detection of demagnetization faults in surface-mounted permanent magnet synchronous motors by means of the zero-sequence voltage component. IEEE Trans. Energy Convers. 2012, 27, 42–51. [Google Scholar] [CrossRef]
- Urresty, J.C.; Riba, J.R.; Romeral, L. Influence of the stator windings configuration in the currents and zero-sequence voltage harmonics in permanent magnet synchronous motors with demagnetization faults. IEEE Trans. Magn. 2013, 49, 4885–4893. [Google Scholar] [CrossRef]
- Casadei, D.; Filippetti, F.; Rossi, C.; Stefani, A. Magnets faults characterization for permanent magnet synchronous motors. In Proceedings of the IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, Cargese, France, 31 August–3 September 2009; pp. 1–6. [Google Scholar]
- Hong, J.; Hyun, D.; Lee, S.B.; Yoo, J.Y.; Lee, K.W. Automated monitoring of magnet quality for permanent-magnet synchronous motors at standstill. IEEE Trans. Ind. Appl. 2010, 46, 1397–1405. [Google Scholar] [CrossRef]
- Hong, J. Detection and classification of rotor demagnetization and eccentricity faults for PM synchronous motors. IEEE Trans. Ind. Appl. 2012, 48, 923–932. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, M.; Li, Y.; Li, M. On-line estimation of permanent magnet flux linkage ripple for PMSM based on a Kalman filter. In Proceedings of the 32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 1171–1175. [Google Scholar]
- Min, Y.; Huang, W.; Yang, J.; Zhao, Y. On-line estimation of permanent-magnet flux and temperature rise in stator winding for PMSM. In Proceedings of the 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Xu, W.; Jiang, Y.; Mu, C.; Blaabjerg, F. Improved nonlinear flux observer-based second-order SOIFO for PMSM sensorless control. IEEE Trans. Power Electron. 2019, 34, 565–579. [Google Scholar] [CrossRef] [Green Version]
- Kashif, S.A.R.; Saqib, M.A. ANN-based flux observer for the sensor-less control of a permanent magnet synchronous motor. In Proceedings of the 20th Australasian Universities Power Engineering Conference, Christchurch, New Zealand, 5–8 December 2010; pp. 1–6. [Google Scholar]
- Uddin, M.N.; Zou, H.; Azevedo, F. Online loss minimization based adaptive flux observer for direct torque and flux control of PMSM drive. IEEE Trans. Ind. Appl. 2016, 52, 425–431. [Google Scholar] [CrossRef]
- Xiao, X.; Chen, C.; Zhang, M. Magnet demagnetization observation or permanent magnet synchronous motor. In Proceedings of the International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 3216–3219. [Google Scholar]
- Xiao, X.; Chen, C. Reduction of torque ripple due to demagnetization in PMSM using current compensation. IEEE Trans. Appl. Supercond. 2010, 20, 1068–1071. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Mukherjee, K.; Kar, N.C. Online PMSM magnet flux-linkage estimation for rotor magnet condition monitoring using measured speed harmonics. IEEE Trans. Ind. Appl. 2017, 53, 2786–2794. [Google Scholar] [CrossRef]
- Anderson, B. Exponential stability of linear equations arising in adaptive identification. IEEE Trans. Autom. Control 1977, 22, 83–88. [Google Scholar] [CrossRef]
- Ullah, Z.; Lee, S.T.; Siddiqi, M.R.; Hur, J. Online diagnosis and severity estimation of partial and uniform irreversible demagnetization fault in interior permanent magnet synchronous motor. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1682–1686. [Google Scholar]



| Parameter | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| λ1 (Wb) | 0.31 | 0.23 | 0.16 | 0.23 | 0.16 |
| λ5 (Wb) | 6.75 × 10−3 | 5.06 × 10−3 | 3.38 × 10−3 | 9.25 × 10−3 | 1.12 × 10−2 |
| λ7 (Wb) | 5.35 × 10−3 | 4.01 × 10−3 | 2.68 × 10−3 | 5.04 × 10−3 | 4.78 × 10−3 |
| λ11 (Wb) | 3.17 × 10−3 | 2.38 × 10−3 | 1.59 × 10−3 | 3.44 × 10−3 | 3.54 × 10−3 |
| PMSM Parameters | Resolver Parameters | ||
|---|---|---|---|
| Pole pairs | 2 | Pole pairs | 1 |
| Phase resistance | 3 Ω | Input voltage | 5 V ± 0.2 (AC) |
| Phase inductance | 1 mH | Input frequency | 10 kHz |
| Rated speed | 3000 r/min | Output voltage | >2 V |
| Back EMF coefficient | 0.09 V/rad·s−1 | Transformer radio | 0.5 ± 5° |
| Sliding friction torque | 0.06 Nm | Zero deviation | ≤10′ |
| Parameter | Observed Value |
|---|---|
| λ1 (Wb) | 0.0449 |
| λ3 (Wb) | 3.43 × 10−5 |
| λ5 (Wb) | 1.89 × 10−9 |
| λ7 (Wb) | 1.19 × 10−9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, L.; Wu, Z. On-Line Detection of Demagnetization for Permanent Magnet Synchronous Motor via Flux Observer. Machines 2022, 10, 354. https://doi.org/10.3390/machines10050354
Cao L, Wu Z. On-Line Detection of Demagnetization for Permanent Magnet Synchronous Motor via Flux Observer. Machines. 2022; 10(5):354. https://doi.org/10.3390/machines10050354
Chicago/Turabian StyleCao, Liqian, and Zhong Wu. 2022. "On-Line Detection of Demagnetization for Permanent Magnet Synchronous Motor via Flux Observer" Machines 10, no. 5: 354. https://doi.org/10.3390/machines10050354
APA StyleCao, L., & Wu, Z. (2022). On-Line Detection of Demagnetization for Permanent Magnet Synchronous Motor via Flux Observer. Machines, 10(5), 354. https://doi.org/10.3390/machines10050354






