Multidisciplinary Collaborative Design and Optimization of Turbine Rotors Considering Aleatory and Interval Mixed Uncertainty under a SORA Framework
Abstract
:1. Introduction
2. Multidisciplinary Design Optimization under Aleatory and Interval Uncertainties
2.1. RBMDO Optimization Model Based on PMA
2.2. Multidisciplinary Uncertainty Analysis Method Considering Aleatory and Interval Uncertainties
2.3. Multidisciplinary Optimization Solution Considering Aleatory and Interval Uncertainties
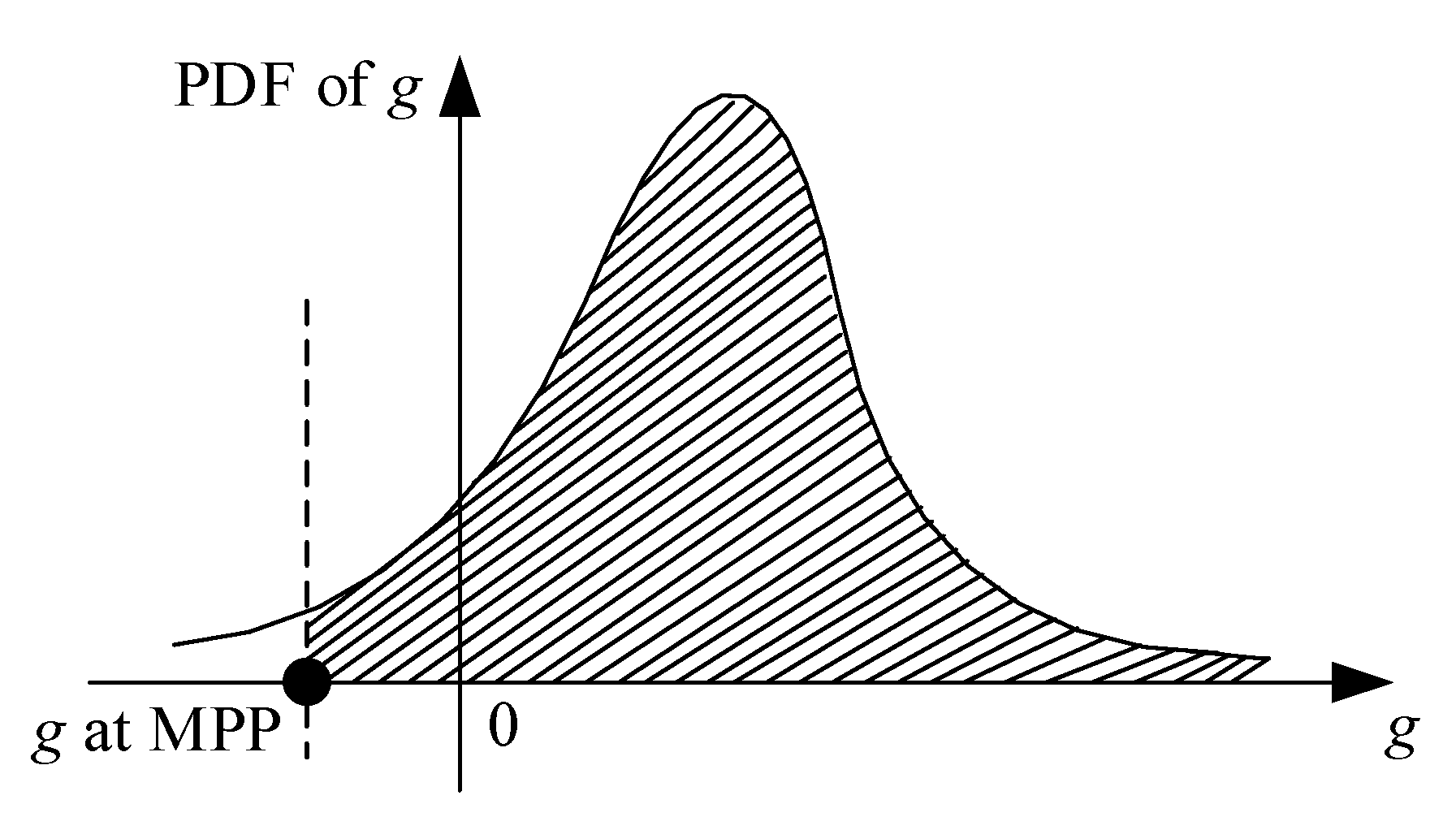
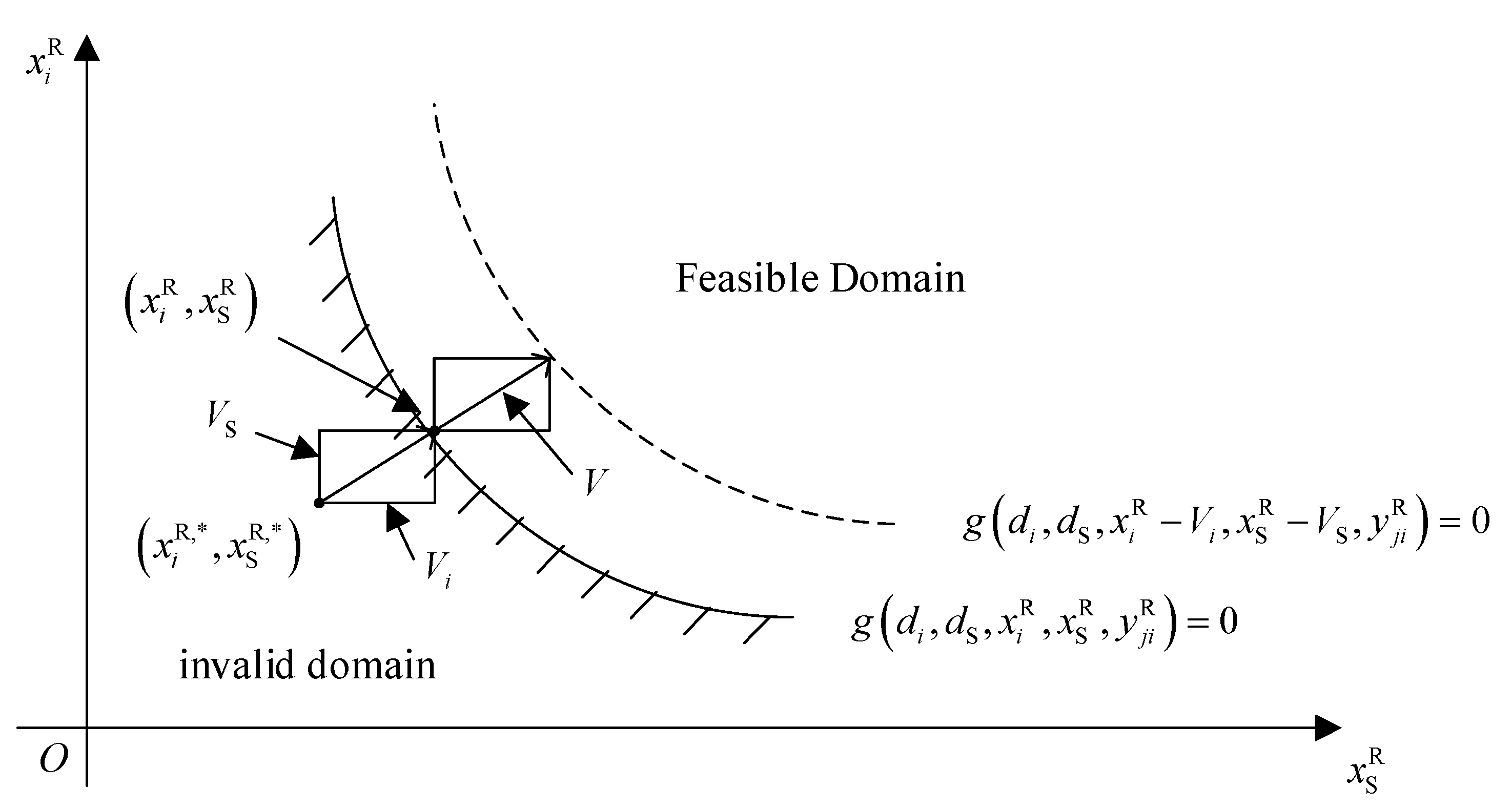
2.3.1. SORA Strategy
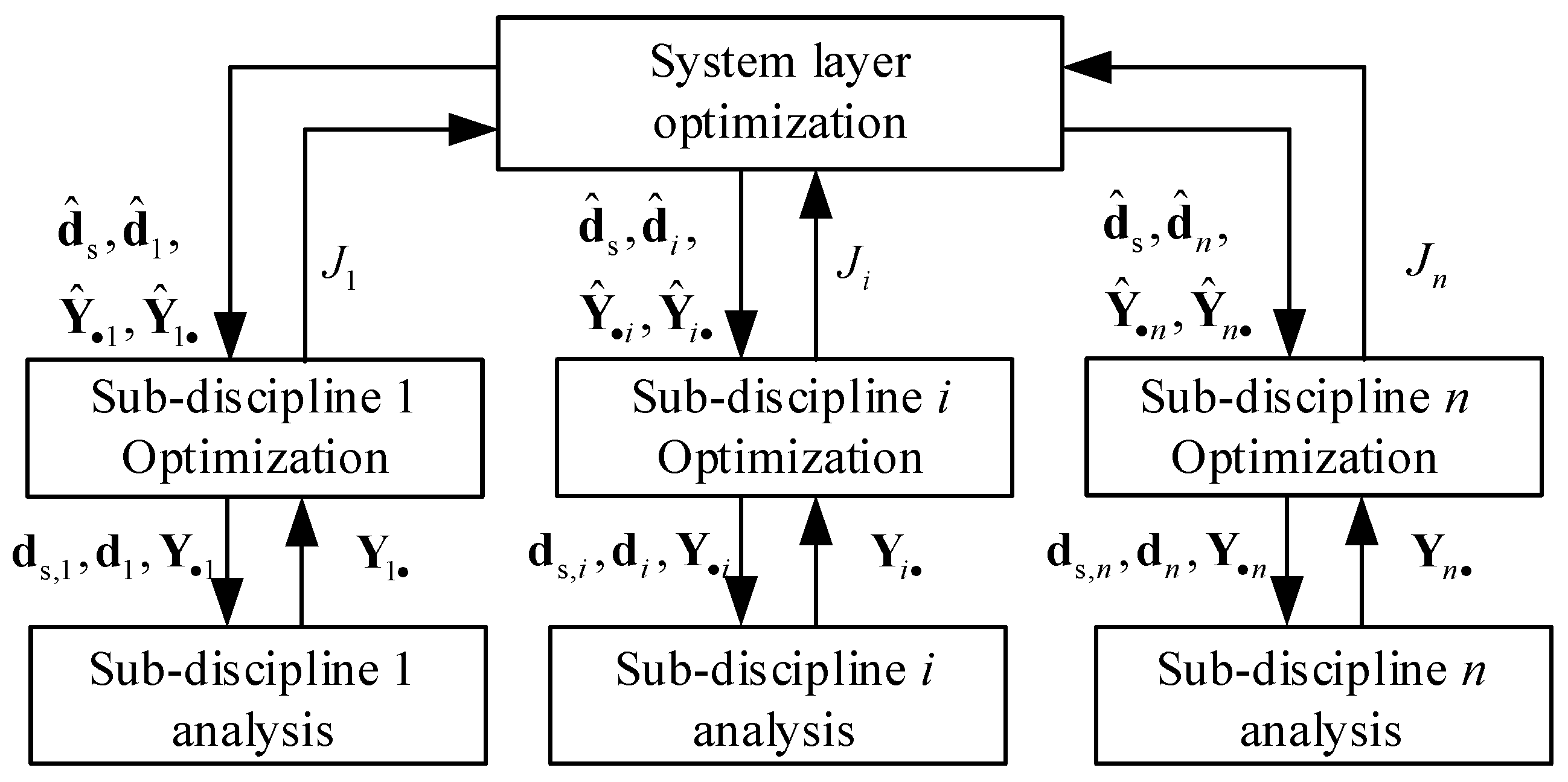
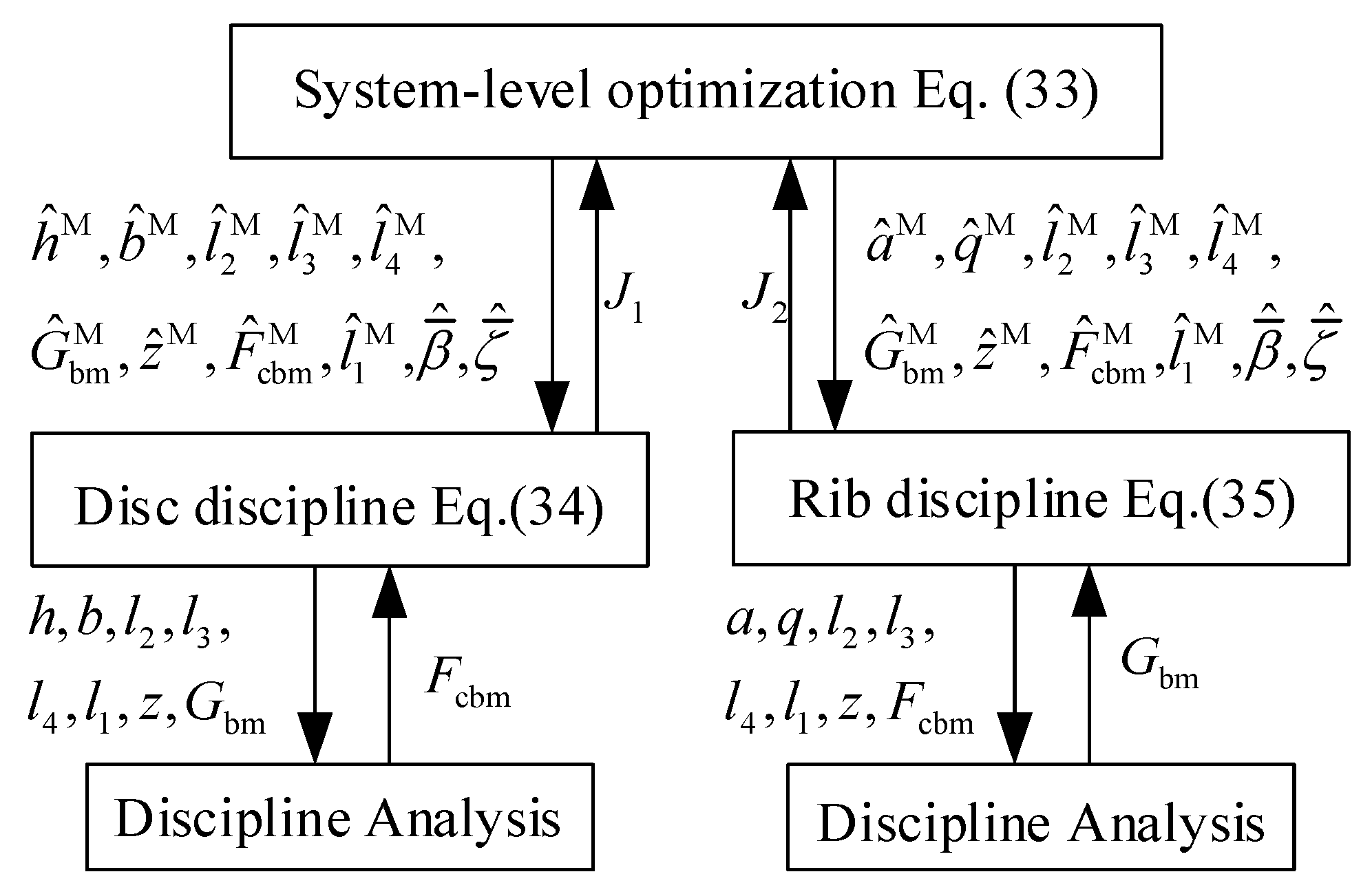
2.3.2. CO Algorithm
2.3.3. Optimization Solution
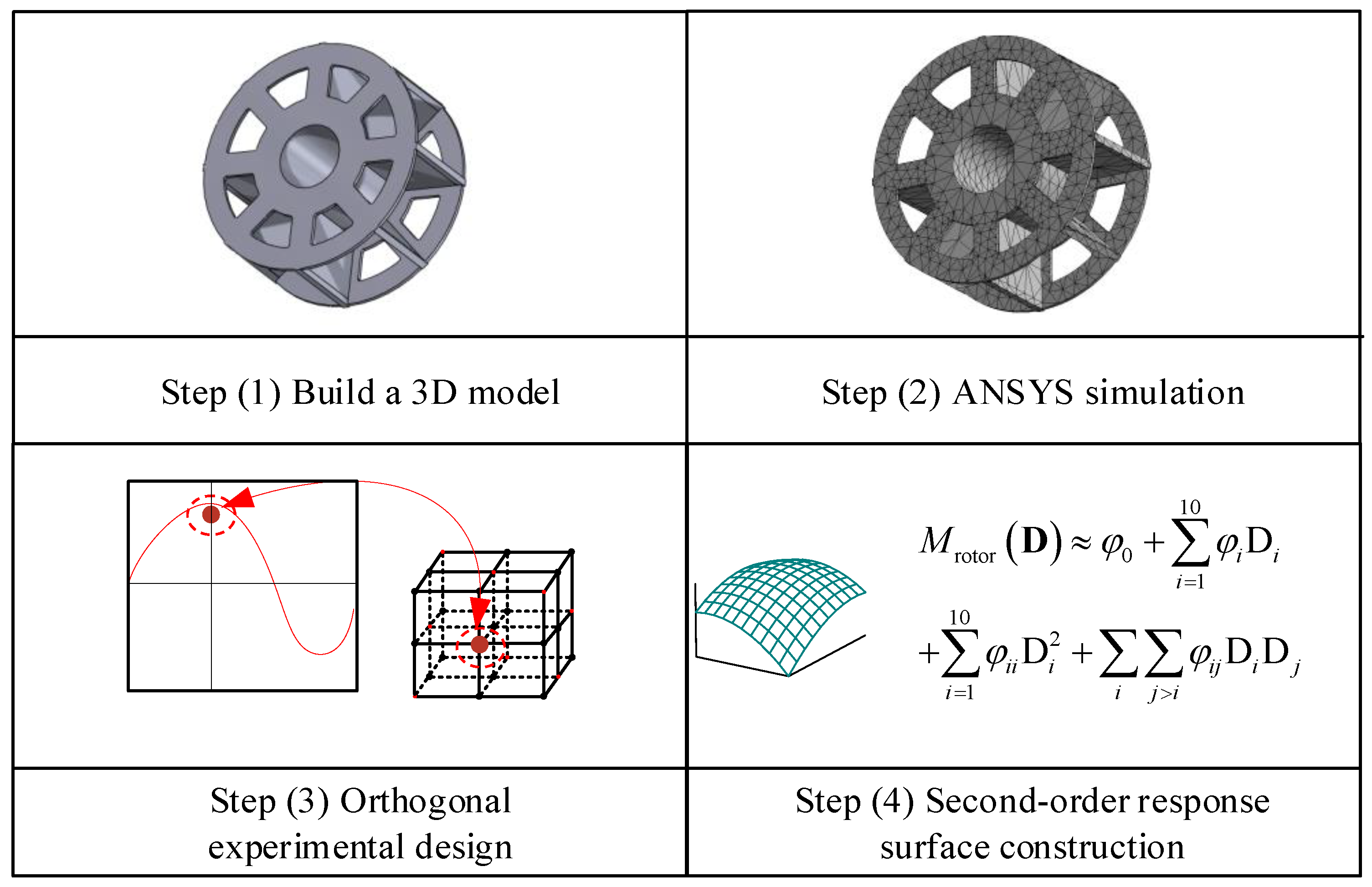
3. Response Surface Modeling of Rotor Mechanism Based on Virtual Prototype
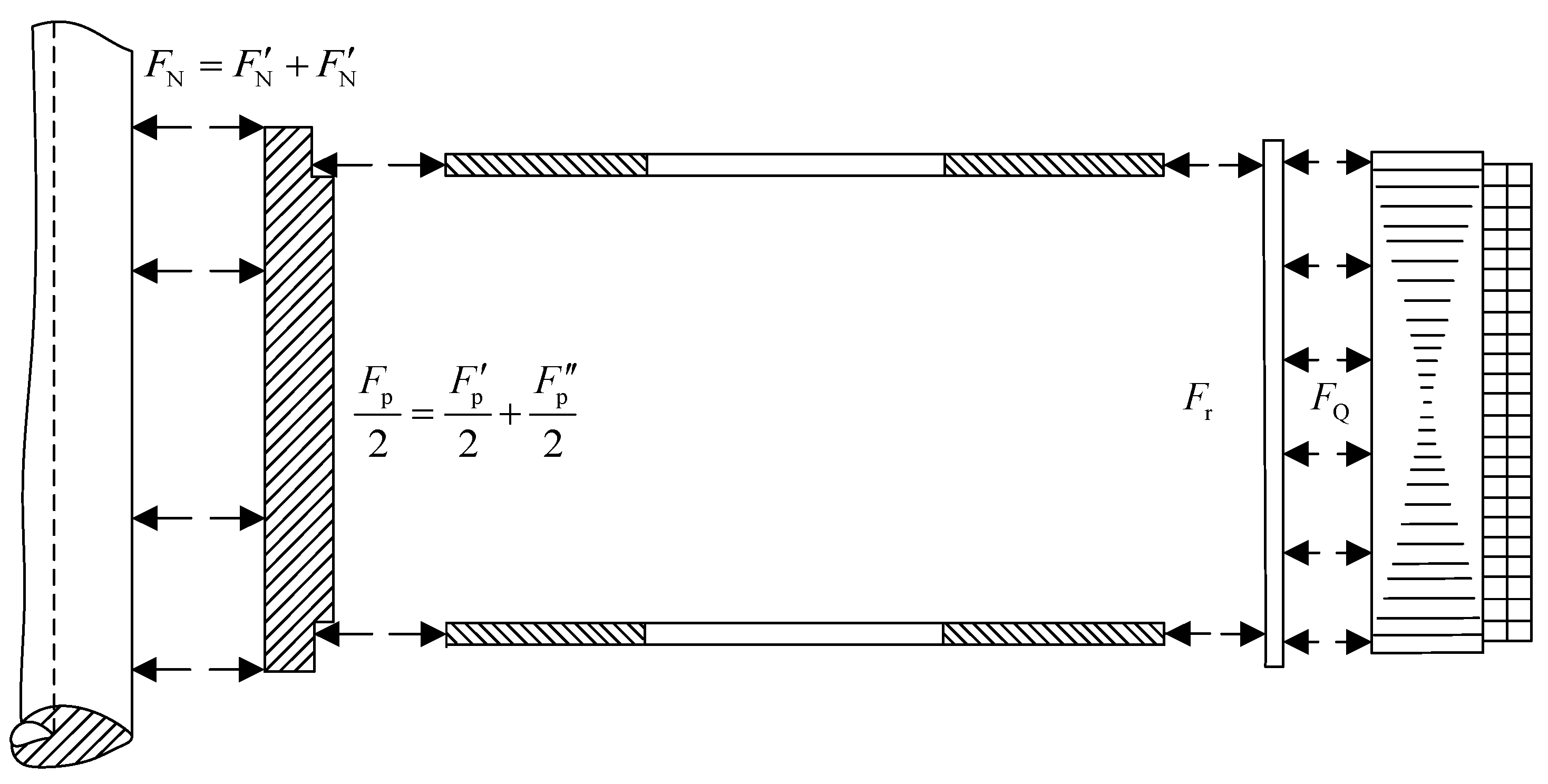
3.1. Discipline Division and Design Optimization of the Rotor Mechanism
3.2. Response Surface Modeling of Rotor Mechanism Based on Virtual Prototype
4. Uncertainty Optimal Analysis of Rotor Mechanism
4.1. Uncertainty Analysis
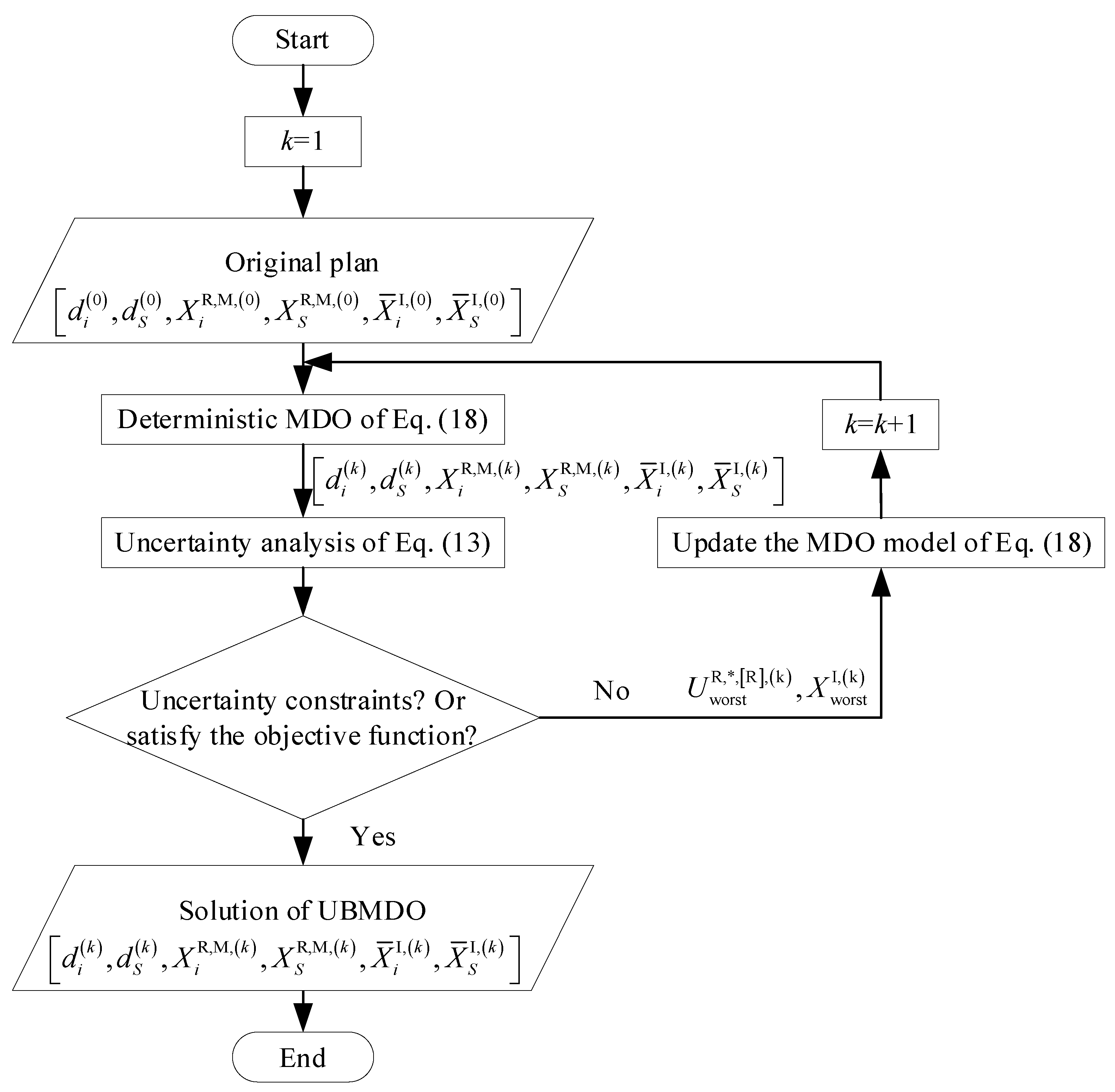
4.2. Optimization Considering Uncertainty
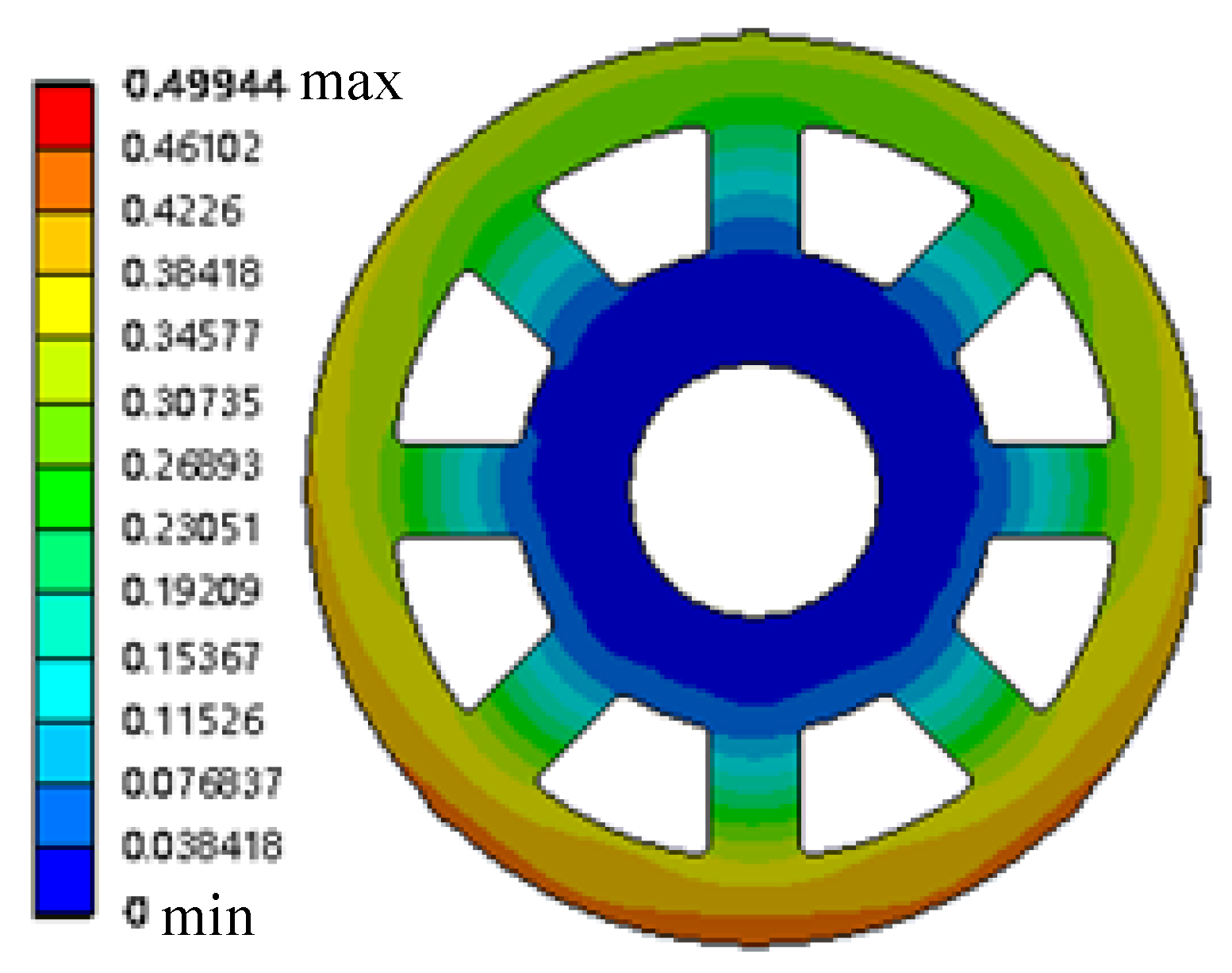
5. Analysis of Rotor Design Optimization Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| objective function | |
| vector of deterministic design variables | |
| vector of uncertain design variables | |
| vector of coupled variables | |
| constraint function | |
| uncertainty constraint | |
| reliability | |
| reliability index | |
| DV | vector of design variables |
| midpoint of the interval variable value | |
| auxiliary design variable | |
| compatibility constraint of the i-th subject | |
| shared variable of the i-th subject | |
| rotor weight | |
| stress | |
| correction coefficient | |
| gravity of the rib | |
| centrifugal force received by the rib | |
| cooperating force between the wheel hub and the disc | |
| cooperating force between the disc and the rib | |
| yoke action |
References
- Agarwal, H.; Renaud, J.E.; Preston, E.L.; Padmanabhan, D. Uncertainty quantification using evidence theory in multidisciplinary design optimization. Reliab. Eng. Syst. Saf. 2004, 85, 281–294. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Helton, J.C.; Joslyn, C.A.; Wojtkiewicz, S.F.; Ferson, S. Challenge problems: Uncertainty in system response given uncertain parameters. Reliab. Eng. Syst. Saf. 2004, 85, 11–19. [Google Scholar] [CrossRef]
- Klir, G.J. Generalized information theory: Aims, results, and open problems. Reliab. Eng. Syst. Saf. 2004, 85, 21–38. [Google Scholar] [CrossRef]
- Meng, D.; Lv, Z.; Yang, S.; Wang, H.; Xie, T.; Wang, Z. A time-varying mechanical structure reliability analysis method based on performance degradation. Structures 2021, 34, 3247–3256. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; Lin, T.; Wang, J.; Yang, H.; Lv, Z. RBMDO using gaussian mixture model-based second-order mean-value saddlepoint approximation. CMES-Comp. Model. Eng. 2022, in press. [Google Scholar]
- Ai, Q.; Yuan, Y.; Mahadevan, S.; Jiang, X. Probabilistic degradation modelling of circular tunnels assembled from segmental linings. Struct. Concrete. 2016, 17, 257–273. [Google Scholar] [CrossRef]
- Su, X.; Li, L.; Qian, H.; Mahadevan, S.; Deng, Y. A new rule to combine dependent bodies of evidence. Soft Comput. 2019, 23, 9793–9799. [Google Scholar] [CrossRef]
- Su, X.; Li, L.; Shi, F.; Qian, H. Research on the fusion of dependent evidence based on mutual information. IEEE Access 2018, 6, 71839–71845. [Google Scholar] [CrossRef]
- Zhu, S.P.; Huang, H.Z.; Peng, W.; Wang, H.K.; Mahadevan, S. Probabilistic physics of failure-based framework for fatigue life prediction of aircraft gas turbine discs under uncertainty. Reliab. Eng. Syst. Saf. 2016, 146, 1–12. [Google Scholar] [CrossRef]
- Meng, D.; Hu, Z.; Guo, J.; Lv, Z.; Xie, T.; Wang, Z. An uncertainty-based structural design and optimization method with interval Taylor expansion. Structures 2021, 33, 4492–4500. [Google Scholar] [CrossRef]
- Jiang, C.; Zheng, J.; Han, X. Probability-interval hybrid uncertainty analysis for structures with both aleatory and epistemic uncertainties: A review. Struct. Multidiscip. Optim. 2018, 57, 2485–2502. [Google Scholar] [CrossRef]
- Hüllermeier, E.; Waegeman, W. Aleatoric and epistemic uncertainty in machine learning: An introduction to concepts and methods. Mach. Learn. 2021, 110, 457–506. [Google Scholar] [CrossRef]
- Zhi, P.; Li, Y.; Chen, B.; Li, M.; Liu, G. Fuzzy optimization design-based multi-level response surface of bogie frame. Int. J. Struct. Integr. 2019, 10, 134–148. [Google Scholar] [CrossRef]
- Li, H.S.; Dong, Q.Y.; Yuan, J.Y. Augmented Lagrangian teaching–learning-based optimization for structural design. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 2195–2213. [Google Scholar] [CrossRef]
- Meng, D.; Wang, H.; Yang, S.; Lv, Z.; Hu, Z.; Wang, Z. Fault analysis of wind power rolling bearing based on EMD feature extraction. CMES-Comp. Model. Eng. 2022, 130, 543–558. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, C.; Yang, Y. A novel methodology of reliability-based multidisciplinary design optimization under hybrid interval and fuzzy uncertainties. Comput. Methods Appl. Mech. Eng. 2018, 337, 439–457. [Google Scholar] [CrossRef]
- Benaouali, A.; Kachel, S. Multidisciplinary design optimization of aircraft wing using commercial software integration. Aerosp. Sci. Technol. 2019, 92, 766–776. [Google Scholar] [CrossRef]
- Zhu, D.; Zhou, J.; Liu, C.; Wang, Z. A short review of reliability-based design optimization. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Shaanxi, China, 8–11 October 2020. [Google Scholar]
- Dutta, S.; Putcha, C. Reliability-Based Design Optimization of a Large-Scale Truss Structure using Polynomial Chaos Expansion Metamodel; Reliability, Safety and Hazard Assessment for Risk-based Technologies; Springer: Singapore, 2020; pp. 481–488. [Google Scholar]
- Cho, H.; Choi, K.K.; Shin, J. Iterative most probable point search method for problems with a mixture of random and interval variables. J. Mech. Design 2020, 142, 071703. [Google Scholar] [CrossRef]
- Sun, W.; Guo, Z. Mathematical modeling and nonlinear vibration analysis of a coupled hydro-generator shaft-foundation system. Commun. Nonlinear Sci. 2021, 98, 105776. [Google Scholar] [CrossRef]
- Mao, X.; Pavesi, G.; Zheng, Y. Francis-type reversible turbine field investigation during fast closure of wicket gates. J. Fluids Eng. 2018, 140, 061103. [Google Scholar]
- Salehi, S.; Nilsson, H.; Lillberg, E.; Edh, N. An in-depth numerical analysis of transient flow field in a Francis turbine during shutdown. Renew. Energ. 2021, 179, 2322–2347. [Google Scholar] [CrossRef]
- Goyal, R.; Gandhi, B.K. Review of hydrodynamics instabilities in Francis turbine during off-design and transient operations. Renew. Energ. 2018, 116, 697–709. [Google Scholar] [CrossRef]
- Unterluggauer, J.; Sulzgruber, V.; Doujak, E.; Bauer, C. Experimental and numerical study of a prototype Francis turbine startup. Renew. Energ. 2020, 157, 1212–1221. [Google Scholar] [CrossRef]
- Yao, S.; Griffith, D.T.; Chetan, M.; Bay, C.J.; Damiani, R.; Kaminski, M.; Loth, E. A gravo-aeroelastically scaled wind turbine rotor at field-prototype scale with strict structural requirements. Renew. Energ. 2020, 156, 535–547. [Google Scholar] [CrossRef]
- Ciappi, L.; Fiaschi, D.; Niknam, P.H.; Talluri, L. Computational investigation of the flow inside a Tesla turbine rotor. Energy 2019, 173, 207–217. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K. Four decades of research into the augmentation techniques of Savonius wind turbine rotor. J. Energ. Resour. Technol. 2018, 140, 050801. [Google Scholar] [CrossRef]
- Nya, R.M.; Abdullah, S.; Singh, S.S.K. Reliability-based fatigue life of vehicle spring under random loading. Int. J. Struct. Integr. 2019, 10, 737–748. [Google Scholar]
- Kebir, T.; Correia, J.; Benguediab, M.; De Jesus, A.M. Numerical study of fatigue damage under random loading using Rainflow cycle counting. Int. J. Struct. Integr. 2020, 12, 149–162. [Google Scholar] [CrossRef]
- Gao, X.; Su, X.; Qian, H.; Pan, X. Dependence assessment in human reliability analysis under uncertain and dynamic situations. Nucl. Eng. Technol. 2022, 54, 948–958. [Google Scholar] [CrossRef]
- Ai, Q.; Yuan, Y.; Mahadevan, S.; Jiang, X. Maintenance strategies optimisation of metro tunnels in soft soil. Struct. Infrastruct. Eng. 2017, 13, 1093–1103. [Google Scholar] [CrossRef]
- Du, W.; Luo, Y.; Wang, Y. A time-variant performance measure approach for dynamic reliability based design optimization. Appl. Math. Model. 2019, 76, 71–86. [Google Scholar] [CrossRef]
- Keshtegar, B.; Hao, P. Enriched self-adjusted performance measure approach for reliability-based design optimization of complex engineering problems. Appl. Math. Model. 2018, 57, 37–51. [Google Scholar] [CrossRef]
- Keshtegar, B.; Hao, P. A hybrid descent mean value for accurate and efficient performance measure approach of reliability-based design optimization. Comput. Methods Appl. Mech. Eng. 2018, 336, 237–259. [Google Scholar] [CrossRef]
- Chen, L.; Deng, Y. An improved evidential Markov decision making model. Appl. Intell. 2022, 52, 8008–8017. [Google Scholar] [CrossRef]
- Du, X.; Sudjianto, A.; Chen, W. An integrated framework for optimization under uncertainty using inverse reliability strategy. J. Mech. Design 2004, 126, 562–570. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, C.; Hu, J.; Wang, X.; Qiu, Z. Sequential multidisciplinary design optimization and reliability analysis under interval uncertainty. Aerosp. Sci. Technol. 2018, 80, 508–519. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, C.; Wang, X.; Liu, G.; Shi, Q. Sequential optimization and fuzzy reliability analysis for multidisciplinary systems. Struct. Multidiscip. Optim. 2019, 60, 1079–1095. [Google Scholar] [CrossRef]
- Du, X.; Guo, J.; Beeram, H. Sequential optimization and reliability assessment for multidisciplinary systems design. Struct. Multidiscip. Optim. 2008, 35, 117–130. [Google Scholar] [CrossRef]
- Li, H.S.; Wang, X.W.; Nan, H.; Liu, M. Application of a sampling-based method for estimation of cumulative failure probability functions of mechanisms. Mech. Mach. Theory. 2021, 155, 104050. [Google Scholar] [CrossRef]
- Wu, Q.; Deng, Y.; Xiong, N. Exponential negation of a probability distribution. Soft Comput. 2022, 26, 2147–2156. [Google Scholar] [CrossRef]
- Meng, D.; Xie, T.; Wu, P.; He, C.; Hu, Z.; Lv, Z. An uncertainty-based design optimization strategy with random and interval variables for multidisciplinary engineering systems. Structures 2021, 32, 997–1004. [Google Scholar] [CrossRef]
- Narayanan, G. Probabilistic fatigue model for cast alloys of aero engine applications. Int. J. Struct. Integr. 2021, 12, 454–469. [Google Scholar] [CrossRef]
- Li, H.S.; Wang, T.; Yuan, J.Y.; Zhang, H. A sampling-based method for high-dimensional time-variant reliability analysis. Mech. Syst. Signal Process. 2019, 126, 505–520. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Peng, W.; Zhang, X.C. Computational-experimental approaches for fatigue reliability assessment of turbine bladed disks. Int. J. Mech. Sci. 2018, 142, 502–517. [Google Scholar] [CrossRef]
- Zhu, S.P.; Keshtegar, B.; Seghier, M.E.A.B.; Zio, E.; Taylan, O. Hybrid and enhanced PSO: Novel first order reliability method-based hybrid intelligent approaches. Comput. Methods Appl. Mech. Eng. 2022, 393, 114730. [Google Scholar] [CrossRef]
- Abd Rahim, A.A.; Abdullah, S.; Singh, S.S.K.; Nuawi, M.Z. Reliability assessment on automobile suspension system using wavelet analysis. Int. J. Struct. Integr. 2019, 10, 602–611. [Google Scholar] [CrossRef]
- Huang, H.Z.; Zhang, X.; Liu, Y.; Meng, D.; Wang, Z. Enhanced sequential optimization and reliability assessment for reliability-based design optimization. J. Mech. Sci. Technol. 2012, 26, 2039–2043. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, P.; Wu, D.; Liu, Z.; Ge, H.; Zhang, S.; Yang, X. A new collaborative optimization method for a distributed energy system combining hybrid energy storage. Sustain. Cities Soc. 2021, 75, 103330. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, J.; Wu, D.; Fan, G.; Zhang, S.; Yang, X.; Ge, H. Two-phase collaborative optimization and operation strategy for a new distributed energy system that combines multi-energy storage for a nearly zero energy community. Energy Convers. Manag. 2021, 230, 113800. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; Zhang, Y.; Zhu, S.P. Structural reliability analysis and uncertainties-based collaborative design and optimization of turbine blades using surrogate model. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1219–1227. [Google Scholar] [CrossRef]
- Meng, D.; Li, Y.; He, C.; Guo, J.; Lv, Z.; Wu, P. Multidisciplinary design for structural integrity using a collaborative optimization method based on adaptive surrogate modelling. Mater. Design 2021, 206, 109789. [Google Scholar] [CrossRef]
- Xiao, F. CED: A distance for complex mass functions. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1525–1535. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F. CEQD: A complex mass function to predict interference effects. IEEE Trans. Cybern. 2021, 1–13. Available online: https://ieeexplore.ieee.org/abstract/document/9314051 (accessed on 14 May 2022). [CrossRef] [PubMed]
- Ai, Q.; Yuan, Y.; Shen, S.L.; Wang, H.; Huang, X. Investigation on inspection scheduling for the maintenance of tunnel with different degradation modes. Tunn. Undergr. Sp. Tech. 2020, 106, 103589. [Google Scholar] [CrossRef]
- Jahan, A.; Ismail, M.Y.; Sapuan, S.M.; Mustapha, F. Material screening and choosing methods-a review. Mater. Design 2010, 31, 696–705. [Google Scholar] [CrossRef]
- Skjong, S.; Rindarøy, M.; Kyllingstad, L.T.; Æsøy, V.; Pedersen, E. Virtual prototyping of maritime systems and operations: Applications of distributed co-simulations. J. Mar. Sci. Technol. 2018, 23, 835–853. [Google Scholar] [CrossRef] [Green Version]
- Park, H.S.; Dang, D.V.; Nguyen, T.T. Development of a flexible roll forming machine for cutting curved parts with virtual prototyping technology. J. Adv. Mech. Des. Syst. 2019, 13, JAMDSM0033. [Google Scholar] [CrossRef] [Green Version]
- Xiao, F. CaFtR: A fuzzy complex event processing method. Int. J. Fuzzy Syst. 2022, 24, 1098–1111. [Google Scholar] [CrossRef]
- Xue, Y.; Deng, Y. Extending set measures to orthopair fuzzy sets. Int. J. Uncertain. Fuzz. 2022, 30, 63–91. [Google Scholar] [CrossRef]







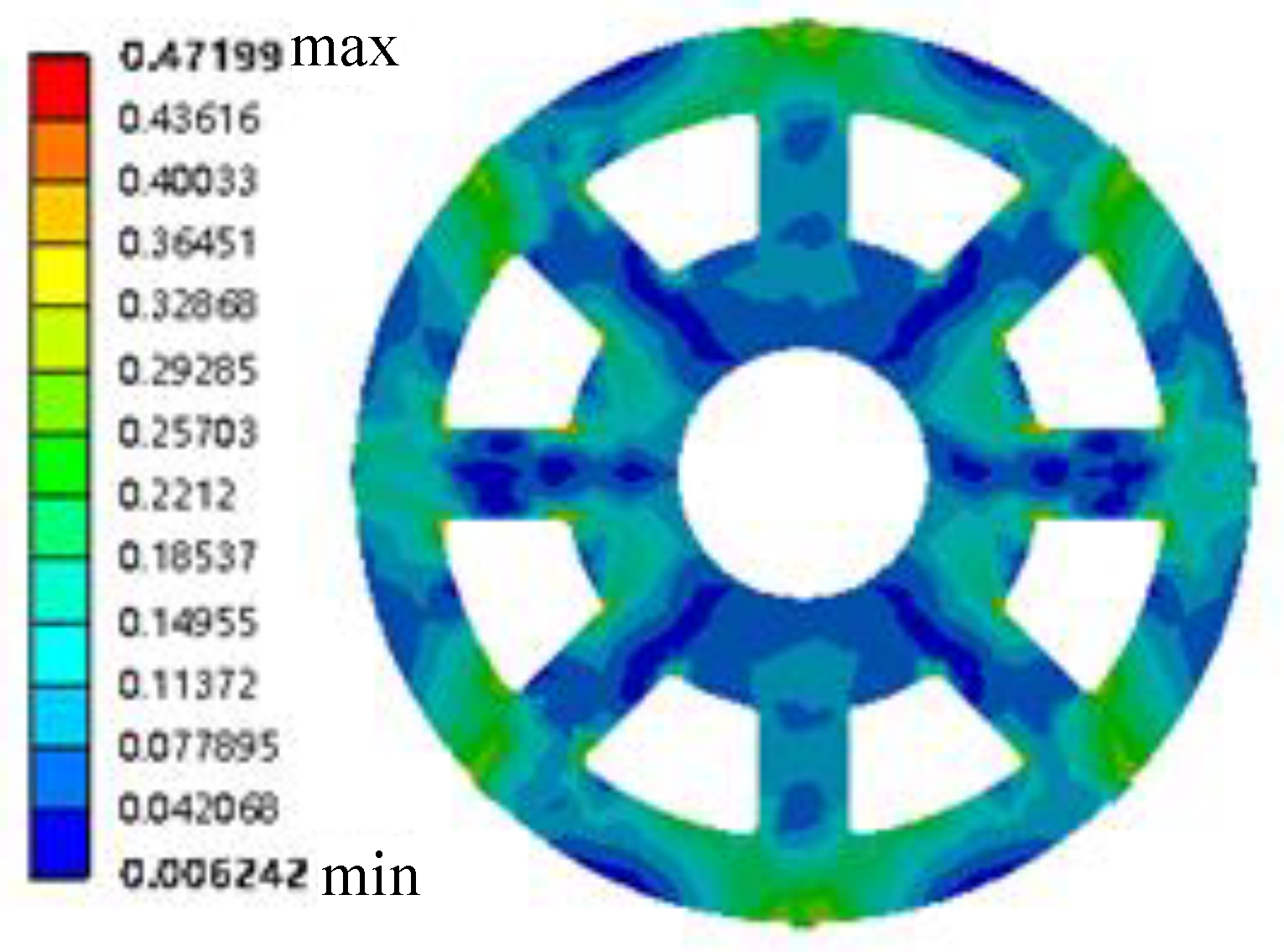



| Design Variable | Design Variable Lower Bound | Design Variable Upper Bound | |
|---|---|---|---|
| Disk discipline local variables | h (mm) | 30 | 45 |
| b (mm) | 0 | 482 | |
| Rebar discipline local variables | a (mm) | 60 | 80 |
| q (mm) | 50 | 70 | |
| Coupled variable | Gbm (kgf) | 23.5 | 44.1 |
| Fcbm (kgf) | 315.8 | 642.1 | |
| Shared variable | z (mm) | 0 | 20 |
| l1 (mm) | 140 | 200 | |
| l2 (mm) | 0 | 780 | |
| l3 (mm) | 0 | 780 | |
| l4 (mm) | 0 | 780 |
| Aleatory Variables | Mean | Standard Deviation | Distribution Type | Aleatory Variable | Mean | Standard Deviation | Distribution Type |
|---|---|---|---|---|---|---|---|
| h | hM | 0.01 hM | Normal distribution | q | qM | 0.01 qM | Normal distribution |
| b | bM | 0.01 bM | Normal distribution | Gbm | Normal distribution | ||
| l2 | Normal distribution | z | zM | 0.01 zM | Normal distribution | ||
| l3 | Normal distribution | Fcbm | Normal distribution | ||||
| l4 | Normal distribution | l1 | Normal distribution | ||||
| a | aM | 0.01 aM | Normal distribution |
| Interval Variable | Upper Bound of the Interval | Lower Bound of Interval |
|---|---|---|
| β | 1.05 | 1.08 |
| ζ | 0 | 0.96 |
| Design Variable | Optimized Value | Design Variable | Optimized Value |
|---|---|---|---|
| h (mm) | 41 | l4 (mm) | 331 |
| b (mm) | 240 | a (mm) | 71 |
| l2 (mm) | 221 | q (mm) | 65 |
| l3 (mm) | 138 | l1 (mm) | 158 |
| z (mm) | 18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, R.; Li, H.; Xie, T.; Lv, Z.; Meng, D.; Yang, W. Multidisciplinary Collaborative Design and Optimization of Turbine Rotors Considering Aleatory and Interval Mixed Uncertainty under a SORA Framework. Machines 2022, 10, 445. https://doi.org/10.3390/machines10060445
Yuan R, Li H, Xie T, Lv Z, Meng D, Yang W. Multidisciplinary Collaborative Design and Optimization of Turbine Rotors Considering Aleatory and Interval Mixed Uncertainty under a SORA Framework. Machines. 2022; 10(6):445. https://doi.org/10.3390/machines10060445
Chicago/Turabian StyleYuan, Rong, Haiqing Li, Tianwen Xie, Zhiyuan Lv, Debiao Meng, and Wenke Yang. 2022. "Multidisciplinary Collaborative Design and Optimization of Turbine Rotors Considering Aleatory and Interval Mixed Uncertainty under a SORA Framework" Machines 10, no. 6: 445. https://doi.org/10.3390/machines10060445






