Curvature Correction of a Notched Continuum Robot Based on a Static Model Considering Large Deformation and Friction Effect
Abstract
:1. Introduction
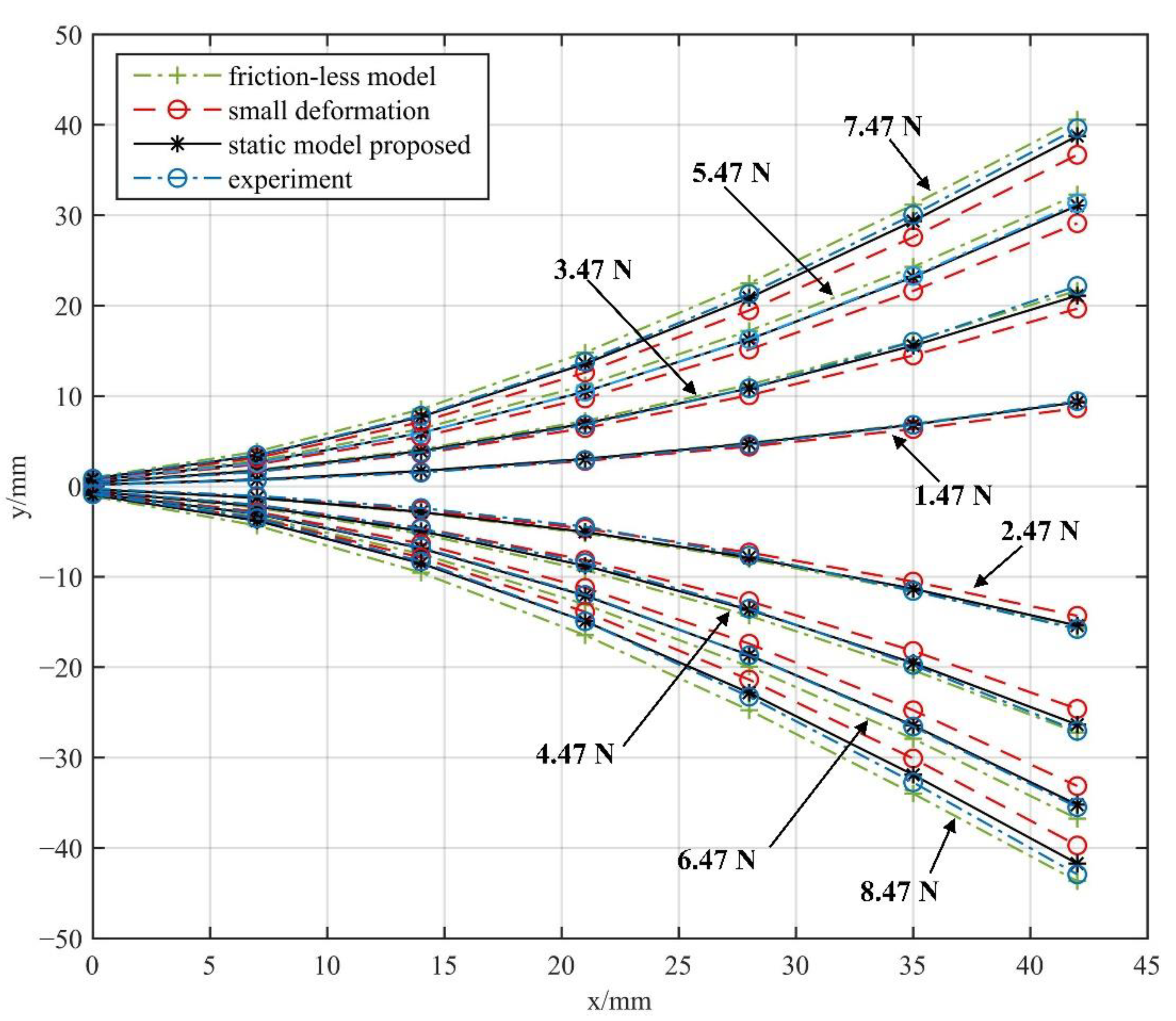
- A static model of the NCR considering large deformation is proposed. The RMSE of the bending angle of every notch based on the large deformation assumption is 0.43°, significantly smaller than the small deformation assumption (1.47°).
- Based on the static model, a piecewise constant curvature correction method of NCR is proposed. The exact single-notch deformation parameters are solved. And the method is validated by experiments and simulations.
- The friction effect and the coupling effect of forces between multiple notches are considered in the model. The experimental results show that the error of the static model based on large deformation (2.4409°) is significantly smaller than that of the static models, which are based on small deformation and friction-less assumption (10.0972°, 5.1016°).
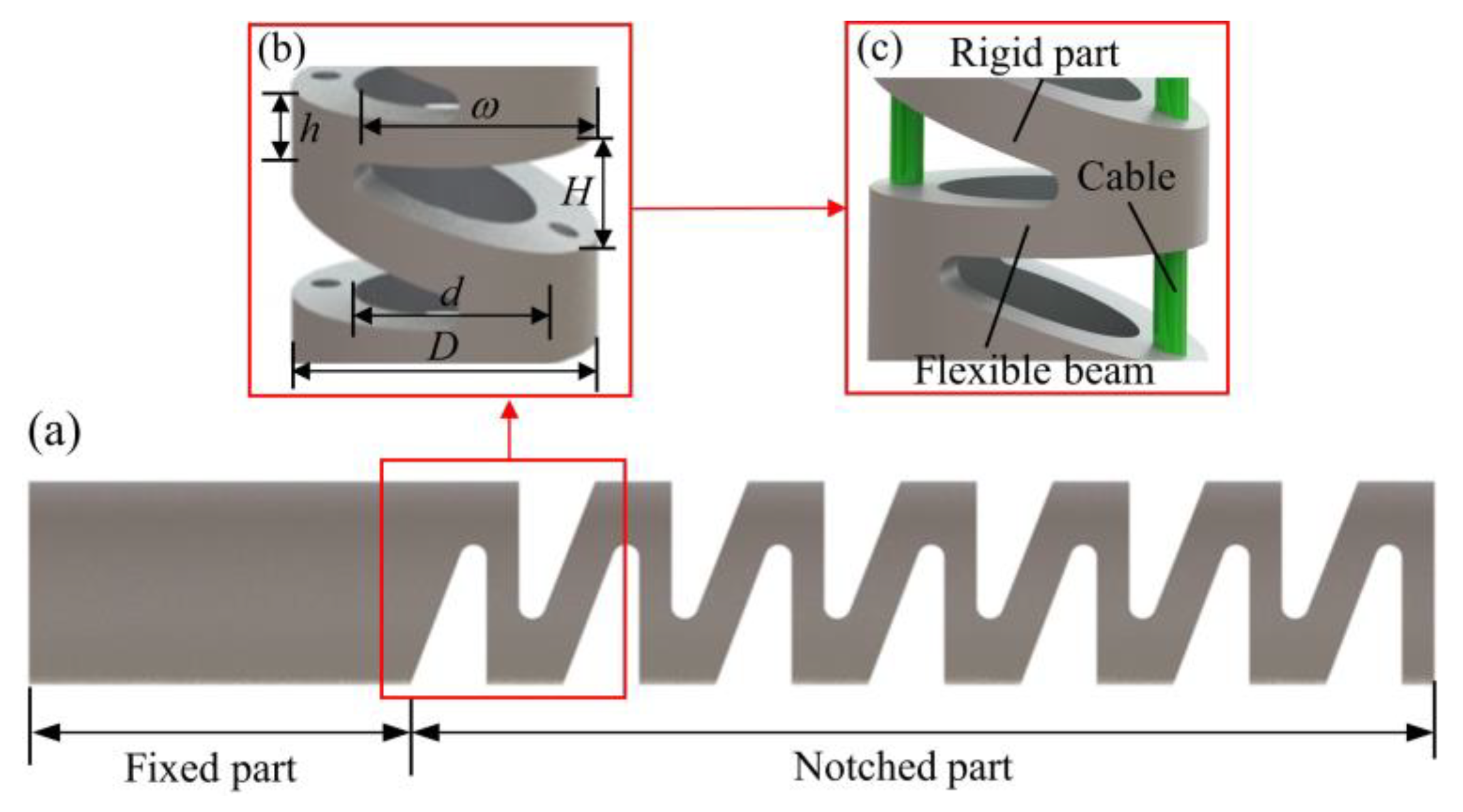
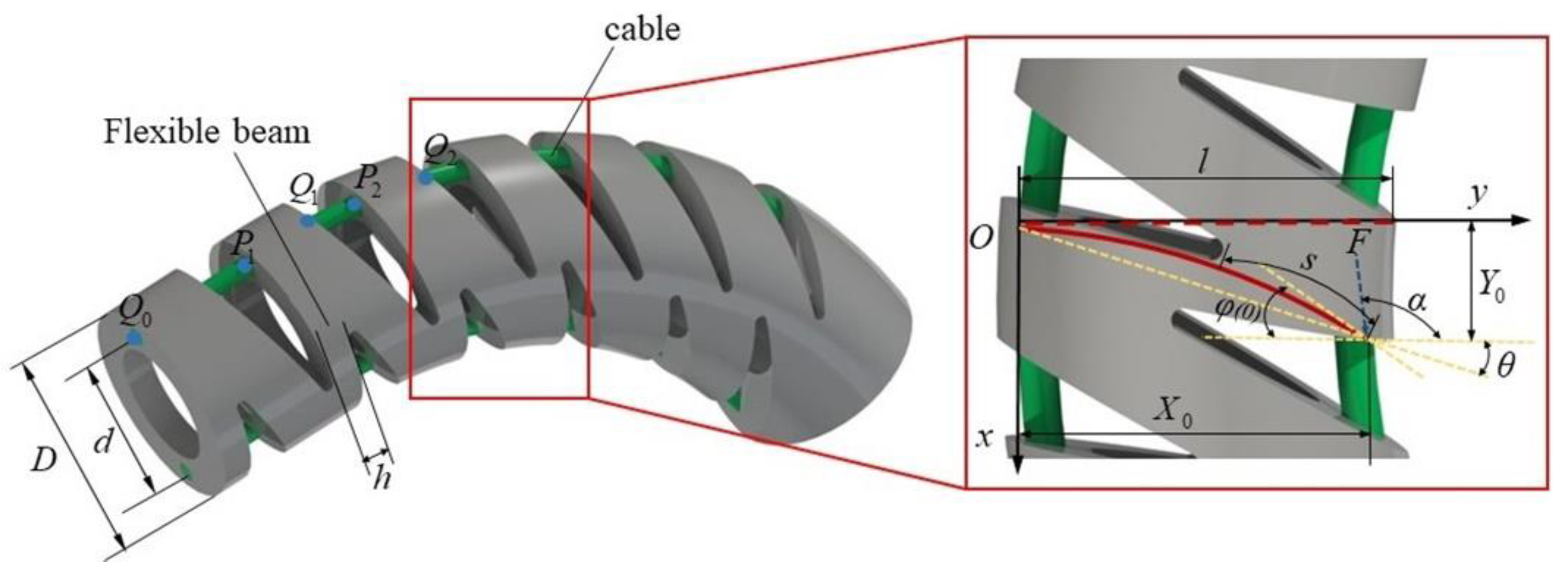
2. The Structure of the NCR
3. Large Deformation Static Model
- Since the volume of the rigid part is much larger than that of the flexible part, the deformation of the rigid parts in the backbone can be ignored.
- The NCR has two degrees of freedom: bending and rotation.
- The friction between the cable and the NCR is obtained by the Coulomb model.
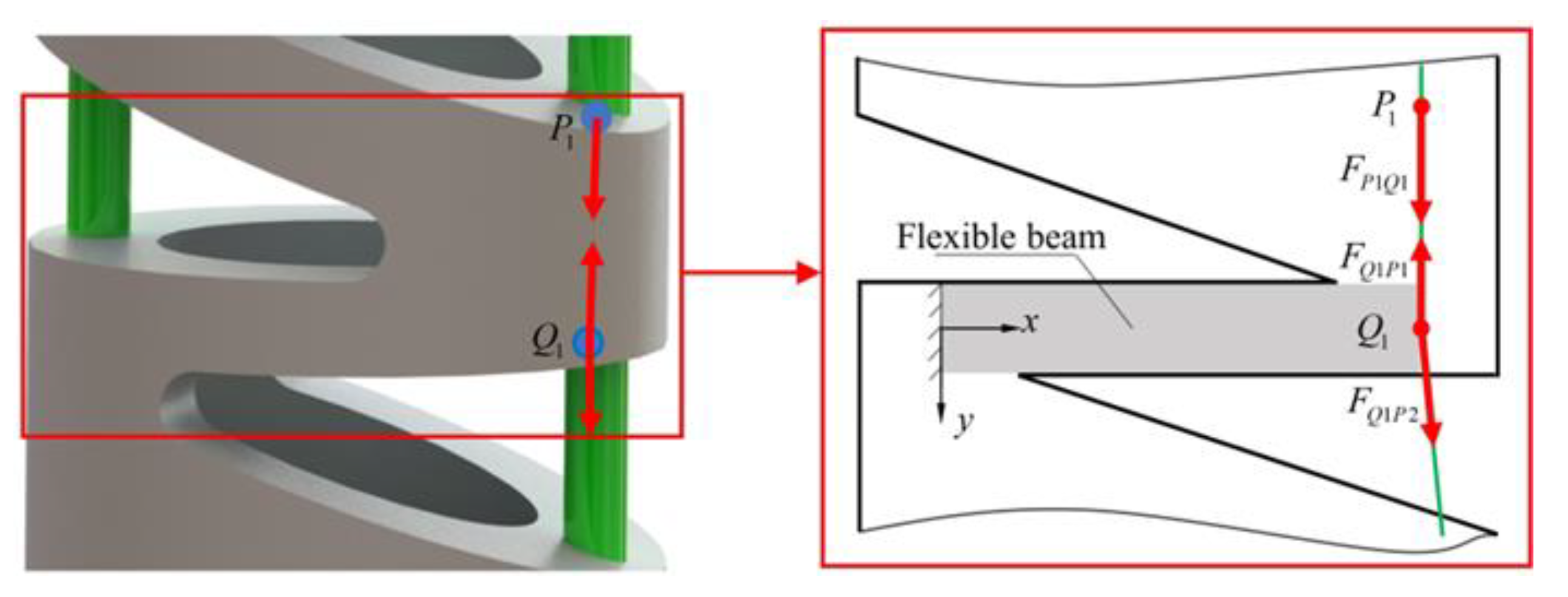
3.1. Static Modeling of a Single Notch
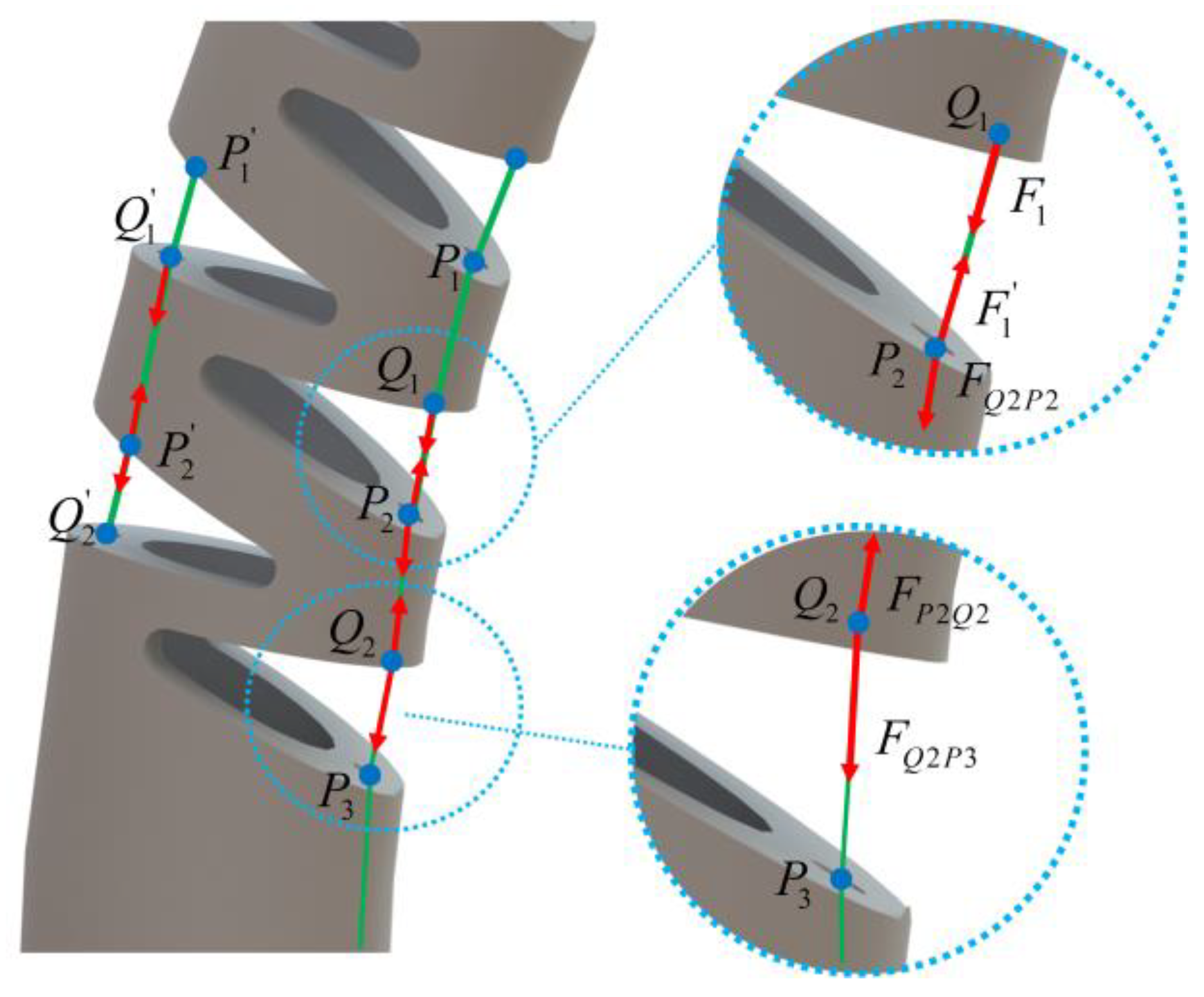
3.2. Solution of Load at Large Deformation Beam in Each Notch
3.3. Elliptic Integral Based on Equivalent Large Deformation Beam
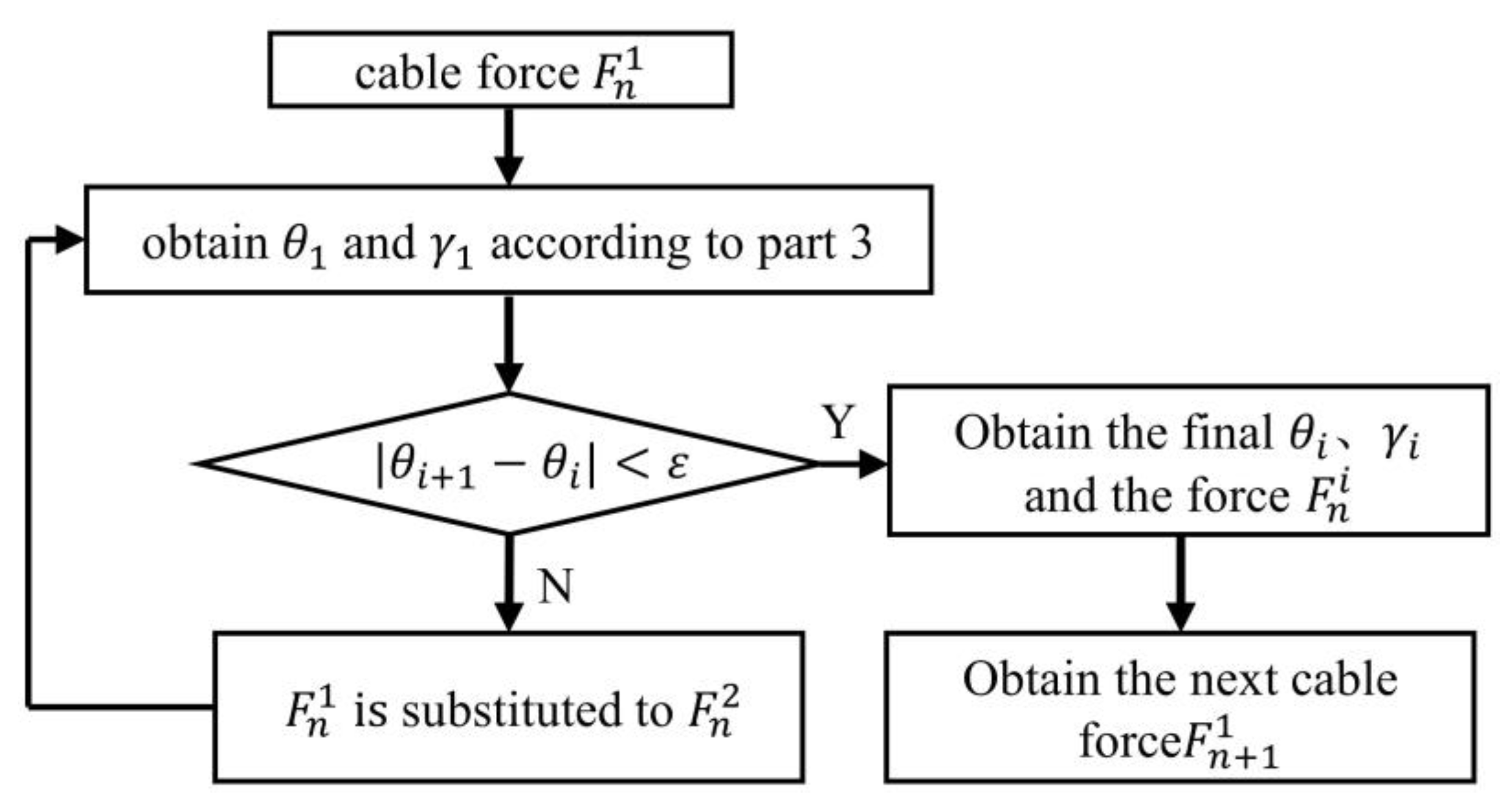
3.4. Curvature Correction and Solution of Deformation Parameters of the NCR
- First, an end cable force is preset, assuming that the cable is perpendicular to the equivalent beam (i.e., ). The deflection angle is calculated according to the large deformation assumption derived earlier in this paper, and the angle between the cable is calculated in the coordinate system using the coordinates.
- Obtain new force at the obtained angle .
- By repeating this process several times, the angle error eventually becomes zero. At this stage, the most updated and are the bending angle and cable force angle of notch 1 with the correct cable force being .
- Then, can be obtained via .
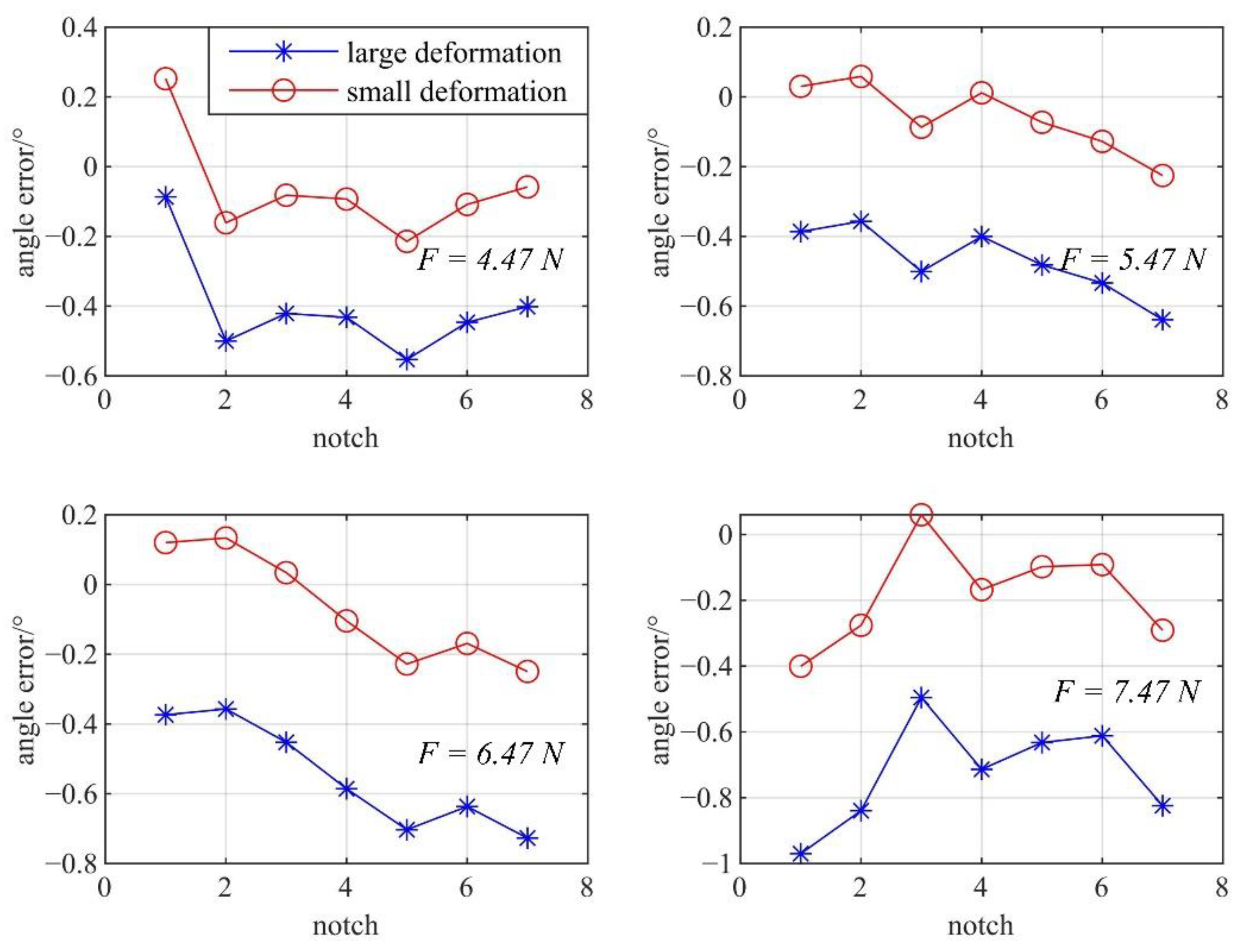
4. Determination of Friction Coefficient
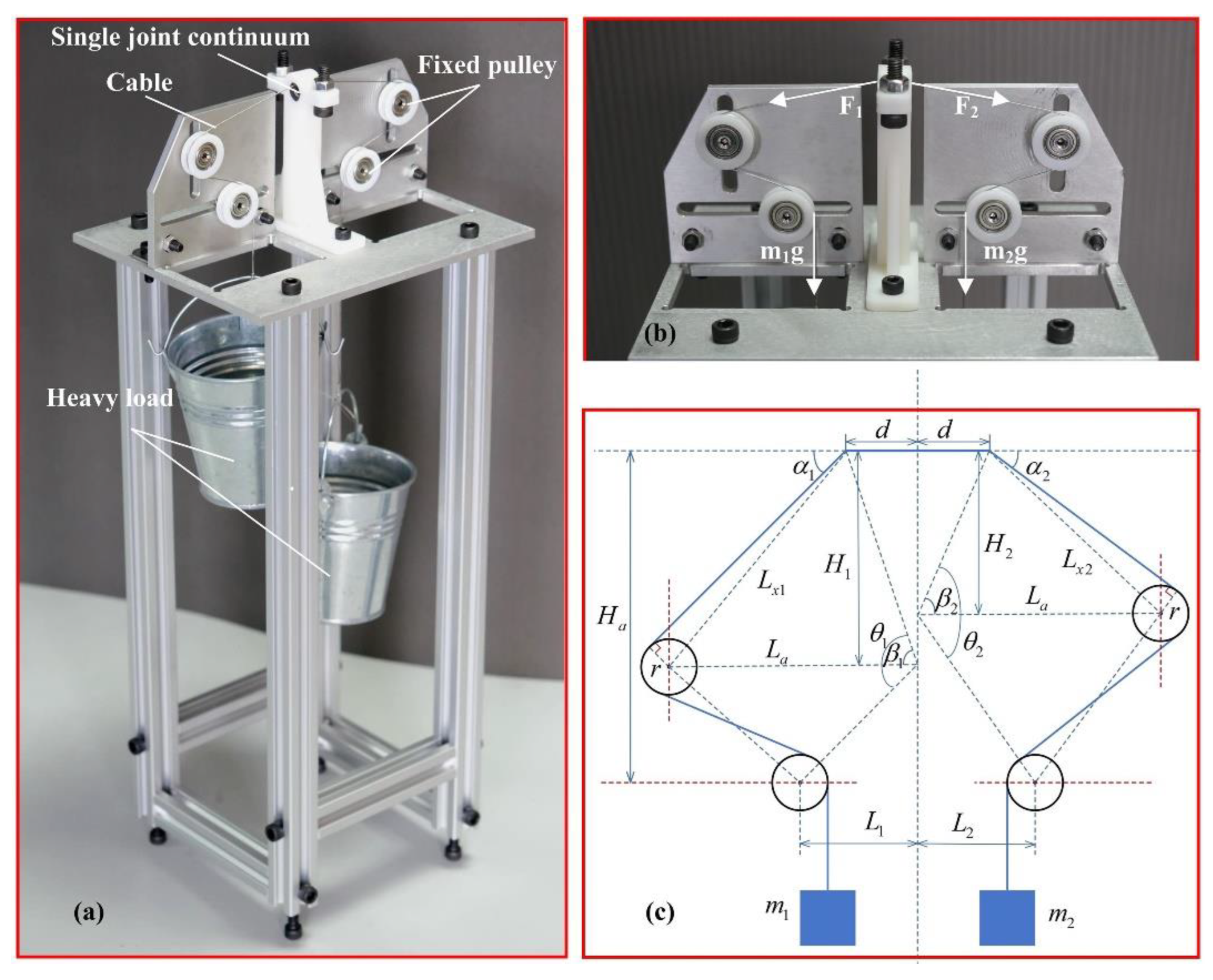
5. Accuracy Verification Experiment of the Static Model
5.1. Experimental Setup
5.2. Calibration of Elastic Modulus
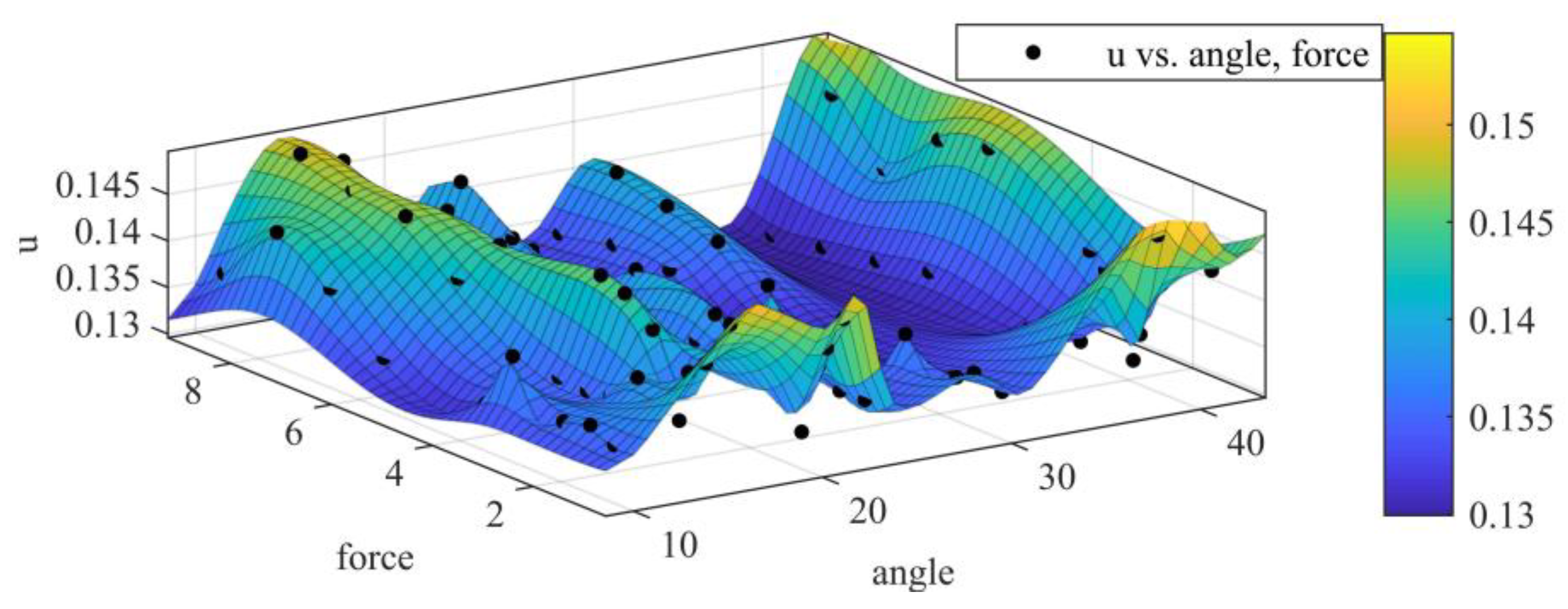
5.3. Error and Result Analysis
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Trivedi, D.; Rahn, C.D.; Kier, W.M.; Walker, I.D. Soft robotics: Biological inspiration, state of the art, and future research. Appl. Bionics Biomech. 2008, 5, 99–117. [Google Scholar] [CrossRef]
- Webster, R.J.; Okamura, A.M.; Cowan, N.J. Toward active cannulas: Miniature snake-like surgical robots. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2857–2863. [Google Scholar]
- Hannan, M.W.; Walker, I.D. Analysis and experiments with an elephant’s trunk robot. Adv. Robot. 2001, 15, 847–858. [Google Scholar] [CrossRef] [PubMed]
- Tsukagoshi, H.; Kitagawa, A.; Segawa, M. Active hose: An artificial elephant’s nose with maneuverability for rescue operation. In Proceedings of the Proceedings 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, Korea, 21–26 May 2001; pp. 2454–2459. [Google Scholar]
- Napadow, V.J.; Kamm, R.D.; Gilbert, R.J. A biomechanical model of sagittal tongue bending. J. Biomech. Eng. 2002, 124, 547–556. [Google Scholar] [CrossRef]
- Rone, W.S.; Ben-Tzvi, P. Continuum robotic tail loading analysis for mobile robot stabilization and maneuvering. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014; p. V05AT08A009. [Google Scholar]
- Guglielmino, E.; Tsagarakis, N.; Caldwell, D.G. An octopus anatomy-inspired robotic arm. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3091–3096. [Google Scholar]
- Webster, R.J., III; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Nakadate, R.; Iwasa, T.; Onogi, S.; Arata, J.; Oguri, S.; Okamoto, Y.; Akahoshi, T.; Eto, M.; Hashizume, M. Surgical Robot for Intraluminal Access: An Ex Vivo Feasibility Study. Cyborg Bionic Syst. 2020, 2020, 8378025. [Google Scholar] [CrossRef]
- Ohuchida, K. Robotic Surgery in Gastrointestinal Surgery. Cyborg Bionic Syst. 2020, 2020, 9724807. [Google Scholar] [CrossRef]
- So, J.; Kim, U.; Kim, Y.B.; Seok, D.-Y.; Yang, S.Y.; Kim, K.; Park, J.H.; Hwang, S.T.; Gong, Y.J.; Choi, H.R. Shape Estimation of Soft Manipulator Using Stretchable Sensor. Cyborg Bionic Syst. 2021, 2021, 9843894. [Google Scholar] [CrossRef]
- Chiluisa, A.J.; Van Rossum, F.J.; Gafford, J.B.; Labadie, R.F.; Webster, R.J.; Fichera, L. Computational optimization of notch spacing for a transnasal ear endoscopy continuum robot. In Proceedings of the 2020 International Symposium on Medical Robotics (ISMR), Atlanta, GA, USA, 18–20 November 2020; pp. 188–194. [Google Scholar]
- Eastwood, K.W.; Swarup, A.; Francis, P.; Alvara, A.N.; Chen, H.; Looi, T.; Naguib, H.E.; Drake, J.M. A steerable neuroendoscopic instrument using compliant contact-aided joints and monolithic articulation. J. Med. Devices 2020, 14, 025002. [Google Scholar] [CrossRef]
- Ding, J.; Goldman, R.E.; Xu, K.; Allen, P.K.; Fowler, D.L.; Simaan, N. Design and coordination kinematics of an insertable robotic effectors platform for single-port access surgery. IEEE/ASME Trans. Mechatron. 2012, 18, 1612–1624. [Google Scholar] [CrossRef]
- Zhang, G.; Du, F.; Xue, S.; Cheng, H.; Zhang, X.; Song, R.; Li, Y. Design and Modeling of a Bio-Inspired Compound Continuum Robot for Minimally Invasive Surgery. Machines 2022, 10, 468. [Google Scholar] [CrossRef]
- York, P.A.; Swaney, P.J.; Gilbert, H.B.; Webster, R.J. A wrist for needle-sized surgical robots. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1776–1781. [Google Scholar]
- Kutzer, M.D.; Segreti, S.M.; Brown, C.Y.; Armand, M.; Taylor, R.H.; Mears, S.C. Design of a new cable-driven manipulator with a large open lumen: Preliminary applications in the minimally-invasive removal of osteolysis. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2913–2920. [Google Scholar]
- Eastwood, K.W.; Azimian, H.; Carrillo, B.; Looi, T.; Naguib, H.E.; Drake, J.M. Kinetostatic design of asymmetric notch joints for surgical robots. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 2381–2387. [Google Scholar]
- Francis, P.; Eastwood, K.W.; Bodani, V.; Price, K.; Upadhyaya, K.; Podolsky, D.; Azimian, H.; Looi, T.; Drake, J. Miniaturized instruments for the da Vinci research kit: Design and implementation of custom continuum tools. IEEE Robot. Autom. Mag. 2017, 24, 24–33. [Google Scholar] [CrossRef]
- Li, S.; Hao, G. Current trends and prospects in compliant continuum robots: A survey. Actuators 2021, 10, 145. [Google Scholar] [CrossRef]
- Yip, M.C.; Camarillo, D.B. Model-less hybrid position/force control: A minimalist approach for continuum manipulators in unknown, constrained environments. IEEE Robot. Autom. Lett. 2016, 1, 844–851. [Google Scholar] [CrossRef]
- Xu, K.; Simaan, N. An investigation of the intrinsic force sensing capabilities of continuum robots. IEEE Trans. Robot. 2008, 24, 576–587. [Google Scholar] [CrossRef]
- Zheng, T.; Branson, D.T.; Guglielmino, E.; Kang, R.; Medrano Cerda, G.A.; Cianchetti, M.; Follador, M.; Godage, I.S.; Caldwell, D.G. Model validation of an octopus inspired continuum robotic arm for use in underwater environments. J. Mech. Robot. 2013, 5, 021004. [Google Scholar] [CrossRef]
- Bergeles, C.; Gosline, A.H.; Vasilyev, N.V.; Codd, P.J.; Pedro, J.; Dupont, P.E. Concentric tube robot design and optimization based on task and anatomical constraints. IEEE Trans. Robot. 2015, 31, 67–84. [Google Scholar] [CrossRef]
- Legrand, J.; Ourak, M.; Vandebroek, T.; Vander Poorten, E. A large displacement model for superelastic material side-notched tube instruments. Int. J. Mech. Sci. 2021, 197, 106329. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, H.; Wang, X.; Liang, B. Approximate piecewise constant curvature equivalent model and their application to continuum robot configuration estimation. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 1929–1936. [Google Scholar]
- Du, Z.; Yang, W.; Dong, W. Kinematics modeling of a notched continuum manipulator. J. Mech. Robot. 2015, 7, 041017. [Google Scholar] [CrossRef]
- Gao, A.; Murphy, R.J.; Liu, H.; Iordachita, I.I.; Armand, M. Mechanical model of dexterous continuum manipulators with compliant joints and tendon/external force interactions. IEEE/ASME Trans. Mechatron. 2016, 22, 465–475. [Google Scholar] [CrossRef]
- Jones, B.A.; Gray, R.L.; Turlapati, K. Three dimensional statics for continuum robotics. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 2659–2664. [Google Scholar]
- Rucker, D.C.; Webster III, R.J. Statics and dynamics of continuum robots with general tendon routing and external loading. IEEE Trans. Robot. 2011, 27, 1033–1044. [Google Scholar] [CrossRef]
- Eastwood, K.W.; Francis, P.; Azimian, H.; Swarup, A.; Looi, T.; Drake, J.M.; Naguib, H.E. Design of a contact-aided compliant notched-tube joint for surgical manipulation in confined workspaces. J. Mech. Robot. 2018, 10, 015001. [Google Scholar] [CrossRef]
- Wei, D.; Wenlong, Y.; Dawei, H.; Zhijiang, D. Modeling of flexible arm with triangular notches for applications in single port access abdominal surgery. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 588–593. [Google Scholar]
- Fichera, L.; Dillon, N.P.; Zhang, D.; Godage, I.S.; Siebold, M.A.; Hartley, B.I.; Noble, J.H.; Russell, P.T.; Labadie, R.F.; Webster, R.J. Through the eustachian tube and beyond: A new miniature robotic endoscope to see into the middle ear. IEEE Robot. Autom. Lett. 2017, 2, 1488–1494. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Ping, Z.; Zuo, S. Miniature continuum manipulator with three degrees-of-freedom force sensing for retinal microsurgery. J. Mech. Robot. 2021, 13, 041002. [Google Scholar] [CrossRef]
- Simaan, N.; Xu, K.; Wei, W.; Kapoor, A.; Kazanzides, P.; Taylor, R.; Flint, P. Design and integration of a telerobotic system for minimally invasive surgery of the throat. Int. J. Robot. Res. 2009, 28, 1134–1153. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Wang, H.; Tian, S.; Zhang, F. Modeling of notched variable stiffness continuum flexible snake-like robot. In Proceedings of the 2018 International Automatic Control Conference (CACS), Taoyuan, Taiwan, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Yang, Z.; Yang, W.; Du, Z. Kinematics modelling of tendon-driven continuum manipulator with crossed notches. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Hong Kong, 12–14 December 2017; p. 012005. [Google Scholar]
- Wang, H.; Wang, X.; Yang, W.; Du, Z. Design and kinematic modeling of a notch continuum manipulator for laryngeal surgery. Int. J. Control Autom. Syst. 2020, 18, 2966–2973. [Google Scholar] [CrossRef]
- Lee, K. Large deflections of cantilever beams of non-linear elastic material under a combined loading. Int. J. Non-Linear Mech. 2002, 37, 439–443. [Google Scholar] [CrossRef]
- Walker, A.; Hall, D. An analysis of the large deflections of beams using the Rayleigh-Ritz finite element method. Aeronaut. Q. 1968, 19, 357–367. [Google Scholar] [CrossRef]
- Tada, Y.; Lee, G.C. Finite element solution to an elastica problem of beams. Int. J. Numer. Methods Eng. 1970, 2, 229–241. [Google Scholar] [CrossRef]
- Beléndez, T.; Neipp, C.; Beléndez, A. Large and small deflections of a cantilever beam. Eur. J. Phys. 2002, 23, 371. [Google Scholar] [CrossRef]
- Mutyalarao, M.; Bharathi, D.; Rao, B.N. Large deflections of a cantilever beam under an inclined end load. Appl. Math. Comput. 2010, 217, 3607–3613. [Google Scholar] [CrossRef]
- Bisshopp, K.; Drucker, D. Large deflection of cantilever beams. Q. Appl. Math. 1945, 3, 272–275. [Google Scholar] [CrossRef]
- Howell, L.L.; Midha, A. Parametric deflection approximations for end-loaded, large-deflection beams in compliant mechanisms. J. Mech. Des. 1995, 117, 156–165. [Google Scholar] [CrossRef]
- Kimball, C.; Tsai, L.-W. Modeling of flexural beams subjected to arbitrary end loads. J. Mech. Des. 2002, 124, 223–235. [Google Scholar] [CrossRef]
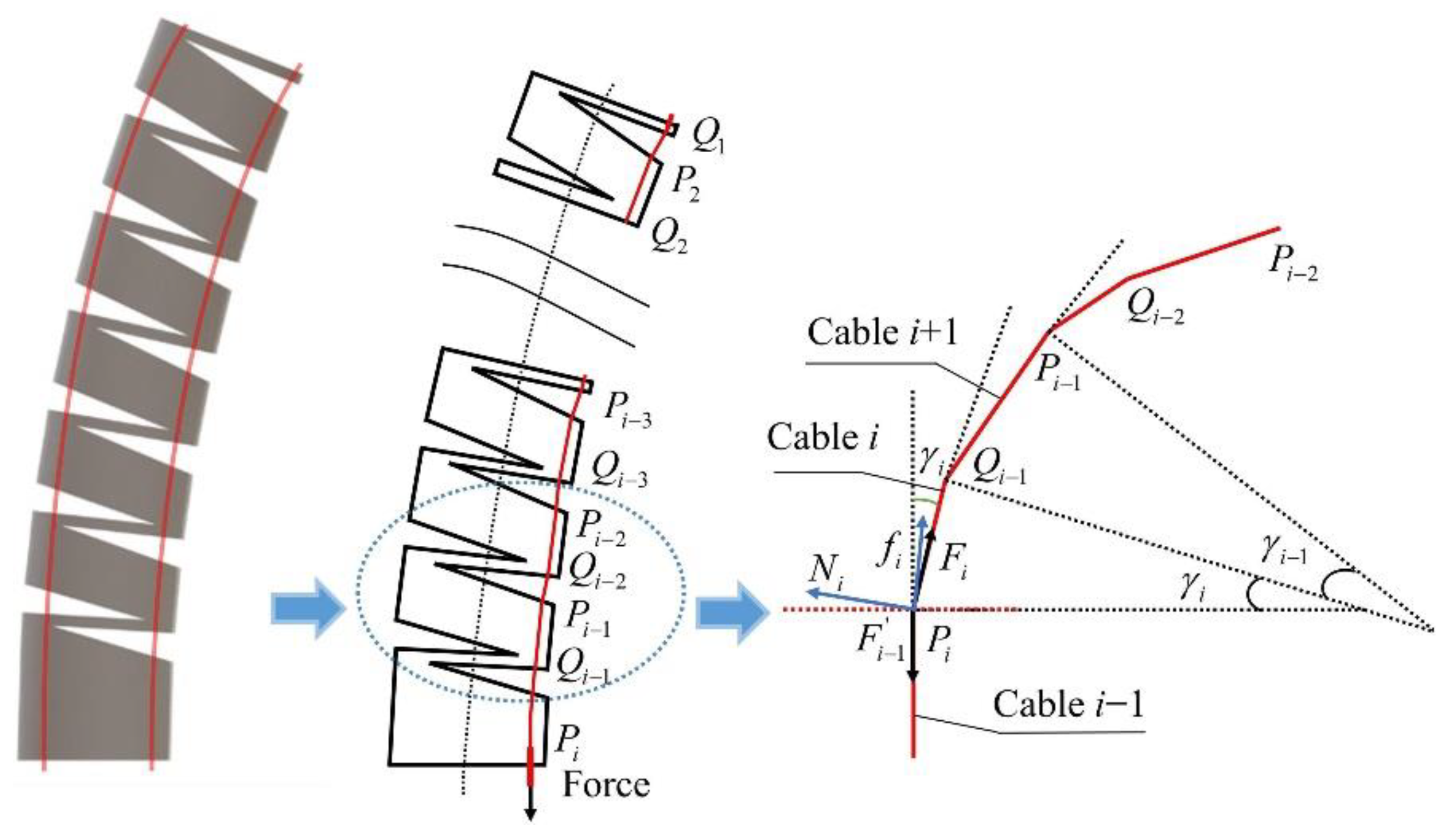
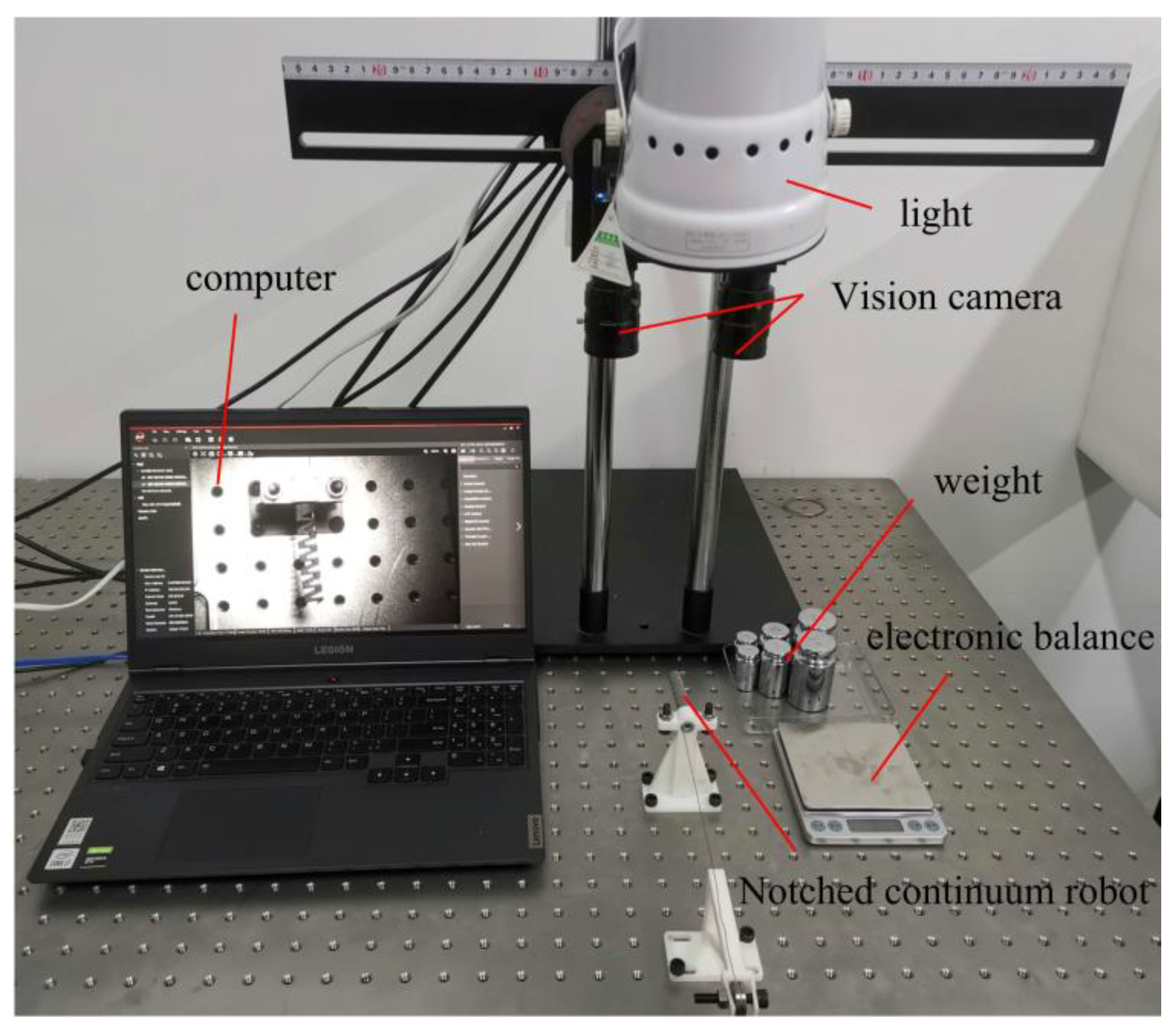



| Parameter | Description |
|---|---|
| Fi | Tension force on cable i |
| Fi−1 | Tension force on cable i − 1 |
| Ni | Supporting force exerted by the continuum robot |
| fi | Friction force exerted by the continuum robot |
| Ni′ | The supporting force applied by the cable to the continuum robot (not shown in the figure) |
| fi′ | Friction force applied by the cable to the continuum robot (not shown in the figure) |
| γi | The angle between cable i and the cable i − 1 |
| Parameter | Unit/mm |
|---|---|
| D | 10 |
| d | 6 |
| h | 1.5 |
| H | 3.5 |
| ω | 6.9 |
| material | Nylon |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Shang, S.; Zhang, G.; Xue, S.; Cheng, H.; Qi, P.; Du, F. Curvature Correction of a Notched Continuum Robot Based on a Static Model Considering Large Deformation and Friction Effect. Machines 2022, 10, 778. https://doi.org/10.3390/machines10090778
Liu J, Shang S, Zhang G, Xue S, Cheng H, Qi P, Du F. Curvature Correction of a Notched Continuum Robot Based on a Static Model Considering Large Deformation and Friction Effect. Machines. 2022; 10(9):778. https://doi.org/10.3390/machines10090778
Chicago/Turabian StyleLiu, Jiaxing, Sibo Shang, Gang Zhang, Shaowei Xue, Hao Cheng, Peng Qi, and Fuxin Du. 2022. "Curvature Correction of a Notched Continuum Robot Based on a Static Model Considering Large Deformation and Friction Effect" Machines 10, no. 9: 778. https://doi.org/10.3390/machines10090778
APA StyleLiu, J., Shang, S., Zhang, G., Xue, S., Cheng, H., Qi, P., & Du, F. (2022). Curvature Correction of a Notched Continuum Robot Based on a Static Model Considering Large Deformation and Friction Effect. Machines, 10(9), 778. https://doi.org/10.3390/machines10090778







