Adaptive Neuro-Fuzzy Control of Active Vehicle Suspension Based on
Abstract
:1. Introduction
- Dynamic Controller Transition and Data Collection: The proposed methodology introduces dynamic switching between controllers based on road characteristics, a novel approach for improving suspension system performance. An emphasis on meticulous manual controller transitions and comprehensive data collection across various road profiles distinguishes this approach, paving the way for data-driven suspension optimization. The combination of fuzzy logic and neural network techniques allows the ANFIS controller to provide continuous and smooth control actions as the input conditions change. This smooth transition helps avoid sudden changes in control output, which can contribute to system stability and improved performance.
- Pioneering Utilization of ANFIS Controller as a Hybrid Controller Training Approach: One of the key innovations in this research is the training of the ANFIS controller using input–output data from both the and controllers. This hybrid training approach leverages the knowledge and performance characteristics of both controller types to enhance the capabilities of the ANFIS controller, resulting in a unique and powerful control system for suspension optimization.
2. Problem Formulation and Design Method
2.1. Quarter-Car Model
2.2. Design Objectives
- Ride comfort: Ride comfort is commonly assessed by quantifying the RMS value of acceleration experienced by passengers [7]. To attain optimal ride comfort, it is imperative to minimize this value to the greatest extent possible within the frequency range of passenger body sensitivity, typically falling between 1 Hz and 8 Hz [31]. When road roughness is predominantly modeled as white noise or impulse input (as is frequently the case), enhancing ride comfort involves the minimization of the norm of the transfer function from road displacement to chassis acceleration (), with appropriate weighting applied to the relevant frequencies. However, if the road disturbances include more complex waveforms than white noise (such as deterministic patterns), achieving optimal ride comfort may require the use of performance.
- Road-holding: To achieve good road-holding, it is necessary to maintain continuous contact between the tires and the road surface. In the context of a given road profile, this objective can be accomplished by minimizing the or norms of the transfer function from the road disturbance to tire displacement (). It is essential to emphasize that maintaining rigid contact between the tires and the road necessitates that the dynamic tire load does not surpass the static load [14], i.e.,This fact can be utilized to normalize the dynamic tire load.
- Suspension stroke limits: Suspension deflection () plays a crucial role in achieving the required road-holding specifications, and it is imperative to maintain the deflection limits to ensure optimal ride comfort and prevent any structural damage to the system. As a result, it becomes imperative to confine the transfer function within the established upper and lower bounds to achieve the desired outcomes. Deviating from these limits can result in compromised ride comfort and have an adverse impact on the overall performance of the vehicle. To avoid excessive suspension bottoming, it has to consider the limitations of suspension deflection and incorporate appropriate measures to maintain optimal performance, as follows:
- Control signal: The control signal is produced by a hydraulic actuator and is constrained due to its saturation. It is hypothesized that the normalized control signal is bounded, as expressed by the inequality:
2.3. Review of and H∞ Design Frameworks
2.3.1. Synthesis
2.3.2. H∞ Synthesis
3. Adaptive Neuro-Fuzzy Inference Systems (ANFIS)
- Layer 1: Every node in this layer is depicted as a square shape, each associated with a specific membership function:where the superscripts above and below denote the layer number and the node index within the layer, respectively. The input to the i-th node in this layer is denoted by x (or y), while represents the corresponding linguistic term associated with this node (e.g., “small”, “large”, etc.). In this specific case, the membership function, denoted as , is selected to have a bell-shaped form with a maximum value of 1 and a minimum value of 0, as illustrated below:The parameter set corresponds to the specific parameters of the bell-shaped membership function. Any variation in the values of these parameters will result in changes to the shape of the bell-shaped function accordingly. As a result, a wide range of membership functions can be induced for the linguistic value by adjusting the values of these parameters.
- Layer 2: Each node in this layer is represented by a circular shape denoted by the symbol П, indicating that the incoming signals are multiplied. The output of the node is calculated as the T-norm (logical AND) multiplication of the input signals, as follows:where and are the membership functions for the input variables x and y, respectively, associated with the i-th node, and represents the logical AND operator. The resulting value represents the firing strength or degree of membership for the i-th rule. Each output node corresponds to the firing strength of a specific rule.
- Layer 3: Every node within this layer is a fixed node, symbolized by a circular shape marked as N. This layer executes a normalization procedure involving summation and arithmetic division. Specifically, the i-th node computes the ratio of the i-th rule’s firing strength to the total sum of all rules’ firing strengths, as follows:The computed values, denoted as , are termed normalized firing strengths. These values signify the extent of the contribution of each rule towards the ultimate output of the ANFIS model.
- Layer 4: Each node in this layer is represented by a square shape and performs the multiplication of the normalized output of layer 3, , with the “then” part of the fuzzy rule, denoted as , as follows:The set of parameters are referred to as the consequent parameters, and they determine the shape and position of the output surface of the ANFIS model.
- Layer 5: The presented neural network architecture comprises a single node characterized by a circular shape and identified as Σ. The output of this layer is calculated through the algebraic summation of the input signals, represented as follows:Here, and denote the weight and input signal of the i-th input node, respectively. The output represents the weighted sum of the input signals normalized by the sum of the weights.
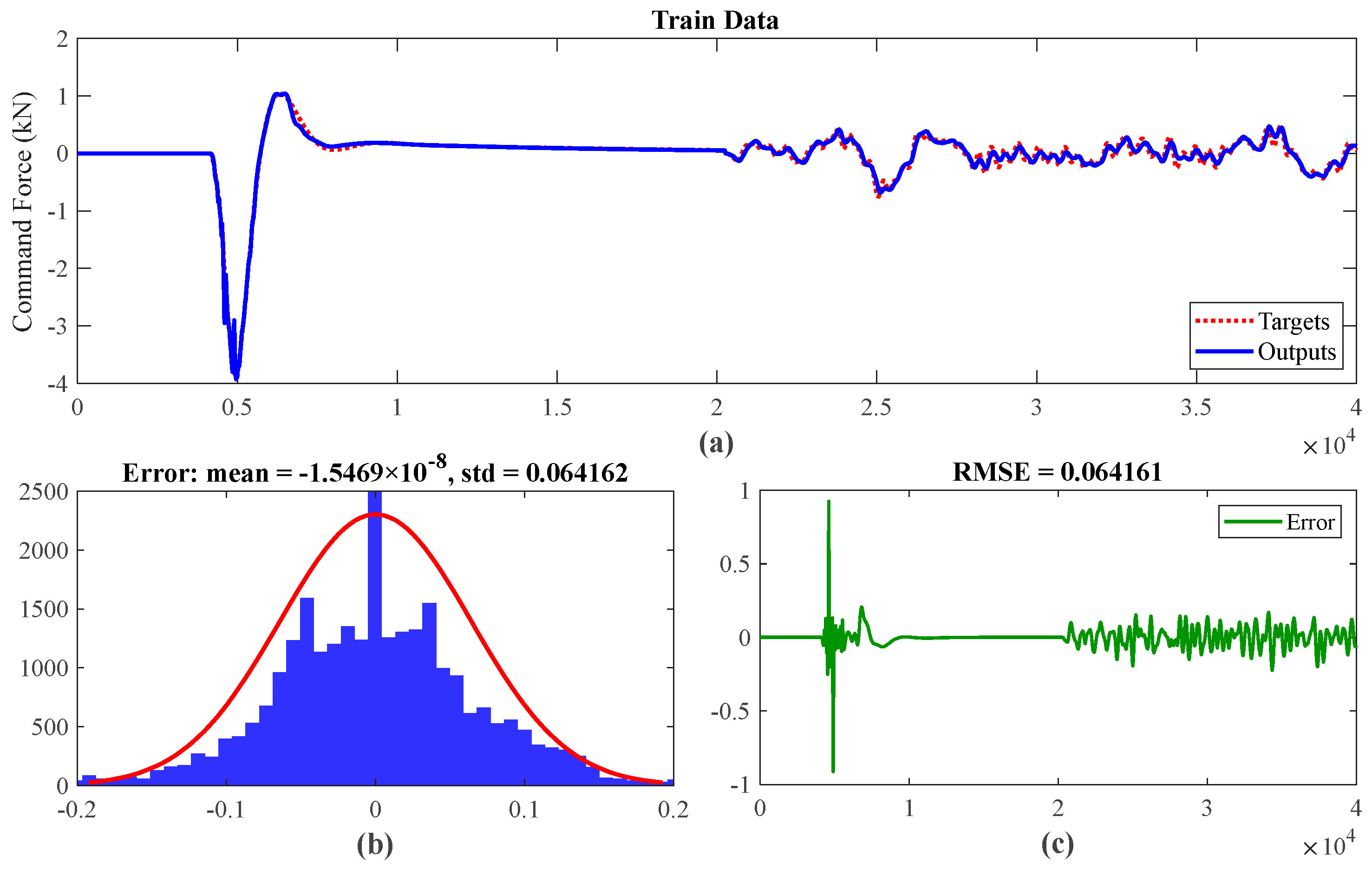
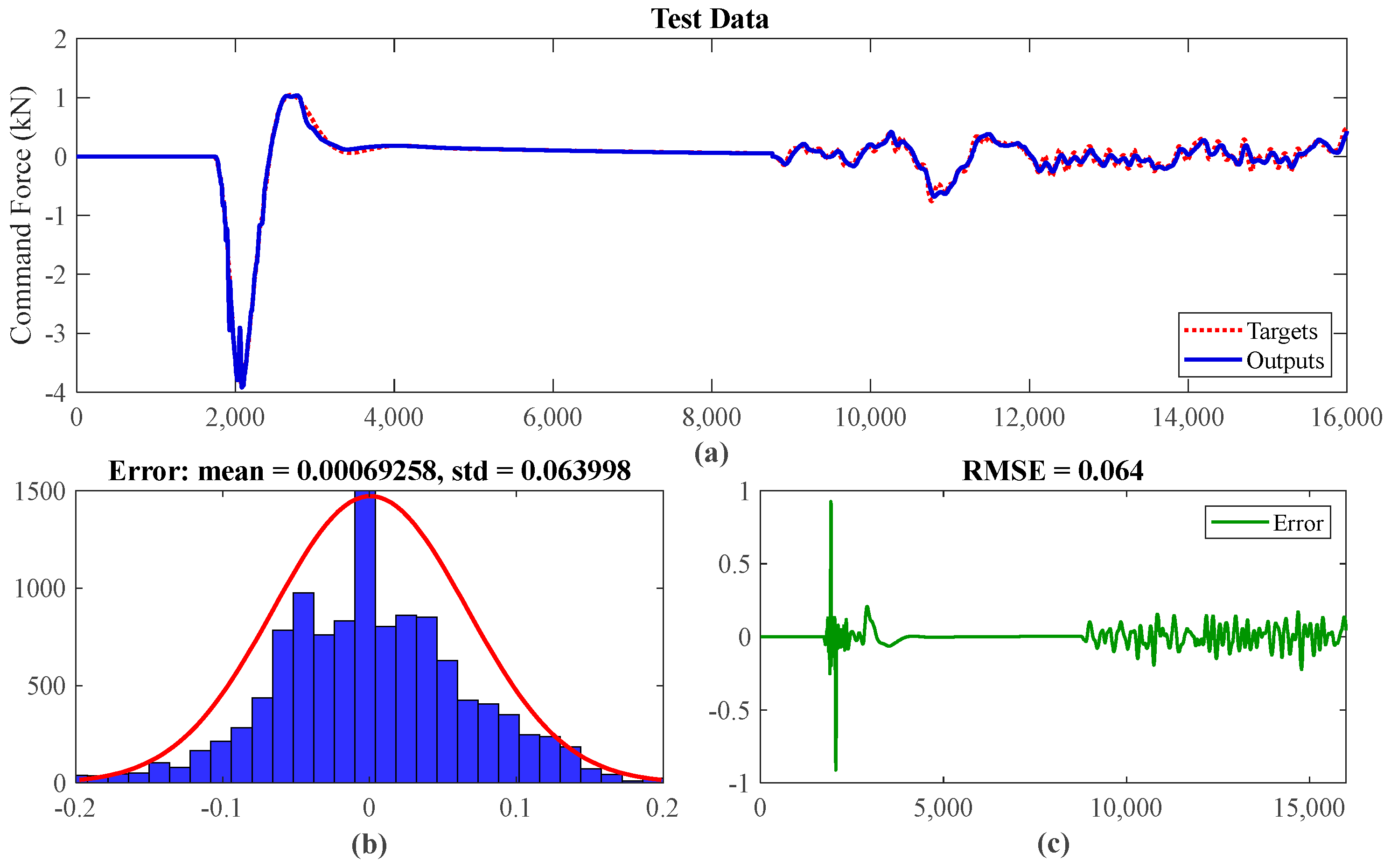
ANFIS Design
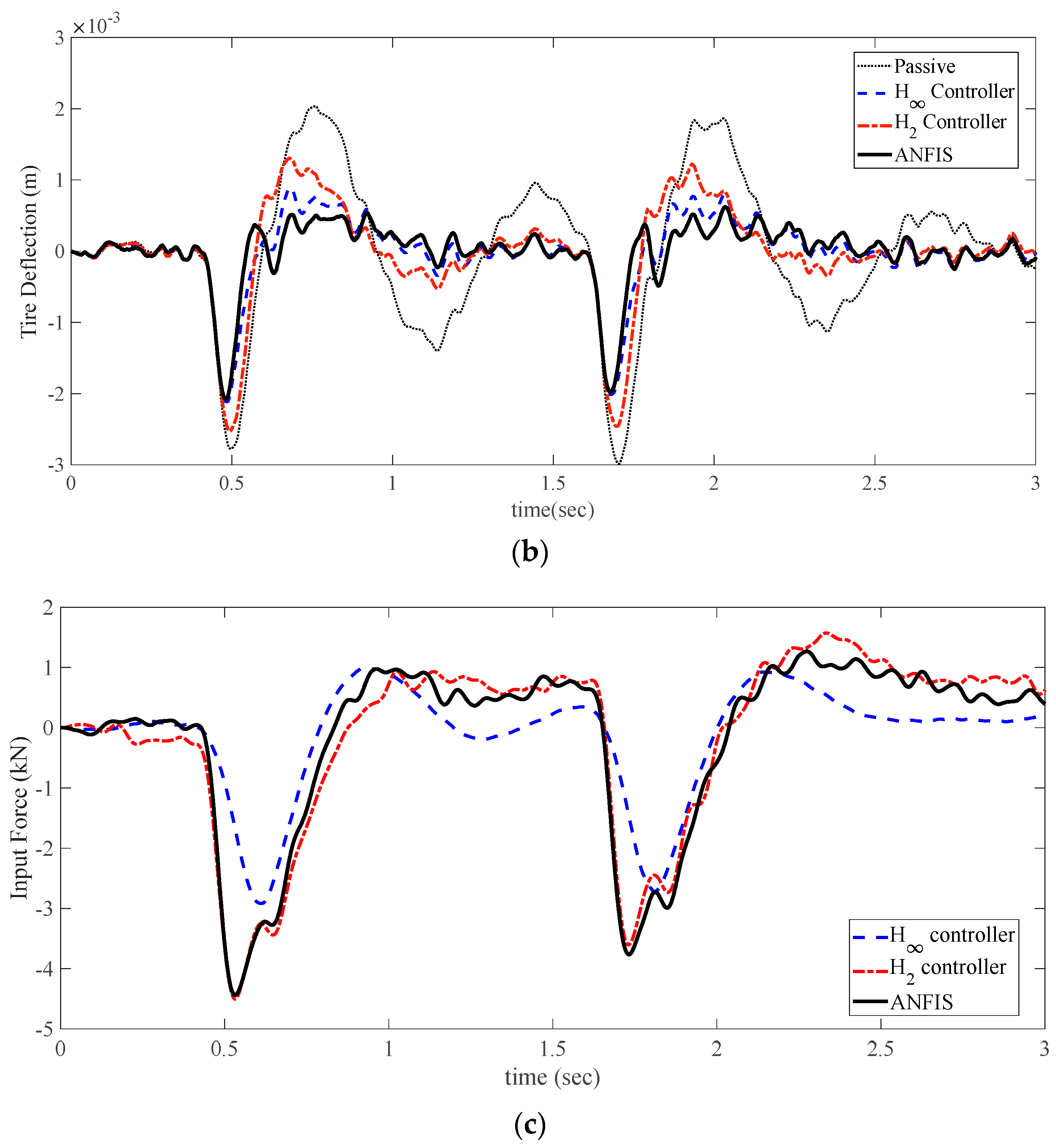
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Badri, P.; Amini, A.; Sojoodi, M. Robust fixed-order dynamic output feedback controller design for nonlinear uncertain suspension system. Mech. Syst. Signal Process. 2016, 80, 137–151. [Google Scholar] [CrossRef]
- Ma, M.; Chen, H. Constrained H2 control of active suspensions using LMI optimization. In Proceedings of the 2006 Chinese Control Conference, Harbin, China, 7–11 August 2006. [Google Scholar]
- Viadero-Monasterio, F.; Boada, B.; Boada, M.; Díaz, V. H∞ Dynamic output feedback control for a networked control active suspension system under actuator faults. Mech. Syst. Signal Process. 2022, 162, 108050. [Google Scholar] [CrossRef]
- Sun, W.; Gao, H.; Yao, B. Adaptive robust vibration control of full-car active suspensions with electrohydraulic actuators. IEEE Trans. Control. Syst. Technol. 2013, 21, 2417–2422. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Wang, J. Robust gain-scheduling energy-to-peak control of vehicle lateral dynamics stabilisation. Veh. Syst. Dyn. 2014, 52, 309–340. [Google Scholar] [CrossRef]
- Jin, X.; Wang, J.; Sun, S.; Li, S.; Yang, J.; Yan, Z. Design of constrained robust controller for active suspension of in-wheel-drive electric vehicles. Mathematics 2021, 9, 249. [Google Scholar] [CrossRef]
- Akbari, A.; Lohmann, B. Output feedback H∞/GH2 preview control of active vehicle suspensions: A comparison study of LQG preview. Veh. Syst. Dyn. 2010, 48, 1475–1494. [Google Scholar] [CrossRef]
- Akbari Alvanagh, A. Multi-Objective H_Infinity/GH_2 Preview Control of Active Vehicle Suspensions. Ph.D. Dessertation, Technische Universität München, München, Germany, 2009. [Google Scholar]
- Youn, I.; Khan, M.; Uddin, N.; Youn, E.; Tomizuka, M. Road disturbance estimation for the optimal preview control of an active suspension systems based on tracked vehicle model. Int. J. Automot. Technol. 2017, 18, 307–316. [Google Scholar] [CrossRef]
- Burl, J.B. Linear Optimal Control: H (2) and H (Infinity) Methods; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1998. [Google Scholar]
- Jurisch, M. Vertical trajectory planning: An optimal control approach for active suspension systems in autonomous vehicles. Veh. Syst. Dyn. 2022, 60, 3788–3809. [Google Scholar] [CrossRef]
- Malekshahi, A.; Mirzaei, M. Designing a non-linear tracking controller for vehicle active suspension systems using an optimization process. Int. J. Automot. Technol. 2012, 13, 263–271. [Google Scholar] [CrossRef]
- Saglam, F.; Unlusoy, Y.S. Adaptive ride comfort and attitude control of vehicles equipped with active hydro-pneumatic suspension. Int. J. Veh. Des. 2016, 71, 31–51. [Google Scholar] [CrossRef]
- Sun, W.; Pan, H.; Gao, H. Filter-based adaptive vibration control for active vehicle suspensions with electrohydraulic actuators. IEEE Trans. Veh. Technol. 2015, 65, 4619–4626. [Google Scholar] [CrossRef]
- Mousavi, Y.; Alfi, A.; Kucukdemiral, I.B.; Fekih, A. Tube-based model reference adaptive control for vibration suppression of active suspension systems. IEEE/CAA J. Autom. Sin. 2022, 9, 728–731. [Google Scholar] [CrossRef]
- Al Aela, A.M.; Kenne, J.-P.; Angue Mintsa, H. A novel adaptive and nonlinear electrohydraulic active suspension control system with zero dynamic tire liftoff. Machines 2020, 8, 38. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, C.; Liu, Y.-J.; Wang, R.; Tong, S. Performance improvement of active suspension constrained system via neural network identification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7089–7098. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, H.; Ma, K.; Liu, Z.; Chen, C. Neural adaptive self-triggered control for uncertain nonlinear systems with input hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6206–6214. [Google Scholar] [CrossRef]
- Na, J.; Huang, Y.; Wu, X.; Su, S.-F.; Li, G. Adaptive finite-time fuzzy control of nonlinear active suspension systems with input delay. IEEE Trans. Cybern. 2019, 50, 2639–2650. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.H.; Li, S.; Chen, D.; Liao, L. Tracking control of redundant mobile manipulator: An RNN based metaheuristic approach. Neurocomputing 2020, 400, 272–284. [Google Scholar] [CrossRef]
- Khan, A.H.; Li, S.; Luo, X. Obstacle avoidance and tracking control of redundant robotic manipulator: An RNN-based metaheuristic approach. IEEE Trans. Ind. Inform. 2019, 16, 4670–4680. [Google Scholar] [CrossRef]
- Han, S.-Y.; Dong, J.-F.; Zhou, J.; Chen, Y.-H. Adaptive fuzzy PID control strategy for vehicle active suspension based on road evaluation. Electronics 2022, 11, 921. [Google Scholar] [CrossRef]
- Al Aela, A.M.; Kenne, J.-P.; Mintsa, H.A. Adaptive neural network and nonlinear electrohydraulic active suspension control system. J. Vib. Control. 2022, 28, 243–259. [Google Scholar] [CrossRef]
- Na, J.; Huang, Y.; Wu, X.; Liu, Y.-J.; Li, Y.; Li, G. Active suspension control of quarter-car system with experimental validation. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 4714–4726. [Google Scholar] [CrossRef]
- Joseph, S.B.; Dada, E.G.; Abidemi, A.; Oyewola, D.O.; Khammas, B.M. Metaheuristic algorithms for PID controller parameters tuning: Review, approaches and open problems. Heliyon 2022, 8, e09399. [Google Scholar] [CrossRef] [PubMed]
- Mozaffari, A.; Doosthoseini, A.; Azad, N.L. Predictive control of suspension systems through combining dynamic matrix and constrained variable structure controllers. J. Dyn. Syst. Meas. Control. 2016, 138, 121007. [Google Scholar] [CrossRef]
- Rodriguez-Guevara, D.; Favela-Contreras, A.; Beltran-Carbajal, F.; Sotelo, C.; Sotelo, D. An MPC-LQR-LPV controller with quadratic stability conditions for a nonlinear half-car active suspension system with electro-hydraulic actuators. Machines 2022, 10, 137. [Google Scholar] [CrossRef]
- Rodriguez-Guevara, D.; Favela-Contreras, A.; Beltran-Carbajal, F.; Sotelo, D.; Sotelo, C. Active suspension control using an MPC-LQR-LPV controller with attraction sets and quadratic stability conditions. Mathematics 2021, 9, 2533. [Google Scholar] [CrossRef]
- Chen, G.; Jiang, Y.; Tang, Y.; Xu, X. Revised adaptive active disturbance rejection sliding mode control strategy for vertical stability of active hydro-pneumatic suspension. ISA Trans. 2023, 132, 490–507. [Google Scholar] [CrossRef]
- Rath, J.J.; Defoort, M.; Sentouh, C.; Karimi, H.R.; Veluvolu, K.C. Output-constrained robust sliding mode based nonlinear active suspension control. IEEE Trans. Ind. Electron. 2020, 67, 10652–10662. [Google Scholar] [CrossRef]
- Hrovat, D. Survey of advanced suspension developments and related optimal control applications. Automatica 1997, 33, 1781–1817. [Google Scholar] [CrossRef]
- Esmaeili, J.S.; Akbari, A.; Karimi, H.R. Load-dependent LPV/H2 output-feedback control of semi-active suspension systems equipped with MR damper. Int. J. Veh. Des. 2015, 68, 119–140. [Google Scholar] [CrossRef]
- Esmaeili, J.S.; Akbari, A.; Mirzaei, M. LPV H2 control of semi-active suspensions. In Proceedings of the 2nd International Conference on Control, Instrumentation and Automation (ICCIA 2011), Shiraz, Iran, 27–29 December 2011. [Google Scholar]
- Jing, H.; Li, X.; Karimi, H. Output-feedback based H∞ control for active suspension systems with control delay. IEEE Trans. Ind. Electron. 2014, 61, 436–446. [Google Scholar]
- Gáspár, P.; Szaszi, I.; Bokor, J. Design of robust controllers for active vehicle suspension using the mixed µ synthesis. Veh. Syst. Dyn. 2003, 40, 193–228. [Google Scholar] [CrossRef]
- Jin, X.; Wang, J.; He, X.; Yan, Z.; Xu, L.; Wei, C.; Yin, G. Improving vibration performance of electric vehicles based on in-wheel motor-active suspension system via robust finite frequency control. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1631–1643. [Google Scholar] [CrossRef]
- Poussot-Vassal, C.; Sename, O.; Dugard, L.; Gaspar, P.; Szabo, Z.; Bokor, J. A new semi-active suspension control strategy through LPV technique. Control. Eng. Pract. 2008, 16, 1519–1534. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Gahinet, P.; Nemirovskii, A.; Laub, A.J.; Chilali, M. The LMI control toolbox. In Proceedings of the 1994 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; IEEE: Piscataway, NJ, USA, 1994. [Google Scholar]
- Scherer, C.; Weiland, S. Linear Matrix Inequalities in Control; Lecture Notes; Dutch Institute for Systems and Control: Delft, The Netherlands, 2000; Volume 3. [Google Scholar]
- Scherer, C.; Gahinet, P.; Chilali, M. Multiobjective output-feedback control via LMI optimization. IEEE Trans. Autom. Control. 1997, 42, 896–911. [Google Scholar] [CrossRef]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]







| Symbol | Description | Value |
|---|---|---|
| Sprung mass | 315 kg | |
| Unsprung mass | 37.5 kg | |
| Suspension stiffness | 29,500 N/m | |
| Tire stiffness | 210,000 N/m | |
| Suspension damping coefficient | 1500 N·s/m | |
| Suspension deflection limits | [−8, 6] cm |
| System | Force (kN) | |||
|---|---|---|---|---|
| Passive | 0.203 | 0.103 | 0 | |
| controller | 0.097 | 0.091 | 1.51 | |
| controller | 0.138 | 0.073 | 1.20 | |
| ANFIS | 0.077 | 0.97 | 1.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmaeili, J.S.; Akbari, A.; Farnam, A.; Azad, N.L.; Crevecoeur, G.
Adaptive Neuro-Fuzzy Control of Active Vehicle Suspension Based on
Esmaeili JS, Akbari A, Farnam A, Azad NL, Crevecoeur G.
Adaptive Neuro-Fuzzy Control of Active Vehicle Suspension Based on
Esmaeili, Jaffar Seyyed, Ahmad Akbari, Arash Farnam, Nasser Lashgarian Azad, and Guillaume Crevecoeur.
2023. "Adaptive Neuro-Fuzzy Control of Active Vehicle Suspension Based on
Esmaeili, J. S., Akbari, A., Farnam, A., Azad, N. L., & Crevecoeur, G.
(2023). Adaptive Neuro-Fuzzy Control of Active Vehicle Suspension Based on






