Nonlinear Dynamics and Vibration Localization of Shrouded Blisk with Contact and Friction Effects
Abstract
1. Introduction
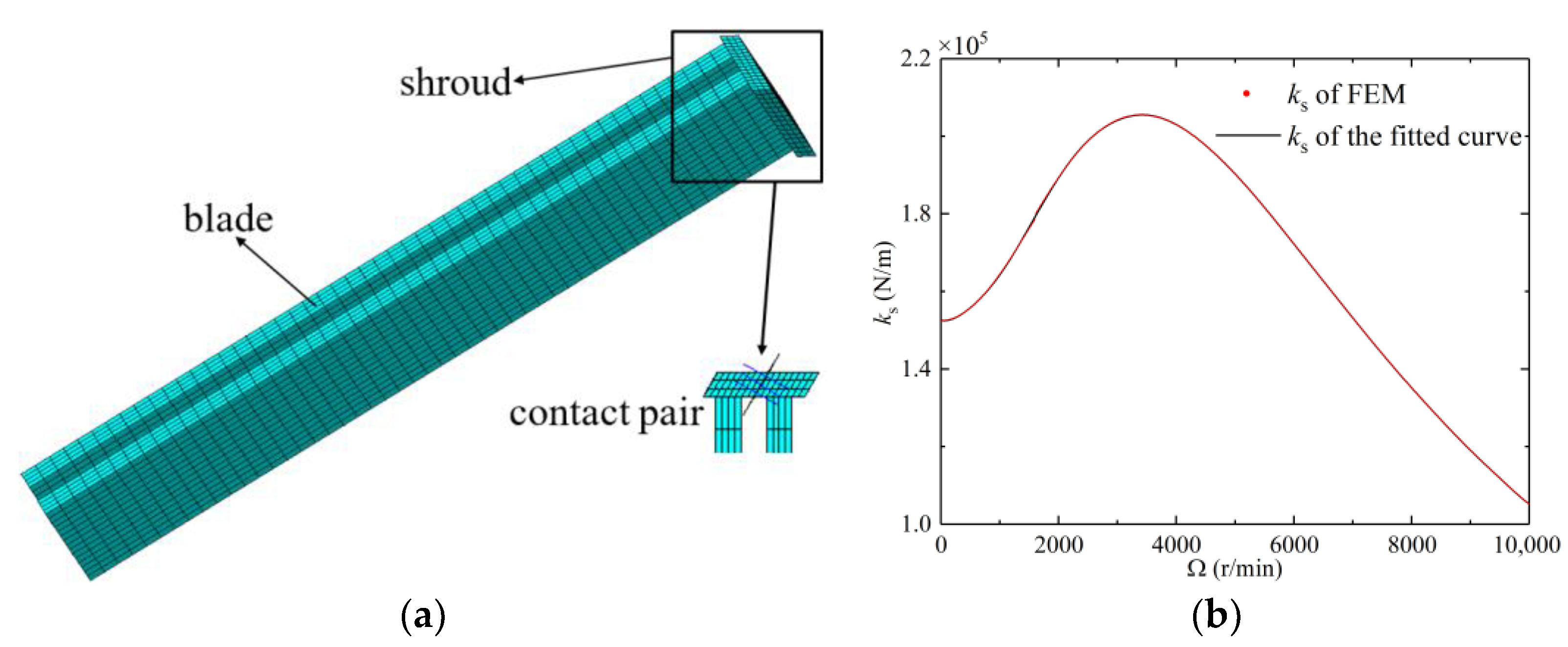
2. Dynamics Modelling of Shrouded Blisk
- The torsion of the blade body in the spanwise direction is generally small in view of turbine design for short blades. When short blades are concerned, the change in the circumferential velocity in the blade’s spanwise direction can be assumed small. Consequently, the directions of the relative velocity of the fluid to the blade vary limitedly in the same direction, and thus the torsion angle is idealized to be small for short blades.
- The bending rigidity of the blade is generally large compared with a long blade, and the modal couplings between in-plane and out-of-plane motions due to geometrically nonlinearity is weak enough to be ignored.
- When the installation angle is small, the aerodynamic force normal to the blade surface stands mainly in the plane of blisk rotation [20], meaning the in-plane component of the force is much larger than its out-of-plane counterpart. Under the same assumption of small installation angle, the principal axes of the blade cross-section are arranged in such a way that the bending rigidity in the out-of-plane direction overwhelms that in the in-plane directions. Hence, it is reasonable not to consider the out-of-plane motions in the present study owing to the small load and large bending rigidity in the out-of-plane.
2.1. Dynamic Modeling
2.2. Governing Equations
3. Nonlinear Dynamics and Vibration Localization of Shrouded Blisk
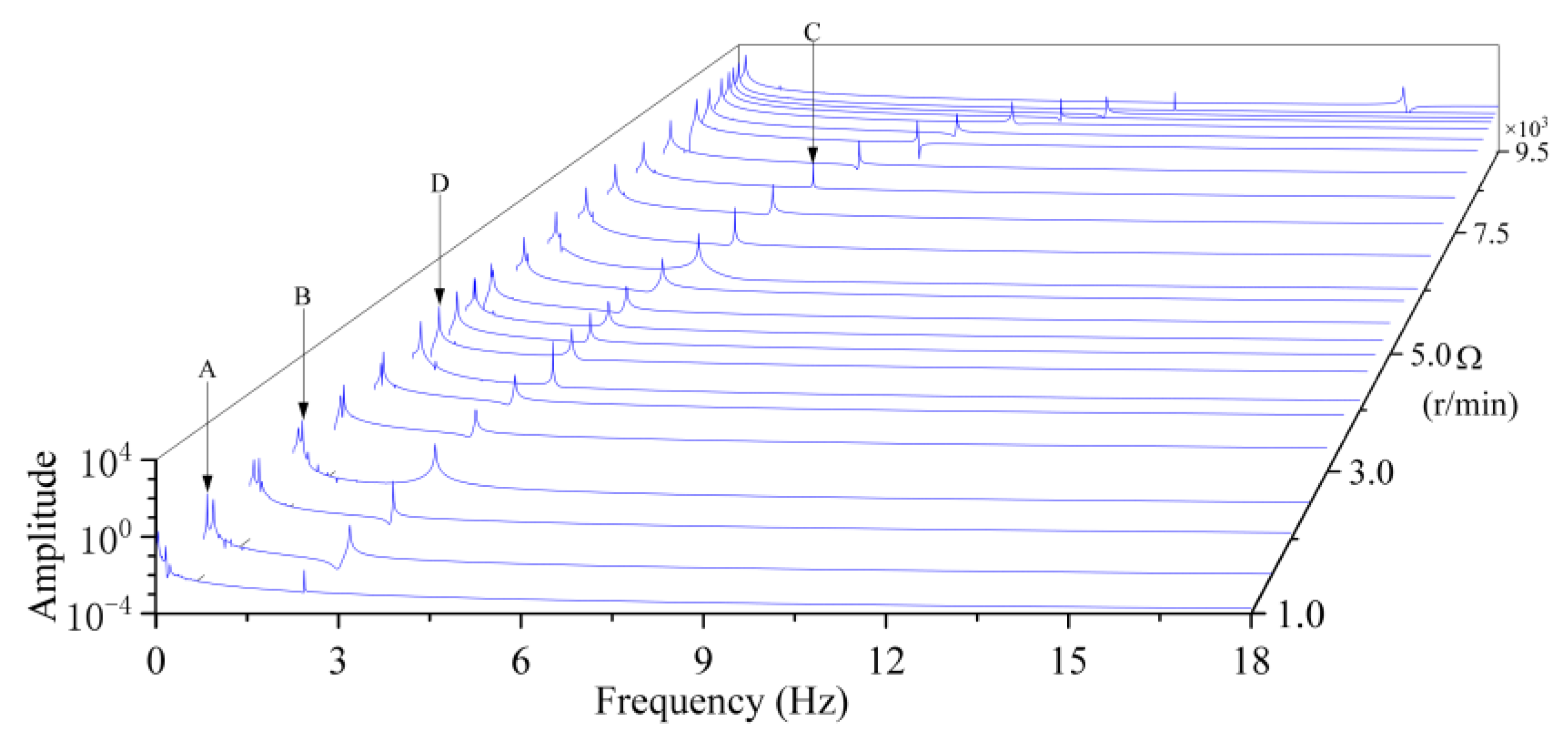
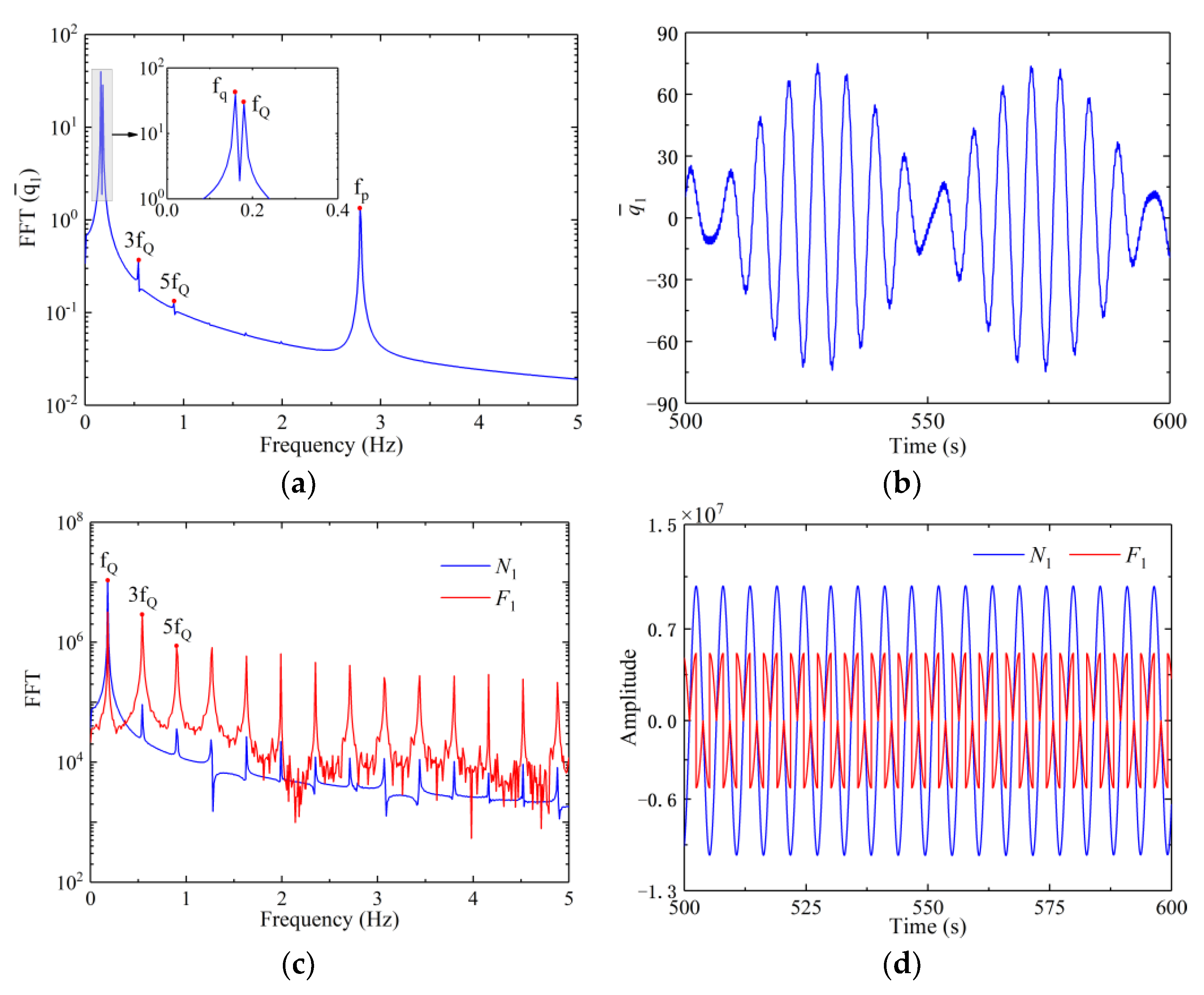
3.1. Steady-State Response, Primary Resonance and Beat
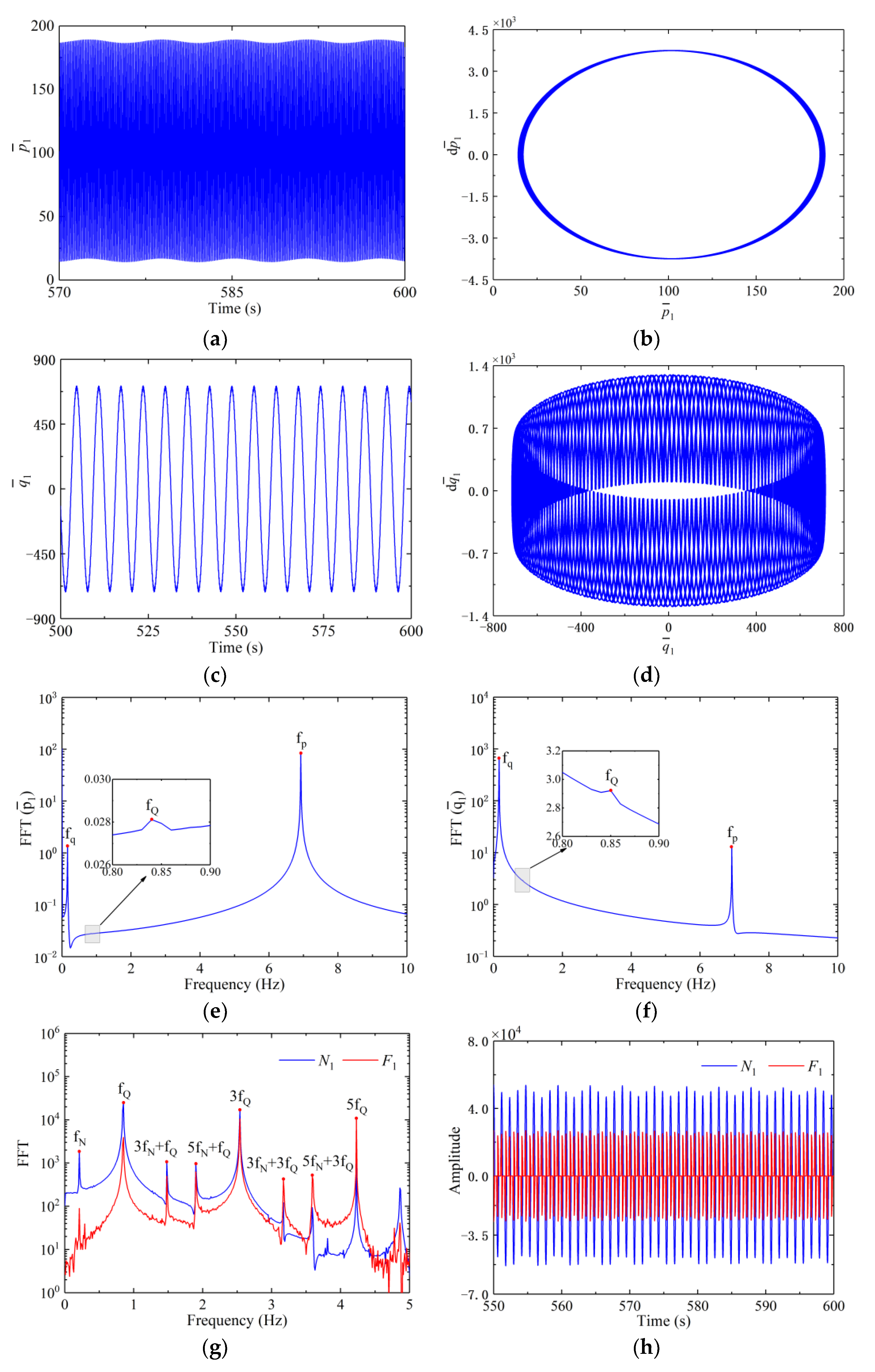
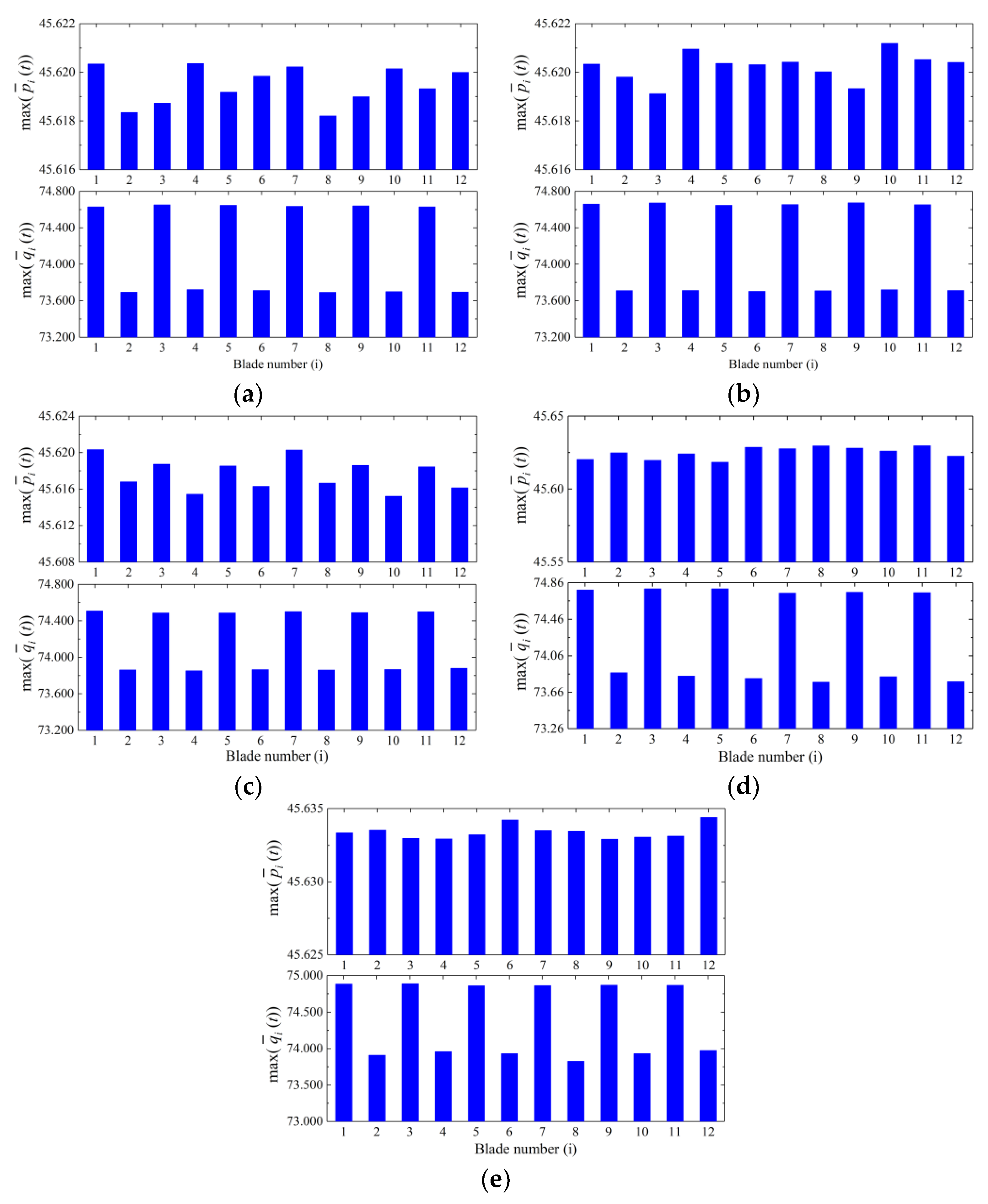
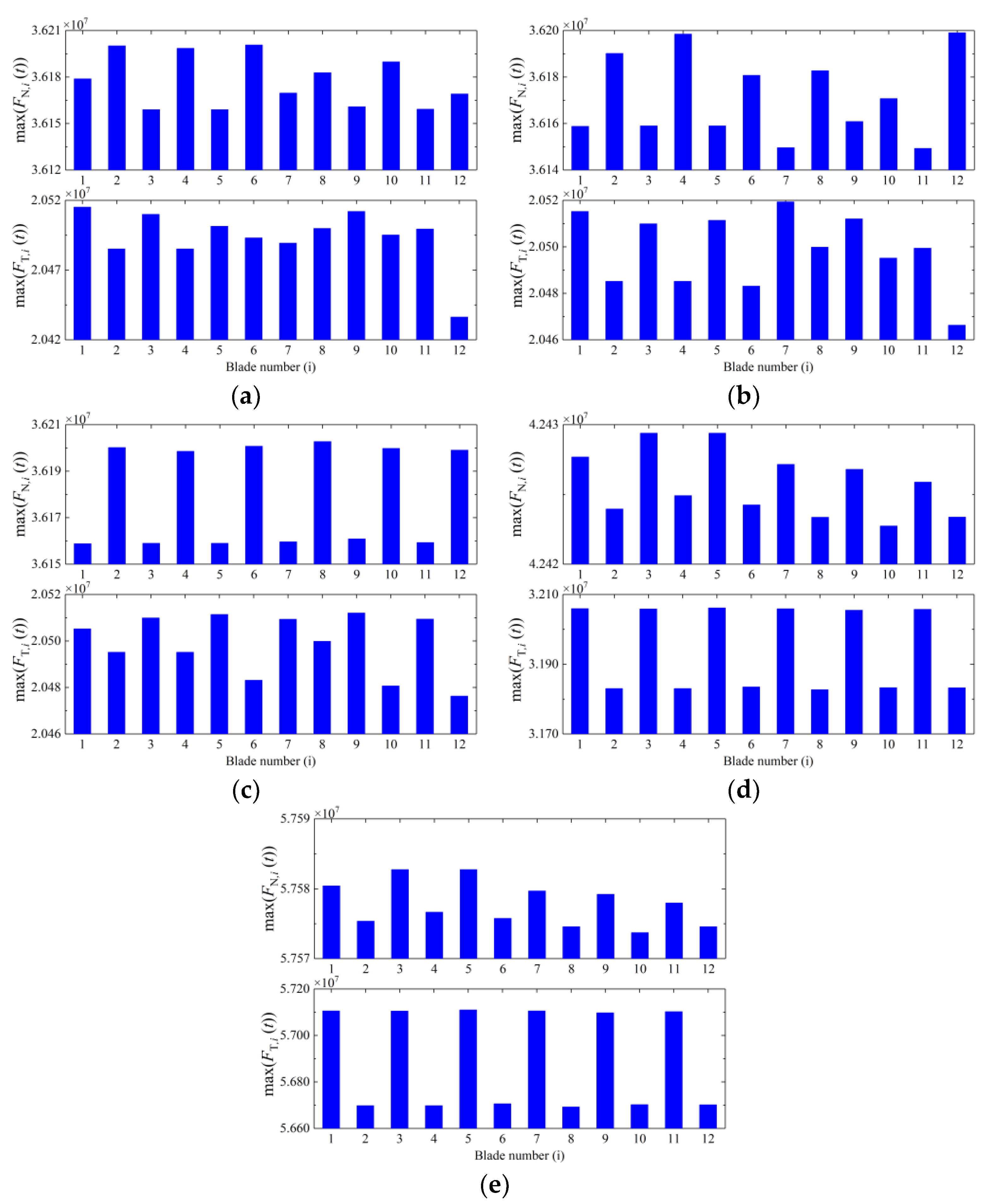
3.2. Localization of Vibration of Blades
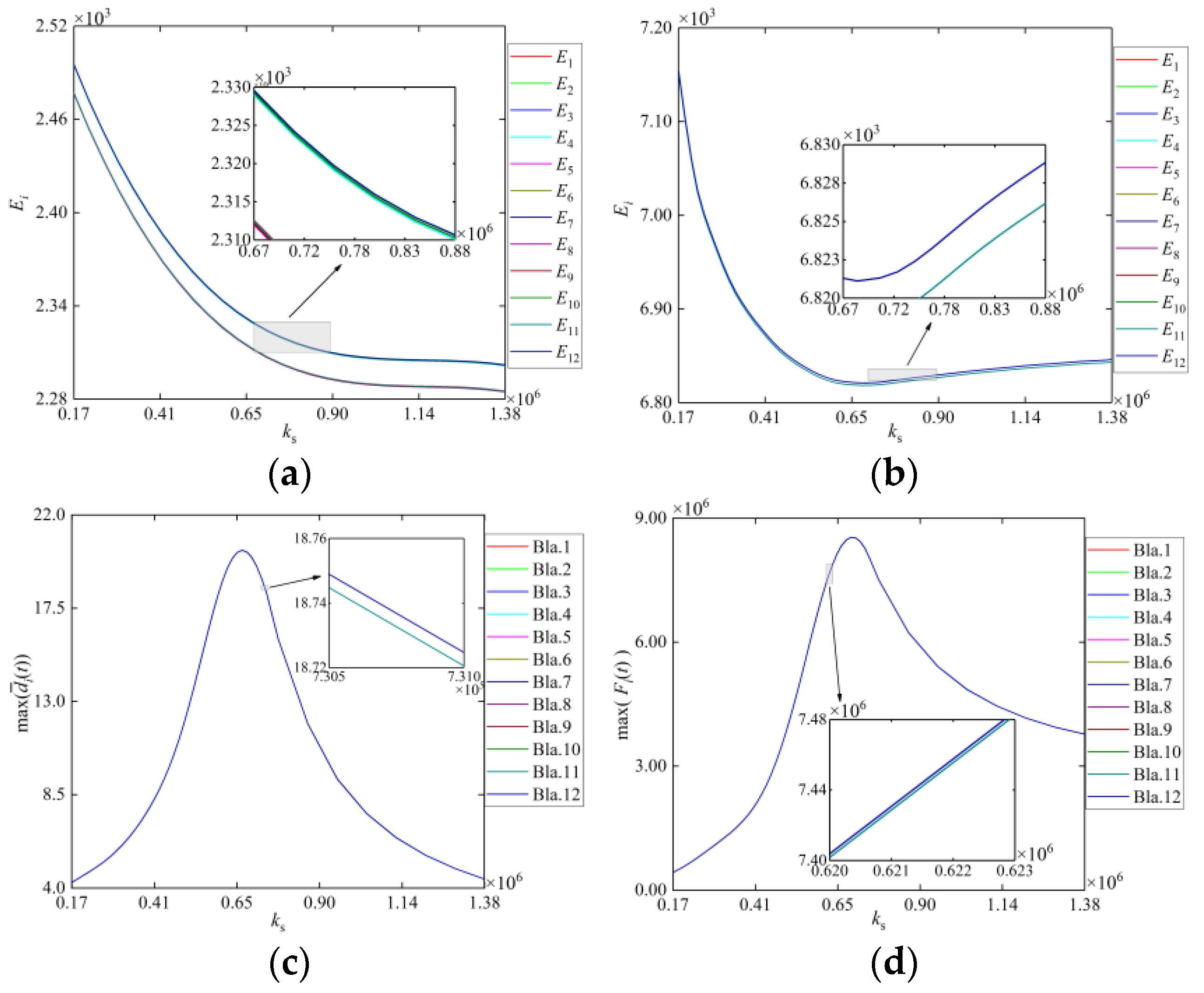
3.3. Effect of Coupling Stiffness on the Localization of Vibration
3.4. Power of Blade Vibration under Localization of Vibration
4. Conclusions
- (1)
- With the increase of rotation speed, the primary resonance, beat and quasi-periodic vibration appear successively due to the contact and friction between shrouds.
- (2)
- The localization of vibration occurs in tuned shrouded blisks only when the beat exists, i.e., frequency of free vibration slightly differs from the frequency of the forced vibration caused by the contact and friction of shrouds. Further, the level of such localization increases as the blade-disk coupling becomes strong.
- (3)
- The power of the blade motion drops consistently with the contact stiffness of the shrouds in the localization of vibration, which is different from the non-localization case.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Nomenclature of the Most Important Quantities
| Symbol | Parameter Names | Symbol | Parameter Names |
|---|---|---|---|
| , | Viscous damping coefficients in the spanwise and flapwise directions | Aerodynamic force | |
| , | Viscous damping coefficients of the disk | ||
| Normal distance between the shrouds | , | Spanwise and flapwise displacements of the blade | |
| Radius of the disk | Relative velocity aligning with the contact surfaces of the i-th and (i-1)-th shrouds | ||
| EA, EI | Tensile and bending stiffness of the blade | , | Instantaneous center of disk in the X-, Y-directions |
| Friction force of the i-th shroud | Tilt angle of shrouds | ||
| Normal contact stiffness between adjacent shrouds | Tuning parameter | ||
| , | Stiffness coefficients of the shaft to the disk | Gap between adjacent shrouds | |
| L | Length of the blade | Number of inlet vanes in the upstream of the blades | |
| mass of the disk | , | Coefficients of minimum kinetic friction and maximum static friction | |
| mass of the shrouds | Linear mass density of the blades | ||
| Normal force of the i-th shroud | Rotation speed | ||
| n | Total number of blades | Variate after nondimensionalize | |
| , | The j-th modal coordinates of the i-th blade |
Appendix B. Coefficients in Governing Equations
Appendix C. Friction Force with Different Contact States
- There is no contact between adjacent shrouds. In this case, one has , and the value of the friction force on the shroud interface is zero.
- Contact exists between the i-th and (i-1)-th shrouds. In this case, one has , and three scenarios can happen as follows.
- (a)
- If the i-th shroud is slipping relatively to the (i-1)-th shroud, . The sliding friction of the i-th blade is expressed as
- (b)
- If the i-th shroud is sticking relatively to the (i-1)-th shroud, one has , , , . In the flapwise direction the equation becomesThe flapwise equation of the (i-1)-th blade is expressed asFurther, one hasThe static friction forces is written as
- (c)
- If but , the friction force reverses its direction. At this moment, the i-th shroud is slipping relatively to the (i-1)-th shroud.
- There is contact between consecutive shrouds. It is assumed that the j-th shroud is connected to its adjacent shrouds, and thus . Two different statuses are differentiated in this situation.
- (a)
- If both the j-th shrouds are sticking relatively to adjacent shrouds, , , , . In flapwise direction of the -th shroud, the equation of motion readsThe flapwise equation of the l-th blade readsThe flapwise equation of the (i-1)-th blade readsBased on Equations (A17)–(A19). The sticking friction force of the -th blade is derived, asSimilarly, the static friction force of the r-th blade is
- (b)
- If the m-th shroud is slipping relatively to the (m-1)-th shroud whole other shrouds are sticking relatively to adjacent shrouds, . Different from Equations (A20) and (A21), the sliding friction force of the m-th blade becomes
Appendix D. Process of the Dichotomy Method
Appendix E. Parameters of the Finite Element Model
| Parameter Names | Value |
|---|---|
| The length and width of the blade cross section | 0.01, 0.15 m |
| The length, width and thickness of the shroud | 0.01, 0.15, 0.02 m |
| Density | 4500 kg/m3 |
| Young’s modulus | 116 GPa |
| Poisson’s ratio | 0.3 |
References
- Carter, T.J. Common failures in gas turbine blades. Eng. Fail. Anal. 2005, 12, 237–247. [Google Scholar] [CrossRef]
- Cigeroglu, E. Development of Microslip Friction Models and Forced Response Prediction Methods for Frictionally Constrained Turbine Blades. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2007. [Google Scholar]
- Chu, S.; Cao, D.; Sun, S.; Pan, J.; Wang, L. Impact vibration characteristics of a shrouded blade with asymmetric gaps under wake flow excitations. Nonlinear Dyn. 2013, 72, 539–554. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Chen, D.Z.; Yang, C.H. Influence on Coupling Vibration of Rotor System with Grouped Blades due to Mistuned Lacing Wire. Appl. Mech. Mater. 2011, 101–102, 1119–1125. [Google Scholar] [CrossRef]
- Ma, H.; Xie, F.; Nai, H.; Wen, B. Vibration characteristics analysis of rotating shrouded blades with impacts. J. Sound Vib. 2016, 378, 92–108. [Google Scholar] [CrossRef]
- Chatterjee, A.; Kotambkar, M.S. Modal characteristics of turbine blade packets under lacing wire damage induced mistuning. J. Sound Vib. 2015, 343, 49–70. [Google Scholar] [CrossRef]
- Petrov, E.P.; Sanliturk, K.Y.; Ewins, D.J. A New Method for Dynamic Analysis of Mistuned Bladed Disks Based on the Exact Relationship Between Tuned and Mistuned Systems. J. Eng. Gas Turbines Power 2002, 124, 586–597. [Google Scholar] [CrossRef]
- Petrov, E.P. Method for direct parametric analysis of nonlinear forced response of bladed disks with friction contact interfaces. J. Turbomach. 2004, 126, 654–662. [Google Scholar] [CrossRef]
- Karimi, A.H.; Shadmani, M. Nonlinear vibration analysis of a beam subjected to a random axial force. Arch. Appl. Mech. 2019, 89, 385–402. [Google Scholar] [CrossRef]
- Iwan, W.D. On a Class of Models for the Yielding Behavior of Continuous and Composite Systems. J. Appl. Mech. 1967, 34, 612–617. [Google Scholar] [CrossRef]
- Griffin, J.H. Friction Damping of Resonant Stresses in Gas Turbine Engine Airfoils. J. Eng. Power 1980, 102, 329–333. [Google Scholar] [CrossRef]
- Menq, C.H.; Bielak, J.; Griffin, J.H. The influence of microslip on vibratory response, part I: A new microslip model. J. Sound Vib. 1986, 107, 279–293. [Google Scholar] [CrossRef]
- Cigeroglu, E.; An, N.; Menq, C.H. A microslip friction model with normal load variation induced by normal motion. Nonlinear Dyn. 2007, 50, 609–626. [Google Scholar] [CrossRef]
- Yang, B.D.; Menq, C.H. Characterization of 3D contact kinematics and prediction of resonant response of structures having 3D frictional constraint. J. Sound Vib. 1998, 217, 909–925. [Google Scholar] [CrossRef]
- Peterka, F.; Vacík, J. Transition to chaotic motion in mechanical systems with impacts. J. Sound Vib. 1992, 154, 95–115. [Google Scholar] [CrossRef]
- Peterka, F. Bifurcations and transition phenomena in an impact oscillator. Chaos Solitons Fractals 1996, 7, 1635–1647. [Google Scholar] [CrossRef]
- Brach, R.M. Mechanical Impact Dynamics: Rigid Body Collisions; John Wiley & Sons: New York, NY, USA, 1991; pp. 248–249. ISBN 0471508454. [Google Scholar]
- Liu, Y.; Shangguan, B.; Xu, Z. A friction contact stiffness model of fractal geometry in forced response analysis of a shrouded blade. Nonlinear Dyn. 2012, 70, 2247–2257. [Google Scholar] [CrossRef]
- Li, C.; Liu, X.; Tang, Q.; Chen, Z. Modeling and nonlinear dynamics analysis of a rotating beam with dry friction support boundary conditions. J. Sound Vib. 2021, 498, 115978. [Google Scholar] [CrossRef]
- He, B.; Ouyang, H.; He, S.; Mei, Y. Dynamic analysis of integrally shrouded group blades with rubbing and impact. Nonlinear Dyn. 2018, 92, 2159–2175. [Google Scholar] [CrossRef]
- Mashayekhi, F.; Nobari, A.S.; Zucca, S. Hybrid reduction of mistuned bladed disks for nonlinear forced response analysis with dry friction. Int. J. Non-Linear Mech. 2019, 116, 73–84. [Google Scholar] [CrossRef]
- She, H.; Li, C.; Tang, Q.; Wen, B. Veering and merging analysis of nonlinear resonance frequencies of an assembly bladed disk system. J. Sound Vib. 2021, 493, 115818. [Google Scholar] [CrossRef]
- Wei, S.T.; Pierre, C. Localization Phenomena in Mistuned Assemblies with Cyclic Symmetry Part II: Forced Vibrations. J. Vib. Acoust. 1988, 110, 439–449. [Google Scholar] [CrossRef]
- Fang, X.; Tang, J.; Jordan, E.; Murphy, K.D. Crack induced vibration localization in simplified bladed-disk structures. J. Sound Vib. 2006, 291, 395–418. [Google Scholar] [CrossRef]
- Picou, A.; Capiez-Lernout, E.; Soize, C.; Mbaye, M. Robust dynamic analysis of detuned-mistuned rotating bladed disks with geometric nonlinearities. Comput. Mech. 2020, 65, 711–730. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, D.; Xie, Y. Vibration analysis of mistuned damped blades with nonlinear friction and contact. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1505–1521. [Google Scholar] [CrossRef]
- Pesaresi, L.; Armand, J.; Schwingshackl, C.W.; Salles, L.; Wong, C. An advanced underplatform damper modelling approach based on a microslip contact model. J. Sound Vib. 2018, 436, 327–340. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Yang, Z.; She, H. A new method of micro-slip contact normal pressure modeling and its application in the dynamic analysis of the dovetail–tenon–mortise jointed blades. Mech. Based Des. Struct. Mach. 2022. [Google Scholar] [CrossRef]
- Joannin, C.; Chouvion, B.; Thouverez, F.; Mbaye, J.P. Nonlinear Modal Analysis of Mistuned Periodic Structures Subjected to Dry Friction. J. Eng. Gas Turbines Power 2016, 138, 072504. [Google Scholar] [CrossRef]
- Thouverez, F.; Grolet, A.; Gibert, C. Non-linear periodic solutions of bladed disks. In Proceedings of the Eurodyn 2014: Ix International Conference on Structural Dynamics, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- Mehrdad Pourkiaee, S.; Zucca, S. A Reduced Order Model for Nonlinear Dynamics of Mistuned Bladed Disks With Shroud Friction Contacts. J. Eng. Gas Turbines Power 2019, 141, 011031. [Google Scholar] [CrossRef]
- She, H.; Li, C.; Tang, Q.; Ma, H.; Wen, B. Computation and investigation of mode characteristics in nonlinear system with tuned/mistuned contact interface. Front. Mech. Eng. 2020, 15, 133–150. [Google Scholar] [CrossRef]
- Vakakis, A.F.; Manevitch, L.I.; Mikhlin, Y.V.; Pilipchuk, V.N.; Zevin, A.A. Normal Modes and Localization in Nonlinear Systems; John Wiley & Sons: New York, NY, USA, 1996; pp. 285–304. ISBN 0-471-13319-1. [Google Scholar]
- Vakakis, A.F.; Cetinkaya, C. Mode localization in a class of multidegree-of-freedom nonlinear systems with cyclic system. SIAM J. Appl. Math. 1993, 53, 265–282. [Google Scholar] [CrossRef][Green Version]
- Grolet, A.; Thouverez, F. Vibration analysis of a nonlinear system with cyclic symmetry. J. Eng. Gas Turbines Power 2010, 133, 022502. [Google Scholar] [CrossRef]
- Fontanela, F.; Grolet, A.; Salles, L.; Hoffmann, N. Computation of quasi-periodic localised vibrations in nonlinear cyclic and symmetric structures using harmonic balance methods. J. Sound Vib. 2019, 438, 54–65. [Google Scholar] [CrossRef]
- Berger, E. Friction modeling for dynamic system simulation. Appl. Mech. Rev. 2002, 55, 535–577. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; McGraw-Hill Companies: New York, NY, USA, 2001; pp. 399–401. ISBN 0-07-118174-1. [Google Scholar]
- Shadmani, M.; Tikani, R.; Ziaei-Rad, S. On using a distributed-parameter model for modal analysis of a mistuned bladed disk rotor and extracting the statistical properties of its in-plane natural frequencies. J. Sound Vib. 2019, 438, 324–343. [Google Scholar] [CrossRef]




| Notation | Value | Notation | Value |
|---|---|---|---|
| 1·N·s·m−1 | 5 N·s·m−1 | ||
| 0.5 m | EI | 1.45 × 103 N·m2 | |
| EA | 1.74 × 108 N | 1.0 × 107 N·m−1 | |
| L | 0.5 m | 14.04 kg | |
| 0.135 kg | 50 N | ||
| rad | 5 s·m−1 | ||
| 2.0 × 10−5 m | 1 | ||
| 0.5 | 0.3 | ||
| 6.75 kg·m−1 | Ω | 6000 r·min−1 |
| General case, r/min | 0.0 | 0.0 |
| The beat case, r/min | −3.902 × 10−5 | −1.197 × 10−4 |
| Contact- and friction free, r/min | 0.0 | 0.0 |
| 0.01 | −5.024 × 10−5 | 1.190 × 10−5 |
| 0.1 | 2.003 × 10−5 | −3.704 × 10−5 |
| 1 | −3.902 × 10−5 | −1.197 × 10−5 |
| 10 | 2.429 × 10−5 | 0.0017 |
| 100 | 6.471 × 10−5 | 0.0063 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, G.; Wang, Y. Nonlinear Dynamics and Vibration Localization of Shrouded Blisk with Contact and Friction Effects. Machines 2023, 11, 238. https://doi.org/10.3390/machines11020238
Yuan G, Wang Y. Nonlinear Dynamics and Vibration Localization of Shrouded Blisk with Contact and Friction Effects. Machines. 2023; 11(2):238. https://doi.org/10.3390/machines11020238
Chicago/Turabian StyleYuan, Gaofei, and Yuefang Wang. 2023. "Nonlinear Dynamics and Vibration Localization of Shrouded Blisk with Contact and Friction Effects" Machines 11, no. 2: 238. https://doi.org/10.3390/machines11020238
APA StyleYuan, G., & Wang, Y. (2023). Nonlinear Dynamics and Vibration Localization of Shrouded Blisk with Contact and Friction Effects. Machines, 11(2), 238. https://doi.org/10.3390/machines11020238






