Online O-Ring Stress Prediction and Bolt Tightening Sequence Optimization Method for Solid Rocket Motor Assembly
Abstract
1. Introduction
2. Elastic–Plastic Model of Rubber O-Ring
3. Assembly Simulation of the O-Ring
3.1. Assembly Condition Parameters
3.2. Selection of the Parameter Space
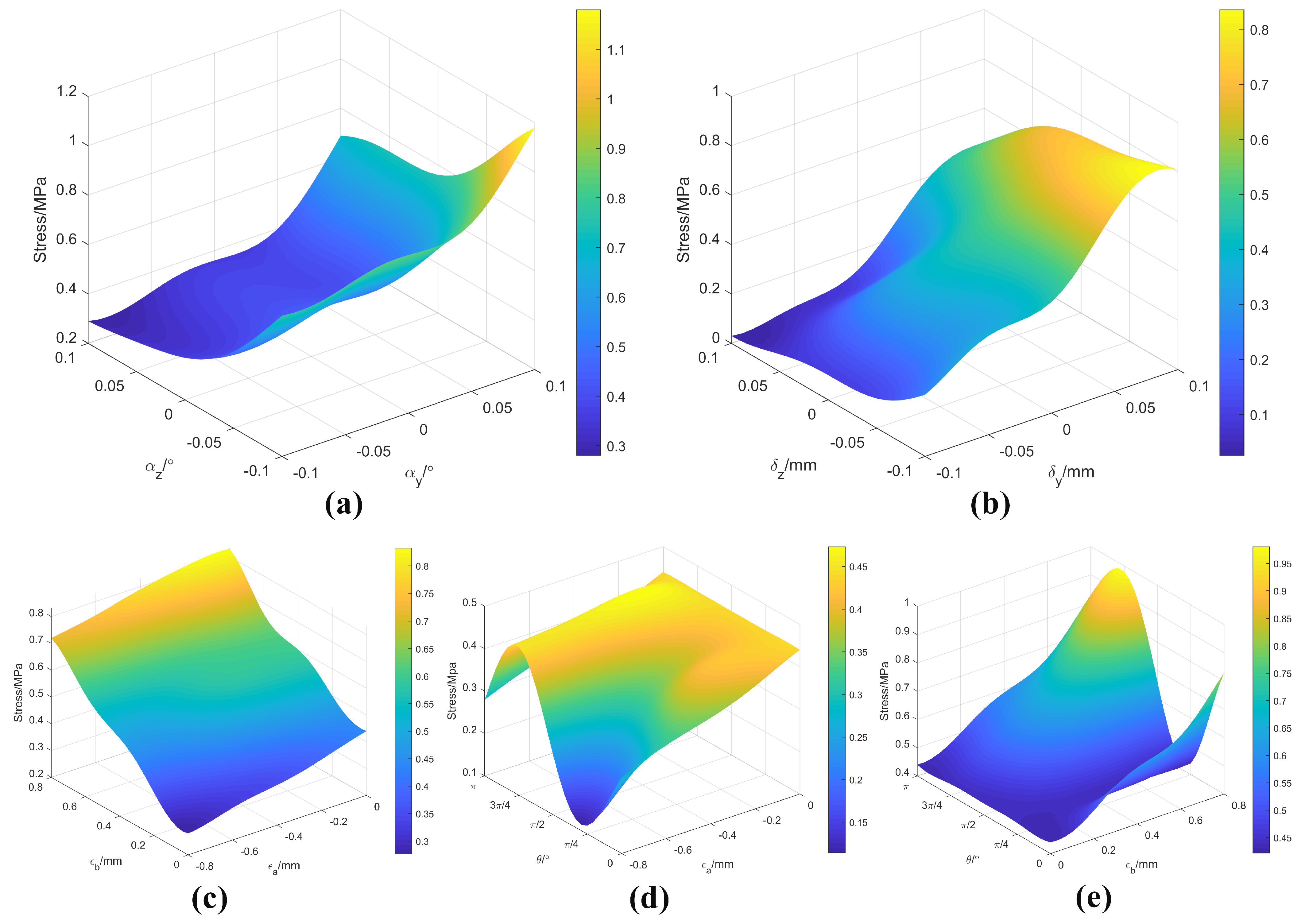
3.3. Finite Element Analysis of the O-Ring
4. Data Set Expansion Technology
5. Kriging-Based Stress Prediction Model
5.1. Kriging Prediction Modeling
5.2. Optimization of the GEK Model
6. Prediction Process
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SRM | Solid rocket motor |
| FEM | Finite element method |
| FEA | Finite element analysis |
| LHS | Latin hypercube sampling |
| GAN | Generative adversarial networks |
| CTGAN | Conditional tabular generative adversarial networks |
| RSM | Response surface method |
| GEK | Gradient-enhanced Kriging |
| MSE | Mean squared error |
| DOF | Degree of freedom |
| GA | Genetic algorithm |
References
- Dalal, S.R.; Fowlkes, E.B.; Hoadley, B. Risk analysis of the space shuttle: Pre-Challenger prediction of failure. J. Am. Stat. Assoc. 1989, 84, 945–957. [Google Scholar] [CrossRef]
- Sivakumar, V.; Palaninathan, R. FE analysis of contact pressure prediction on O-rings used in solid rocket booster segment joints. Int. J. Sci. Eng. Appl. 2012, 1, 8–16. [Google Scholar] [CrossRef]
- Jingdong, L.; Lipei, H. Research on recognition algorithm of seal fitting point based on compressibility control. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 6259–6264. [Google Scholar]
- Shao, Y.; Kang, R. A life prediction method for O-ring static seal structure based on Physics of Failure. In Proceedings of the 2014 Prognostics and System Health Management Conference (PHM-2014 Hunan), Zhangiiajie, China, 24–27 August 2014; pp. 16–21. [Google Scholar]
- Sun, L.; Gu, X.; Feng, L.; Di, Y. Reliability analysis of rubber O-rings used in the rockets. In Proceedings of the 2016 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bali, Indonesia, 4–7 December 2016; pp. 1392–1396. [Google Scholar]
- Zine, A.; Benseddiq, N.; Abdelaziz, M.N. Rubber fatigue life under multiaxial loading: Numerical and experimental investigations. Int. J. Fatigue 2011, 33, 1360–1368. [Google Scholar] [CrossRef]
- Choi, J.; Quagliato, L.; Lee, S.; Shin, J.; Kim, N. Multiaxial fatigue life prediction of polychloroprene rubber (CR) reinforced with tungsten nano-particles based on semi-empirical and machine learning models. Int. J. Fatigue 2021, 145, 106136. [Google Scholar] [CrossRef]
- He, G.; Zhao, Y.; Yan, C. Application of tabular data synthesis using generative adversarial networks on machine learning-based multiaxial fatigue life prediction. Int. J. Press. Vessel. Pip. 2022, 199, 104779. [Google Scholar] [CrossRef]
- Bárkányi, Á.; Chovan, T.; Nemeth, S.; Abonyi, J. Modelling for digital twins—potential role of surrogate models. Processes 2021, 9, 476. [Google Scholar] [CrossRef]
- Cao, R.; Sun, Z.; Wang, J.; Guo, F. A single-loop reliability analysis strategy for time-dependent problems with small failure probability. Reliab. Eng. Syst. Saf. 2022, 219, 108230. [Google Scholar] [CrossRef]
- Zhu, Q.; Han, Q.; Liu, J.; Yu, C. High-Accuracy Finite Element Model Updating a Framed Structure Based on Response Surface Method and Partition Modification. Aerospace 2023, 10, 79. [Google Scholar] [CrossRef]
- Dong, K.; Sun, Z. Application of Kriging Model to Gear Wear Calculation under Mixed Elastohydrodynamic Lubrication. Machines 2022, 10, 490. [Google Scholar] [CrossRef]
- Kim, B.; Lee, S.B.; Lee, J.; Cho, S.; Park, H.; Yeom, S.; Park, S.H. A comparison among Neo-Hookean model, Mooney-Rivlin model, and Ogden model for chloroprene rubber. Int. J. Precis. Eng. Manuf. 2012, 13, 759–764. [Google Scholar] [CrossRef]
- Bibel, G.D.; Ezell, R.M. An Improved Flange Bolt-Up Procedure Using Experimentally Determined Elastic Interaction Coefficients. J. Press. Vessel Technol. 1992, 114, 439–443. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wang, J.; Zhang, J.; Zhu, X.; Xu, Z. Research on Process Planning Method of Aerospace Engine Bolt Tightening Based on Digital Twin. Machines 2022, 10, 1048. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Xu, L.; Veeramachaneni, K. Synthesizing tabular data using generative adversarial networks. arXiv 2018, arXiv:1811.11264. [Google Scholar]
- Xu, L.; Skoularidou, M.; Cuesta-Infante, A.; Veeramachaneni, K. Modeling tabular data using conditional gan. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. South. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Ulaganathan, S.; Couckuyt, I.; Dhaene, T.; Degroote, J.; Laermans, E. High dimensional Kriging metamodelling utilising gradient information. Appl. Math. Model. 2016, 40, 5256–5270. [Google Scholar] [CrossRef]
- Han, Z.H.; Görtz, S.; Zimmermann, R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function. Aerosp. Sci. Technol. 2013, 25, 177–189. [Google Scholar] [CrossRef]
- Chung, H.S.; Alonso, J. Design of a low-boom supersonic business jet using cokriging approximation models. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002; p. 5598. [Google Scholar]
- Chung, H.S.; Alonso, J. Using gradients to construct cokriging approximation models for high-dimensional design optimization problems. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 317. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
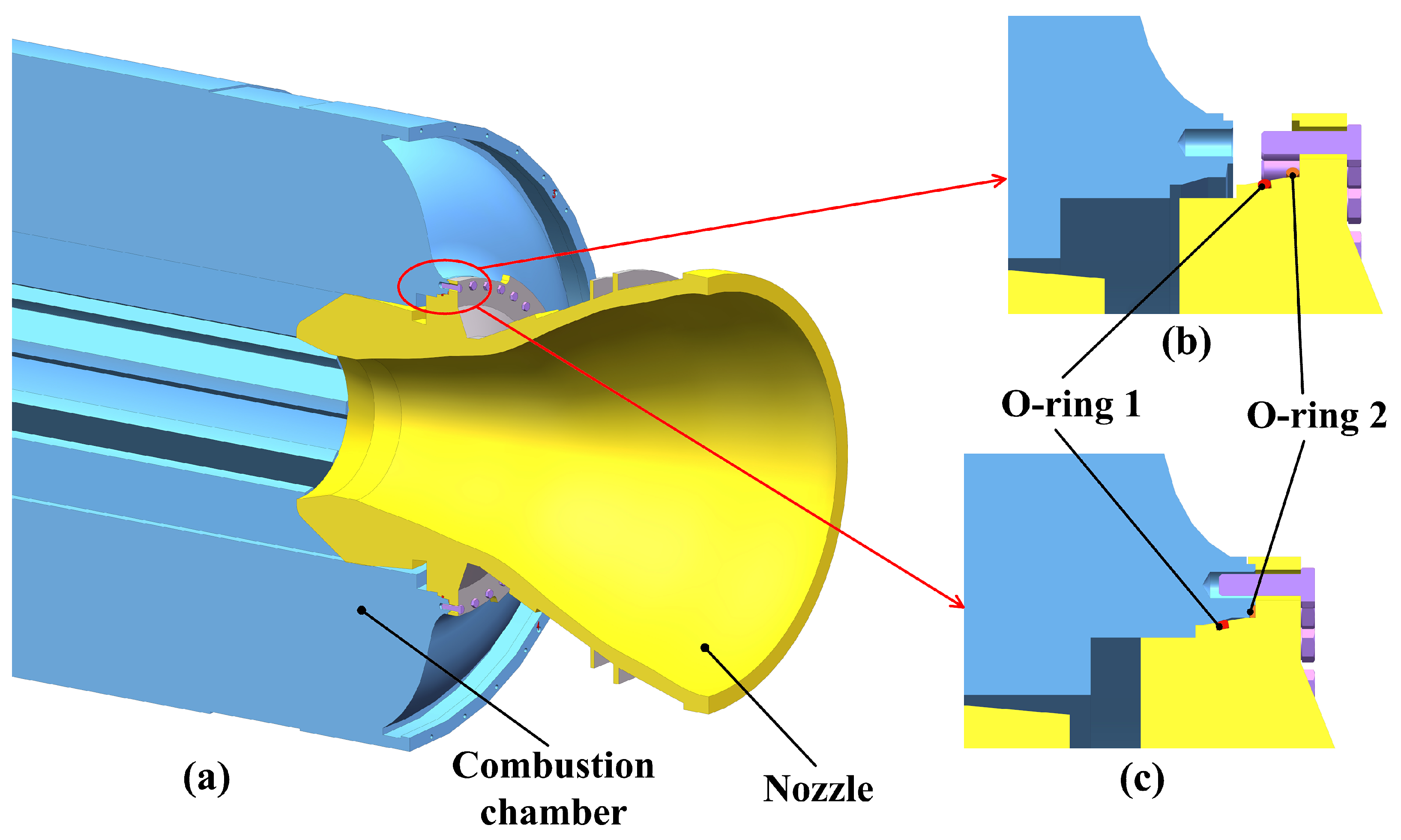
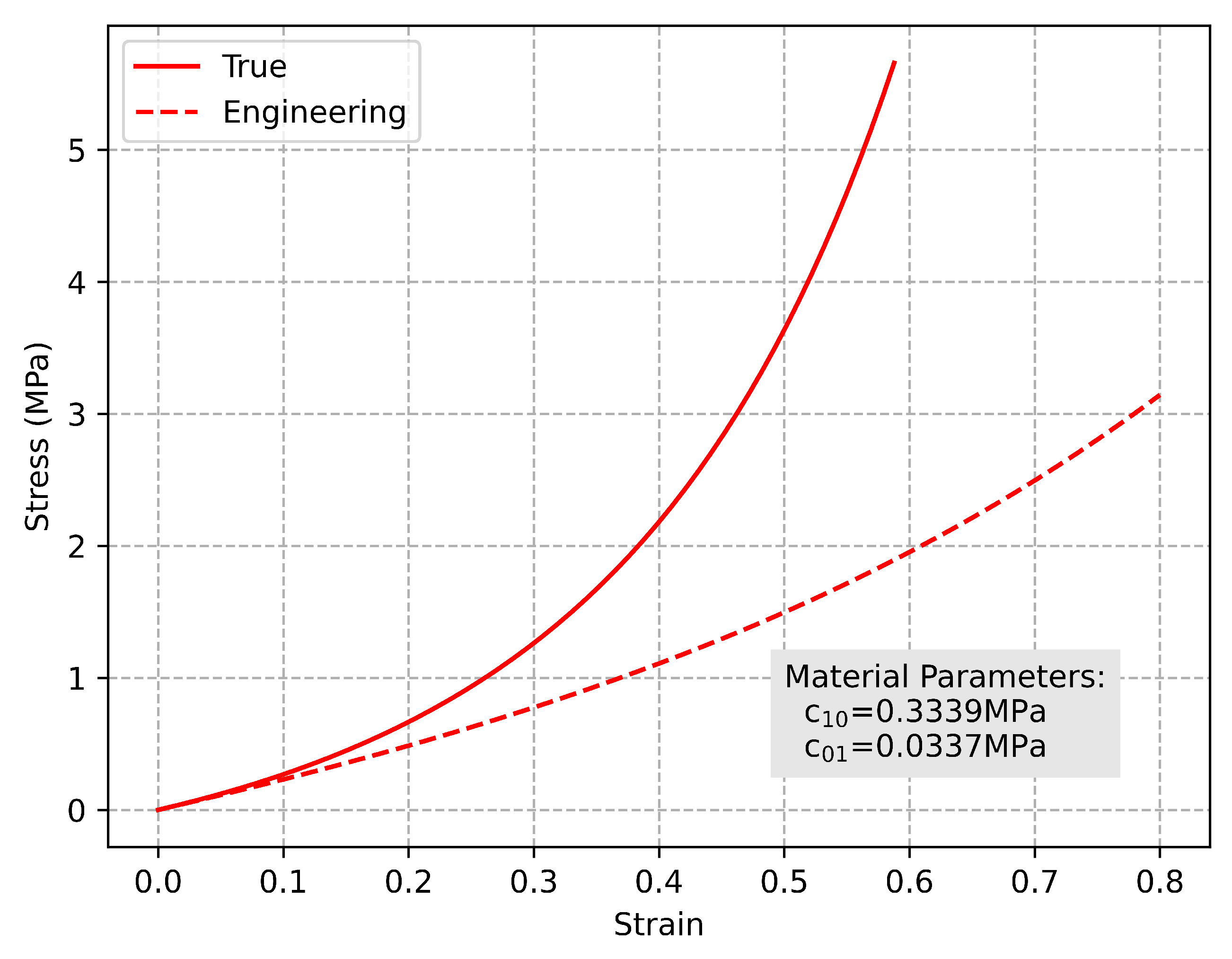
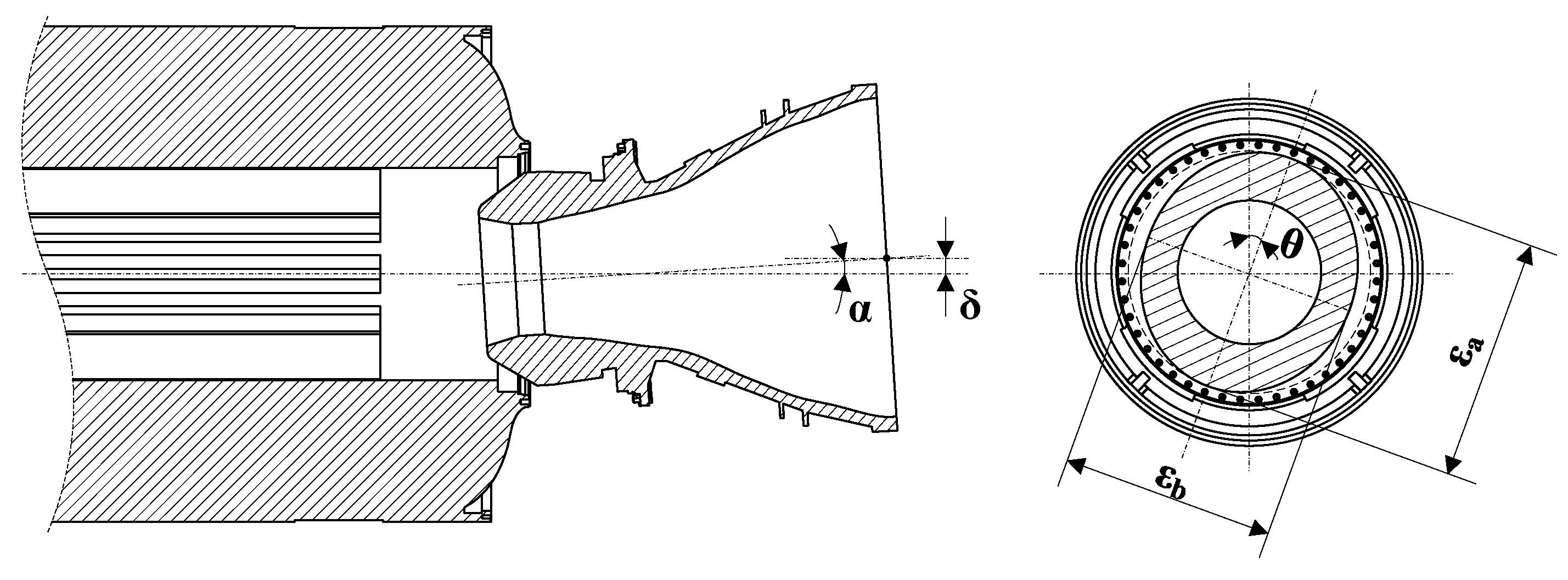


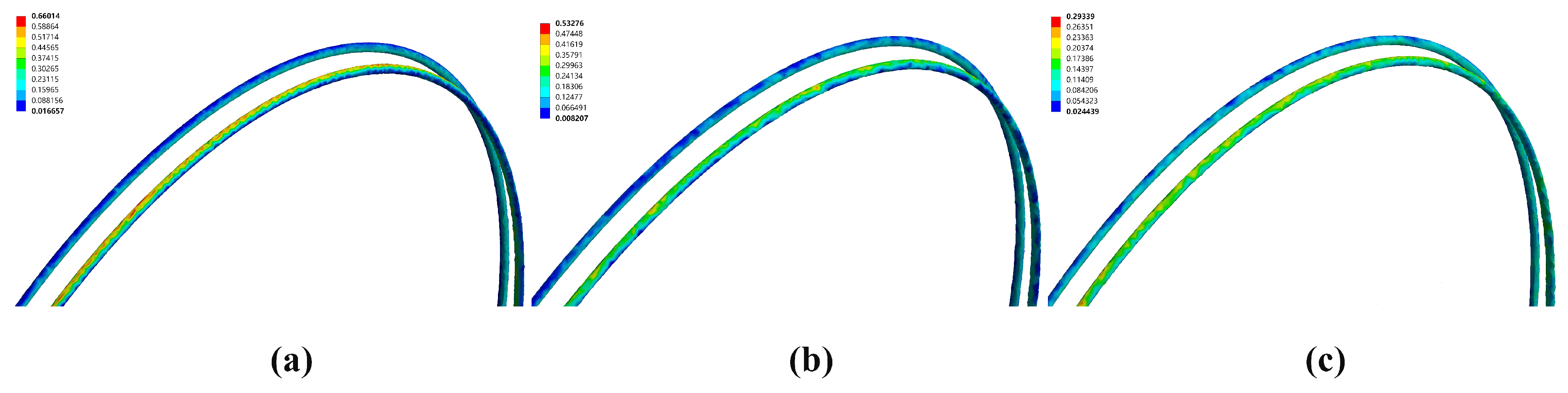




| /MPa | /MPa | |
|---|---|---|
| 0.8 | 0.3339 | 0.0337 |
| Pattern | Tightening Method | Percentage/% |
|---|---|---|
| 1 | single-robot clockwise | 13.57 |
| 2 | single-robot diagonal | 23.63 |
| 3 | double-robots clockwise | 23.95 |
| 4 | double-robots diagonal | 38.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, Y.; Wang, J.; Cao, R.; Xu, Z. Online O-Ring Stress Prediction and Bolt Tightening Sequence Optimization Method for Solid Rocket Motor Assembly. Machines 2023, 11, 387. https://doi.org/10.3390/machines11030387
Zhang J, Wang Y, Wang J, Cao R, Xu Z. Online O-Ring Stress Prediction and Bolt Tightening Sequence Optimization Method for Solid Rocket Motor Assembly. Machines. 2023; 11(3):387. https://doi.org/10.3390/machines11030387
Chicago/Turabian StyleZhang, Jiachuan, Yuanyu Wang, Junyi Wang, Runan Cao, and Zhigang Xu. 2023. "Online O-Ring Stress Prediction and Bolt Tightening Sequence Optimization Method for Solid Rocket Motor Assembly" Machines 11, no. 3: 387. https://doi.org/10.3390/machines11030387
APA StyleZhang, J., Wang, Y., Wang, J., Cao, R., & Xu, Z. (2023). Online O-Ring Stress Prediction and Bolt Tightening Sequence Optimization Method for Solid Rocket Motor Assembly. Machines, 11(3), 387. https://doi.org/10.3390/machines11030387





