Comparative Study on Health Monitoring of a Marine Engine Using Multivariate Physics-Based Models and Unsupervised Data-Driven Models
Abstract
:1. Introduction
2. Theory of Data-Driven Models
2.1. Principle Component Analysis
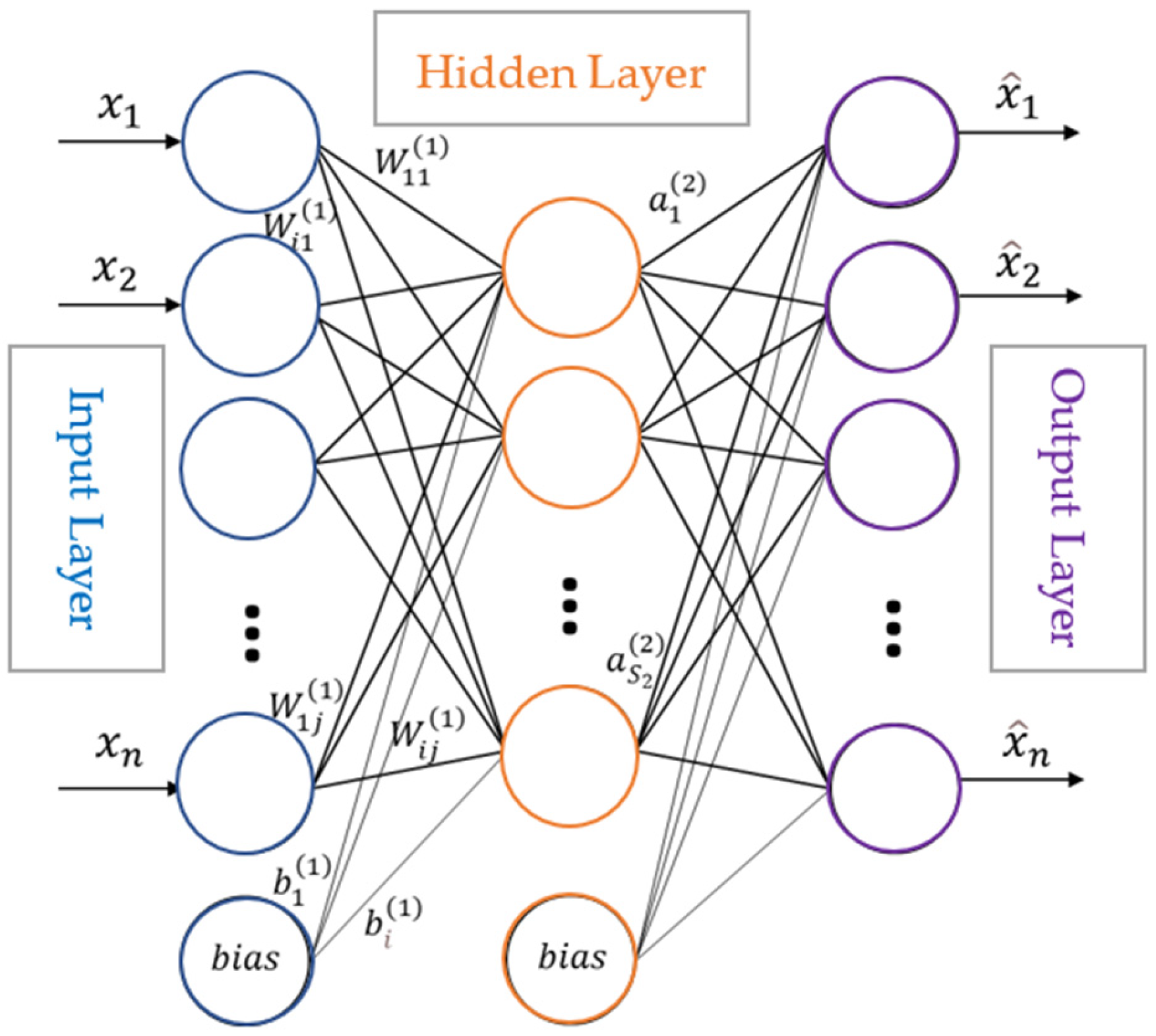
2.2. Sparse Autoencoder Model
2.3. Status Indicator for Machine Health
3. Physics-Based Multivariate Models
4. Marine Engine Test Rig
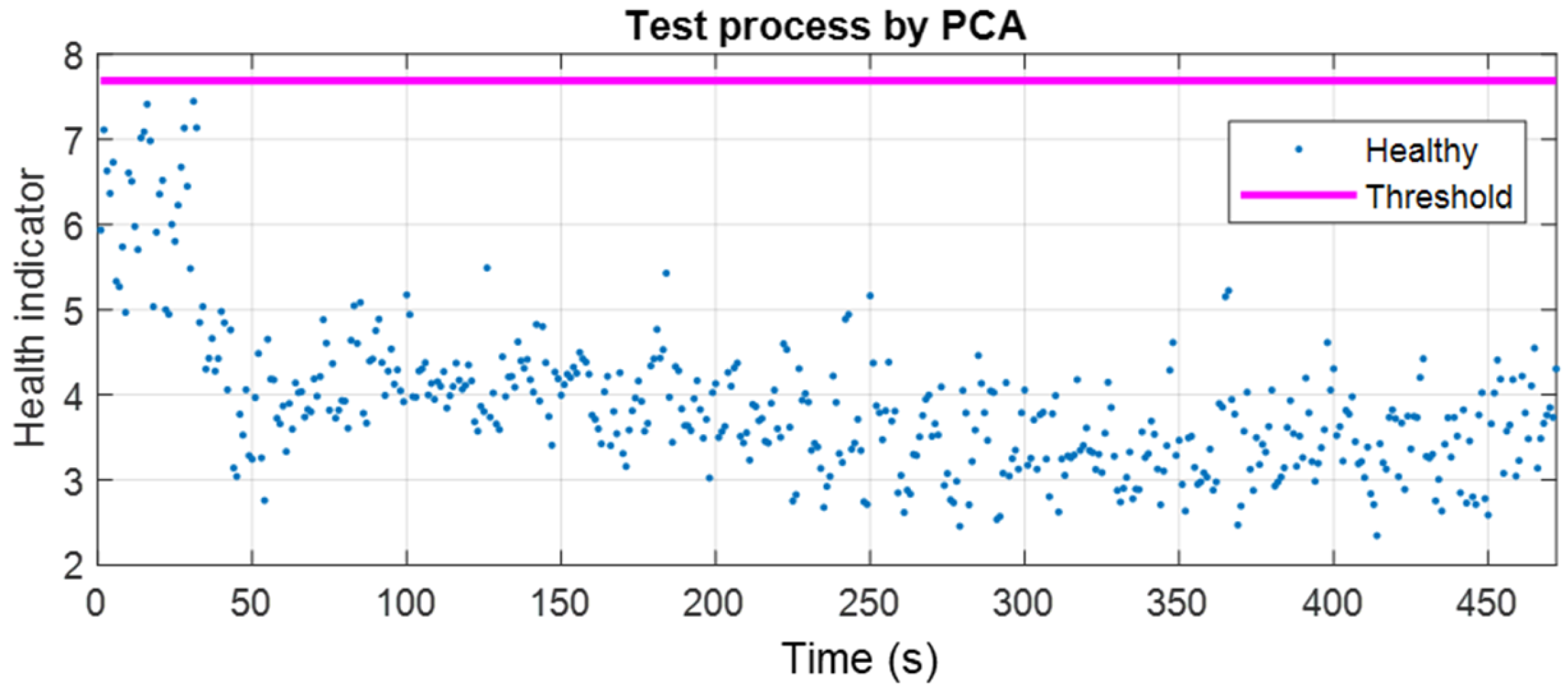
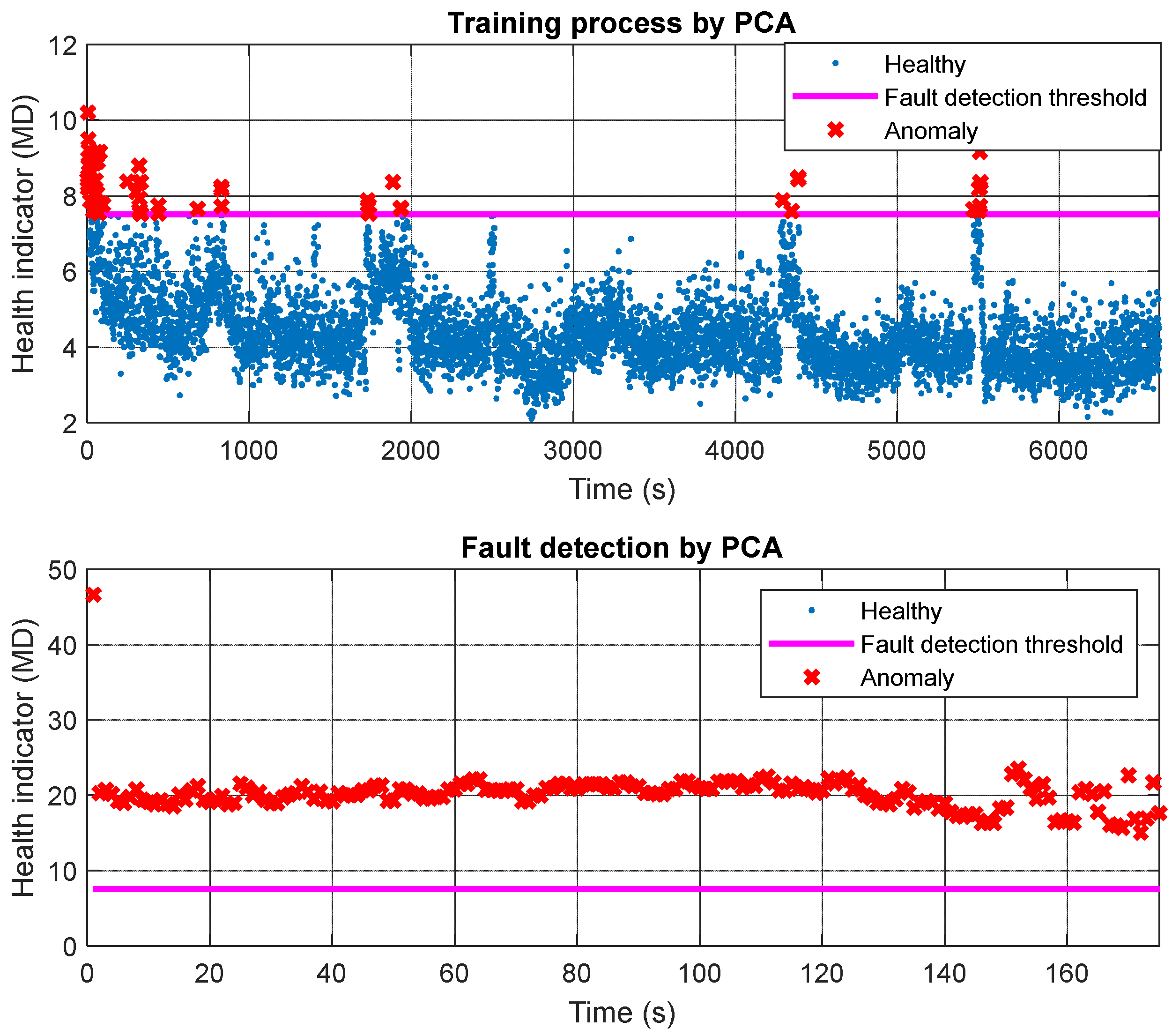
5. Case Studies
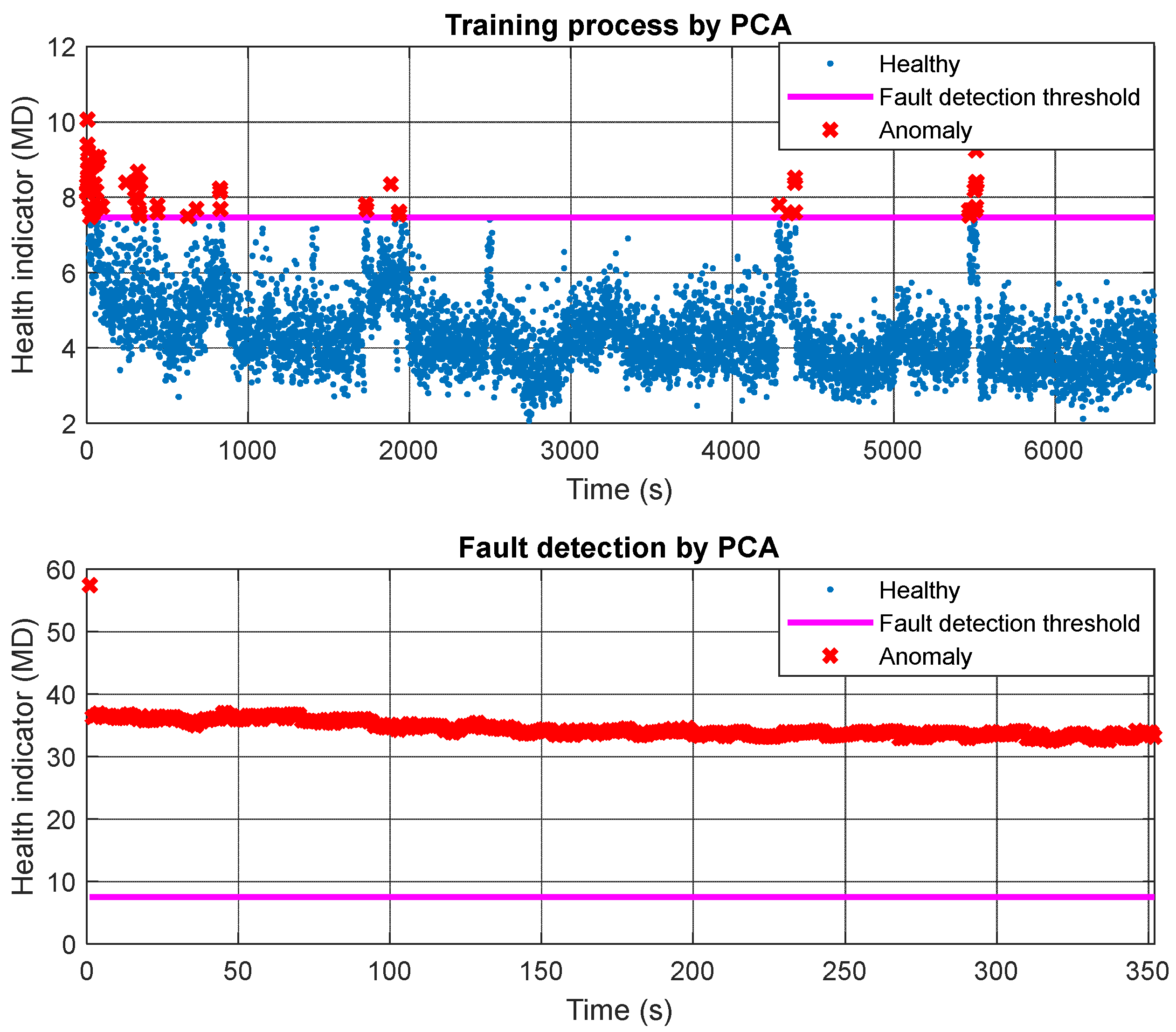
5.1. Filter Blockage
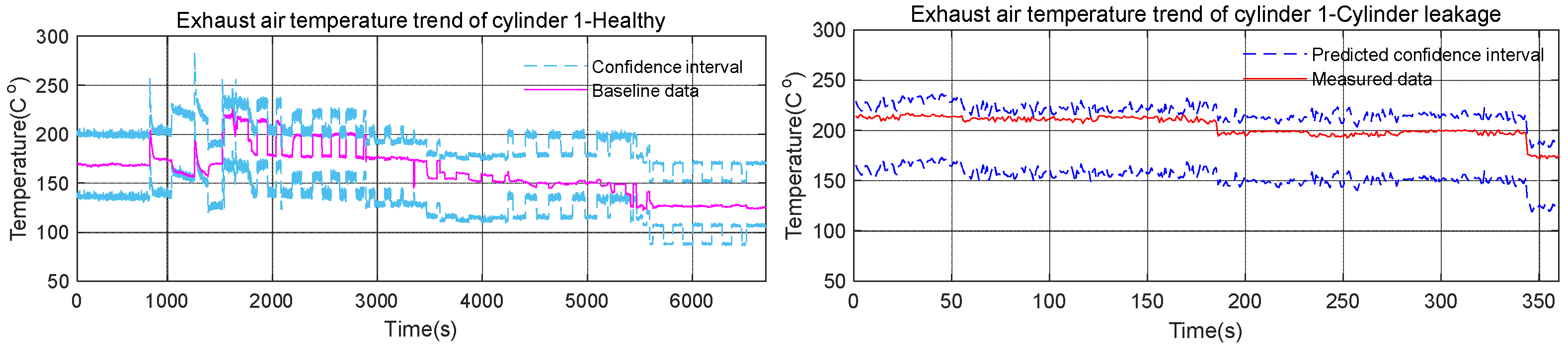
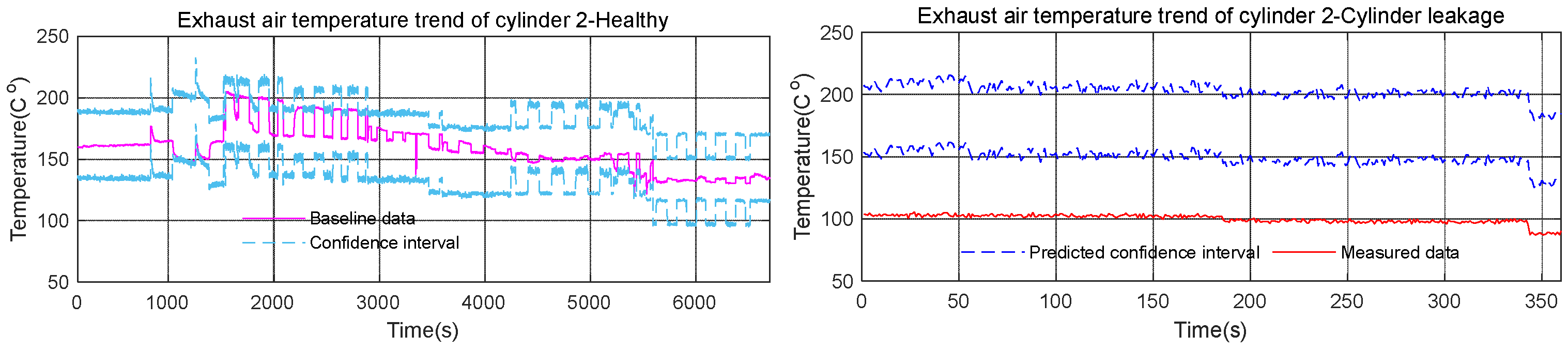
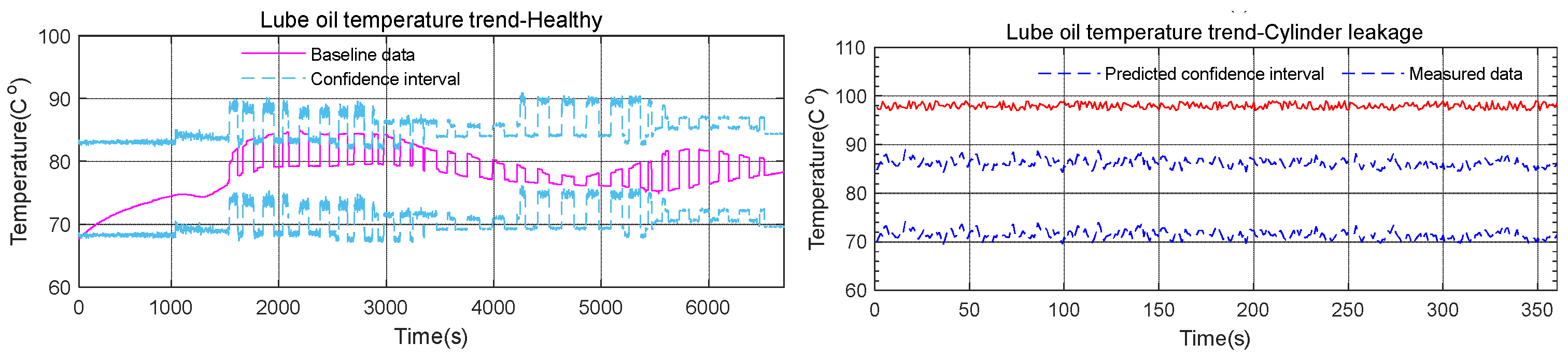
5.2. Cylinder Leakage
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Castresana, J.; Gabiña, G.; Martin, L.; Basterretxea, A.; Uriondo, Z. Marine diesel engine ANN modelling with multiple output for complete engine performance map. Fuel 2022, 319, 123873. [Google Scholar] [CrossRef]
- Ou, S.; Yu, Y.; Yang, J. Identification and reconstruction of anomalous sensing data for combustion analysis of marine diesel engines. Measurement 2022, 193, 110960. [Google Scholar] [CrossRef]
- Liu, L.; Chen, X.; Liu, D.; Du, J.; Li, W. Combustion phase identification for closed-loop combustion control by resonance excitation in marine diesel engines. Mech. Syst. Signal Process. 2022, 163, 108115. [Google Scholar] [CrossRef]
- Fog, T.L.; Hansen, L.K.; Larsen, J.; Hansen, H.; Madsen, L.; Sorensen, P.; Hansen, E.; Pedersen, P. On condition monitoring of exhaust valves in marine diesel engines. In Proceedings of the Neural Networks for Signal Processing IX: Proceedings of the 1999 IEEE Signal Processing Society Workshop, Madison, WI, USA, 25 August 1999; pp. 554–563. [Google Scholar]
- Sun, L.; Ren, X.; Zhou, H.; Li, G.; Yang, W.; Zhao, J.; Liu, Y. Machining Quality Prediction of Marine Diesel Engine Block Based on Error Transmission Network. Machines 2022, 10, 1081. [Google Scholar] [CrossRef]
- Sakellaridis, N.F.; Raptotasios, S.I.; Antonopoulos, A.K.; Mavropoulos, G.C.; Hountalas, D.T. Development and validation of a new turbocharger simulation methodology for marine two stroke diesel engine modelling and diagnostic applications. Energy 2015, 91, 952–966. [Google Scholar] [CrossRef]
- Chen, K.; Mao, Z.; Zhao, H.; Jiang, Z.; Zhang, J. A Variational Stacked Autoencoder with Harmony Search Optimizer for Valve Train Fault Diagnosis of Diesel Engine. Sensors 2020, 20, 223. [Google Scholar] [CrossRef]
- Han, P.; Ellefsen, A.L.; Li, G.; Holmeset, F.T.; Zhang, H. Fault Detection With LSTM-Based Variational Autoencoder for Maritime Components. IEEE Sens. J. 2021, 21, 21903–21912. [Google Scholar] [CrossRef]
- Bai, H.; Zhan, X.; Yan, H.; Wen, L.; Yan, Y.; Jia, X. Research on Diesel Engine Fault Diagnosis Method Based on Stacked Sparse Autoencoder and Support Vector Machine. Electronics 2022, 11, 2249. [Google Scholar] [CrossRef]
- Yan, X.; Sheng, C.; Zhao, J.; Yang, K.; Li, Z. Study of on-line condition monitoring and fault feature extraction for marine diesel engines based on tribological information. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2014, 229, 291–300. [Google Scholar] [CrossRef]
- Wang, J.; Sun, X.; Zhang, C.; Ma, X. An integrated methodology for system-level early fault detection and isolation. Expert Syst. Appl. 2022, 201, 117080. [Google Scholar] [CrossRef]
- Fu, C.; Sinou, J.-J.; Zhu, W.; Lu, K.; Yang, Y. A state-of-the-art review on uncertainty analysis of rotor systems. Mech. Syst. Signal Process. 2023, 183, 109619. [Google Scholar] [CrossRef]
- Lynch, C.; Hagras, H.; Callaghan, V. Using Uncertainty Bounds in the Design of an Embedded Real-Time Type-2 Neuro-Fuzzy Speed Controller for Marine Diesel Engines. In Proceedings of the 2006 IEEE International Conference on Fuzzy Systems, Vancouver, BC, Canada, 16–21 July 2006; pp. 1446–1453. [Google Scholar]
- Fu, C.; Ren, X.; Yang, Y. Vibration Analysis of Rotors Under Uncertainty Based on Legendre Series. J. Vib. Eng. Technol. 2019, 7, 43–51. [Google Scholar] [CrossRef]
- Wang, R.; Chen, H.; Guan, C. A Bayesian inference-based approach for performance prognostics towards uncertainty quantification and its applications on the marine diesel engine. ISA Trans. 2021, 118, 159–173. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Gao, Z.; Cao, L.; Dong, F.; Zou, Y.; Wang, K.; Zhang, Y.; Sun, P. Marine Systems and Equipment Prognostics and Health Management: A Systematic Review from Health Condition Monitoring to Maintenance Strategy. Machines 2022, 10, 72. [Google Scholar] [CrossRef]
- Wang, X.; Cai, Y.; Li, A.; Zhang, W.; Yue, Y.; Ming, A. Intelligent fault diagnosis of diesel engine via adaptive VMD-Rihaczek distribution and graph regularized bi-directional NMF. Measurement 2021, 172, 108823. [Google Scholar] [CrossRef]
- Xi, W.; Li, Z.; Tian, Z.; Duan, Z. A feature extraction and visualization method for fault detection of marine diesel engines. Measurement 2018, 116, 429–437. [Google Scholar] [CrossRef]
- Liu, Y.; Gan, H.; Cong, Y.; Hu, G. Research on fault prediction of marine diesel engine based on attention-LSTM. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 237, 508–519. [Google Scholar] [CrossRef]
- Hou, L.; Zhang, J.; Du, B. A fault diagnosis model of marine diesel engine fuel oil supply system using PCA and optimized SVM. In Journal of Physics: Conference Series, Proceedings of the 4th International Conference on Artificial Intelligence, Automation and Control Technologies (AIACT 2020), Hangzhou, China, 24–26 April 2020; IOP Publishing Ltd.: Bristol, UK, 2020; p. 012045. [Google Scholar]
- Wang, X.; Kruger, U.; Irwin, G.W.; McCullough, G.; McDowell, N. Nonlinear PCA with the local approach for diesel engine fault detection and diagnosis. IEEE Trans. Control Syst. Technol. 2007, 16, 122–129. [Google Scholar] [CrossRef]
- Zhong, K.; Li, J.; Wang, J.; Han, M. Fault Detection for Marine Diesel Engine Using Semi-supervised Principal Component Analysis. In Proceedings of the 2019 9th International Conference on Information Science and Technology (ICIST), Hulunbuir, China, 2–5 August 2019; pp. 146–151. [Google Scholar]
- Wang, S.; Wang, J.; Ding, X. An Intelligent Fault Diagnosis Scheme Based On PCA-BP Neural Network for the Marine Diesel Engine. IOP Conf. Ser. Mater. Sci. Eng. 2020, 782, 032079. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, K.; Gao, J.; Che, X. Autoencoder and Deep Neural Network based Energy Consumption Analysis of Marine Diesel Engine. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; pp. 1692–1696. [Google Scholar]
- Qu, C.; Zhou, Z.; Liu, Z.; Jia, S. Predictive anomaly detection for marine diesel engine based on echo state network and autoencoder. Energy Rep. 2022, 8, 998–1003. [Google Scholar] [CrossRef]
- Velasco-Gallego, C.; Lazakis, I. Analysis of variational autoencoders for imputing missing values from sensor data of marine systems. J. Ship Res. 2022, 66, 193–203. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L. Principal Component Analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Liang, X.; Duan, F.; Bennett, I.; Mba, D. A Sparse Autoencoder-Based Unsupervised Scheme for Pump Fault Detection and Isolation. Appl. Sci. 2020, 10, 6789. [Google Scholar] [CrossRef]
- De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D.L. The Mahalanobis distance. Chemom. Intell. Lab. Syst. 2000, 50, 1–18. [Google Scholar] [CrossRef]
- Ghorbani, H. Mahalanobis distance and its application for detecting multivariate outliers. Facta Univ. Ser. Math. Inform. 2019, 3, 583–595. [Google Scholar] [CrossRef]
- Sarmadi, H.; Entezami, A.; Saeedi Razavi, B.; Yuen, K.V. Ensemble learning-based structural health monitoring by Mahalanobis distance metrics. Struct. Control Health Monit. 2021, 28, e2663. [Google Scholar] [CrossRef]
- Odiowei, P.E.P.; Cao, Y. Nonlinear Dynamic Process Monitoring Using Canonical Variate Analysis and Kernel Density Estimations. IEEE Trans. Ind. Inform. 2010, 6, 36–45. [Google Scholar] [CrossRef]

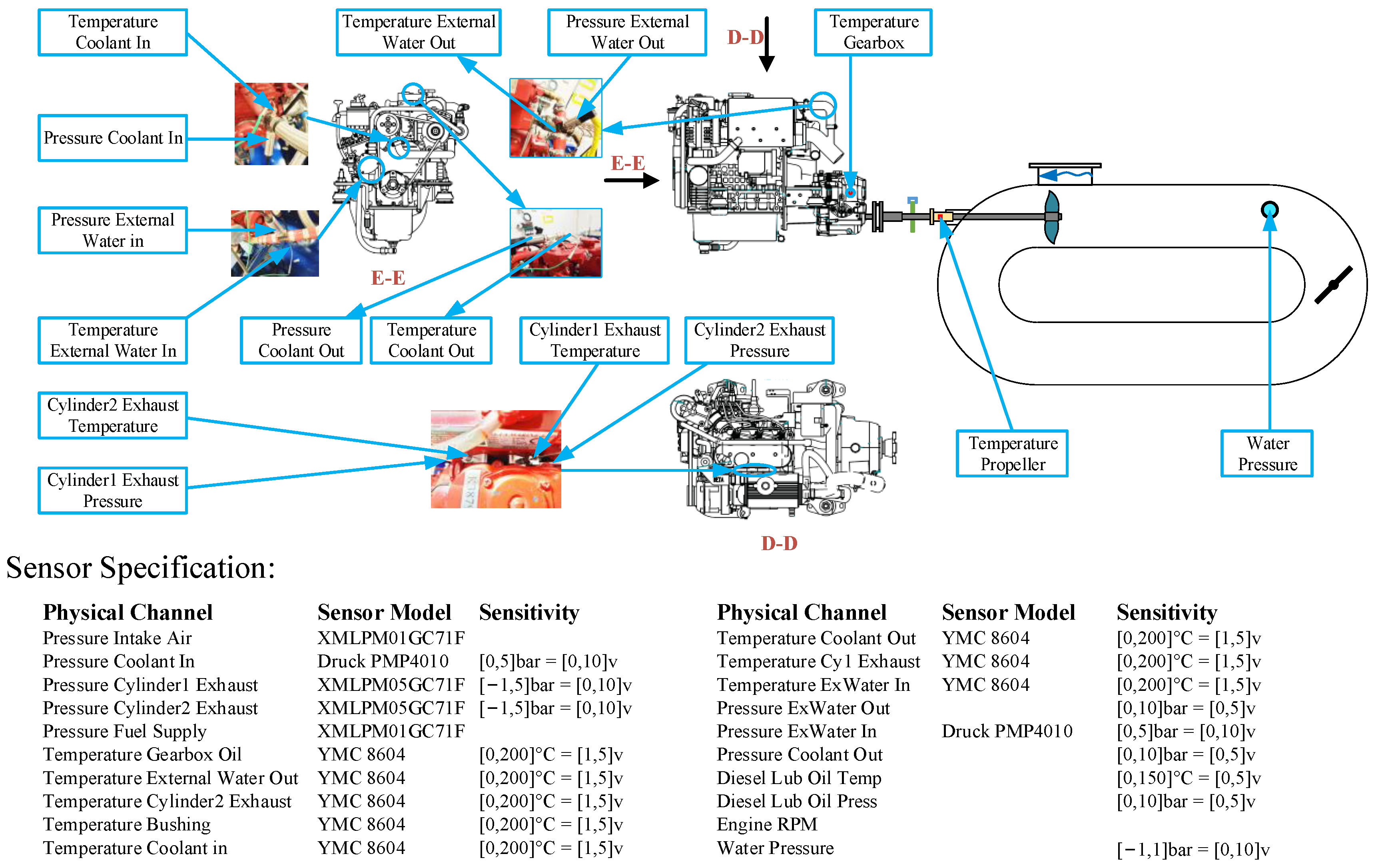



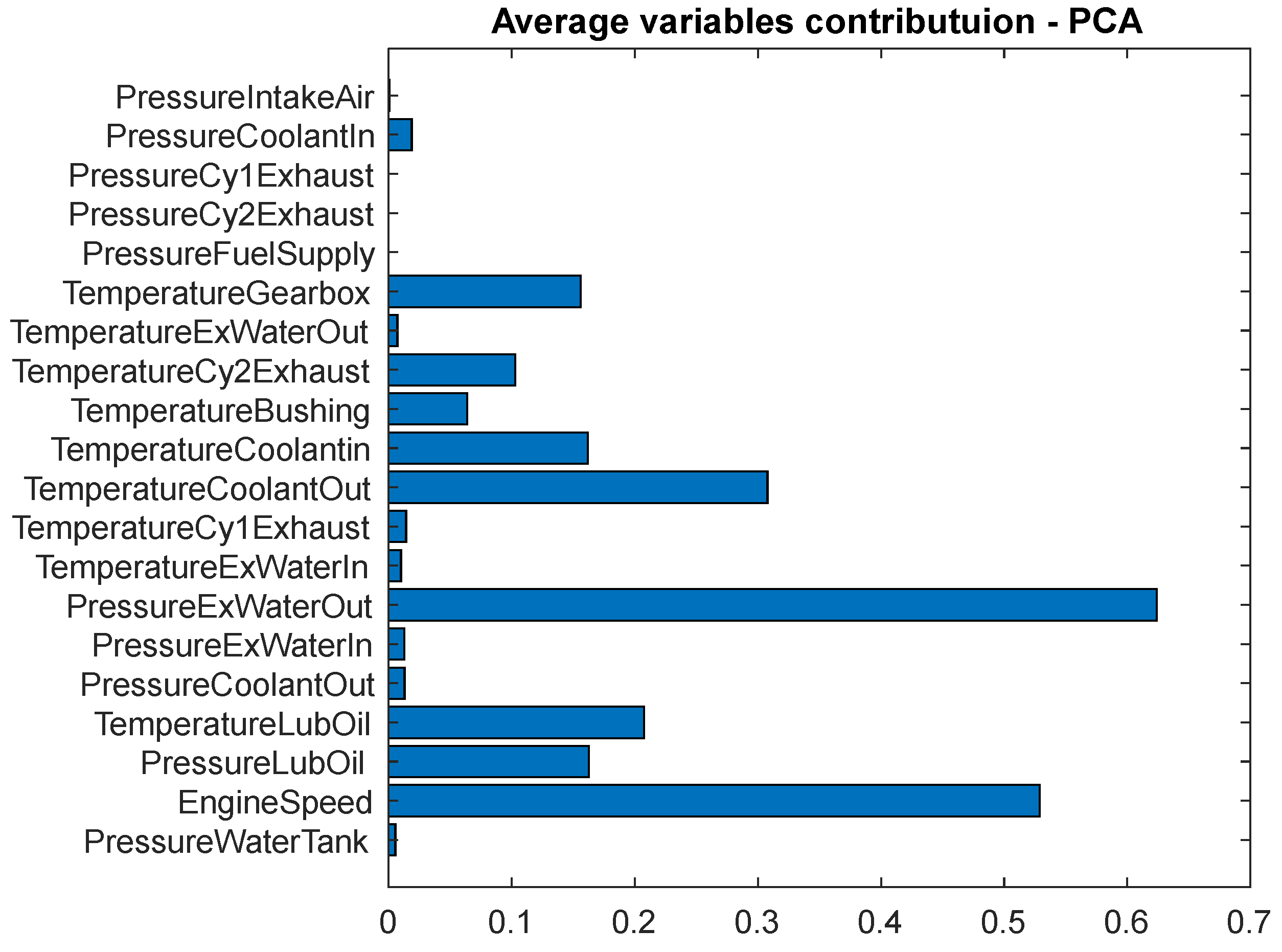
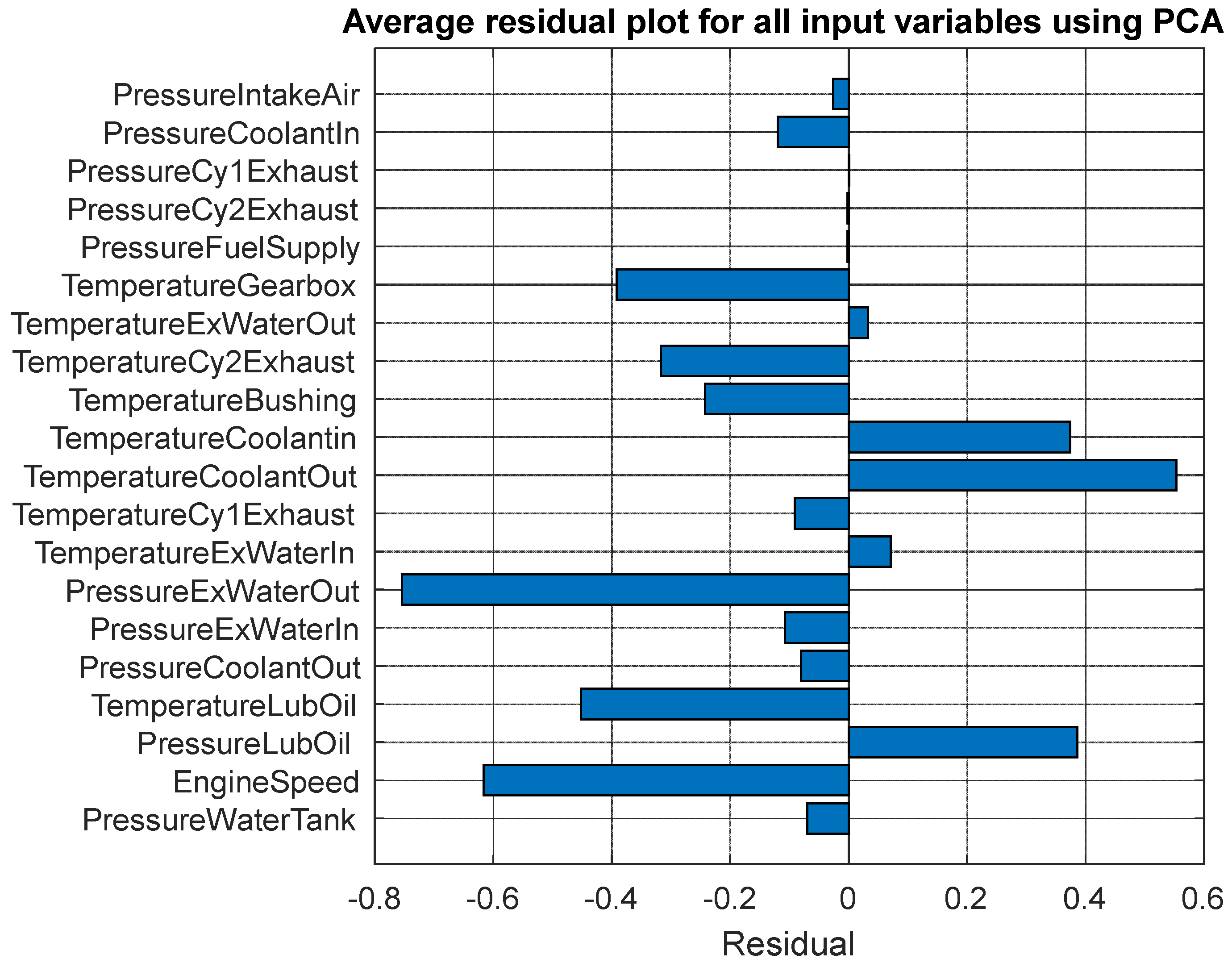


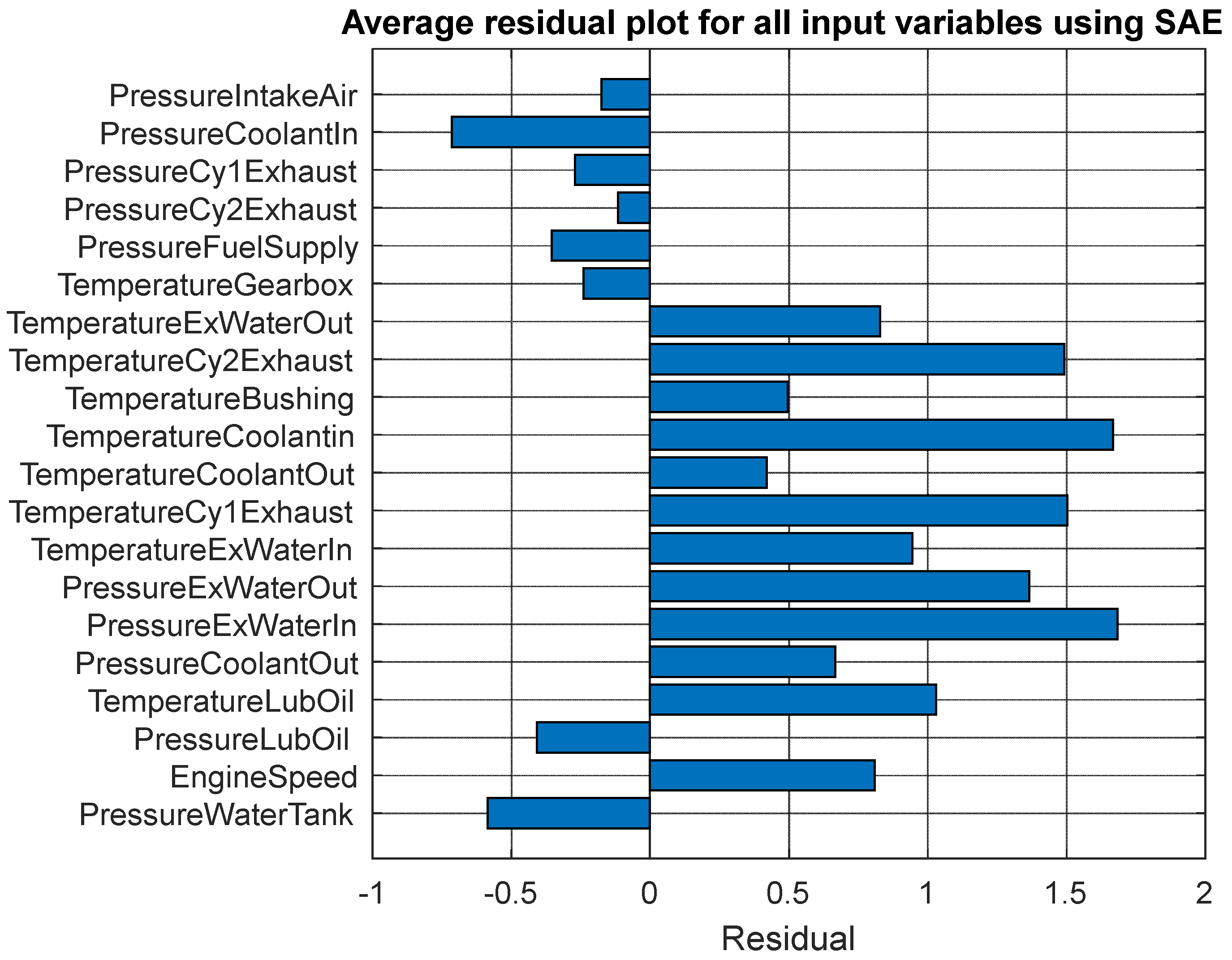


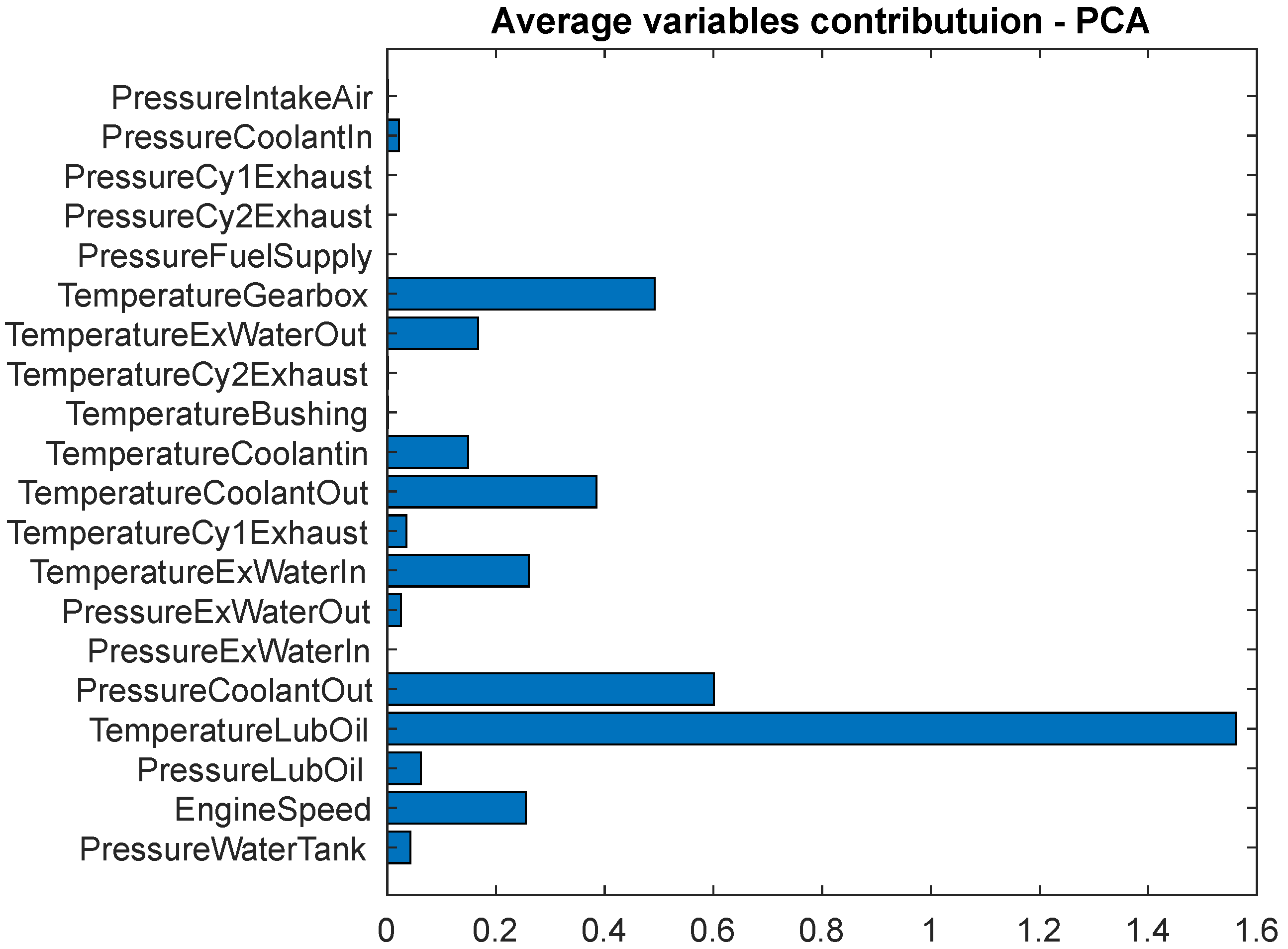
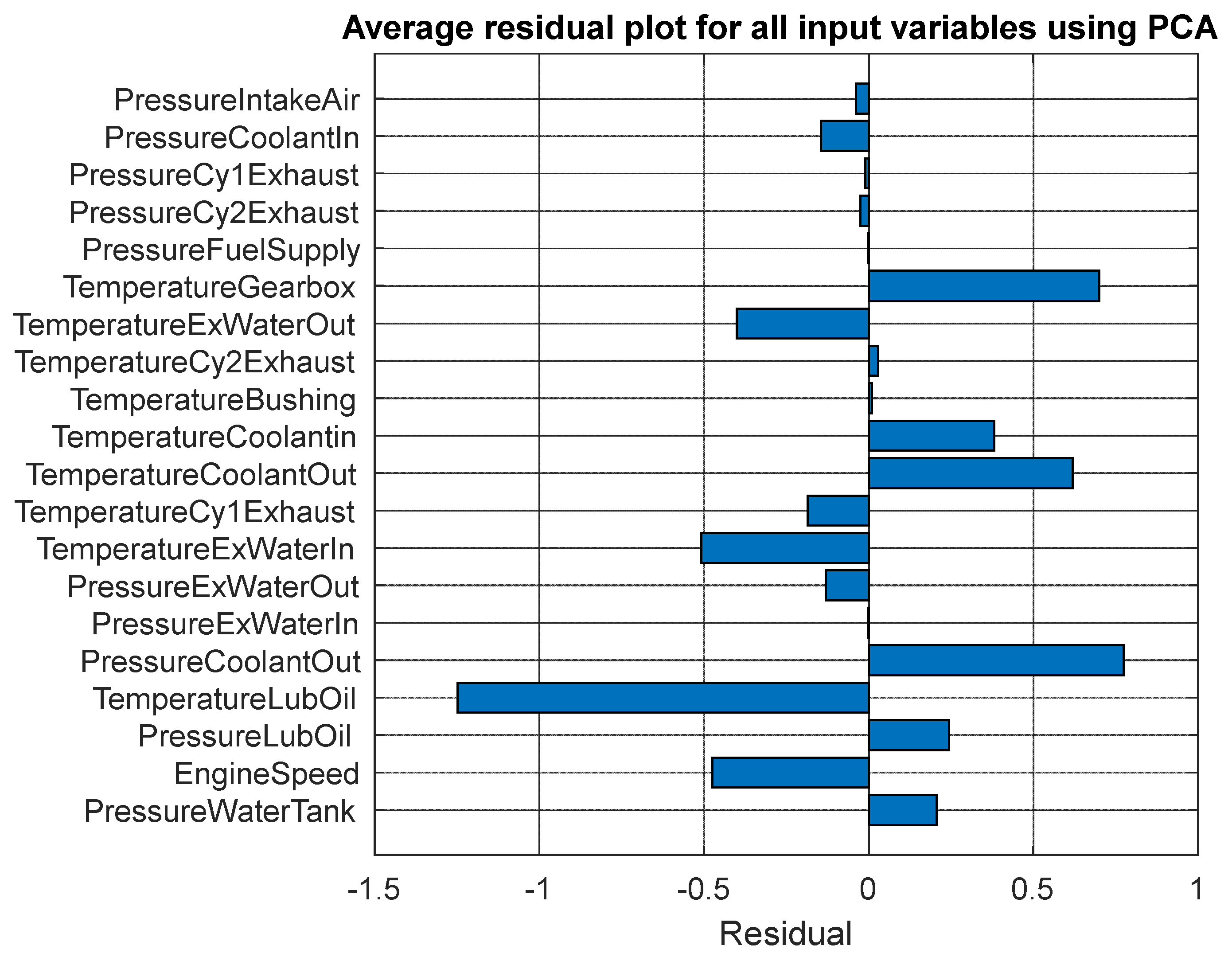

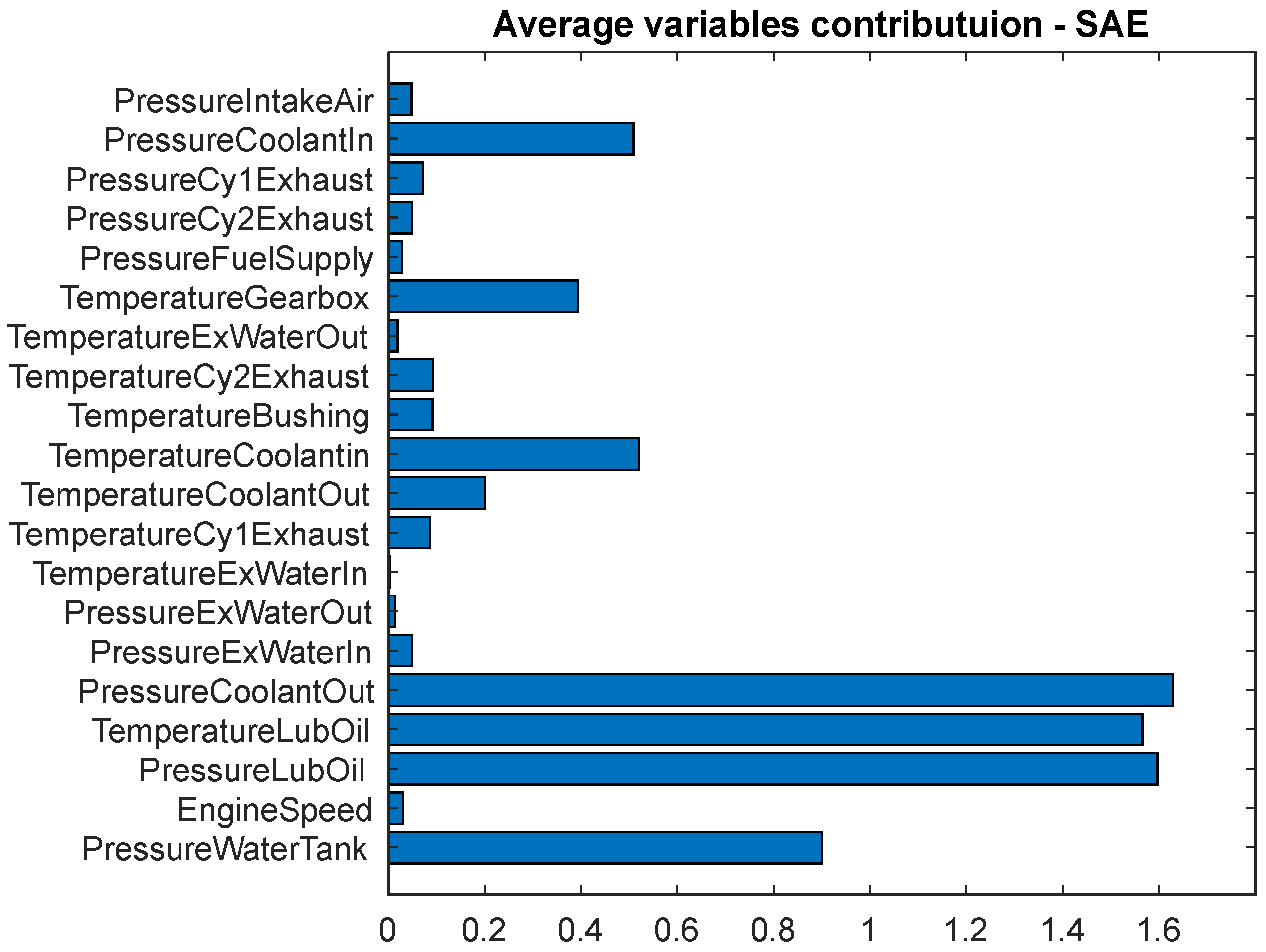
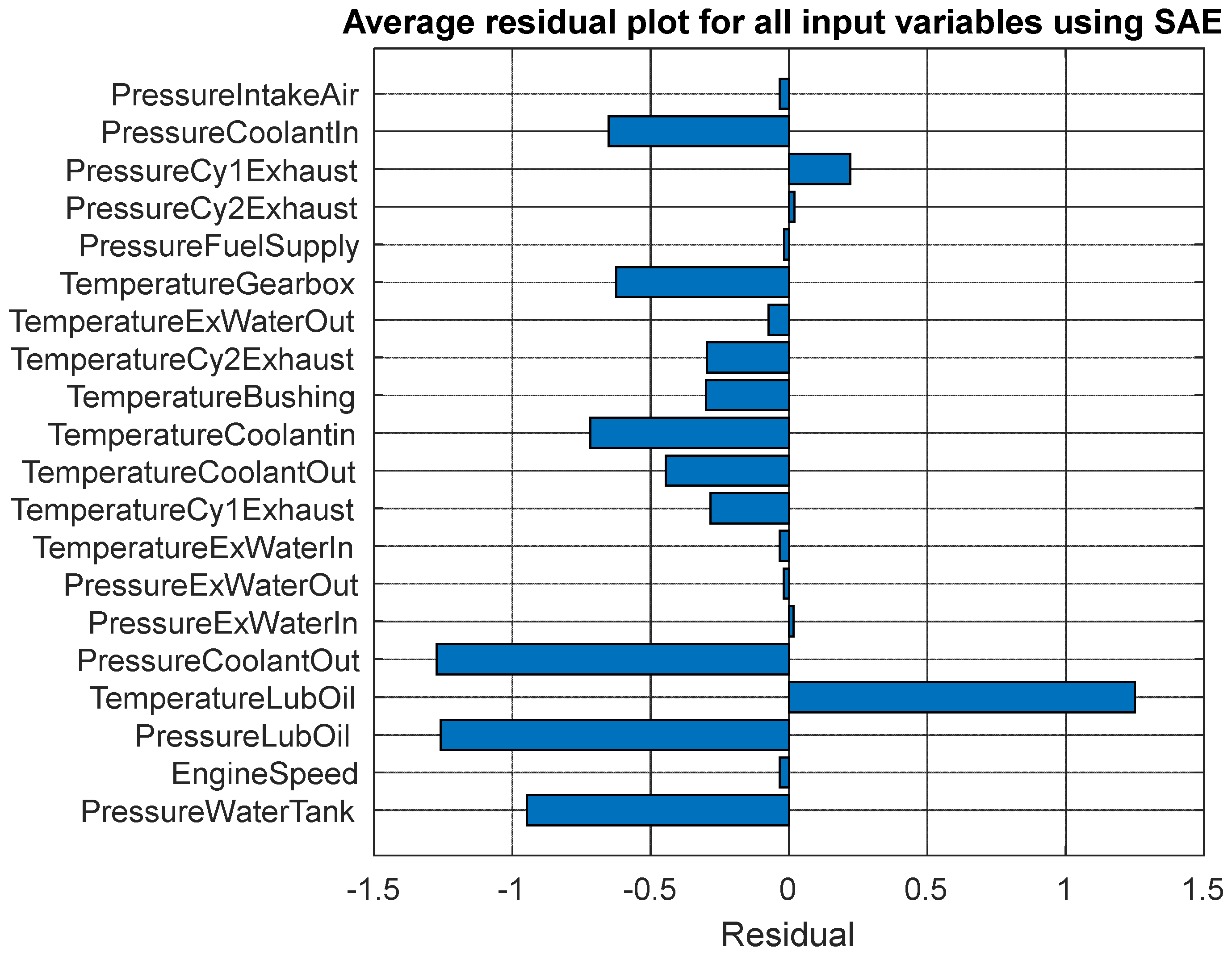
| No. | Short Form | Detail |
|---|---|---|
| 1 | Pressure Intake Air | Intake air pressure of engine |
| 2 | Pressure Coolant In | Internal coolant water pressure at inlet |
| 3 | Pressure Coolant Out | Internal coolant water pressure at outlet |
| 4 | Pressure Cy1 Exhaust | Exhaust air pressure of cylinder 1 |
| 5 | Pressure Cy2 Exhaust | Exhaust air pressure of cylinder 2 |
| 6 | Pressure Fuel Supply | Pressure of fuel supply to engine |
| 7 | Pressure Ex Water In | External coolant water pressure at inlet |
| 8 | Pressure Ex Water Out | External coolant water pressure at outlet |
| 9 | Pressure Lub Oil | Lube oil pressure |
| 10 | Pressure Water Tank | Water pressure in water tank/load level |
| 11 | Engine Speed RPM | Averaged rotating speed of shaft |
| 12 | Temperature Gearbox | Gearbox housing temperature |
| 13 | Temperature Bushing | Journal bearing (before propeller) oil temperature |
| 14 | Temperature Coolant in | Internal coolant water temperature at inlet |
| 15 | Temperature Coolant Out | Internal coolant water temperature at outlet |
| 16 | Temperature Cy1 Exhaust | Exhaust air temperature of cylinder 1 |
| 17 | Temperature Cy2 Exhaust | Exhaust air temperature of cylinder 2 |
| 18 | Temperature Ex Water In | External coolant water temperature at inlet |
| 19 | Temperature Ex Water Out | External coolant water temperature at outlet |
| 20 | Temperature Lub Oil | Lube oil temperature |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Liang, X.; Li, Q.; Lu, K.; Gu, F.; Ball, A.D.; Zheng, Z. Comparative Study on Health Monitoring of a Marine Engine Using Multivariate Physics-Based Models and Unsupervised Data-Driven Models. Machines 2023, 11, 557. https://doi.org/10.3390/machines11050557
Fu C, Liang X, Li Q, Lu K, Gu F, Ball AD, Zheng Z. Comparative Study on Health Monitoring of a Marine Engine Using Multivariate Physics-Based Models and Unsupervised Data-Driven Models. Machines. 2023; 11(5):557. https://doi.org/10.3390/machines11050557
Chicago/Turabian StyleFu, Chao, Xiaoxia Liang, Qian Li, Kuan Lu, Fengshou Gu, Andrew D. Ball, and Zhaoli Zheng. 2023. "Comparative Study on Health Monitoring of a Marine Engine Using Multivariate Physics-Based Models and Unsupervised Data-Driven Models" Machines 11, no. 5: 557. https://doi.org/10.3390/machines11050557
APA StyleFu, C., Liang, X., Li, Q., Lu, K., Gu, F., Ball, A. D., & Zheng, Z. (2023). Comparative Study on Health Monitoring of a Marine Engine Using Multivariate Physics-Based Models and Unsupervised Data-Driven Models. Machines, 11(5), 557. https://doi.org/10.3390/machines11050557










