Dynamic Modeling and Analysis of an RV Reducer Considering Tooth Profile Modifications and Errors
Abstract
1. Introduction
2. Quasi-Static Analysis of Cycloid–Pin Gear Pairs
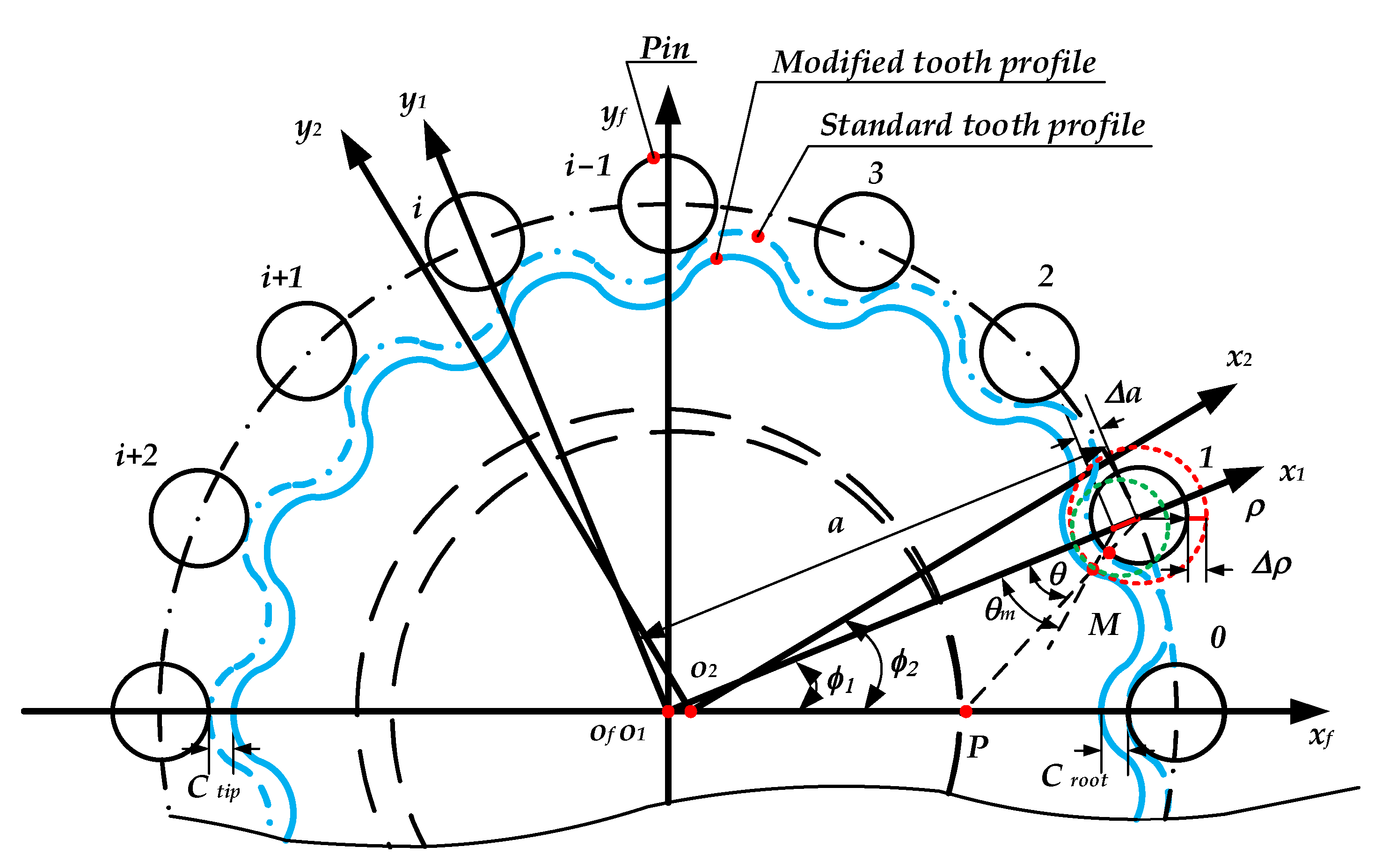
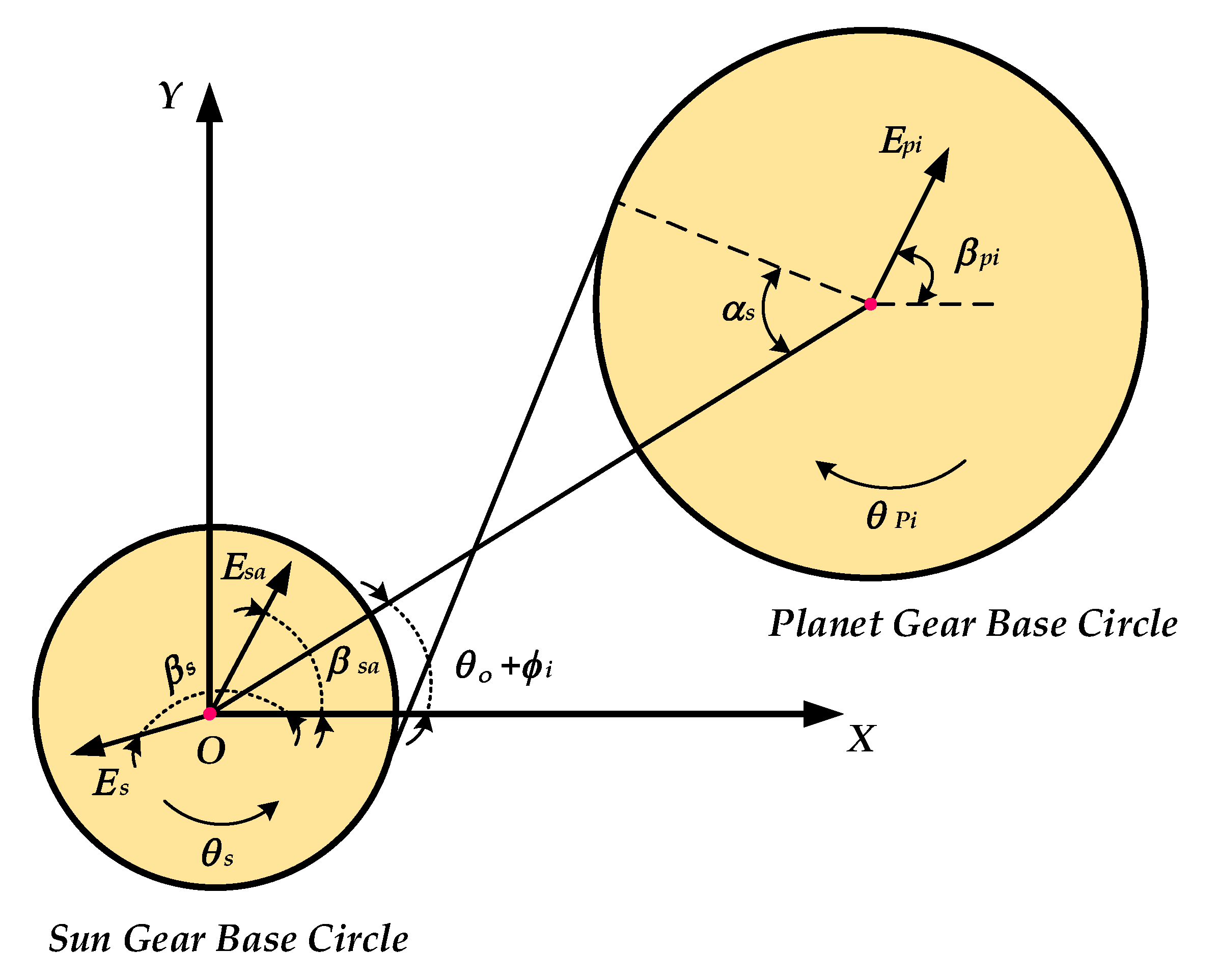
2.1. Tooth Contact Analysis of Cycloid–Pin Gear Pairs
2.2. Loaded Tooth Contact Analysis of Cycloid–Pin Gear Pairs
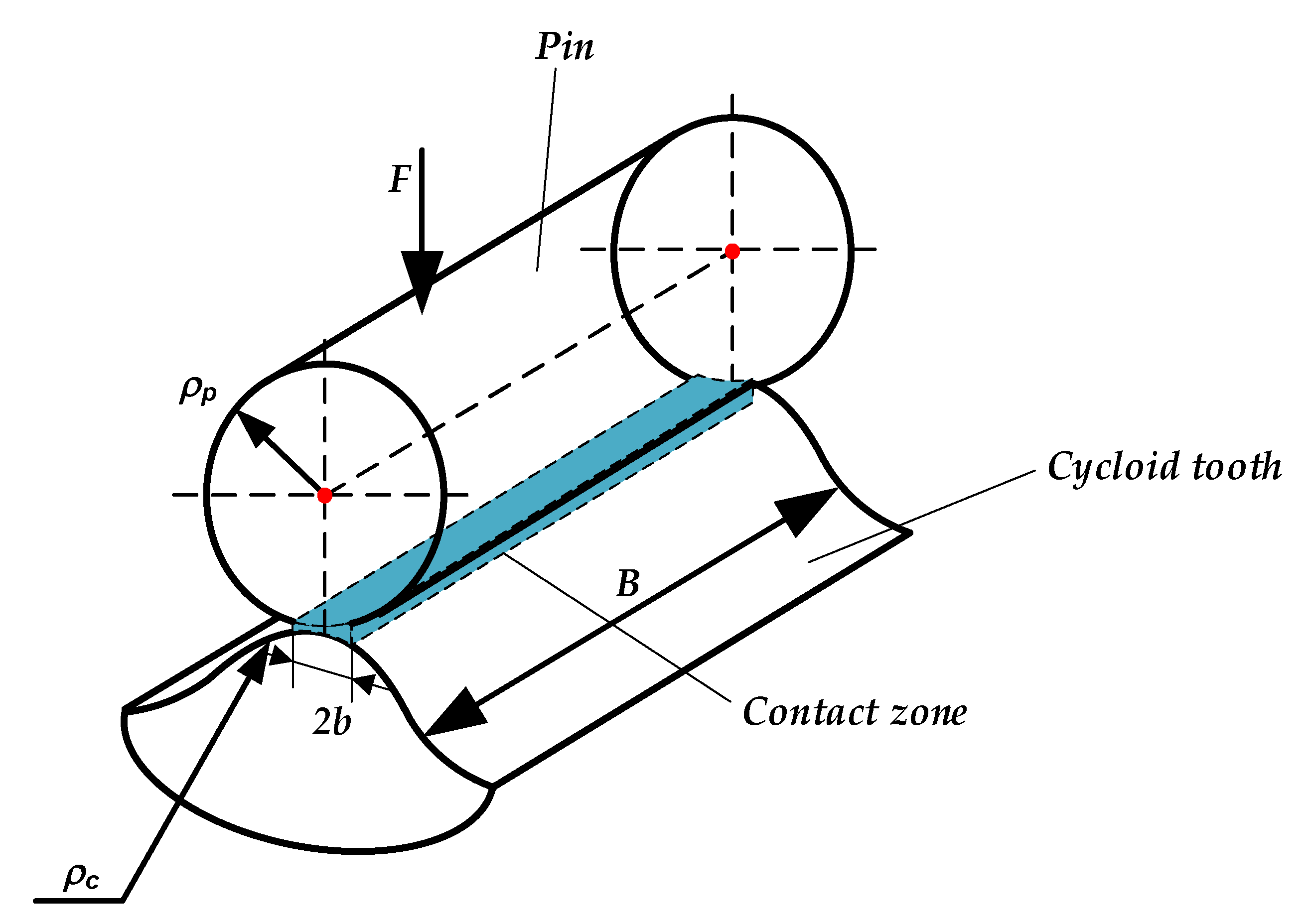
2.2.1. Hertzian Contact Stiffness
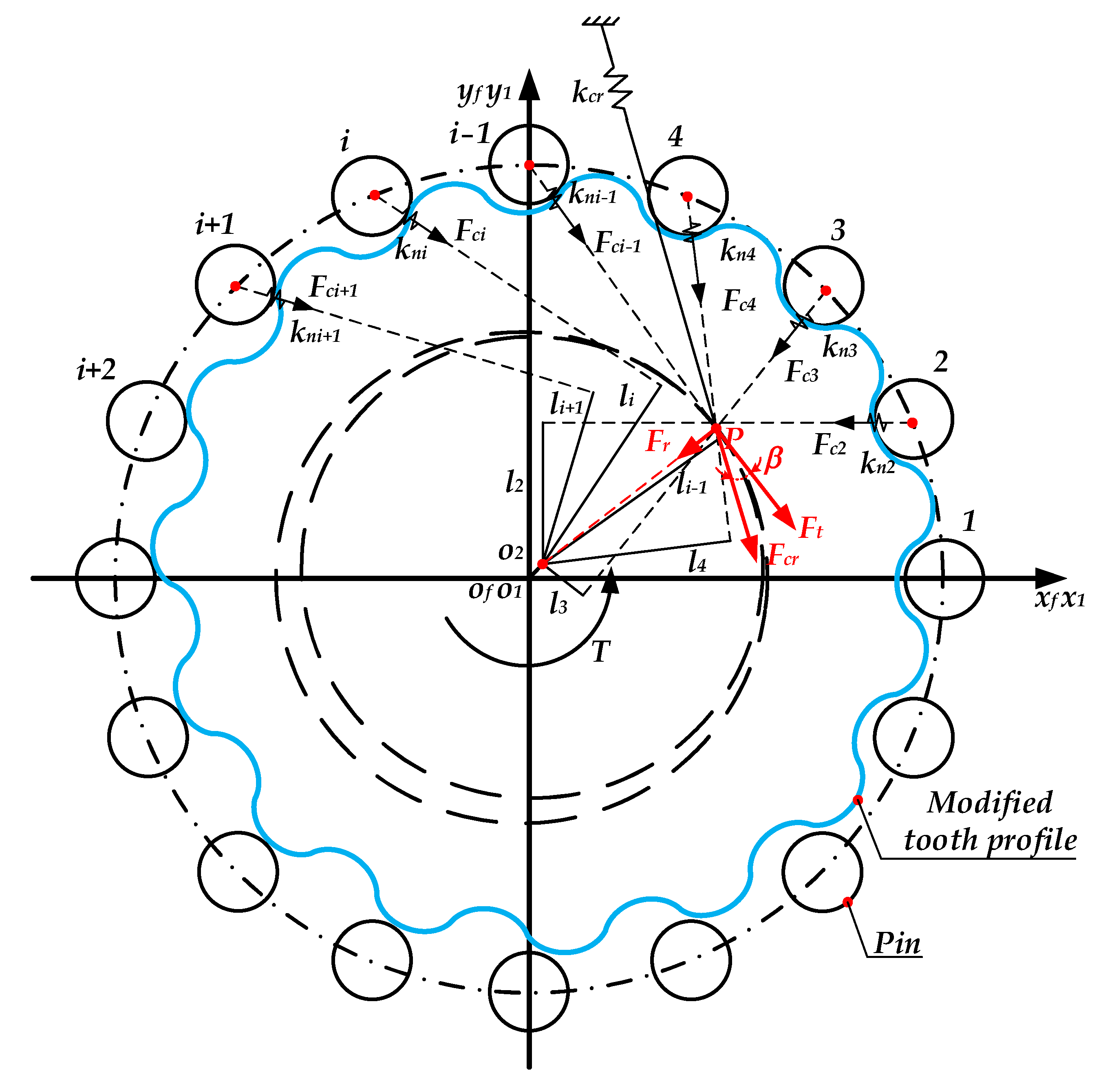
2.2.2. Compatibility and Equilibrium Conditions
2.3. Equivalent Pressure Angle and Mesh Stiffness
3. Dynamic Model of RV Reducer
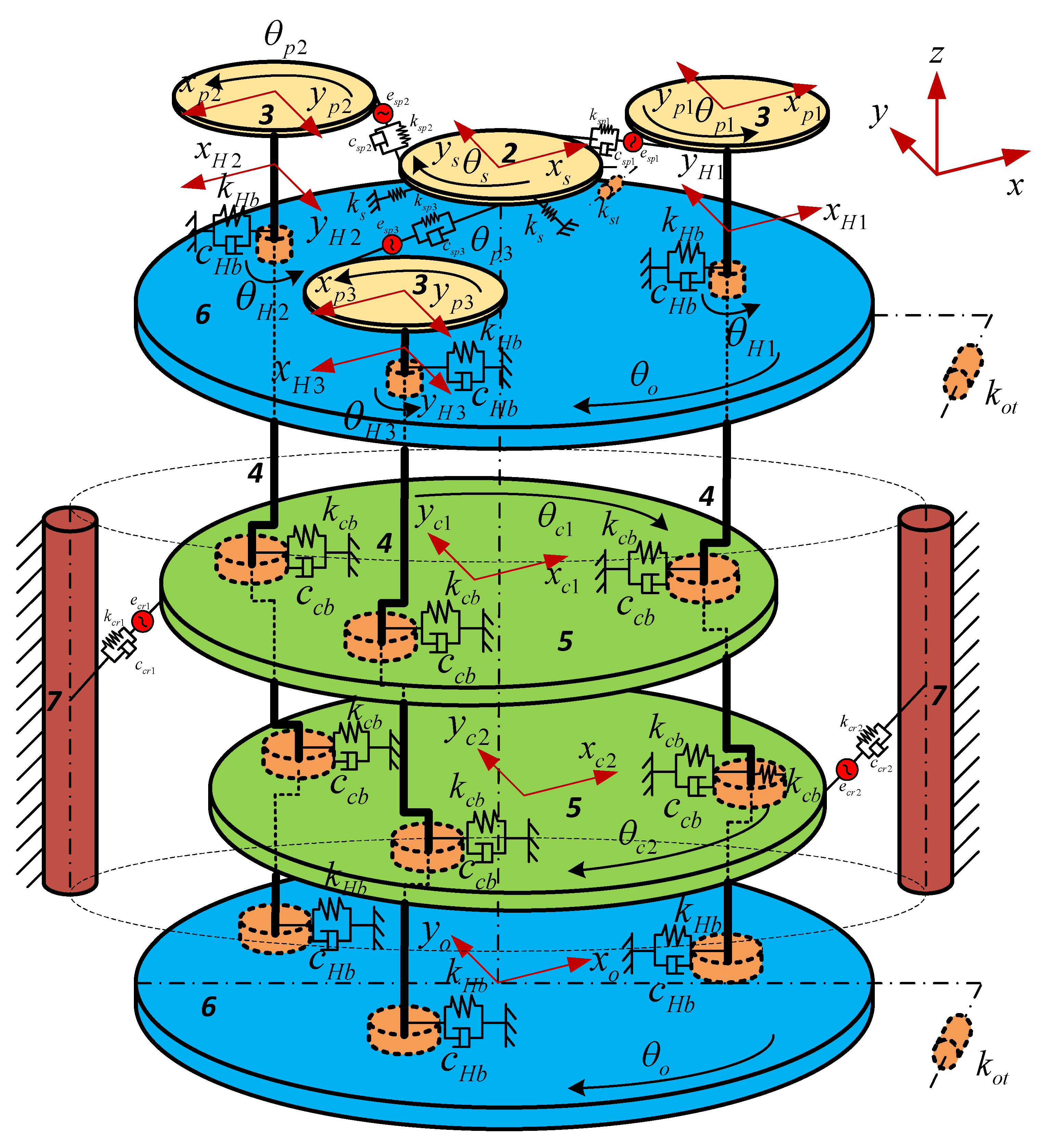
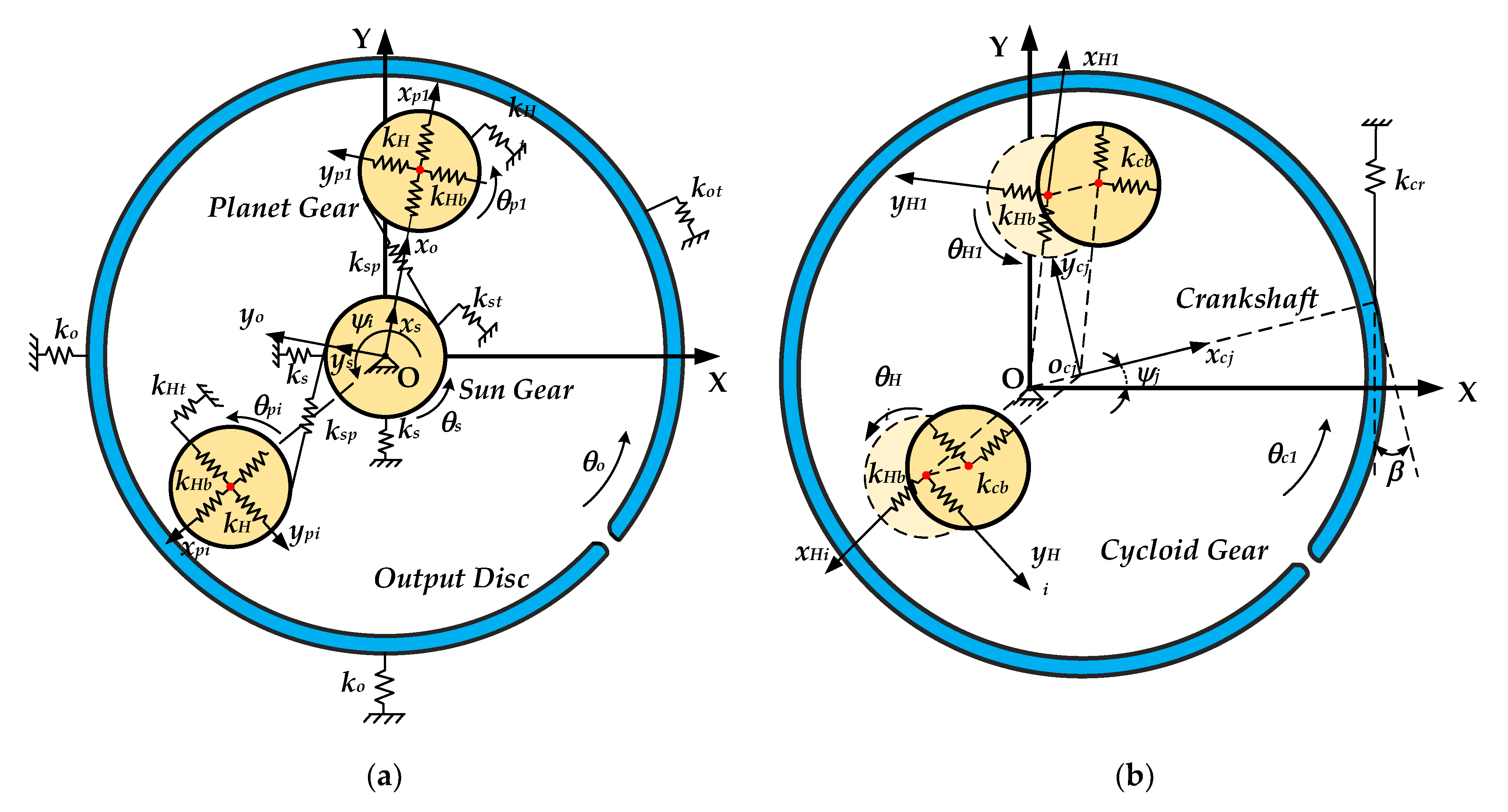
3.1. Basic Assumptions and Coordinate Systems
- (1)
- The whole structural distortion of the gears and output disc is negligible.
- (2)
- Each component vibrates in the plane normal to its axis.
- (3)
- The system is simplified as a lumped parameter model with gears and supports simplified as springs.
- (4)
- Each involute planetary gear with the same material properties and design parameters is distributed along the circumference.
- (5)
- The lubrication condition is negligible to avoid uncertainness and complexity.
3.2. Mesh Stiffness Excitation and System Error Analysis
3.2.1. Mesh Stiffness Excitation
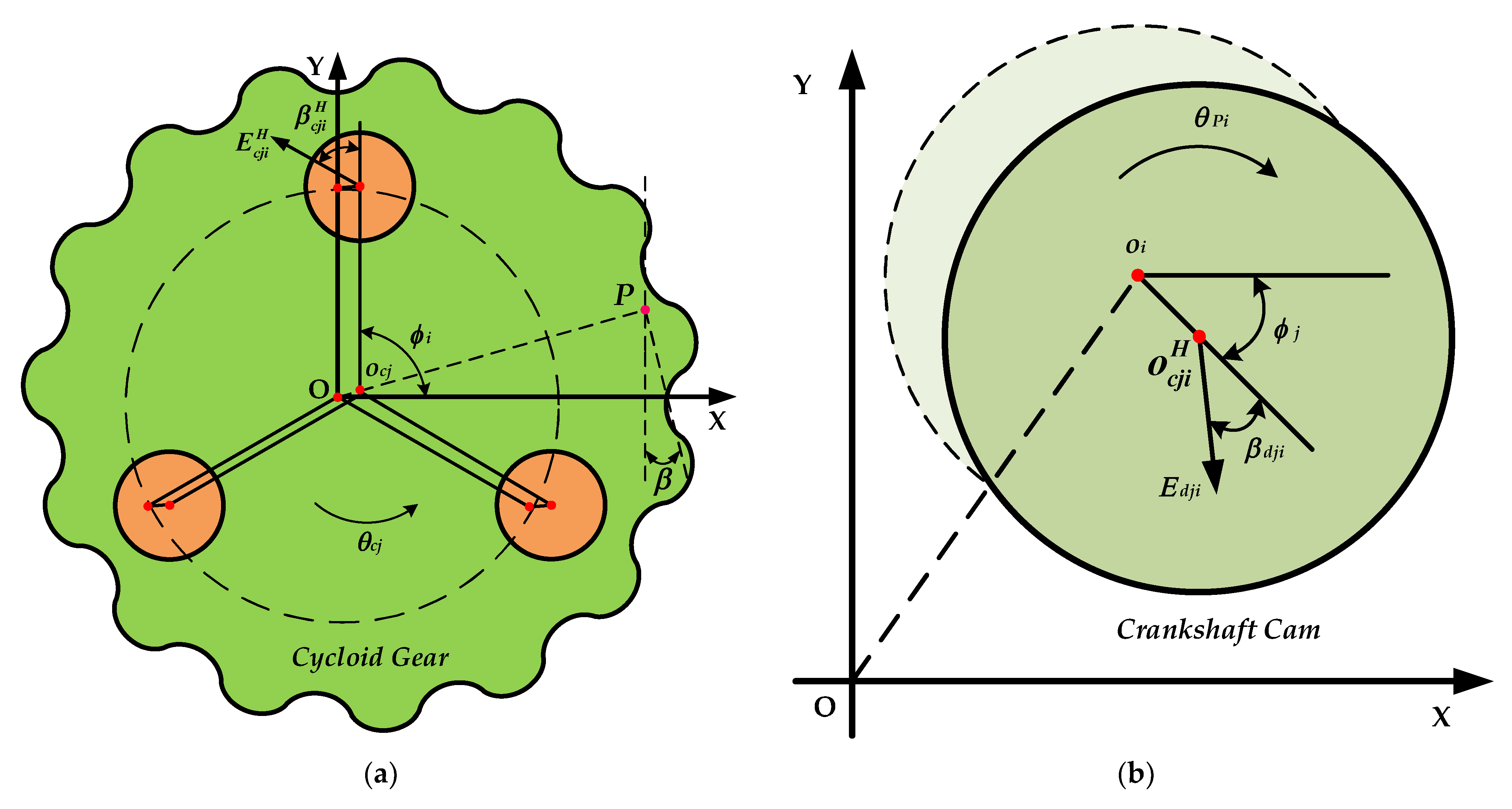
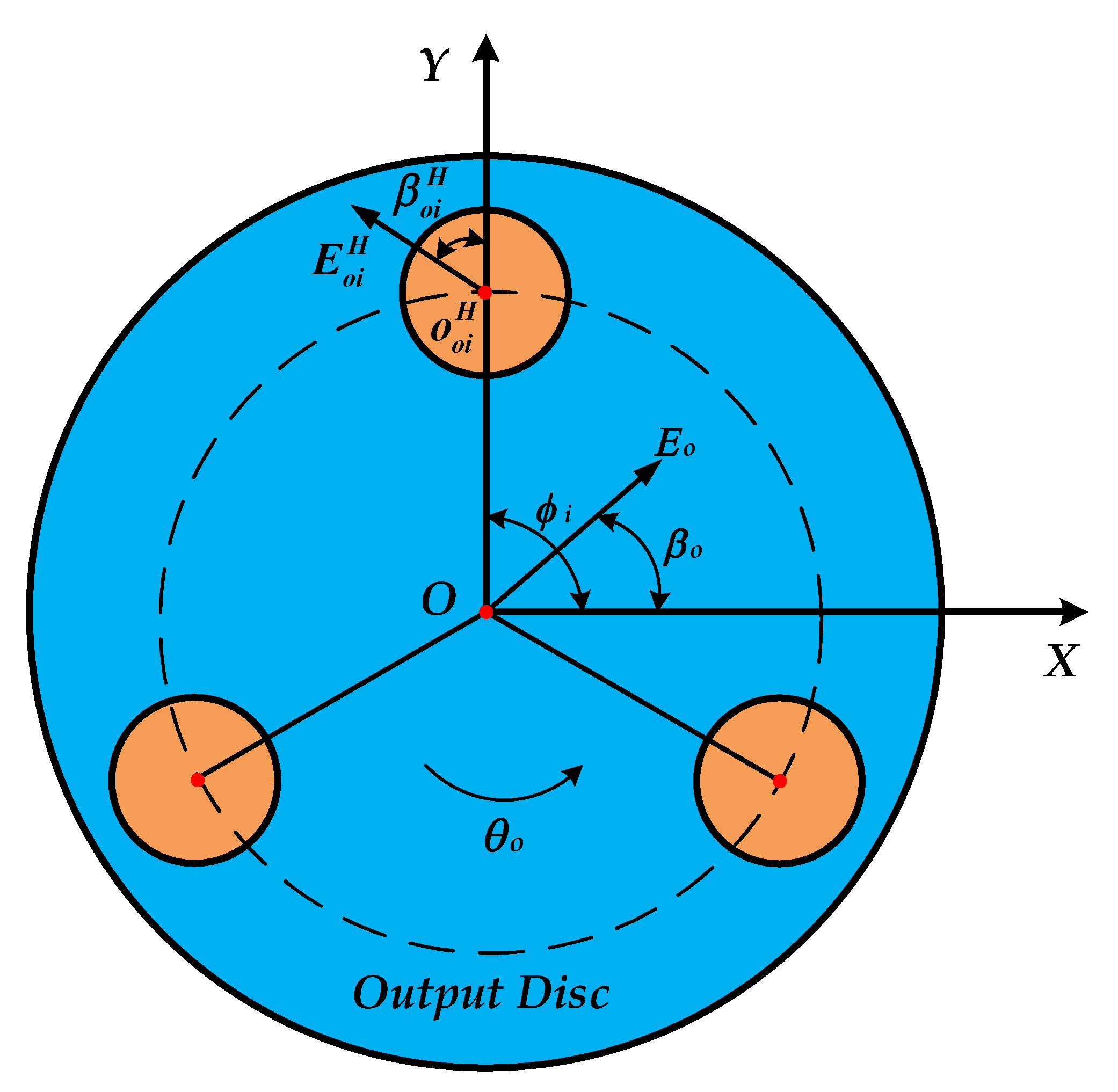
3.2.2. System Error Analysis
- (1)
- Equivalent error between the sun and planet gear at the mesh and support positions.
- (2)
- Equivalent error of the cycloid-pin gear drive at the mesh and support positions.
- (3)
- Equivalent error of the output disc at the contact or support position.
3.3. Formulations of Motion Equations
3.3.1. Relative Displacements
- (1)
- Relative displacement projection of the sun and planet gears along the mesh line.
- (2)
- Relative displacement projection of the crankshaft and cycloid gear along the translational direction of the crankshaft.
- (3)
- Relative displacement projection of the crankshaft and the output disc along the translational direction of the crankshaft.
- (4)
- Relative displacement projection of the cycloid gear and pins along the mesh line.
3.3.2. Motion Equations
4. Analysis Results and Discussion
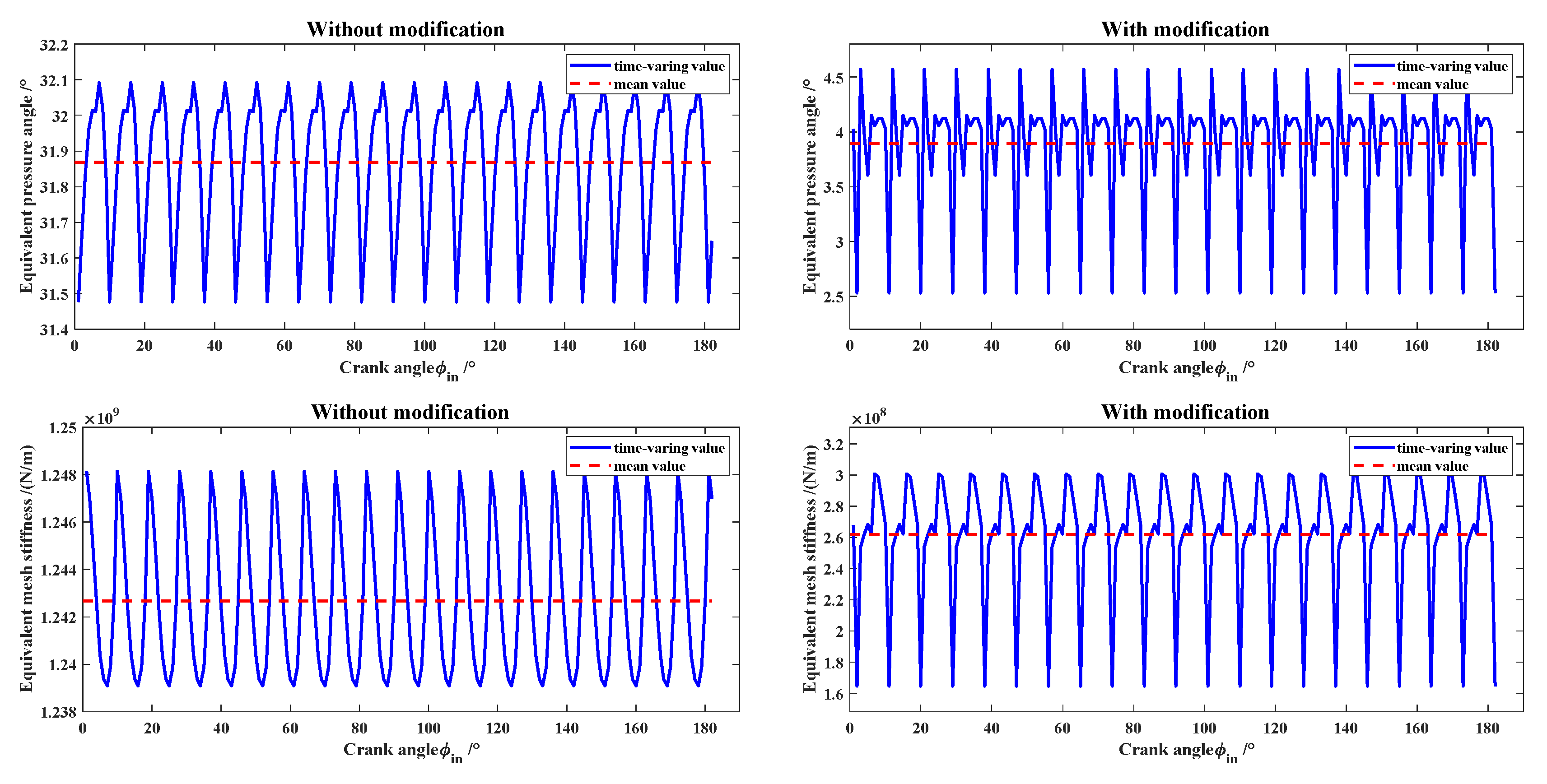
4.1. Numerical Solution of Equivalent Pressure Angle and Mesh Stiffness
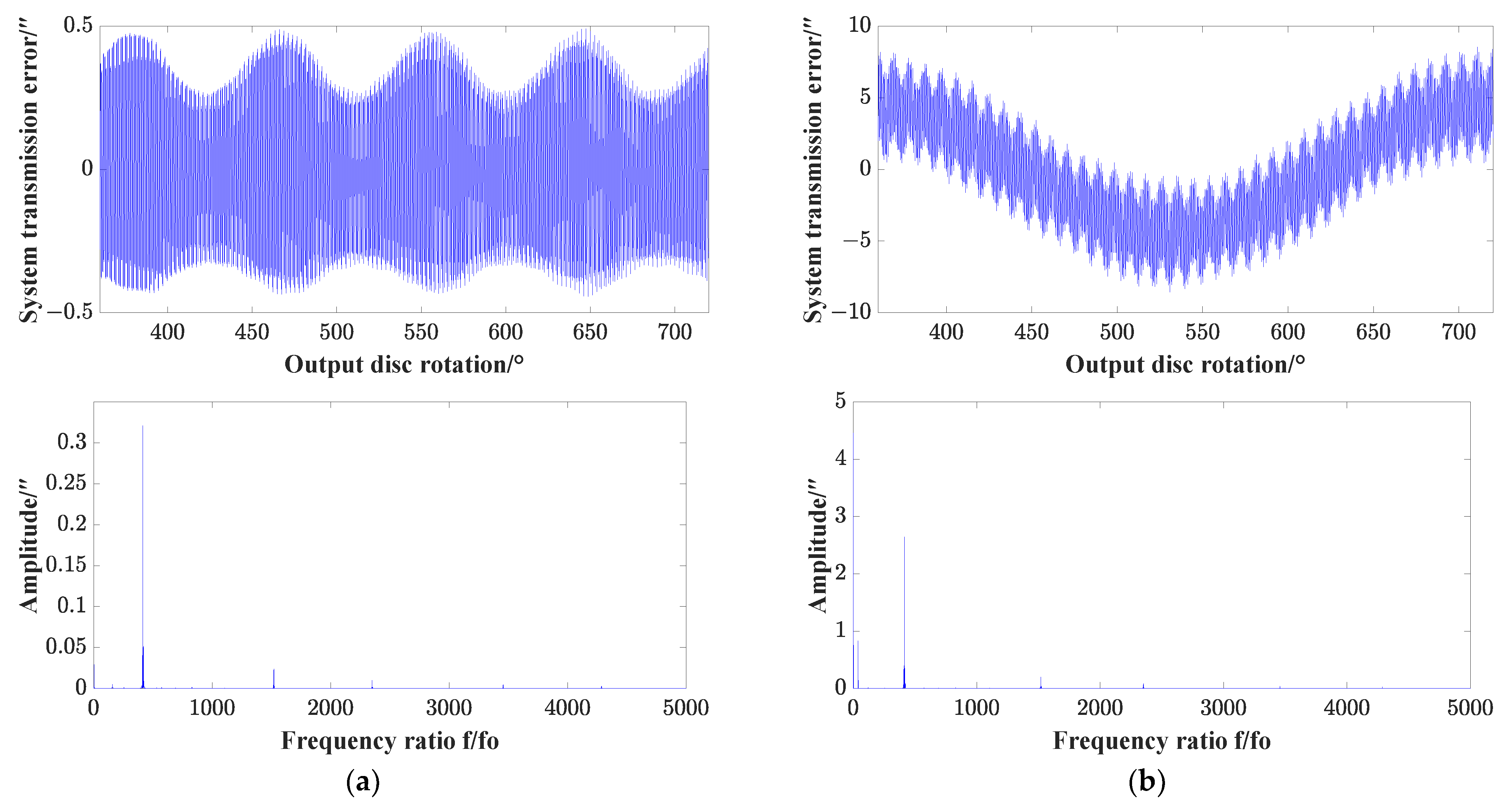
4.2. Dynamic Responses in the Time Domain
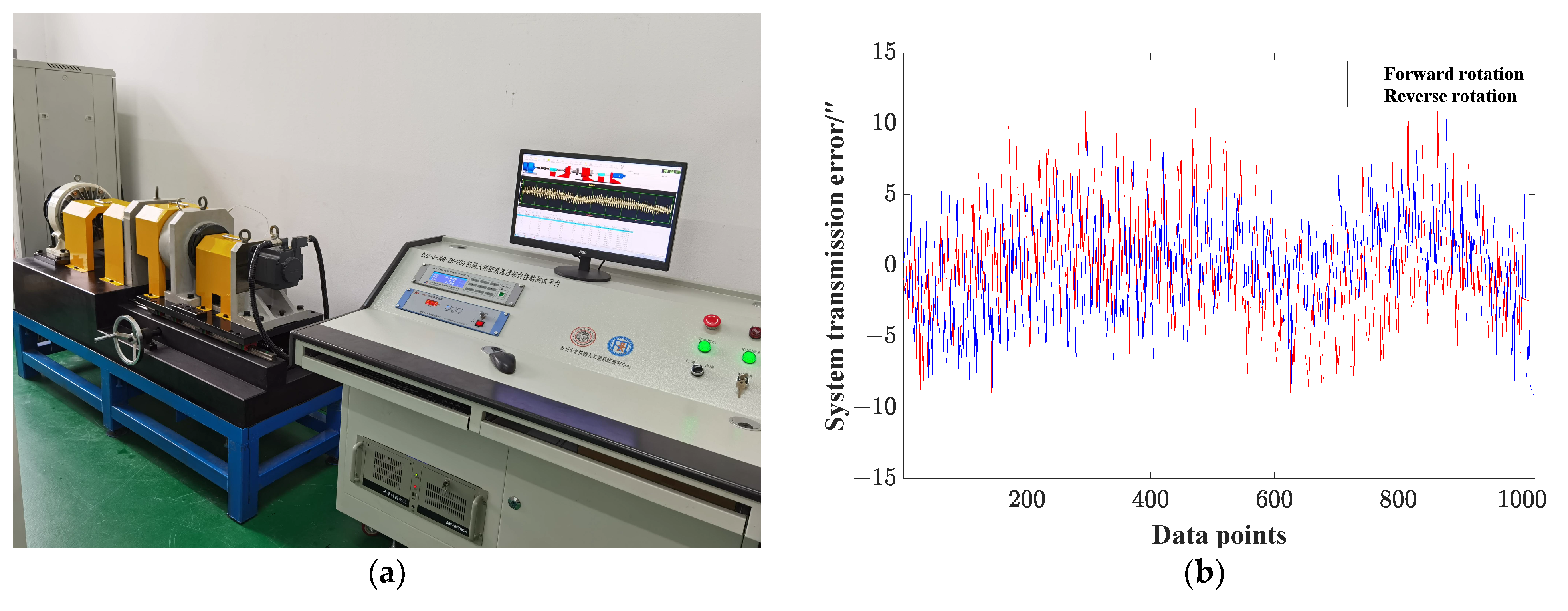
4.3. Effects of System Errors on the Dynamic Transmission Error
5. Conclusions
- Through quasi-static analysis based on the LTCA, the tooth profile modifications have a significant effect on the values of the equivalent pressure angle and mesh stiffness of the cycloid–pin gear pair, which should be adequately considered in the dynamic model of the RV reducers.
- The motion trajectories and phase plane diagrams are vulnerable to influence from the system errors of the components. From the phase plane diagrams, it can be seen whether the system motion state is under the quasi-static or chaotic state, and many kinds of variation characteristics of the time domain diagrams are disclosed.
- The system errors of the components significantly affect the dynamic transmission error magnitude and variation rule, illustrating that error is truly an important factor related to transmission precision.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, T.X.; Zhou, J.X.; Deng, X.Z.; Li, J.B.; Xing, C.R.; Su, J.X.; Wang, H.L. A manufacturing error measurement methodology for a rotary vector reducer cycloidal gear based on a gear measuring center. Meas. Sci. Technol. 2018, 29, 075006. [Google Scholar] [CrossRef]
- Chen, B.K.; Zhong, H.; Liu, J.Y.; Li, C.Y.; Fang, T.T. Generation and investigation of a new cycloid drive with double contact. Mech. Mach. Theory 2012, 49, 270–283. [Google Scholar] [CrossRef]
- Li, S.T. Design and strength analysis methods of the trochoidal gear reducers. Mech. Mach. Theory 2014, 81, 140–154. [Google Scholar] [CrossRef]
- Huang, Y.C.; Du, X.S.; Zhu, C.C.; Ni, G.X.; Ullah, N.; Liu, H. Mesh stiffness analysis of beveloid gears for the rotating vector transmission. Mech. Sci. Technol. 2019, 33, 3943–3953. [Google Scholar] [CrossRef]
- Li, T.X.; Xu, H.; Tian, M. A loaded analysis method for RV cycloidal-pin transmission based on the minimum energy principle. Strojniski Vestn.-J. Mech. Eng. 2020, 66, 655–667. [Google Scholar] [CrossRef]
- Jang, D.J.; Kim, Y.C.; Hong, E.P.; Kim, G.S. Geometry design and dynamic analysis of a modified cycloid reducer with epitrochoid tooth profile. Mech. Mach. Theory 2021, 164, 17. [Google Scholar] [CrossRef]
- Jin, S.-S.; Tong, X.-T.; Wang, Y.-L. Influencing factors on rotate vector reducer dynamic transmission error. Int. J. Autom. Technol. 2019, 13, 545–556. [Google Scholar] [CrossRef]
- Wang, H.; Shi, Z.Y.; Yu, B.; Xu, H. Transmission performance analysis of RV reducers influenced by profile modification and load. Appl. Sci. 2019, 9, 4099. [Google Scholar] [CrossRef]
- Wang, S.; Tan, J.; Gu, J.J.; Huang, D.S. Study on torsional vibration of RV reducer based on time-varying stiffness. Vib. Eng. Technol. 2021, 9, 73–84. [Google Scholar] [CrossRef]
- Xu, L.X.; Chen, B.K.; Li, C.Y. Dynamic modelling and contact analysis of bearing-cycloid-pinwheel transmission mechanisms used in joint rotate vector reducers. Mech. Mach. Theory 2019, 137, 432–458. [Google Scholar] [CrossRef]
- Wu, K.Y.; Shih, Y.P.; Lee, J.J. Kinematic error analysis of the rotor vector gear reducer with machining tolerances. Braz. Soc. Mech. Sci. Eng. 2020, 42, 16. [Google Scholar] [CrossRef]
- Li, T.X.; Tian, M.; Xu, H.T.; Deng, X.Z.; An, X.T.; Su, J.X. Meshing contact analysis of cycloidal-pin gear in RV reducer considering the influence of manufacturing error. Braz. Soc. Mech. Sci. Eng. 2020, 42, 14. [Google Scholar] [CrossRef]
- Li, X.; Li, C.Y.; Wang, Y.W.; Chen, B.K.; Lim, T.C. Analysis of a cycloid speed reducer considering tooth profile modification and clearance-fit output mechanism. Mech. Des. 2017, 139, 12. [Google Scholar] [CrossRef]
- Li, T.X.; An, X.T.; Deng, X.Z.; Li, J.F.; Li, Y.L. A new tooth profile modification method of cycloidal gears in precision reducers for robots. Appl. Sci. 2020, 10, 1266. [Google Scholar] [CrossRef]
- Huang, C.H.; Tsai, S.J. A study on loaded tooth contact analysis of a cycloid planetary gear reducer considering friction and bearing roller stiffness. Adv. Mech. Des. Syst. Manuf. 2017, 11, 17. [Google Scholar] [CrossRef]
- Hsieh, C.F.; Jian, W.S. The effect on dynamics of using various transmission designs for two-stage cycloidal speed reducers. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. Eng. Sci. 2016, 230, 665–681. [Google Scholar] [CrossRef]
- Yang, Y.H.; Chen, C.; Wang, S.Y. Response sensitivity to design parameters of RV reducer. Chin. J. Mech. Eng. 2018, 31, 13. [Google Scholar] [CrossRef]
- Hao, C.Y.; Feng, G.B.; Sun, H.G.; Li, H.P. Rigid-flexible coupling dynamics simulation of planetary gear transmission based on MFBD. J. Vibroeng. 2017, 19, 5668–5678. [Google Scholar] [CrossRef]
- Hsieh, C.-F. Dynamics Analysis of cycloidal speed reducers with pinwheel and nonpinwheel designs. Mech. Des. 2014, 136, 091008. [Google Scholar] [CrossRef]
- Huang, C.; Wang, J.X.; Xiao, K.; Li, M.; Li, J.Y. Dynamic characteristics analysis and experimental research on a new type planetary gear apparatus with small tooth number difference. Mech. Sci. Technol. 2013, 27, 1233–1244. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, A.; Qin, D.; Lim, T.C.; Shu, R.; Lin, X.; Meng, F. A coupling dynamics analysis method for a multistage planetary gear system. Mech. Mach. Theory 2017, 110, 27–49. [Google Scholar] [CrossRef]
- Wang, H.W.; Zhang, T.; Liu, G.; Wu, L.Y. System-structure coupling dynamic analysis of planetary gears. Math. Probl. Eng. 2015, 2015, 350616. [Google Scholar] [CrossRef]
- Chen, X.H.; Yang, X.K.; Zuo, M.J.; Tian, Z.G. Planetary gearbox dynamic modeling considering bearing clearance and sun gear tooth crack. Sensors 2021, 21, 2638. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.Q.; Li, X.A.; Yang, M.D.; Wang, F.; Han, X. Non-random vibration analysis of rotate vector reducer. Sound Vib. 2023, 542, 22. [Google Scholar] [CrossRef]
- Matejić, M.; Blagojević, M.; Kostić, N.; Petrović, N.; Marjanović, N. Efficiency Analysis of New Two-Stage Cycloid Drive Concept. Tribol. Ind. 2020, 42, 337–343. [Google Scholar] [CrossRef]
- Bednarczyk, S. Analysis of the cycloidal reducer output mechanism while taking into account machining deviations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 7299–7313. [Google Scholar] [CrossRef]
- Blagojevic, M.; Matejic, M.; Kostic, N. Dynamic Behaviour of a Two-Stage Cycloidal Speed Reducer of a New Design Concept. Teh. Vjesn.-Tech. Gaz. 2018, 25, 291–298. [Google Scholar]
- Gorla, C.; Davoli, P.; Rosa, F.; Longoni, C.; Chiozzi, F.; Samarani, A. Theoretical and experimental analysis of a cycloidal speed reducer. J. Mech. Des. 2008, 130, 112604. [Google Scholar] [CrossRef]
- Efremenkov, E.A.; Shanin, S.A.; Martyushev, N.V. Development of an Algorithm for Computing the Force and Stress Parameters of a Cycloid Reducer. Mathematics 2023, 11, 993. [Google Scholar] [CrossRef]
- Maccioni, L.; Concli, F.; Blagojevic, M. A new three-stage gearbox concept for high reduction ratios: Use of a nested-cycloidal architecture to increase the power density. Mech. Mach. Theory 2023, 181, 105203. [Google Scholar] [CrossRef]
- Li, X.; Chen, B.K.; Wang, Y.W.; Lim, T.C. Mesh stiffness calculation of cycloid-pin gear pair with tooth profile modification and eccentricity error. Cent. South Univ. 2018, 25, 1717–1731. [Google Scholar] [CrossRef]


| Parameter Symbols | Descriptions | Values |
|---|---|---|
| ns | Tooth number of sun gear | 12 |
| np | Tooth number of planet gear | 36 |
| nr | Pin number | 40 |
| nc | Tooth number of cycloid gear | 39 |
| m | Modulus (mm) | 1.5 |
| α | Pressure angle (°) | 20 |
| ρ | Pin radius (mm) | 3 |
| a | Pin position radius (mm) | 85.8 |
| e | Eccentricity (mm) | 1.3 |
| i | Reduction ratio | 121 |
| rb | Radius of pin gear (mm) | 88 |
| B | Gear width (mm) | 12 |
| Parameter Symbols | Descriptions | Values |
|---|---|---|
| ms | Mass of sun gear (kg) | 1.3 |
| mp | Mass of planet gear (kg) | 0.88 |
| mH | Mass of crank shaft (kg) | 0.4 |
| mc | Mass of cycloid gear (kg) | 2.76 |
| mo | Mass of output disc (kg) | 15.33 |
| Js | Inertial of sun gear (kg· mm) | |
| Jp | Inertial of planet gear (kg· mm) | |
| JH | Inertial of crank shaft (kg· mm) | |
| Jc | Inertial of cycloid gear (kg· mm) | 0.0209 |
| Jo | Inertial of planet carrier (kg· mm) | 0.106 |
| kst | Torsional stiffness of sun gear (Nm/rad) | |
| ks | Radial supporting stiffness of sun gear (N/m) | |
| kHt | Torsional stiffness of crankshaft (Nm/rad)) | |
| kH | Bending stiffness of crankshaft (N/m) | |
| kHb | Supporting bearing stiffness of crankshaft (N/m) | |
| kcb | Turning-arm bearing stiffness of cycloid gear (N/m) | |
| ko | Radial supporting stiffness of output disc (N/m) |
| Parameters | Descriptions | Values |
|---|---|---|
| Machining eccentricity error of sun gear (mm, °) | ||
| Machining eccentricity error of planet gear (mm, °) | ||
| Assembly error of sun gear (mm, °) | ||
| Eccentricity error of crankshaft hole in the cycloid gear (mm, °) | ||
| Eccentricity error of crankshaft cam (mm, °) | ||
| Eccentricity error of crankshaft hole in the output disc (mm, °) | ||
| Assembly eccentricity error of output disc (mm, °) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Huang, J.; Ding, C.; Guo, R.; Niu, W. Dynamic Modeling and Analysis of an RV Reducer Considering Tooth Profile Modifications and Errors. Machines 2023, 11, 626. https://doi.org/10.3390/machines11060626
Li X, Huang J, Ding C, Guo R, Niu W. Dynamic Modeling and Analysis of an RV Reducer Considering Tooth Profile Modifications and Errors. Machines. 2023; 11(6):626. https://doi.org/10.3390/machines11060626
Chicago/Turabian StyleLi, Xuan, Jiaqing Huang, Chuancang Ding, Ran Guo, and Weilong Niu. 2023. "Dynamic Modeling and Analysis of an RV Reducer Considering Tooth Profile Modifications and Errors" Machines 11, no. 6: 626. https://doi.org/10.3390/machines11060626
APA StyleLi, X., Huang, J., Ding, C., Guo, R., & Niu, W. (2023). Dynamic Modeling and Analysis of an RV Reducer Considering Tooth Profile Modifications and Errors. Machines, 11(6), 626. https://doi.org/10.3390/machines11060626







