Analytical Sensitivity Analysis of Dynamic Problems with Direct Differentiation of Generalized-α Time Integration
Abstract
1. Introduction
2. Sensitivity Analysis with Generalized-α Time Integration
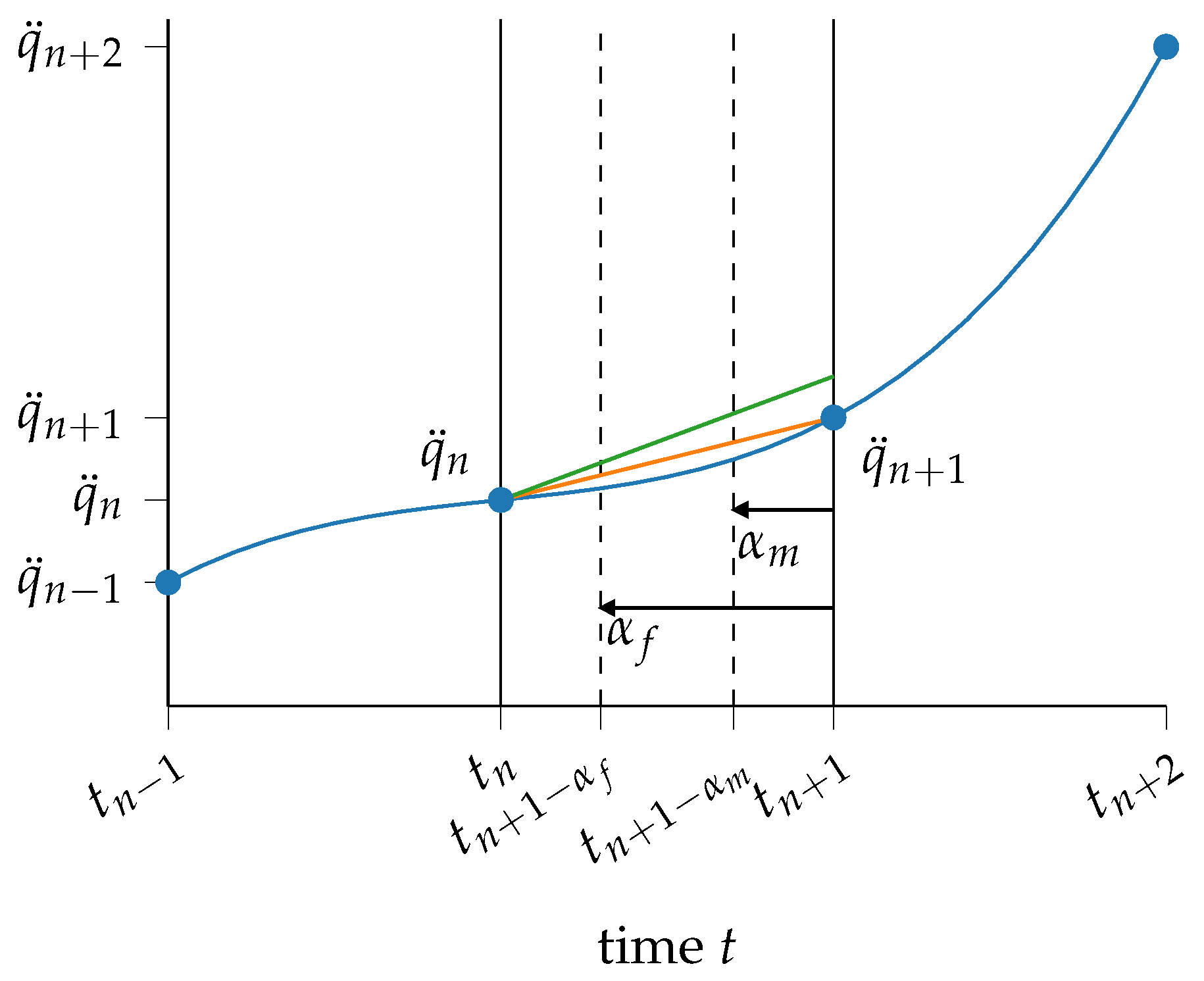
2.1. Generalized- Time Integration
2.2. Structural Dynamics
2.3. Flexible Multibody Dynamics
3. Numerical Results
3.1. Structural Dynamics
- sensitivities of position 2 with respect to stiffness 1 and mass 2 (Figure 4);
- sensitivities of velocity 2 with respect to stiffness 1 and mass 2 (Figure 5);
- sensitivities of acceleration 2 with respect to stiffness 1, stiffness 2 and mass 2 (Figure 6);
- sensitivities of acceleration 3 with respect to stiffness 1 and mass 2 (Figure 6).
- sensitivity of velocity 2 with respect to stiffness 2 (Figure 5);
- sensitivity of velocity 2 with respect to mass 3 (Figure 5);
- sensitivity of acceleration 2 with respect to stiffness 2 (Figure 6);
- sensitivity of acceleration 2 with respect to mass 3 (Figure 6).
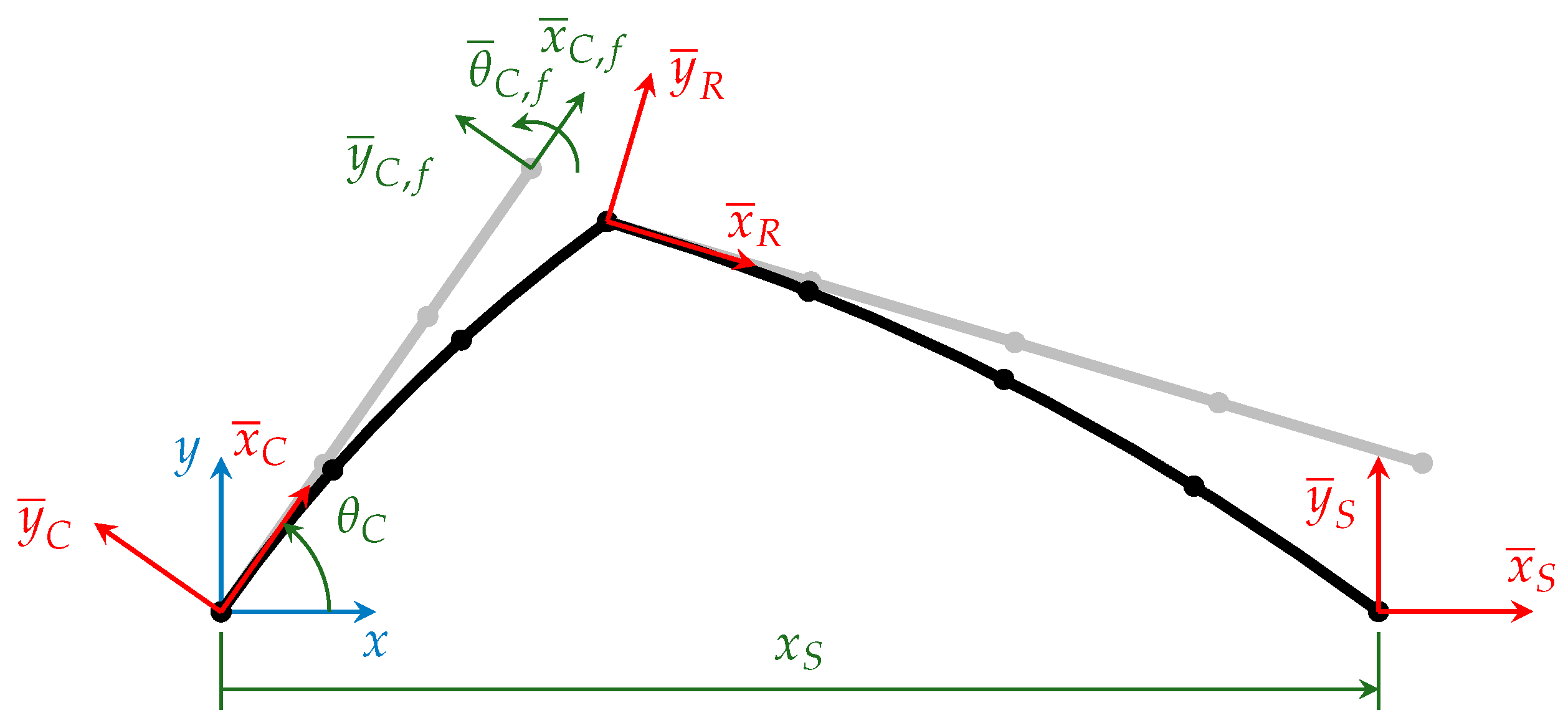
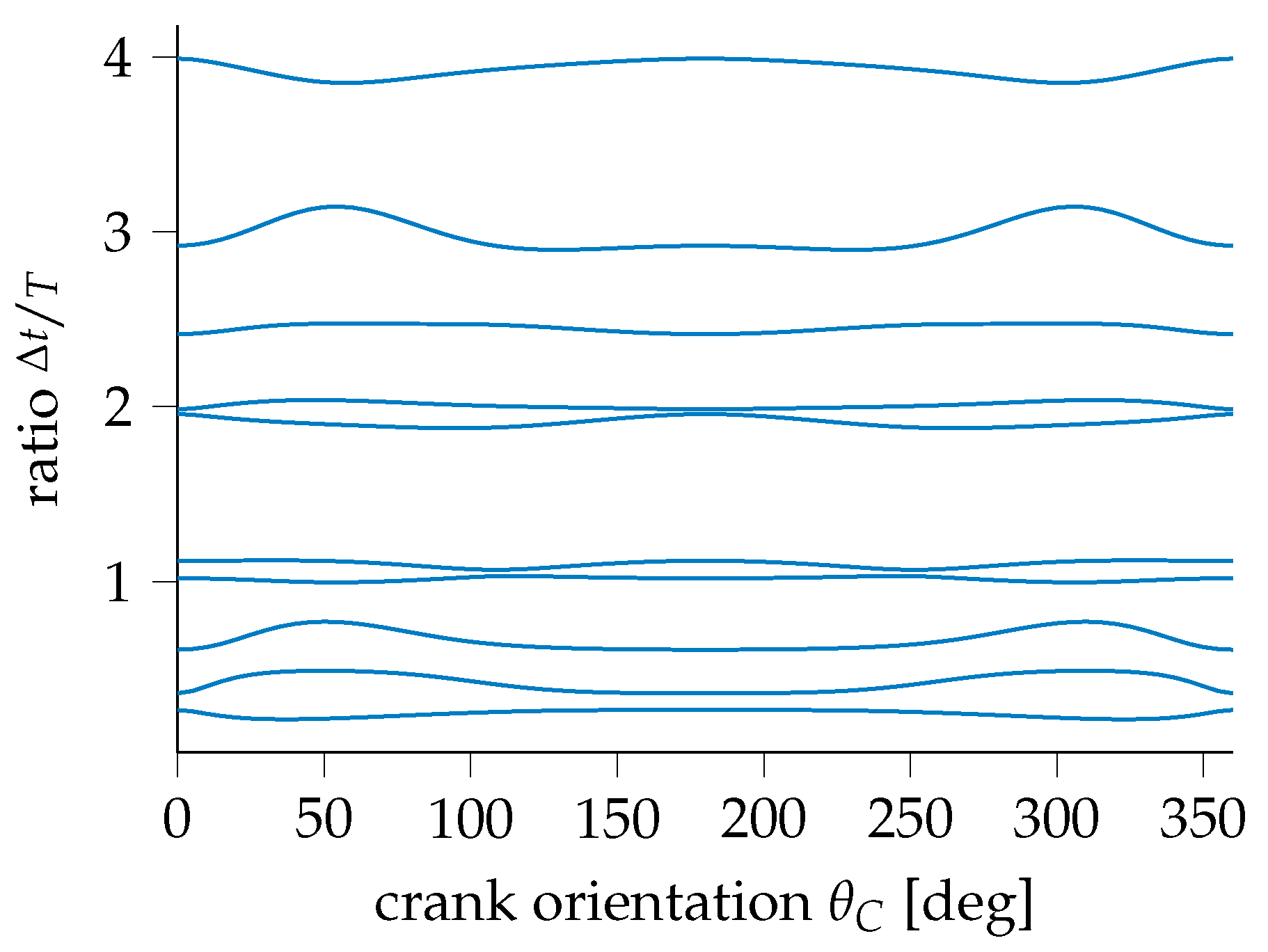
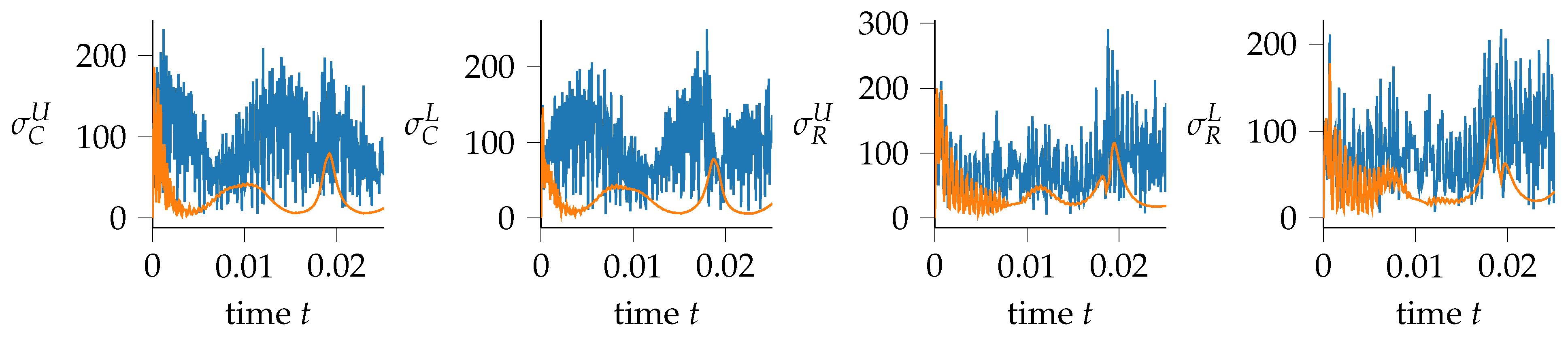
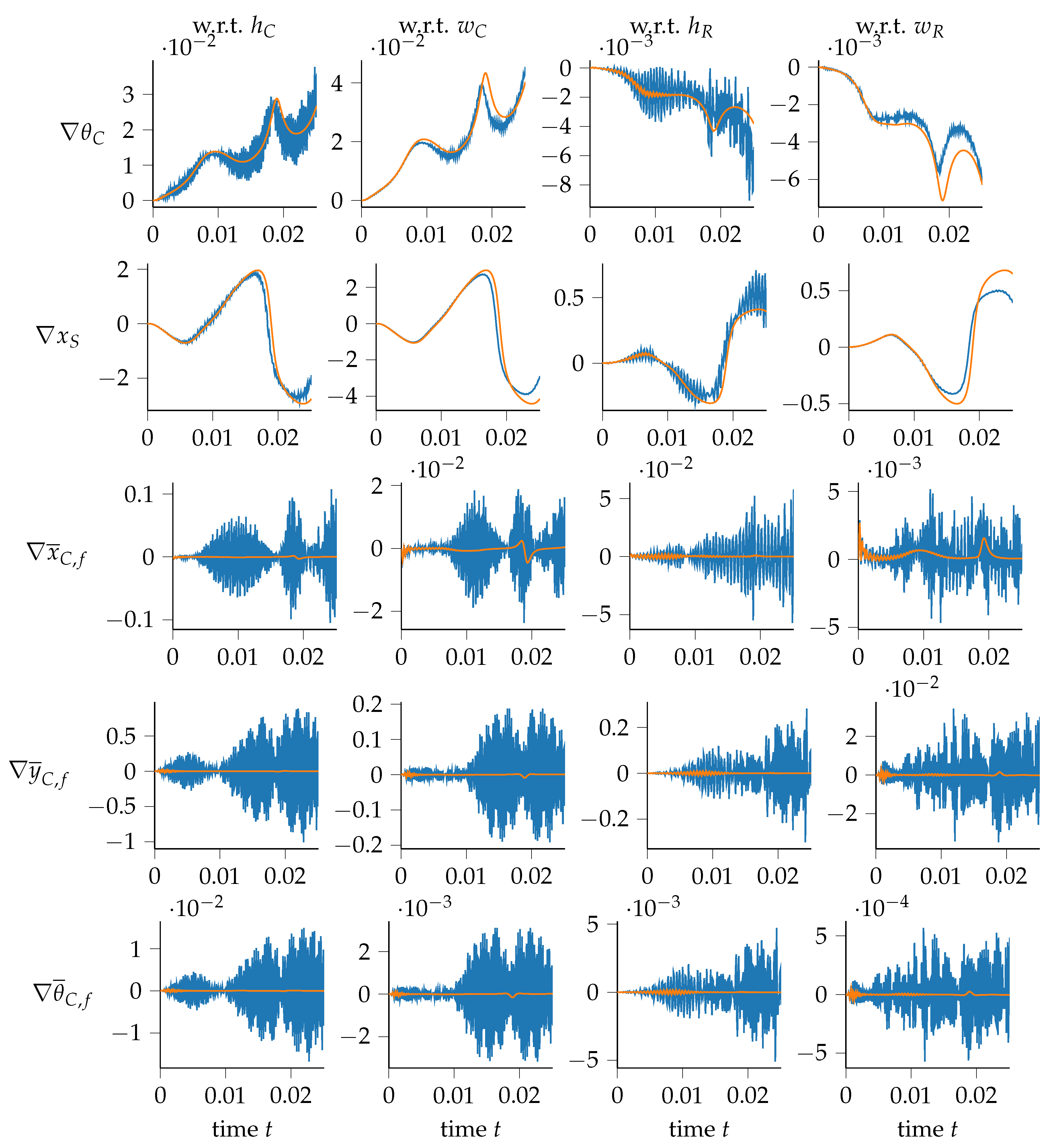
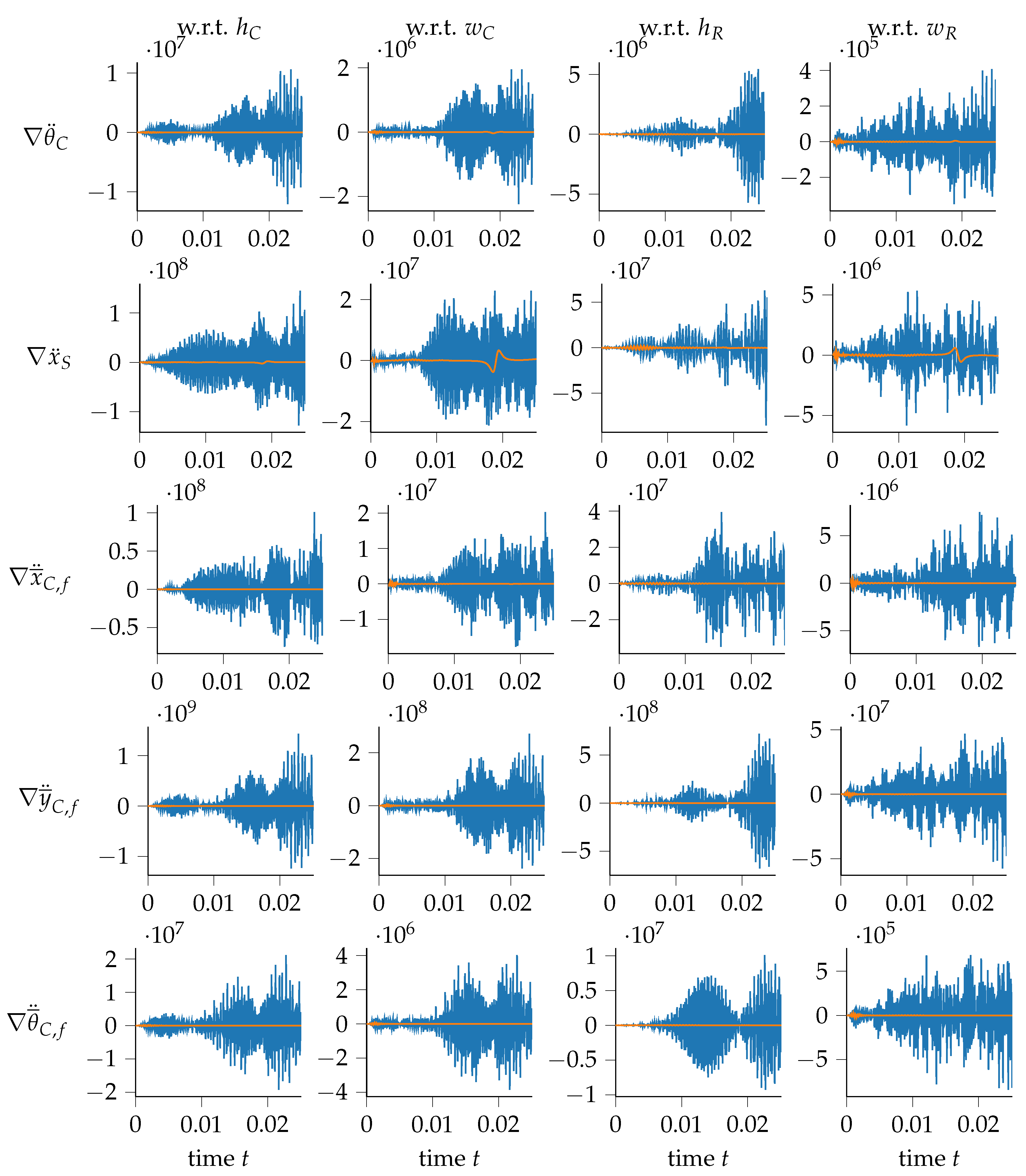
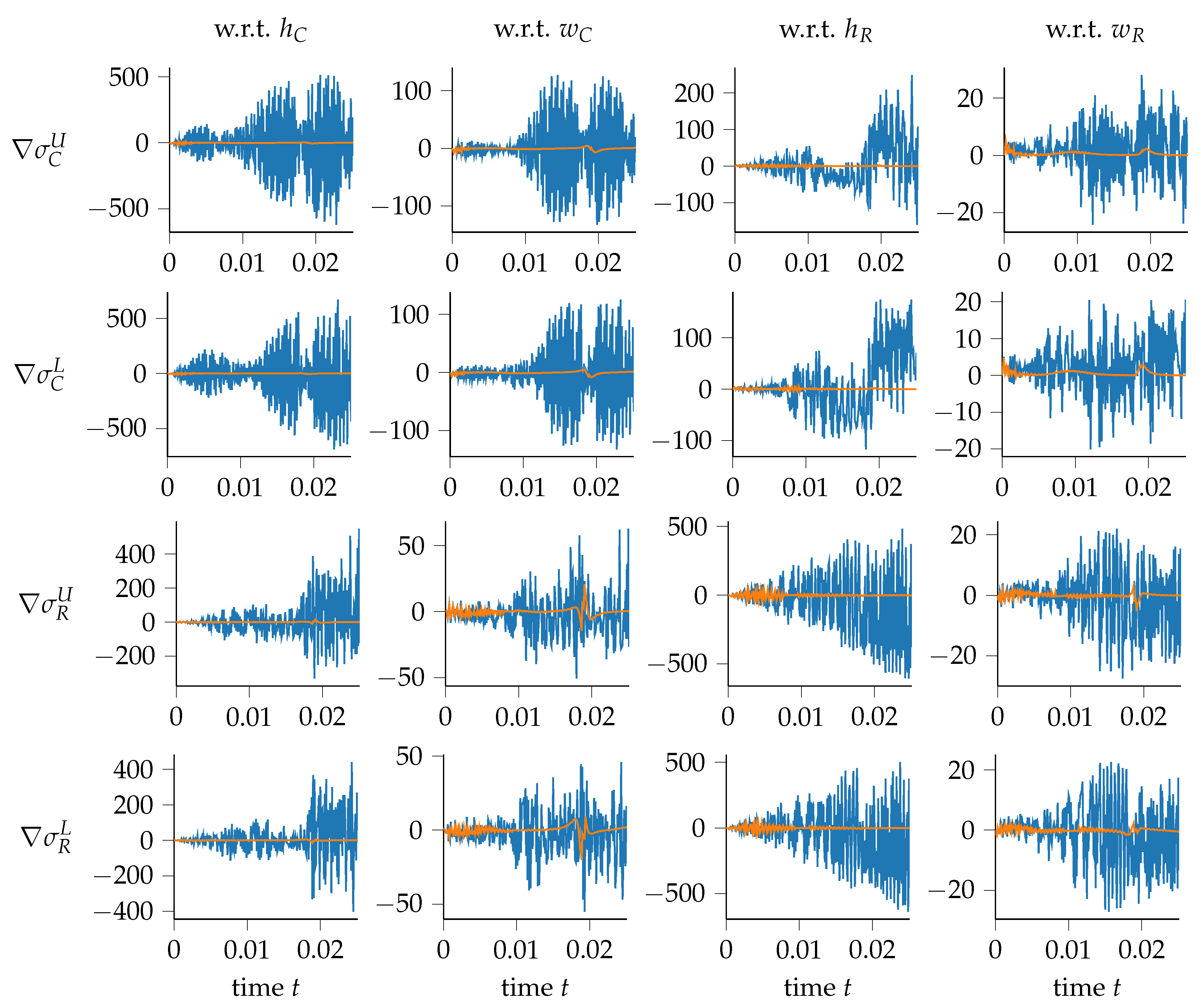
3.2. Flexible Slider–Crank Mechanism
- sensitivities of with respect to and ;
- sensitivities of with respect to , , and .
- sensitivities of with respect to and ;
- sensitivities of with respect to ;
- sensitivities of with respect to , and ;
- sensitivities of with respect to ; , and ;
- sensitivities of with respect to , , and .
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Effective Equations of Motion for Structural Dynamics
Appendix A.1. Primal Analysis
Appendix A.2. Sensitivity Analysis
Appendix B. Derivation of Effective Equations of Motion for Flexible Multibody Dynamics
Appendix B.1. Primal Analysis
Appendix B.2. Nonlinear Solver
Appendix B.3. Sensitivity Analysis
References
- Hien, T.D.; Kleiber, M. Stochastic design sensitivity in structural dynamics. Int. J. Numer. Methods Eng. 1991, 32, 1247–1265. [Google Scholar] [CrossRef]
- Cho, S.; Choi, K.K. Design sensitivity analysis and optimization of non-linear transient dynamics. Part I–sizing design. Int. J. Numer. Methods Eng. 2000, 48, 351–373. [Google Scholar] [CrossRef]
- Cho, S.; Choi, K.K. Design sensitivity analysis and optimization of non-linear transient dynamics. Part II–configuration design. Int. J. Numer. Methods Eng. 2000, 48, 375–399. [Google Scholar] [CrossRef]
- van Keulen, F.; Haftka, R.; Kim, N. Review of options for structural design sensitivity analysis—Part 1: Linear systems. Comput. Methods Appl. Mech. Eng. 2005, 194, 3213–3243. [Google Scholar] [CrossRef]
- Martins, J.R.R.A.; Hwang, J.T. Review and unification of methods for computing derivatives of multidisciplinary computational models. AIAA J. 2013, 51, 2582–2599. [Google Scholar] [CrossRef]
- Tortorelli, D.A.; Michaleris, P. Design sensitivity analysis: Overview and review. Inverse Probl. Eng. 1994, 1, 71–105. [Google Scholar] [CrossRef]
- Wehrle, E.; Gufler, V. Lightweight engineering design of nonlinear dynamic systems with gradient-based structural design optimization. In Proceedings of the Munich Symposium on Lightweight Design 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 44–57. [Google Scholar] [CrossRef]
- Wehrle, E. Optimal lightweight engineering via a three-block solver scheme for mechanical analysis. In Optimal Design and Control of Multibody Systems; Nachbagauer, K., Held, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2024; Volume 42, pp. 16–29. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Hilber, H.M.; Hughes, T.J.R.; Taylor, R.L. Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq. Eng. Struct. Dyn. 1977, 5, 283–292. [Google Scholar] [CrossRef]
- Wood, W.L.; Bossak, M.; Zienkiewicz, O.C. An alpha modification of Newmark’s method. Int. J. Numer. Methods Eng. 1980, 15, 1562–1566. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method. J. Appl. Mech. 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Gufler, V.; Wehrle, E.; Vidoni, R. Sensitivity analysis of flexible multibody dynamics with generalized-α time integration and Baumgarte stabilization: A study on numerical stability. In Mechanisms and Machine Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 147–155. [Google Scholar] [CrossRef]
- Griewank, A.; Walther, A. Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, 2nd ed.; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Naumann, U. The Art of Differentiating Computer Programs: An Introduction to Algorithmic Differentiation; SIAM: Philadelphia, PA, USA, 2012. [Google Scholar]
- Callejo, A.; Dopico, D. Direct sensitivity analysis of multibody systems: A vehicle dynamics benchmark. J. Comput. Nonlinear Dyn. 2019, 14, 021004. [Google Scholar] [CrossRef]
- Margossian, C.C. A review of automatic differentiation and its efficient implementation. WIREs Data Min. Knowl. Discov. 2019, 9, e1305. [Google Scholar] [CrossRef]
- Pi, T.; Zhang, Y.; Chen, L. First order sensitivity analysis of flexible multibody systems using absolute nodal coordinate formulation. Multibody Syst. Dyn. 2012, 27, 153–171. [Google Scholar] [CrossRef]
- Held, A.; Knüfer, S.; Seifried, R. Structural sensitivity analysis of flexible multibody systems modeled with the floating frame of reference approach using the adjoint variable method. Multibody Syst. Dyn. 2016, 40, 287–302. [Google Scholar] [CrossRef]
- Boopathy, K.; Kennedy, G. Adjoint-based derivative evaluation methods for flexible multibody systems with rotorcraft applications. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- Martins, J.R.R.A.; Kennedy, G.J. Enabling large-scale multidisciplinary design optimization through adjoint sensitivity analysis. Struct. Multidiscip. Optim. 2021, 64, 2959–2974. [Google Scholar] [CrossRef]
- Nachbagauer, K.; Oberpeilsteiner, S.; Sherif, K.; Steiner, W. The use of the adjoint method for solving typical optimization problems in multibody dynamics. J. Comput. Nonlinear Dyn. 2015, 10, 061011. [Google Scholar] [CrossRef]
- Lauß, T.; Oberpeilsteiner, S.; Steiner, W.; Nachbagauer, K. The discrete adjoint method for parameter identification in multibody system dynamics. Multibody Syst. Dyn. 2017, 42, 397–410. [Google Scholar] [CrossRef]
- Boopathy, K.; Kennedy, G.J. Parallel finite element framework for rotorcraft multibody dynamics and discrete adjoint sensitivities. Aiaa J. 2019, 57, 3159–3172. [Google Scholar] [CrossRef]
- Boopathy, K. Adjoint Based Design Optimization of Systems with Time Dependent Physics and Probabilistically Modeled Uncertainties. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2020. [Google Scholar]
- Ebrahimi, M.; Butscher, A.; Cheong, H.; Iorio, F. Design optimization of dynamic flexible multibody systems using the discrete adjoint variable method. Comput. Struct. 2019, 213, 82–99. [Google Scholar] [CrossRef]
- Nejat, A.A.; Moghadasi, A.; Held, A. Adjoint sensitivity analysis of flexible multibody systems in differential-algebraic form. Comput. Struct. 2020, 228, 106–148. [Google Scholar] [CrossRef]
- Held, A. On design sensitivities in the structural analysis and optimization of flexible multibody systems. Multibody Syst. Dyn. 2022, 54, 53–74. [Google Scholar] [CrossRef]
- Solano, D.; Sarojini, D.; Rajaram, D.; Mavris, D.N. Adjoint-based analysis and optimization of beam-like structures subjected to dynamic loads. Struct. Multidiscip. Optim. 2022, 65, 52. [Google Scholar] [CrossRef]
- Haug, E.J.; Arora, J.S. Design sensitivity analysis of elastic mechanical systems. Comput. Methods Appl. Mech. Eng. 1978, 15, 35–62. [Google Scholar] [CrossRef]
- Hsieh, C.C.; Arora, J.S. Structural design sensitivity analysis with general boundary conditions: Dynamic problem. Int. J. Numer. Methods Eng. 1985, 21, 267–283. [Google Scholar] [CrossRef]
- Baier, H.; Seeßelberg, C.; Specht, B. Optimierung in der Strukturmechanik; Vieweg: Braunschweig/Wiesbaden, Germany, 1994. [Google Scholar] [CrossRef]
- Trier, S.; Marthinsen, A.; Sivertsen, O. Design sensitivities by the adjoint variable method in nonlinear structural dynamics. In Proceedings of the SIMS Simulation Conference, Trondheim, Norway, 11–13 June 1996. [Google Scholar]
- Michaleris, P.; Tortorelli, D.A.; Vidal, C.A. Tangent operators and design sensitivity formulations for transient non-linear coupled problems with applications to elastoplasticity. Int. J. Numer. Methods Eng. 1994, 37, 2471–2499. [Google Scholar] [CrossRef]
- Bhalerao, K.D.; Poursina, M.; Anderson, K.S. An efficient direct differentiation approach for sensitivity analysis of flexible multibody systems. Multibody Syst. Dyn. 2010, 23, 121–140. [Google Scholar] [CrossRef]
- Zhu, Y. Sensitivity Analysis and Optimization of Multibody Systems. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2014. [Google Scholar]
- Dopico, D.; Zhu, Y.; Sandu, A.; Sandu, C. Direct and adjoint sensitivity analysis of ordinary differential equation multibody formulations. J. Comput. Nonlinear Dyn. 2014, 10, 011012. [Google Scholar] [CrossRef]
- Callejo, A.; Sonneville, V.; Bauchau, O. Discrete adjoint method for the sensitivity analysis of flexible multibody systems. J. Comput. Nonlinear Dyn. 2018, 14, 021001. [Google Scholar] [CrossRef]
- Cao, Z.; Yao, J.; Jia, Z.; Liang, D. Transient response sensitivity analysis of localized nonlinear structure using direct differentiation method. Machines 2022, 10, 1039. [Google Scholar] [CrossRef]
- Haug, E.J.; Ehle, P.E. Second-order design sensitivity analysis of mechanical system dynamics. Int. J. Numer. Methods Eng. 1982, 18, 1699–1717. [Google Scholar] [CrossRef]
- Ding, J.Y.; Pan, Z.K.; Chen, L.Q. Second order adjoint sensitivity analysis of multibody systems described by differential-algebraic equations. Multibody Syst. Dyn. 2007, 18, 599–617. [Google Scholar] [CrossRef]
- Belotti, R.; Palomba, I.; Wehrle, E.; Vidoni, R. An approximation-based design optimization approach to eigenfrequency assignment for flexible multibody systems. Appl. Sci. 2021, 11, 11558. [Google Scholar] [CrossRef]
- Palomba, I.; Vidoni, R. Flexible-link multibody system eigenvalue analysis parameterized with respect to rigid-body motion. Appl. Sci. 2019, 9, 5156. [Google Scholar] [CrossRef]
- Brüls, O.; Lemaire, E.; Duysinx, P.; Eberhard, P. Multibody dynamics. In Multibody Dynamics: Computational Methods and Applications; Arczewski, K., Blajer, W., Fraczek, J., Wojtyra, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Chapter Optimization of Multibody Systems and Their Structural Components; pp. 49–68. [Google Scholar] [CrossRef]
- Gufler, V.; Wehrle, E.; Vidoni, R. Multiphysical design optimization of multibody systems: Application to a Tyrolean weir cleaning mechanism. In Proceedings of the 3rd International Conference of IFToMM Italy, Naples, Italy, 9–11 September 2020. [Google Scholar] [CrossRef]
- Gufler, V.; Wehrle, E.; Achleitner, J.; Vidoni, R. A semi-analytical approach to sensitivity analysis with flexible multibody dynamics of a morphing forward wing section. Multibody Syst. Dyn. 2023, 58, 1–20. [Google Scholar] [CrossRef]
- Gufler, V.; Zwölfer, A.; Wehrle, E. Analytical derivatives of flexible multibody dynamics with the floating frame of reference formulation. Multibody Syst. Dyn. 2022, 60, 257–288. [Google Scholar] [CrossRef]
- Brüls, O.; Golinval, J. The generalized-α method in mechatronic applications. ZAMM 2006, 86, 748–758. [Google Scholar] [CrossRef]
- Jansen, K.E.; Whiting, C.H.; Hulbert, G.M. A generalized-α method for integrating the filtered Navier–Stokes equations with a stabilized finite element method. Comput. Methods Appl. Mech. Eng. 2000, 190, 305–319. [Google Scholar] [CrossRef]
- Köbis, M.A.; Arnold, M. Convergence of generalized-α time integration for nonlinear systems with stiff potential forces. Multibody Syst. Dyn. 2015, 37, 107–125. [Google Scholar] [CrossRef]
- Bestle, D. Analyse und Optimierung von Mehrkörpersystemen; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar] [CrossRef]
- Haug, E.J.; Arora, J.S. Applied Optimal Design: Mechanical and Structural Systems; John Wiley & Sons: Hoboken, NJ, USA, 1979. [Google Scholar]
- Gufler, V.; Wehrle, E.; Zwölfer, A. A review of flexible multibody dynamics for gradient-based design optimization. Multibody Syst. Dyn. 2021, 53, 379–409. [Google Scholar] [CrossRef]
- Shabana, A.A. Flexible multibody dynamics: Review of past and recent developments. Multibody Syst. Dyn. 1997, 1, 189–222. [Google Scholar] [CrossRef]
- Shabana, A.A. Dynamics of Multibody Systems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Petzold, L.; Lötstedt, P. Numerical solution of nonlinear differential equations with algebraic constraints II: Practical implications. SIAM J. Sci. Stat. Comput. 1986, 7, 720–733. [Google Scholar] [CrossRef]
- Bottasso, C.L.; Bauchau, O.A.; Cardona, A. Time-step-size-independent conditioning and sensitivity to perturbations in the numerical solution of index three differential algebraic equations. SIAM J. Sci. Comput. 2007, 29, 397–414. [Google Scholar] [CrossRef][Green Version]
- Bauchau, O.A. Flexible Multibody Dynamics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Dopico, D.; González, F.; Luaces, A.; Saura, M.; García-Vallejo, D. Direct sensitivity analysis of multibody systems with holonomic and nonholonomic constraints via an index-3 augmented Lagrangian formulation with projections. Nonlinear Dyn. 2018, 93, 2039–2056. [Google Scholar] [CrossRef]
- Baumgarte, J. Stabilization of constraints and integrals of motion in dynamical systems. Comput. Methods Appl. Mech. Eng. 1972, 1, 1–16. [Google Scholar] [CrossRef]
- Gufler, V.; Wehrle, E.; Vidoni, R. Analytical sensitivity analysis of flexible multibody dynamics with index-1 differential-algebraic equations and Baumgarte stabilization. Int. J. Mech. Control 2023, 24, 3–14. [Google Scholar]
- Arnold, M.; Brüls, O. Convergence of the generalized-α scheme for constrained mechanical systems. Multibody Syst. Dyn. 2007, 18, 185–202. [Google Scholar] [CrossRef]
- Bathe, K.J.; Noh, G. Insight into an implicit time integration scheme for structural dynamics. Comput. Struct. 2012, 98–99, 1–6. [Google Scholar] [CrossRef]
- Huang, C.; Fu, M. A composite collocation method with low-period elongation for structural dynamics problems. Comput. Struct. 2018, 195, 74–84. [Google Scholar] [CrossRef]
- Kadapa, C.; Dettmer, W.; Perić, D. On the advantages of using the first-order generalised-alpha scheme for structural dynamic problems. Comput. Struct. 2017, 193, 226–238. [Google Scholar] [CrossRef]
- Malakiyeh, M.M.; Shojaee, S.; Javaran, S.H. Development of a direct time integration method based on Bezier curve and 5th-order Bernstein basis function. Comput. Struct. 2018, 194, 15–31. [Google Scholar] [CrossRef]
- Namadchi, A.H.; Jandaghi, E.; Alamatian, J. A new model-dependent time integration scheme with effective numerical damping for dynamic analysis. Eng. Comput. 2020, 37, 2543–2558. [Google Scholar] [CrossRef]
- Noh, G.; Bathe, K.J. The Bathe time integration method with controllable spectral radius: The ρ∞-Bathe method. Comput. Struct. 2019, 212, 299–310. [Google Scholar] [CrossRef]
- Shojaee, S.; Rostami, S.; Abbasi, A. An unconditionally stable implicit time integration algorithm: Modified quartic B-spline method. Comput. Struct. 2015, 153, 98–111. [Google Scholar] [CrossRef]
- Wen, W.; Wei, K.; Lei, H.; Duan, S.; Fang, D. A novel sub-step composite implicit time integration scheme for structural dynamics. Comput. Struct. 2017, 182, 176–186. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Englewood Cliffs, NJ, USA, 1996; p. 1037. [Google Scholar]
- Kreisselmeier, G.; Steinhauser, R. Systematic control design by optimizing a vector performance index. In Proceedings of the International Federation of Active Controls Symposium on Computer-Aided Design of Control Systems, Zürich, Switzerland, 29–31 August 1979. [Google Scholar] [CrossRef]
- Martins, J.R.R.A.; Poon, N.M.K. On structural optimization using constraint aggregation. In Proceedings of the 6th World Congress on Structural and Multidisciplinary Optimization, Rio de Janeiro, Brazi, 30 May–3 June 2005. [Google Scholar]
- Duddeck, F. Multidisciplinary optimization of car bodies. Struct. Multidiscip. Optim. 2008, 35, 375–389. [Google Scholar] [CrossRef]
- Kurtaran, H.; Eskandarian, A.; Marzougui, D.; Bedewi, N.E. Crashworthiness design optimization using successive response surface approximations. Comput. Mech. 2002, 29, 409–421. [Google Scholar] [CrossRef]
- Langer, H. Extended Evolutionary Algorithms for Multiobjective and Discrete Design Optimization of Structure. Ph.D. Dissertation, Lehrstuhl für Leichtbau, Technische Universität München, Munich, Germany, 2005. [Google Scholar]
- Boursier Niutta, C.; Wehrle, E.J.; Duddeck, F.; Belingardi, G. Surrogate modeling in design optimization of structures with discontinuous responses: A new approach for ill-posed problems in crashworthiness design. Struct. Multidiscip. Optim. 2018, 57, 1857–1869. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sábester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; Wiley: Hoboken, NJ, USA, 2008; p. 227. [Google Scholar]
- Xu, Q.; Wehrle, E.; Baier, H. Knowledge-based surrogate modeling in engineering design optimization. In Surrogate-Based Modeling and Optimization; Koziel, S., Leifsson, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 313–336. [Google Scholar] [CrossRef]

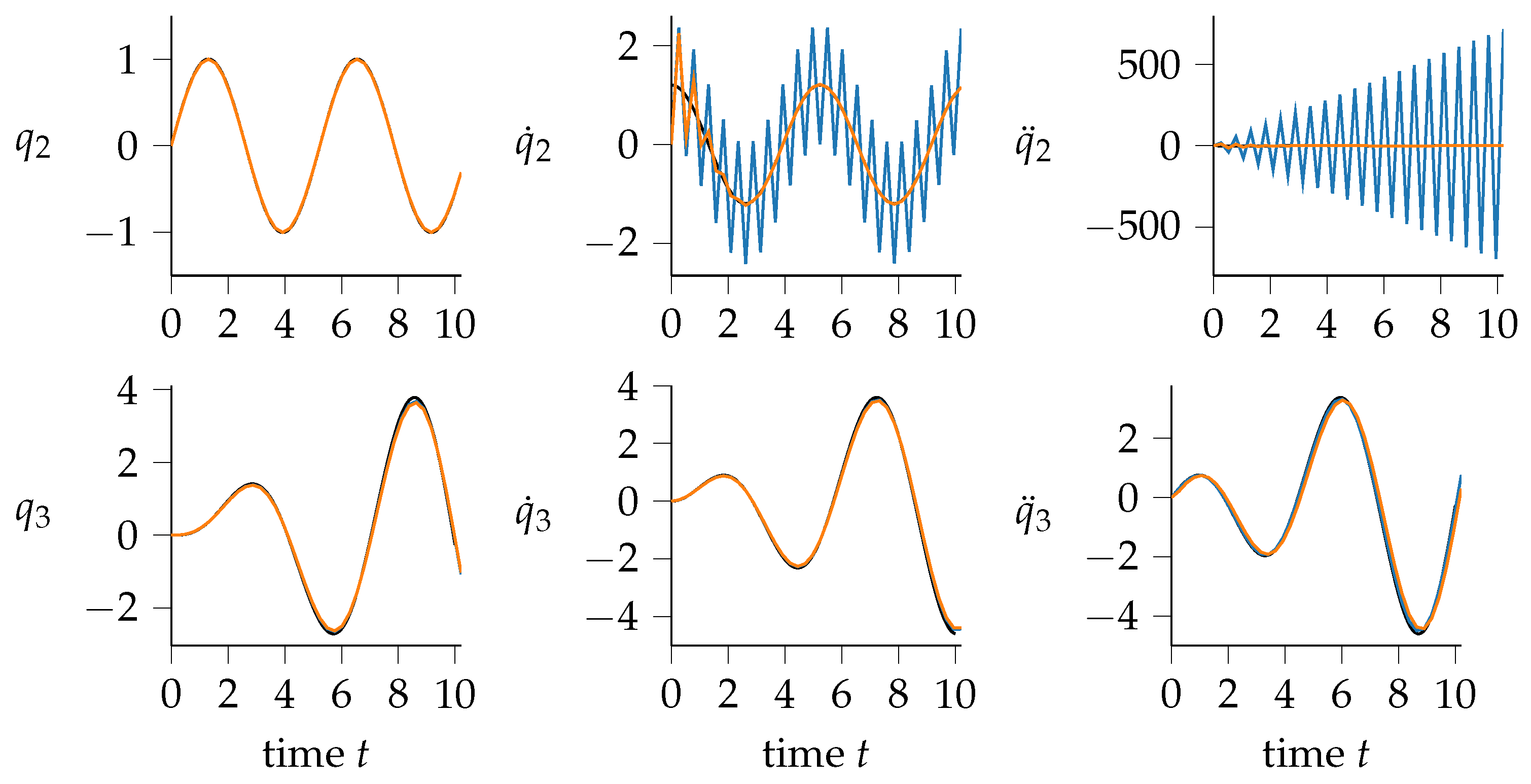

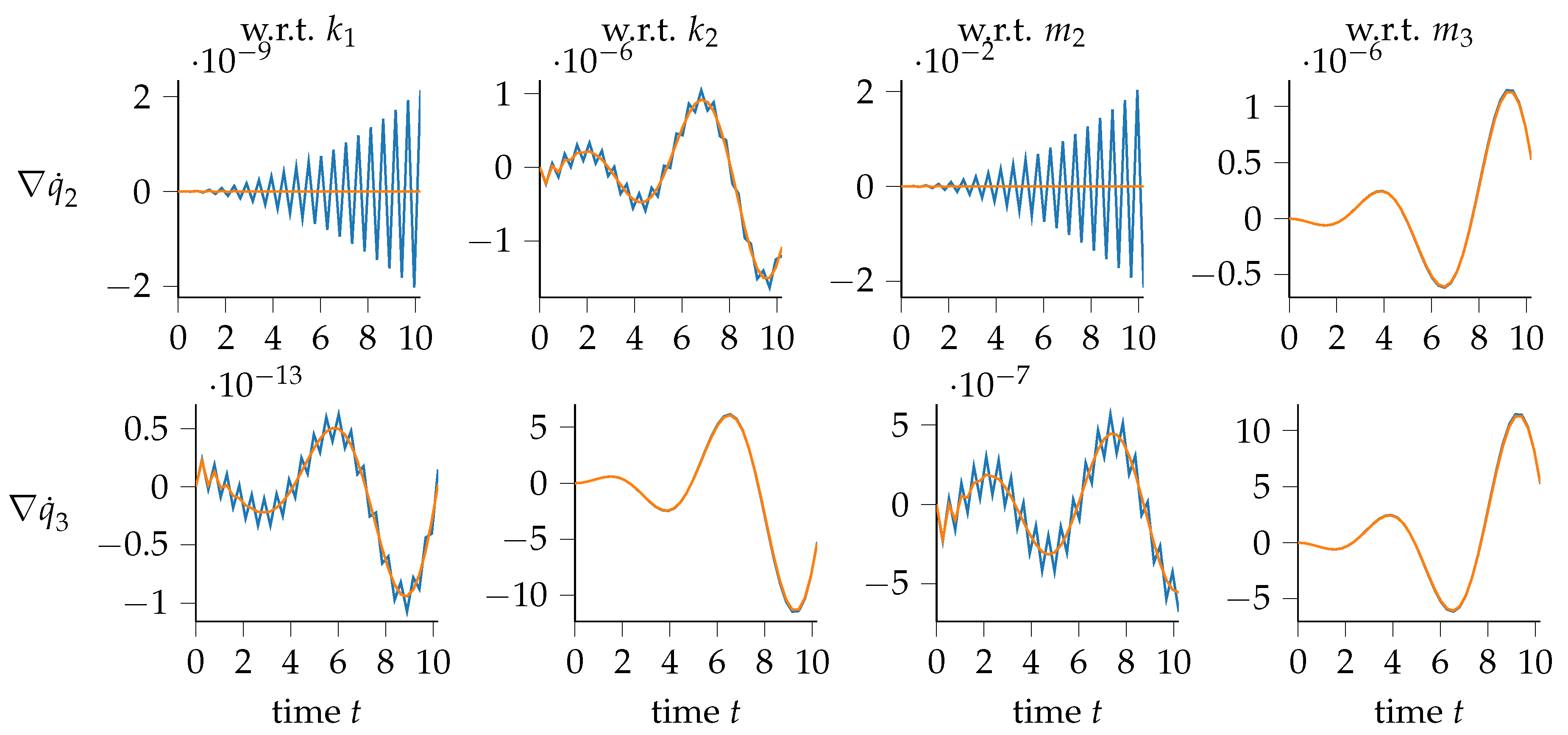




| Time Integration | Sensitivity Analysis | Calculation Time | Speedup |
|---|---|---|---|
| Newmark-β | None | 0.0555 | – |
| Newmark-β | Finite differencing | 0.2088 | – |
| Newmark-β | Analytical | 0.1023 | 2.0410 |
| Generalized-α | None | 0.0458 | – |
| Generalized-α | Finite differencing | 0.2122 | – |
| Generalized-α | Analytical | 0.0993 | 2.1370 |
| Property | Symbol | Crank | Rod | Slider | Units |
|---|---|---|---|---|---|
| Width | w | 20 | 20 | 30 | mm |
| Height | h | 30 | 30 | 30 | mm |
| Length | ℓ | 120 | 180 | 40 | mm |
| Property | Symbol | Value | Units |
|---|---|---|---|
| Density | |||
| Elastic modulus | E | 210,000 | |
| Poisson ratio | 0.3 | − |
| Time Integration | Sensitivity Analysis | Calculation Time [mm:ss] | Speedup |
|---|---|---|---|
| Newmark-β | None | 03:44 | – |
| Newmark-β | Finite differencing | 18:12 | – |
| Newmark-β | Analytical | 04:29 | 4.0595 |
| Generalized-α | None | 02:42 | – |
| Generalized-α | Finite differencing | 13:22 | – |
| Generalized-α | Analytical | 03:30 | 3.8190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wehrle, E.; Gufler, V. Analytical Sensitivity Analysis of Dynamic Problems with Direct Differentiation of Generalized-α Time Integration. Machines 2024, 12, 128. https://doi.org/10.3390/machines12020128
Wehrle E, Gufler V. Analytical Sensitivity Analysis of Dynamic Problems with Direct Differentiation of Generalized-α Time Integration. Machines. 2024; 12(2):128. https://doi.org/10.3390/machines12020128
Chicago/Turabian StyleWehrle, Erich, and Veit Gufler. 2024. "Analytical Sensitivity Analysis of Dynamic Problems with Direct Differentiation of Generalized-α Time Integration" Machines 12, no. 2: 128. https://doi.org/10.3390/machines12020128
APA StyleWehrle, E., & Gufler, V. (2024). Analytical Sensitivity Analysis of Dynamic Problems with Direct Differentiation of Generalized-α Time Integration. Machines, 12(2), 128. https://doi.org/10.3390/machines12020128








