Research on Grinding Force Prediction of Flexible Abrasive Disc Grinding Process of TC17 Titanium Alloy
Abstract
1. Introduction
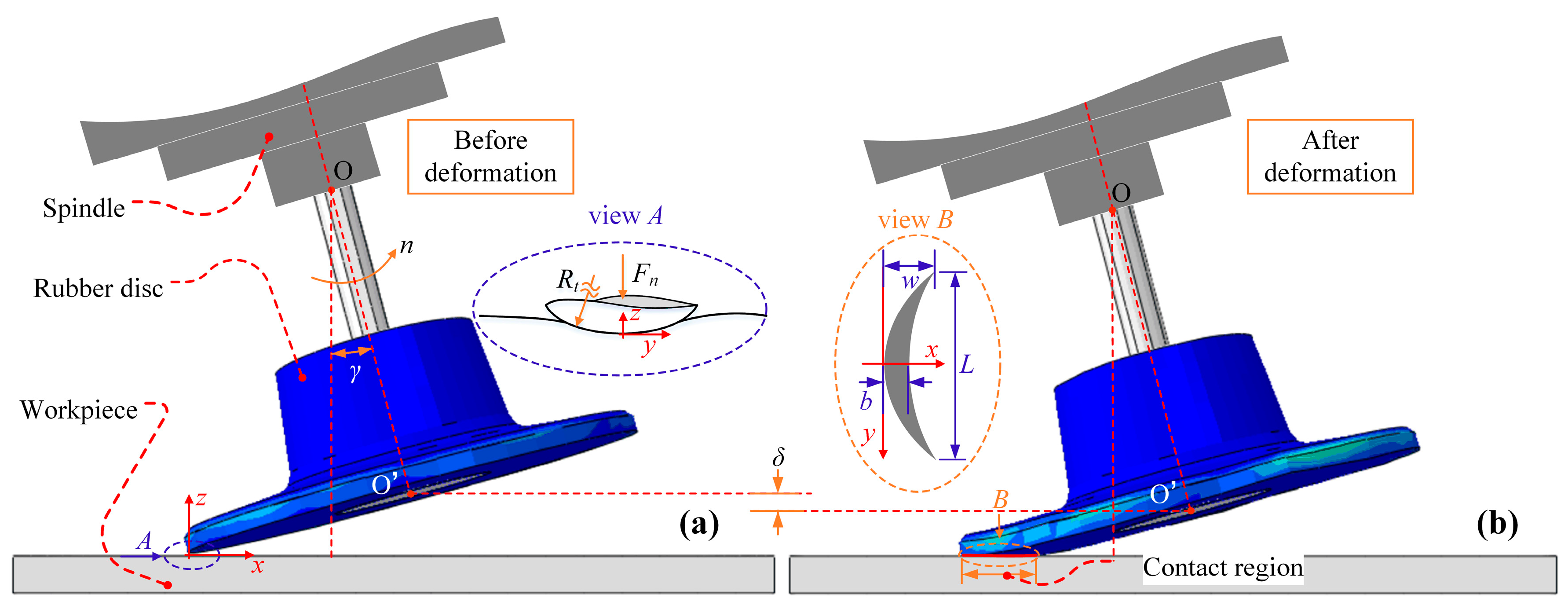
2. Characteristics of the Abrasive Disc Grinding Process
3. Characteristics of the Abrasive Disc Grinding Process
3.1. Macroscopic Grinding Force
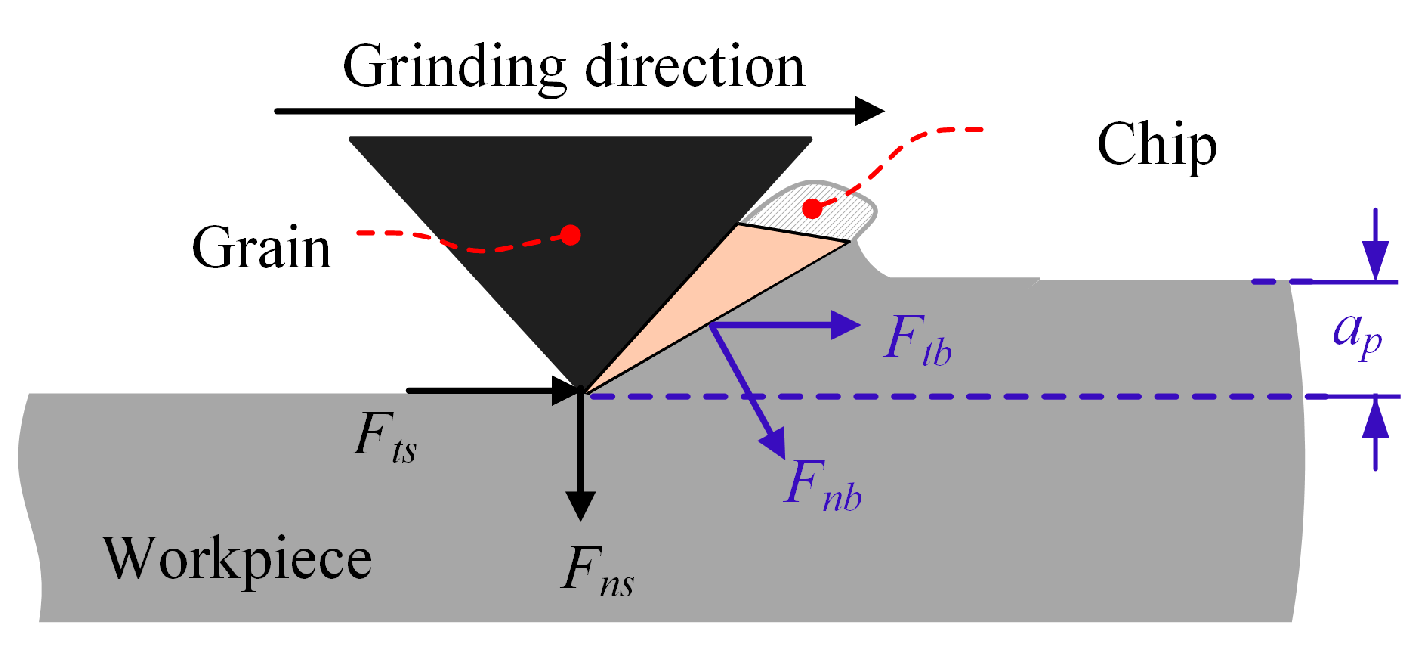
3.2. Microscopic Grinding Force
4. TC17 Abrasive Disc Grinding Experiment
4.1. Influence of Grinding Parameters on Normal Force
4.2. Multi-Factor Orthogonal Experiment
5. Prediction Model of Normal Grinding Force
5.1. Analysis of the Experimental Results Using Response Surface Optimization
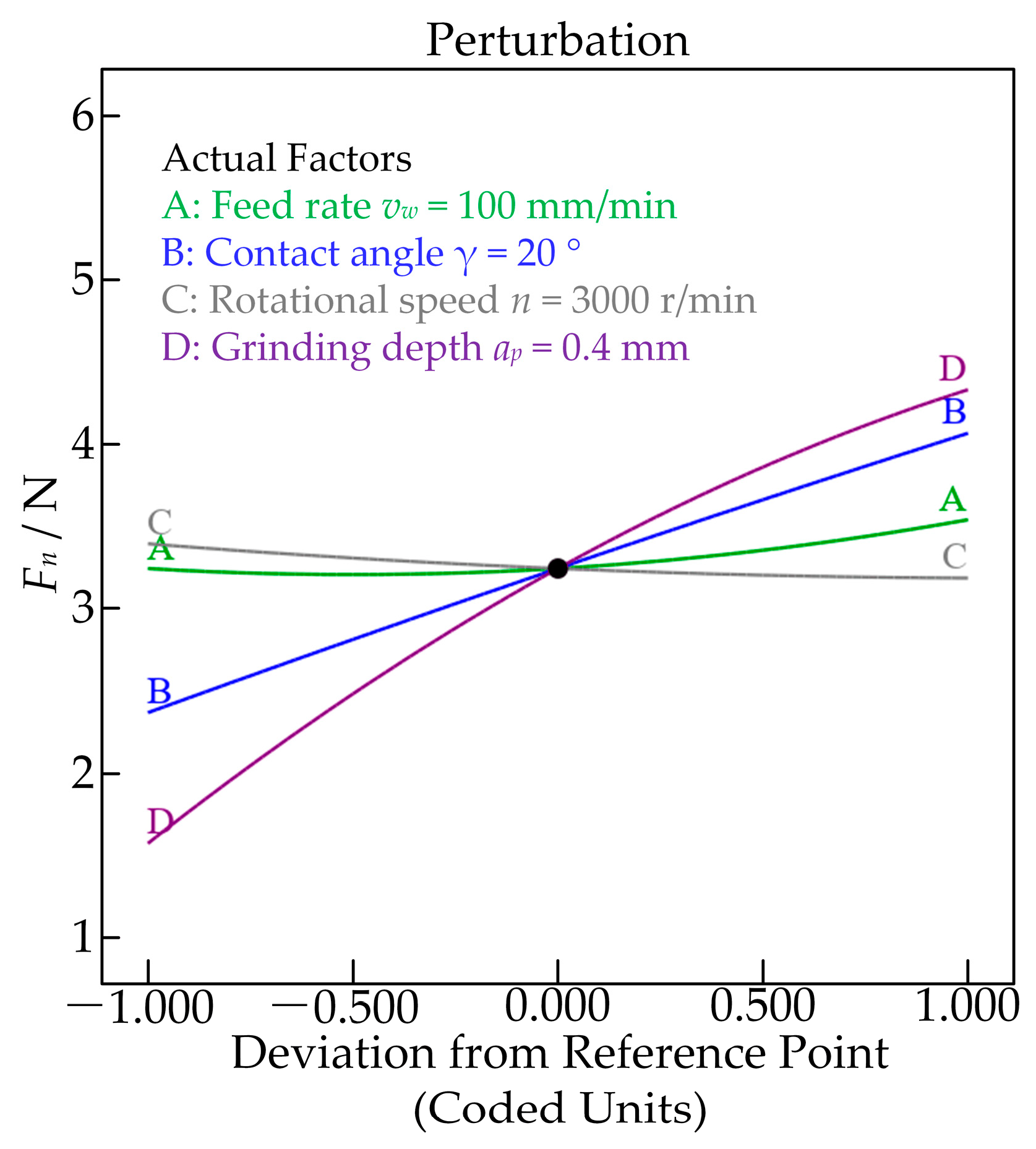
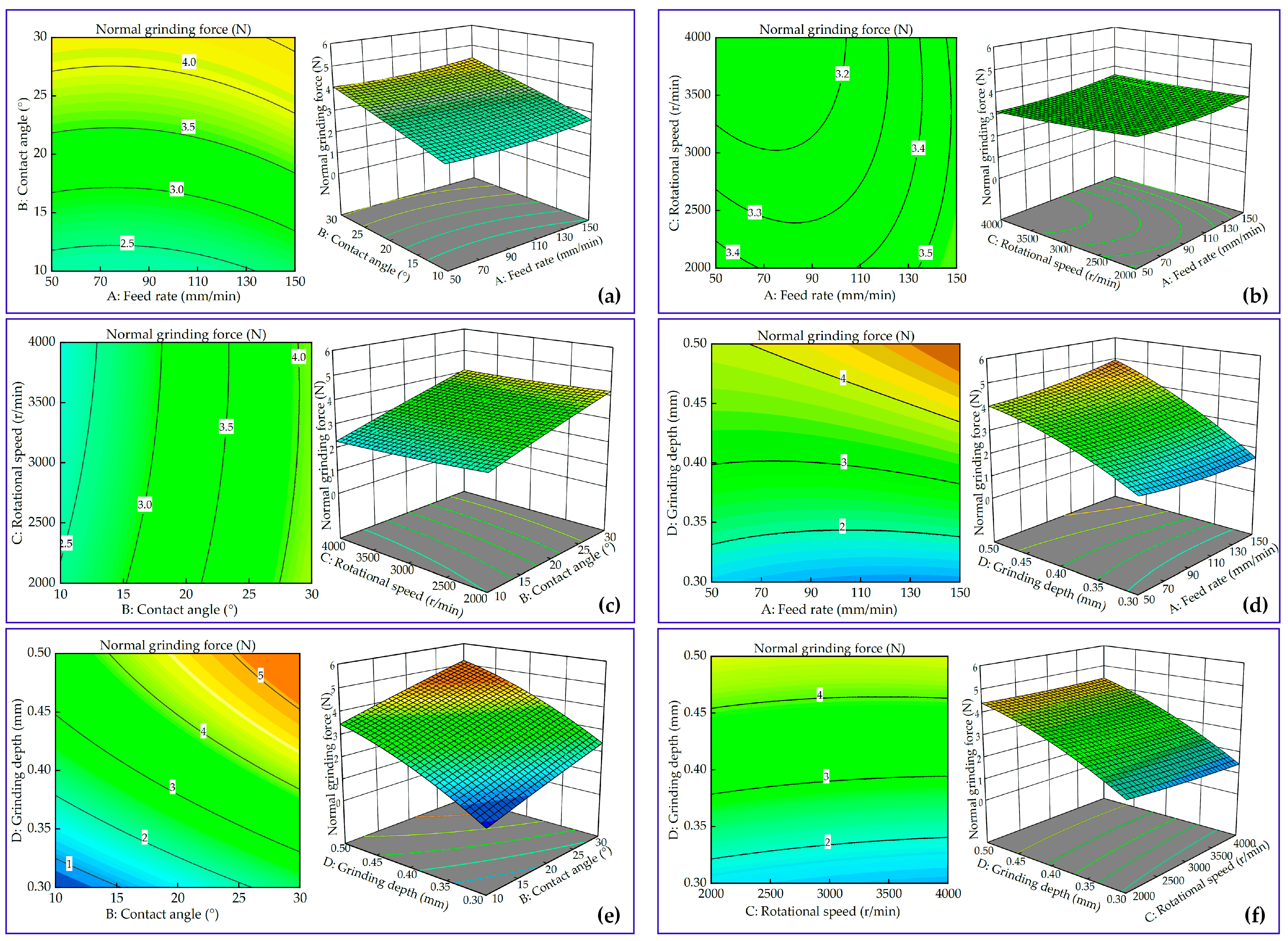
5.2. Interaction Effect of Process Parameters on Normal Grinding Forces
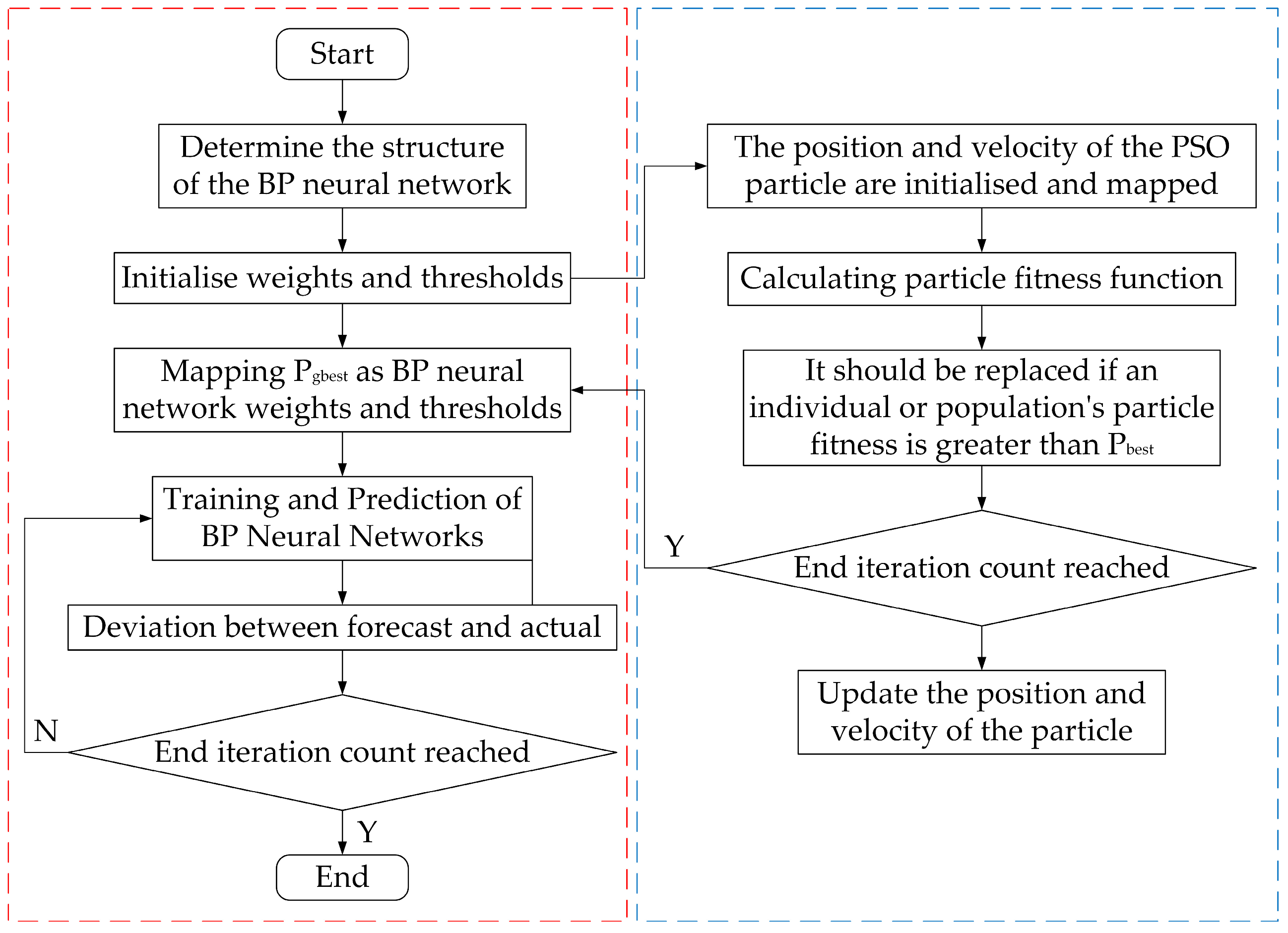
5.3. Prediction of Normal Grinding Force Based on PSO-BP
5.3.1. Principle of PSO-BP Neural Network
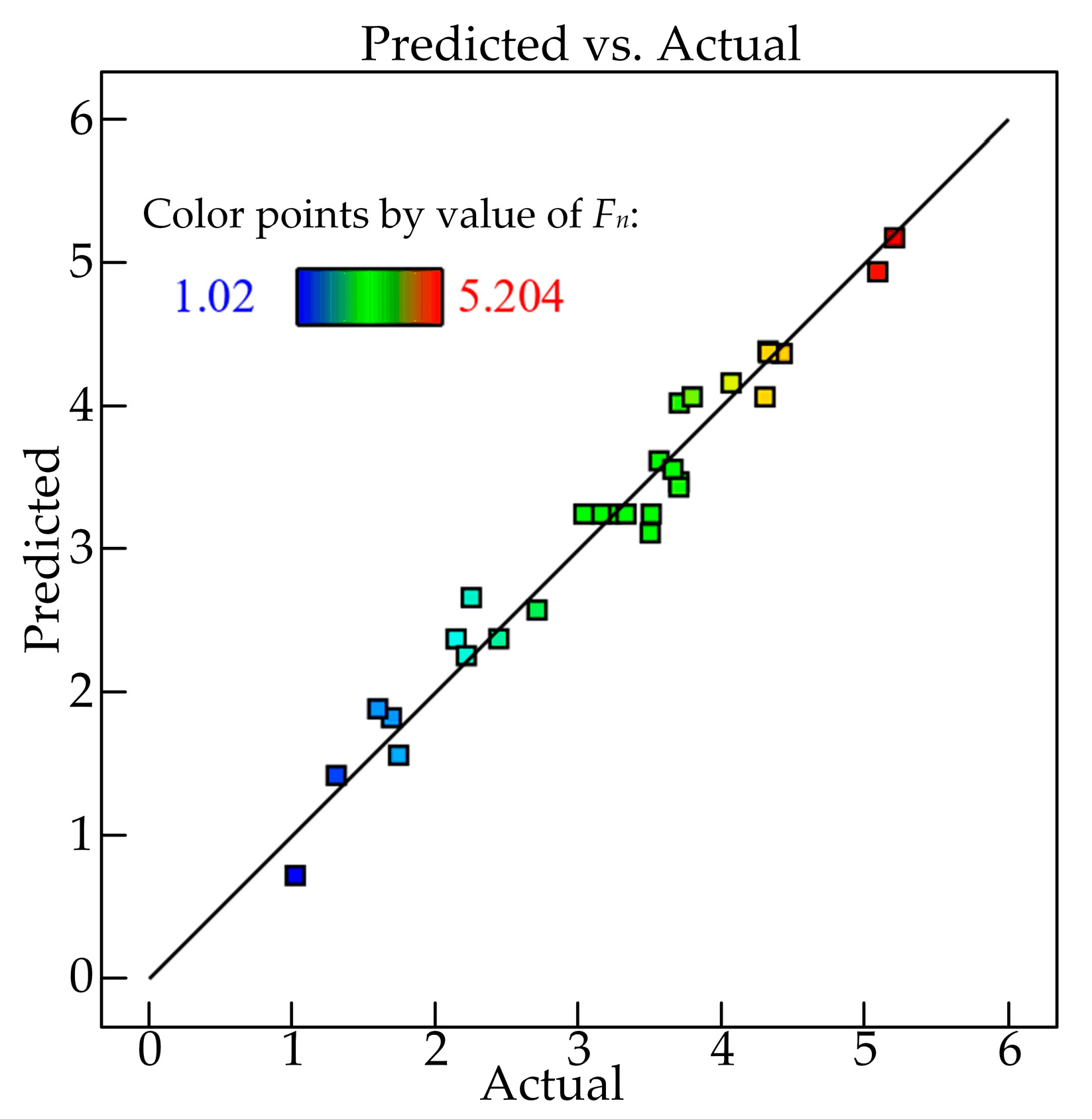
5.3.2. Analysis of PSO-BP Neural Network Prediction Results
5.4. Comparison of the Results of Two Prediction Models
6. Conclusions
- (1)
- The abrasive disc grinding process was analyzed and considered as a flexible process to adapt to different curved surfaces. The normal grinding force model was established from macroscopic and microscopic perspectives, which showed that the contact angle, grinding depth, rotational speed, and feed rate were the main factors.
- (2)
- The normal grinding force significantly increased with the increase of the grinding depth and contact angle, slightly increased with the increase of the feed rate, and slightly decreased with the increase of the rotational speed. The regression model of normal grinding force was developed, and the ANOVA results showed that the interaction of the feed rate and grinding depth was the more influential factor.
- (3)
- The normal grinding force prediction model based on the PSO-BP neural network was carried out. The coefficient of determination, R2, of the training and test set data verified the accuracy and reliability of the model. The maximum absolute and relative errors of the training and test data in the model were 0.22 N and 4.2%, respectively.
- (4)
- Comparing the PSO-BP and BBD prediction models and their generalization ability, the added prediction experimental results showed that the MAE and MRE of the above two prediction models were 0.22 N and 0.16 N, and 13.3% and 10.9%, respectively. The results showed that the BBD model was more effective and accurate in predicting the normal grinding force.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Q.; Sun, Q.; Xin, S.; Chen, Y.; Wu, C.; Wang, H.; Xu, J.; Wan, M.; Zeng, W.; Zhao, Y. High-strength titanium alloys for aerospace engineering applications: A review on melting-forging process. Mater. Sci. Eng. A 2022, 845, 143260. [Google Scholar] [CrossRef]
- Williams, J.C.; Boyer, R.R. Opportunities and Issues in the Application of Titanium Alloys for Aerospace Components. Metals 2020, 10, 705. [Google Scholar] [CrossRef]
- Chen, L.-Y.; Cui, Y.-W.; Zhang, L.-C. Recent Development in Beta Titanium Alloys for Biomedical Applications. Metals 2020, 10, 1139. [Google Scholar] [CrossRef]
- Arunachalam, A.P.S.; Idapalapati, S. Material removal analysis for compliant polishing tool using adaptive meshing technique and Archard wear model. Wear 2019, 418–419, 140–150. [Google Scholar] [CrossRef]
- Arunachalam, A.P.S.; Idapalapati, S.; Subbiah, S.; Lim, Y.W. A novel retractable stiffener-based disk-shaped active compliant polishing tool. J. Manuf. Porcess. 2020, 51, 83–94. [Google Scholar] [CrossRef]
- Yao, C.; Tan, L.; Yang, P.; Zhang, D. Effects of tool orientation and surface curvature on surface integrity in ball end milling of TC17. Int. J. Adv. Manuf. Technol. 2018, 94, 1699–1710. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, X.; Feng, M.; Li, S.; Pan, X.; Feng, W. Research on Adaptive Control of Grinding Force for Carbide Indexable Inserts Grinding Process Based on Spindle Motor Power. Machines 2022, 10, 802. [Google Scholar] [CrossRef]
- Lei, X.; Xiang, D.; Peng, P.; Liu, G.; Li, B.; Zhao, B.; Gao, G. Establishment of dynamic grinding force model for ultrasonic-assisted single abrasive high-speed grinding. J. Mater. Process. Technol. 2022, 300, 117420. [Google Scholar] [CrossRef]
- Bie, W.; Zhao, B.; Gao, G.; Chen, F.; Chen, H. Grinding force assessment in tangential ultrasonic vibration-assisted grinding gear: Analytical model and experimental verification. Int. J. Adv. Manuf. Technol. 2023, 126, 5457–5474. [Google Scholar] [CrossRef]
- Li, H.; Chen, T.; Duan, Z.; Zhang, Y.; Li, H. A grinding force model in two-dimensional ultrasonic-assisted grinding of silicon carbide. J. Mater. Process. Technol. 2022, 304, 117568. [Google Scholar] [CrossRef]
- Song, K.; Xiao, G.; Chen, S.; Liu, X.; Huang, Y. A new force-depth model for robotic abrasive belt grinding and confirmation by grinding of the Inconel 718 alloy. Robot. CIM-INT. Manuf. 2023, 80, 102483. [Google Scholar] [CrossRef]
- Song, K.; Xiao, G.; Chen, S.; Li, S. Analysis of thermal-mechanical causes of abrasive belt grinding for titanium alloy. Int. J. Adv. Manuf. Technol. 2021, 113, 3241–3260. [Google Scholar] [CrossRef]
- Li, L.; Ren, X.; Feng, H.; Chen, H.; Chen, X. A novel material removal rate model based on single grain force for robotic belt grinding. J. Manuf. Porcess. 2021, 68, 1–12. [Google Scholar] [CrossRef]
- Yan, S.; Xu, X.; Yang, Z.; Zhu, D.; Ding, H. An improved robotic abrasive belt grinding force model considering the effects of cut-in and cut-off. J. Manuf. Porcess. 2019, 37, 496–508. [Google Scholar] [CrossRef]
- Liu, M.; Li, C.; Zhang, Y.; Yang, M.; Gao, T.; Cui, X.; Wang, X.; Xu, W.; Zhou, Z.; Liu, B.; et al. Analysis of grinding mechanics and improved grinding force model based on randomized grain geometric characteristics. Chinese J. Aeronaut. 2023, 36, 160–193. [Google Scholar] [CrossRef]
- Tao, H.; Liu, Y.; Zhao, D.; Lu, X. Prediction and measurement for grinding force in wafer self-rotational grinding. Int. J. Mech. Sci. 2023, 258, 108530. [Google Scholar] [CrossRef]
- Yi, J.; Yi, T.; Deng, H.; Chen, B.; Zhou, W. Theoretical modeling and experimental study on grinding force of straight groove structured grinding wheel. Int. J. Adv. Manuf. Technol. 2023, 124, 3407–3421. [Google Scholar] [CrossRef]
- Jamshidi, H.; Budak, E. An analytical grinding force model based on individual grit interaction. J. Mater. Process. Technol. 2020, 283, 116700. [Google Scholar] [CrossRef]
- Jamshidi, H.; Gurtan, M.; Budak, E. Identification of active number of grits and its effects on mechanics and dynamics of abrasive processes. J. Mater. Process. Technol. 2019, 273, 116239. [Google Scholar] [CrossRef]
- Jamshidi, H.; Budak, E. On the prediction of surface burn and its thickness in grinding processes. CIRP Ann. 2021, 70, 285–288. [Google Scholar] [CrossRef]
- Ma, X.; Cai, Z.; Yao, B.; Chen, G.; Liu, W.; Qiu, K. Dynamic grinding force model for face gear based on the wheel-gear contact geometry. J. Mater. Process. Technol. 2022, 306, 117633. [Google Scholar] [CrossRef]
- Cai, S.; Cai, Z.; Lin, C. Modeling of the generating face gear grinding force and the prediction of the tooth surface topography based on the abrasive differential element method. CIRP J. Manuf. Sci. Technol. 2023, 41, 80–93. [Google Scholar] [CrossRef]
- Meng, Q.; Guo, B.; Wu, G.; Xiang, Y.; Guo, Z.; Jia, J.; Zhao, Q.; Li, K.; Zeng, Z. Dynamic force modeling and mechanics analysis of precision grinding with microstructured wheels. J. Mater. Process. Technol. 2023, 314, 117900. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Q.; Chen, H.; Chen, L.; Qu, S.; Wang, Z.; Yu, T. A grinding force predictive model and experimental validation for the laser-assisted grinding (LAG) process of zirconia ceramic. J. Mater. Process. Technol. 2022, 302, 117492. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, Z.; Li, S.; Shi, Z.; Wen, D.; Jiang, J.; Zhang, Z. Grinding force modelling for ductile-brittle transition in laser macro-micro-structured grinding of zirconia ceramics. Ceram. Int. 2019, 45, 18487–18500. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, J.; Li, S.; Wen, D. Laser textured Ti-6Al-4V surfaces and grinding performance evaluation using CBN grinding wheels. Opt. Laser. Technol. 2019, 109, 389–400. [Google Scholar] [CrossRef]
- Zhou, H.; Ding, W.; Li, Z.; Su, H.-H. Predicting the grinding force of titanium matrix composites using the genetic algorithm optimizing back-propagation neural network model. P.I. Mech. Eng. B-J. Eng. 2019, 233, 1157–1167. [Google Scholar] [CrossRef]
- Gu, P.; Zhu, C.; Tao, Z.; Yu, Y. A grinding force prediction model for SiCp/Al composite based on single-abrasive-grain grinding. Int. J. Adv. Manuf. Technol. 2020, 109, 1563–1581. [Google Scholar] [CrossRef]
- Duan, J.; An, J.; Wu, Z.; Huai, W.; Gao, F. Contact characteristics and material removal mechanism of aerospace blade abrasive disc grinding. J. Mech. Eng. 2023, 59, 349–360. Available online: http://www.cjmenet.com.cn/CN/10.3901/JME.2023.17.349 (accessed on 7 February 2024).
- Arunachalam, A.P.S.; Idapalapati, S. Three-dimensional topography modelling of regular prismatic grain coated abrasive discs. Int. J. Adv. Manuf. Technol. 2018, 96, 3521–3532. [Google Scholar] [CrossRef]
- Spence, D.A. The hertz contact problem with finite friction. J. Elast. 1975, 5, 297–319. [Google Scholar] [CrossRef]
- Zhu, W.-L.; Yang, Y.; Li, H.N.; Axinte, D.; Beaucamp, A. Theoretical and experimental investigation of material removal mechanism in compliant shape adaptive grinding process. Int. J. Mach. Tool. Manuf. 2019, 142, 76–97. [Google Scholar] [CrossRef]
- Lv, L.; Deng, Z.; Yue, W.; Wan, L.; Liu, T. Modeling Analysis of Grinding Process Driven by Single Grain Grinding Mechanism and Data Fusion. J. Mech. Eng. 2023, 59, 200–215. [Google Scholar] [CrossRef]
- Malkin, S.; Guo, C. Grinding Technology: Theory and Application of Machining with Abrasives, 2nd ed.; Industrial Press Inc.: New York, USA, 2008; pp. 43–74. [Google Scholar]
- Sharma, V.; Kumar, V. Application of Box-Behnken design and response surface methodology for multi-optimization of laser cutting of AA5052/ZrOsub2/sub metal−matrix composites. P. I. Mech. Eng. L-J. Mat. 2018, 232, 652–668. [Google Scholar] [CrossRef]









| Parameter | n (r/min) | γ (°) | ap (mm) | vw (mm/min) | |
|---|---|---|---|---|---|
| No. | |||||
| 1 | 2000, 3000, 4000, 5000, 6000 | 15 | 0.3 | 100 | |
| 2 | 3000 | 10, 15, 20, 25, 30 | 0.3 | 100 | |
| 3 | 3000 | 15 | 0.3, 0.4, 0.5, 0.6, 0.7 | 100 | |
| 4 | 3000 | 15 | 0.3 | 50, 100, 150, 200, 250 | |
| Level of Factor | A | B | C | D |
|---|---|---|---|---|
| Feed Rate, vw/mm/min | Contact Angle, γ/° | Rotational Speed, n/r·min−1 | Grinding Depth, ap/mm | |
| −1 | 50 | 10 | 2000 | 0.3 |
| 0 | 100 | 20 | 3000 | 0.4 |
| 1 | 150 | 30 | 4000 | 0.5 |
| No. | Factors | Response | Factors | Response | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| vw (mm/min) | γ (°) | n (r/min) | ap (mm) | Fn (N) | No. | vw (mm/min) | γ (°) | n (r/min) | ap (mm) | Fn (N) | |
| 1 | 100 | 20 | 3000 | 0.4 | 3.329 | 16 | 100 | 20 | 4000 | 0.3 | 1.306 |
| 2 | 100 | 30 | 3000 | 0.3 | 2.440 | 17 | 150 | 30 | 3000 | 0.4 | 4.420 |
| 3 | 50 | 10 | 3000 | 0.4 | 2.143 | 18 | 50 | 20 | 3000 | 0.3 | 1.596 |
| 4 | 100 | 20 | 2000 | 0.3 | 1.691 | 19 | 50 | 30 | 3000 | 0.4 | 4.299 |
| 5 | 50 | 20 | 4000 | 0.4 | 3.498 | 20 | 100 | 20 | 3000 | 0.4 | 3.153 |
| 6 | 50 | 20 | 3000 | 0.5 | 3.701 | 21 | 100 | 10 | 3000 | 0.5 | 3.697 |
| 7 | 100 | 20 | 2000 | 0.5 | 4.320 | 22 | 150 | 20 | 3000 | 0.5 | 5.086 |
| 8 | 100 | 20 | 3000 | 0.4 | 3.214 | 23 | 150 | 20 | 4000 | 0.4 | 3.657 |
| 9 | 150 | 20 | 3000 | 0.3 | 1.741 | 24 | 100 | 20 | 4000 | 0.5 | 4.325 |
| 10 | 150 | 20 | 2000 | 0.4 | 3.560 | 25 | 100 | 10 | 3000 | 0.3 | 1.020 |
| 11 | 100 | 30 | 4000 | 0.4 | 3.791 | 26 | 100 | 20 | 3000 | 0.4 | 3.505 |
| 12 | 50 | 20 | 2000 | 0.4 | 3.699 | 27 | 100 | 10 | 4000 | 0.4 | 2.214 |
| 13 | 150 | 10 | 3000 | 0.4 | 2.249 | 28 | 100 | 30 | 2000 | 0.4 | 4.063 |
| 14 | 100 | 20 | 3000 | 0.4 | 3.034 | 29 | 100 | 10 | 2000 | 0.4 | 2.708 |
| 15 | 100 | 30 | 3000 | 0.5 | 5.204 | ||||||
| Source | Sum of Squares | df | Mean Square | F Value | p-Value |
|---|---|---|---|---|---|
| Model | 33.16 | 14 | 2.37 | 28.37 | <0.0001 |
| A | 0.2631 | 1 | 0.2631 | 3.15 | 0.0976 |
| B | 8.65 | 1 | 8.65 | 103.55 | <0.0001 |
| C | 0.1302 | 1 | 0.1302 | 1.59 | 0.2322 |
| D | 22.79 | 1 | 22.79 | 272.99 | <0.0001 |
| AB | 0.0001 | 1 | 0.0001 | 0.0007 | 0.9797 |
| AC | 0.0222 | 1 | 0.0222 | 0.2659 | 0.6142 |
| AD | 0.3844 | 1 | 0.3844 | 4.60 | 0.0499 |
| BC | 0.0123 | 1 | 0.0123 | 0.1476 | 0.7067 |
| BD | 0.0019 | 1 | 0.0019 | 0.0227 | 0.8825 |
| CD | 0.0380 | 1 | 0.0380 | 0.4554 | 0.5108 |
| A2 | 0.1423 | 1 | 0.1423 | 1.70 | 0.2128 |
| B2 | 0.0047 | 1 | 0.0047 | 0.0566 | 0.8154 |
| C2 | 0.0137 | 1 | 0.0137 | 0.1644 | 0.6913 |
| D2 | 0.5535 | 1 | 0.5535 | 6.63 | 0.0220 |
| Residual | 1.17 | 14 | 0.0835 | ||
| Lack of fit | 1.04 | 10 | 0.1040 | 3.24 | 0.1345 |
| Pure error | 0.1286 | 4 | 0.0321 | ||
| Cor total | 34.33 | 28 |
| Name | Value | Name | Value |
|---|---|---|---|
| Std.Dev. | 0.2890 | R2 | 0.9659 |
| Mean | 3.20 | Adjusted R2 | 0.9319 |
| C.V.% | 9.04 | Predicted R2 | 0.8196 |
| Adeq Precision | 21.4325 |
| Sample | vw (mm/min) | α (°) | n (r/min) | ap (mm) | Experiment Value (N) | BBD Predicted Value (N) | PSO-BP Predicted Value (N) |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 15 | 3000 | 0.4 | 2.82 | 2.814 | 2.755 |
| 2 | 100 | 15 | 3000 | 0.5 | 3.76 | 3.889 | 3.948 |
| 3 | 100 | 15 | 2000 | 0.3 | 1.48 | 1.430 | 1.315 |
| 4 | 100 | 15 | 4000 | 0.3 | 1.24 | 0.971 | 1.061 |
| 5 | 50 | 15 | 3000 | 0.3 | 1.14 | 1.468 | 1.041 |
| 6 | 250 | 15 | 3000 | 0.3 | 1.67 | 1.983 | 1.104 |
| 7 | 100 | 20 | 3000 | 0.3 | 1.45 | 1.575 | 1.752 |
| 8 | 100 | 30 | 3000 | 0.3 | 2.44 | 2.375 | 2.695 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.; Wu, Z.; Ren, J.; Zhang, G. Research on Grinding Force Prediction of Flexible Abrasive Disc Grinding Process of TC17 Titanium Alloy. Machines 2024, 12, 143. https://doi.org/10.3390/machines12020143
Duan J, Wu Z, Ren J, Zhang G. Research on Grinding Force Prediction of Flexible Abrasive Disc Grinding Process of TC17 Titanium Alloy. Machines. 2024; 12(2):143. https://doi.org/10.3390/machines12020143
Chicago/Turabian StyleDuan, Jihao, Zhuofan Wu, Jianbo Ren, and Gaochen Zhang. 2024. "Research on Grinding Force Prediction of Flexible Abrasive Disc Grinding Process of TC17 Titanium Alloy" Machines 12, no. 2: 143. https://doi.org/10.3390/machines12020143
APA StyleDuan, J., Wu, Z., Ren, J., & Zhang, G. (2024). Research on Grinding Force Prediction of Flexible Abrasive Disc Grinding Process of TC17 Titanium Alloy. Machines, 12(2), 143. https://doi.org/10.3390/machines12020143





