An Analysis of the WPT Function for Pattern Optimization to Detect Defects in Bearings
Abstract
1. Introduction
2. Experimental Measurements
3. Wavelet Packet Transform
4. Methodology for the Selection of the Mother Wavelet
- WPT decomposition: The WPT is applied with a decomposition level of 9 to ensure that there is a narrow band of frequencies that include the fault frequency for each case. This is applied for each mother wavelet and for all conditions tested.
- Energy of the packets’ calculation is calculated using Equation (4), but only for the packet that includes the fault frequency for each case.
- The energy variation () calculation The energy variation of the packet that includes the fault frequency is calculated with Equation (5), where the energy of the healthy condition and the energy of the defective condition are used. The larger variation, the better the results. It has been considered that an increase of 50% is a good value of energy increase for a correct detection of the defect; so, to be less restrictive, mother wavelets with an energy variation lower than 45% were discarded.
- Reliability analysis: Energy values of the packet that include the fault frequency and that, by using each preselected mother wavelet, are entered into an intelligent classification system in which defective and healthy conditions are distinguished in two different classes; thus, the output would yield a value if an energy value belonged to the healthy or defective condition. This procedure will be performed for each defect (inner and outer race) separately. The model used for this is a medium Gaussian SVM, as SVM is proven to be fast, reliable, and very useful for these procedures [28]. Within the type of SVM, the medium Gaussian is the one that yields the highest success rate in this case. This was checked with a MATLAB® application called ‘classification learner’, where different models can be trained. This model was also selected in bearing works, such as [35]. The hyperplane that best separates the classes or conditions is calculated with a kernel function, in this case, medium Gaussian [36]. The model is trained with cross-validation, which protects against overfitting by partitioning the data set into folds (in this case, the maximum possible, 50), and estimates the accuracy on each fold. The mother wavelet with the highest success rate is selected, which means that data using that mother wavelet can be better separated in classes or conditions (healthy or defective), offering better defect detection ability.
5. Selection of the Mother Wavelet
6. Comparative Study
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hodge, V.J.; O’Keefe, S.; Weeks, M.; Moulds, A. Wireless Sensor Networks for Condition Monitoring in the Railway Industry: A Survey. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1088–1106. [Google Scholar] [CrossRef]
- Sakib, N.; Wuest, T. Challenges and Opportunities of Condition-Based Predictive Maintenance: A Review. Procedia CIRP 2018, 78, 267–272. [Google Scholar] [CrossRef]
- Senapaty, G.; Rao, U.S. Vibration Based Condition Monitoring of Rotating Machinery. MATEC Web Conf. 2018, 144, 01021. [Google Scholar] [CrossRef]
- Vishwakarma, M.; Purohit, R.; Harshlata, V.; Rajput, P. Vibration Analysis & Condition Monitoring for Rotating Machines: A Review. Mater. Today Proc. 2017, 4, 2659–2664. [Google Scholar] [CrossRef]
- Wang, N.; Liu, X. Bearing Fault Diagnosis Method Based on Hilbert Envelope Demodulation Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2018, 436, 012009. [Google Scholar] [CrossRef]
- Jin, S.; Lee, S.-K. Bearing Fault Detection Utilizing Group Delay and the Hilbert-Huang Transform. J. Mech. Sci. Technol. 2017, 31, 1089–1096. [Google Scholar] [CrossRef]
- Osman, S.; Wang, W. A Normalized Hilbert-Huang Transform Technique for Bearing Fault Detection. J. Vib. Control 2016, 22, 2771–2787. [Google Scholar] [CrossRef]
- Wescoat, E.; Mears, L.; Goodnough, J.; Sims, J. Frequency Energy Analysis in Detecting Rolling Bearing Faults. Procedia Manuf. 2020, 48, 980–991. [Google Scholar] [CrossRef]
- Liu, H.; Li, D.; Yuan, Y.; Zhang, S.; Zhao, H.; Deng, W. Fault Diagnosis for a Bearing Rolling Element Using Improved VMD and HT. Appl. Sci. 2019, 9, 1439. [Google Scholar] [CrossRef]
- Gu, J.; Peng, Y.; Lu, H.; Chang, X.; Cao, S.; Chen, G.; Cao, B. An Optimized Variational Mode Decomposition Method and Its Application in Vibration Signal Analysis of Bearings. Struct. Health Monit. 2022, 21, 2386–2407. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault Diagnosis of Ball Bearings Using Continuous Wavelet Transform. Appl. Soft Comput. 2011, 11, 2300–2312. [Google Scholar] [CrossRef]
- Guo, J.; Liu, X.; Li, S.; Wang, Z. Bearing Intelligent Fault Diagnosis Based on Wavelet Transform and Convolutional Neural Network. Shock Vib. 2020, 2020, e6380486. [Google Scholar] [CrossRef]
- Patil, A.; Gaikwad, J.; Kulkarni, J. Bearing Fault Diagnosis Using Discrete Wavelet Transform and Artificial Neural Network. In Proceedings of the 2016 2nd International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT), Bangalore, India, 21–23 July 2016; pp. 399–405. [Google Scholar]
- Nabhan, A.; Ghazaly, N.; Samy, A.; Mousa, M.O. Bearing Fault Detection Techniques—A Review. Turk. J. Eng. Sci. Technol. 2015, 3, 1–18. [Google Scholar]
- Wan, L.; Zhang, G.; Li, H.; Li, C. A Novel Bearing Fault Diagnosis Method Using Spark-Based Parallel ACO-K-Means Clustering Algorithm. IEEE Access 2021, 9, 28753–28768. [Google Scholar] [CrossRef]
- Saruhan, H.; Sandemir, S.; Çiçek, A.; Uygur, I. Vibration Analysis of Rolling Element Bearings Defects. J. Appl. Res. Technol. JART 2014, 12, 384–395. [Google Scholar] [CrossRef]
- Li, H.; Fu, L.; Zheng, H. Bearing Fault Diagnosis Based on Amplitude and Phase Map of Hermitian Wavelet Transform. J. Mech. Sci. Technol. 2011, 25, 2731–2740. [Google Scholar] [CrossRef]
- Graney, B.; Starry, K. Rolling Element Bearing Analysis. Mater. Eval. 2012, 70, 78–85. [Google Scholar]
- Castejón, C.; Lara, O.; GARCIA-PRADA, J.C. Automated Diagnosis of Rolling Bearings Using MRA and Neural Networks. Mech. Syst. Signal Process. 2010, 24, 289–299. [Google Scholar] [CrossRef]
- Hernández, A.; Castejón, C.; García-Prada, J.C.; Padrón, I.; Marichal, G.N. Wavelet Packets Transform Processing and Genetic Neuro-Fuzzy Classification to Detect Faulty Bearings. Adv. Mech. Eng. 2019, 11, 1687814019831185. [Google Scholar] [CrossRef]
- Gómez, M.J.; Castejón, C.; GARCIA-PRADA, J.C. Incipient Fault Detection in Bearings Through the Use of WPT Energy and Neural Networks. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations; Springer: Berlin/Heidelberg, Germany, 2014; pp. 63–72. ISBN 978-3-642-39347-1. [Google Scholar]
- Xu, Y.; Xiu, S. A New and Effective Method of Bearing Fault Diagnosis Using Wavelet Packet Transform Combined with Support Vector Machine. J. Comput. 2011, 6, 2502–2509. [Google Scholar] [CrossRef]
- Xiong, S.; Zhou, H.; He, S.; Zhang, L.; Xia, Q.; Xuan, J.; Shi, T. A Novel End-To-End Fault Diagnosis Approach for Rolling Bearings by Integrating Wavelet Packet Transform into Convolutional Neural Network Structures. Sensors 2020, 20, 4965. [Google Scholar] [CrossRef] [PubMed]
- Nikolaou, N.G.; Antoniadis, I.A. Rolling Element Bearing Fault Diagnosis Using Wavelet Packets. NDT E Int. 2002, 35, 197–205. [Google Scholar] [CrossRef]
- Rafiee, J.; Rafiee, M.A.; Tse, P.W. Application of Mother Wavelet Functions for Automatic Gear and Bearing Fault Diagnosis. Expert Syst. Appl. 2010, 37, 4568–4579. [Google Scholar] [CrossRef]
- Lou, X.; Loparo, K.A. Bearing Fault Diagnosis Based on Wavelet Transform and Fuzzy Inference. Mech. Syst. Signal Process. 2004, 18, 1077–1095. [Google Scholar] [CrossRef]
- Purushotham, V.; Narayanan, S.; Prasad, S.A.N. Multi-Fault Diagnosis of Rolling Bearing Elements Using Wavelet Analysis and Hidden Markov Model Based Fault Recognition. NDT E Int. 2005, 38, 654–664. [Google Scholar] [CrossRef]
- Zamorano, M.; Gómez Garcia, M.J.; Castejón, C. Selection of a Mother Wavelet as Identification Pattern for the Detection of Cracks in Shafts. J. Vib. Control 2022, 28, 3152–3161. [Google Scholar] [CrossRef]
- Wai Keng, N.; Leong, M.; Hee, L.; Abdelrhman, A. Wavelet Analysis: Mother Wavelet Selection Methods. Appl. Mech. Mater. 2013, 393, 953–958. [Google Scholar]
- Ao, H.; Junsheng, C.; Jinde, Z.; Truong, T. Roller Bearing Fault Diagnosis Method Based on Chemical Reaction Optimization and Support Vector Machine. J. Comput. Civ. Eng. 2014, 29, 04014077. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, L. Fault Diagnosis of Bearing Based on Improved Refined Composite Hierarchical Fuzzy Entropy and Least Squares Support Vector Machine. J. Vib. Eng. Technol. 2022, 10, 3025–3036. [Google Scholar] [CrossRef]
- Wang, M.; Wang, W.; Zeng, J.; Zhang, Y. An Integrated Method Based on Sparrow Search Algorithm Improved Variational Mode Decomposition and Support Vector Machine for Fault Diagnosis of Rolling Bearing. J. Vib. Eng. Technol. 2022, 10, 2893–2904. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing; Academic Press: Cambridge, MA, USA, 1999; ISBN 978-0-12-466606-1. [Google Scholar]
- Zamorano, M.; Gómez, M.J.; Castejón, C. Optimal Selection of the Mother Wavelet in WPT Analysis and Its Influence in Cracked Railway Axles Detection. Machines 2023, 11, 493. [Google Scholar] [CrossRef]
- Lin, S.-L. Application of Machine Learning to a Medium Gaussian Support Vector Machine in the Diagnosis of Motor Bearing Faults. Electronics 2021, 10, 2266. [Google Scholar] [CrossRef]
- Noble, W. What is a support vector machine? Nat. Biotechnol 2006, 24, 1565–1567. [Google Scholar] [CrossRef] [PubMed]
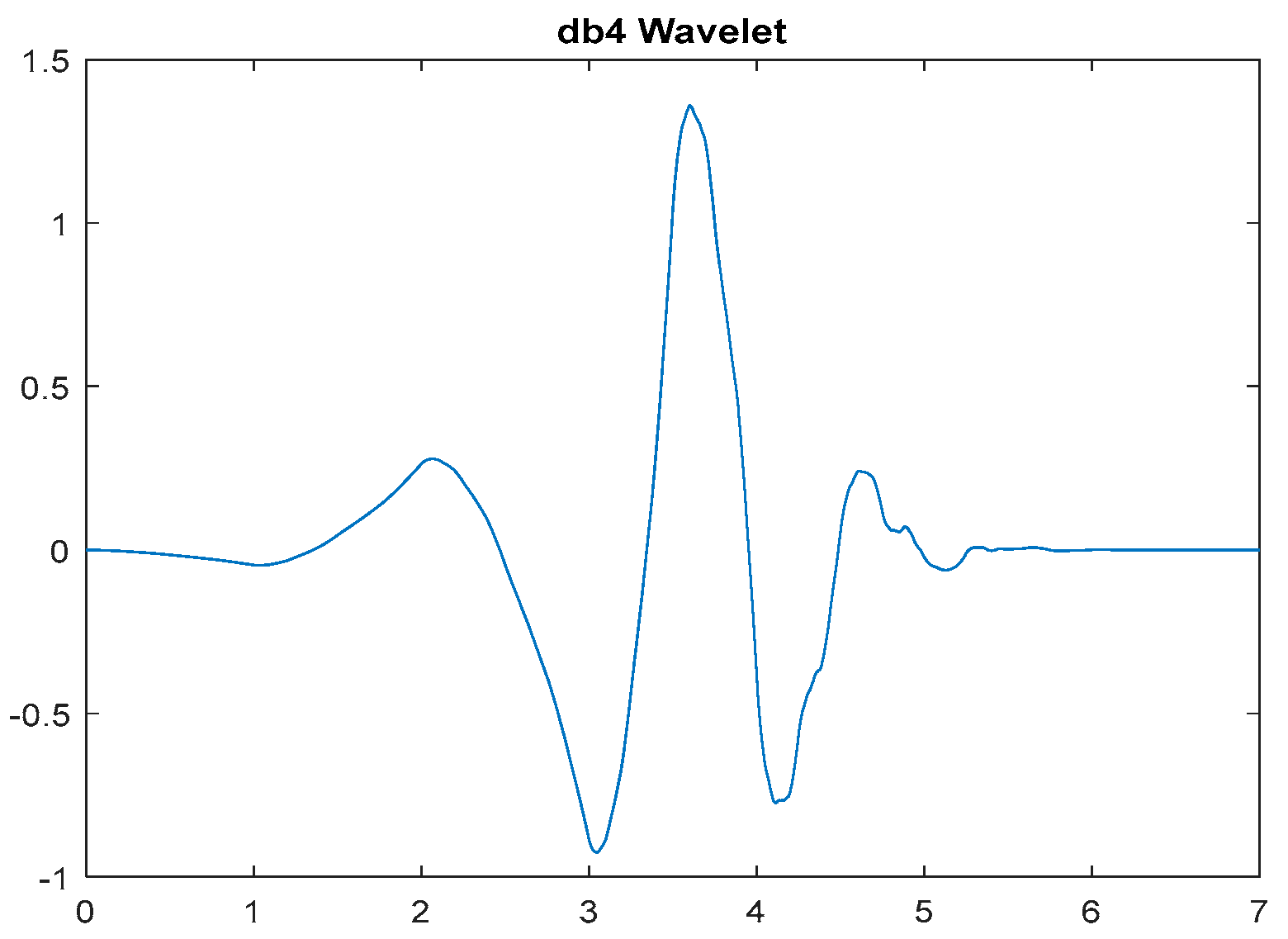

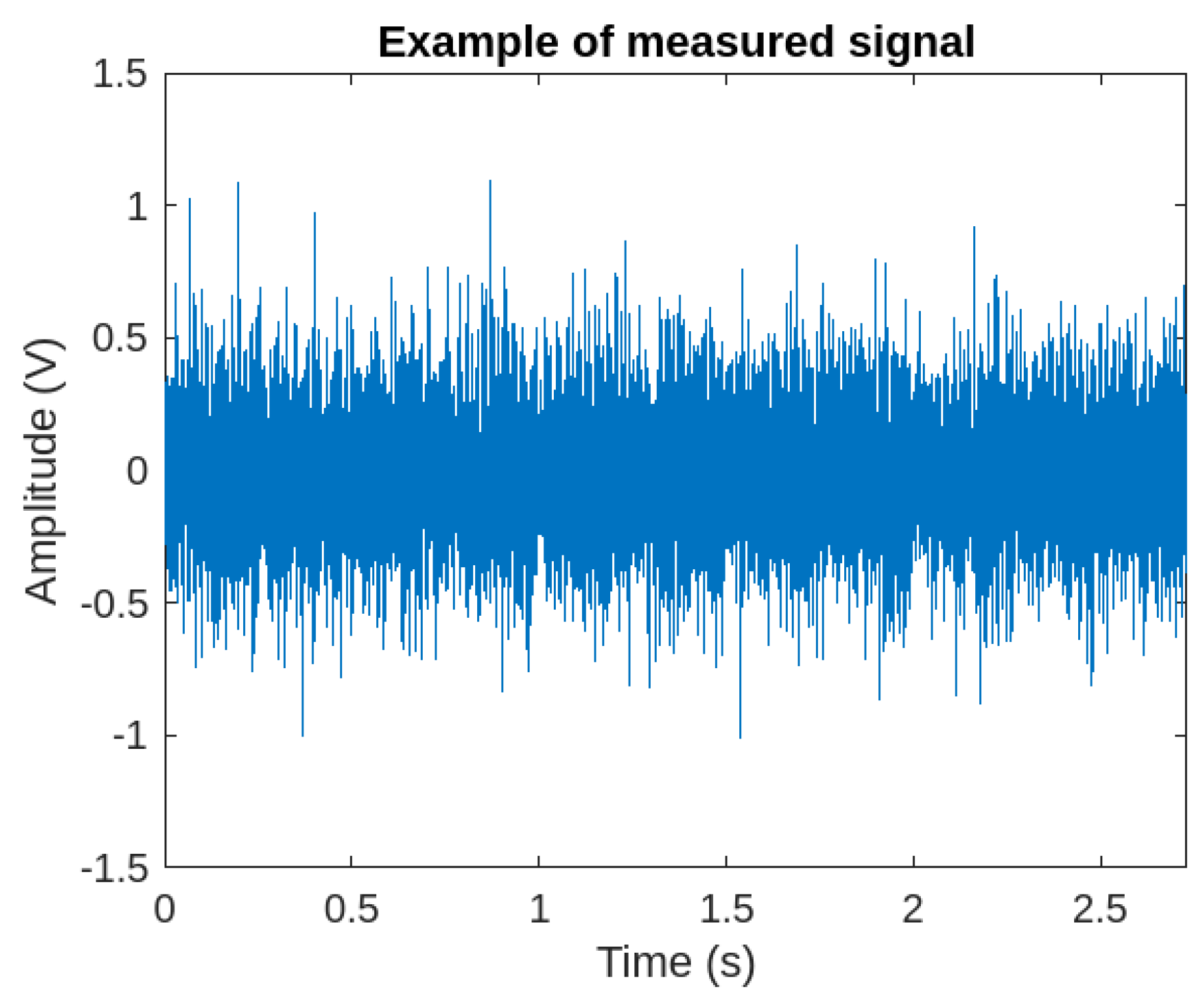
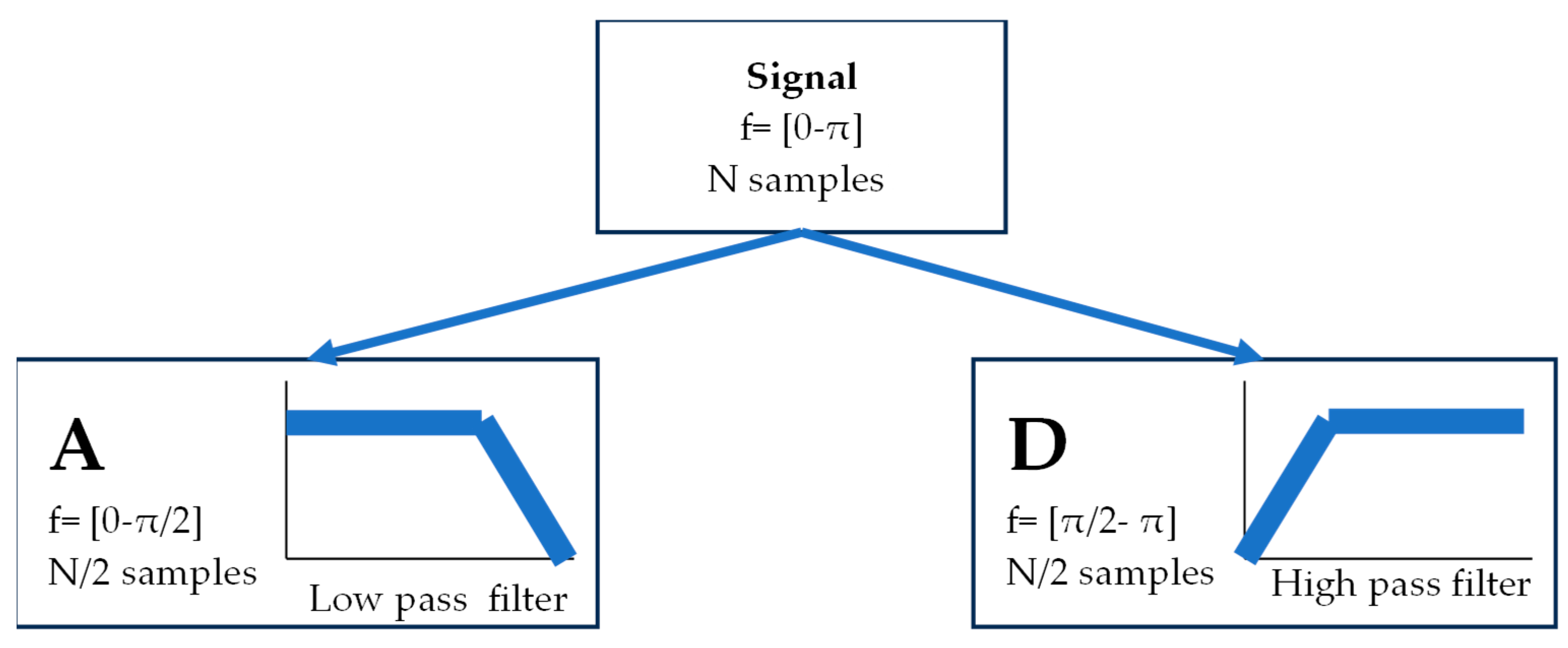
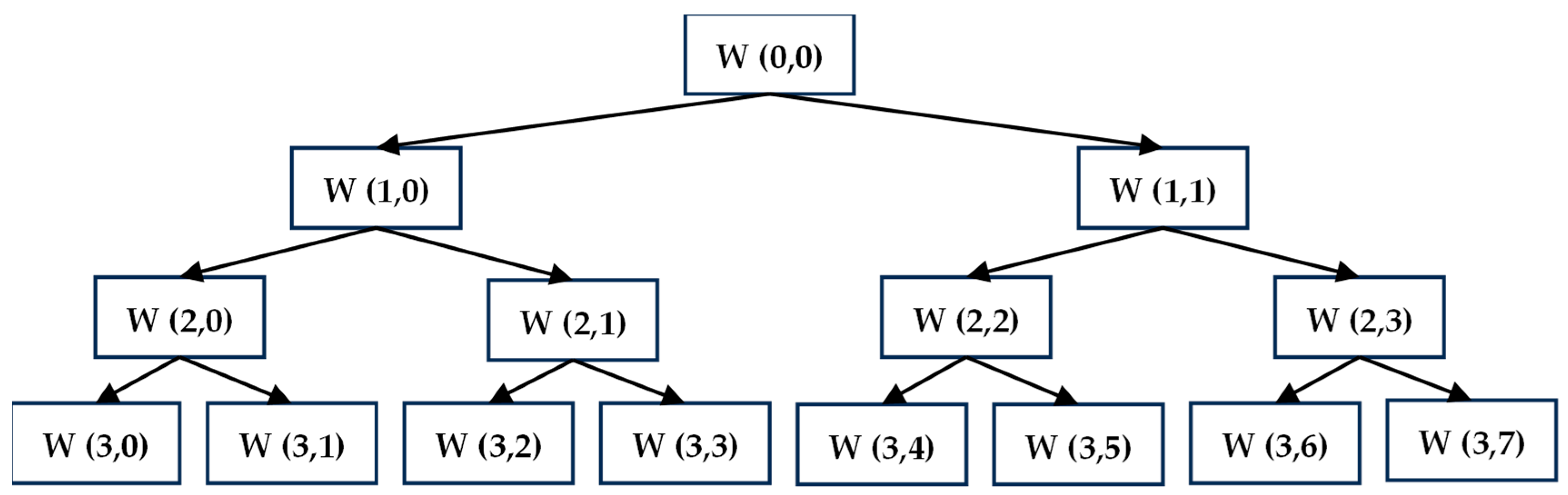


| Parameter | Value |
|---|---|
| Inside diameter (mm) | 15.875 |
| External diameter (mm) | 46.990 |
| Pitch diameter (mm) | 33.490 |
| Number of balls | 8 |
| Ball diameter (mm) | 7.940 |
| Contact angle (°) | 0 |
| Defect | Equation | Fault Frequency (Hz) |
|---|---|---|
| Inner-race | 296.90 | |
| Outer-race | 183.10 |
| Mother Wavelet | Packet Energy (Healthy) | Packet Energy (Defective) | Energy Variation (%) | Success Rate (Medium Gaussian SVM) |
|---|---|---|---|---|
| Db2 | 0.43996569 | 0.80853792 | 83.7729477 | 95.5 |
| Db4 | 0.44766094 | 0.66096363 | 47.648 | 97 |
| Db5 | 0.50546822 | 0.85437674 | 69.0267975 | 94 |
| Db7 | 0.71454683 | 1.05436438 | 47.5570715 | 94.5 |
| Coif1 | 0.44742314 | 0.84940592 | 89.8439841 | 94 |
| Coif2 | 0.47662413 | 0.69887133 | 46.6294465 | 94 |
| Coif5 | 0.70220691 | 1.04223496 | 48.4227731 | 95.5 |
| Sym2 | 0.43996569 | 0.80853792 | 83.7729477 | 95.5 |
| Sym10 | 0.60534282 | 0.90802633 | 50.0019986 | 94.5 |
| Mother Wavelet | Packet Energy (Healthy) | Packet Energy (Defective) | Energy Variation (%) | Success Rate (Medium Gaussian SVM) |
|---|---|---|---|---|
| Db2 | 0.49198327 | 0.789115 | 60.3946819 | 71 |
| Db3 | 0.50836819 | 0.81486114 | 60.2895611 | 70 |
| Db4 | 0.53372075 | 0.85502631 | 60.2010631 | 71.5 |
| Db6 | 0.59761903 | 0.92234262 | 54.3362186 | 68 |
| Db7 | 0.57977949 | 0.85406113 | 47.3079253 | 68 |
| Db8 | 0.60210136 | 0.93850256 | 55.8711909 | 68.5 |
| Db9 | 0.79225172 | 1.21221911 | 53.0093376 | 69 |
| Db10 | 1.34578002 | 2.24824047 | 67.0585406 | 65.5 |
| Coif1 | 0.6097671 | 1.12022517 | 83.7136115 | 73 |
| Coif2 | 0.47797477 | 0.7754434 | 62.2352168 | 73.5 |
| Coif3 | 0.51382459 | 0.75850003 | 47.618476 | 71.5 |
| Coif5 | 0.66420104 | 0.98927322 | 48.9418358 | 75.5 |
| Sym2 | 0.49198327 | 0.789115 | 60.3946819 | 71 |
| Sym3 | 0.50836819 | 0.81486114 | 60.2895611 | 70 |
| Sym4 | 0.45582653 | 0.73745731 | 61.7846387 | 74.5 |
| Sym6 | 0.43257976 | 0.69043591 | 59.6089279 | 77 |
| Sym7 | 0.44147311 | 0.64677369 | 46.503528 | 69 |
| Sym8 | 0.42405694 | 0.66162416 | 56.0224809 | 74.5 |
| Sym9 | 0.43521722 | 0.63831325 | 46.6654397 | 66 |
| Sym10 | 0.42586168 | 0.64213376 | 50.7845827 | 73 |
| Mother Wavelet | Success Rate (Medium Gaussian SVM) (%) |
|---|---|
| Db2 | 77.6 |
| Db4 | 80.3 |
| Db7 | 67.2 |
| Coif1 | 78.3 |
| Coif2 | 76.3 |
| Coif5 | 76.3 |
| Sym2 | 76.6 |
| Sym10 | 65.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamorano, M.; Gómez, M.J.; Castejon, C. An Analysis of the WPT Function for Pattern Optimization to Detect Defects in Bearings. Machines 2024, 12, 207. https://doi.org/10.3390/machines12030207
Zamorano M, Gómez MJ, Castejon C. An Analysis of the WPT Function for Pattern Optimization to Detect Defects in Bearings. Machines. 2024; 12(3):207. https://doi.org/10.3390/machines12030207
Chicago/Turabian StyleZamorano, Marta, María Jesús Gómez, and Cristina Castejon. 2024. "An Analysis of the WPT Function for Pattern Optimization to Detect Defects in Bearings" Machines 12, no. 3: 207. https://doi.org/10.3390/machines12030207
APA StyleZamorano, M., Gómez, M. J., & Castejon, C. (2024). An Analysis of the WPT Function for Pattern Optimization to Detect Defects in Bearings. Machines, 12(3), 207. https://doi.org/10.3390/machines12030207








