An Intelligent Diagnostic Method for Wear Depth of Sliding Bearings Based on MGCNN
Abstract
1. Introduction
- Different from the current research focus on the lubrication and antiwear performance of sliding bearings, this paper aims to dynamically diagnose and quantitatively evaluate the wear state during the operation of bearings. In typical situations, MWD directly impacts bearing performance, yet is often challenging to measure directly in real time. Conversely, vibration signals can be continuously collected through external sensors. Leveraging the vibration signals collected during the operation of sliding bearings, this paper proposes an end-to-end approach to infer the MWD affecting bearing performance, enabling the diagnosis of bearing conditions. This bridges a gap in the current research landscape of sliding bearings by providing an intelligent diagnostic method.
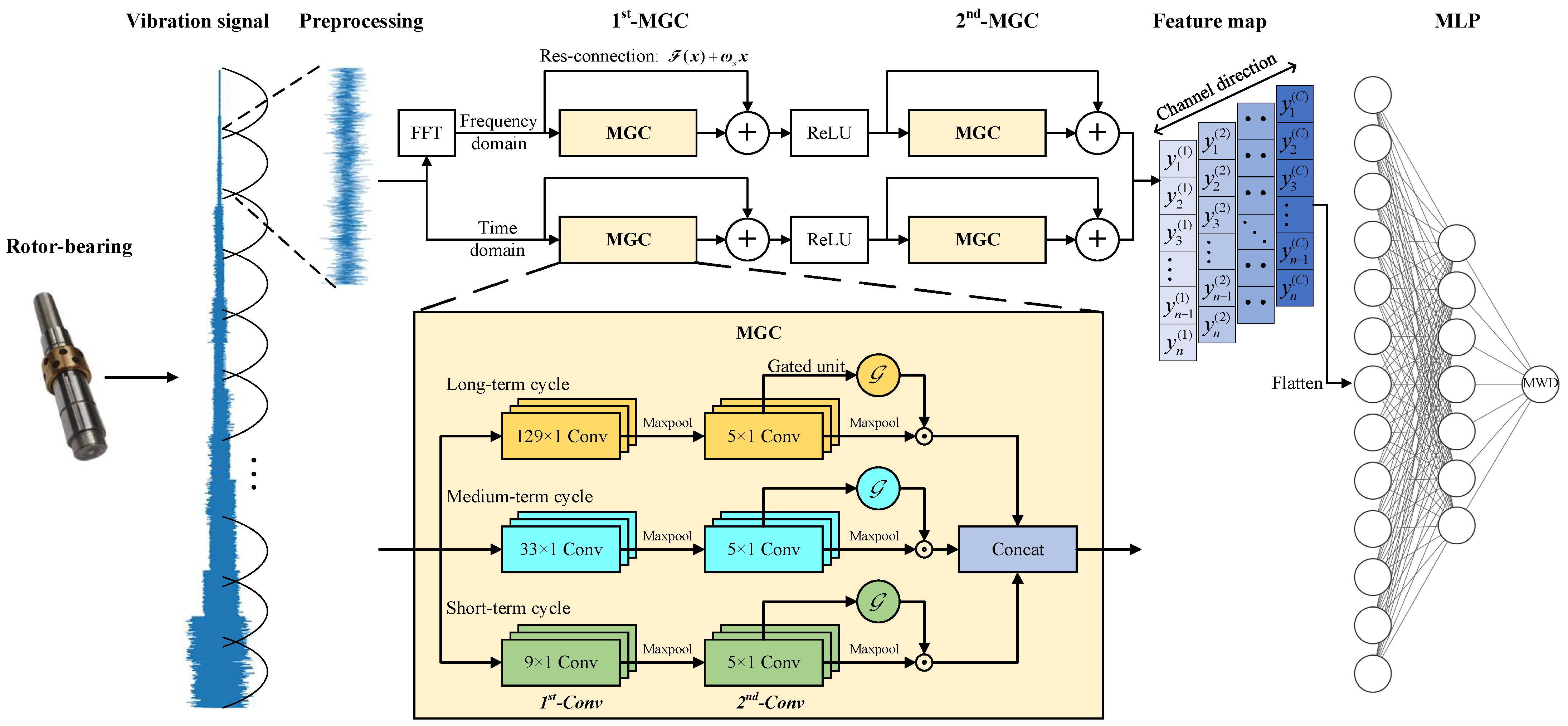
- An MGCNN intelligent diagnostic model is constructed, with vibration signals as input and the bearing’s MWD as output. Considering the periodic characteristics of rotating machinery, the established MGCNN model adopts a dual-path parallel structure in both time-domain and frequency-domain to fully extract valid information from bearing vibration signals, thereby enhancing the model’s prior knowledge. The MGC module is designed, which utilizes three channels for long-term, medium-term, and short-term cycles to extract multiscale information from vibration signals; meanwhile, gated units are designed to assign weights to feature vectors through nonlinear mappings. By amplifying the weights of important features and disregarding unimportant ones, the control of information flow is achieved.
- Building upon the diagnostic results of the proposed method, this paper further conducts predictive maintenance for sliding bearings. By setting a predefined wear threshold, this paper determines a bearing’s remaining useful life, facilitating predictive maintenance for bearings and equipment.
2. Bearing Vibration Signals and Deep Neural Networks
2.1. Wear State and Diagnosis of Sliding Bearing
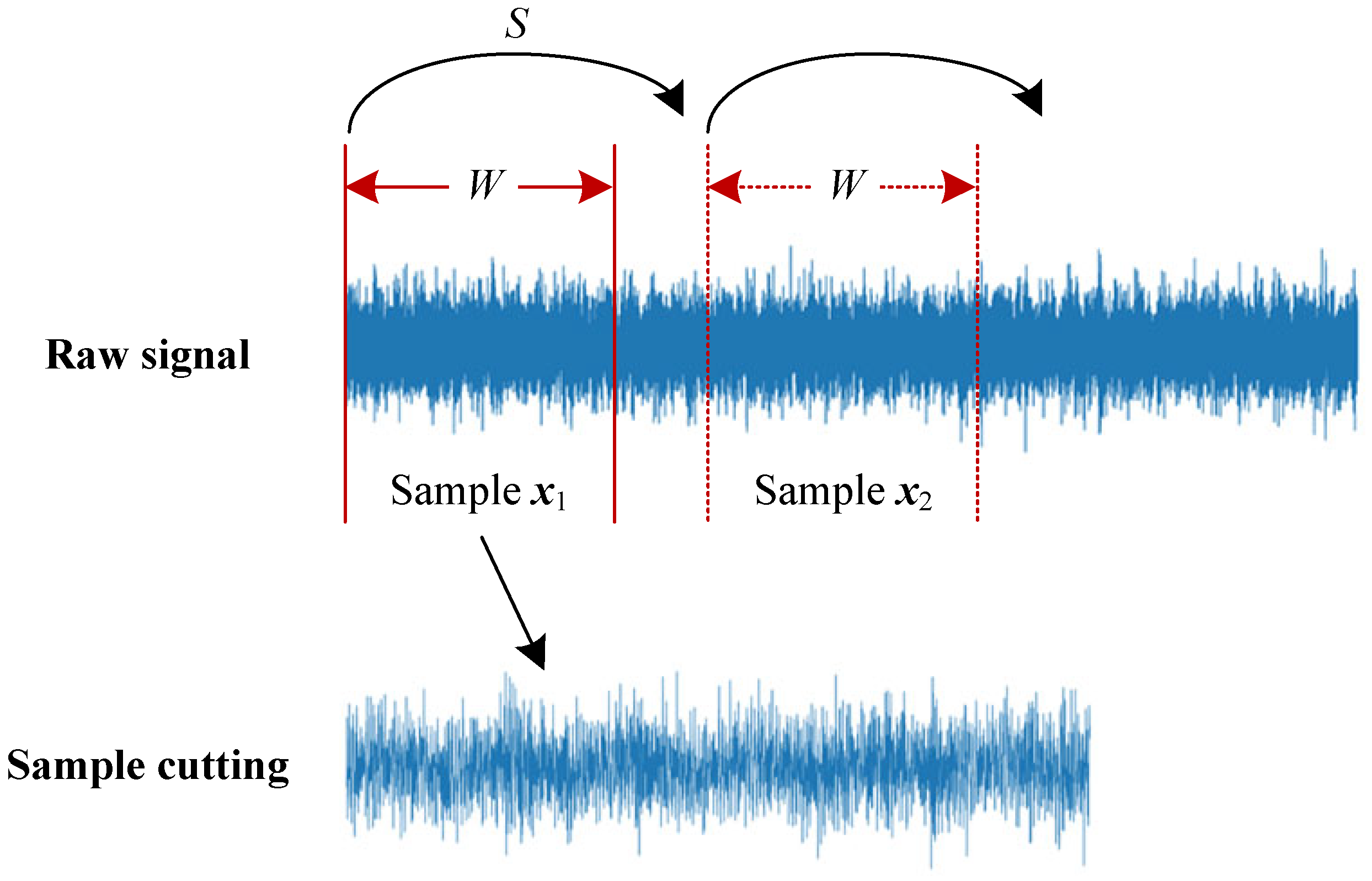
2.2. Sample Cutting and Preprocessing
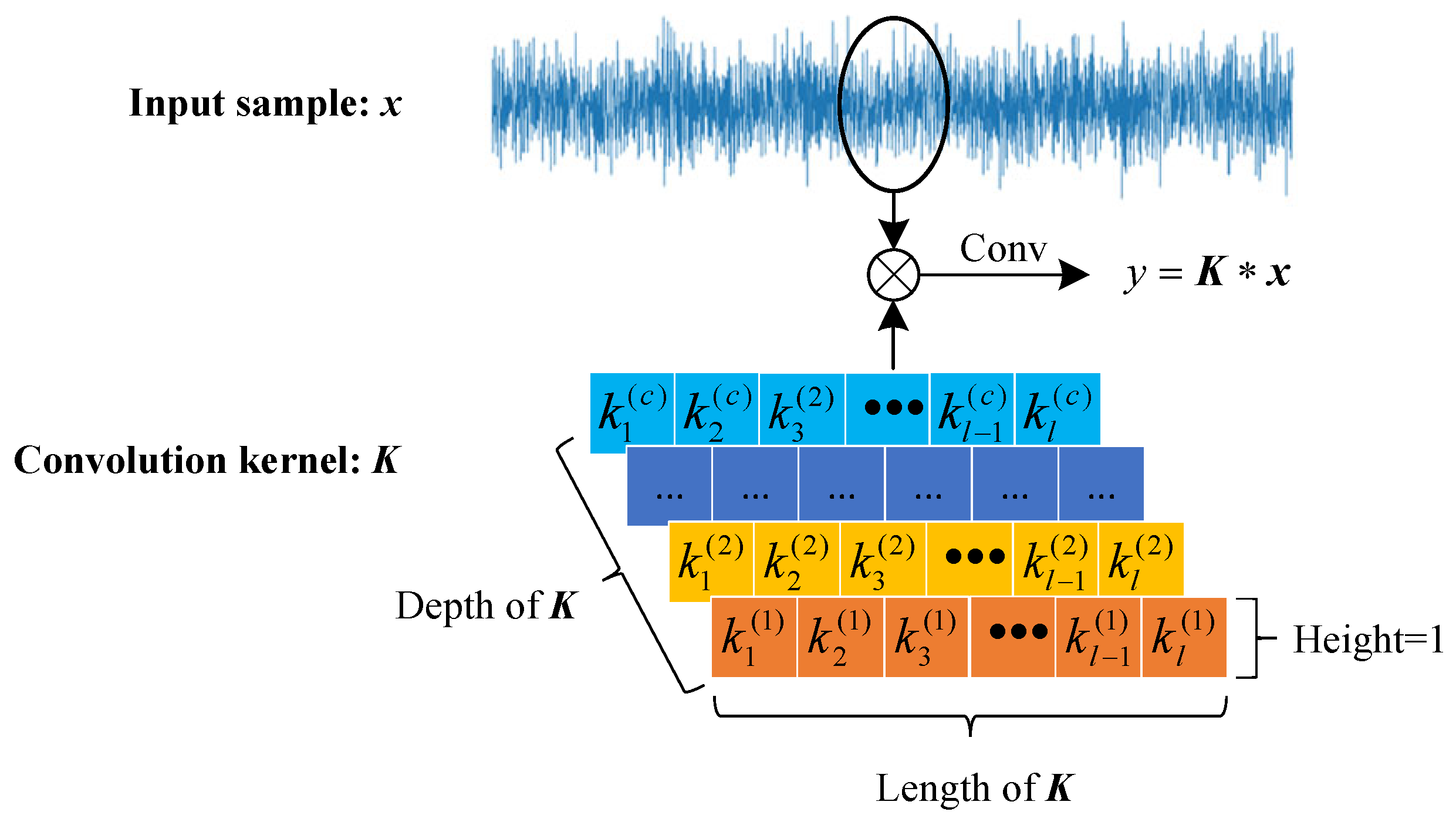
2.3. Convolutional Neural Network
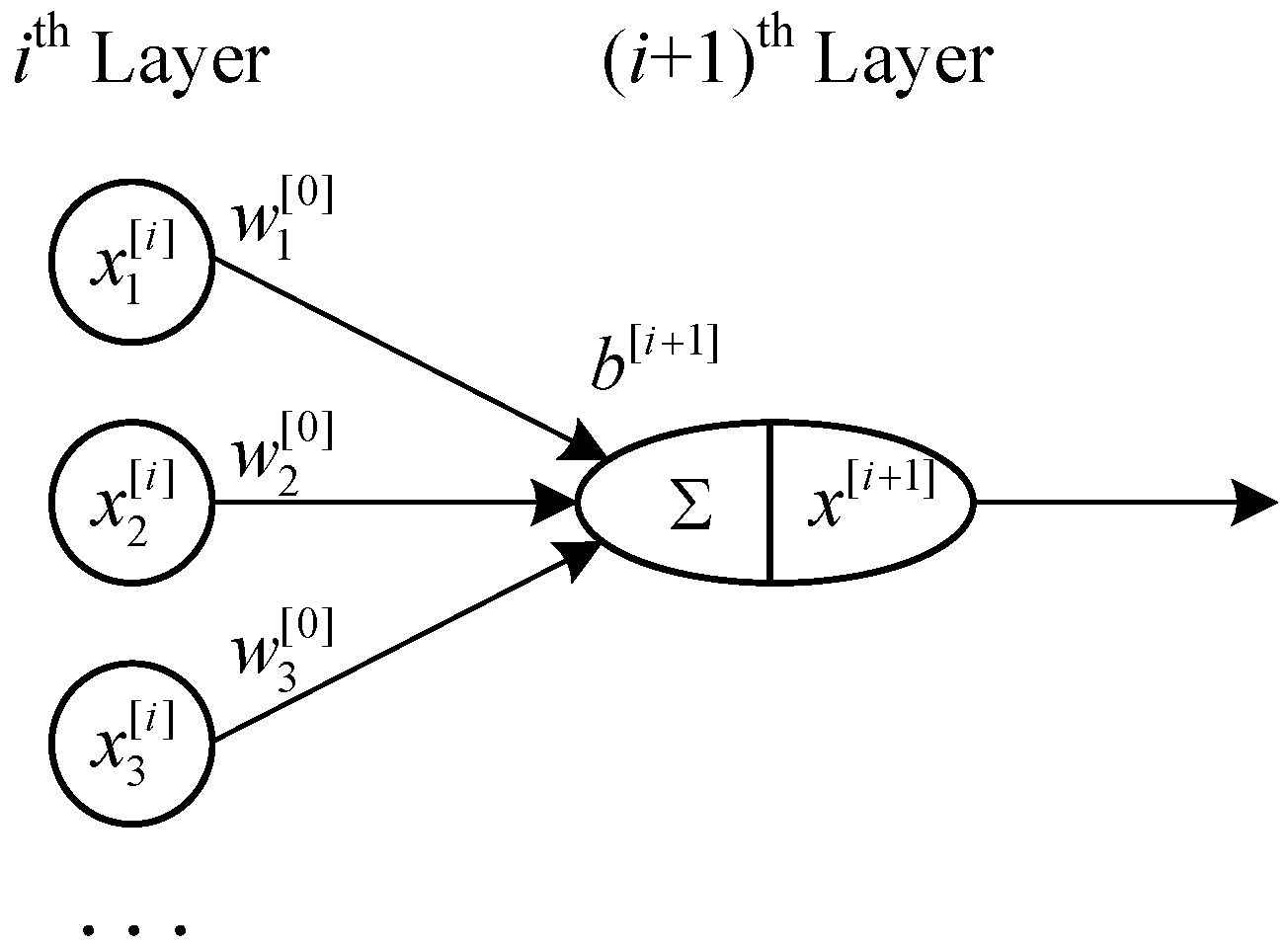
2.4. Fully Connected Neural Network
| Algorithm 1 Adam [51] |
|
3. Multiscale Gated Convolutional Neural Network
3.1. Overall Structure of the MGCNN
3.2. Structure of the MGC Module
3.3. Detailed Model Parameters
4. Experiment and Discussion
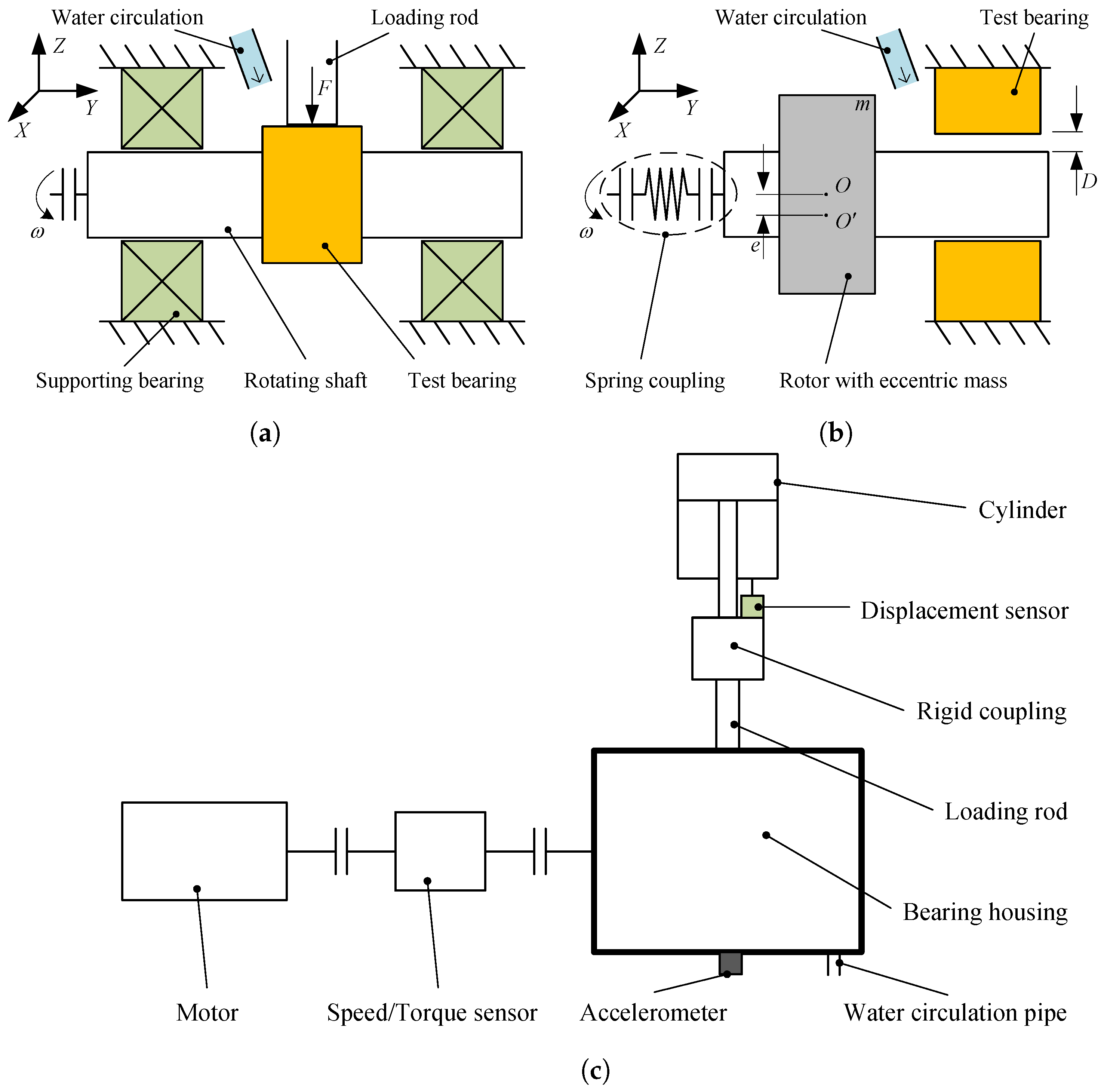
4.1. Wear and Vibration Test of Sliding Bearings
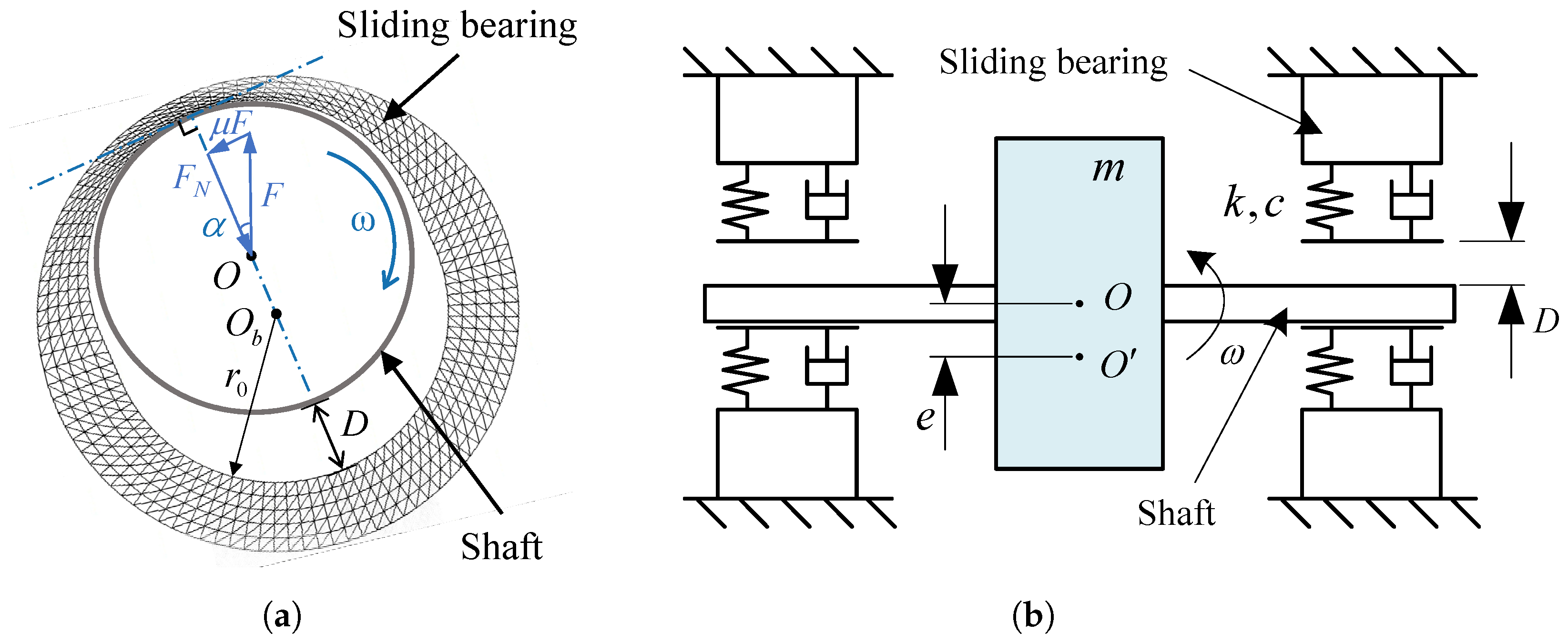
- During the sliding bearing wear test stage, the inner surface of the bearing contacts the middle section of the shaft, and the bearing remains stationary in the circumferential direction while being subjected to a fixed direction and amplitude load radially. The two ends of the shaft are supported by cylindrical roller bearings, which are constrained axially and radially, and maintain a constant speed rotation in the circumferential direction, as shown in Figure 9a. In this stage, the test bearing transitions from a healthy state to a worn state.
- In the vibration measurement stage of the worn bearing, the worn test bearing is fixed in a bearing housing as a support for one end of the shaft, while the other end of the shaft is connected to an electric motor through a spring coupling. An eccentric mass block m is attached to the shaft, with an eccentricity e, and the shaft rotates at a constant speed in the circumferential direction. As shown in Figure 9b, D is the clearance between the journal and the bearing, which is also the maximum wear depth of the bearing.
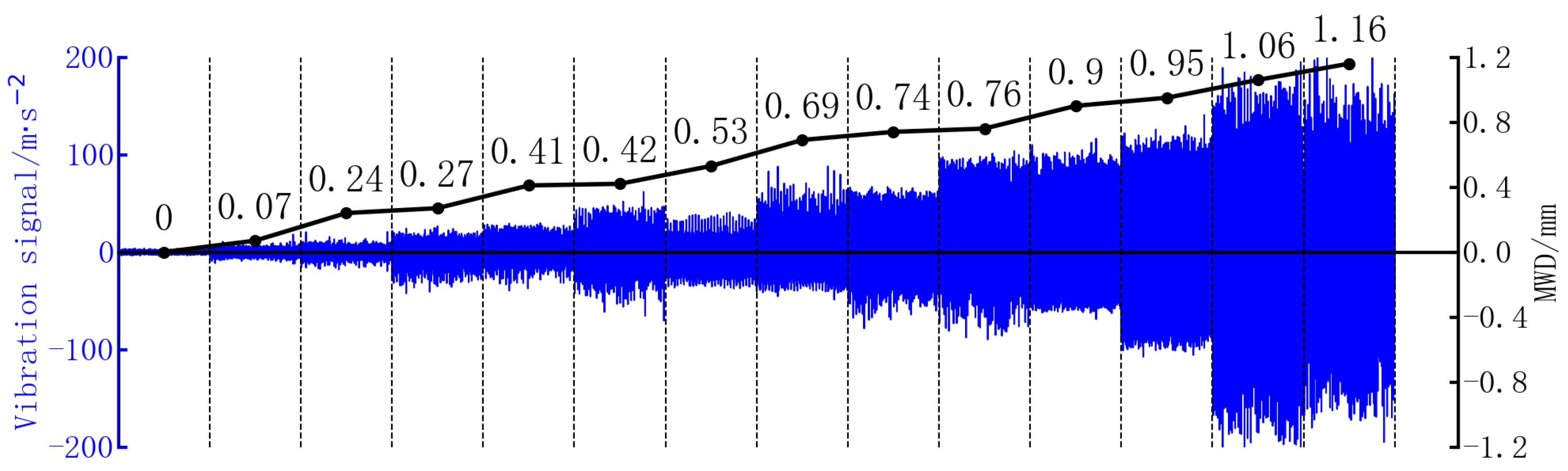
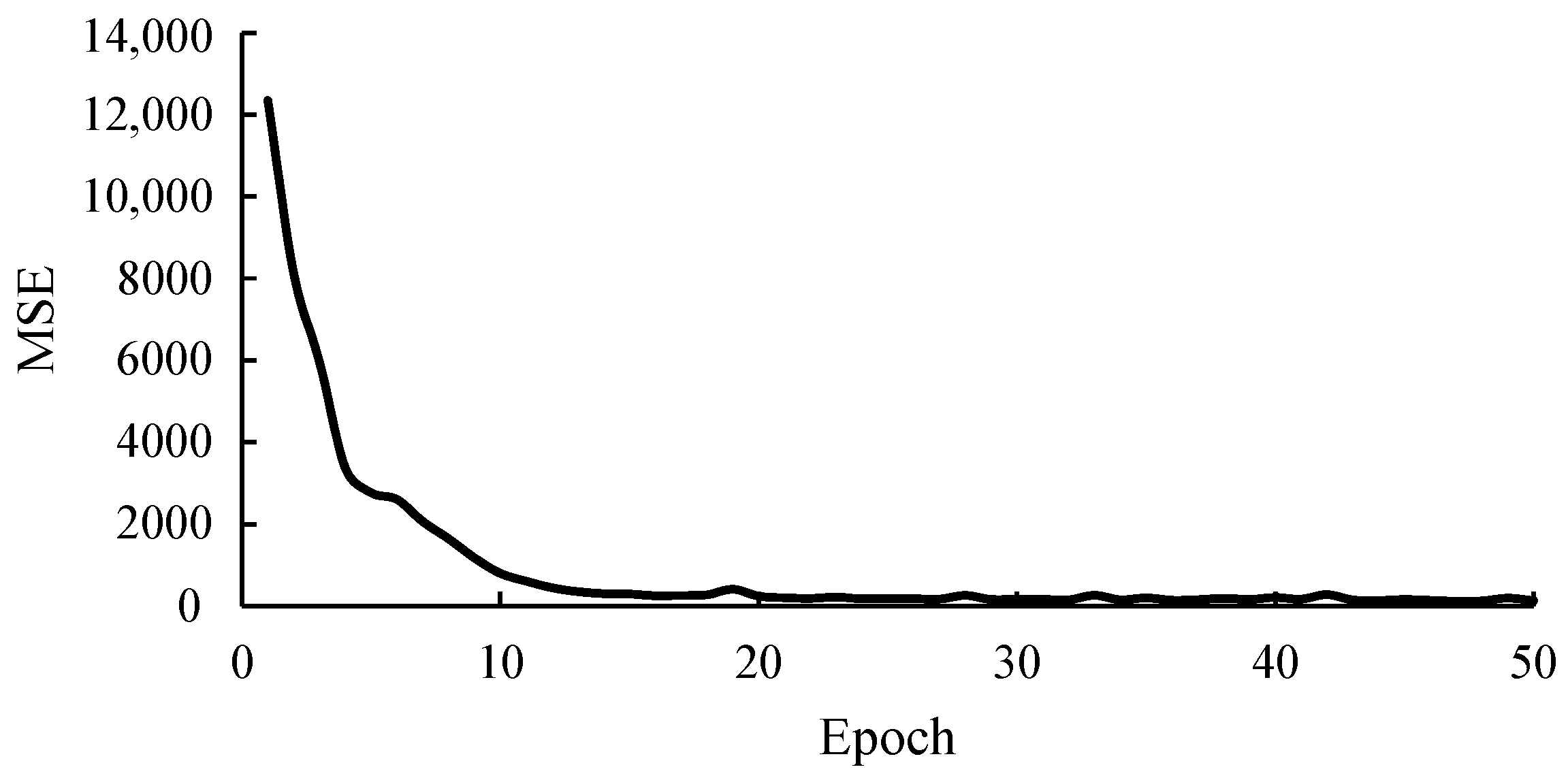
4.2. Wear Depth Diagnosis
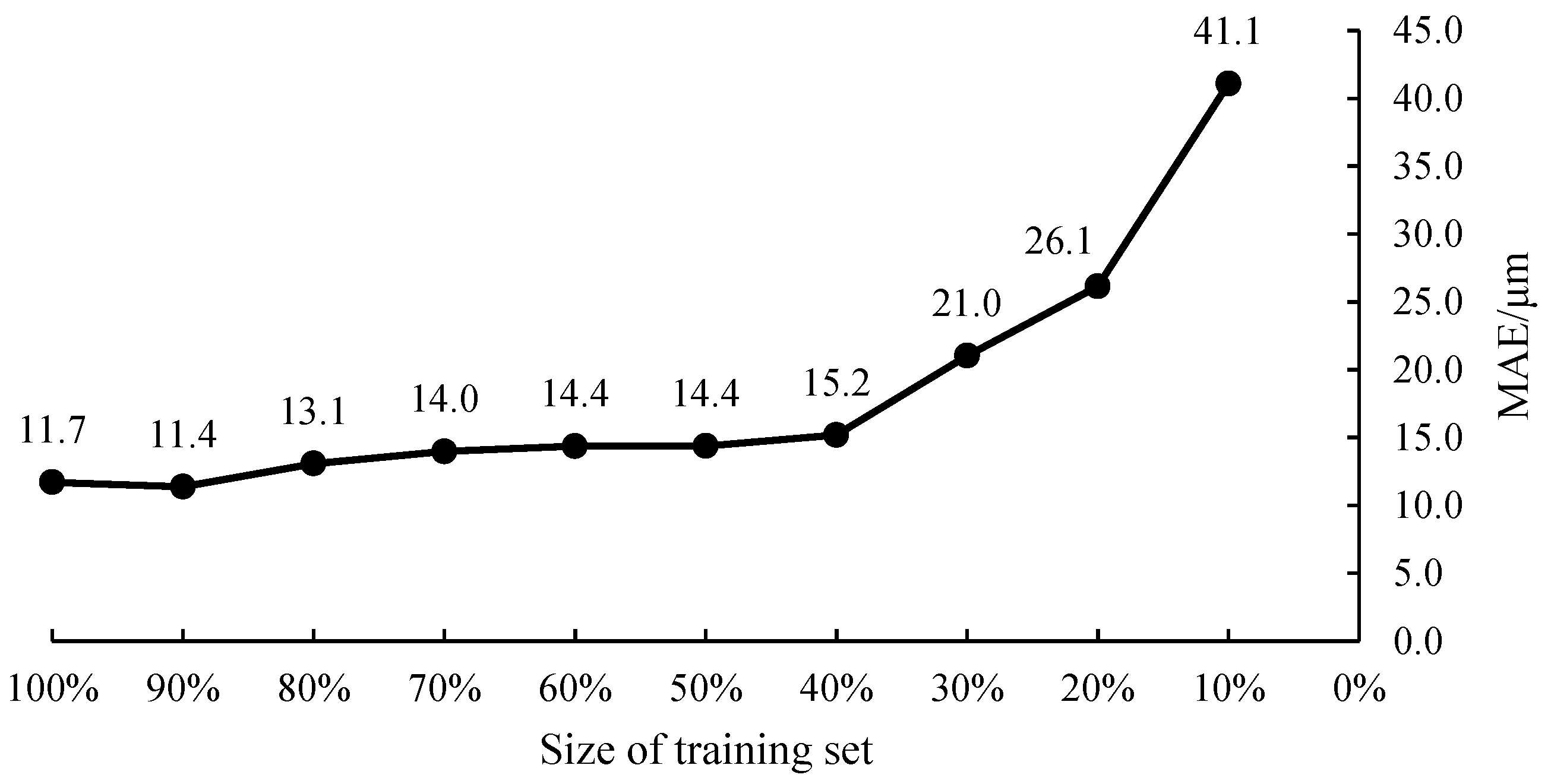
4.3. Impact of Dataset Size on Model Performance
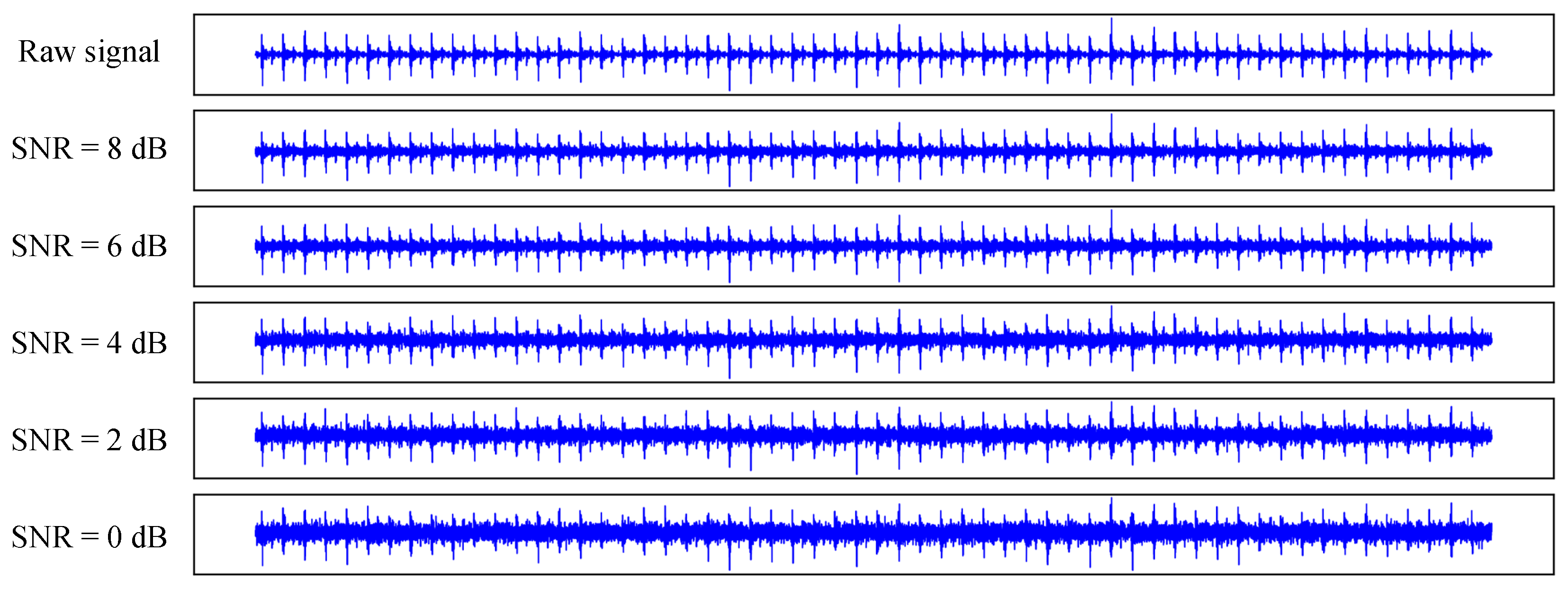
4.4. Impact of Noise on Model Performance
- Strategy 1: Noise at a specific SNR was not added to the training or validation sets but only to the test set. The test results are shown in Table 5.
- Strategy 2: Noise at a specific SNR was added to all training, validation, and test sets. The test results are shown in Table 6.
- Strategy 3: Noise at one specific SNR was added to the test set, while the remaining four SNRs were added to the training and validation sets. For example, the test set was subjected to 0 dB of noise, whereas the training and validation sets were exposed to noise levels of SNR = [8 dB, 6 dB, 4 dB, 2 dB], resulting in a quadrupling of the training set size. The test results are shown in Table 7.
4.5. Prognosis of Remaining Useful Life
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ozsarac, U.; Findik, F.; Durman, M. The wear behaviour investigation of sliding bearings with a designed testing machine. Mater. Des. 2007, 28, 345–350. [Google Scholar] [CrossRef]
- Du, F.; Li, D.; Sa, X.; Li, C.; Yu, Y.; Li, C.; Wang, J.; Wang, W. Overview of friction and wear performance of sliding bearings. Coatings 2022, 12, 1303. [Google Scholar] [CrossRef]
- Shi, G.; Yu, X.; Meng, H.; Zhao, F.; Wang, J.; Jiao, J.; Jiang, H. Effect of surface modification on friction characteristics of sliding bearings: A review. Tribol. Int. 2023, 177, 107937. [Google Scholar] [CrossRef]
- Wang, L.; Kong, X.; Yu, G.; Li, W.; Li, M.; Jiang, A. Error estimation and cross-coupled control based on a novel tool pose representation method of a five-axis hybrid machine tool. Int. J. Mach. Tools Manuf. 2022, 182, 103955. [Google Scholar] [CrossRef]
- Luo, R.; Cao, P.; Dai, Y.; Fu, Y.; Zhao, F.; Huang, Y.; Yang, Q. Rotating machinery fault diagnosis theory and implementation. Instrum. Tech. Sens. 2014, 3, 107–110. [Google Scholar]
- Li, Y.; Tan, Y.; Ma, L.; Yao, J.; Zhang, Z. Wear reliability modeling and simulation analysis of ceramic plain bearing. Lubr. Eng. 2023, 48, 167–171. [Google Scholar]
- Bigoni, C.; Hesthaven, J.S. Simulation-based Anomaly Detection and Damage Localization: An application to Structural Health Monitoring. Comput. Methods Appl. Mech. Eng. 2020, 363, 112896. [Google Scholar] [CrossRef]
- Saxena, A.; Goebel, K.; Simon, D.; Eklund, N. Damage propagation modeling for aircraft engine run-to-failure simulation. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–9. [Google Scholar]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, PHM’12, Minneapolis, MN, USA, 23–27 September 2012; pp. 1–8. [Google Scholar]
- Lei, Y.; Han, T.; Wang, B.; Li, N.; Yan, T.; Yang, J. XJTU-SY rolling element bearing accelerated life test datasets: A tutorial. J. Mech. Eng. 2019, 55, 1–6. [Google Scholar]
- Vencl, A.; Gašić, V.; Stojanović, B. Fault Tree Analysis of Most Common Rolling Bearing Tribological Failures. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Galati, Romania, 22–24 September 2016; IOP Publishing: Bristol, UK, 2017; Volume 174, p. 012048. Available online: https://iopscience.iop.org/article/10.1088/1757-899X/174/1/012048 (accessed on 10 April 2024).
- Li, H.; Zhang, Q.; Qin, X.; Sun, Y. Fault diagnosis method for rolling bearings based on short-time Fourier transform and concolution neural network. J. Vib. Shock 2018, 37, 124–131. [Google Scholar]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. Deep transfer network with joint distribution adaptation: A new intelligent fault diagnosis framework for industry application. ISA Trans. 2020, 97, 269–281. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, L.; Wu, J.; Lai, H. Reliability modeling and evaluation of CNC machine tools for a general state of repair. J. Tsinghua Univ. Sci. Technol. 2022, 62, 965–970. [Google Scholar]
- Wang, L.; Zhu, B.; Wu, J.; Tao, Z. Fault analysis of circular tool magazine based on Bayesian network. J. Jilin Univ. Eng. Technol. Ed. 2022, 52, 280–287. [Google Scholar]
- Luo, J. New Techniques of Influencing the Development of Manuvacturing Industry. Res. China Mark. Regul. 2020, 12–14. [Google Scholar]
- Alexander, P.; Evgeny, T. Procedure for simulation of stable thermal conductivity of bearing assemblies. Adv. Eng. Lett. 2023, 2, 58–63. [Google Scholar] [CrossRef]
- Baron, P.; Pivtorak, O.; Ivan, J.; Kočiško, M. Assessment of the Correlation between the Monitored Operating Parameters and Bearing Life in the Milling Head of a CNC Computer Numerical Control Machining Center. Machines 2024, 12, 188. [Google Scholar] [CrossRef]
- Wen, S. Study on lubrication theory-progress and thinking-over. Tribology 2007, 6, 497–503. [Google Scholar]
- Yang, J.; Yang, S.; Chen, C.; Wang, Y.; Wu, W. Rearch on sliding bearings and rotor system stability. J. Aerosp. Power 2008, 23, 1420–1426. [Google Scholar]
- Martsinkovsky, V.; Yurko, V.; Tarelnik, V.; Filonenko, Y. Designing thrust sliding bearings of high bearing capacity. Procedia Eng. 2012, 39, 148–156. [Google Scholar] [CrossRef]
- Chasalevris, A.C.; Nikolakopoulos, P.G.; Papadopoulos, C.A. Dynamic effect of bearing wear on rotor-bearing system response. J. Vib. Acoust. 2013, 135, 011008. [Google Scholar] [CrossRef]
- Lin, L.; He, M.; Ma, W.; Wang, Q.; Zhai, H.; Deng, C. Dynamic Characteristic Analysis of the Multi-Stage Centrifugal Pump Rotor System with Uncertain Sliding Bearing Structural Parameters. Machines 2022, 10, 473. [Google Scholar] [CrossRef]
- Tang, D.; Xiang, G.; Guo, J.; Cai, J.; Yang, T.; Wang, J.; Han, Y. On the optimal design of staved water-lubricated bearings driven by tribo-dynamic mechanism. Phys. Fluids 2023, 35, 093611. [Google Scholar] [CrossRef]
- Tofighi-Niaki, E.; Safizadeh, M.S. Dynamic of a flexible rotor-bearing system supported by worn tilting journal bearings experiencing rub-impact. Lubricants 2023, 11, 212. [Google Scholar] [CrossRef]
- Yang, T.; Xiang, G.; Cai, J.; Wang, L.; Lin, X.; Wang, J.; Zhou, G. Five-DOF nonlinear tribo-dynamic analysis for coupled bearings during start-up. Int. J. Mech. Sci. 2024, 296, 109068. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, X.; Zhang, L.; Wang, X.; Wang, C.; Wang, H.; Zhao, X. Effect of surface roughness, viscosity-pressure relationship and elastic deformation on lubrication performance of misaligned journal bearings. Ind. Lubr. Tribol. 2014, 66, 337–345. [Google Scholar] [CrossRef]
- Engel, T.; Lechler, A.; Verl, A. Sliding bearing with adjustable friction properties. Cirp-Ann.-Manuf. Technol. 2016, 65, 353–356. [Google Scholar] [CrossRef]
- Ren, G. A new method to calculate water film stiffness and damping for water lubricated bearing with multiple axial grooves. Chin. J. Mech. Eng. 2020, 33, 1–18. [Google Scholar] [CrossRef]
- Tang, D.; Xiao, K.; Xiang, G.; Cai, J.; Fillon, M.; Wang, D.; Su, Z. On the nonlinear time-varying mixed lubrication for coupled spiral microgroove water-lubricated bearings with mass conservation cavitation. Tribol. Int. 2024, 193, 109381. [Google Scholar] [CrossRef]
- Ojala, N.; Valtonen, K.; Heino, V.; Kallio, M.; Aaltonen, J.; Siitonen, P.; Kuokkala, V.T. Effects of composition and microstructure on the abrasive wear performance of quenched wear resistant steels. Wear 2014, 317, 225–232. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, G.; Zhu, L.; Wang, H.; Han, C.; Li, Z.; Wang, H.; Yong, Q.; Huang, Y. Structure–performance evolution mechanism of the wear failure process of coated spherical plain bearings. Eng. Fail. Anal. 2022, 135, 106097. [Google Scholar] [CrossRef]
- Kumar Rajak, S.; Kumar, D.; Seetharam, R.; Tandon, P. Mechanical and dry sliding wear analysis of porcelain reinforced SAE660 bronze bearing alloy composite fabricated by stir casting method. Mater. Today Proc. 2023, 87, 210–214. [Google Scholar] [CrossRef]
- Yin, Y.; Jiao, M.; Xie, T.; Zheng, Z.; Liu, K.; Yu, J.; Tian, M. Research progress in sliding bearing materials. Lubr. Eng. 2006, 183–187. [Google Scholar]
- Jeon, H.G.; Cho, D.H.; Yoo, J.H.; Lee, Y.Z. Wear Prediction of Earth-Moving Machinery Joint Bearing via Correlation between Wear Coefficient and Film Parameter: Experimental Study. Tribol. Trans. 2018, 61, 808–815. [Google Scholar] [CrossRef]
- König, F.; Ouald Chaib, A.; Jacobs, G.; Sous, C. A multiscale-approach for wear prediction in journal bearing systems—From wearing-in towards steady-state wear. Wear 2019, 426-427, 1203–1211. [Google Scholar] [CrossRef]
- Dai, J.; Tian, L. A Novel Prognostic Method for Wear of Sliding Bearing Based on SFENN. In Proceedings of the Intelligent Robotics and Applications, Hangzhou, China, 5–7 July 2023; Yang, H., Liu, H., Zou, J., Yin, Z., Liu, L., Yang, G., Ouyang, X., Wang, Z., Eds.; Springer Nature: Singapore, 2023; pp. 212–225. [Google Scholar]
- Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Process. 2018, 102, 37–58. [Google Scholar] [CrossRef]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond empirical risk minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Chen, S.; Shang, P. Financial time series analysis using the relation between MPE and MWPE. Phys. A Stat. Mech. Appl. 2020, 537, 122716. [Google Scholar] [CrossRef]
- Petrauskiene, V.; Ragulskiene, J.; Zhu, H.; Wang, J.; Cao, M. The discriminant statistic based on MPE-MWPE relationship and non-uniform embedding. J. Meas. Eng. 2022, 10, 150–163. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Bottou, L. Stochastic gradient descent tricks. In Neural Networks: Tricks of the Trade: Second Edition; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–436. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zhang, X. Modern Signal Processing; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2022. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part IV 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Dai, J.; Tian, L.; Han, T.; Chang, H. Digital Twin for wear degradation of sliding bearing based on PFENN. Adv. Eng. Inform. 2024, 61, 102512. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y.; Hu, Q. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs. Mech. Syst. Signal Process. 2007, 21, 2280–2294. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster–Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
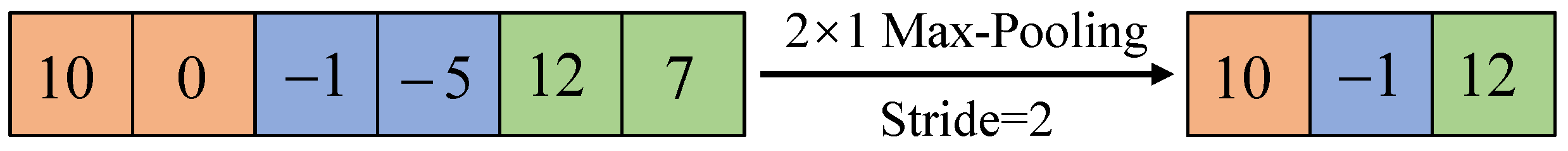





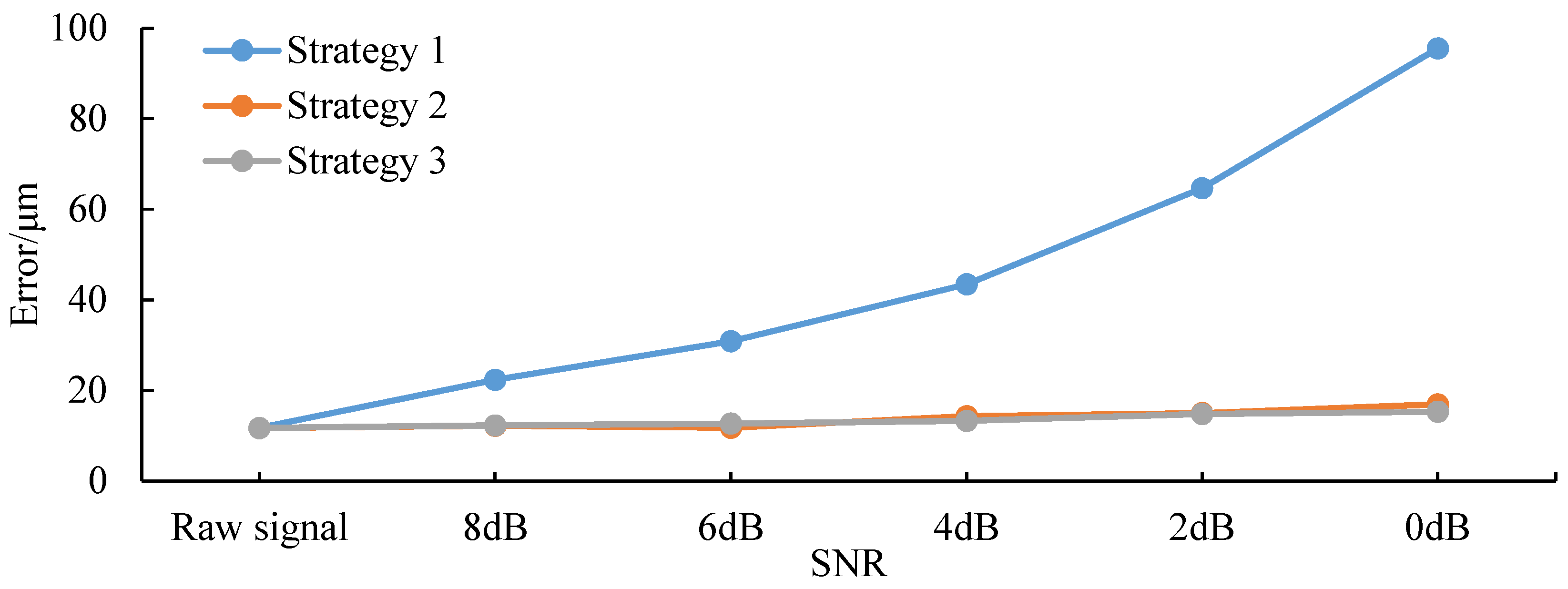

| Layer | Number of Channels | Convolution Kernel | Max Pooling | Gated Unit | |||||
|---|---|---|---|---|---|---|---|---|---|
| Input | Output | Size | Stride | Size | Stride | ||||
| -MGC (time-domain) | Long-term cycle | 1 | 16 | 129 × 1 | 1 | ||||
| -Conv | Medium-term cycle | 1 | 16 | 33 × 1 | 1 | 4 × 1 | 2 | Sigmoid | |
| Short-term cycle | 1 | 16 | 9 × 1 | 1 | |||||
| -Conv | 16 | 16 | 5 × 1 | 2 | 4 × 1 | 2 | / | ||
| Res-connection | 1 | 48 | 1 × 1 | 8 | / | / | / | ||
| -MGC (time-domain) | Long-term cycle | 48 | 16 | 129 × 1 | 1 | ||||
| -Conv | Medium-term cycle | 48 | 16 | 33 × 1 | 1 | 4 × 1 | 2 | Sigmoid | |
| Short-term cycle | 48 | 16 | 9 × 1 | 1 | |||||
| -MGC in time-domain | 16 | 16 | 5 × 1 | 2 | 4 × 1 | 2 | / | ||
| Res-connection | 48 | 48 | 1 × 1 | 8 | / | / | / | ||
| -MGC (frequency-domain) | Long-term cycle | 1 | 16 | 129 × 1 | 1 | ||||
| -Conv | Medium-term cycle | 1 | 16 | 33 × 1 | 1 | 4 × 1 | 2 | Sigmoid | |
| Short-term cycle | 1 | 16 | 9 × 1 | 1 | |||||
| -Conv | 16 | 16 | 5 × 1 | 2 | 4 × 1 | 2 | / | ||
| Res-connection | 1 | 48 | 1 × 1 | 8 | / | / | / | ||
| -MGC (frequency-domain) | Long-term cycle | 48 | 16 | 129 × 1 | 1 | ||||
| -Conv | Medium-term cycle | 48 | 16 | 33 × 1 | 1 | 4 × 1 | 2 | Sigmoid | |
| Short-term cycle | 48 | 16 | 9 × 1 | 1 | |||||
| -Conv | 16 | 16 | 5 × 1 | 2 | 4 × 1 | 2 | / | ||
| Res-connection | 48 | 48 | 1 × 1 | 8 | / | / | / | ||
| MLP | Flatten | Channels: 48→1; activation function: ReLU; Dropout = 0.5 | |||||||
| 1st layer | Length of feature vectors: 2304→20; activation function: ReLU | ||||||||
| 2nd layer | Length of feature vectors: 20→1; activation function: ReLU | ||||||||
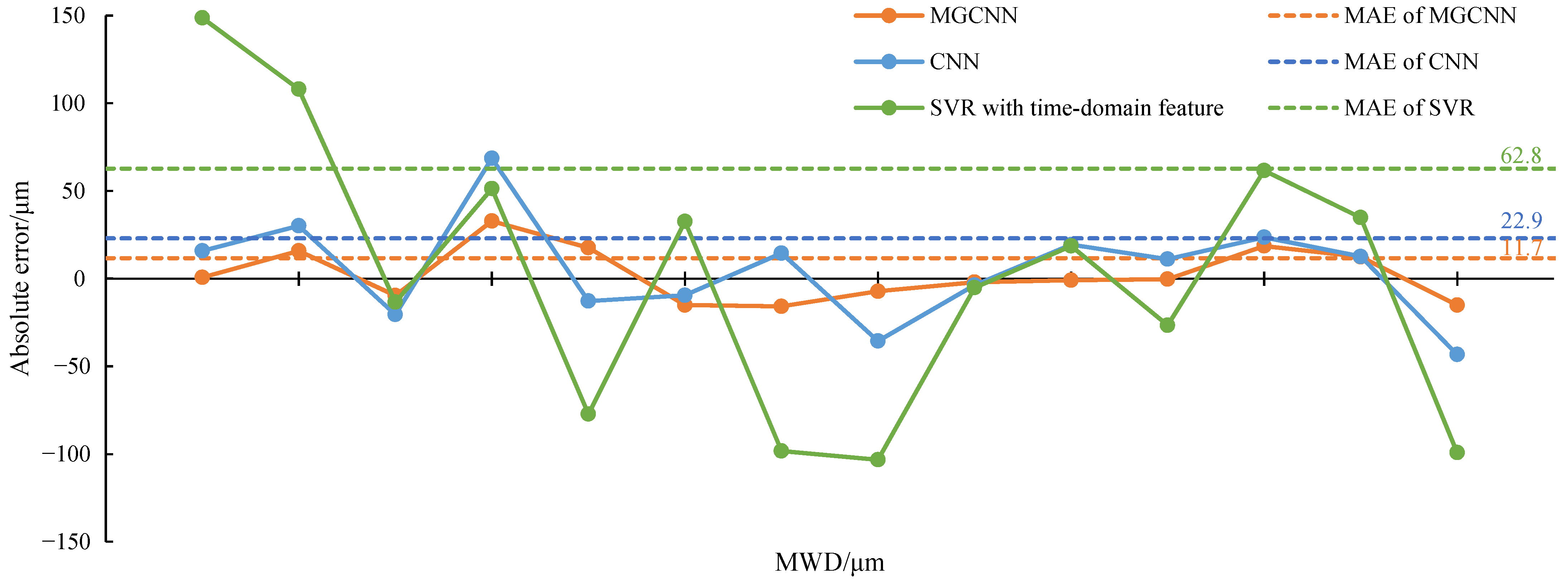
| True Value/m | MGCNN | CNN | SVR-1 | SVR-2 | ||||
|---|---|---|---|---|---|---|---|---|
| Output | Error | Output | Error | Output | Error | Output | Error | |
| 0 | 0.7 | 0.7 | 15.8 | 15.8 | 322.5 | 322.5 | 148.7 | 148.7 |
| 70 | 85.8 | 15.8 | 100.1 | 30.1 | 371.3 | 301.3 | 178 | 108 |
| 240 | 230.4 | −9.6 | 219.5 | −20.5 | 385.0 | 145.0 | 226.6 | −13.4 |
| 270 | 302.8 | 32.8 | 338.6 | 68.6 | 408.6 | 138.6 | 321.3 | 51.3 |
| 410 | 427.6 | 17.6 | 397.2 | −12.8 | 417.8 | 7.8 | 332.8 | −77.2 |
| 420 | 404.9 | −15.1 | 410.5 | −9.5 | 428.6 | 8.6 | 452.6 | 32.6 |
| 530 | 514.2 | −15.8 | 544.5 | 14.5 | 435.1 | −94.9 | 431.7 | −98.3 |
| 690 | 682.8 | −7.2 | 654.4 | −35.6 | 441.8 | −248.2 | 586.7 | −103.3 |
| 740 | 738.0 | −2.0 | 736.3 | −3.7 | 448.6 | −291.4 | 734.8 | −5.2 |
| 760 | 759.1 | −0.9 | 779.4 | 19.4 | 449.2 | −310.8 | 778.6 | 18.6 |
| 900 | 899.7 | −0.3 | 911.1 | 11.1 | 473.8 | −426.2 | 873.4 | −26.6 |
| 950 | 968.6 | 18.6 | 973.6 | 23.6 | 478.5 | −471.5 | 1011.6 | 61.6 |
| 1060 | 1072.4 | 12.4 | 1072.6 | 12.6 | 489.1 | −570.9 | 1094.8 | 34.8 |
| 1160 | 1144.9 | −15.1 | 1116.7 | −43.3 | 478.0 | −682 | 1060.8 | −99.2 |
| MAE | 11.7 | 22.9 | 287.1 | 62.8 | ||||
| True Value/m | MGCNN | CNN | SVR-1 | SVR-2 | ||||
|---|---|---|---|---|---|---|---|---|
| Output | Error | Output | Error | Output | Error | Output | Error | |
| 240 | 176.9 | −63.1 | 184.4 | −55.6 | 390.1 | 150.1 | 131.5 | −108.5 |
| 530 | 557.4 | 27.4 | 584.0 | 54.0 | 428.2 | −101.8 | 363.2 | −166.8 |
| 760 | 797.4 | 37.4 | 808.0 | 48.0 | 448.1 | −311.9 | 846.3 | 86.3 |
| MAE | 42.6 | 52.4 | 187.9 | 120.5 | ||||
| True Value | Size of Training Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 90% | 80% | 70% | 60% | 50% | 40% | 30% | 20% | 10% | |
| 0 | 1.1 | 5.1 | 4.7 | 2.4 | 6.6 | 8.2 | 9.9 | 33.2 | 66.1 |
| 70 | 91.8 | 84.6 | 86.7 | 93.4 | 86.3 | 97.3 | 111.3 | 108.5 | 131.9 |
| 240 | 237.1 | 234.5 | 231.7 | 235.3 | 231.7 | 233.0 | 218.5 | 202.8 | 199.4 |
| 270 | 302.4 | 307.7 | 302.8 | 306.3 | 311.4 | 311.2 | 327.1 | 327.7 | 331.6 |
| 410 | 421.3 | 422.1 | 428.4 | 430.2 | 428.8 | 410.5 | 405.1 | 406.7 | 369.3 |
| 420 | 402.0 | 404.4 | 403.1 | 403.5 | 402.1 | 408.1 | 420.4 | 420.1 | 453.6 |
| 530 | 520.6 | 516.2 | 517.4 | 518.5 | 519.6 | 517.1 | 520.3 | 527.8 | 529.3 |
| 690 | 678.8 | 685.8 | 682.5 | 683.1 | 683.0 | 684.4 | 673.9 | 664.5 | 651.1 |
| 740 | 735.4 | 733.2 | 733.9 | 731.6 | 732.8 | 734.2 | 734.6 | 731.5 | 741.4 |
| 760 | 760.7 | 763.6 | 761.3 | 763.5 | 763.1 | 769.2 | 778.5 | 788.1 | 817.1 |
| 900 | 903.5 | 905.2 | 904.5 | 905.4 | 907.8 | 908.9 | 919.8 | 918.4 | 939.1 |
| 950 | 973.1 | 975.9 | 979.1 | 976.1 | 970.3 | 977.1 | 981.9 | 996.9 | 999.6 |
| 1060 | 1067.1 | 1074.1 | 1075.7 | 1075.3 | 1075.7 | 1074.4 | 1081.8 | 1087.2 | 1105.7 |
| 1160 | 1147.7 | 1140.9 | 1138.8 | 1139.6 | 1139.5 | 1127.2 | 1123.9 | 1120.6 | 1121.9 |
| MAE | 11.4 | 13.1 | 14.0 | 14.4 | 14.4 | 15.2 | 21.0 | 26.1 | 41.1 |
| Models in k-Fold Cross-Validation | Raw Signal | SNR | ||||
|---|---|---|---|---|---|---|
| 8 dB | 6 dB | 4 dB | 2 dB | 0 dB | ||
| No.1 | / | 23.0 | 30.2 | 40.1 | 56.7 | 80.0 |
| No.2 | / | 21.2 | 30.2 | 43.7 | 66.1 | 101.1 |
| No.3 | / | 22.3 | 32.0 | 46.3 | 67.7 | 99.6 |
| No.4 | / | 23.3 | 30.8 | 42.7 | 66.5 | 102.9 |
| No.5 | / | 22.0 | 31.2 | 44.4 | 66.4 | 94.2 |
| Mean | 11.7 | 22.4 | 30.9 | 43.4 | 64.7 | 95.6 |
| Models in k-Fold Cross-Validation | Raw Signal | SNR | ||||
|---|---|---|---|---|---|---|
| 8 dB | 6 dB | 4 dB | 2 dB | 0 dB | ||
| No.1 | / | 11.6 | 10.0 | 14.0 | 14.6 | 16.4 |
| No.2 | / | 13.4 | 13.2 | 15.0 | 15.8 | 17.5 |
| No.3 | / | 12.7 | 12.1 | 13.8 | 14.2 | 17.5 |
| No.4 | / | 12.4 | 11.6 | 15.4 | 15.5 | 15.7 |
| No.5 | / | 10.8 | 11.8 | 12.9 | 14.8 | 17.4 |
| Mean | 11.7 | 12.2 | 11.7 | 14.2 | 15.0 | 16.9 |
| Models in k-Fold Cross-Validation | Raw Signal | SNR | ||||
|---|---|---|---|---|---|---|
| 8 dB | 6 dB | 4 dB | 2 dB | 0 dB | ||
| No.1 | / | 11.9 | 12.7 | 14.3 | 13.9 | 15.4 |
| No.2 | / | 11.3 | 14.5 | 13.8 | 13.9 | 14.6 |
| No.3 | / | 13.0 | 12.7 | 13.8 | 14.5 | 15.6 |
| No.4 | / | 12.2 | 12.5 | 10.5 | 15.5 | 17.1 |
| No.5 | / | 12.9 | 10.8 | 13.7 | 16.1 | 13.6 |
| Mean | 11.7 | 12.2 | 12.6 | 13.2 | 14.8 | 15.3 |
| Current Time (min) | Actual RUL (min) | Predicted RUL (min) | Error (min) |
|---|---|---|---|
| 0 | 170 | 7 | −163 |
| 34 | 136 | 14 | −122 |
| 77 | 93 | 120 | 27 |
| 80 | 90 | 69 | −21 |
| 104 | 66 | 52 | −14 |
| 124 | 46 | 58 | 12 |
| 146 | 24 | 57 | 33 |
| 150 | 20 | 35 | 15 |
| 151 | 19 | 29 | 10 |
| 161 | 9 | 26 | 17 |
| 167 | 3 | 13 | 10 |
| 170 | 0 | 4 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Tian, L.; Chang, H. An Intelligent Diagnostic Method for Wear Depth of Sliding Bearings Based on MGCNN. Machines 2024, 12, 266. https://doi.org/10.3390/machines12040266
Dai J, Tian L, Chang H. An Intelligent Diagnostic Method for Wear Depth of Sliding Bearings Based on MGCNN. Machines. 2024; 12(4):266. https://doi.org/10.3390/machines12040266
Chicago/Turabian StyleDai, Jingzhou, Ling Tian, and Haotian Chang. 2024. "An Intelligent Diagnostic Method for Wear Depth of Sliding Bearings Based on MGCNN" Machines 12, no. 4: 266. https://doi.org/10.3390/machines12040266
APA StyleDai, J., Tian, L., & Chang, H. (2024). An Intelligent Diagnostic Method for Wear Depth of Sliding Bearings Based on MGCNN. Machines, 12(4), 266. https://doi.org/10.3390/machines12040266








