Electromagnetic Characterization of Permanent Magnet Eddy Current Structures Based on Backplane Distance Adjustment
Abstract
:1. Introduction
2. Structure and Operation Principles of Permanent Magnet Eddy Current Switching Seal
3. Modeling and Analysis of Permanent Magnet Eddy Current Structures
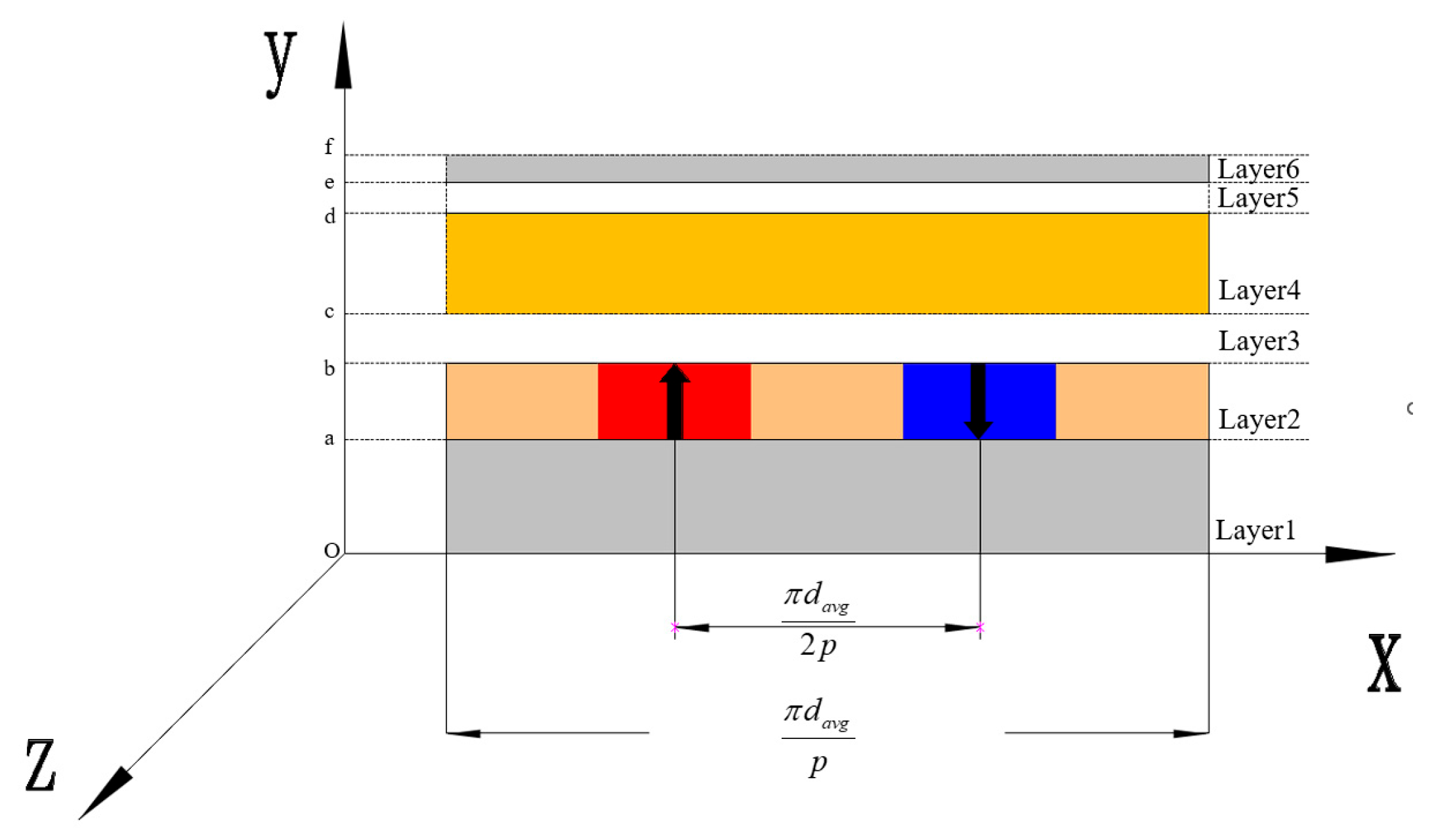
3.1. Model and Assumptions
- Layer 1: Magnet disc backplane layer;
- Layer 2: Permanent magnet array layer;
- Layer 3: Working air gap layer;
- Layer 4: Copper layer;
- Layer 5: Backplane air gap layer;
- Layer 6: Conductor disc backplane layer.
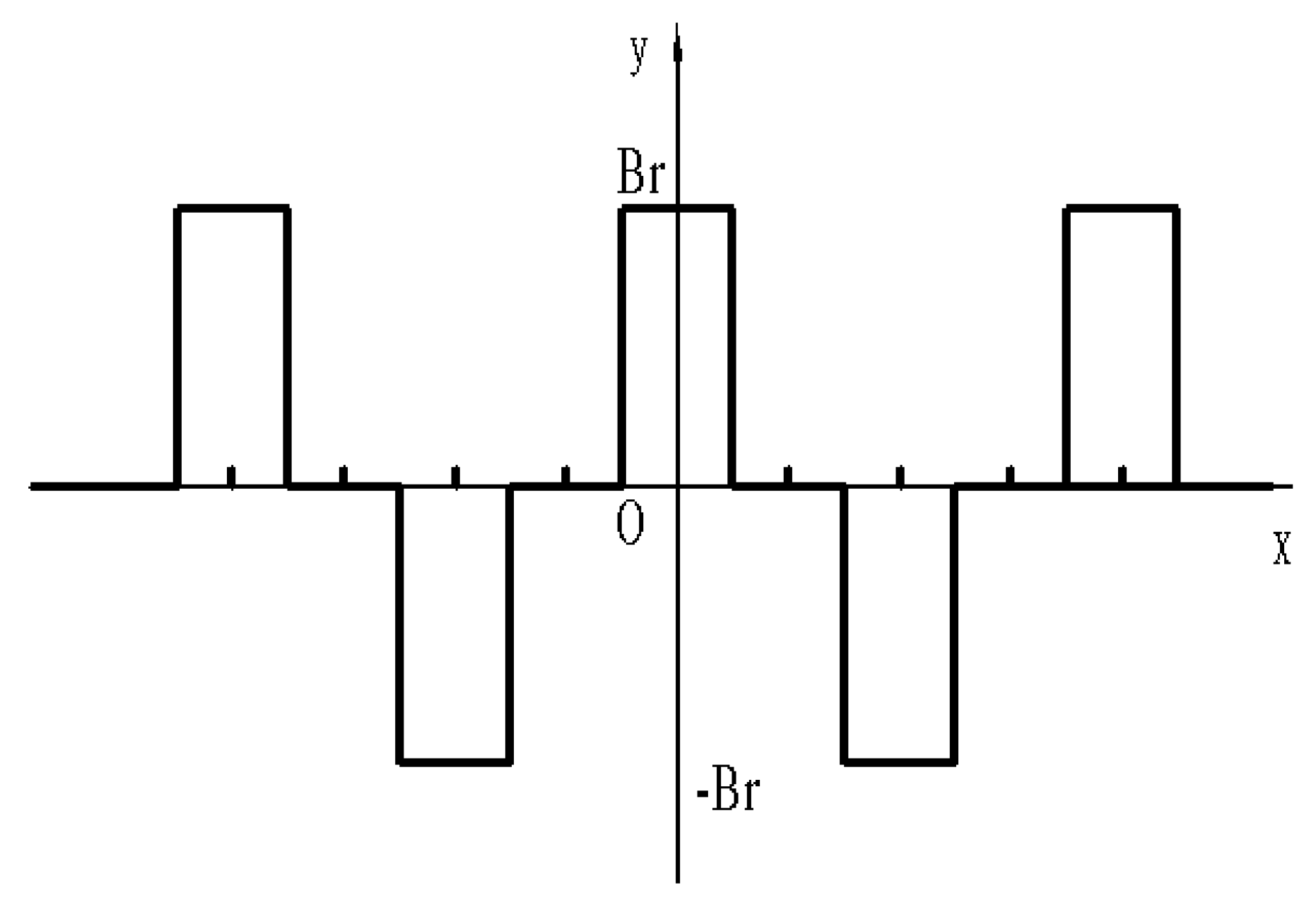
3.2. Model Analysis and Control Equations
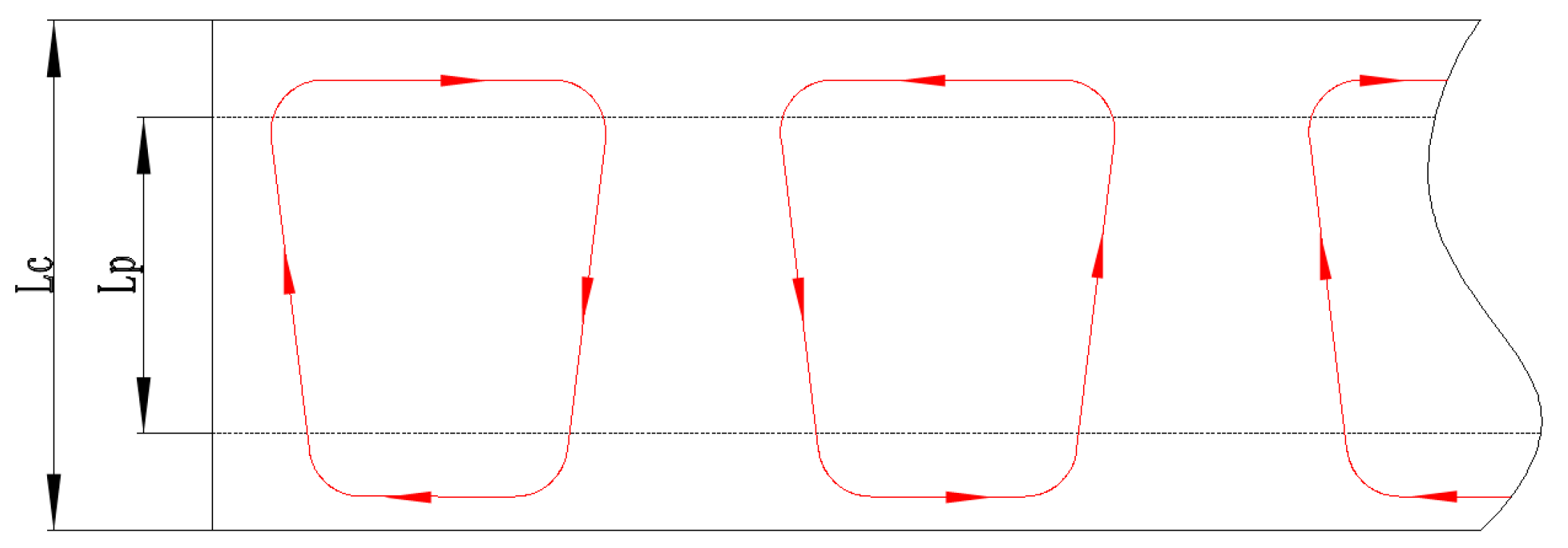
3.3. The Boundary Conditions
3.4. Torque Equation
3.5. Axial Force Equation
4. Finite Element Analysis of the Electromagnetic Field in Permanent Magnet Eddy Current Structures
- The permanent magnet material is neodymium iron boron, uniformly magnetized along the axial direction, and the demagnetization caused by thermal conduction due to eddy current effects is not considered.
- The magnetic conductor is an isotropic material.
- Only components related to electromagnetic effects in the model are considered, namely, the permanent magnet, copper conductor disc, conductor disc backplane, and the magnetic shielding effect of the conductor disc yoke iron. The electromagnetic effects of other metal components are neglected, and their structures are treated as air.
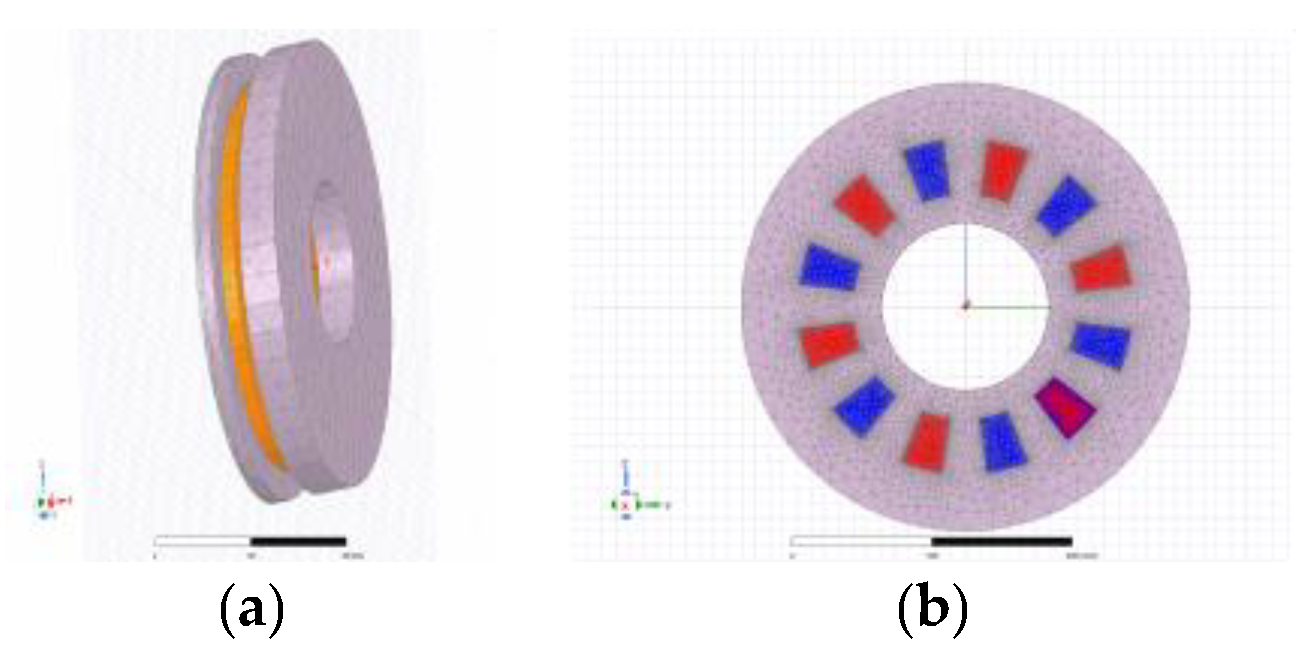
4.1. Finite Element Model Meshing Results
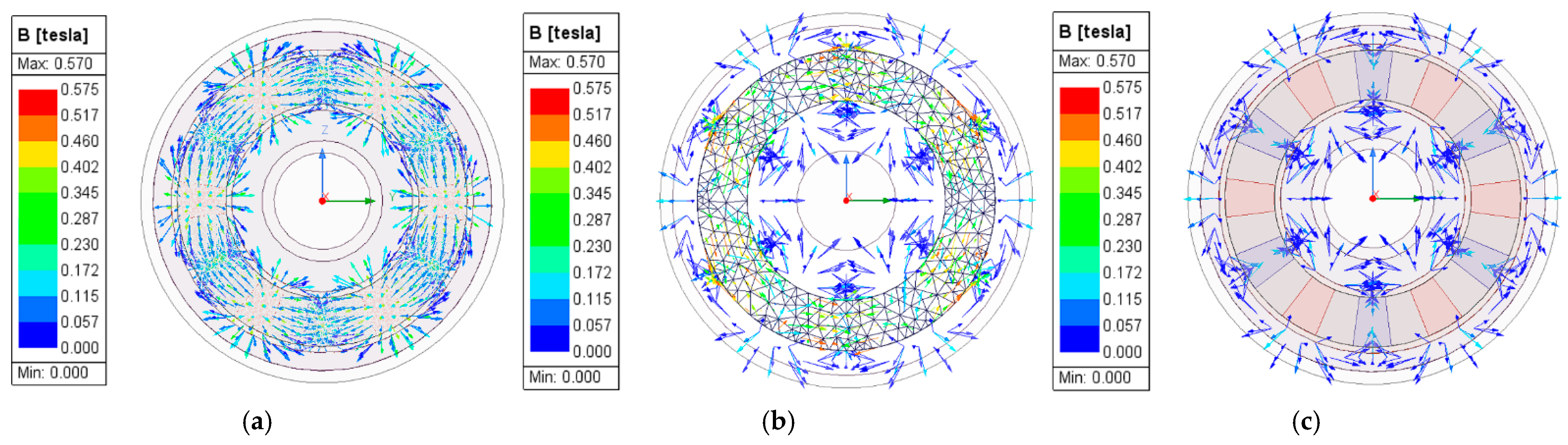
4.2. Static Magnetic Field Results of the Permanent Magnet Eddy Current Structure
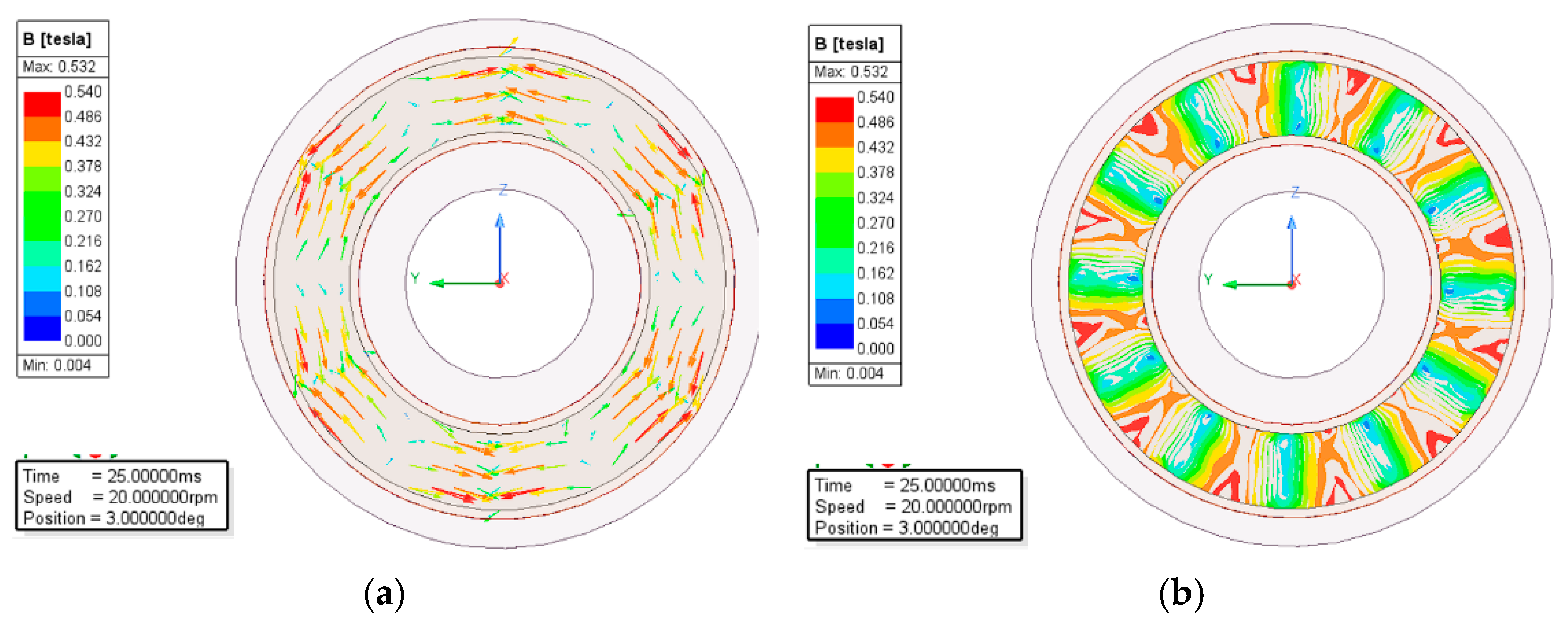
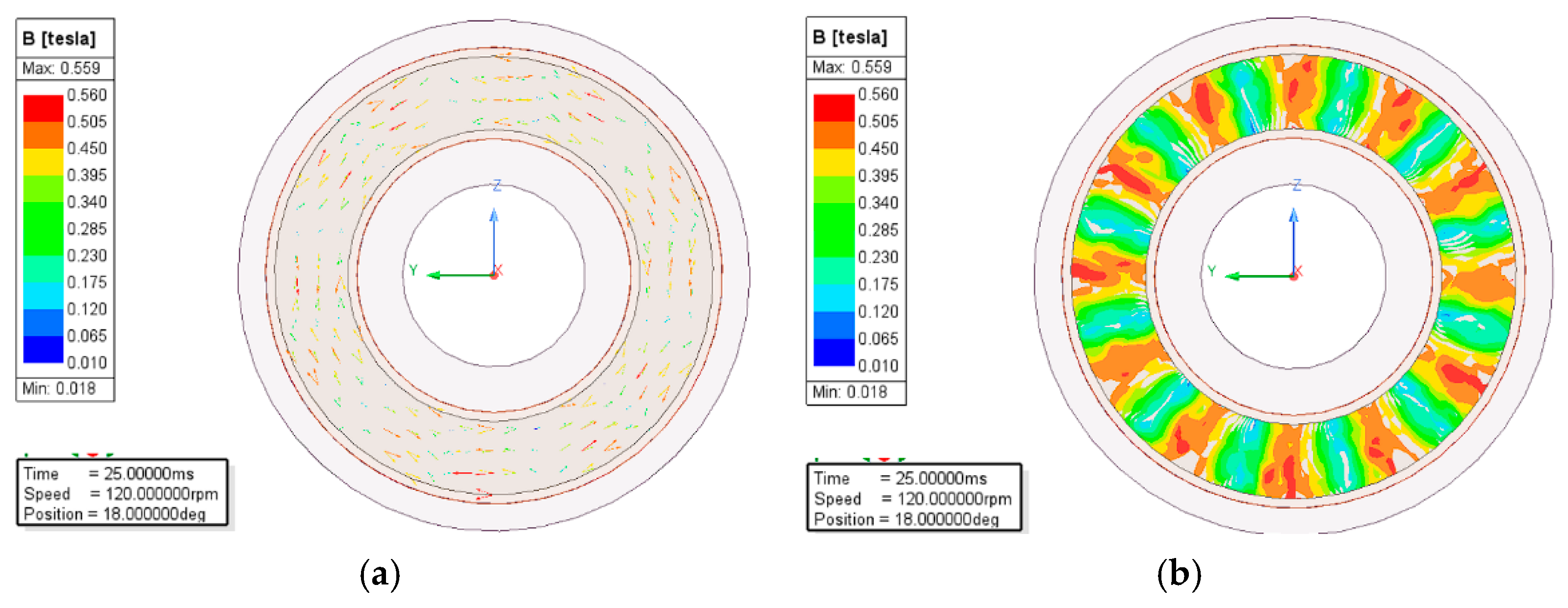
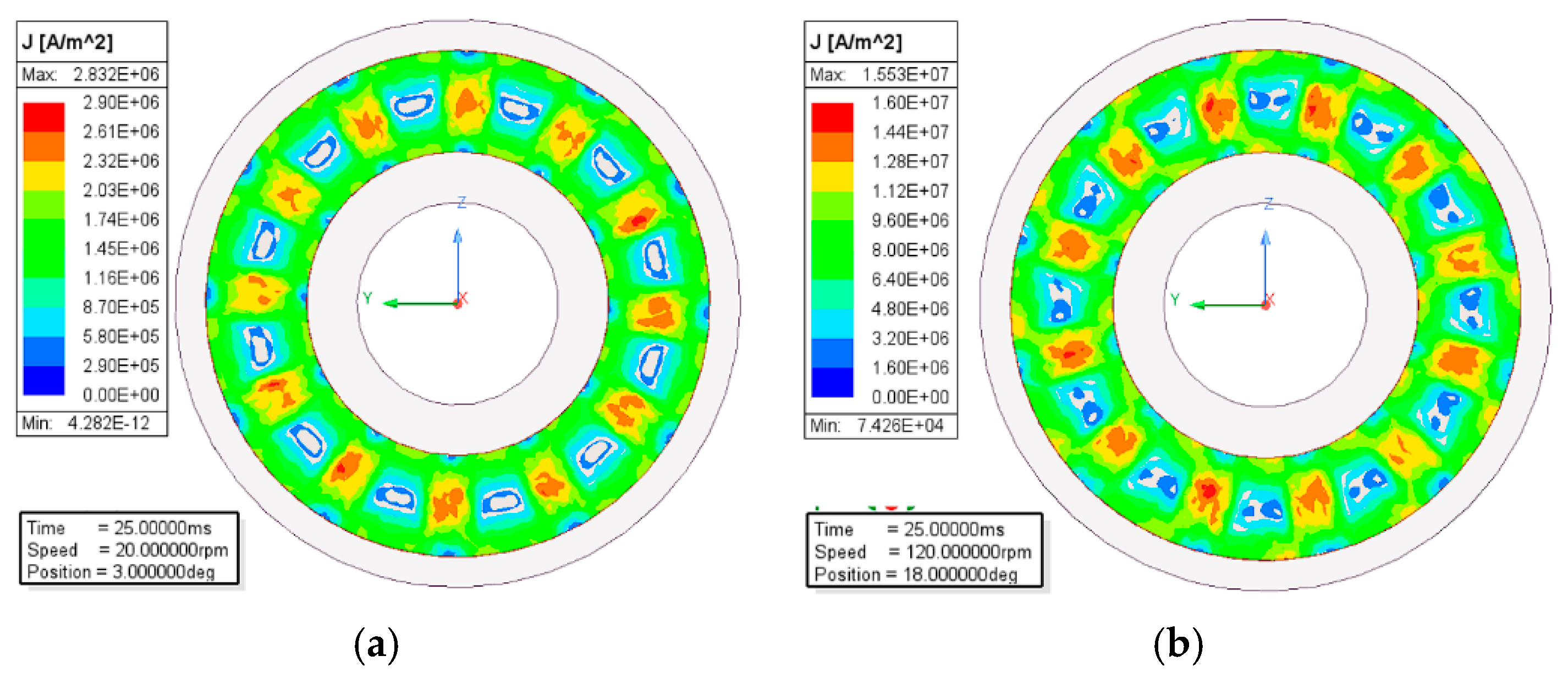
4.3. Transient Magnetic Field Results of the Permanent Magnet Eddy Current Structure
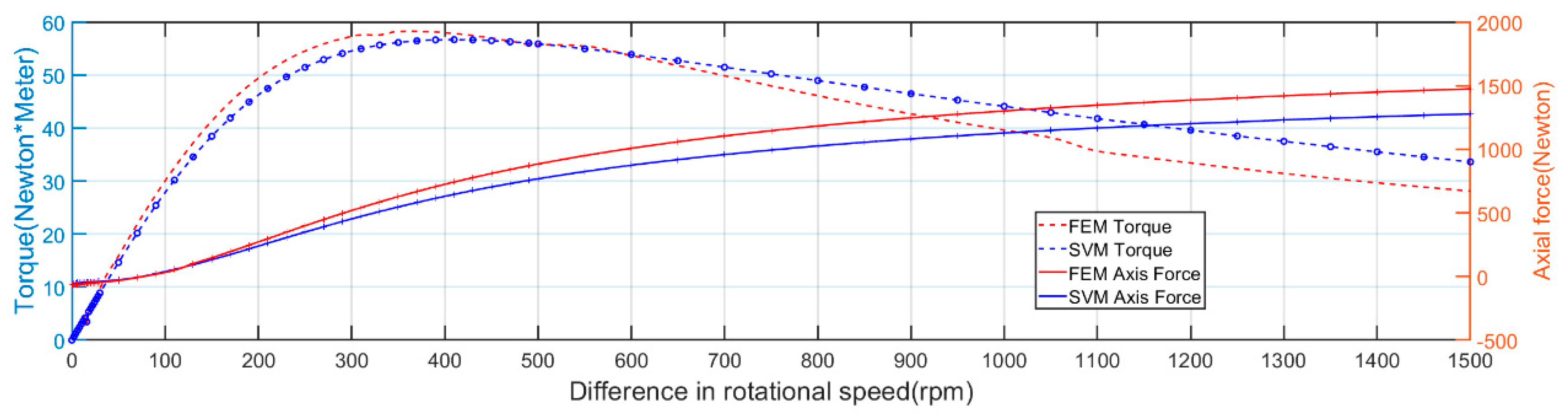
4.4. Transmission Characteristics of the Permanent Magnet Eddy Current Structure
5. Experiments and Results
5.1. Test Prototypes and Test Methods
5.2. Test Results
6. Conclusions
- This study utilized the method of separation of variables to solve the electromagnetic field of the permanent magnet eddy current structure with a gap between the conductor disc and the backplane, and we derived the calculation methods for torque and axial force. Validation against results obtained using finite element methods showed that the analytical results were accurate, particularly under low-slip conditions, thus making this method suitable for electromagnetic field design calculations for such low-slip disc-type structures.
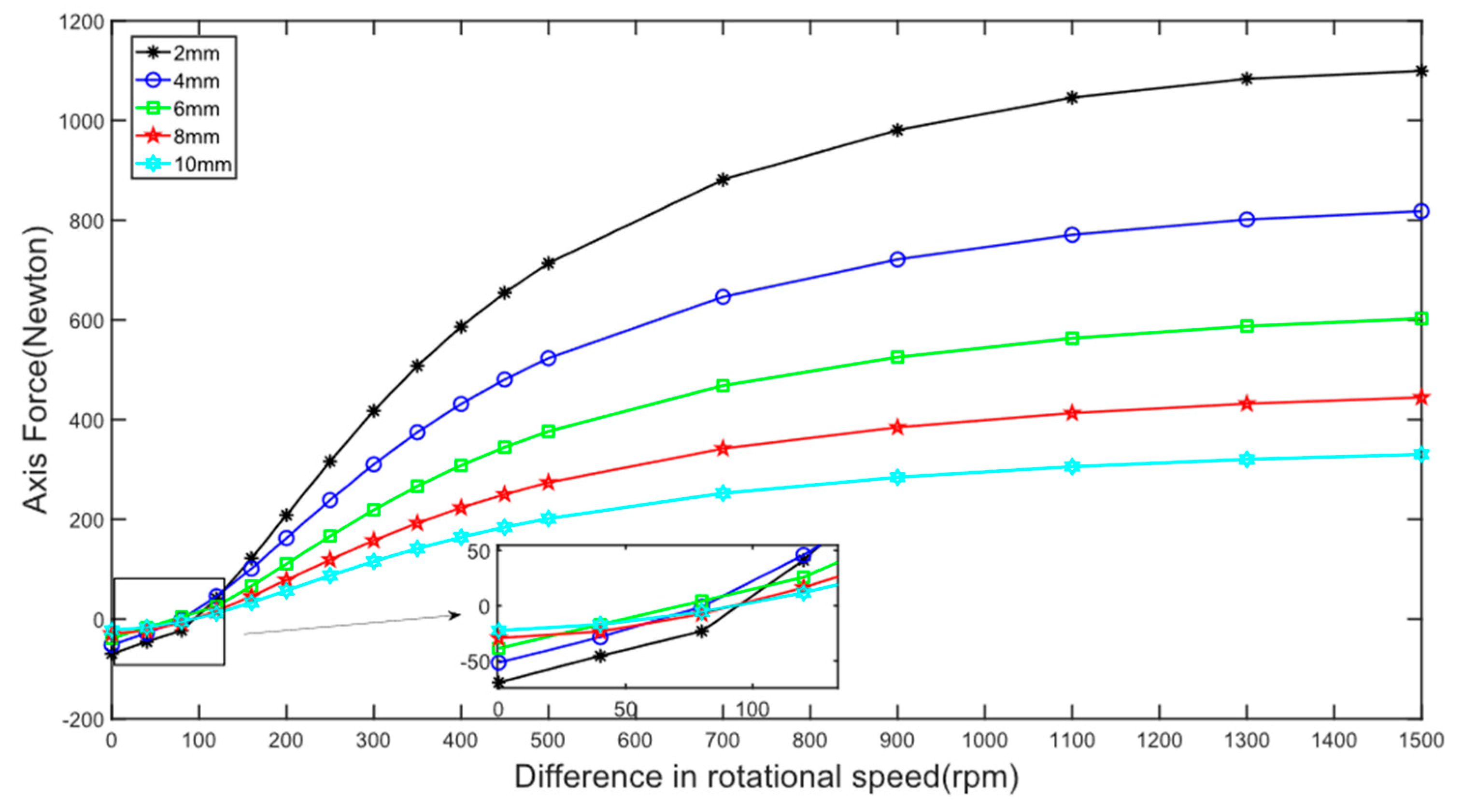
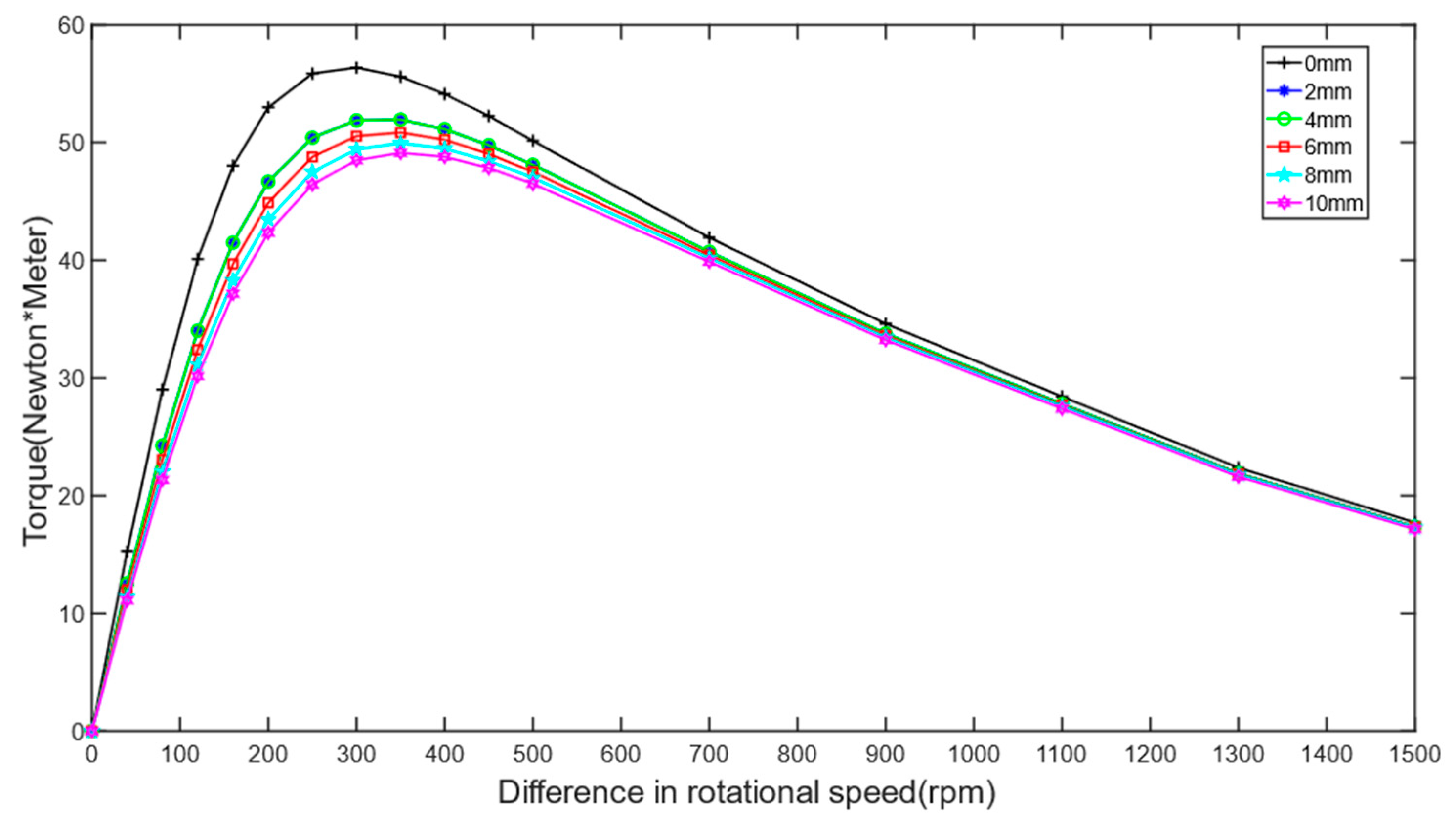
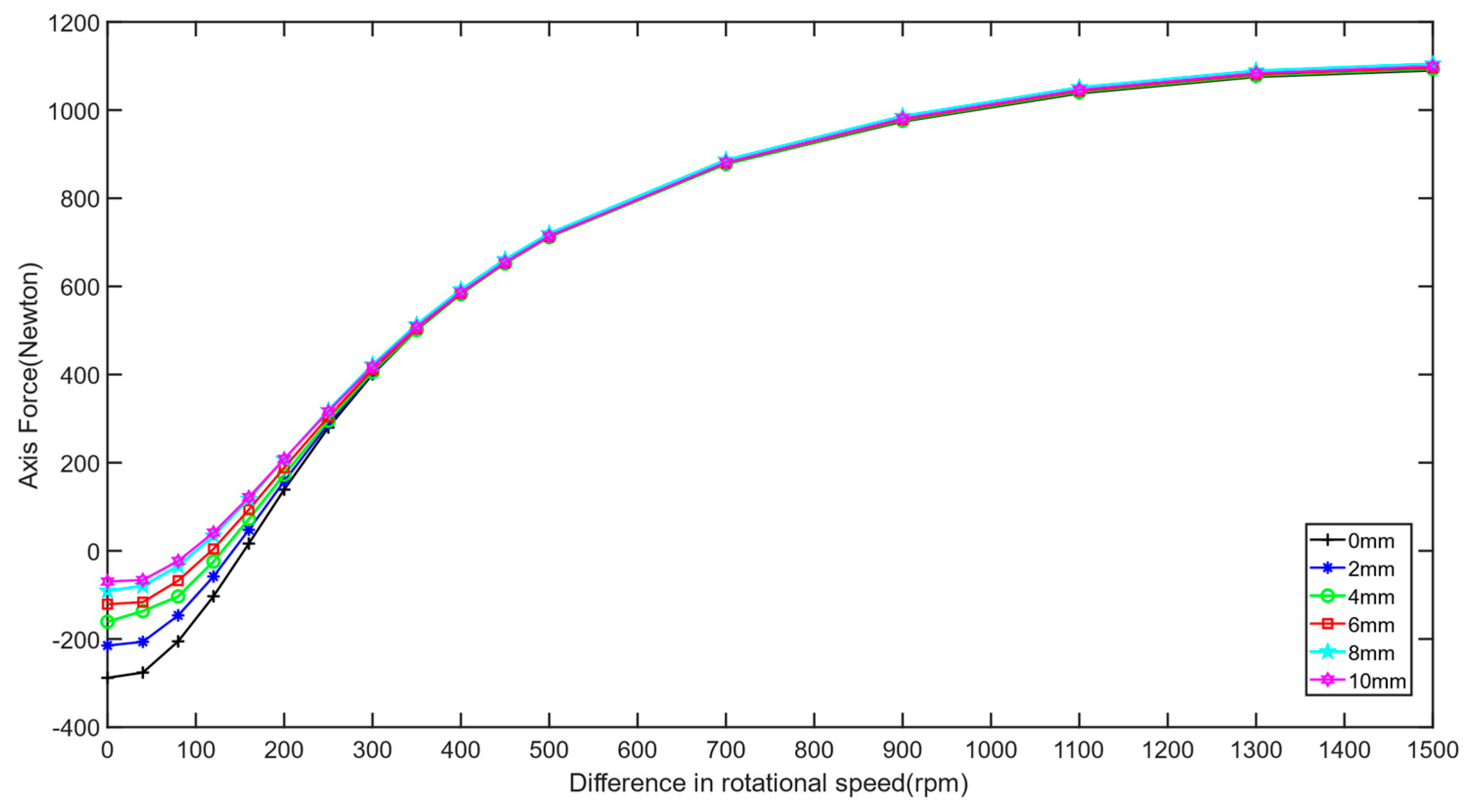
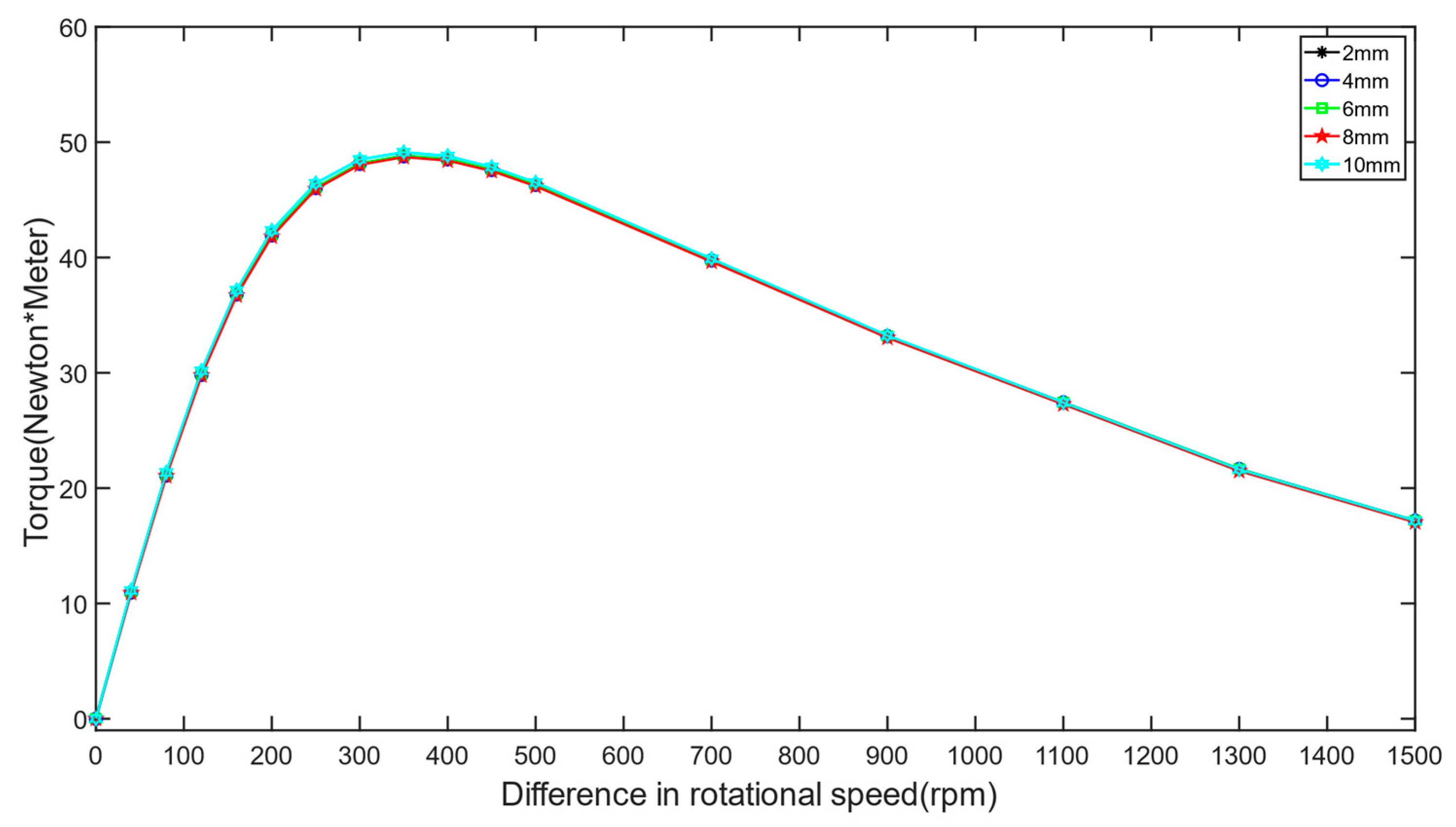
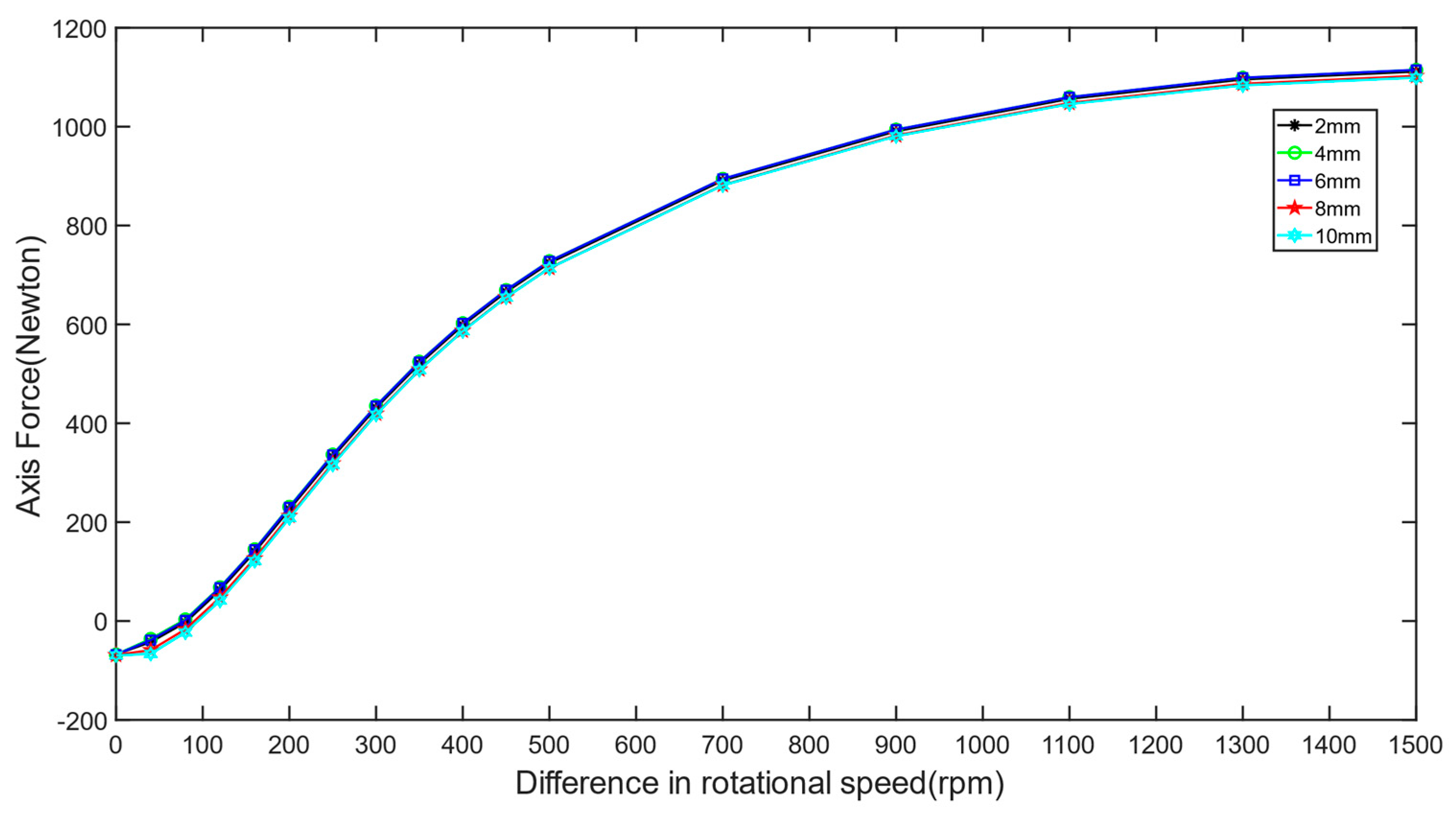
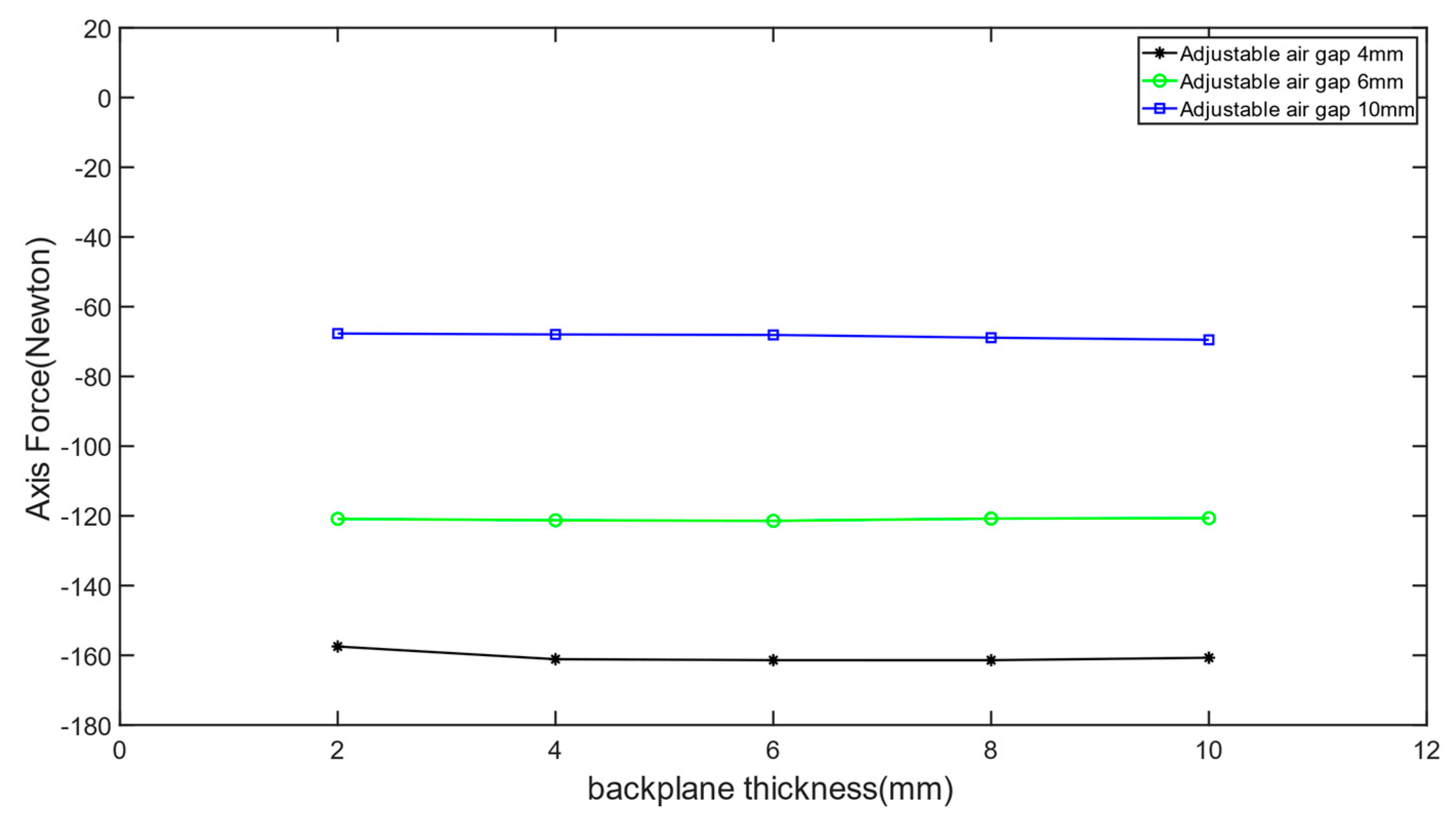
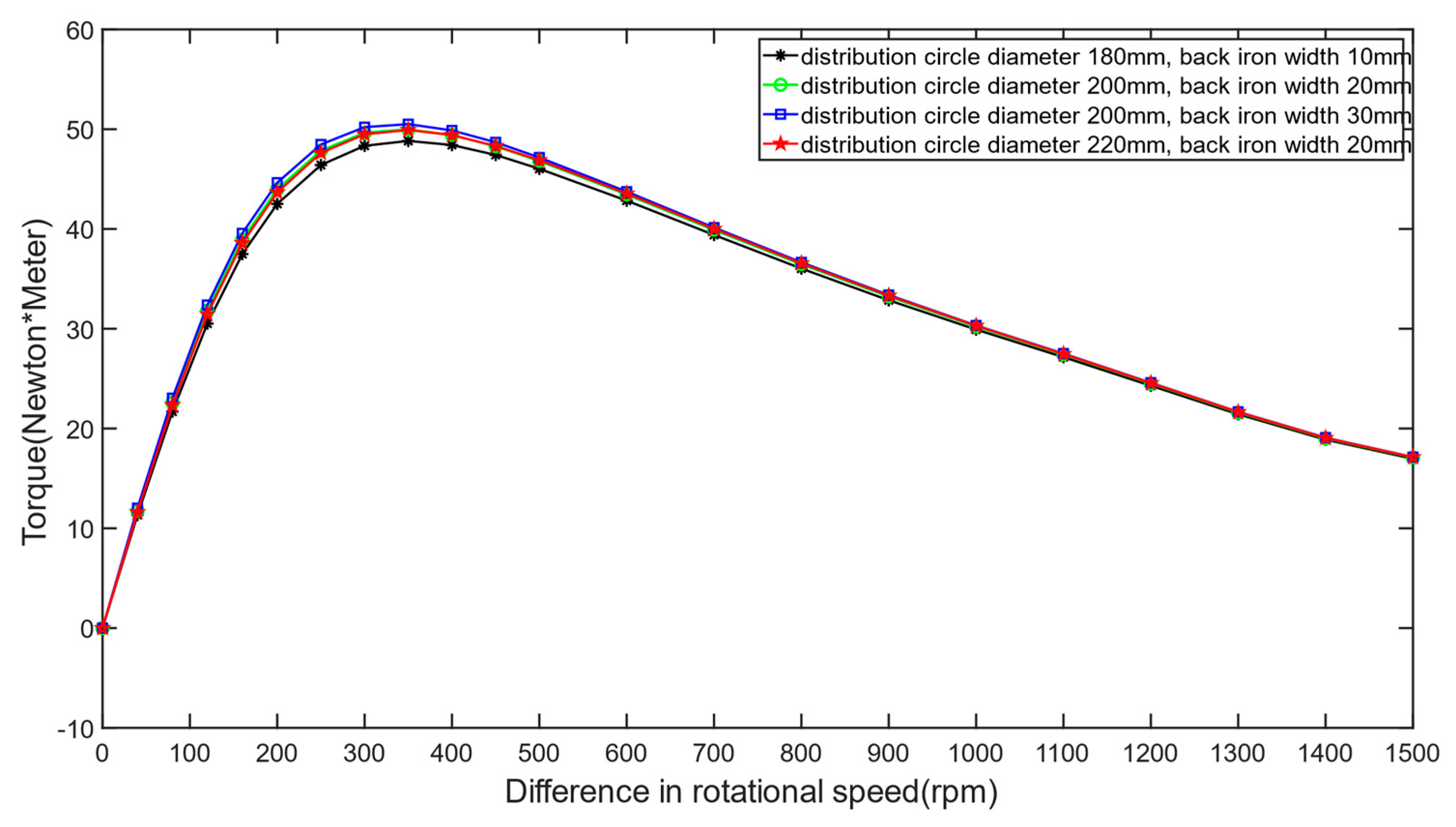
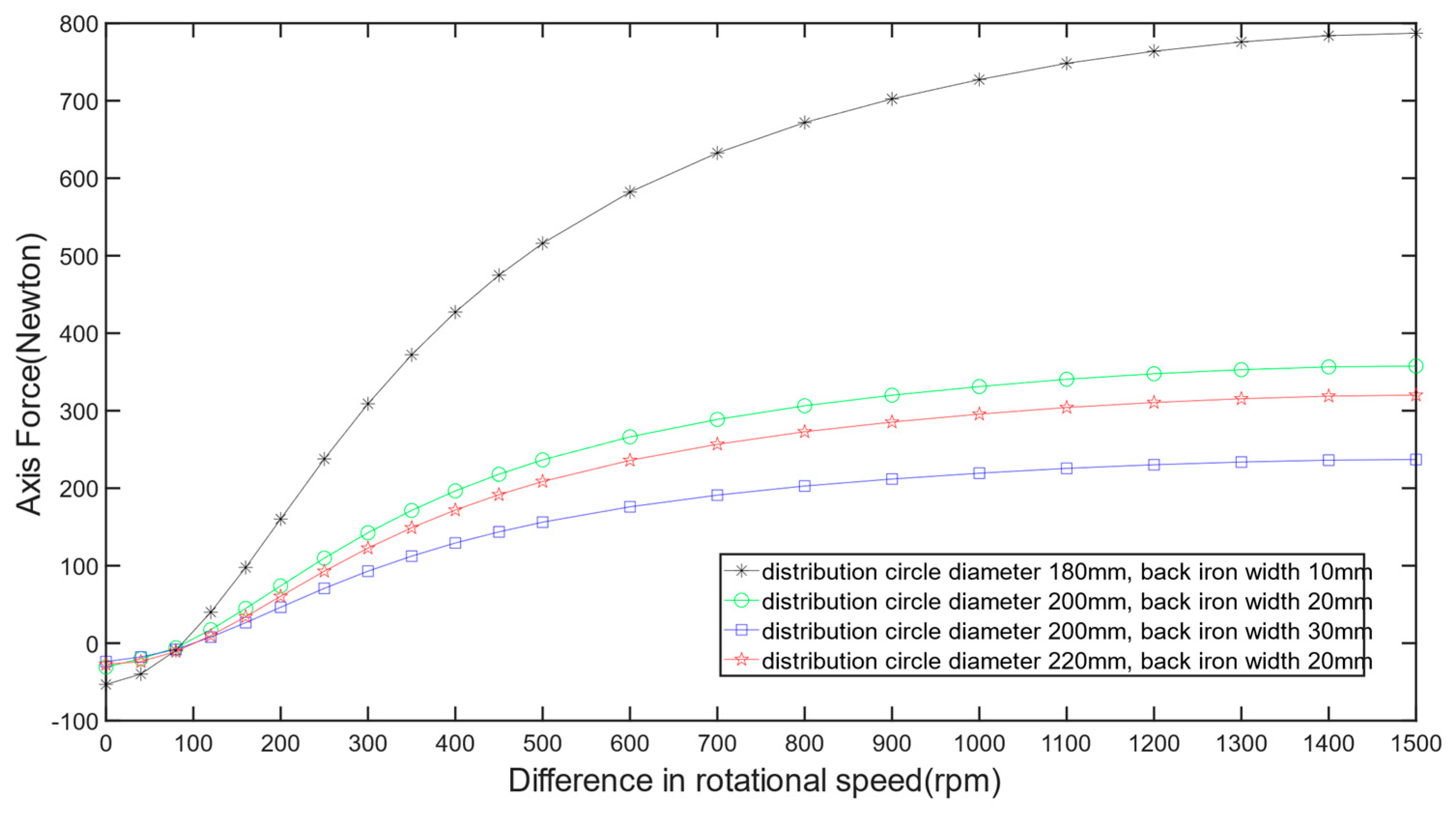
- The working air gap of the permanent magnet eddy current structure plays a dominant role in the transmitted torque and axial force. Both torque and axial force decrease with increasing working air gap. The backplane air gap significantly influences the transmission characteristics of the switch-type seal in the low-slip region, leading to decreased torque transmission and initial axial force with increasing backplane air gap. However, in the high-slip region, the backplane air gap has little effect on the transmission characteristics.
- The transmission characteristics of the permanent magnet eddy current structure show no significant relationship with the thickness of the conductor disc’s backplane. However, under low-slip conditions, axial force and torque are related to the area of the conductor disc’s backplane facing the permanent magnet, with larger facing areas resulting in greater transmitted axial force and torque.
7. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Governing Equations for Electromagnetic Fields
Appendix B. Solving the Governing Equations of Electromagnetic Fields Using the Method of Separated Variables
Appendix C. Detailed Boundary Conditions
References
- Li, F. Research Status on Internal Spraying Technology of Gateway Driving Equipment. Coal Sci. Technol. 2017, 45, 89–92. [Google Scholar] [CrossRef]
- Cheng, D. Machinery Design Manual, 6th ed.; Chemical Industry Press: Beijing, China, 2016; Volume 3, pp. 276–301. [Google Scholar]
- Yang, C. Transmission Characteristics of Axial Asynchronous Permanent Magnet Couplings. J. Mech. Eng. 2014, 50, 76–84. [Google Scholar] [CrossRef]
- Dai, X.; Liang, Q.; Cao, J.; Long, Y.; Mo, J.; Wang, S. Analytical Modeling of Axial-Flux Permanent Magnet Eddy Current Couplings with a Slotted Conductor Topology. IEEE Trans. Magn. 2016, 52, 8000315. [Google Scholar] [CrossRef]
- Yang, C.; Zhu, L.; Wu, Y. Speed Regulation Characteristics of Slotted Disc-Type Asynchronous Magnetic Coupler. Electr. Mach. Control. J. 2021, 25, 130–138. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, R.; Xiao, M. Torque and speed performance study of disk type synchronous magnetic coupler. Sci. Bull. Mech. Eng. 2022, 84, 211–222. [Google Scholar]
- Boules, N. Prediction of No-Load Flux Density Distribution in Permanent Magnet Machines. IEEE Trans. Ind. Appl. 1985, A-21, 633–643. [Google Scholar] [CrossRef]
- Shi, T. Analytical Modeling, Analyzing and Optimal Designing of Permanent Magnet Eddy-Current Couplings. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2018. [Google Scholar]
- Zhang, Z.; Han, Q.; Xu, X.; Yan, Y.; Peng, C. Air Gap Magnetic Field Calculation of Permanent Magnet Direct Drive Generator Based on Conformal Mapping and Magnetic Equivalent Circuit Method. Trans. China Electrotech. Soc. 2023, 38, 703–710. [Google Scholar]
- Smith, A.C.; Willsamson, H.; Benhama, N.; Counter, L.F. Magnetic Drive Couplings. In Proceedings of the International Electric Machines and Drives Conference, Canterbury, UK, 13 September 1999. [Google Scholar]
- Wang, J.; Lin, H.; Fang, S.; Huang, Y. A General Analytical Model of Permanent Magnet Eddy Current Couplings. IEEE Trans. Magn. 2014, 50, 8000109. [Google Scholar] [CrossRef]
- Razavi, H.K.; Lamperth, M.U. Eddy-Current Coupling with Slotted Conductor Disk. IEEE Trans. Magn. 2006, 42, 405–410. [Google Scholar] [CrossRef]
- Dai, X.; Liang, Q.; Ren, C.; Cao, J.; Mo, J.; Wang, S. Analytical Solution of Magnetic Field in Permanent-Magnet Eddy-Current Couplings by Considering the Effects of Slots and Iron-Core Protrusions. J. Magn. 2015, 20, 273–283. [Google Scholar] [CrossRef]
- Yang, F.; Liu, L. Magnetic Field Analysis of Permanent Magnet Magnetic Coupler Based on Ansoft Maxwell. In Proceedings of the Application of Artificial Intelligence and Modern Information Technology in the Coal Industry 2019 Annual Conference; China Coal Society Mine Mechatronics Professional Committee: Enshi, China, 2019; pp. 88–90. [Google Scholar]
- Wolfgang Nolting Electrodynamics; Springer: Cham, Switzerland, 2016; ISBN 9783319401676.
- Arfken, G.B.; Weber, H.J.; Harris, F.E. Mathematical Methods for Physicists a Comprehensive Guide; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 9780123846549. [Google Scholar]
- Conway, J. Functions of One Complex Variable; Springer Nature: Berlin/Heidelberg, Germany, 1973. [Google Scholar]
- Russell, R.; Norsworthy, K.J. Eddy Currents and Wall Losses in Screened-Rotor Induction Motors. Proc. IEE-Part A Power Eng. 1958, 105, 163–175. [Google Scholar] [CrossRef]
- Wang, M.; Kou, B.; Zhang, L.; Xu, J. Characteristics Analysis for Axial-Flux Permanent Magnet Eddy Current Brake with Slotted Disc. Available online: https://ieeexplore.ieee.org/document/9845986 (accessed on 11 August 2022).
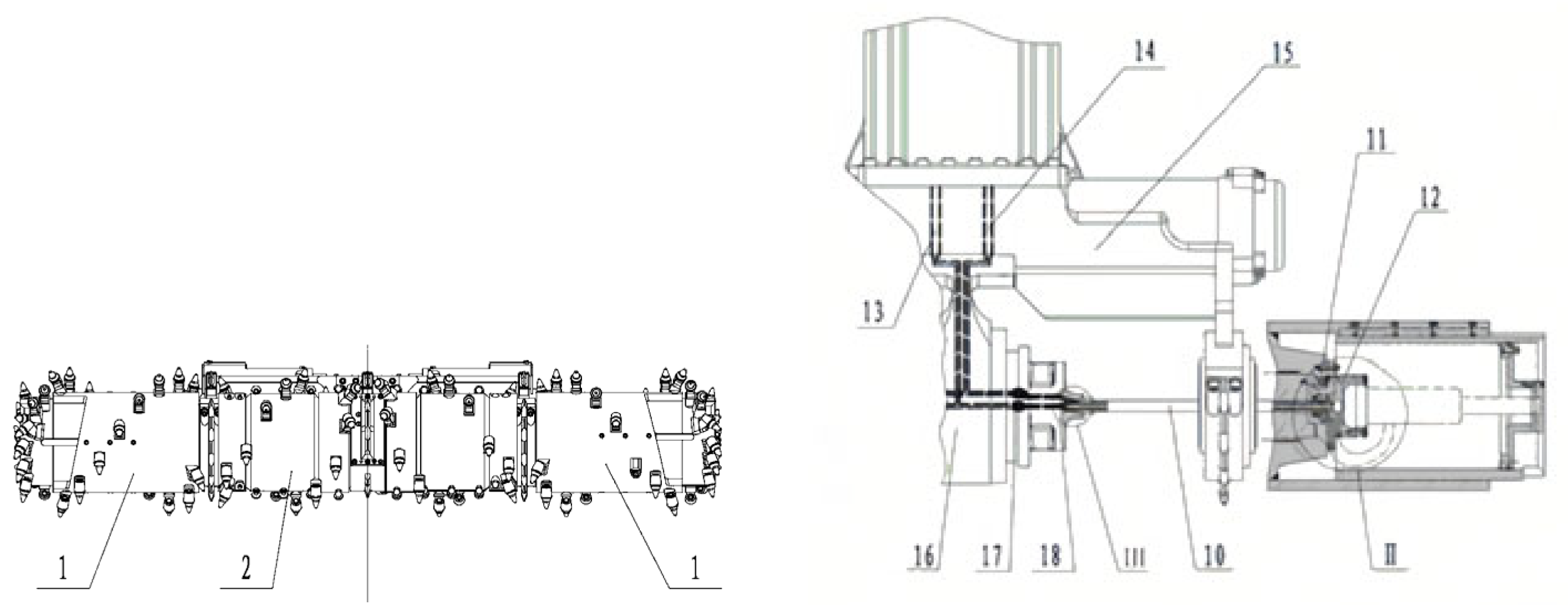
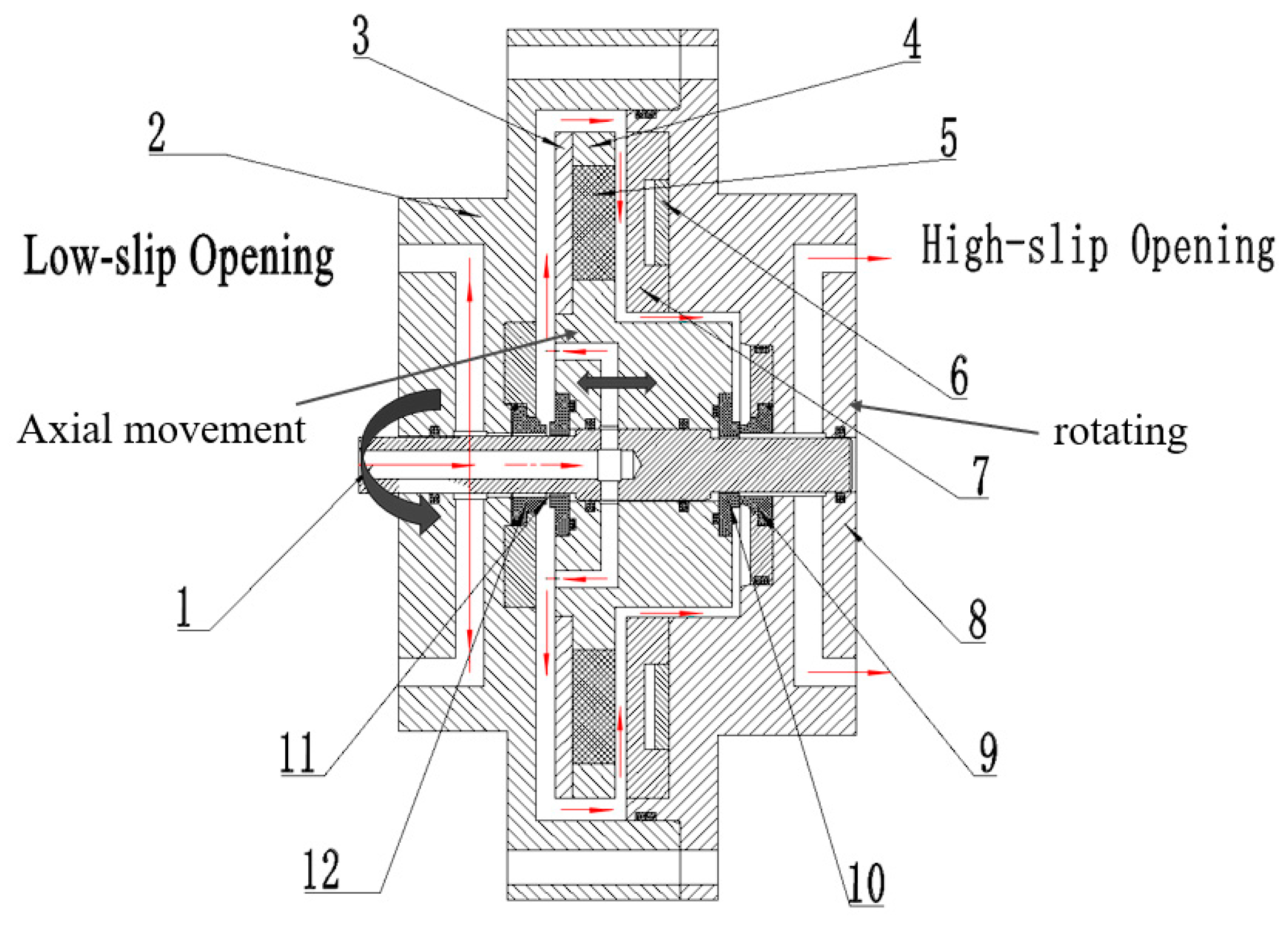
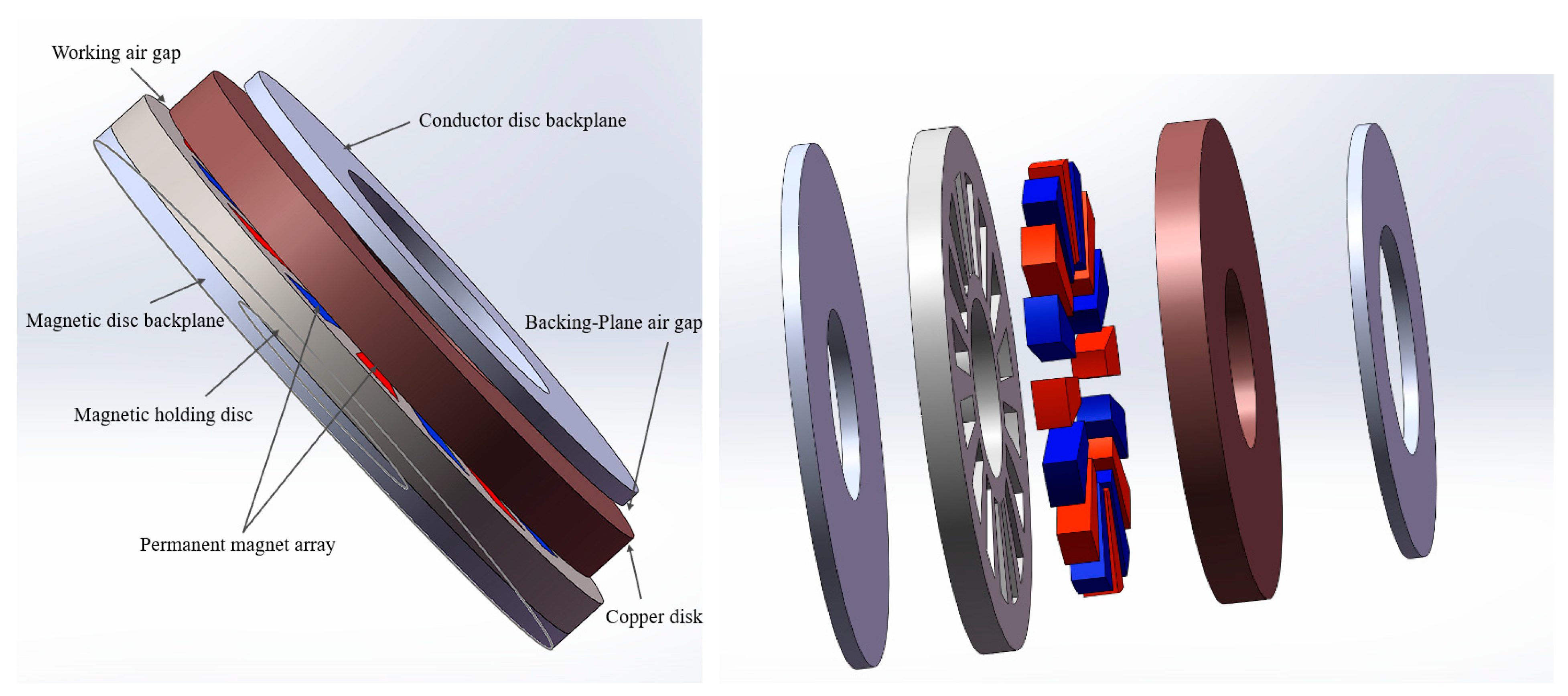
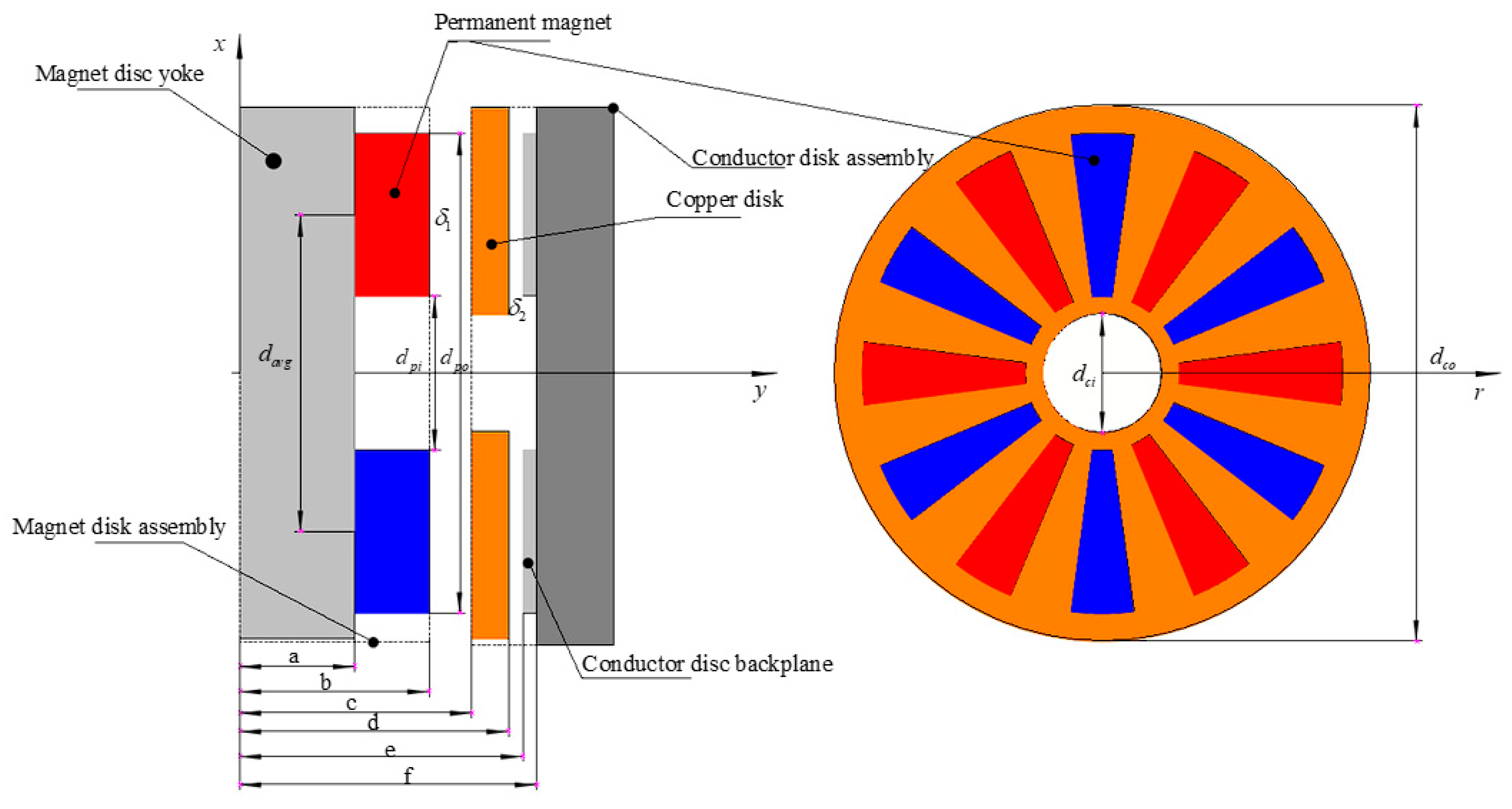








| Structure Name | Material | Outer Diameter (mm) | Inner Diameter (mm) | Thickness (mm) |
|---|---|---|---|---|
| Water inlet | 022Cr17Ni12Mo2 | 20 | 12 | - |
| Left flange | 06Cr19Ni10 | 360 | 22 | 70 |
| Magnetic disc backplane | 45# | 280 | 110 | 6 |
| Magnetic holding disc | 06Cr19Ni10 | 280 | 50.6 | 12 |
| Permanent magnet array | NdFeB35 | 240 | 160 | 12 |
| Conductor disc backplane | 45# | 240 | 160 | 5 |
| Copper conductor | TU2 | 280 | 50 | 15 |
| Right flange | 06Cr19Ni10 | 360 | 20 | 65 |
| Right dynamic ring | Nitrile rubber | 28 | 22 | 5 |
| Right stationary ring | Filled with PTFE resin | 30 | 20.5 | 5.5 |
| Left dynamic ring | Silicon carbide | 26 | 22 | 4 |
| Left stationary ring | M106 K | 28 | 21 | 5.5 |
| Structural Parameters | Symbolic | Value |
|---|---|---|
| Permanent magnet inner diameter | 160 mm | |
| Permanent magnet outer diameter | 240 mm | |
| Permanent magnet distribution circle diameter | 200 mm | |
| Permanent magnet pole pair number | 12 | |
| Permanent magnet duty ratio | 0.5 | |
| Copper disc inner diameter | 150 mm | |
| Copper disc outer diameter | 250 mm | |
| Working air gap | 2 mm~10 mm | |
| Backplane air gap | 0 mm~10 mm | |
| Difference in rotational speed | 0~1500 rpm |
| Definition | Symbolic | Value |
|---|---|---|
| Vacuum permeability | 4π × 10−7 H/m | |
| Relative permeability of magnet disc backplane and conductor backplane | 2000 | |
| Relative permeability of copper | 0.999991 | |
| Relative permeability of air | 1 | |
| Relative permeability of permanent magnet | 1.0997785406 | |
| Permanent magnet remanence | 1.22 T | |
| Relative coercivity of permanent magnet | −8.9 × 105 A/m | |
| Conductivity of copper | 5.7 × 107 S/m | |
| Conductivity of magnet disc backplane and conductor backplane | 2.0 × 107 S/m |
| Instrument Composition | Model | Parameters |
|---|---|---|
| Geared motors | YB3-380V-40-axis 3 kW | Speed RPM1480 Ratio 20 |
| DAC | USB-6008 | 12-Bit,10 kS/s |
| Flow sensors | FLYW110 | 0.8~8 m3/h,1.5%F.S. |
| Pressure sensors | CYB-20SA | 0~6.3 Mpa, 0.25%F.S. |
| Converter | G120 | 3AC380V |
| Upper computer | Region R9000P | 3.2 GHz |
| Shockproof pressure gauge | YN63-Ⅰ | 0~6.3 Mpa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Wang, T.; Song, T.; Guo, W. Electromagnetic Characterization of Permanent Magnet Eddy Current Structures Based on Backplane Distance Adjustment. Machines 2024, 12, 343. https://doi.org/10.3390/machines12050343
Wu Y, Wang T, Song T, Guo W. Electromagnetic Characterization of Permanent Magnet Eddy Current Structures Based on Backplane Distance Adjustment. Machines. 2024; 12(5):343. https://doi.org/10.3390/machines12050343
Chicago/Turabian StyleWu, Yipeng, Teng Wang, Tao Song, and Wenxiao Guo. 2024. "Electromagnetic Characterization of Permanent Magnet Eddy Current Structures Based on Backplane Distance Adjustment" Machines 12, no. 5: 343. https://doi.org/10.3390/machines12050343
APA StyleWu, Y., Wang, T., Song, T., & Guo, W. (2024). Electromagnetic Characterization of Permanent Magnet Eddy Current Structures Based on Backplane Distance Adjustment. Machines, 12(5), 343. https://doi.org/10.3390/machines12050343






