Brush Seal Performance with Ideal Gas Working Fluid under Static Rotor Condition
Abstract
:1. Introduction
2. Numerical Approach for the Leakage Flow Characteristic of the Brush Seal
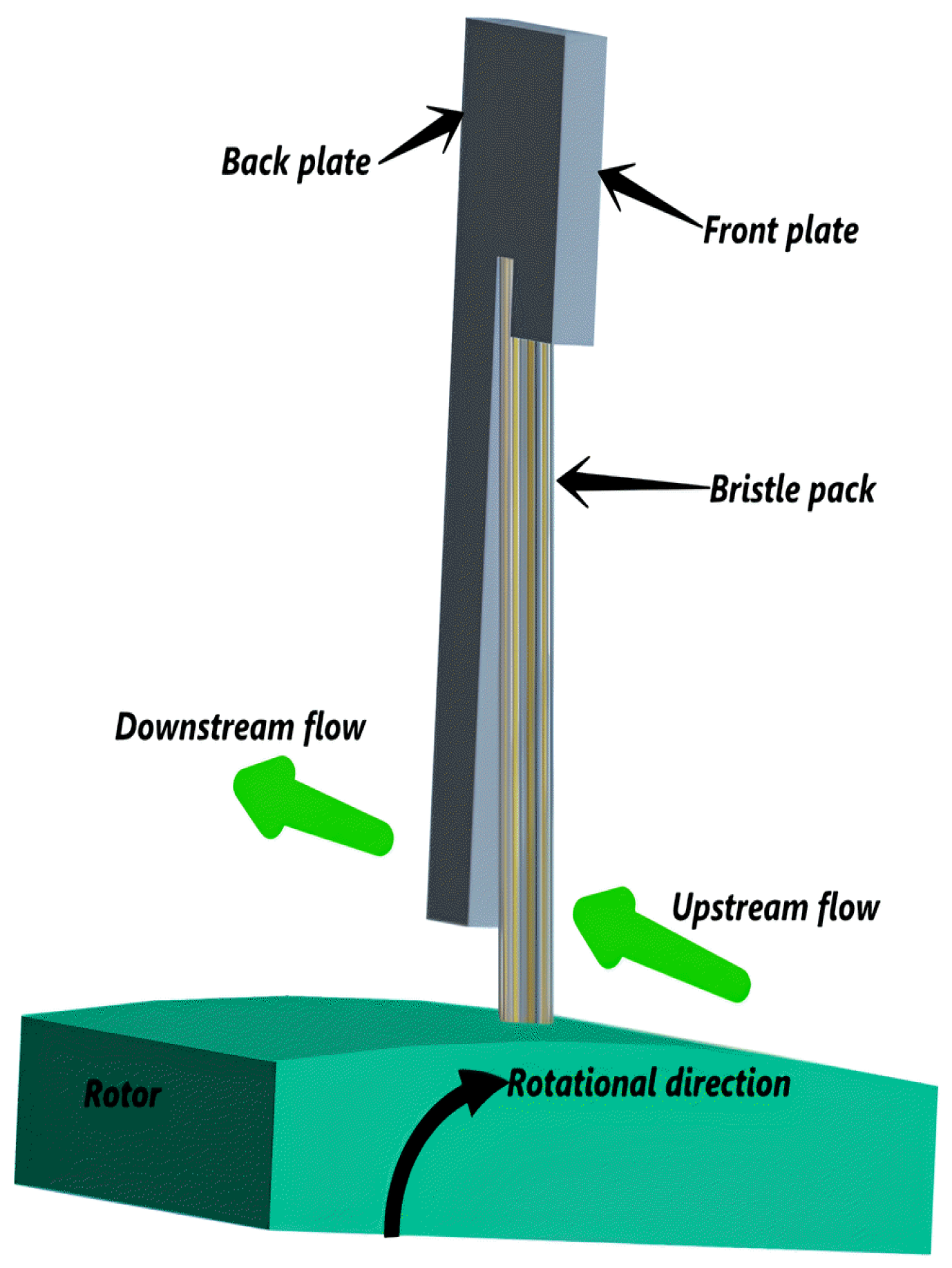
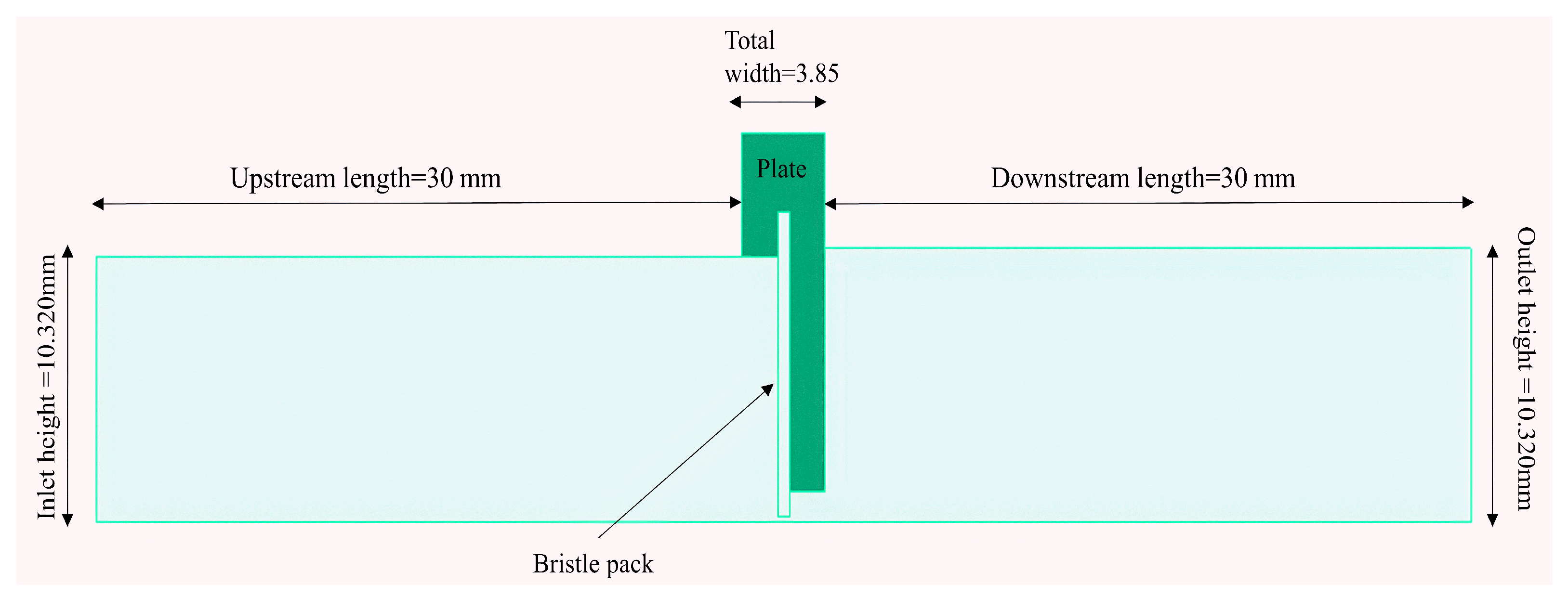
2.1. Problem Description
2.2. Theoretical Approach of Porous Medium
- Ignore the influence of shaft curvature.
- Reasonably ignores bristle bending.
- The leakage of air from the brush seal is an ideal compressible gas.
- The bristles that make up the brush seal are made of Haynes 25 and are uniform in shape.
- The bristles are not drawn individually; instead, the entirety of the region is considered a porous medium.
3. Porous Media Solver Model for Brush Seal
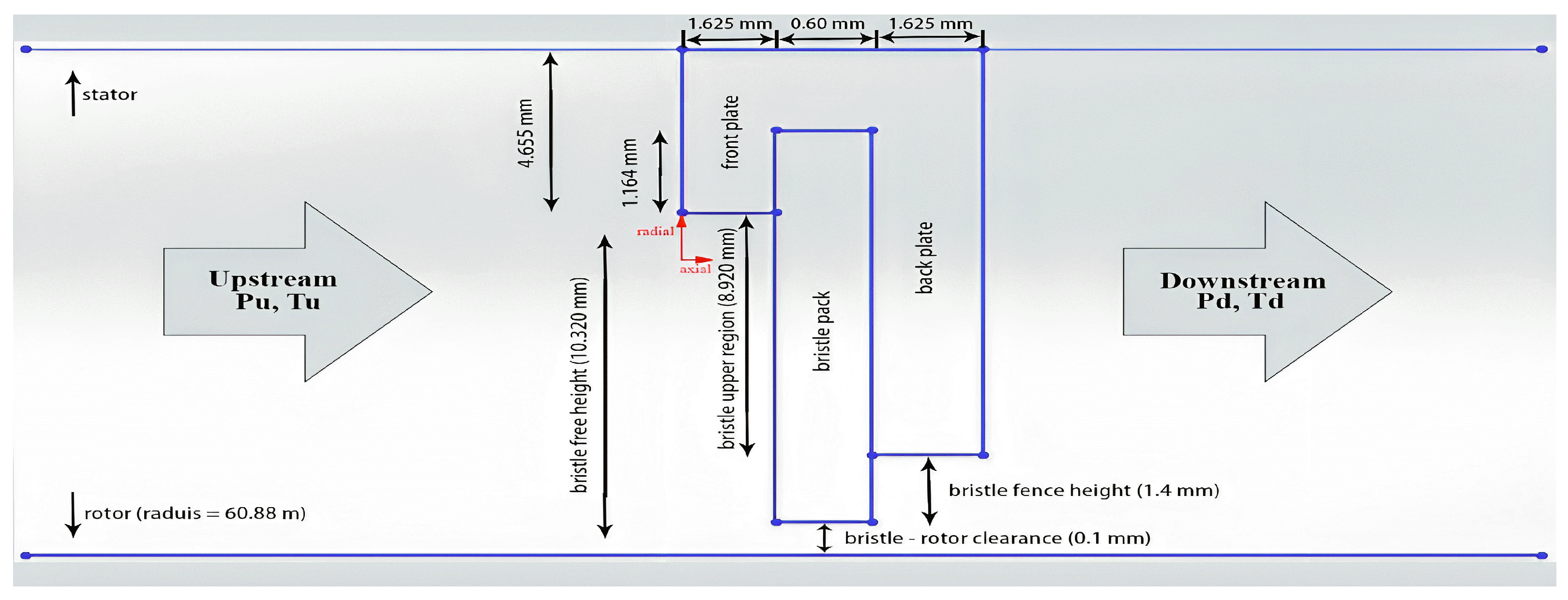
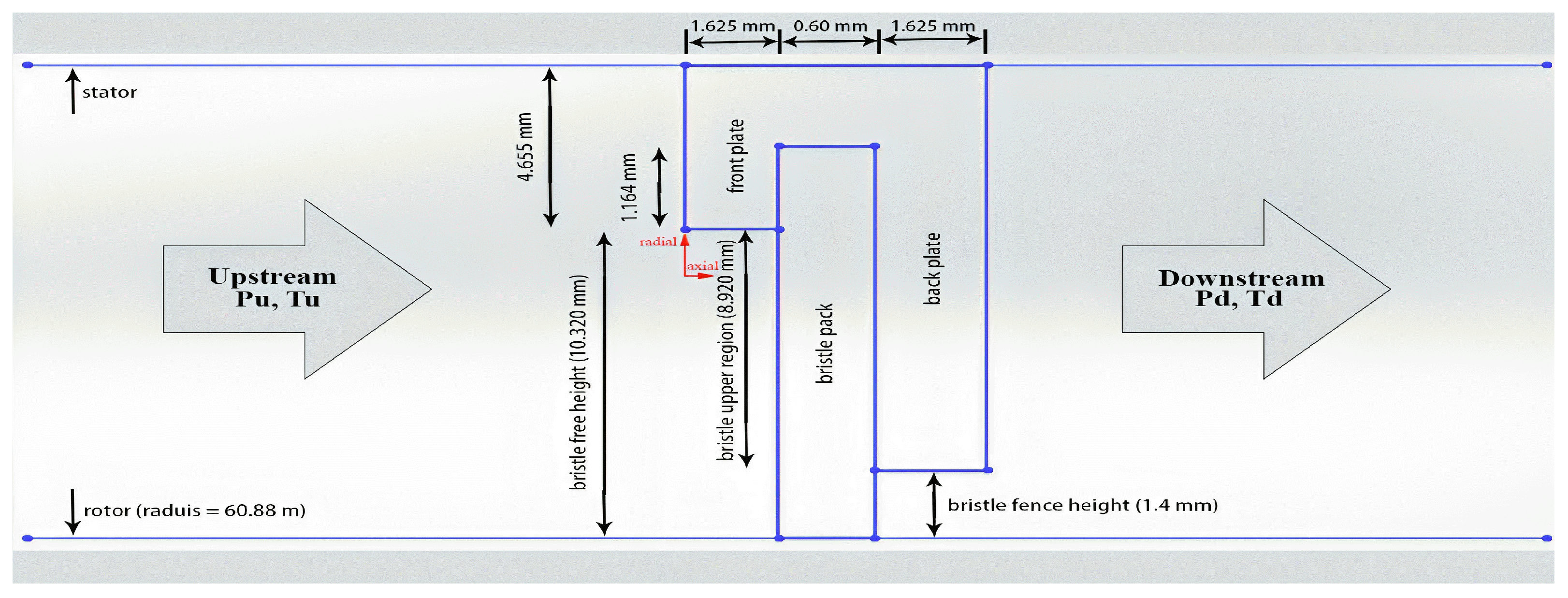
3.1. Geometric Specifications
3.2. Boundary Conditions
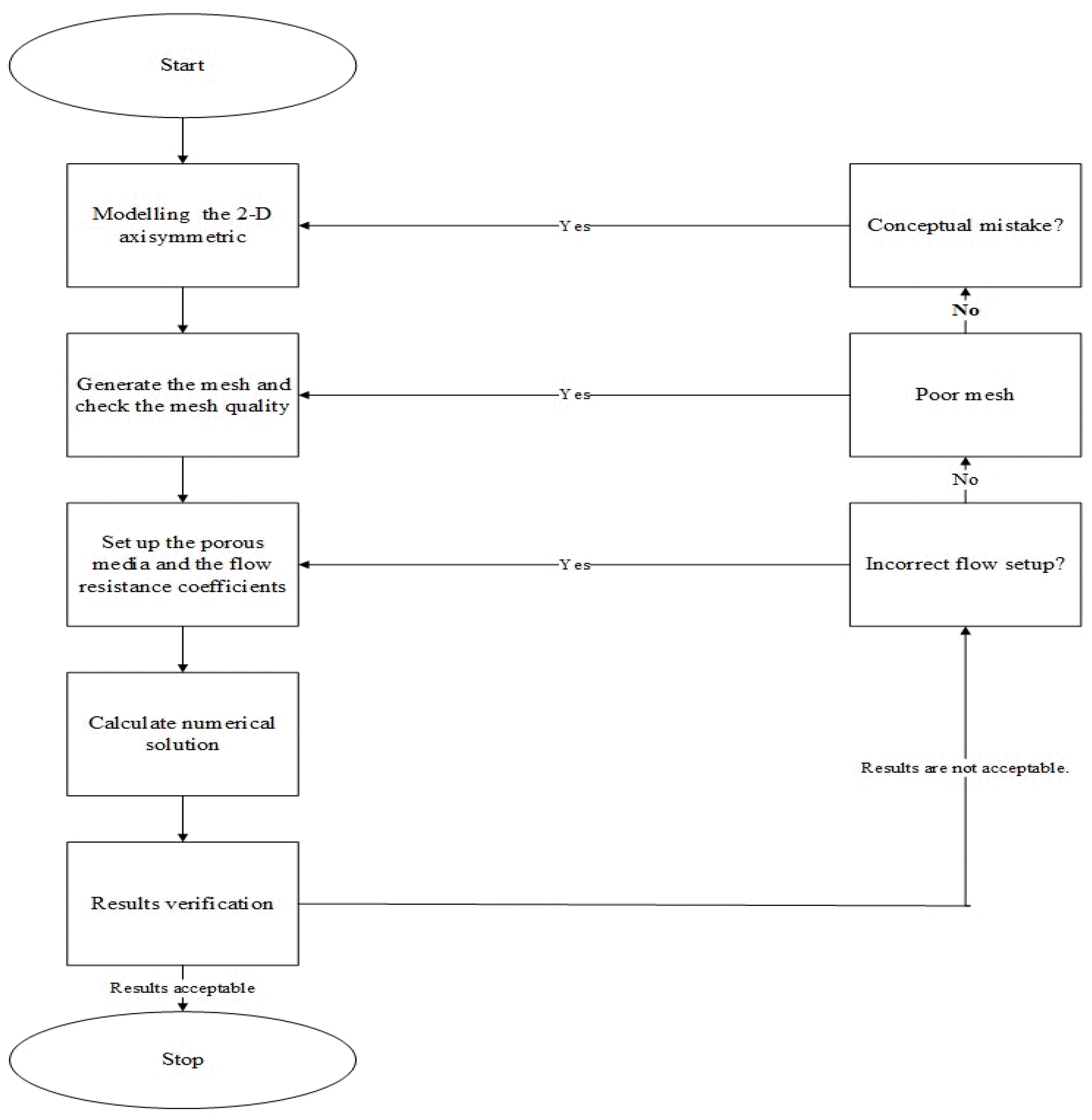
3.3. Numerical Methods
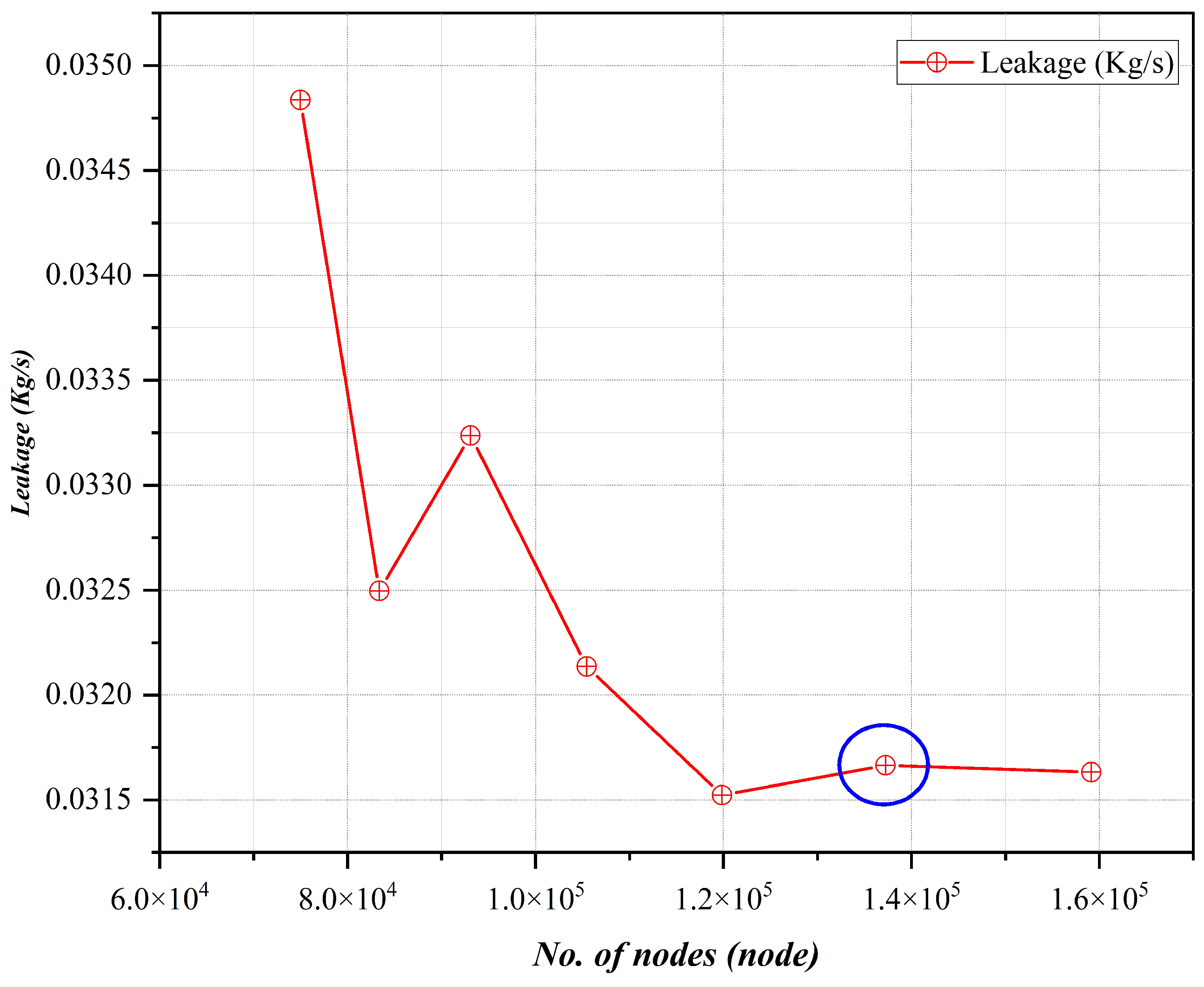
3.4. Mesh Quality Inspection
3.5. Validating the Precision of the Porous Medium Model
4. Results and Discussions
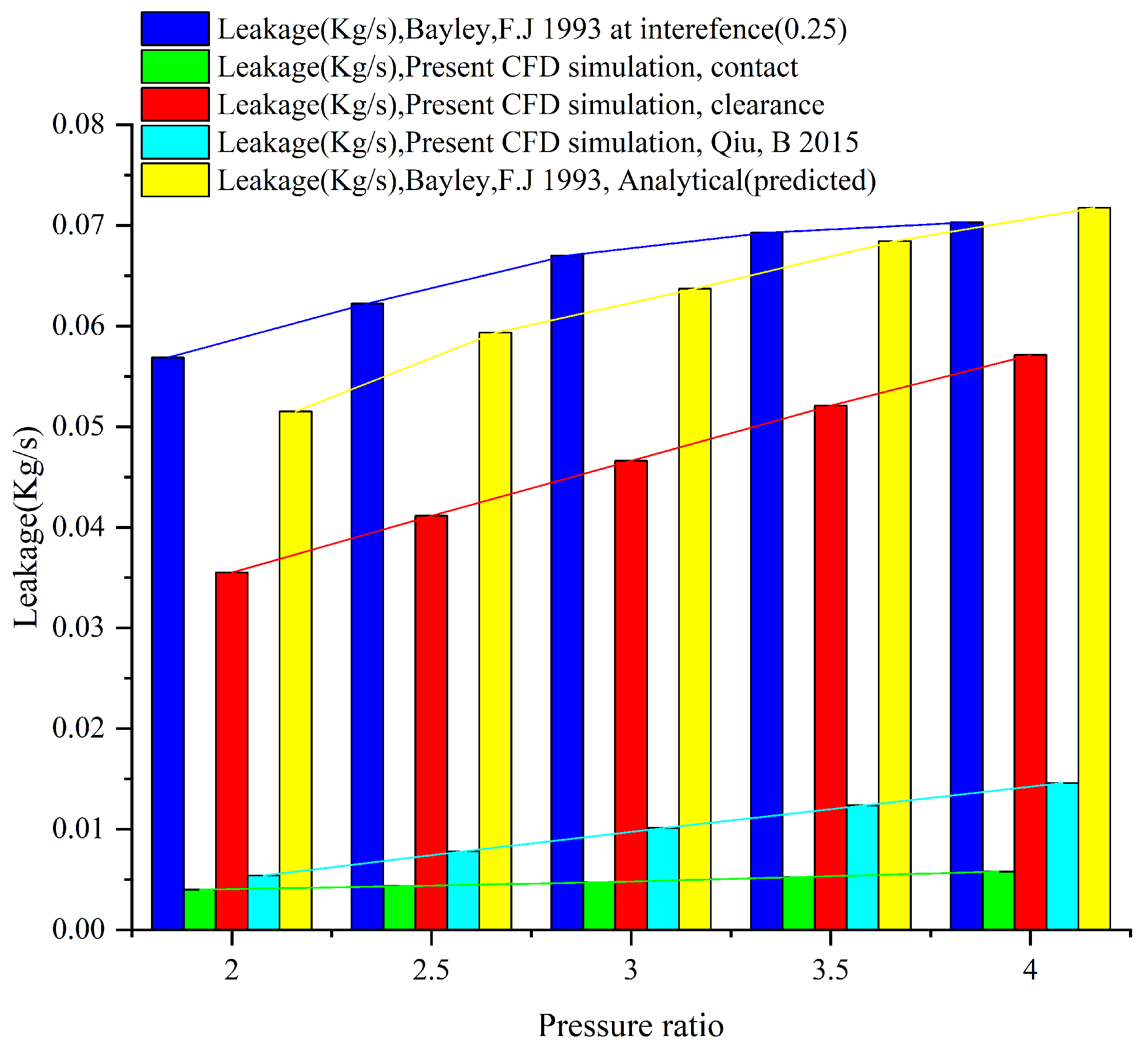
4.1. Leakage Flow with Different Pressure Ratios
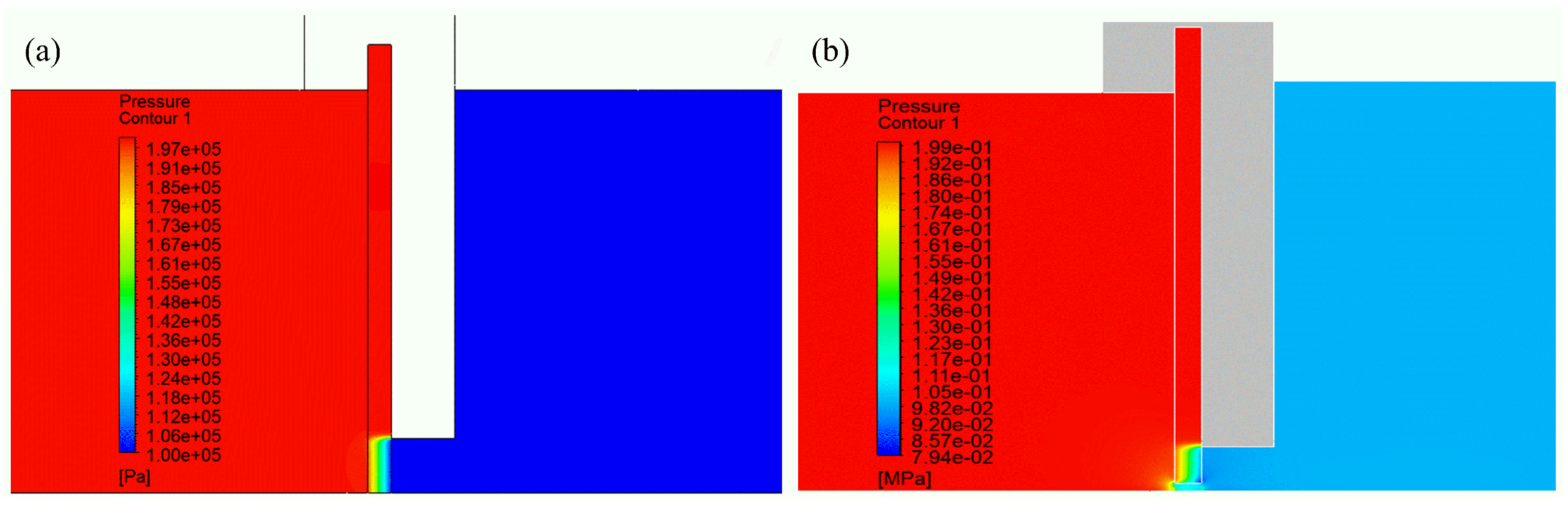
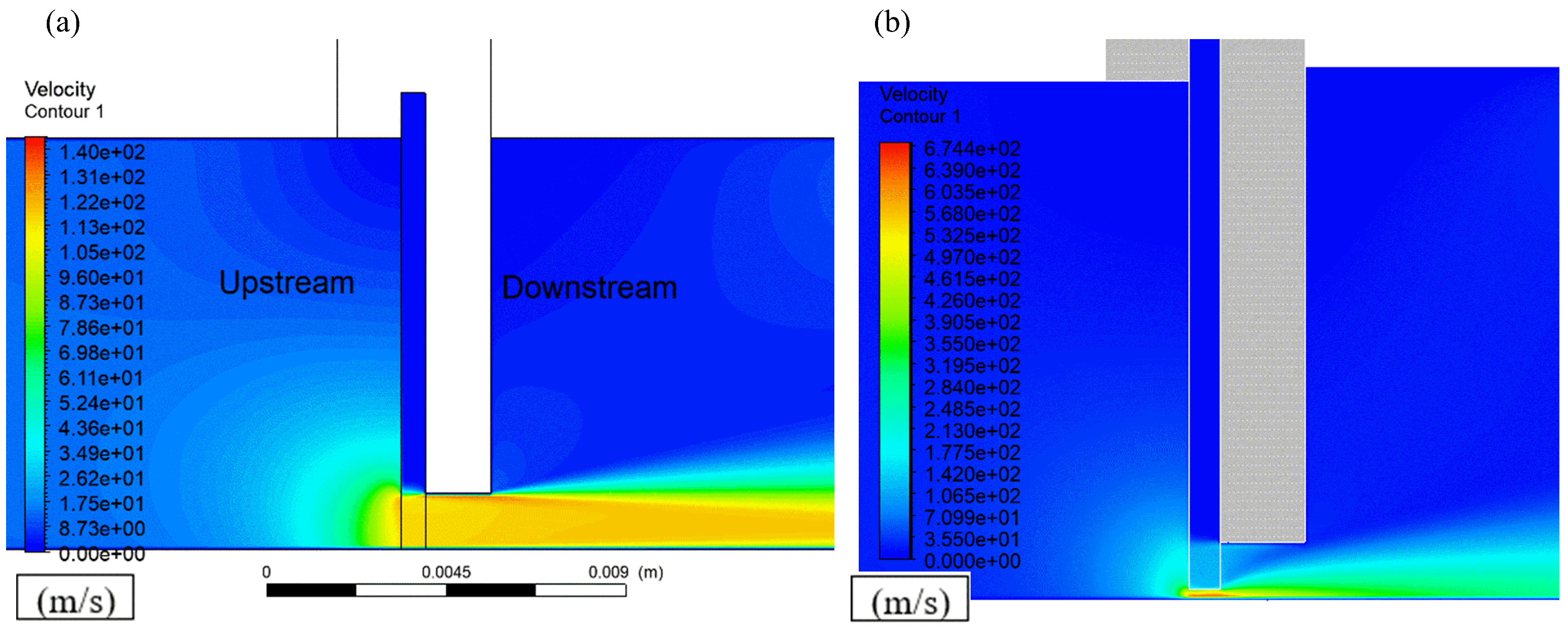
4.2. Pressure Contour Distribution
4.3. Velocity Contour Distribution
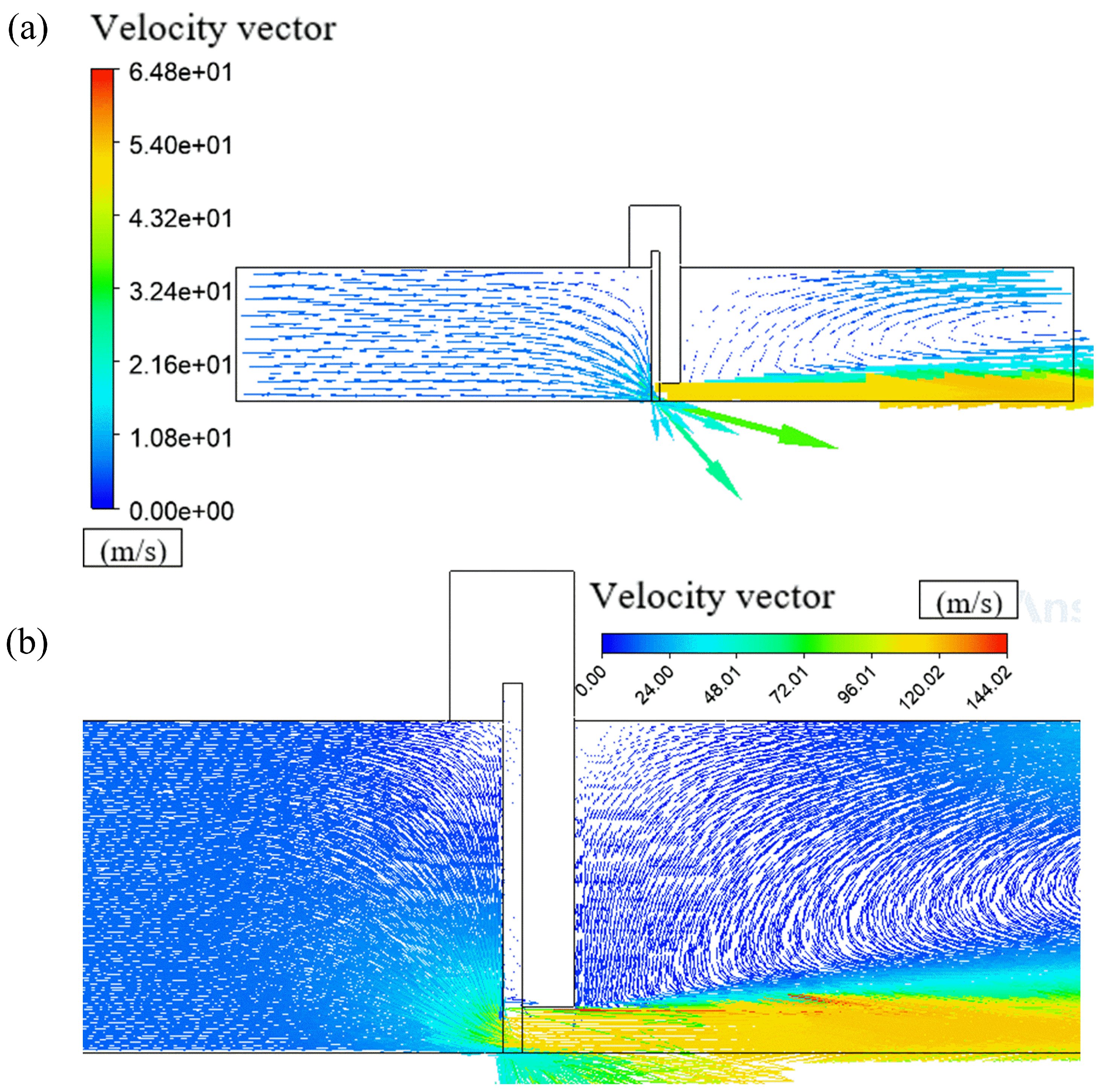
4.4. Velocity Vector Distribution
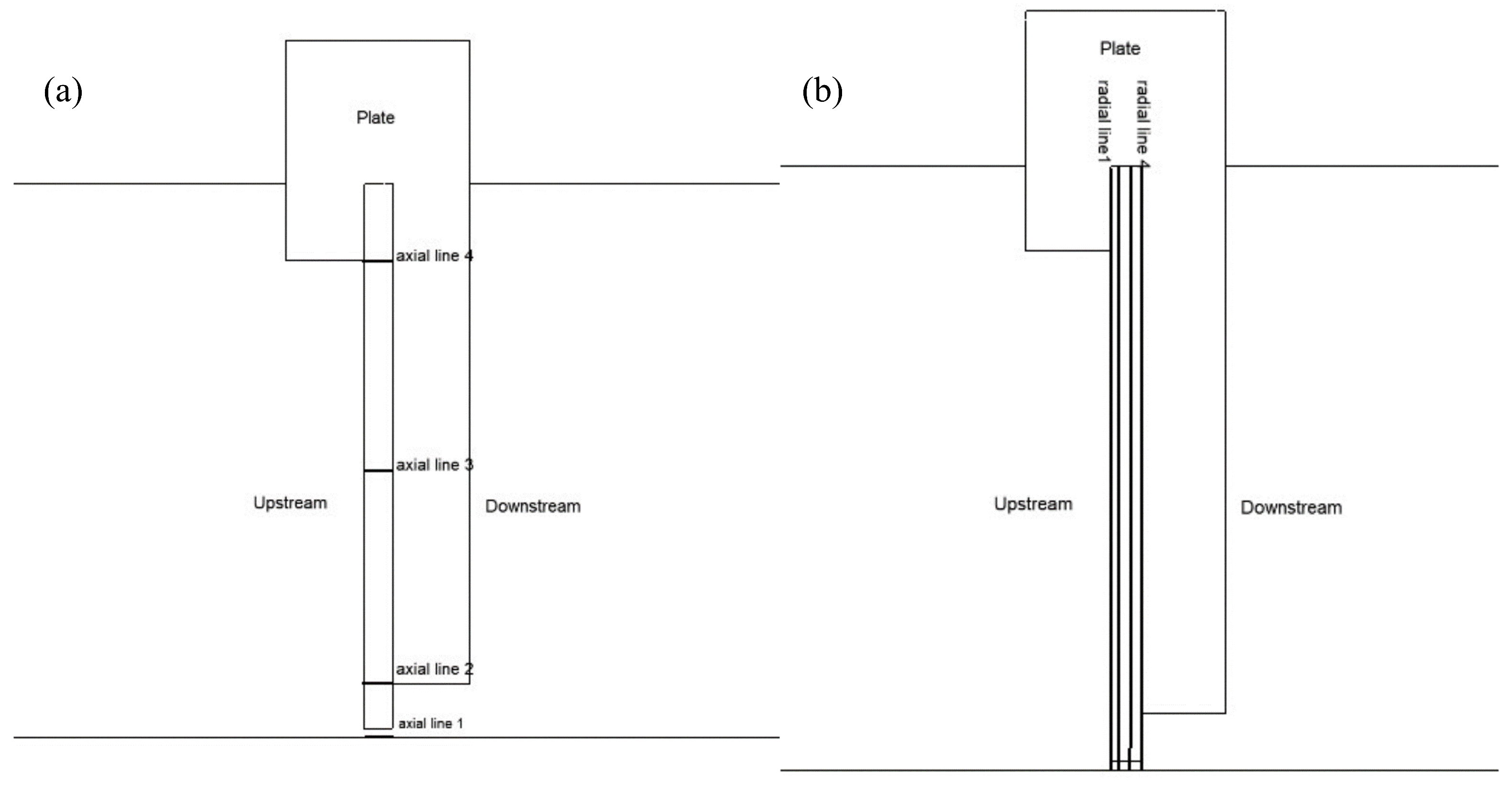
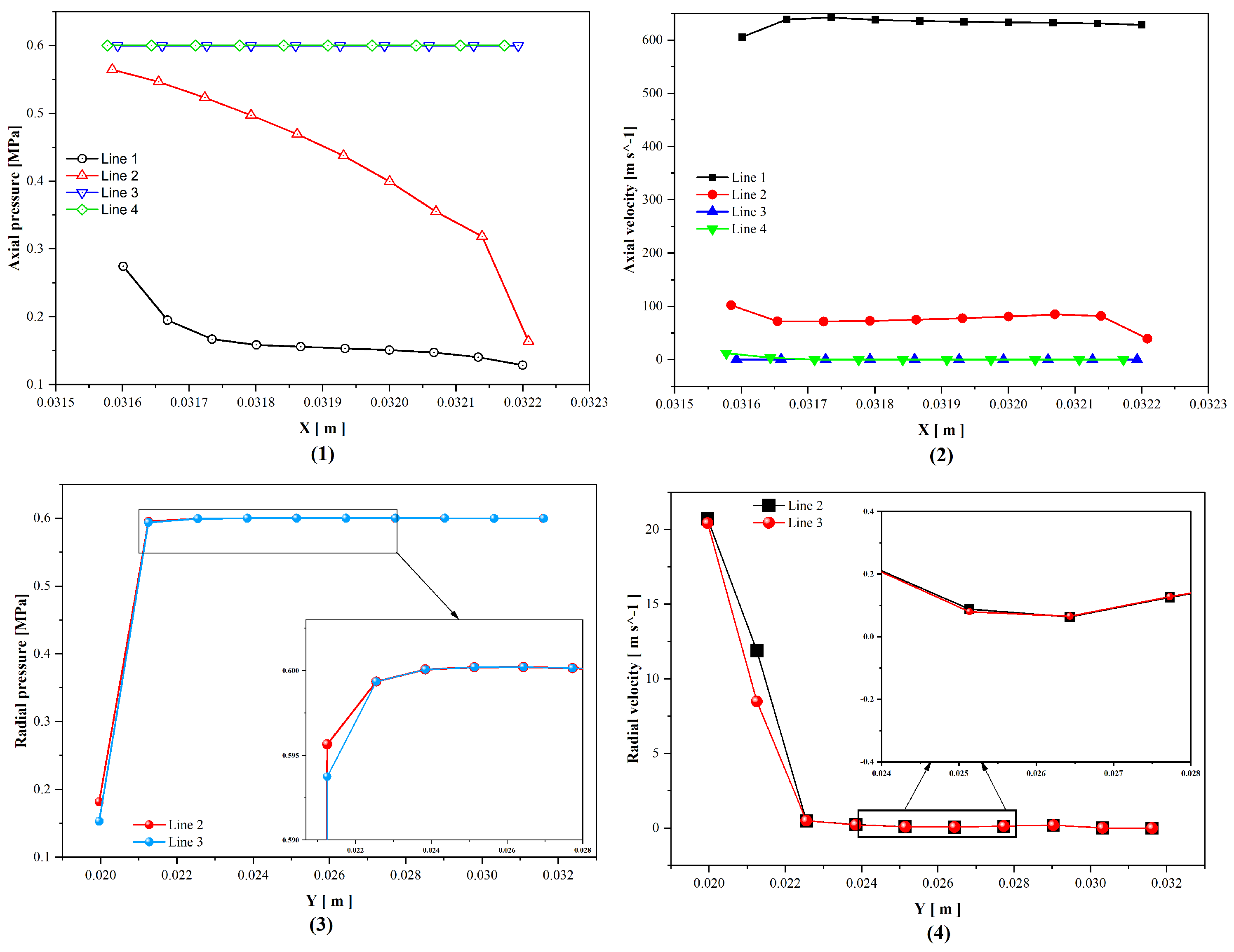
4.5. Radial and Axial Velocity and Pressure in Brush Seals at Contact and Clearance Structures
5. Conclusions
- In our simulation, the focus was on compressible flow. The model geometry was adopted from the research conducted by Bayley and Long, as in the previous experimental research. From the simulation results, we found that the compressible flow did not have a significant impact on the results. However, the long calculation time associated with the compressible flow model should be considered as a trade-off.
- While optimal brush seal performance is achieved when the bristle pack maintains full contact with the rotor surface, the practical limitations often necessitate operation with a small clearance structure due to factors such as rotor deviation, transient conditions, or bristle wear.
- The fluid velocity reached a maximum value near the rotor surface, indicating jet-like behavior at the outlet, and the pressure at the free end of the bristle pack reached its minimum value at this point; furthermore, both contact and clearance structures demonstrated a significant increase in leakage rate with an increasing pressure ratio, but the leakage rate under the contact model consistently remained lower than that of the clearance model, highlighting the superior sealing performance achieved under the contact model.
- The leakage rates for both the contact and clearance structures increased in different ways as the pressure ratio rose. This shows how important the pressure ratio is when judging the performance of a brush seal. The simulated leakage rate agreed well with both experimental results and previous simulation results across the entire pressure ratio range. This proves that the proposed method for figuring out resistance coefficients in porous media is correct.
- While the current investigation examined the leakage flow behavior of brush seals under different structural configurations, further research is necessary to investigate the influence of rotor rotations on leakage flow and to characterize the optimal sealing performance under varying operational parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ai | Viscous resistance coefficient [1/] |
| Bi | Inertial resistance coefficient [1/m] |
| Fi | Additional resistance source term of the bristles to the fluid |
| Rp | Pressure ratio |
| Pi | Pressure inlet |
| Pd | Pressure outlet |
| va | Average flow velocity |
| d | Bristle diameter |
| Vs | Bristle volume |
| V | Total volume |
| N | Bristle pack density [bristles/unit length] |
| Dr | Rotor diameter |
Greek Symbols
| Bristle lay angle [degree] | |
| Density [kg/] | |
| Porosity (ratio of the void volume to the total volume (voids and bristles)) | |
| Dynamic viscosity [kg/(m·s)], also can be called friction coefficient |
Abbreviations
| CFD | Computational fluid dynamics |
| RANS | Reynolds-averaged Navier–Stokes |
| 2D | Two-dimensional model |
References
- Pekris, M.J.; Franceschini, G.; Gillespie, D.R. An Investigation of Flow, Mechanical and Thermal Performance of Conventional and Pressure-Balanced Brush Seals. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 44700, pp. 2141–2153. [Google Scholar]
- Li, J.; Yang, J.; Shi, L.; Yang, R.; Feng, Z. Analytical Investigations on the Contact Force Between Bristle Packs and Shaft Surface of Brush Seals. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 44700, pp. 2211–2218. [Google Scholar]
- Fellenstein, J.A.; Dellacorte, C. A new tribological test for candidate brush seal materials evaluation. Tribol. Trans. 1996, 39, 173–179. [Google Scholar] [CrossRef]
- Qiu, B.; Li, J. Numerical investigations on the heat transfer behavior of brush seals using combined computational fluid dynamics and finite element method. J. Heat Transf. 2013, 135, 122601. [Google Scholar] [CrossRef]
- Chupp, R.E.; Hendricks, R.C.; Lattime, S.B.; Steinetz, B.M. Sealing in turbomachinery. J. Propuls. Power 2006, 22, 313–349. [Google Scholar] [CrossRef]
- Neef, M.; Sulda, E.; Sürken, N.; Walkenhorst, J. Design features and performance details of brush seals for turbine applications. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2006; Volume 4238, pp. 1385–1392. [Google Scholar]
- Song, X.; Liu, M.; Hu, X.; Wang, X.; Liao, T.; Sun, J. Numerical analysis of flow across brush elements based on a 2-D staggered tube banks model. Aerospace 2021, 8, 19. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Yan, X.; Li, J. Investigations on the leakage and heat transfer characteristics of brush seal part 1: Leakage characteristics. J. Eng. Thermophys. 2017, 38, 482–489. [Google Scholar]
- Lee, J.J.; Kang, S.Y.; Kim, T.S.; Byun, S.S. Thermo-economic analysis on the impact of improving inter-stage packing seals in a 500 MW class supercritical steam turbine power plant. Appl. Therm. Eng. 2017, 121, 974–983. [Google Scholar] [CrossRef]
- Atkinson, E.; Bristol, B. Effects of material choices on brush seal performance. Lubr. Eng. 1992, 48, 740–746. [Google Scholar]
- Song, X.; Liu, M.; Yang, J. Numerical analysis of leakage performance of brush seal based on a 2-d tube bank model and porous medium model considering the effect of compressible gas. Int. J. Fluid Mach. Syst. 2022, 15, 329–343. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Z. Theoretical Model of Bristle Performance Analysis in Brush Seal. In Proceedings of the 4th China-Japan International Conference on History of Mechanical Technology, Beijing, China, 1 November 2004. [Google Scholar]
- Chew, J.; Hogg, S. Porosity modeling of brush seals. J. Tribol. 1997, 119, 769–775. [Google Scholar] [CrossRef]
- Chew, J.; Lapworth, B.; Millener, P. Mathematical modeling of brush seals. Int. J. Heat Fluid Flow 1995, 16, 493–500. [Google Scholar] [CrossRef]
- Pröstler, S. Modellierung und Numerische Berechnungen von Wellenabdichtungen in Bürstenbauart; Verlag Dr. Hut: München, Germany, 2005. [Google Scholar]
- Dogu, Y. Investigation of brush seal flow characteristics using bulk porous medium approach. J. Eng. Gas Turbines Power 2005, 127, 136–144. [Google Scholar] [CrossRef]
- Wiid, J.J.F. The Experimental and Numerical Investigation of the Influence of Shaft Rotation on Leakage Rate of Non-Contacting Seals Found in Turbine Applications; University of Pretoria: Pretoria, South Africa, 2018. [Google Scholar]
- Gresham, T.G.; Weaver, B.K.; Wood, H.G.; Untaroiu, A. Characterization of Brush Seal Permeability. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 49781, p. V05AT15A031. [Google Scholar]
- Bayley, F.; Long, C. A combined experimental and theoretical study of flow and pressure distributions in a brush seal. J. Eng. Gas Turbines Power 1993, 115, 404–410. [Google Scholar] [CrossRef]
- Huang, X.G.; Wu, D. Design of experiment platform and investigation of flow field and heat transfer in straight labyrinth seal. J. Propuls. Technol. 1999, 20, 80–85. [Google Scholar]
- Ding, S.; Tao, Z.; Xu, G. Numerical simulation of fluid flow and heat transfer of a brush seal configuration. J. Propuls. Technol. 1999, 20, 65–67. [Google Scholar]
- Cao, G.; Ji, H.; Ji, G. Experimental and numerical study on the leakage characteristics of brush seals at the early stage of operating. J. Propul. Technol. 2010, 31, 478–482. [Google Scholar]
- Carlile, J.; Hendricks, R.; Yoder, D. Brush seal leakage performance with gaseous working fluids at static and low rotor speed conditions. J. Eng. Gas Turbines Power 1993, 115, 397–403. [Google Scholar] [CrossRef]
- Turner, M.; Chew, J.; Long, C. Experimental investigation and mathematical modeling of clearance brush seals. J. Eng. Gas Turbines Power 1998, 120, 573–579. [Google Scholar] [CrossRef]
- Pugachev, A.; Helm, P. Calibration of porous medium models for brush seals. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 83–91. [Google Scholar] [CrossRef]
- Yue, C.; Bitian, S.; Lanzhu, Z. Leakage performance predictions of a brush seal based on fluid–solid coupling method. Sci. Prog. 2020, 103, 0036850419897221. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Peng, N. Study of heat transfer and leakage characteristics of brush seals based on local temperature non-equilibrium model. Machines 2022, 10, 823. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Li, Z.; Yan, X. Numerical comparison of leakage flow and rotordynamic characteristics for two types of labyrinth seals with baffles. J. Eng. Gas Turbines Power 2020, 142, 091008. [Google Scholar] [CrossRef]
- Qiu, B.; Li, J.; Feng, Z. Investigation of conjugate heat transfer in brush seals using porous media approach under local thermal non-equilibrium conditions. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56734, p. V05CT15A009. [Google Scholar]
- Görgün, E. A Study of Porous Media Resistance Coefficients for Brush Seals. Ph.D. Thesis, Sabanci University, Istanbul, Turkey, 2014. [Google Scholar]
- ANSYS FLUENT 12.0 Theory Guide. 2009. Volume 67. pp. 291–329. Available online: https://www.afs.enea.it/project/neptunius/docs/fluent/html/th/main_pre.htm (accessed on 5 July 2024).
- Chen, L.; Wood, P.; Jones, T.; Chew, J. Detailed experimental studies of flow in large scale brush seal model and a comparison with CFD predictions. J. Eng. Gas Turbines Power 2000, 122, 672–679. [Google Scholar] [CrossRef]








| Directions | Inertial Resistance Coefficient | Viscous Resistance Coefficient |
|---|---|---|
| radial | 1 × | 1 × |
| axial | 7.5 × | 4.5 × |
| Parameters | Values |
|---|---|
| Rotor diameter | 121.76 mm |
| Front plate inside diameter | 142.40 mm |
| Brush seal outside diameter | 151.71 mm |
| Bristle fence height | 1.40 mm |
| Brush seal axial thickness | 3.53 mm |
| Bristle pack thickness | 0.60 mm |
| Bristle diameter | 0.0762 mm |
| Bristle lay angle | 45° |
| Bristle pack density | 200/mm circumference |
| Parameters | Values |
|---|---|
| Fluid | Air ideal gas |
| Inlet total pressure Pin | 0.20 to 0.60 (MPa) |
| Outlet static pressure Pout | 0.1 (MPa) |
| Pressure ratio | 2 to 6 |
| Inlet total temperature | 293.15 (K) |
| Bristle lay angle | 45 (degrees) |
| Number of bristle rows in the rotor axial direction | 11 (rows) |
| Average size of voids among bristles | 0.009525 (mm) |
| Porosity | 0.195 |
| Clearance | 0.1 (mm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.A.M.; Liu, M.; Kang, Y.; Wang, J.; Idriss, A.I.B.; Tin, N.T.T. Brush Seal Performance with Ideal Gas Working Fluid under Static Rotor Condition. Machines 2024, 12, 476. https://doi.org/10.3390/machines12070476
Ahmed AAM, Liu M, Kang Y, Wang J, Idriss AIB, Tin NTT. Brush Seal Performance with Ideal Gas Working Fluid under Static Rotor Condition. Machines. 2024; 12(7):476. https://doi.org/10.3390/machines12070476
Chicago/Turabian StyleAhmed, Altyib Abdallah Mahmoud, Meihong Liu, Yuchi Kang, Juan Wang, Aboubaker I. B. Idriss, and Nguyen Thi Trung Tin. 2024. "Brush Seal Performance with Ideal Gas Working Fluid under Static Rotor Condition" Machines 12, no. 7: 476. https://doi.org/10.3390/machines12070476
APA StyleAhmed, A. A. M., Liu, M., Kang, Y., Wang, J., Idriss, A. I. B., & Tin, N. T. T. (2024). Brush Seal Performance with Ideal Gas Working Fluid under Static Rotor Condition. Machines, 12(7), 476. https://doi.org/10.3390/machines12070476