Calculation of Wear of Railway Wheels with Multibody Codes: Benchmarking of the Modelling Choices
Abstract
:1. Introduction
2. Model
2.1. Wear Calculation
2.2. Vehicle–Track MB Model
2.2.1. Vehicle Model
- Four wheelsets, each one with six DOFs.
- Eight axle boxes that are only allowed to rotate with respect to their wheelset (1 DOF per body).
- Two bogie-frame bodies, which feature six DOFs each and model the FIAT bogie used on the vehicle.
- Two bolsters that have all six DOFs.
- One carbody with six DOFs.
2.2.2. Track Model
2.2.3. Wheel–Rail Contact Model
3. Results
4. Conclusions
- With respect to Archard’s law, the KP law is less affected by changes in the contact reference damping applied to avoid numerical instabilities in the calculation of the wheel–rail contact forces. Nonetheless, a preliminary tuning of the reference damping should always be performed to ensure reliable results in terms of wear depth and worn profile shape. Conversely, the number of discretization elements on the contact patch has a negligible impact on the wear depth distribution, but it can threaten the convergence of the numerical integrator during the simulation, especially when using the EE method.
- For the KP law, the wear rate decreases with the curve radius, as all curves in the wear regime are severe in the simulations shown in the paper. On the other hand, Archard’s law does not feature a monotonous dependency of wear rate on curve radius because wider curves can be run at a higher speed, shifting from the mild 1 region to the severe region of the KTH wear map.
- Although the outcomes of the present paper suggest that the energetic KP law ensures more stability in the simulation and less dependency on modelling parameters, it is a less solid law in the literature, with many uncertainties on the wear coefficients and transition between the mild and severe regimes.
- The EE method, which considers an equivalent elliptic patch, provides wear depth distributions in good agreement with the outputs of the DE method, which considers a non-elliptic patch shape for the calculation of the tangential forces and wear depth. As the discrepancies between the two methods can be considered lower than the uncertainties related to the choice of the wear coefficients, and since the computational time can increase by one order of magnitude when shifting from the EE to the DE method, the EE method is believed to be the proper approach for the sake of the numerical simulation of the evolution of railway wheel profile shapes.
- It is demonstrated that the SIMPACK algorithm calculates the contact pressure using the total normal force, which is the sum of the elastic term and a damping term. Nonetheless, the simulations shown in the paper highlight that this strategy can produce local wear peaks when using Archard’s law, which states that worn volume is directly proportional to the normal force. These peaks arise when the number of contact patches has an abrupt change, and a new contact patch is generated with a small area, and with a normal force corresponding to the damping contribution only. This leads to large values of contact pressure corresponding to the seizure regime according to the KTH map. To avoid these peaks generated from numerical issues, the present paper suggests calculating the worn volume with the elastic component only, which acts as a sort of filtered normal force.
- Nowadays, the most suitable solution for wear prediction is to rely on the commercial code for the dynamic simulation, whilst developing an external routine to calculate the worn material and worn profile shape. With this strategy, it is possible to avoid numerical peaks more easily, to define track-variable wear coefficients (to consider for instance lubrication) and in general to gain further control of the wear computation with no loss of the unbeatable reliability provided by commercial codes for the dynamic simulation.
- To run iterative wear simulations, with subsequent replacement of the wheel worn profiles, it is essential to adopt a suitable smoothing technique that avoids numerical instabilities whilst not compromising the worn shape of the profile. Consequently, different smoothing and filtering techniques should be tested to find the optimal strategy.
- Experimental activities on dedicated test rigs are planned to tune and validate the wear algorithms for the selected wheel and rail steel materials considering the variation in wear coefficients due to the possible influence of third-body materials at the wheel–rail interface such as lubricants or natural contaminants.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Enblom, R. Deterioration mechanisms in the wheel–rail interface with focus on wear prediction: A literature review. Veh. Syst. Dyn. 2009, 47, 661–700. [Google Scholar] [CrossRef]
- Braghin, F.; Bruni, S.; Lewis, R. Railway wheel wear. In Wheel–Rail Interface Handbook; Lewis, R., Olofsson, U., Eds.; Woodhead Publishing: Cambridge, UK, 2009; pp. 172–210. [Google Scholar]
- Pombo, J.; Desprets, H.; Verardi, R.; Ambrósio, J.; Pereira, M.; Ariaudo, C.; Kuka, N. Wheel wear evolution and its influence on the dynamic behaviour of railway vehicles. In Proceedings of the 7th EUROMECH Solid Mechanics Conference, Lisbon, Portugal, 9–11 September 2009. [Google Scholar]
- Pombo, J. Application of a Computational Tool to Study the Influence of Worn Wheels on Railway Vehicle Dynamics. J. Softw. Eng. Appl. 2012, 5, 51–61. [Google Scholar] [CrossRef]
- Pradhan, S.; Samantaray, A.K.; Bhattacharyya, R. Prediction of railway wheel wear and its influence on the vehicle dynamics in a specific operating sector of Indian railways network. Wear 2018, 406–407, 92–104. [Google Scholar] [CrossRef]
- Pradhan, S.; Samantaray, A.K. A Recursive Wheel Wear and Vehicle Dynamic Performance Evolution Computational Model for Rail Vehicles with Tread Brakes. Vehicles 2019, 1, 88–115. [Google Scholar] [CrossRef]
- H-Nia, S.; Flodin, J.; Casanueva, C.; Asplund, M.; Stichel, S. Predictive maintenance in railway systems: MBS-based wheel and rail life prediction exemplified for the Swedish Iron-Ore line. Veh. Syst. Dyn. 2024, 61, 3–20. [Google Scholar] [CrossRef]
- Ye, Y.; Sun, Y.; Dongfang, S.; Shi, D.; Hecht, M. Optimizing wheel profiles and suspensions for railway vehicles operating on specific lines to reduce wheel wear: A case study. Multibody Syst. Dyn. 2021, 51, 91–122. [Google Scholar] [CrossRef]
- Pires, A.C.; Pacheco, L.A.; Dalvi, I.L.; Endlich, C.S.; Queiroz, J.C.; Antoniolli, F.A.; Santos, G.F.M. The effect of railway wheel wear on reprofiling and service life. Wear 2021, 477. [Google Scholar] [CrossRef]
- EN 14363:2016; Railway Applications—Testing and Simulation for the Acceptance of Running Characteristics of Railway Vehicles—Running Behaviour and Stationary Tests. CEN: Brussels, Belgium, 2016.
- Pombo, J.; Ambrósio, J.; Pereira, M.; Lewis, R.; Dwyer-Joyce, R.; Ariaudo, C.; Kuka, N. A study on wear evaluation of railway wheels based on multibody dynamics and wear computation. Multibody Syst. Dyn. 2010, 24, 347–366. [Google Scholar] [CrossRef]
- Pombo, J.; Ambrósio, J.; Pereira, M.; Lewis, R.; Dwyer-Joyce, R.; Ariaudo, C.; Kuka, N. A railway wheel wear prediction tool based on a multibody software. J. Theor. Appl. Mech. 2010, 48, 751–770. [Google Scholar]
- Pombo, J.; Ambrósio, J.; Pereira, M.; Lewis, R.; Dwyer-Joyce, R.; Ariaudo, C.; Kuka, N. Development of a wear prediction tool for steel railway wheels using three alternative wear functions. Wear 2011, 271, 238–245. [Google Scholar] [CrossRef]
- Enblom, R.; Stichel, S. Industrial implementation of novel procedures for the prediction of railway wheel surface deterioration. Wear 2011, 271, 203–209. [Google Scholar] [CrossRef]
- Bosso, N.; Magelli, M.; Zampieri, N. Simulation of wheel and rail profile wear: A review of numerical models. Railw. Eng. Sci. 2022, 30, 403–436. [Google Scholar] [CrossRef]
- Braghin, F.; Lewis, R.; Dwyer-Joyce, R.S.; Bruni, S. A mathematical model to predict railway wheel profile evolution due to wear. Wear 2006, 261, 1253–1264. [Google Scholar] [CrossRef]
- Jin, X.; Xiao, X.; Wen, Z.; Guo, J.; Zhu, M. An investigation into the effect of train curving on wear and contact stresses of wheel and rail. Tribol. Int. 2009, 42, 475–490. [Google Scholar] [CrossRef]
- Tao, G.; Ren, D.; Wang, L.; Wen, Z.; Jin, X. Online prediction model for wheel wear considering track flexibility. Multibody Syst. Dyn. 2018, 44, 313–334. [Google Scholar] [CrossRef]
- Bosso, N.; Zampieri, N. Numerical stability of co-simulation approaches to evaluate wheel profile evolution due to wear. Int. J. Rail Transp. 2020, 8, 159–179. [Google Scholar] [CrossRef]
- About Simpack 2023.4-Build150, 64bit; Dassault Systems Simulia Corp.: Santa Clara, CA, USA, 2023.
- Krause, H.; Poll, G. Wear of wheel-rail surfaces. Wear 1986, 113, 103–122. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Archard, J.F.; Hirst, W.; Allibone, T.E. The wear of metals under unlubricated conditions. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1956, 236, 397–410. [Google Scholar] [CrossRef]
- Jendel, T. Prediction of wheel profile wear—Comparisons with field measurements. Wear 2002, 253, 89–99. [Google Scholar] [CrossRef]
- Kalker, J.J.; Chudzikiewicz, A. Calculation of the Evolution of the Form of a Railway Wheel Profile Through Wear. In Unilateral Problems in Structural Analysis IV, Proceedings of the Fourth Meeting on Unilateral Problems in Structural Analysis, Capri, Italy, 14–16 June 1989; Piero, G., Maceri, F., Eds.; Birkhäuser: Basel, Switzerland, 1991. [Google Scholar]
- Jendel, T.; Berg, M. Prediction of Wheel Profile Wear. Veh. Syst. Dyn. 2002, 37, 502–513. [Google Scholar] [CrossRef]
- Bosso, N.; Magelli, M.; Zampieri, N. Study on the Influence of the Modelling Strategy in the Calculation of the Worn Profile of Railway Wheels; WIT Press: Southampton, UK, 2022; pp. 65–76. [Google Scholar]
- Ignesti, M.; Innocenti, A.; Marini, L.; Meli, E.; Rindi, A. Development of a model for the simultaneous analysis of wheel and rail wear in railway systems. Multibody Syst. Dyn. 2014, 31, 191–240. [Google Scholar] [CrossRef]
- Kisilowski, J.; Kowalik, R. Method for Determining the Susceptibility of the Track. Appl. Sci. 2022, 12, 12534. [Google Scholar] [CrossRef]
- Kalker, J.J. A Fast Algorithm for the Simplified Theory of Rolling Contact. Veh. Syst. Dyn. 1982, 11, 1–13. [Google Scholar] [CrossRef]
- Ayasse, J.B.; Chollet, H. Determination of the wheel rail contact patch in semi-Hertzian conditions. Veh. Syst. Dyn. 2005, 43, 161–172. [Google Scholar] [CrossRef]
- Quost, X.; Sebes, M.; Eddhahak, A.; Ayasse, J.-B.; Chollet, H.; Gautier, P.-E.; Thouverez, F. Assessment of a semi-Hertzian method for determination of wheel–rail contact patch. Veh. Syst. Dyn. 2006, 44, 789–814. [Google Scholar] [CrossRef]
- Bezin, Y.; Pålsson, B.A. Multibody simulation benchmark for dynamic vehicle-track interaction in switches and crossings: Modelling description and simulation tasks. Veh. Syst. Dyn. 2023, 61, 644–659. [Google Scholar] [CrossRef]
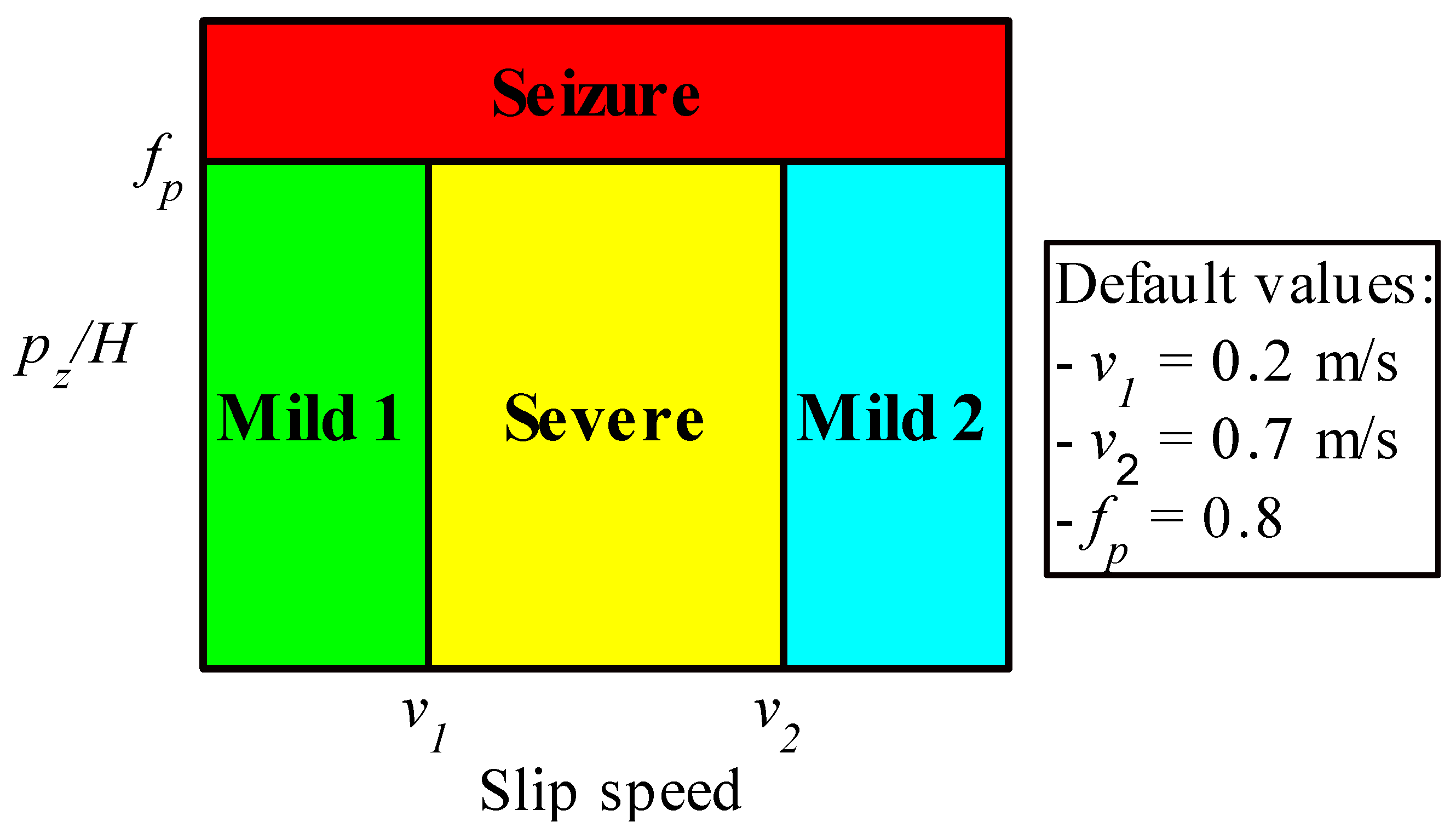
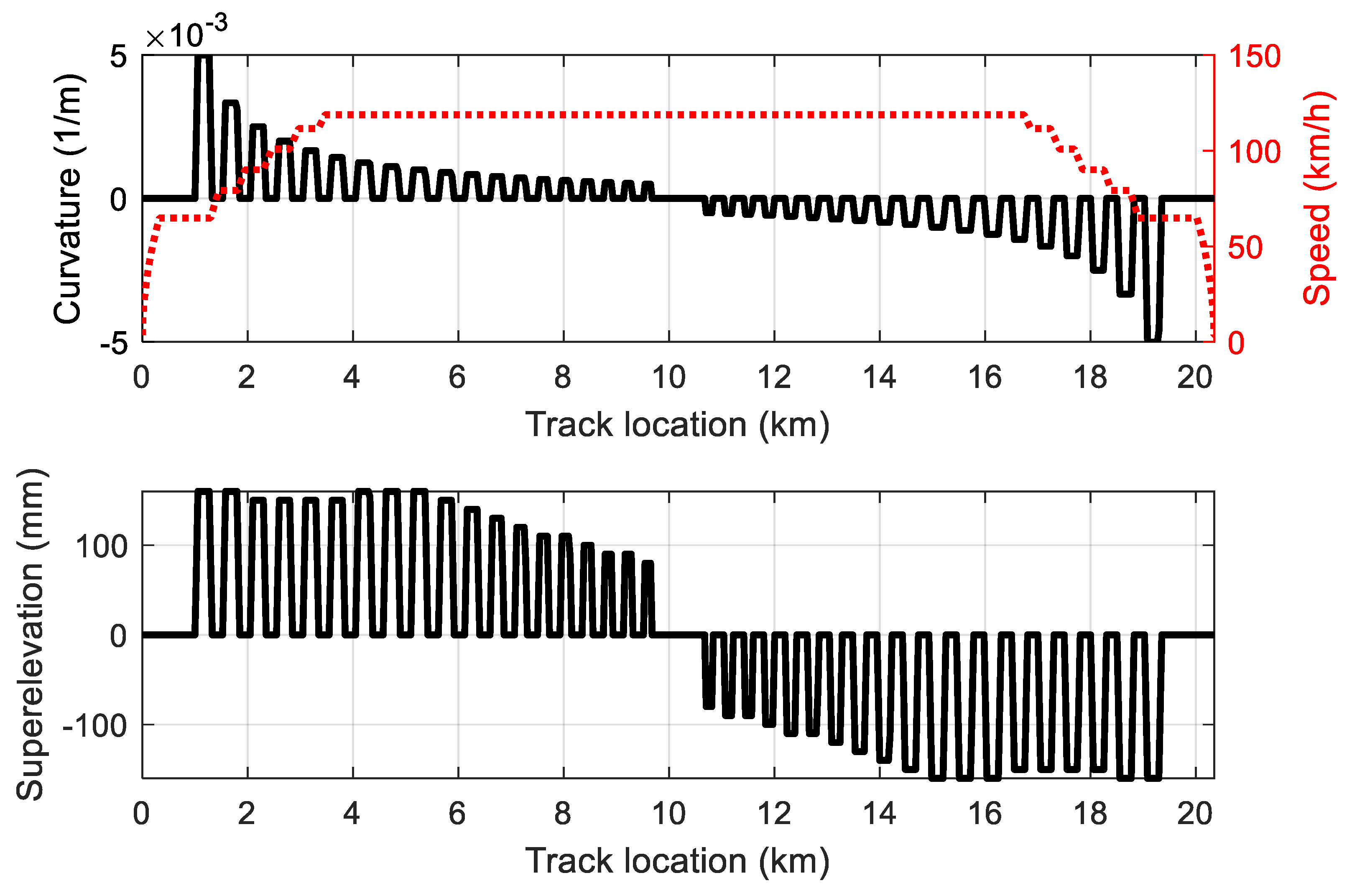
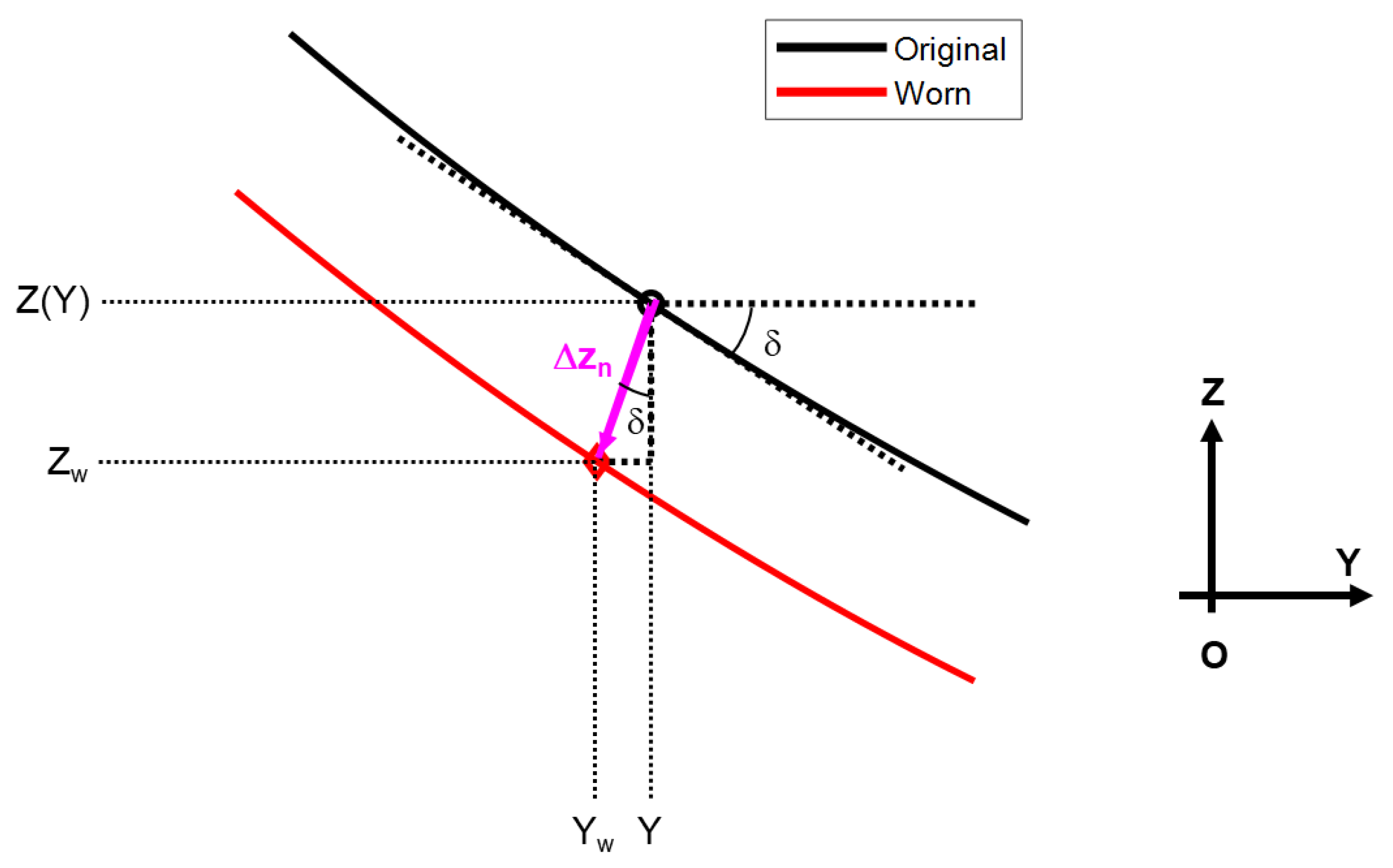




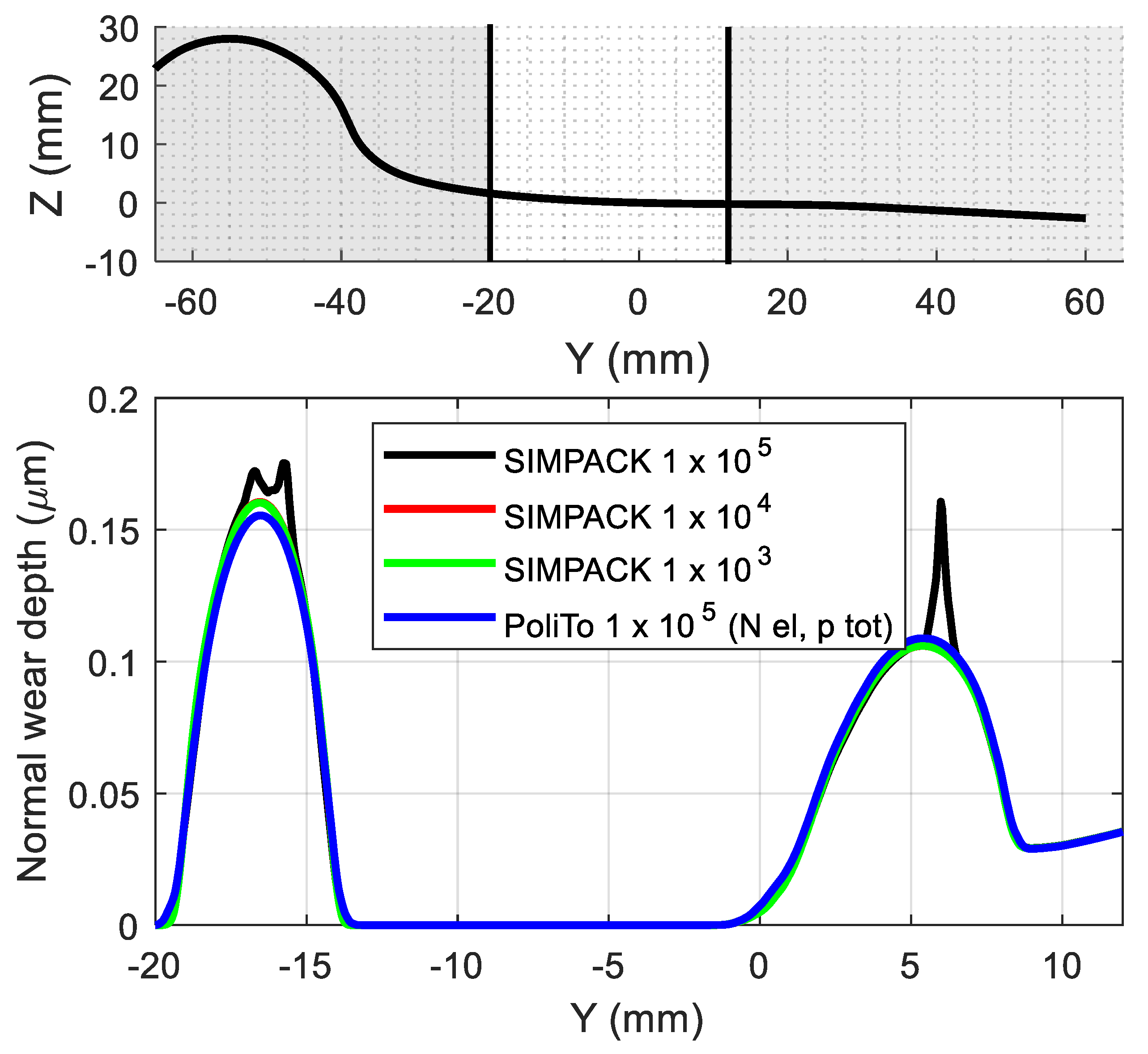
| Wear Region | Wear Coefficient |
|---|---|
| Mild 1 | 1.43 × 10−4 |
| Severe | 1.00 × 10−3 |
| Mild 2 | 1.43 × 10−4 |
| Seizure | 1.00 × 10−2 |
| Quantity | Equivalent Elastic Method | Discrete Elastic Method | ||||
|---|---|---|---|---|---|---|
| Number of elements | 5 | 11 | 23 | 5 | 11 | 23 |
| Normalized CPU time | 1.62 | 1 | 1.39 | 10.62 | 10.75 | 10.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magelli, M.; Zampieri, N. Calculation of Wear of Railway Wheels with Multibody Codes: Benchmarking of the Modelling Choices. Machines 2024, 12, 644. https://doi.org/10.3390/machines12090644
Magelli M, Zampieri N. Calculation of Wear of Railway Wheels with Multibody Codes: Benchmarking of the Modelling Choices. Machines. 2024; 12(9):644. https://doi.org/10.3390/machines12090644
Chicago/Turabian StyleMagelli, Matteo, and Nicolò Zampieri. 2024. "Calculation of Wear of Railway Wheels with Multibody Codes: Benchmarking of the Modelling Choices" Machines 12, no. 9: 644. https://doi.org/10.3390/machines12090644
APA StyleMagelli, M., & Zampieri, N. (2024). Calculation of Wear of Railway Wheels with Multibody Codes: Benchmarking of the Modelling Choices. Machines, 12(9), 644. https://doi.org/10.3390/machines12090644







