Adjustable Speed Control and Damping Analysis of Torsional Vibrations in VSD Compressor Systems
Abstract
:1. Introduction
2. MV Field Case Application
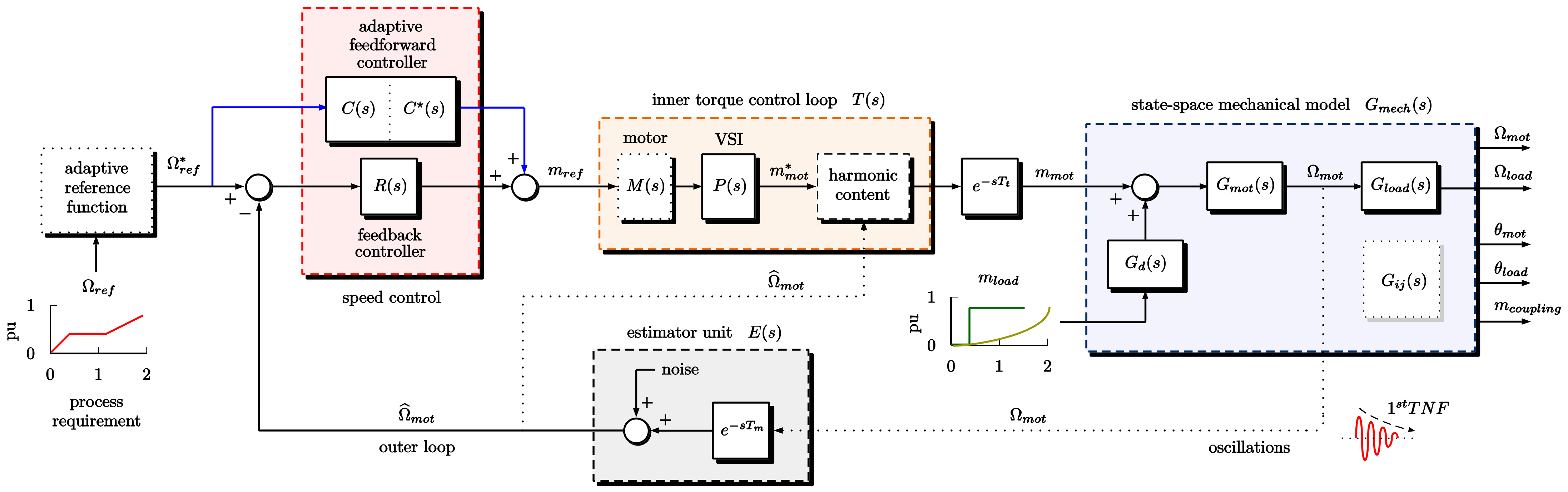
3. Drive train Mechanical Modeling
4. Analysis of the VSD Vibrating Behavior
- The AC-DC-AC topology and the torque spectrum;
- The control loops design and the oscillation characteristics.
- m = 0 and k ≠ 0 → VSI inverter integer harmonic;
- m ≠ 0 and k = 0 → diode-bridge integer harmonic;
- m ≠ 0 and k ≠ 0 → interharmonics DC-link.
5. Campbell Diagram and First Analysis
6. Torque Control Loop
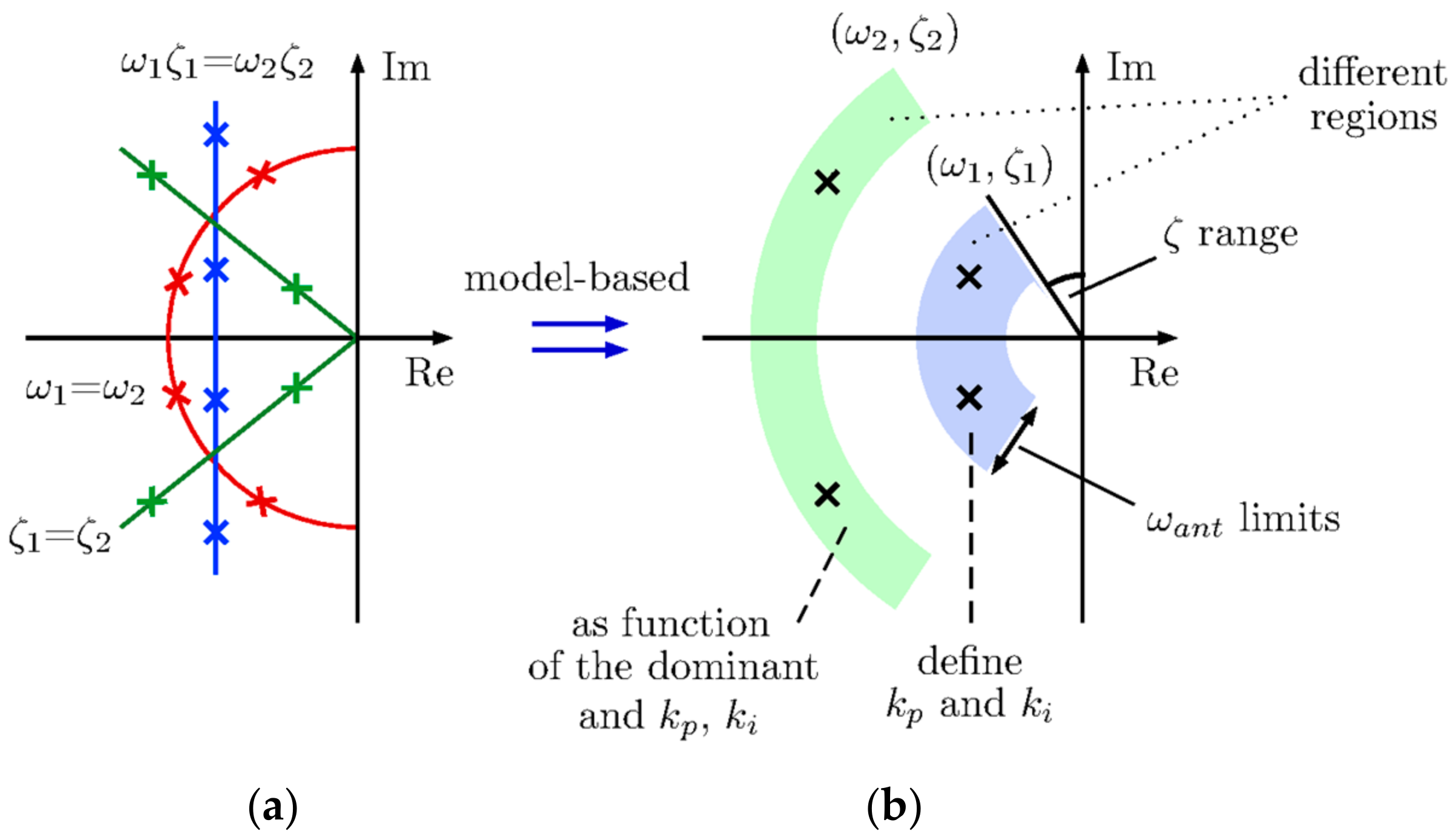
6.1. Feedback Controller Design
- 1.
- From (15), kp and ki are written as a function of the pole pair p1,2, based on {Jmot, Jload, Kel, ω1, ζ1} as in (16):
- 2.
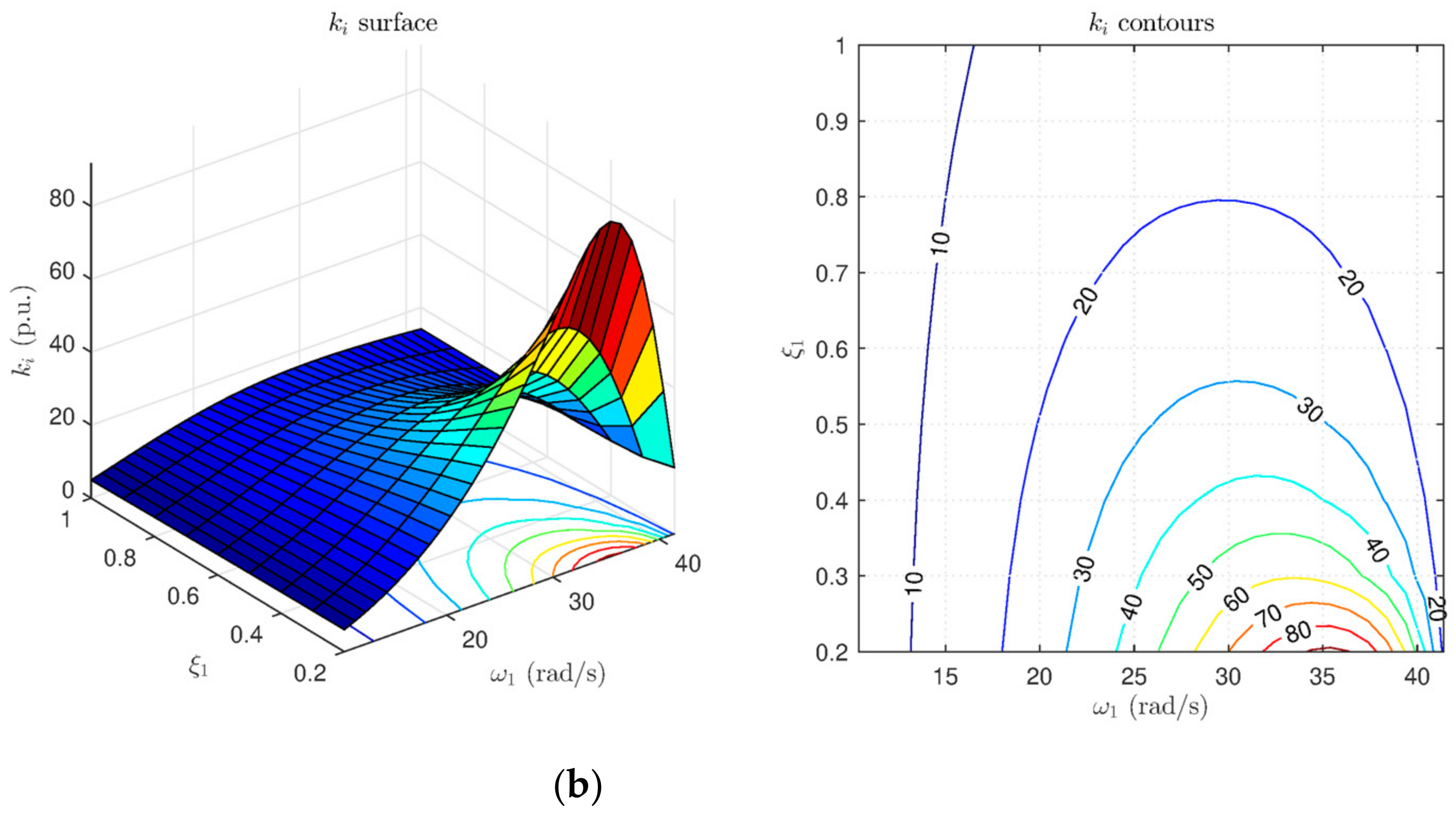
- Choosing the pole-pair p1,2 as the dominant ones, as it follows ω1 < ω2. A fast closed-loop dynamic is guaranteed by settling the frequency boundaries according to ωant as given in (17). In addition, ζ1 should be high in order to have R(s) robustly stable on load torque rejection. The coefficients of p1,2 ⇒ (ω1, ζ1) are chosen through the gains counter plots in Figure 10, then kp, and ki are selected, focusing on the linear parts of the surface.
- 3.
- The resonant coefficients of p3,4 ⇒ (ω2, ζ2) are a function of the previous parameters, as given in (18):
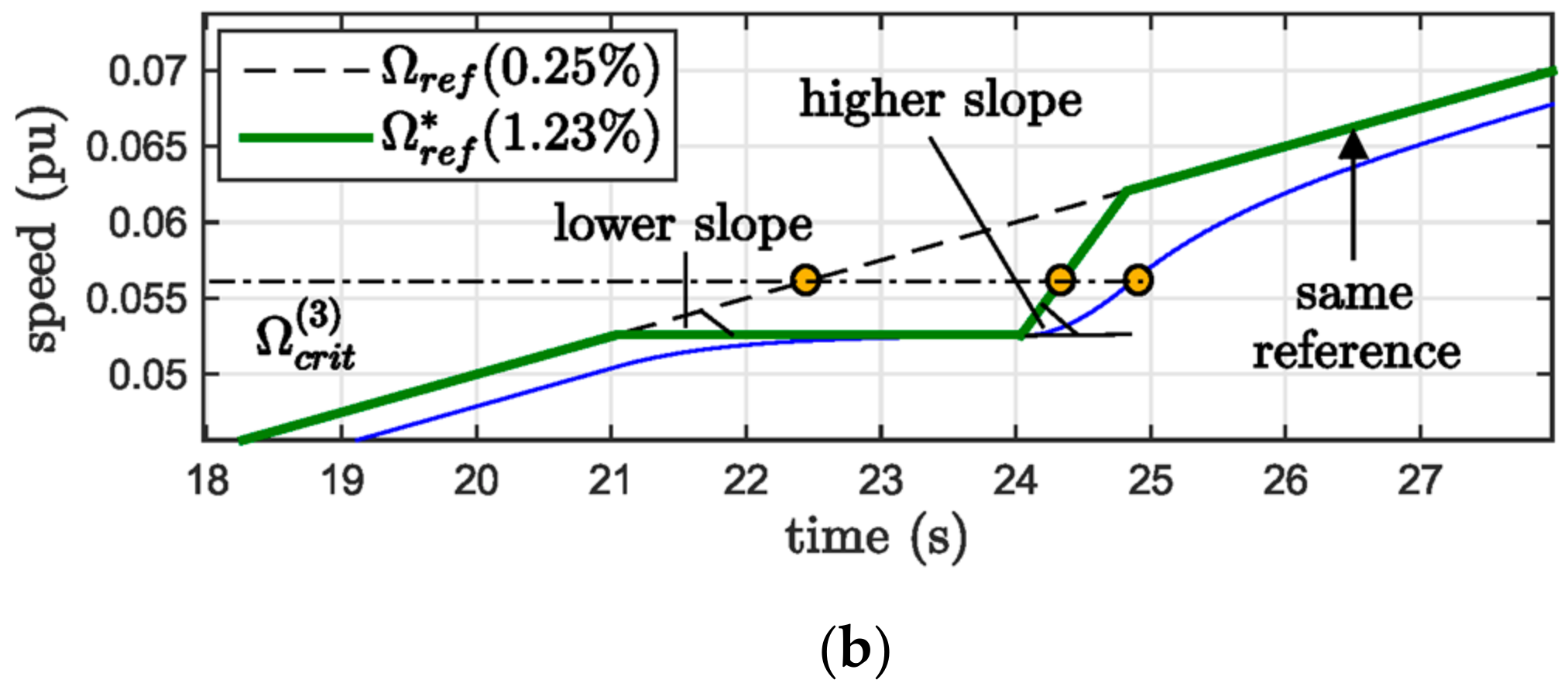
6.2. Feedforward Controller Design
- When a speed step reference Ωref(s) = h/s is applied, where h represents the step size (e.g., h = 1):
- When a speed ramp reference Ωref(s) = h/s2 is applied:
| Algorithm 1. Feedforward Adaptation Pseudocode. |
| 1: α = 1&h = 0.1 ← according to Figure 13 and Figure 14 |
| 2: x = dΩref/dt ← it could be discretized |
| 3: if x > 0 then |
| 4: if x ≥ 20% then ← assuming a step |
| 5: Copt(s) = C(s) ← according to (20) |
| 6: else if 0 < x ≤ 1% then ← keeping limit to 1% |
| 7: Copt(s) = C*(s) ← according to (23) |
| 8: else |
| 9: lower (Ωref,t) ← decrease the ramp* slope |
| 10: goto 3 |
| 11: else if x < 0 then |
| 12: x = |x| and goto 3 |
| 13: else if x = 0 then goto 3 |
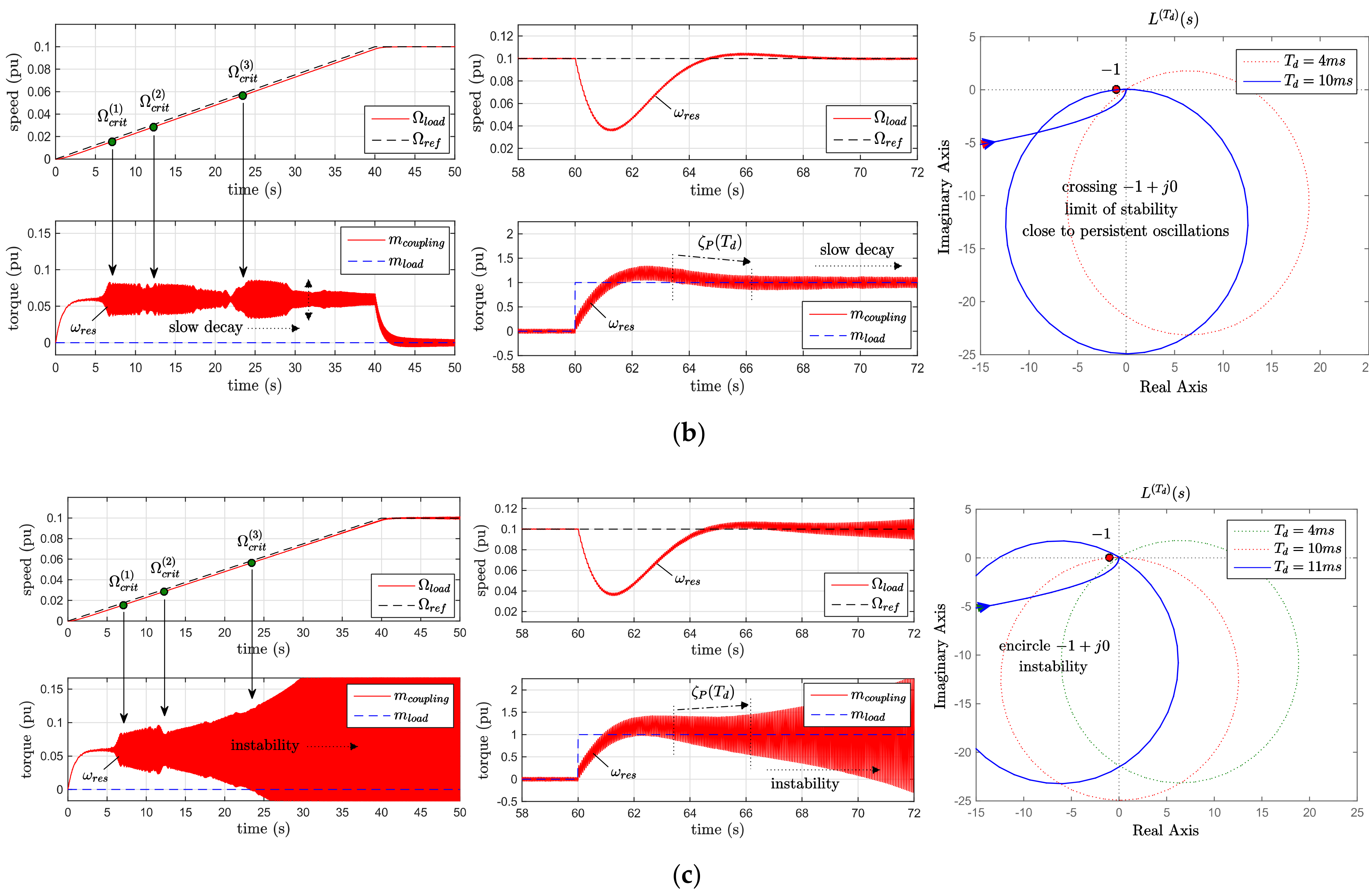
7. Control Stability and Robustness
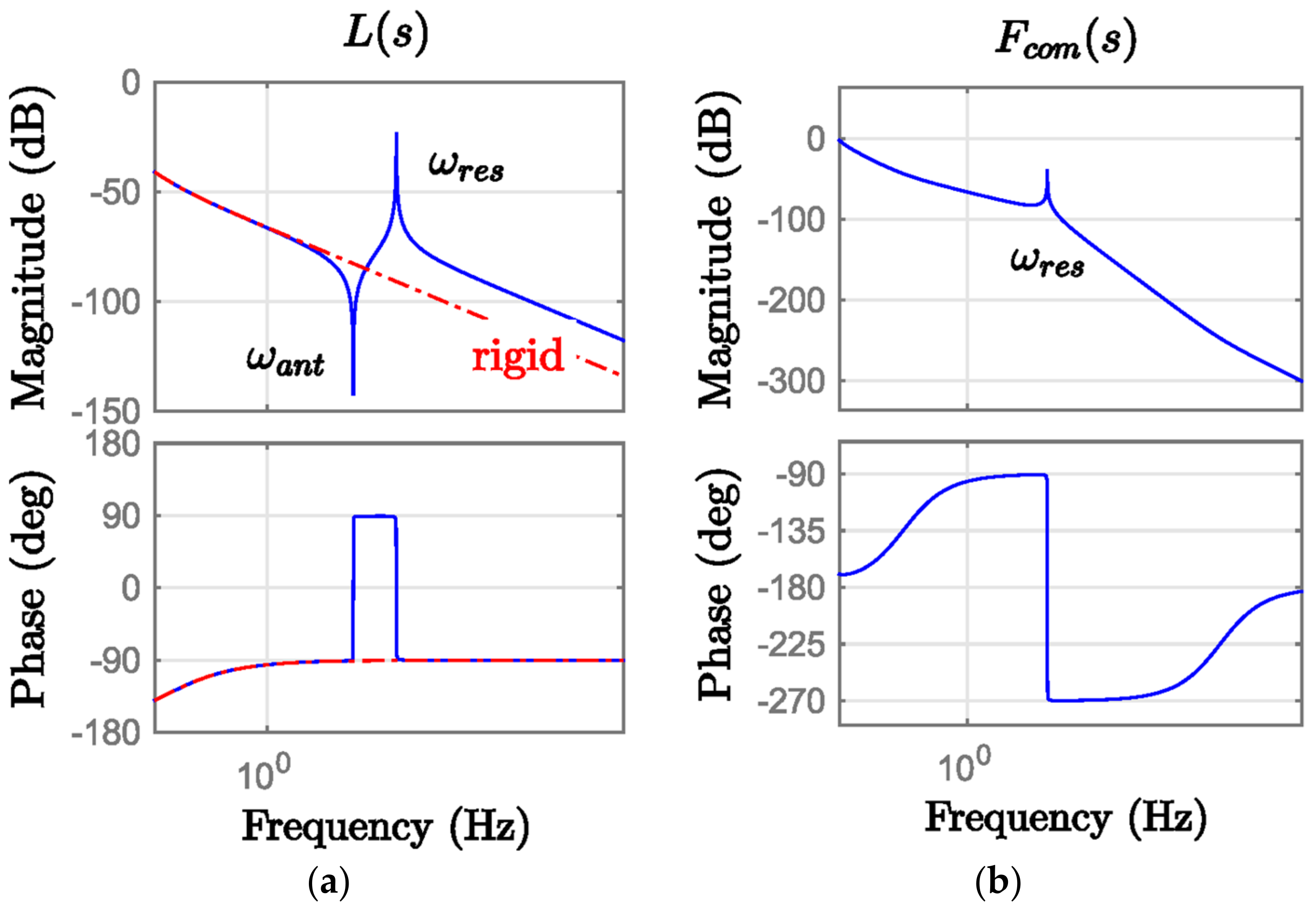
7.1. Nyquist Analysis
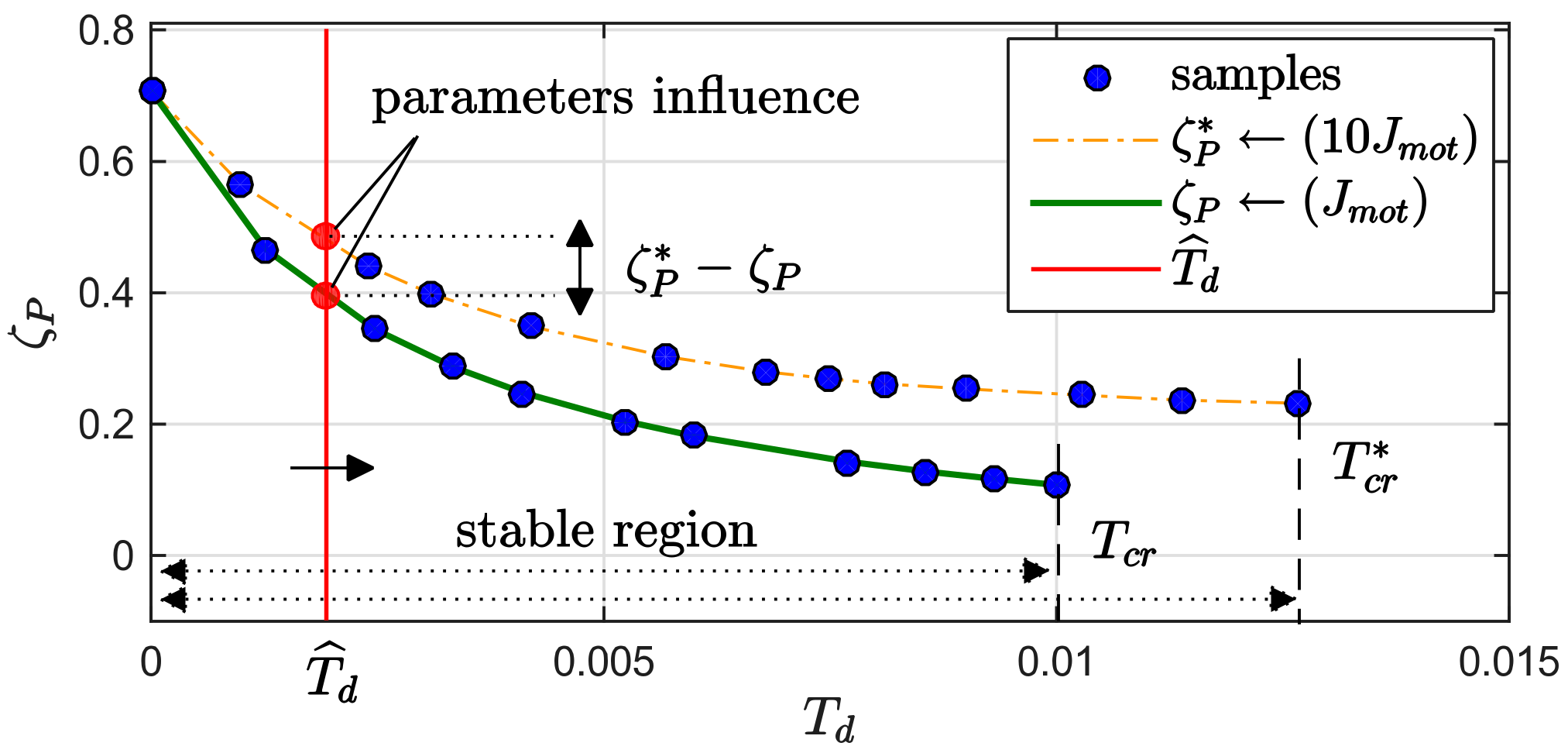
7.2. Process Damping and Characteristics
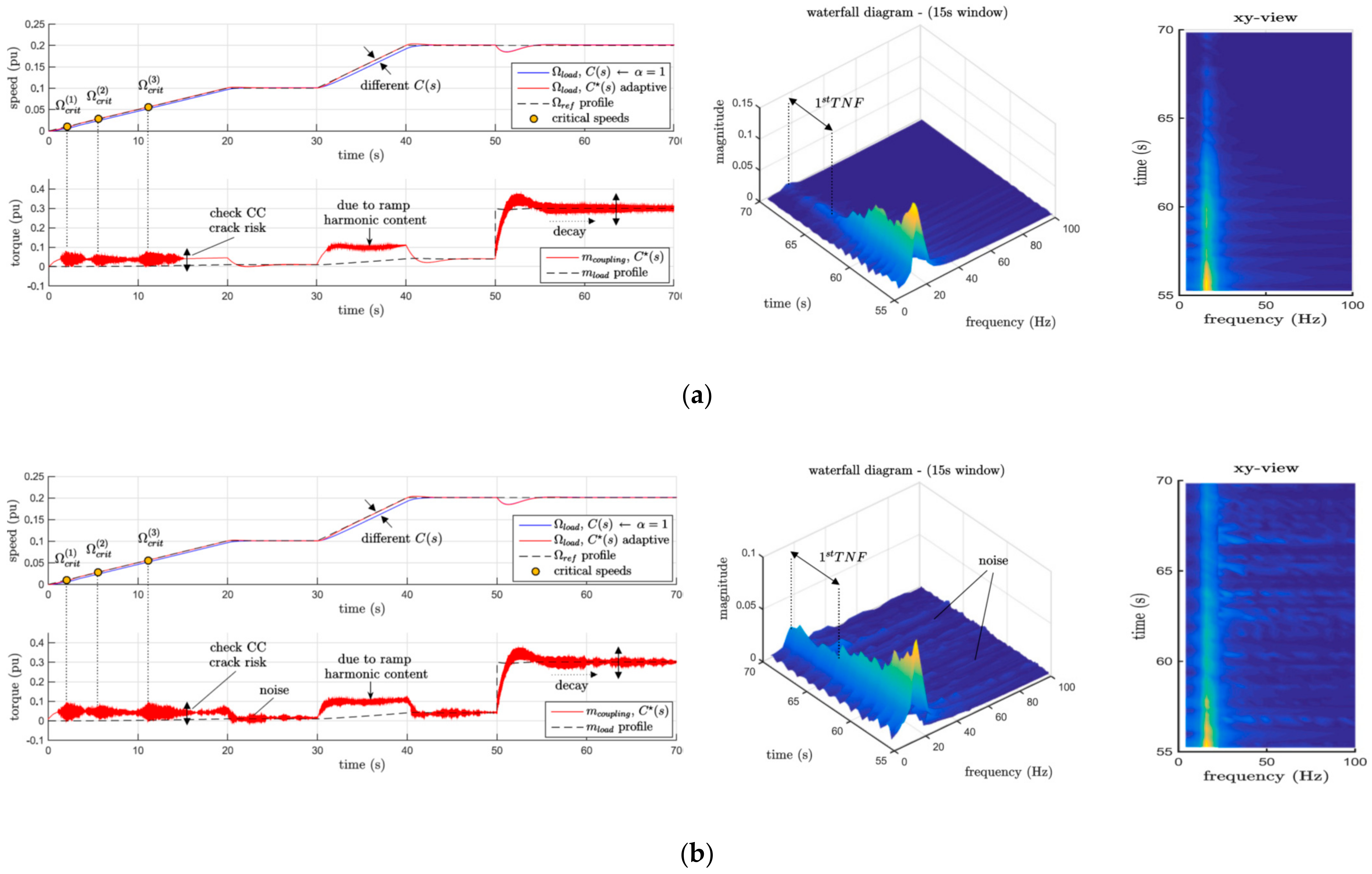
8. HIL Experimental Setup
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muszynski, R.; Deskur, J. Damping of torsional vibrations in highdynamic industrial drives. IEEE Trans. Ind. Electron. 2010, 57, 544–552. [Google Scholar] [CrossRef]
- Holopain, T.; Repo, A.; Niiranen, J. Electromechanical interaction in torsional vibrations of drive train systems including an electrical machine. In Proceedings of the 8th IFToMM International Conference on Rotordynamics, Seoul, Korea, 12–15 September 2010; p. 933. [Google Scholar]
- Del Puglia, S.; Franciscis, S.; Van de Moortel, S.; Jörg, P.; Hattenbach, T.; Sgrò, D.; Antonelli, L.; Falomi, S. A Torsional Interaction Optimization in a LNG Train with Load Commutated Inverter. In Proceedings of the 8th IFToMM International Conference on Rotor Dynamics, Seoul, Korea, 12–15 September 2010. [Google Scholar]
- Song-Manguelle, J.; Schröder, S.; Geyer, T.; Ekemb, G.; Nyobe-Yome, J.M. Prediction of mechanical shaft failures due to pulsating torques of variable-frequency drives. IEEE Trans. Ind. Appl. 2010, 46, 1979–1988. [Google Scholar] [CrossRef]
- Mauri, M.; Rossi, M.; Bruha, M. Generation of Torsional Excitation in a Variable-Speed-Drive System. In Proceedings of the IEEE 23nd International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM, Capri Island, Italy, 22–24 June 2016. [Google Scholar]
- Szabat, K.; Orlowska-Kowalska, T. Vibration suppression in a twomass drive system using PI speed controller and additional feedbacks—Comparative study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Harnefors, L.; Saarakkala, S.E.; Hinkkanen, M. Speed control of electrical drives using classical control methods. IEEE Trans. Ind. Appl. 2013, 49, 889–898. [Google Scholar] [CrossRef]
- Saarakkala, S.E.; Hinkkanen, M.; Zenger, K. Speed control of two-mass mechanical loads in electric drives. In Proceedings of the IEEE Energy Conversion Congress and Exposition, ECCE, Raleigh, NC, USA, 15–20 September 2012; pp. 1246–1253. [Google Scholar]
- Saarakkala, S.E.; Hinkkanen, M. State-space speed control of two mass mechanical systems: Analytical tuning and experimental evaluation. IEEE Trans. Ind. Appl. 2014, 50, 3428–3437. [Google Scholar] [CrossRef] [Green Version]
- Rossi, M.; Marco, M.; Castelli-Dezza, F.; Carmeli, M.S. Discrete multi-layer estimator implementation for sensorless control of elastic drive systems—An industrial case study. In Proceedings of the 14th IMEKO TC10 Workshop on Technical Diagnostics, Milan, Italy, 27–28 June 2016. [Google Scholar]
- Schramm, S.; Sihler, C.; Song-Manguelle, J.; Rotondo, P. Damping torsional interharmonic effects of large drives. IEEE Trans. Power Electron. 2010, 25, 1090–1098. [Google Scholar] [CrossRef]
- Brock, S.; Deskur, J. The problem of measurement and control of speed in a drive with an inaccurate measuring position transducer. In Proceedings of the International Workshop on Advanced Motion Control, Trento, Italy, 26–28 March 2008; Volume 1, pp. 132–136. [Google Scholar]
- Ikeda, H.; Hanamoto, T.; Tsuji, T. Digital Speed Control of Multi-Inertia Resonant System Using Real Time Simulator. In Proceedings of the International Conference on Electrical Machines and Systems, Seoul, Korea, 8–11 October 2007; Volume 10, pp. 1881–1886. [Google Scholar]
- Holopain, T.; Niiranen, J.; Jörg, P.; Andreo, D. Electric Motors and Drives in Torsional Vibration Analysis and Design. In Proceedings of the 42nd Turbimachinery Symposium, Houston, TX, USA, 1–3 October 2013. [Google Scholar]
- Zhang., G.; Furusho, J. Speed control of two-inertia system by PI/PID control. IEEE Trans. Ind. Electron. 2000, 47, 603–609. [Google Scholar] [CrossRef]
- A.P.I. Standard. Tutorial on the API Standard Paragraphs Covering Rotor Dynamics and Balance: An Introduction to Lateral Critical and Train Torsional Analysis and Rotor Balancing; American Petroleum Institute (API): Washington, DC, USA, 1996. [Google Scholar]
- DeWinter, F.; Grainger, L. A practical approach to solving large drive harmonic problems at the design stage. IEEE Trans. Ind. Appl. 1990, 26, 1095–1101. [Google Scholar] [CrossRef]
- Ferretti, G.; Magnani, G.; Rocco, P. Some fundamental limitations in the control of two-mass systems. In Proceedings of the IEEE 2009 International Conference on Mechatronics, ICM, Malaga, Spain, 14–17 April 2009. [Google Scholar]
- Harnefors, L. Proof and application of the positive-net-damping stability criterion. IEEE Trans. Power Syst. 2011, 26, 481–482. [Google Scholar] [CrossRef]
- Kocur., J.; Muench, M. Impact of Electrical Noise on the Torsional Response of VFD Compressor Trains. In Proceedings of the Proceedings of the Forty First Turbomachinery Symposium, Houston, TX, USA, 24–27 September 2012. [Google Scholar]
- Lecchini, A.; Campi, M.C.; Savaresi, S.M. Virtual reference feedback tuning for two degree of freedom controllers. Int. J. Adapt. Control Signal Process. 2002, 16, 355–371. [Google Scholar] [CrossRef] [Green Version]
- Lipo, T.A.; Krause, P.C. Stability analysis of a rectifier-inverter induction motor drive. IEEE Trans. Power Appar. Syst. 1969; PAS-88, 55–66. [Google Scholar]
- Rossi, M.; Mauri, M.; Carmeli, M.S.; Castelli-Dezza, F. Latency Effect in a Variable Speed Control on Torsional Response of Elastic Drive Systems. In Proceedings of the IEEE 22nd International Conference on Electrical Machines, ICEM, Lausanne, Switzerland, 4–7 September 2016; pp. 2282–2288. [Google Scholar]
- Rotondo, P.; Andreo, D.; Falomi, S.; Jörg, P.; Lenzi, A.; Hattenbach, T.; Fioravanti, D.; De Franciscis, S. Combined Torsional and Electromechanical Analysis of an LNG Compression Train with Variable Speed Drive System. In Proceedings of the 38th Turbimachinery Symposium, Houston, TX, USA, 14–17 September 2009; pp. 93–102. [Google Scholar]
- Simond, J.J.; Sapin, A.; Tu Xuan, M.; Wetter, R.; Burmeister, P. 12-Pulse LCI synchronous drive for a 20 MW compressor modeling, simulation and measurements. IAS Annu. Meet. 2005, 4, 2302–2307. [Google Scholar]
- Szabat, K.; Orlowska-Kowalska, T.; Dybkowski, M. Indirect Adaptive Control of Induction Motor Drive System with an Elastic Coupling. IEEE Trans. Ind. Electron. 2009, 56, 4038–4042. [Google Scholar] [CrossRef]
- Tamaoki, T.; Takanezawa, M.; Lu, Z.; Xiao, S.; Kimoto, M.; Morita, N. A study for on-line transfer function analysis, in realizing higher speed response adjustment, in association with variable speed rolling mill motor drive system. In Proceedings of the International Power Electronics Conference—ECCE Asia, IPEC, Sapporo, Japan, 21–24 June 2010; pp. 2516–2519. [Google Scholar]
- Thomsen, S.; Hoffmann, N.; Fuchs, F.W. PI Control, PI-Based State Space Control, and Model-Based Predictive Control for Drive Systems with Elastically Coupled Loads—A Comparative Study. IEEE Trans. Ind. Electron. 2011, 58, 3647–3657. [Google Scholar] [CrossRef]
- Wachel, J.C.; Szenasi, F.R. Analysis of Torsional Vibrations in Rotating Machinery. In Proceedings of the 22sd Turbomachinery Symposium, Dallas, TX, USA, 14–16 September 1993. [Google Scholar]
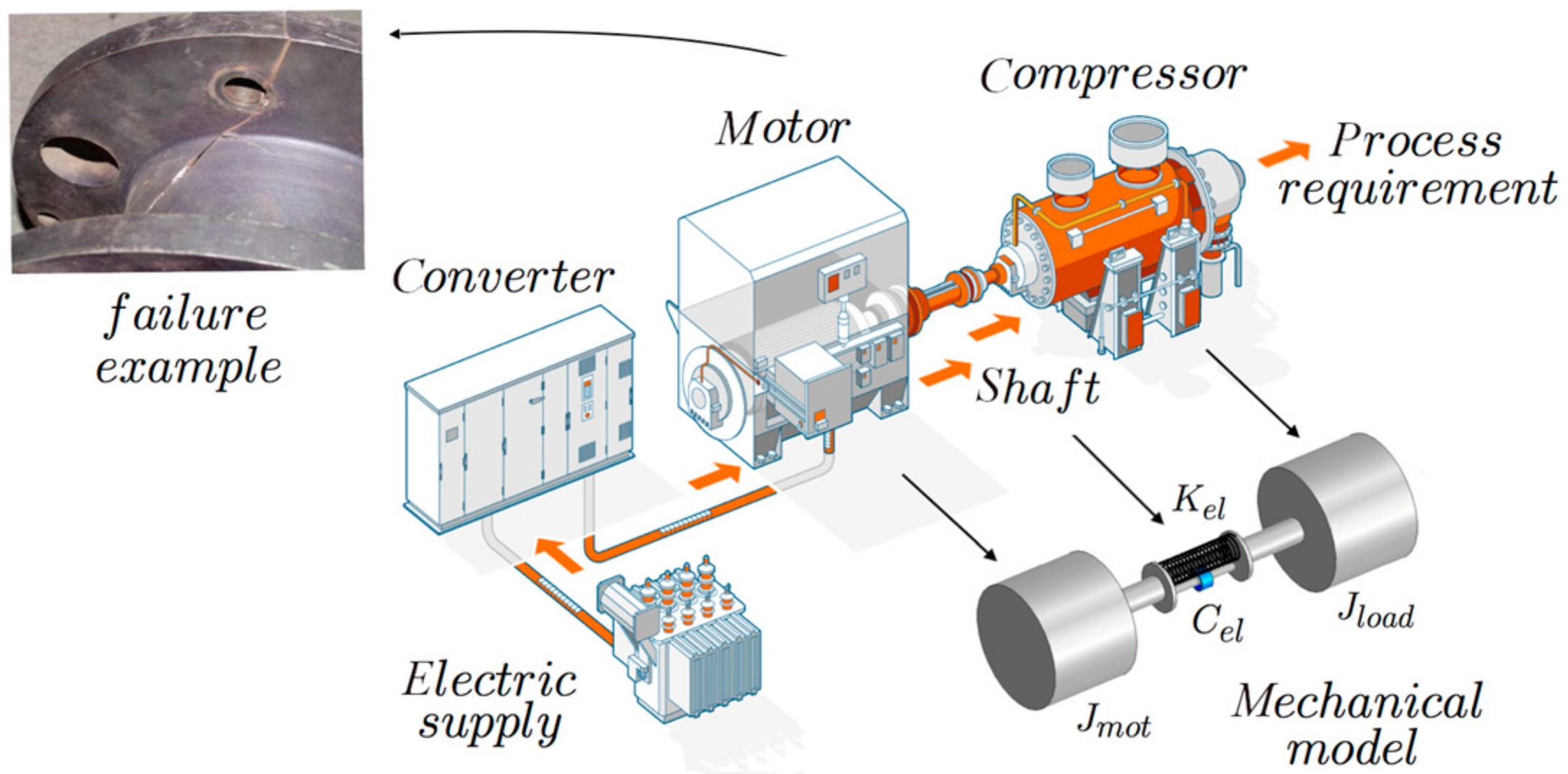
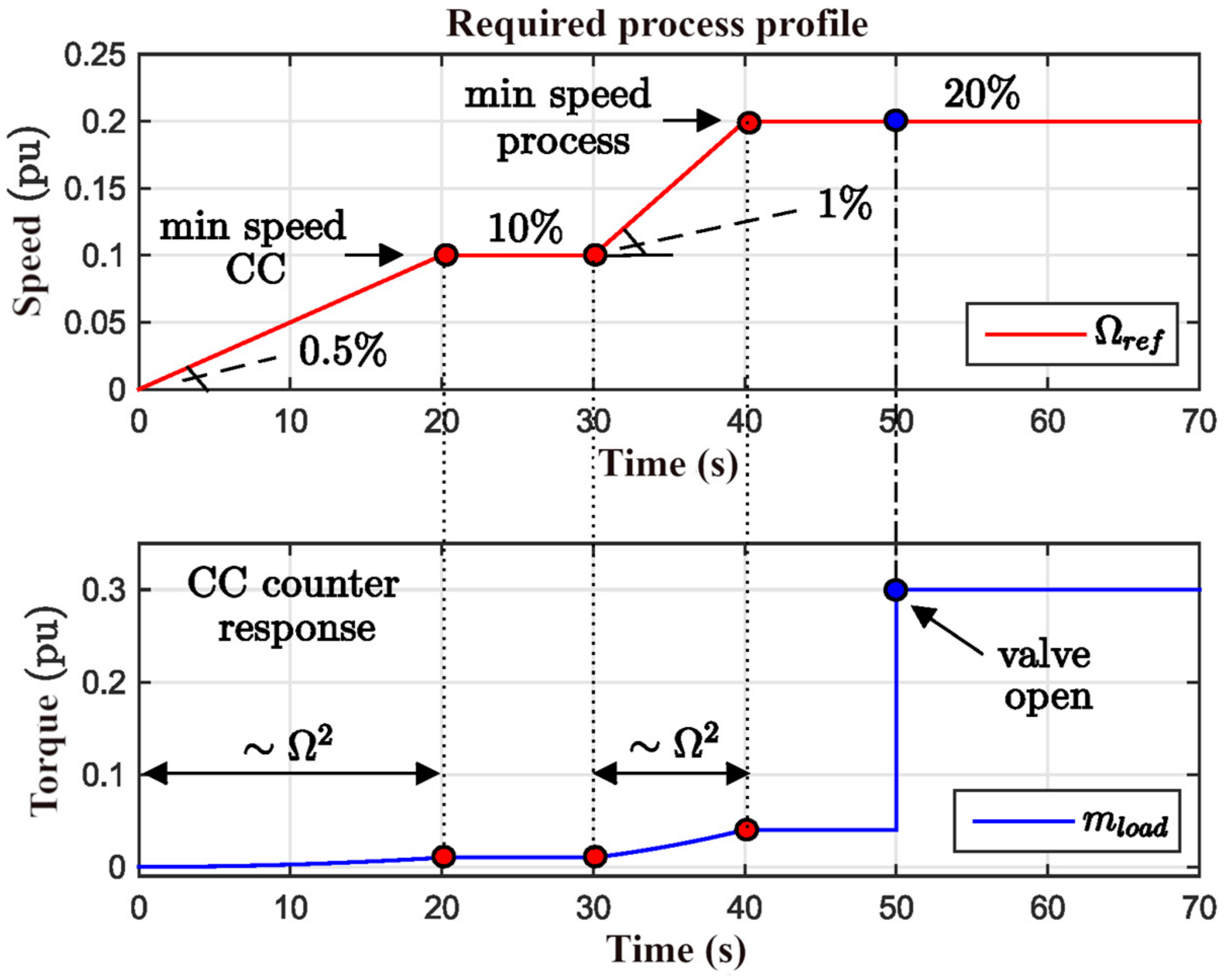
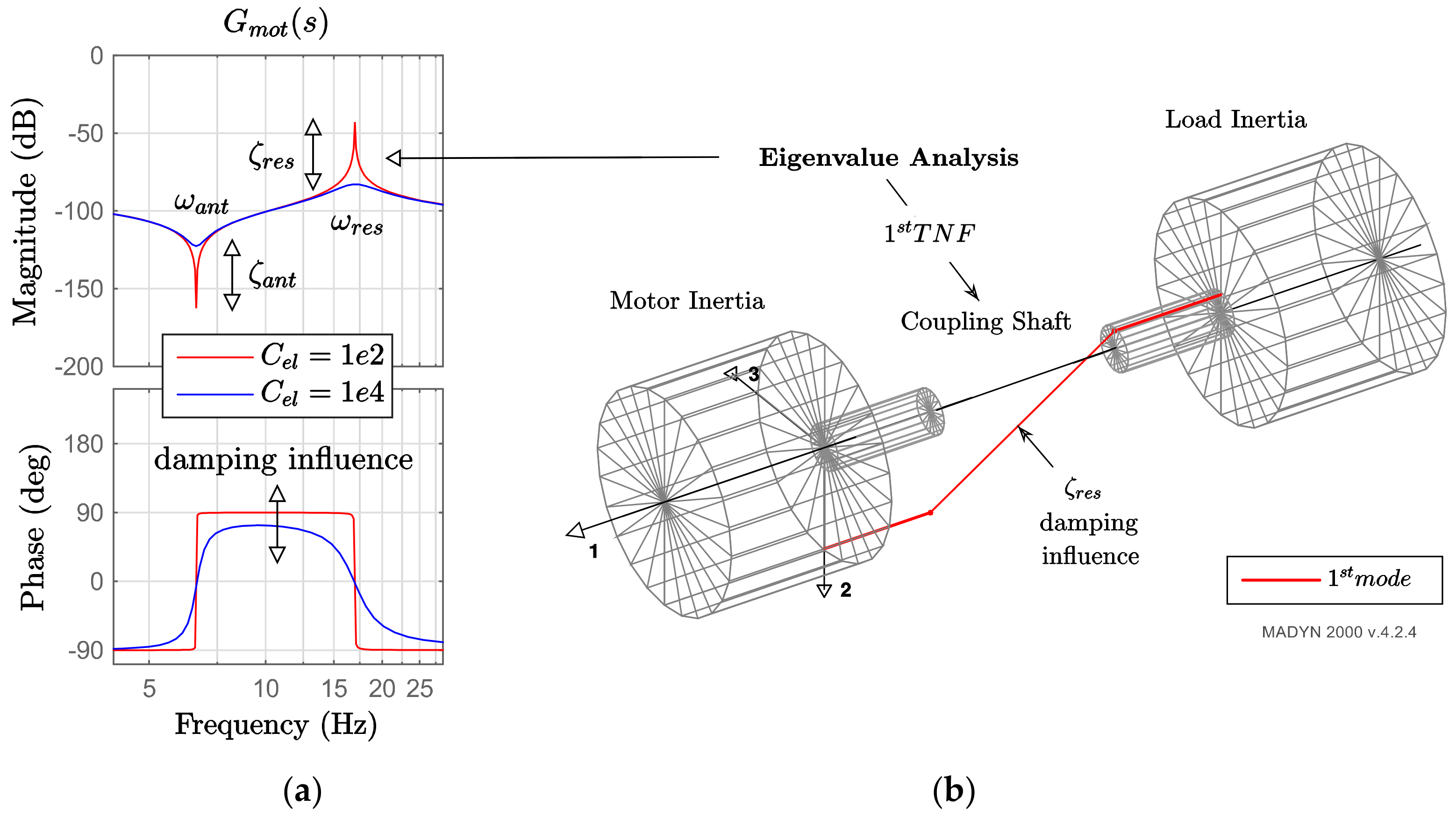


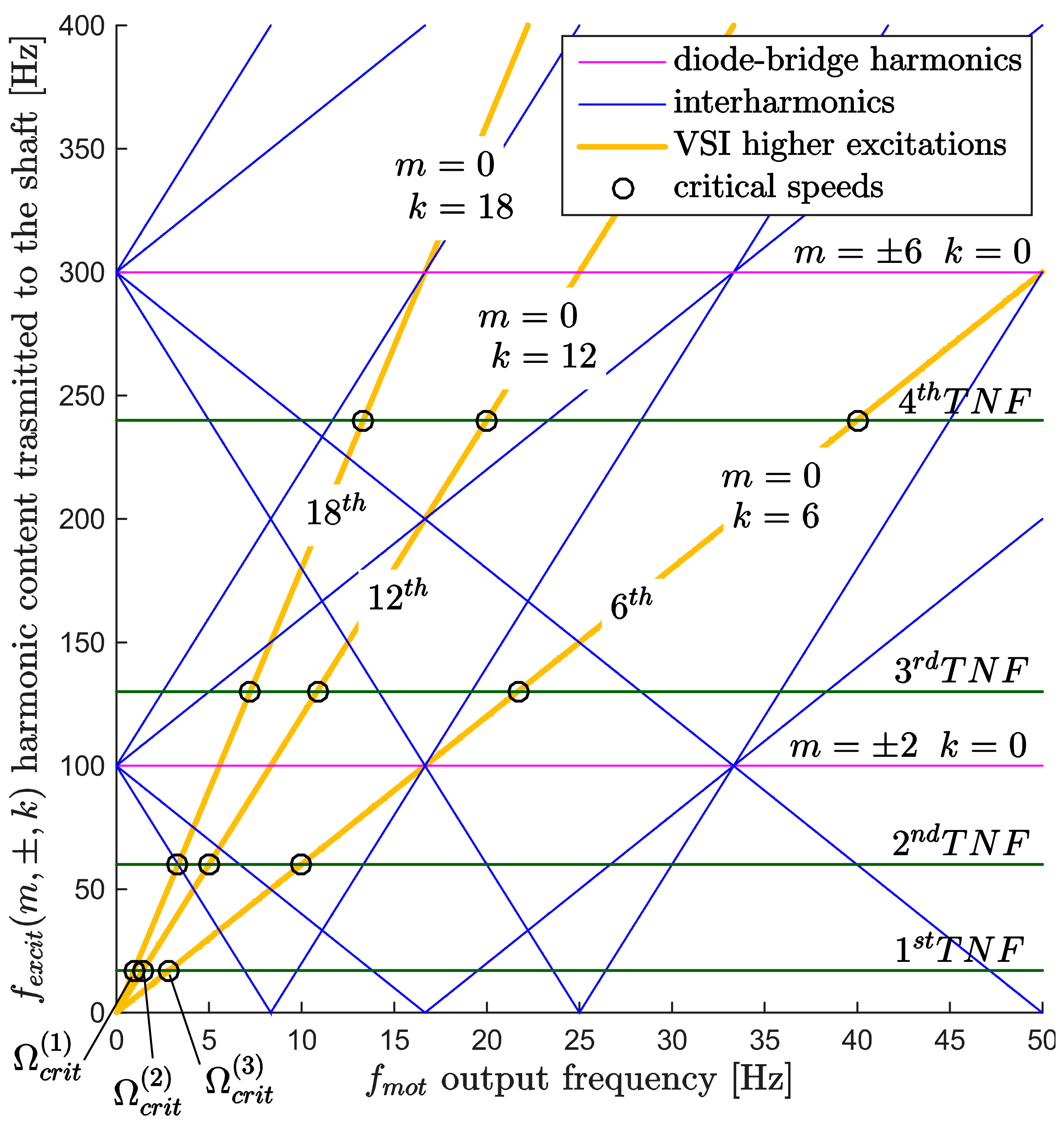


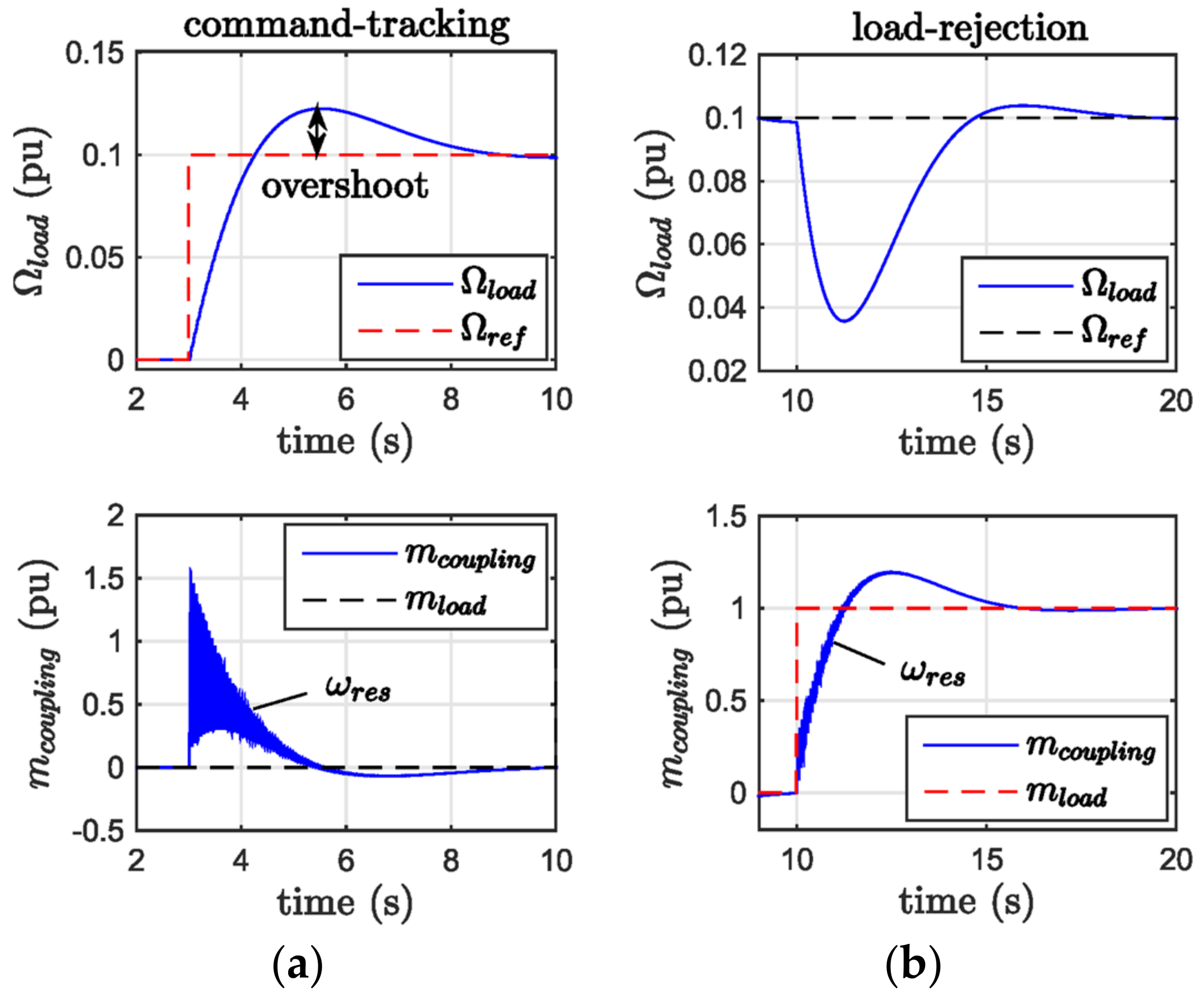
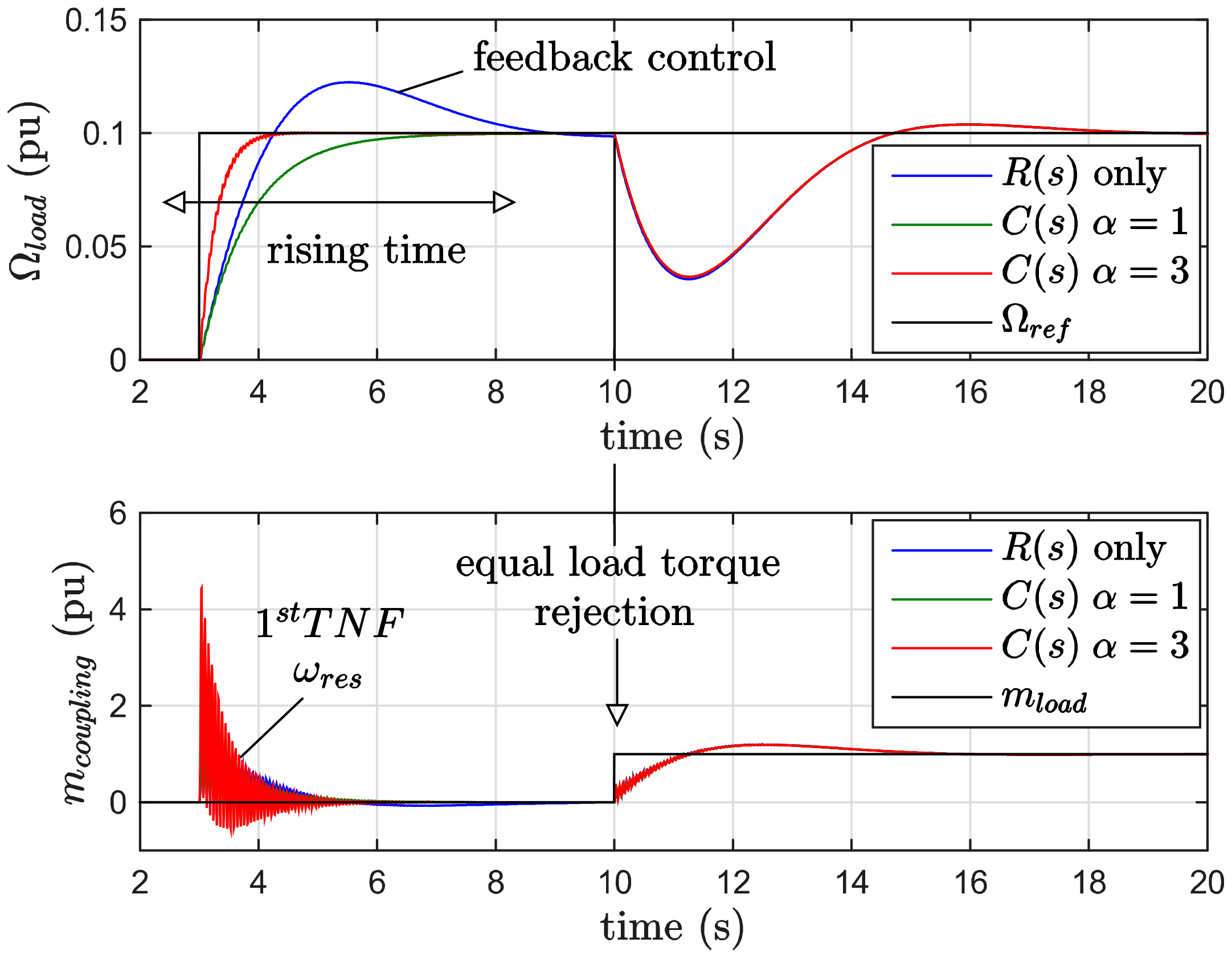
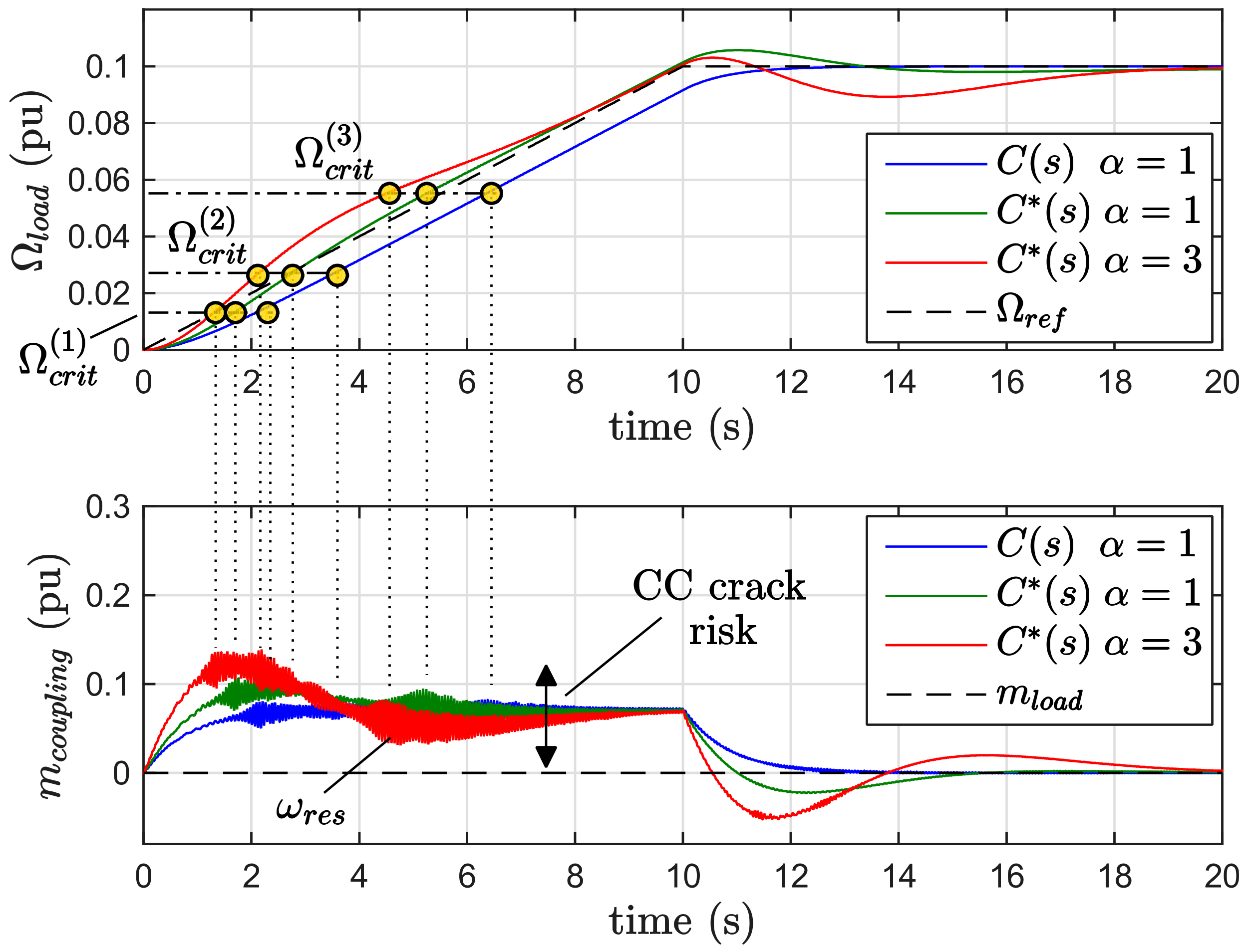
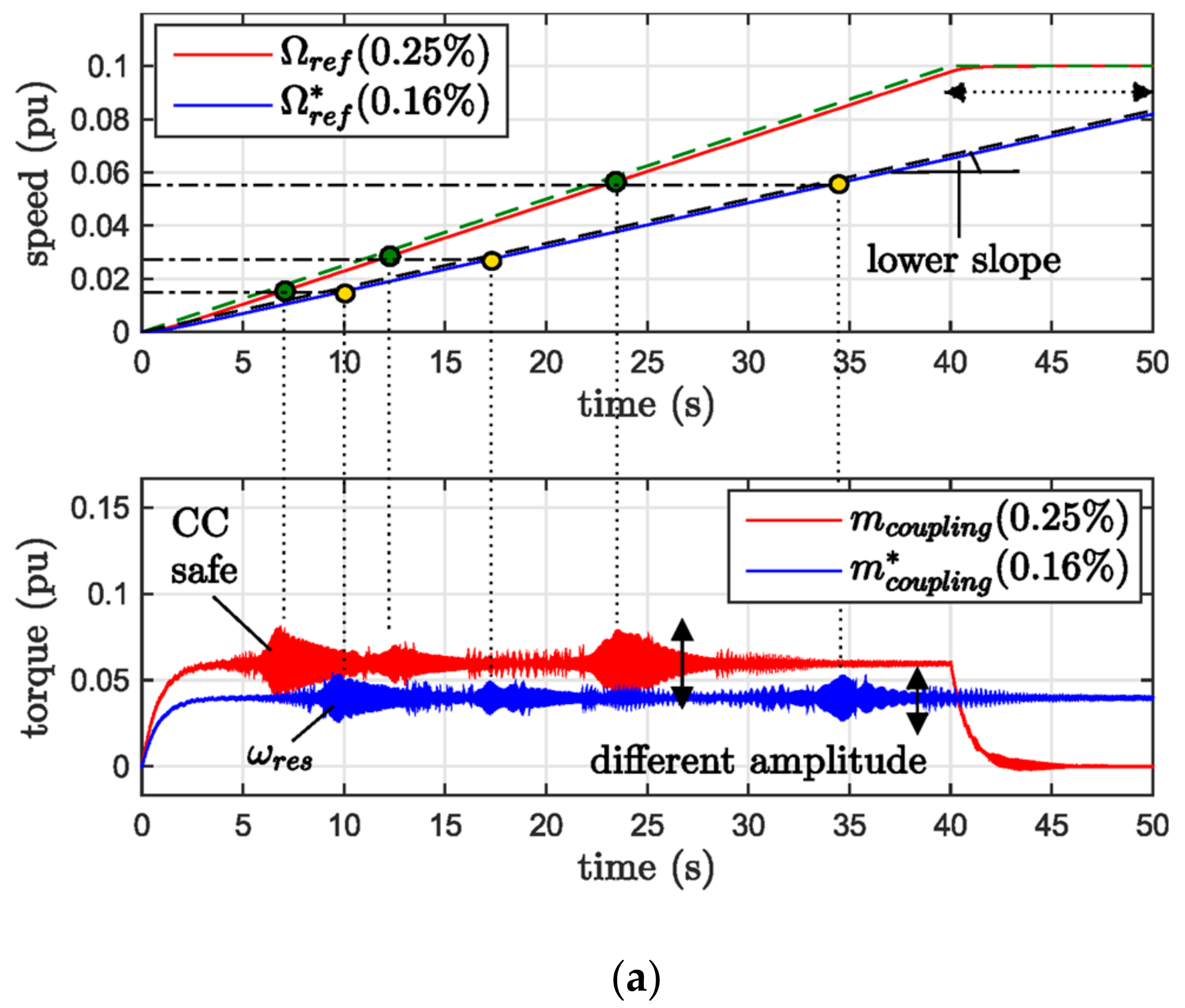



| Electric Data | |
|---|---|
| Voltage vrat (kV) | 6 |
| Current irat (A) | 931 |
| Frequency fline (Hz) | 50 |
| Speed Ωrat (rpm) | 1492.45 |
| Pole pairs npp | 2 |
| Mechanical Data | |
| IM inertia Jmot (Nms2/rad) | 510 |
| Load inertia Jload (Nms2/rad) | 226.3 |
| Stiffness Kel (Nm/rad) | 1.347 × 107 |
| Damping Cel (Nm s/rad) | 100 |
| Static friction fs (Nm) | 0.95 |
| Dynamic friction fv (Nms2/rad2) | 10−4 |
| Crack limit ad mrat (%) | 10 |
| Supply Frequency fline (Hz) | 50 | 50 | 50 |
| Resonance first TNF (Hz) | 17 | 17 | 17 |
| Resonance ωres (rad/s) | 106.76 | 106.76 | 106.76 |
| Integer (m, ±k) | (0, +6) | (0, +12) | (0, +18) |
| Harmonics nk | 6th | 12th | 18th |
| Critical Speeds Ω(i)crit (pu) | (3) 0.056 | (2) 0.028 | (1) 0.019 |
| p1,2 | Pulsation ω1 (Rad/s) | 10.5 |
| Damping ζ1 | 0.55 | |
| Gain kp (pu) | 10 | |
| Gain ki (pu) | 6.5 | |
| p3,4 | Pulsation ω2 (rad/s) | 112.05 |
| Damping ζ2 | 0.34 |
| Simulation | Critical Speeds Ω(1)crit | Mm ≅ 4% |
| Ramp command (0.1 → 0.2) | Mm ≅ 2% | |
| Step command | Mm ≅ 3.5% | |
| HIL | Critical speeds Ω(1)crit | Mm ≅ 4.5% |
| Ramp command (0.1 → 0.2) | Mm ≅ 2.2% | |
| Step command | Mm ≅ 3.5% | |
| Noise level % | ≅1.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi, M.; Carmeli, M.S.; Mauri, M. Adjustable Speed Control and Damping Analysis of Torsional Vibrations in VSD Compressor Systems. Machines 2021, 9, 374. https://doi.org/10.3390/machines9120374
Rossi M, Carmeli MS, Mauri M. Adjustable Speed Control and Damping Analysis of Torsional Vibrations in VSD Compressor Systems. Machines. 2021; 9(12):374. https://doi.org/10.3390/machines9120374
Chicago/Turabian StyleRossi, Mattia, Maria Stefania Carmeli, and Marco Mauri. 2021. "Adjustable Speed Control and Damping Analysis of Torsional Vibrations in VSD Compressor Systems" Machines 9, no. 12: 374. https://doi.org/10.3390/machines9120374
APA StyleRossi, M., Carmeli, M. S., & Mauri, M. (2021). Adjustable Speed Control and Damping Analysis of Torsional Vibrations in VSD Compressor Systems. Machines, 9(12), 374. https://doi.org/10.3390/machines9120374








