Aeroelastic Response of Aircraft Wings to External Store Separation Using Flexible Multibody Dynamics
Abstract
:1. Introduction
2. Method
2.1. Multibody Dynamics
- nonlinear dynamics of rigid and elastic bodies;
- geometrically exact beam and shell elements;
- lumped and super elements;
- smart materials, electric and hydraulic networks and active control;
- essential fixed-wing and rotorcraft aerodynamics; and,
- links to external solvers for co-simulation of multiphysics problems, such as Computational Fluid Dynamics (CFD) and terradynamics.
2.2. Verification
3. Demonstration Model
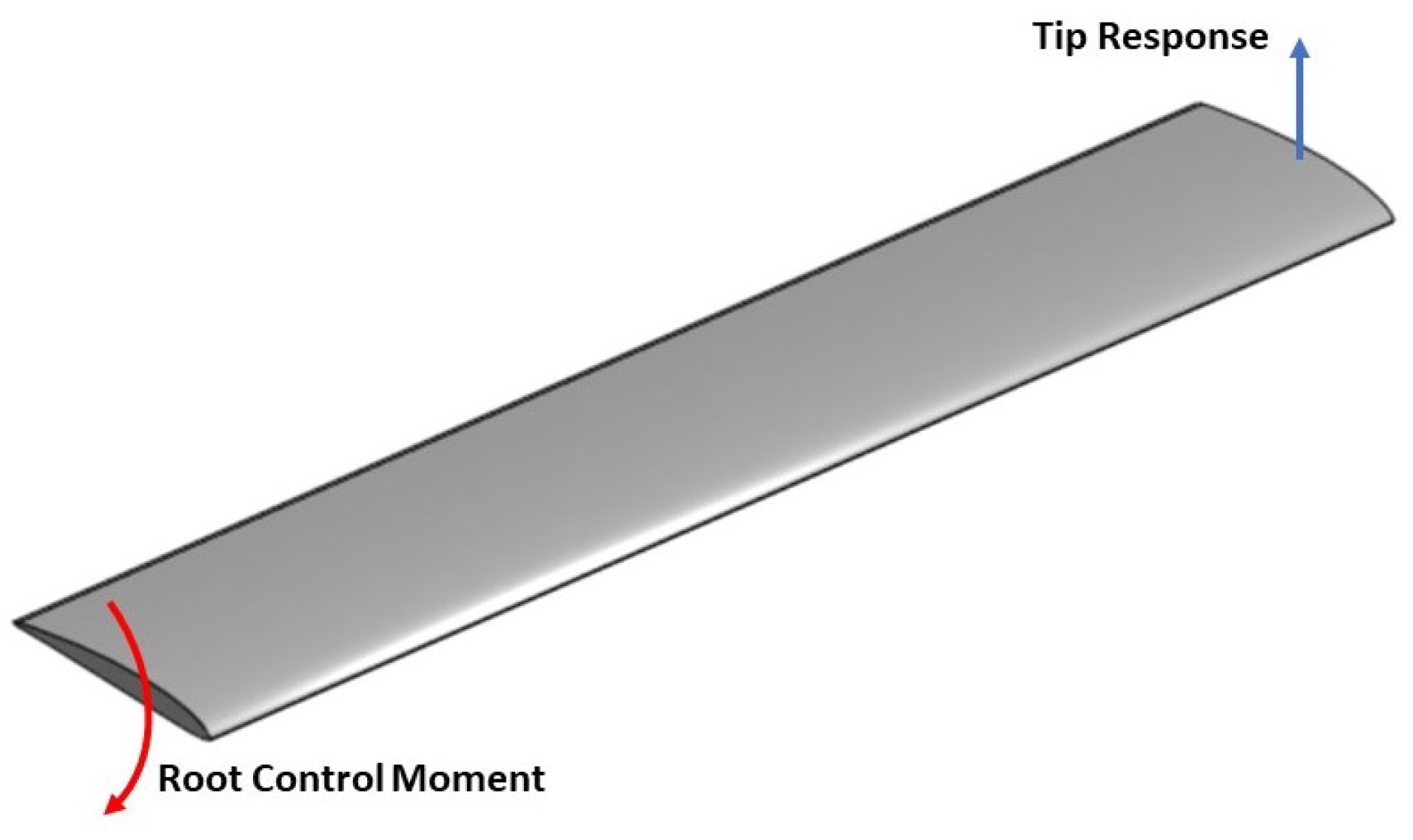
3.1. Aircraft
3.2. MBDyn Model Description
- Simulation parameters: time step, final time, solution tolerances, and iteration limits.
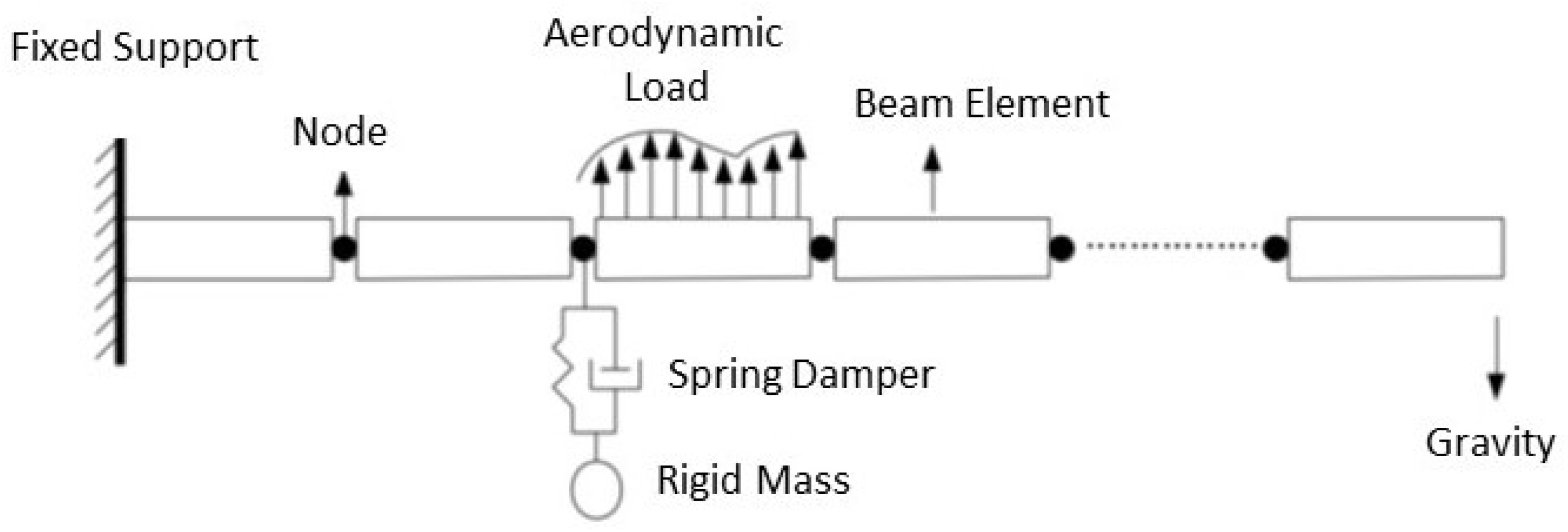
- Structural model: 16 three-node finite-volume beam elements [27] defined the 16 m span wing structure. The whole wing structure required 32 nodes for structural discretization, each was assigned inertial properties.
- Beam cross-section: properties were given as a diagonal (6 × 6) constitutive law matrix, which remains constant along the span.
- Aerodynamic model: the wing was discretized by aerodynamic elements formulated by lifting line theory. The aerodynamic elements included both steady and unsteady aerodynamics, therefore helping to achieve realistic static deflection and dynamic response.
- Boundary condition: ground joint was used to support the wing root.
- Store: a rigid body at m spanwise location was defined to represent the store, which was connected to the wing via spring and damper, as shown in Figure 5. The store has no aerodynamic model attached to it.
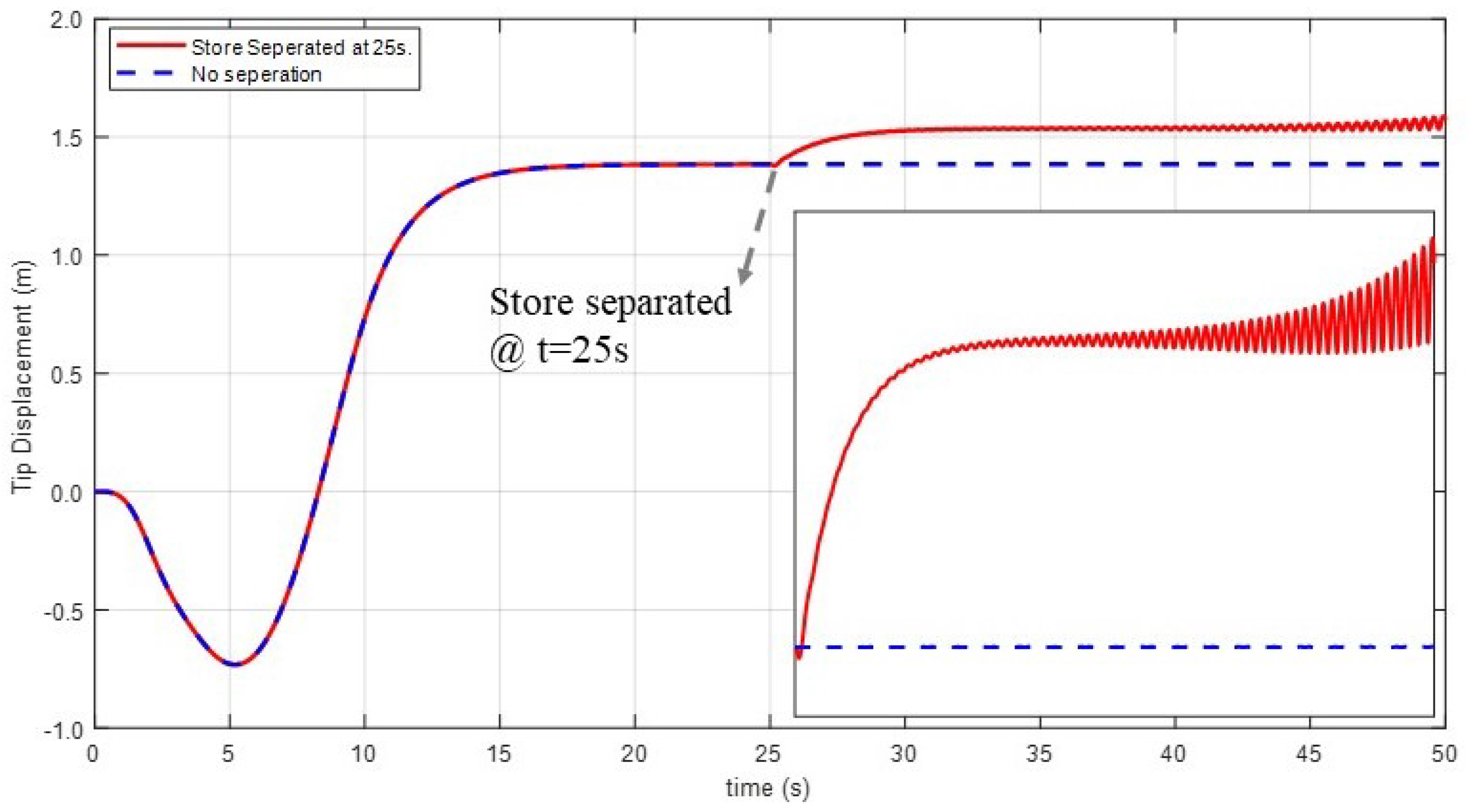
- Separation: the driven element was used to keep the store connected to the wing for t < 25 s. 25 s was defined based on the time required to achieve the steady-state solution of the same wing under the same flight conditions.
- Gravity: introduced to achieve realistic wing static response of a highly flexible wing and motion of the store after separation.
4. Results and Discussion
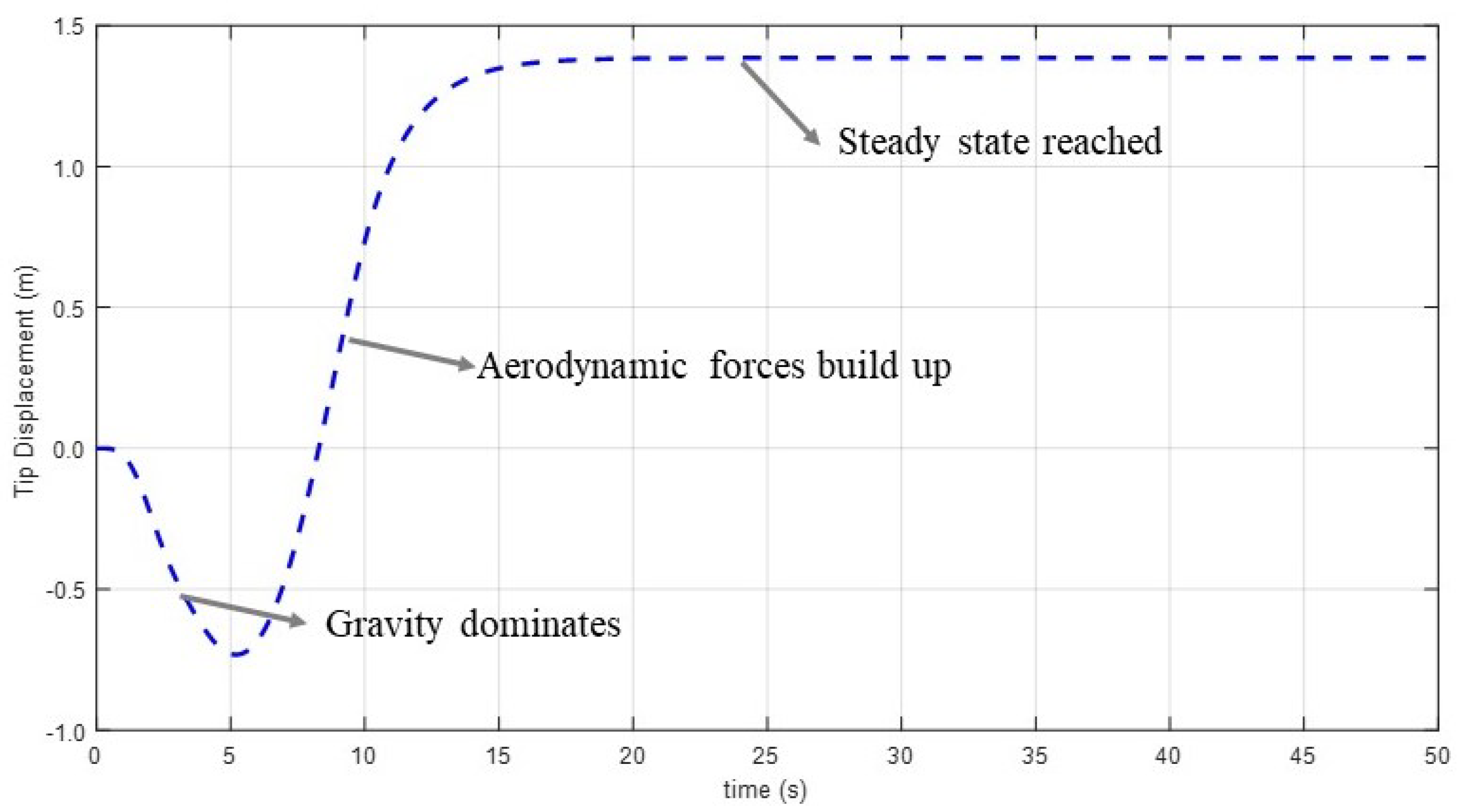
4.1. Simulation without Store Separation
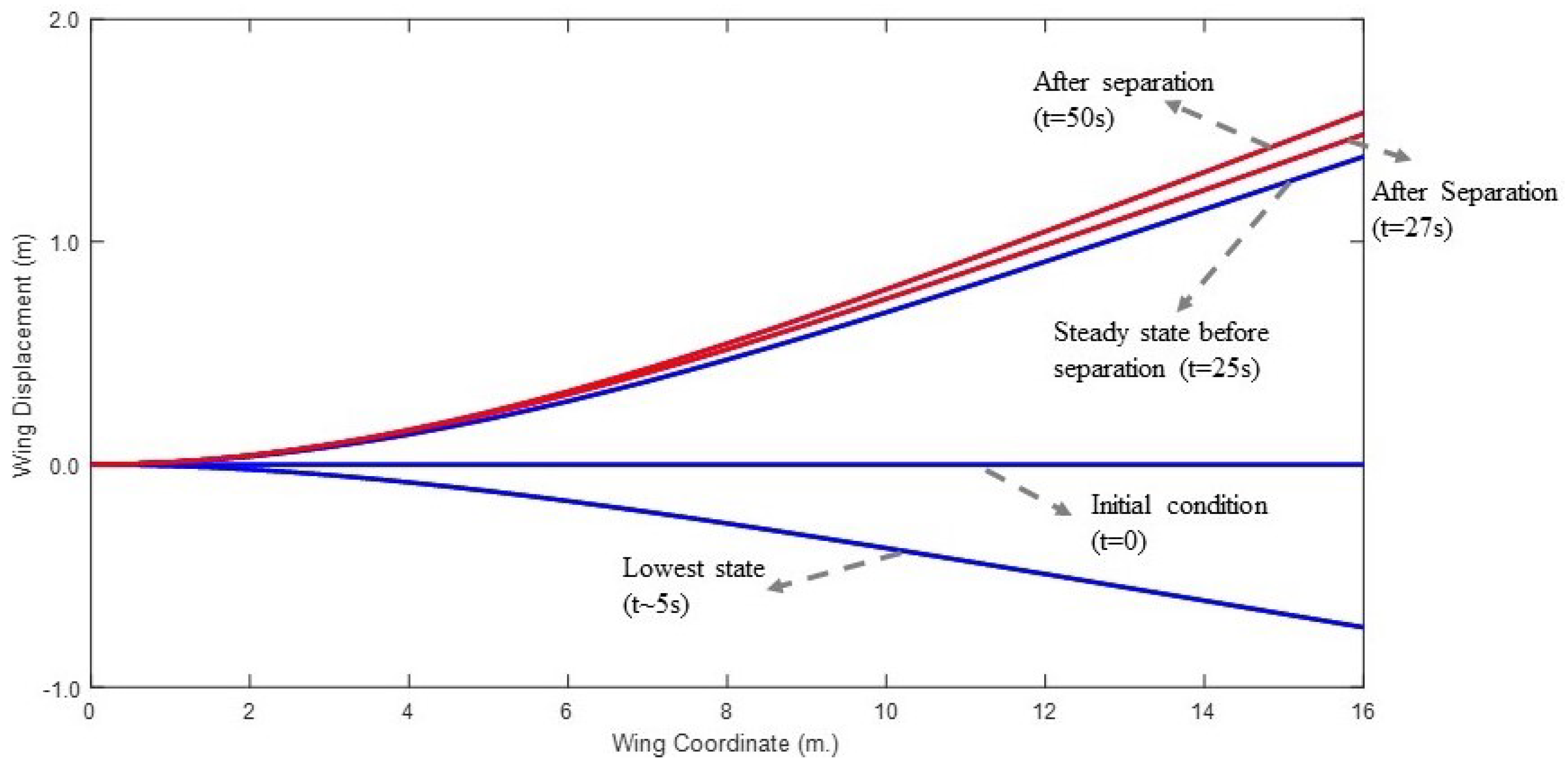
4.2. Wing Response to Store Separation
4.3. Stability Enhancement
4.3.1. Wing Stiffening
4.3.2. Vibration Control
5. Conclusions
- The wing response, which is stable before the response, could be unstable after the separation of the external store.
- A preliminary investigation on wing stiffness showed that a 6 percent increase in the wing structural mass is required to achieve a stable wing.
- As an alternative to the wing stiffening, the diverging wing response after the store separation could be stabilized using a controller. In this case, a moment with maximum 9 amplitude is required.
- The simulations can be repeated for a flying aircraft, including the rigid body motion, fuselage vibrational modes, and flight mechanics derivatives.
- The store can be given aerodynamic characteristics to include the effects of store aerodynamics on the wing stability.
- The store location, store mass, wing airfoil, and the wing structure can be optimized for a safe store separation, while ensuring that the payload carrying capacity of the aircraft is kept the same.
- A flight envelope for stable store separation could be achieved.
Funding
Acknowledgments
Conflicts of Interest
References
- Fredriksen, J.C. International Warbirds: An Illustrated Guide to World Military Aircraft (1914–2000); ABC-CLIO: Santa Barbara, CA, USA, 2001. [Google Scholar]
- Gupta, S.G.; Ghonge, M.M.; Jawandhiya, P.M. Review of Unmanned Aircraft System (UAS). Int. J. Adv. Res. Comput. Eng. Technol. (IJARCET) 2013, 2, 1648–1658. [Google Scholar] [CrossRef]
- Anonymous. Unmanned Aircraft Systems Roadmap 2010–2035; DoD, US Department of Defense: Fort Rucker, AL, USA, 2010. [Google Scholar]
- Valanis, K.; Vachtsevanos, G.J. (Eds.) Handbook of Unmanned Aerial Vehicles; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Lijewski, L.E.; Suhs, N.E. Time-accurate computational fluid dynamics approach to transonic store separation trajectory prediction. J. Aircr. 1994, 31, 886–891. [Google Scholar] [CrossRef]
- Lasek, M.; Sibilski, K.; Lasek, M. Modelling of External Store Separation. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Mizrahi, I.; Raveh, D.E. Wing Elasticity Effects on Store Separation. J. Aircr. 2019, 56, 1231–1249. [Google Scholar] [CrossRef]
- Hua, R.; Zhao, C.; Ye, Z.; Science, Y.J.A. Effect of Elastic Deformation on the Trajectory of Aerial Separation. Aerosp. Sci. Technol. 2015, 45, 128–139. [Google Scholar] [CrossRef]
- Kozak, M.T.; Yildiz, E.N.; Yazicioglu, Y.; Cigeroglu, E. Effects of Aircraft Aeroelastic Deformations on External Store Separation Dynamics. In Proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013. [Google Scholar] [CrossRef]
- Karpel, M.; Presente, E. Structural dynamic loads in response to impulsive excitation. J. Aircr. 1995, 32, 853–861. [Google Scholar] [CrossRef]
- Zhang, S.; Meganathan, A.; Jain, K.; Fuchiwaki, T. Effects of Store Separation on the Aeroelastic Behavior of Wings. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Kariv, D.; Raveh, D.E. Dynamic Response of an Elastic Aircraft to Ripple Store Ejection. J. Aircr. 2020, 57, 635–651. [Google Scholar] [CrossRef]
- Patil, M.J.; Hodges, D.H.; Cesnik, C.E.S. Limit-Cycle Oscillations in High-Aspect RAtio Wings. J. Fluids Struct. 1999, 15, 107–132. [Google Scholar] [CrossRef]
- Tamer, A.; Masarati, P. Aeroelastic Stability Estimation of Control Surfaces with Freeplay Nonlinearity. Aerotec. Missili Spaz. 2017, 96, 154–164. [Google Scholar] [CrossRef]
- Tamer, A.; Masarati, P. Stability of Nonlinear, Time-Dependent Rotorcraft Systems Using Lyapunov Characteristic Exponents. J. Am. Helicopter Soc. 2016, 61, 14–23. [Google Scholar] [CrossRef]
- Masarati, P.; Tamer, A. Sensitivity of trajectory stability estimated by Lyapunov characteristic exponents. Aerosp. Sci. Technol. 2015, 47, 501–510. [Google Scholar] [CrossRef] [Green Version]
- MBDyn: Multibody Dynamics. Available online: http://www.mbdyn.org/ (accessed on 13 March 2021).
- Masarati, P.; Morandini, M.; Mantegazza, P. An efficient formulation for general-purpose multibody/multiphysics analysis. J. Comput. Nonlinear Dyn. 2014, 9, 041001. [Google Scholar] [CrossRef]
- Cavagna, L.; Masarati, P.; Quaranta, G. Coupled Multibody/Computational Fluid Dynamics Simulation of Maneuvering Flexible Aircraft. J. Aircraft 2011, 48, 92–106. [Google Scholar] [CrossRef]
- Mattaboni, M.; Masarati, P.; Quaranta, G.; Mantegazza, P. Multibody Simulation of Integrated Tiltrotor Flight Mechanics, Aeroelasticity, and Control. J. Guid. Control. Dyn. 2012, 35, 1391–1405. [Google Scholar] [CrossRef]
- Cavagna, L.; Fumagalli, A.; Masarati, P.; Morandini, M.; Mantegazza, P. Real-Time Aeroservoelastic Analysis of Wind-Turbines by Free Multibody Software; Springer: Dordrecht, The Netherland, 2011; Volume 23, pp. 69–86. [Google Scholar] [CrossRef]
- Attolico, M.; Masarati, P.; Mantegazza, P. Trajectory Optimization and Real-Time Simulation for Robotics Applications. In Proceedings of the Multibody Dynamics 2005, ECCOMAS Thematic Conference, Madrid, Spain, 21–24 June 2005. [Google Scholar]
- Gundling, C.; Sitaraman, J.; Roget, B.; Masarati, P. Application and validation of incrementally complex models for wind turbine aerodynamics, isolated wind turbine in uniform inflow conditions. Wind Energy 2015, 18, 1893–1916. [Google Scholar] [CrossRef]
- Morandini, M.; Masarati, P. Implementation and Validation of a 4-Node Shell Finite Element. In Proceedings of the ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar]
- Bauchau, O.A.; Wu, G.; Betsch, P.; Cardona, A.; Gerstmayr, J.; Jonker, B.; Masarati, P.; Sonneville, V. Validation of Flexible Multibody Dynamics Beam Formulations using Benchmark Problems. In Proceedings of the 3rd Joint International Conference on Multibody System Dynamics–IMSD, Busan, Korea, 30 June–3 July 2014. [Google Scholar]
- Ripepi, M.; Masarati, P. Reduced Order Models Using Generalized Eigenanalysis. Proc. Inst. Mech. Eng. Part K 2011, 225, 1–14. [Google Scholar] [CrossRef]
- Ghiringhelli, G.L.; Masarati , P.; Mantegazza , P. A multi-body implementation of finite volume beams. AIAA J. 2000, 38, 131–138. [Google Scholar] [CrossRef]
- Prakash, S.; Renjith Kumar, T.; Raja, S.; Dwarakanathan, D.; Subramani, H.; Karthikeyan, C. Active vibration control of a full scale aircraft wing using a reconfigurable controller. J. Sound Vib. 2016, 361, 32–49. [Google Scholar] [CrossRef]
- Astrom, K.J.; Wittenmark, B. Computer-Controlled Systems; Dover: Mineola, NY, USA, 2011. [Google Scholar]

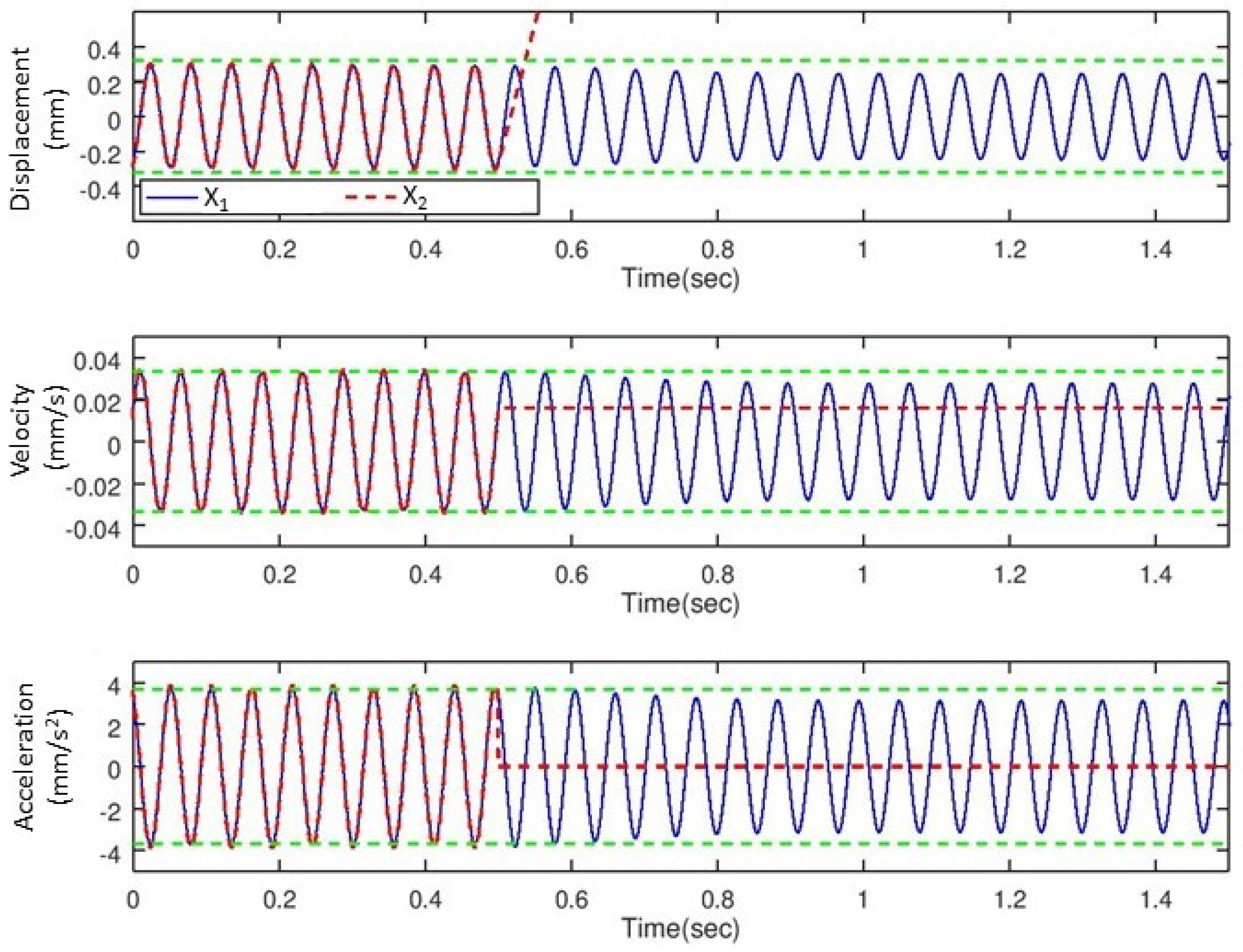





| Parameter | Value |
|---|---|
| Mass () | 7000, 500 (kg) |
| Stiffness () | (N/m) |
| Damping () | (kg × rad/s) |
| Force on main body | 3750 (N) at 20 Hz. |
| Time of store separation | 0.5 s |
| Displacement Amplitude before Separation | Displacement Amplitude after Separation | |
|---|---|---|
| MBDyn Simulation | 0.29 mm | 0.24 mm |
| Analytical Solution | 0.29 mm | 0.24 mm |
| Parameter | Value |
|---|---|
| Time of store separation | 25 s |
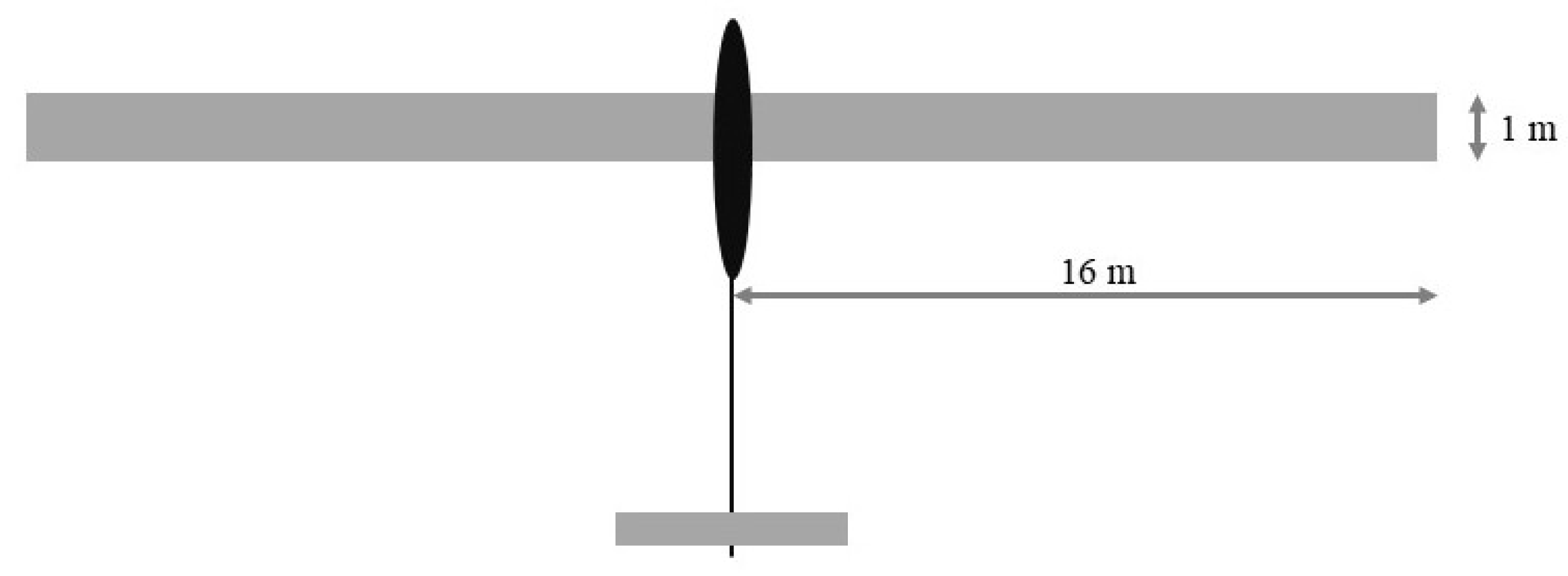
| Half-span | 16 m |
| Chord | 1 m |
| Mass per unit length | 0.75 kg/m |
| Moment of inertia (%50 chord) | 0.1 kgm |
| Span-wise elastic axis | %50 chord |
| Center of gravity | %50 chord |
| Bending rigidity | Nm |
| Torsional rigidity | Nm |
| Bending rigidity (Chordwise) | Nm |
| Altitude | 20 km |
| Density of air | 0.0889 kg/m |
| Parameter | Value |
|---|---|
| Mass of Store | 10 kg |
| Store Support Stiffness | |
| Store location with respect to the wing root | 7 |
| Parameter | Value |
|---|---|
| Altitude | 20 |
| Air Density | 0.089 |
| Flight Speed | 40 kn |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamer, A. Aeroelastic Response of Aircraft Wings to External Store Separation Using Flexible Multibody Dynamics. Machines 2021, 9, 61. https://doi.org/10.3390/machines9030061
Tamer A. Aeroelastic Response of Aircraft Wings to External Store Separation Using Flexible Multibody Dynamics. Machines. 2021; 9(3):61. https://doi.org/10.3390/machines9030061
Chicago/Turabian StyleTamer, Aykut. 2021. "Aeroelastic Response of Aircraft Wings to External Store Separation Using Flexible Multibody Dynamics" Machines 9, no. 3: 61. https://doi.org/10.3390/machines9030061
APA StyleTamer, A. (2021). Aeroelastic Response of Aircraft Wings to External Store Separation Using Flexible Multibody Dynamics. Machines, 9(3), 61. https://doi.org/10.3390/machines9030061






