Possible Ribose Synthesis in Carbonaceous Planetesimals
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory
2.1.1. Formose Reaction Pathway
2.1.2. Initial Concentrations of Reactants
2.2. Computations
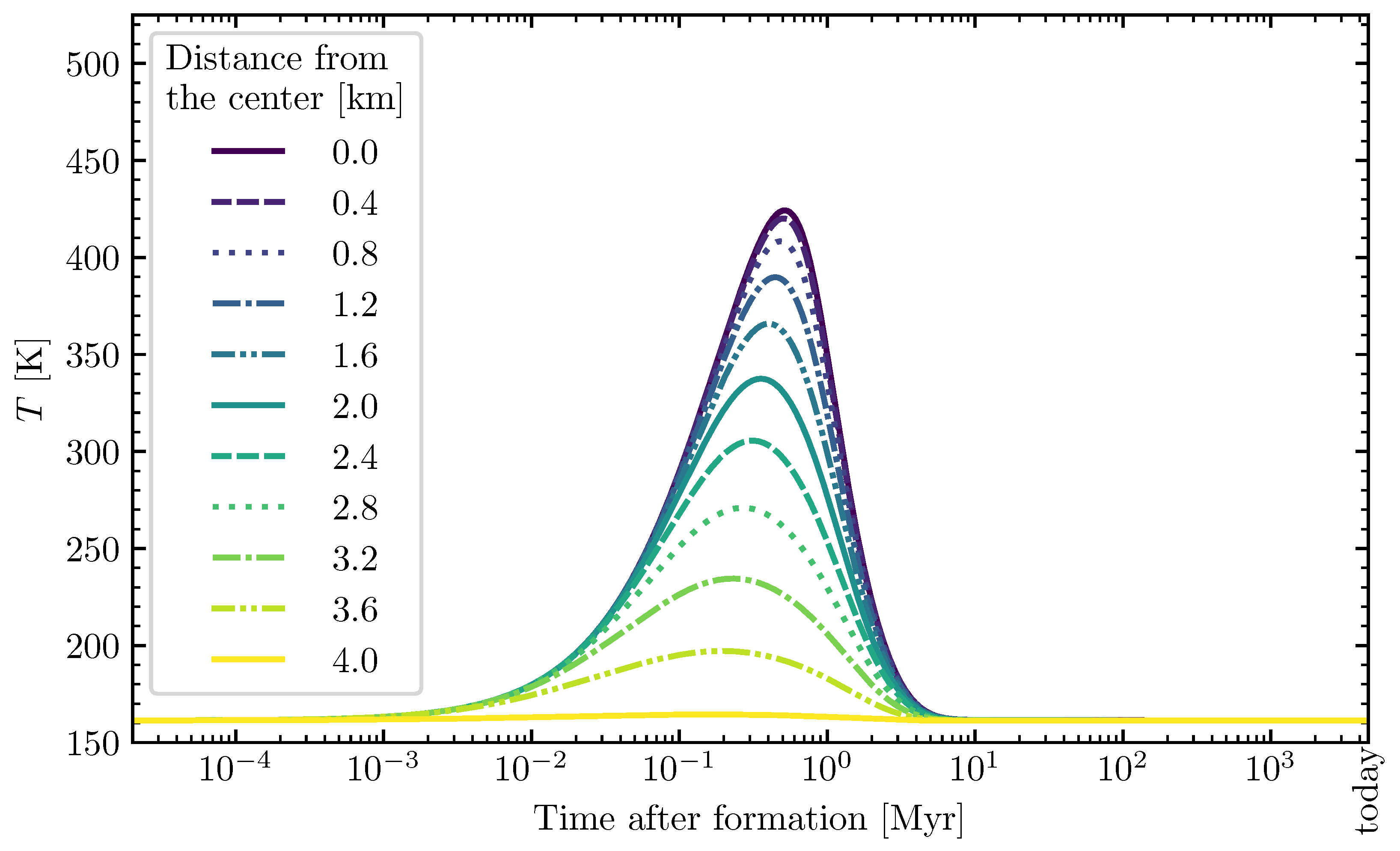
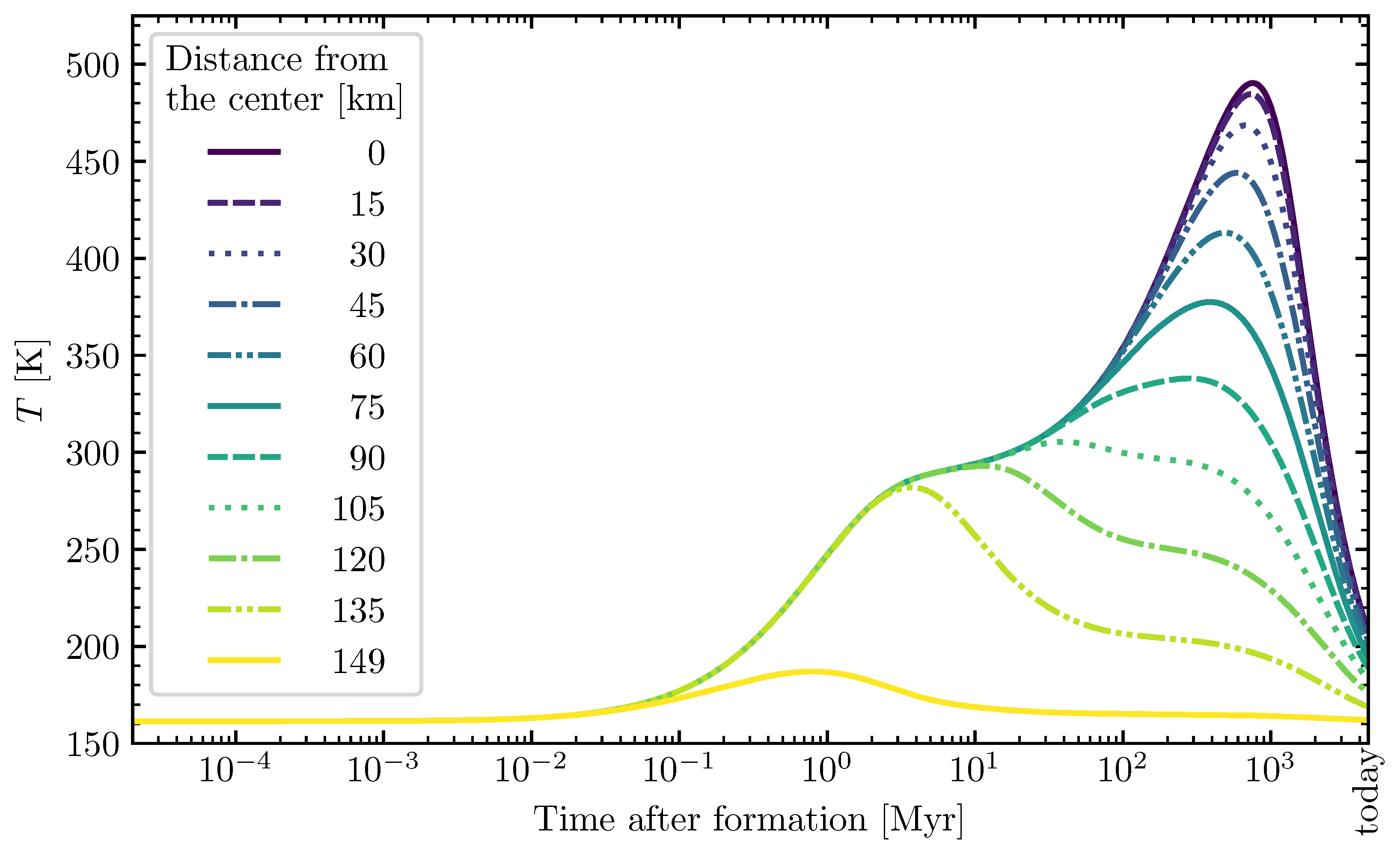
2.2.1. Planetesimal Model
2.2.2. Gibbs Free Energies of Formation of Glycolaldehyde
2.3. Laboratory Experiments
3. Results
3.1. Experimentally Found Yields of Ribose in All 5Cs
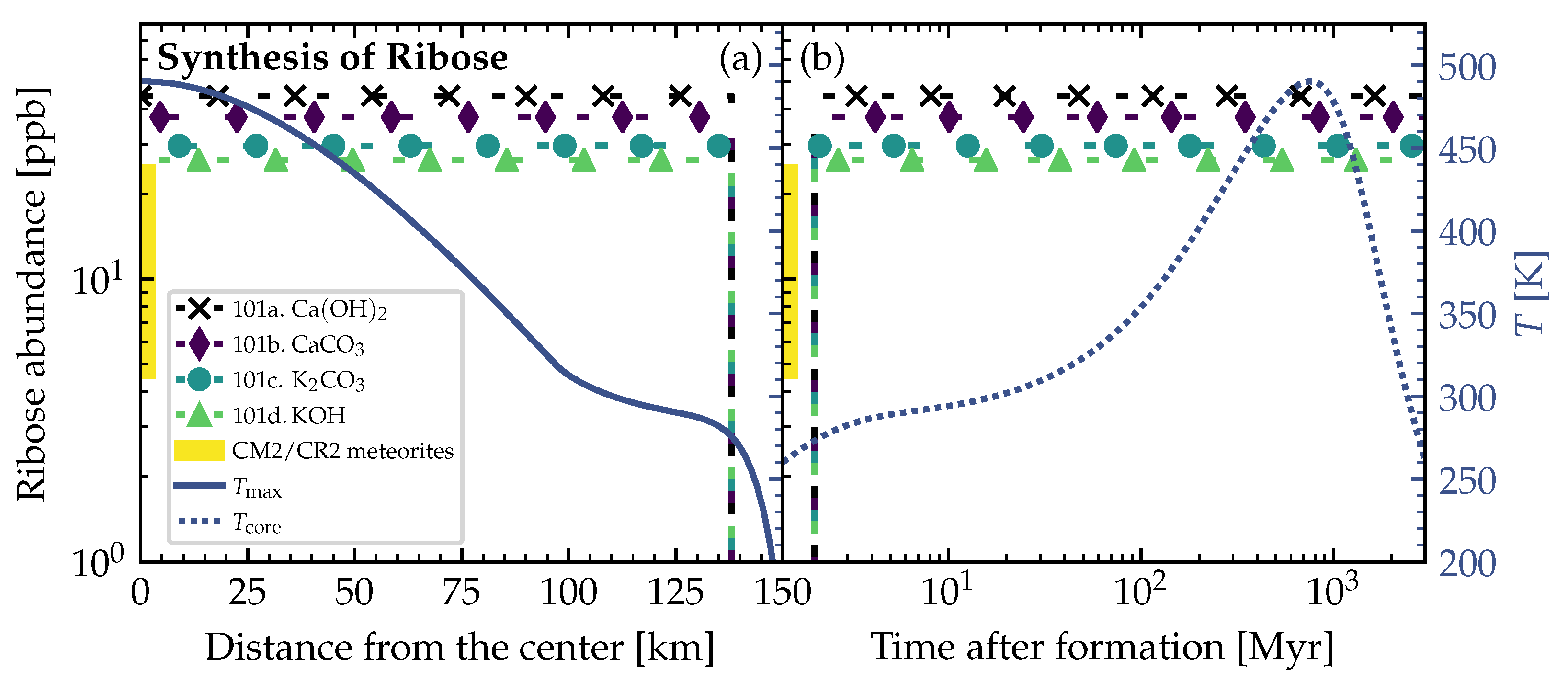
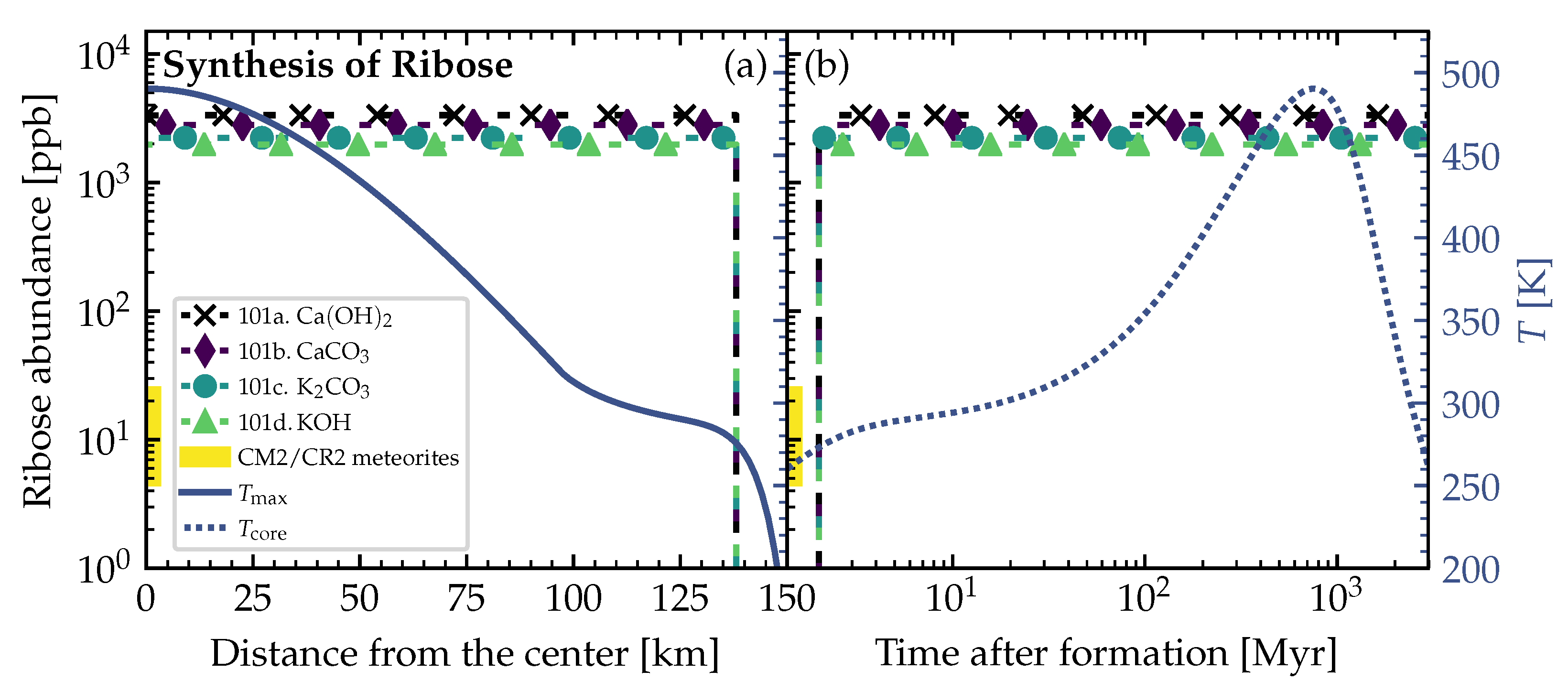
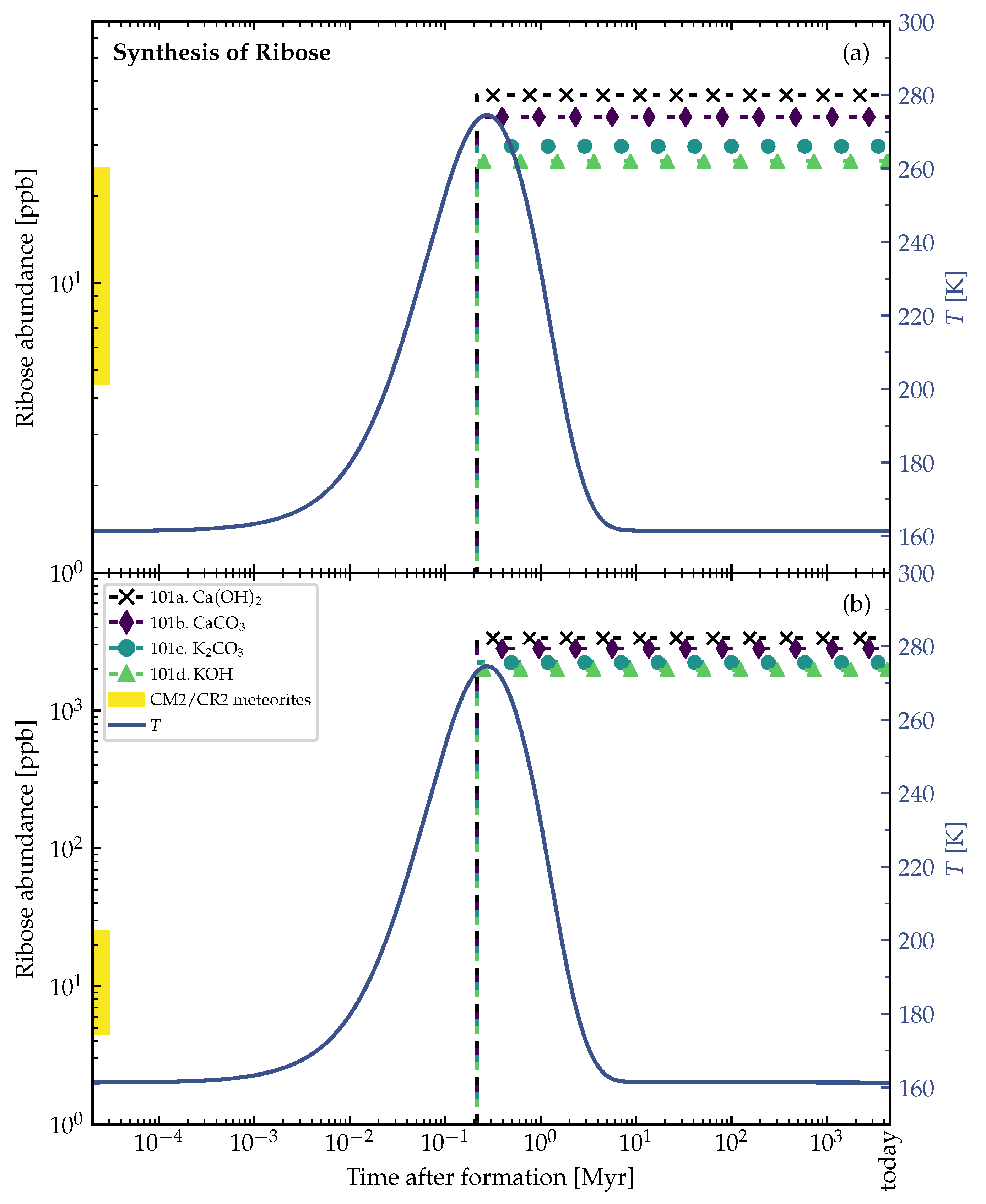
3.2. Theoretically Calculated Ribose Abundances in Planetesimals
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RNA | Ribonucleic acid |
| DNA | Deoxyribonucleic acid |
| 5C | Pentose |
| WLP | Warm little pond/Darwinian pond |
| ppb | Parts per billion |
| ppm | Parts per million |
| CAI | Calcium-aluminium-rich inclusions |
| yr | Year(s) |
| GC-MS | gas chromatography coupled with a mass spectrometer |
| CM2 | Mighei-type chondrites (CM), a group of meteorites, in this case of petrologic type 2 |
| CR2 | Renazzo-type chondrites (CR), a group of meteorites, in this case of petrologic type 2 |
References
- Furukawa, Y.; Chikaraishi, Y.; Ohkouchi, N.; Ogawa, N.O.; Glavin, D.P.; Dworkin, J.P.; Abe, C.; Nakamura, T. Extraterrestrial ribose and other sugars in primitive meteorites. Proc. Natl. Acad. Sci. USA 2019, 116, 24440–24445. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chyba, C.F.; Thomas, P.J.; Brookshaw, L.; Sagan, C. Cometary delivery of organic molecules to the early earth. Science 1990, 249, 366–373. [Google Scholar] [CrossRef] [PubMed]
- Chyba, C.; Sagan, C. Endogenous production, exogenous delivery and impact-shock synthesis of organic molecules: An inventory for the origins of life. Nature 1992, 355, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Gomes, R.; Levison, H.F.; Tsiganis, K.; Morbidelli, A. Origin of the cataclysmic Late Heavy Bombardment period of the terrestrial planets. Nature 2005, 435, 466–469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van Kooten, E.; Schiller, M.; Moynier, F.; Johansen, A.; Haugbølle, T.; Bizzarro, M. Hybrid Accretion of Carbonaceous Chondrites by Radial Transport across the Jupiter Barrier. Astrophys. J. 2021, 910, 70. [Google Scholar] [CrossRef]
- Fischer-Gödde, M.; Elfers, B.M.; Münker, C.; Szilas, K.; Maier, W.D.; Messling, N.; Morishita, T.; Van Kranendonk, M.; Smithies, H. Ruthenium isotope vestige of Earth’s pre-late-veneer mantle preserved in Archaean rocks. Nature 2020, 579, 240–244. [Google Scholar] [CrossRef]
- Pizzarello, S.; Shock, E. Carbonaceous Chondrite Meteorites: The Chronicle of a Potential Evolutionary Path between Stars and Life. Orig. Life Evol. Biosph. 2017, 47, 249–260. [Google Scholar] [CrossRef]
- Rich, A. On the problems of evolution and biochemical information transfer. In Horizons in Biochemistry; Kasha, M., Pullman, B., Eds.; Academic Press: New York, NY, USA, 1962; pp. 103–126. [Google Scholar]
- Gilbert, W. Origin of life: The RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
- Kruger, K.; Grabowski, P.J.; Zaug, A.J.; Sands, J.; Gottschling, D.E.; Cech, T.R. Self-splicing RNA: Autoexcision and autocyclization of the ribosomal RNA intervening sequence of tetrahymena. Cell 1982, 31, 147–157. [Google Scholar] [CrossRef]
- Guerrier-Takada, C.; Gardiner, K.; Marsh, T.; Pace, N.; Altman, S. The RNA moiety of ribonuclease P is the catalytic subunit of the enzyme. Cell 1983, 35, 849–857. [Google Scholar] [CrossRef]
- Guerrier-Takada, C.; Altman, S. Catalytic activity of an RNA molecule prepared by transcription in vitro. Science 1984, 223, 285–286. [Google Scholar] [CrossRef] [PubMed]
- Zaug, A.J.; Cech, T.R. The intervening sequence RNA of tetrahymena is an enzyme. Science 1986, 231, 470–475. [Google Scholar] [CrossRef] [PubMed]
- Cech, T.R. A model for the RNA-catalyzed replication of RNA. Proc. Natl. Acad. Sci. USA 1986, 83, 4360–4363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnston, W.K.; Unrau, P.J.; Lawrence, M.S.; Glasner, M.E.; Bartel, D.P. RNA-Catalyzed RNA Polymerization: Accurate and General RNA-Templated Primer Extension. Science 2001, 292, 1319–1325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vaidya, N.; Manapat, M.L.; Chen, I.A.; Xulvi-Brunet, R.; Hayden, E.J.; Lehman, N. Spontaneous network formation among cooperative RNA replicators. Nature 2012, 491, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Ferris, J.P.; Hill, A.R.; Liu, R.; Orgel, L.E. Synthesis of long prebiotic oligomers on mineral surfaces. Nature 1996, 381, 59–61. [Google Scholar] [CrossRef] [PubMed]
- Ferris, J.P.; Joshi, P.C.; Wang, K.J.; Miyakawa, S.; Huang, W. Catalysis in prebiotic chemistry: Application to the synthesis of RNA oligomers. Adv. Space Res. 2004, 33, 100–105. [Google Scholar] [CrossRef]
- Da Silva, L.; Maurel, M.C.; Deamer, D. Salt-Promoted Synthesis of RNA-like Molecules in Simulated Hydrothermal Conditions. J. Mol. Evol. 2015, 80, 86–97. [Google Scholar] [CrossRef]
- Orgel, L.E. Prebiotic Chemistry and the Origin of the RNA World. Crit. Rev. Biochem. Mol. Biol. 2004, 39, 99–123. [Google Scholar] [CrossRef] [Green Version]
- Toppozini, L.; Dies, H.; Deamer, D.W.; Rheinstädter, M.C. Adenosine Monophosphate Forms Ordered Arrays in Multilamellar Lipid Matrices: Insights into Assembly of Nucleic Acid for Primitive Life. PLoS ONE 2013, 8, e62810. [Google Scholar] [CrossRef] [Green Version]
- Damer, B.; Deamer, D. The Hot Spring Hypothesis for an Origin of Life. Astrobiology 2020, 20, 429–452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becker, S.; Schneider, C.; Okamura, H.; Crisp, A.; Amatov, T.; Dejmek, M.; Carell, T. Wet-dry cycles enable the parallel origin of canonical and non-canonical nucleosides by continuous synthesis. Nat. Commun. 2018, 9, 163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becker, S.; Feldmann, J.; Wiedemann, S.; Okamura, H.; Schneider, C.; Iwan, K.; Crisp, A.; Rossa, M.; Amatov, T.; Carell, T. Unified prebiotically plausible synthesis of pyrimidine and purine RNA ribonucleotides. Science 2019, 366, 76–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuller, W.D.; Sanchez, R.A.; Orgel, L.E. Studies in prebiotic synthesis: VI. Synthesis of purine nucleosides. J. Mol. Biol. 1972, 67, 25–33. [Google Scholar] [CrossRef]
- Fuller, W.D.; Sanchez, R.A.; Orgel, L.E. Studies in prebiotic synthesis. VII: Solid-State Synthesis of Purine Nucleosides. J. Mol. Evol. 1972, 1, 249–257. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Benner, S.A. Prebiotic stereoselective synthesis of purine and noncanonical pyrimidine nucleotide from nucleobases and phosphorylated carbohydrates. Proc. Natl. Acad. Sci. USA 2017, 114, 11315–11320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, H.J.; Benner, S.A. A Direct Prebiotic Synthesis of Nicotinamide Nucleotide. Chem.—Eur. J. 2018, 24, 581–584. [Google Scholar] [CrossRef]
- Nam, I.; Nam, H.G.; Zare, R.N. Abiotic synthesis of purine and pyrimidine ribonucleosides in aqueous microdroplets. Proc. Natl. Acad. Sci. USA 2018, 115, 36–40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pearce, B.K.D.; Pudritz, R.E.; Semenov, D.A.; Henning, T.K. Origin of the RNA world: The fate of nucleobases in warm little ponds. Proc. Natl. Acad. Sci. USA 2017, 114, 11327–11332. [Google Scholar] [CrossRef] [Green Version]
- Paschek, K.; Semenov, D.A.; Pearce, B.K.D.; Lange, K.; Henning, T.K.; Pudritz, R.E. Meteorites and the RNA world II: Synthesis of Nucleobases in Carbonaceous Planetesimals and the Role of Initial Volatile Content. arXiv 2021, arXiv:2112.09160. [Google Scholar] [CrossRef]
- Butlerow, A. Bildung einer zuckerartigen Substanz durch Synthese. Justus Liebigs Ann. Der Chem. 1861, 120, 295–298. [Google Scholar] [CrossRef] [Green Version]
- Breslow, R. On the mechanism of the formose reaction. Tetrahedron Lett. 1959, 1, 22–26. [Google Scholar] [CrossRef]
- Cannizzaro, S. Ueber den der Benzoësäure entsprechenden Alkohol. Justus Liebigs Ann. Der Chem. 1853, 88, 129–130. [Google Scholar] [CrossRef] [Green Version]
- Socha, R.F.; Weiss, A.H.; Sakharov, M.M. Autocatalysis in the formose reaction. React. Kinet. Catal. Lett. 1980, 14, 119–128. [Google Scholar] [CrossRef]
- Fedoseev, G.; Cuppen, H.M.; Ioppolo, S.; Lamberts, T.; Linnartz, H. Experimental evidence for glycolaldehyde and ethylene glycol formation by surface hydrogenation of CO molecules under dense molecular cloud conditions. Mon. Not. R. Astron. Soc. 2015, 448, 1288–1297. [Google Scholar] [CrossRef]
- Eckhardt, A.K.; Linden, M.M.; Wende, R.C.; Bernhardt, B.; Schreiner, P.R. Gas-phase sugar formation using hydroxymethylene as the reactive formaldehyde isomer. Nat. Chem. 2018, 10, 1141–1147. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, Z.; Novalin, S. The Formose Reaction: A Tool to Produce Synthetic Carbohydrates Within a Regenerative Life Support System. Curr. Org. Chem. 2012, 16, 769–788. [Google Scholar] [CrossRef] [Green Version]
- Barber, D.J. Matrix phyllosilicates and associated minerals in C2M carbonaceous chondrites. Geochim. Cosmochim. Acta 1981, 45, 945–970. [Google Scholar] [CrossRef]
- Pearce, B.K.D.; Pudritz, R.E. Seeding The Pregenetic Earth: Meteoritc Abundance of Nucleobases and Potential Reaction Pathways. Astrophys. J. 2015, 807, 85. [Google Scholar] [CrossRef] [Green Version]
- Pearce, B.K.D.; Pudritz, R.E. Meteorites and the RNA World: A Thermodynamic Model of Nucleobase Synthesis within Planetesimals. Astrobiology 2016, 16, 853–872. [Google Scholar] [CrossRef] [Green Version]
- Weber, A.L.; Pizzarello, S. The peptide-catalyzed stereospecific synthesis of tetroses: A possible model for prebiotic molecular evolution. Proc. Natl. Acad. Sci. USA 2006, 103, 12713–12717. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeilani, Y.A.; Nguyen, M.T. Autocatalysis in Formose Reaction and Formation of RNA Nucleosides. J. Phys. Chem. B 2020, 124, 11324–11336. [Google Scholar] [CrossRef] [PubMed]
- Teichert, J.S.; Kruse, F.M.; Trapp, O. Direct Prebiotic Pathway to DNA Nucleosides. Angew. Chem. Int. Ed. 2019, 58, 9944–9947. [Google Scholar] [CrossRef] [PubMed]
- Kruse, F.M.; Teichert, J.S.; Trapp, O. Prebiotic Nucleoside Synthesis: The Selectivity of Simplicity. Chem.—Eur. J. 2020, 26, 14776–14790. [Google Scholar] [CrossRef] [PubMed]
- Saladino, R.; Carota, E.; Botta, G.; Kapralov, M.; Timoshenko, G.N.; Rozanov, A.Y.; Krasavin, E.; Di Mauro, E. Meteorite-catalyzed syntheses of nucleosides and of other prebiotic compounds from formamide under proton irradiation. Proc. Natl. Acad. Sci. USA 2015, 112, E2746–E2755. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Šponer, J.E.; Šponer, J.; Nováková, O.; Brabec, V.; Šedo, O.; Zdráhal, Z.; Costanzo, G.; Pino, S.; Saladino, R.; Di Mauro, E. Emergence of the First Catalytic Oligonucleotides in a Formamide-Based Origin Scenario. Chem.—Eur. J. 2016, 22, 3572–3586. [Google Scholar] [CrossRef] [PubMed]
- Eschenmoser, A. On a Hypothetical Generational Relationship between HCN and Constituents of the Reductive Citric Acid Cycle. Chem. Biodivers. 2007, 4, 554–573. [Google Scholar] [CrossRef] [PubMed]
- Eschenmoser, A. The search for the chemistry of life’s origin. Tetrahedron 2007, 63, 12821–12844. [Google Scholar] [CrossRef]
- Banfalvi, G. Prebiotic Pathway from Ribose to RNA Formation. Int. J. Mol. Sci. 2021, 22, 3857. [Google Scholar] [CrossRef] [PubMed]
- Mumma, M.J.; Charnley, S.B. The Chemical Composition of Comets—Emerging Taxonomies and Natal Heritage. Annu. Rev. Astron. Astrophys. 2011, 49, 471–524. [Google Scholar] [CrossRef]
- Cobb, A.K.; Pudritz, R.E.; Pearce, B.K. Nature’s Starships. II. Simulating the Synthesis of Amino Acids in Meteorite Parent Bodies. Astrophys. J. 2015, 809, 6. [Google Scholar] [CrossRef] [Green Version]
- Burbine, T.H.; Mccoy, T.J.; Meibom, A.; Gladman, B.; Keil, K. Meteoritic Parent Bodies: Their Number and Identification. In Asteroids III; Bottke, W.F., Jr., Cellino, A., Paolicchi, P., Binzel, R.P., Eds.; University of Arizona Press: Tucson, AZ, USA, 2002; pp. 653–667. [Google Scholar]
- Wai, C.M.; Wasson, J.T. Nebular condensation of moderately volatile elements and their abundances in ordinary chondrites. Earth Planet. Sci. Lett. 1977, 36, 1–13. [Google Scholar] [CrossRef]
- Alexander, C.M.O.; Boss, A.P.; Carlson, R.W. The Early Evolution of the Inner Solar System: A Meteoritic Perspective. Science 2001, 293, 64–69. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cassen, P. Nebular thermal evolution and the properties of primitive planetary materials. Meteorit. Planet. Sci. 2001, 36, 671–700. [Google Scholar] [CrossRef]
- Lodders, K. Solar System Abundances and Condensation Temperatures of the Elements. Astrophys. J. 2003, 591, 1220–1247. [Google Scholar] [CrossRef]
- Bland, P.A.; Alard, O.; Benedix, G.K.; Kearsley, A.T.; Menzies, O.N.; Watt, L.E.; Rogers, N.W. Volatile fractionation in the early solar system and chondrule/matrix complementarity. Proc. Natl. Acad. Sci. USA 2005, 102, 13755–13760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Braukmüller, N.; Wombacher, F.; Hezel, D.C.; Escoube, R.; Münker, C. The chemical composition of carbonaceous chondrites: Implications for volatile element depletion, complementarity and alteration. Geochim. Cosmochim. Acta 2018, 239, 17–48. [Google Scholar] [CrossRef]
- Vollstaedt, H.; Mezger, K.; Alibert, Y. Carbonaceous Chondrites and the Condensation of Elements from the Solar Nebula. Astrophys. J. 2020, 897, 82. [Google Scholar] [CrossRef]
- Öberg, K.I.; Bergin, E.A. Astrochemistry and compositions of planetary systems. Phys. Rep. 2021, 893, 1–48. [Google Scholar] [CrossRef]
- Lichtenberg, T.; Krijt, S. System-level Fractionation of Carbon from Disk and Planetesimal Processing. Astrophys. J. Lett. 2021, 913, L20. [Google Scholar] [CrossRef]
- Cuppen, H.M.; Walsh, C.; Lamberts, T.; Semenov, D.; Garrod, R.T.; Penteado, E.M.; Ioppolo, S. Grain Surface Models and Data for Astrochemistry. Space Sci. Rev. 2017, 212, 1–58. [Google Scholar] [CrossRef] [Green Version]
- Ghesquière, P.; Mineva, T.; Talbi, D.; Theulé, P.; Noble, J.A.; Chiavassa, T. Diffusion of molecules in the bulk of a low density amorphous ice from molecular dynamics simulations. Phys. Chem. Chem. Phys. 2015, 17, 11455–11468. [Google Scholar] [CrossRef] [Green Version]
- Johansen, A.; Oishi, J.S.; Mac Low, M.M.; Klahr, H.; Henning, T.; Youdin, A. Rapid planetesimal formation in turbulent circumstellar disks. Nature 2007, 448, 1022–1025. [Google Scholar] [CrossRef] [Green Version]
- Ormel, C.W.; Klahr, H.H. The effect of gas drag on the growth of protoplanets—Analytical expressions for the accretion of small bodies in laminar disks. Astron. Astrophys. 2010, 520, A43. [Google Scholar] [CrossRef] [Green Version]
- Klahr, H.; Schreiber, A. Turbulence Sets the Length Scale for Planetesimal Formation: Local 2D Simulations of Streaming Instability and Planetesimal Formation. Astrophys. J. 2020, 901, 54. [Google Scholar] [CrossRef]
- Visser, R.; van Dishoeck, E.F.; Doty, S.D.; Dullemond, C.P. The chemical history of molecules in circumstellar disks. I. Ices. Astron. Astrophys. 2009, 495, 881–897. [Google Scholar] [CrossRef] [Green Version]
- Semenov, D.; Wiebe, D. Chemical Evolution of Turbulent Protoplanetary Disks and the Solar Nebula. Astrophys. J. Suppl. 2011, 196, 25. [Google Scholar] [CrossRef] [Green Version]
- Drozdovskaya, M.N.; Walsh, C.; van Dishoeck, E.F.; Furuya, K.; Marboeuf, U.; Thiabaud, A.; Harsono, D.; Visser, R. Cometary ices in forming protoplanetary disc midplanes. Mon. Not. R. Astron. Soc. 2016, 462, 977–993. [Google Scholar] [CrossRef]
- Bergner, J.B.; Ciesla, F. Ice Inheritance in Dynamical Disk Models. Astrophys. J. 2021, 919, 45. [Google Scholar] [CrossRef]
- Potapov, A.; McCoustra, M. Physics and chemistry on the surface of cosmic dust grains: A laboratory view. Int. Rev. Phys. Chem. 2021, 40, 299–364. [Google Scholar] [CrossRef]
- Noble, J.A.; Theule, P.; Mispelaer, F.; Duvernay, F.; Danger, G.; Congiu, E.; Dulieu, F.; Chiavassa, T. The desorption of H2CO from interstellar grains analogues. Astron. Astrophys. 2012, 543, A5. [Google Scholar] [CrossRef] [Green Version]
- Burkhardt, C.; Spitzer, F.; Morbidelli, A.; Budde, G.; Render, J.H.; Kruijer, T.S.; Kleine, T. Terrestrial planet formation from lost inner solar system material. Sci. Adv. 2021, 7, eabj7601. [Google Scholar] [CrossRef]
- Johansen, A.; Ronnet, T.; Bizzarro, M.; Schiller, M.; Lambrechts, M.; Nordlund, Å.; Lammer, H. A pebble accretion model for the formation of the terrestrial planets in the Solar System. Sci. Adv. 2021, 7, 444–461. [Google Scholar] [CrossRef] [PubMed]
- Burke, D.J.; Puletti, F.; Brown, W.A.; Woods, P.M.; Viti, S.; Slater, B. Glycolaldehyde, methyl formate and acetic acid adsorption and thermal desorption from interstellar ices. Mon. Not. R. Astron. Soc. 2014, 447, 1444–1451. [Google Scholar] [CrossRef] [Green Version]
- Petersen, S.; Hack, K. The thermochemistry library ChemApp and its applications. Int. J. Mater. Res. 2007, 98, 935–945. [Google Scholar] [CrossRef]
- Dick, J.M. CHNOSZ: Thermodynamic calculations and diagrams for geochemistry. Front. Earth Sci. 2019, 7, 180. [Google Scholar] [CrossRef] [Green Version]
- Free Software Foundation, Inc. GNU Compiler Collection. Available online: https://gcc.gnu.org/ (accessed on 17 November 2021).
- Jakob, W.; Rhinelander, J.; Moldovan, D. pybind11—Seamless operability between C++11 and Python. Available online: https://github.com/pybind/pybind11 (accessed on 17 November 2021).
- Gautier, L. rpy2. Available online: https://github.com/rpy2/rpy2 (accessed on 17 November 2021).
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Lange, K.; Dullemond, C.P.; Trieloff, M.; Blum, J. Institute for Theoretical Astrophysics, Center for Astronomy, Heidelberg University, Heidelberg, Germany. 2022; in preparation. [Google Scholar]
- Mason, B. The carbonaceous chondrites. Space Sci. Rev. 1963, 1, 621–646. [Google Scholar] [CrossRef]
- Paschek, K. prebiotic_synthesis_planetesimal (v1.0). Available online: https://github.com/klauspaschek/prebiotic_synthesis_planetesimal (accessed on 17 November 2021).
- Emberson, J. Amino Acid Synthesis in Meteoritic Parent Bodies. Bachelor’s Thesis, McMaster University, Hamilton, ON, Canada, 2010. [Google Scholar]
- Fernandes, D. Abiotic Amino Acid Synthesis in the Early Solar System. Bachelor’s Thesis, McMaster University, Hamilton, ON, Canada, 2013. [Google Scholar]
- Espinosa-García, J.; Dóbé, S. Theoretical enthalpies of formation for atmospheric hydroxycarbonyls. J. Mol. Struct. 2005, 713, 119–125. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09; Revision E.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Cammi, R.; Tomasi, J. Remarks on the use of the apparent surface charges (ASC) methods in solvation problems: Iterative versus matrix-inversion procedures and the renormalization of the apparent charges. J. Comput. Chem. 1995, 16, 1449–1458. [Google Scholar] [CrossRef]
- Ochterski, J.W. Thermochemistry in Gaussian; Gaussian Inc.: Wallingford, CT, USA, 2000; pp. 1–19. [Google Scholar]
- Curtiss, L.A.; Raghavachari, K.; Redfern, P.C.; Pople, J.A. Assessment of Gaussian-2 and density functional theories for the computation of enthalpies of formation. J. Chem. Phys. 1997, 106, 1063–1079. [Google Scholar] [CrossRef] [Green Version]
- Wagman, D.D.; Evans, W.H.; Parker, V.B.; Schumm, R.H.; Halow, I.; Bailey, S.M.; Churney, K.L.; Nutall, R.L. The NBS tables of chemical thermodynamic properties. J. Phys. Chem. Ref. Data 1982, 11, 2. [Google Scholar]
- Rauchfuß, H. Chemische Evolution und der Ursprung des Lebens; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Omran, A.; Menor-Salvan, C.; Springsteen, G.; Pasek, M. The Messy Alkaline Formose Reaction and Its Link to Metabolism. Life 2020, 10, 125. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Ricardo, A.; Illangkoon, H.I.; Kim, M.J.; Carrigan, M.A.; Frye, F.; Benner, S.A. Synthesis of Carbohydrates in Mineral-Guided Prebiotic Cycles. J. Am. Chem. Soc. 2011, 133, 9457–9468. [Google Scholar] [CrossRef]
- Haas, M.; Lamour, S.; Trapp, O. Development of an advanced derivatization protocol for the unambiguous identification of monosaccharides in complex mixtures by gas and liquid chromatography. J. Chromatogr. A 2018, 1568, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Haas, M.; Lamour, S.; Christ, S.B.; Trapp, O. Mineral-mediated carbohydrate synthesis by mechanical forces in a primordial geochemical setting. Commun. Chem. 2020, 3, 140. [Google Scholar] [CrossRef]
- Zweckmair, T.; Böhmdorfer, S.; Bogolitsyna, A.; Rosenau, T.; Potthast, A.; Novalin, S. Accurate Analysis of Formose Reaction Products by LC–UV: An Analytical Challenge. J. Chromatogr. Sci. 2013, 52, 169–175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Larralde, R.; Robertson, M.P.; Miller, S.L. Rates of decomposition of ribose and other sugars: Implications for chemical evolution. Proc. Natl. Acad. Sci. USA 1995, 92, 8158–8160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Bruijn, J.M.; Kieboom, A.P.G.; Van Bekkiun, H. Alkaline Degradation of Monosaccharides VI1: The Fhucto-Fobmose Reaction of Mixtures of D-Fructose and Formaldehyde. J. Carbohydr. Chem. 1986, 5, 561–569. [Google Scholar] [CrossRef]
- Ricardo, A.; Carrigan, M.A.; Olcott, A.N.; Benner, S.A. Borate Minerals Stabilize Ribose. Science 2004, 303, 196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mills, A.A. Boron in Carbonaceous Chondrites. Nature 1968, 220, 1113–1114. [Google Scholar] [CrossRef]
- Cobb, A.K.; Pudritz, R.E. Nature’s Starships. I. Observed Abundances and Relative Frequencies of Amino Acids in Meteorites. Astrophys. J. 2014, 783, 140. [Google Scholar] [CrossRef] [Green Version]
- Lai, J.C.Y.; Pearce, B.K.; Pudritz, R.E.; Lee, D. Meteoritic abundances of fatty acids and potential reaction pathways in planetesimals. Icarus 2019, 319, 685–700. [Google Scholar] [CrossRef] [Green Version]
- Gilmour, I. Structural and Isotopic Analysis of Organic Matter in Carbonaceous Chondrites. In Treatise on Geochemistry; Elsevier Inc.: Amsterdam, The Netherlands, 2003; Volume 1, pp. 269–290. [Google Scholar] [CrossRef]
- Pizzarello, S.; Cooper, G.W.; Flynn, G.J. The Nature and Distribution of the Organic Material in Carbonaceous Chondrites and Interplanetary Dust Particles. In Meteorites and the Early Solar System II; University of Arizona Press: Tucson, AZ, USA, 2006; pp. 625–651. [Google Scholar]
- Derenne, S.; Robert, F. Model of molecular structure of the insoluble organic matter isolated from Murchison meteorite. Meteorit. Planet. Sci. 2010, 45, 1461–1475. [Google Scholar] [CrossRef]
- Basiuk, V.A.; Navarro-González, R. Pyrolytic Behavior of Amino Acids and Nucleic Acid Bases: Implications for Their Survival during Extraterrestrial Delivery. Icarus 1998, 134, 269–278. [Google Scholar] [CrossRef]
- Pierazzo, E.; Chyba, C.F. Amino acid survival in large cometary impacts. Meteorit. Planet. Sci. 1999, 34, 909–918. [Google Scholar] [CrossRef]
- Brinton, K.L.; Bada, J.L. A reexamination of amino acids in lunar soils: Implications for the survival of exogenous organic material during impact delivery. Geochim. Cosmochim. Acta 1996, 60, 349–354. [Google Scholar] [CrossRef] [Green Version]
- Gull, M.; Mojica, M.A.; Fernández, F.M.; Gaul, D.A.; Orlando, T.M.; Liotta, C.L.; Pasek, M.A. Nucleoside phosphorylation by the mineral schreibersite. Sci. Rep. 2015, 5, 17198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Z.R.; Wang, X. A plausible prebiotic selection of ribose for RNA—Formation, dynamic isolation, and nucleotide synthesis based on metal-doped-clays. Chem 2021, 7, 3292–3308. [Google Scholar] [CrossRef]
- Chen, Q.Q.; Zhao, Z.R.; Wang, X. A Prebiotic Ribosylation of Pyrimidine Nucleobases Enabled by Metal Cations and Clay Minerals. Life 2021, 11, 1381. [Google Scholar] [CrossRef]



| Molecule i | Name | Cometary Concentration | Correction Factor | Predicted Concentration |
|---|---|---|---|---|
| H2O | water | 1 | - | 1 |
| CH2O | formaldehyde | 6.6 × 10−4 | 10−3 | 6.6 × 10−4 |
| C2H4O2 | glycolaldehyde | (0.05–4.00) × 10−4 | - | (0.05–4.00) × 10−4 |
| Catalyst | Name | Maximum Yield of Ribose |
|---|---|---|
| Ca(OH)2 | Calcium hydroxide | 4.1 × 10−2 |
| CaCO3 | Calcium carbonate | 3.5 × 10−2 |
| K2CO3 | Potassium carbonate | 2.7 × 10−2 |
| KOH | Potassium hydroxide | 2.4 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paschek, K.; Kohler, K.; Pearce, B.K.D.; Lange, K.; Henning, T.K.; Trapp, O.; Pudritz, R.E.; Semenov, D.A. Possible Ribose Synthesis in Carbonaceous Planetesimals. Life 2022, 12, 404. https://doi.org/10.3390/life12030404
Paschek K, Kohler K, Pearce BKD, Lange K, Henning TK, Trapp O, Pudritz RE, Semenov DA. Possible Ribose Synthesis in Carbonaceous Planetesimals. Life. 2022; 12(3):404. https://doi.org/10.3390/life12030404
Chicago/Turabian StylePaschek, Klaus, Kai Kohler, Ben K. D. Pearce, Kevin Lange, Thomas K. Henning, Oliver Trapp, Ralph E. Pudritz, and Dmitry A. Semenov. 2022. "Possible Ribose Synthesis in Carbonaceous Planetesimals" Life 12, no. 3: 404. https://doi.org/10.3390/life12030404
APA StylePaschek, K., Kohler, K., Pearce, B. K. D., Lange, K., Henning, T. K., Trapp, O., Pudritz, R. E., & Semenov, D. A. (2022). Possible Ribose Synthesis in Carbonaceous Planetesimals. Life, 12(3), 404. https://doi.org/10.3390/life12030404