Thermodynamic and Kinetic Sequence Selection in Enzyme-Free Polymer Self-Assembly inside a Non-equilibrium RNA Reactor
Abstract
:1. Introduction
2. Models and Methods
2.1. Strands and Complexes

2.2. Elementary Reactions
2.3. Kinetics of Hybridization and Dehybridization
2.4. Hybridization Energy
2.5. Kinetic Stalling
2.6. Effective Cyclic Environment
2.7. Validity of Our Model and Application to Primer Extension
2.8. Parametrization of Rates
2.9. Implementation
3. Results
3.1. Boundary Conditions and Observables
3.2. Overview of Key Findings
3.3. Reference Model without Energetic Bias and Kinetic Stalling

3.4. Energetic Bias in the Absence of Kinetic Stalling
3.5. Loss of Energetic Discrimination Prevents Sequence Selection
3.6. Kinetic Stalling in the Absence of Energetic Bias

3.7. Hydrolysis and Stalling Boost Sequence Selection
3.8. Energetic Bias in the Presence of Kinetic Stalling

3.9. Weak versus Strong Kinetic Stalling
4. Discussion
4.1. Summary
4.2. Prior Work, Our Model, and Future Extensions
4.3. Plausibility of a Binary Alphabet
4.4. Significance for the Emergence of Life
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Terminal Base Pair Energies
| Process | Parameter | Value |
|---|---|---|
| dehybridization |
Appendix B. Examples for Hybridization Energies

Appendix C. Thermodynamics of Hybridization
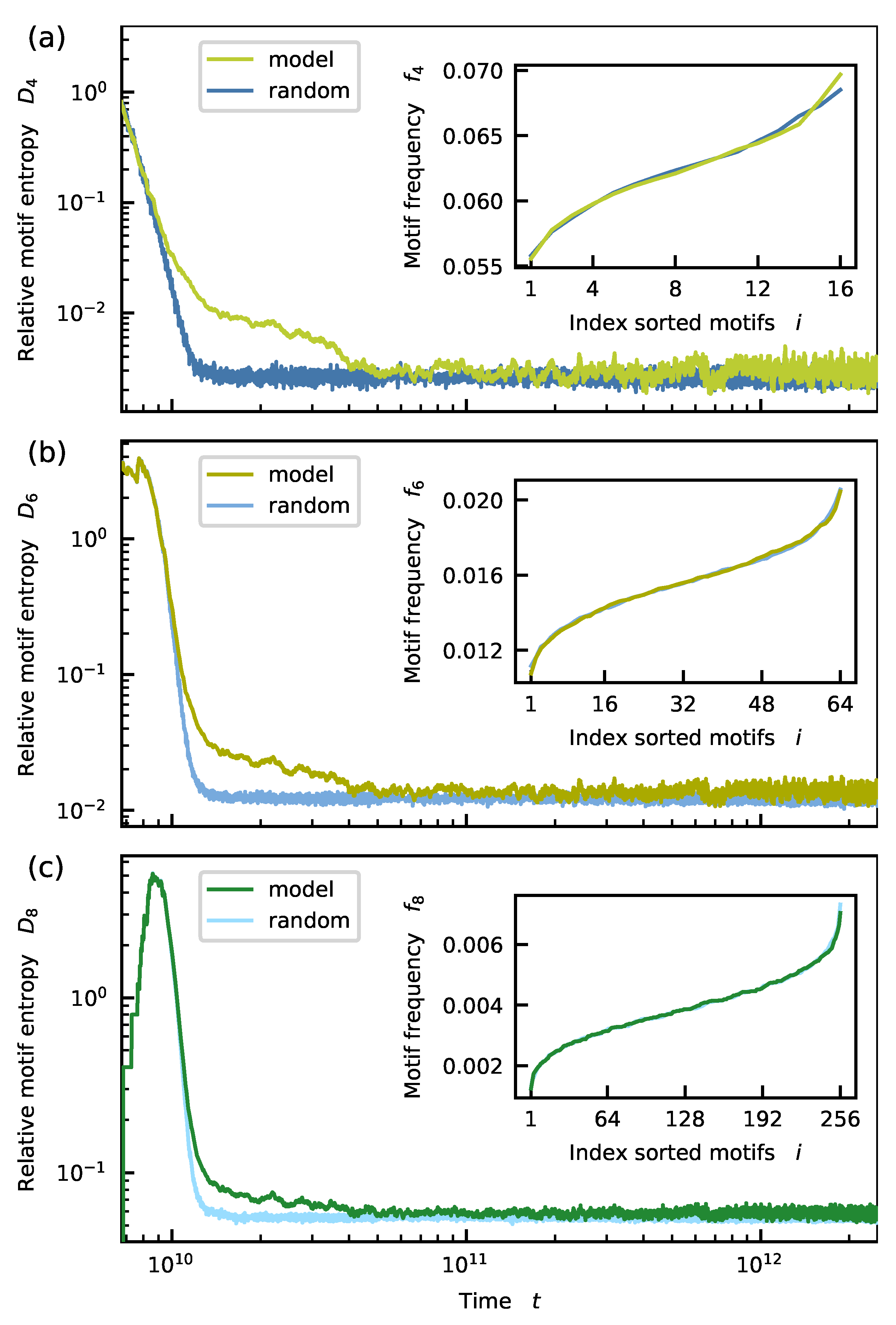
Appendix D. Distribution of Longer Motifs
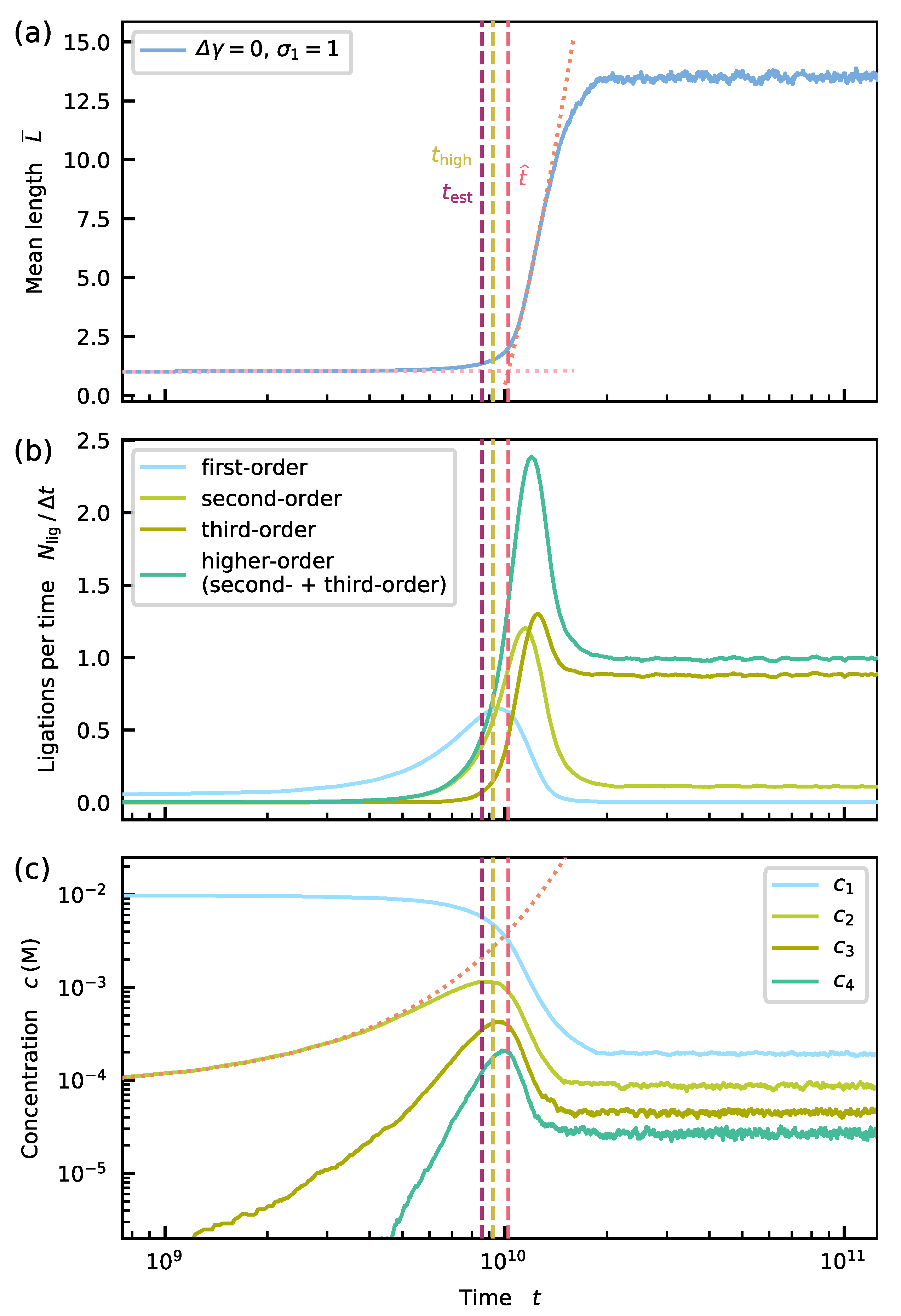
Appendix E. Onset of Growth
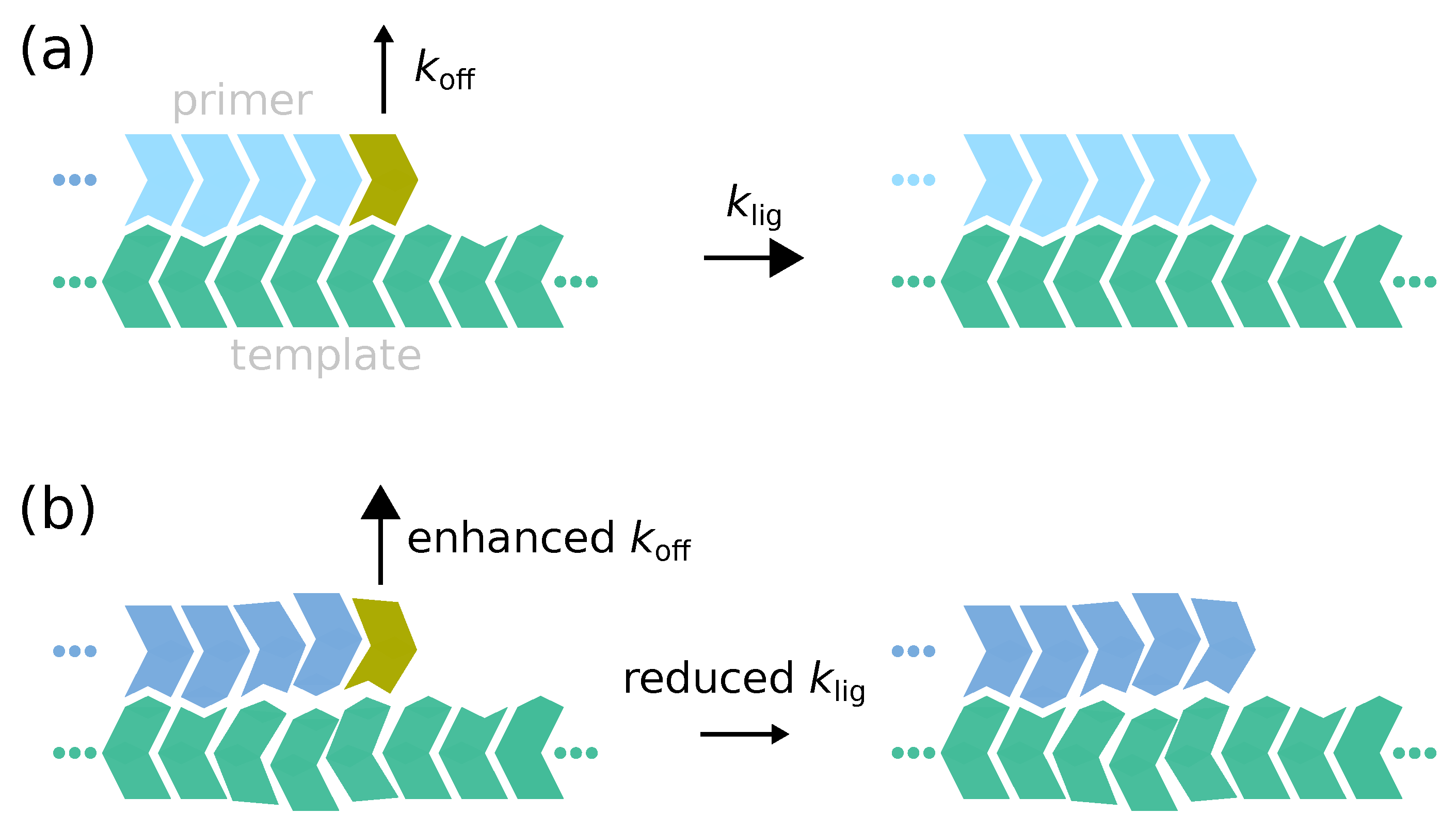
Appendix F. Application to Primer Extension
References
- Doudna, J.A.; Szostak, J.W. RNA-catalysed synthesis of complementary-strand RNA. Nature 1989, 339, 519–522. [Google Scholar] [CrossRef] [PubMed]
- Lorsch, J.R.; Szostak, J.W. In vitro evolution of new ribozymes with polynucleotide kinase activity. Nature 1994, 371, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Johnston, W.K. RNA-Catalyzed RNA Polymerization: Accurate and General RNA-Templated Primer Extension. Science 2001, 292, 1319–1325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wochner, A.; Attwater, J.; Coulson, A.; Holliger, P. Ribozyme-Catalyzed Transcription of an Active Ribozyme. Science 2011, 332, 209–212. [Google Scholar] [CrossRef]
- Attwater, J.; Raguram, A.; Morgunov, A.S.; Gianni, E.; Holliger, P. Ribozyme-catalysed RNA synthesis using triplet building blocks. eLife 2018, 7, e35255. [Google Scholar] [CrossRef]
- Gesteland, R.F.; Cech, T.; Atkins, J.F. (Eds.) The RNA World: The Nature of Modern RNA Suggests a Prebiotic RNA World, 3rd ed.; Number 43 in Cold Spring Harbor Monograph Series; OCLC: ocm60856160; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2006. [Google Scholar]
- Orgel, L.E. Prebiotic Chemistry and the Origin of the RNA World. Crit. Rev. Biochem. Mol. Biol. 2004, 39, 99–123. [Google Scholar] [CrossRef] [Green Version]
- Joyce, G.F. RNA evolution and the origins of life. Nature 1989, 338, 217–224. [Google Scholar] [CrossRef]
- Crick, F. The origin of the genetic code. J. Mol. Biol. 1968, 38, 367–379. [Google Scholar] [CrossRef]
- Orgel, L.E. Evolution of the genetic apparatus. J. Mol. Biol. 1968, 38, 381–393. [Google Scholar] [CrossRef]
- Gilbert, W. Origin of life: The RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
- Szostak, J.W. The Narrow Road to the Deep Past: In Search of the Chemistry of the Origin of Life. Angew. Chem. Int. Ed. 2017, 56, 11037–11043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Powner, M.W.; Gerland, B.; Sutherland, J.D. Synthesis of activated pyrimidine ribonucleotides in prebiotically plausible conditions. Nature 2009, 459, 239–242. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Chmela, V.; Green, N.; Russell, D.; Janicki, M.; Góra, R.; Szabla, R.; Bond, A.; Sutherland, J. Selective prebiotic formation of RNA pyrimidine and DNA purine nucleosides. Nature 2020, 582, 60–66. [Google Scholar] [CrossRef] [PubMed]
- Becker, S.; Thoma, I.; Deutsch, A.; Gehrke, T.; Mayer, P.; Zipse, H.; Carell, T. A high-yielding, strictly regioselective prebiotic purine nucleoside formation pathway. Science 2016, 352, 833–836. [Google Scholar] [CrossRef] [PubMed]
- Mutschler, H.; Wochner, A.; Holliger, P. Freeze–thaw cycles as drivers of complex ribozyme assembly. Nat. Chem. 2015, 7, 502–508. [Google Scholar] [CrossRef] [Green Version]
- Briones, C.; Stich, M.; Manrubia, S.C. The dawn of the RNA World: Toward functional complexity through ligation of random RNA oligomers. RNA 2009, 15, 743–749. [Google Scholar] [CrossRef] [Green Version]
- Toyabe, S.; Braun, D. Cooperative Ligation Breaks Sequence Symmetry and Stabilizes Early Molecular Replication. Phys. Rev. X 2019, 9, 011056. [Google Scholar] [CrossRef] [Green Version]
- Salditt, A.; Keil, L.M.; Horning, D.; Mast, C.; Joyce, G.; Braun, D. Thermal Habitat for RNA Amplification and Accumulation. Phys. Rev. Lett. 2020, 125, 048104. [Google Scholar] [CrossRef]
- Edeleva, E.; Salditt, A.; Stamp, J.; Schwintek, P.; Boekhoven, J.; Braun, D. Continuous nonenzymatic cross-replication of DNA strands with in situ activated DNA Oligonucleotides. Chem. Sci. 2019, 10, 5807–5814. [Google Scholar] [CrossRef] [Green Version]
- Wachowius, F.; Holliger, P. Non-Enzymatic Assembly of a Minimized RNA Polymerase Ribozyme. ChemSystemsChem 2019, 1, 12–15. [Google Scholar] [CrossRef] [Green Version]
- Ferre-D’Amare, A.R.; Scott, W.G. Small Self-cleaving Ribozymes. Cold Spring Harb. Perspect. Biol. 2010, 2, a003574. [Google Scholar] [CrossRef] [Green Version]
- Birikh, K.R.; Heaton, P.A.; Eckstein, F. The Structure, Function and Application of the Hammerhead Ribozyme. Eur. J. Biochem. 1997, 245, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scott, W.G.; Murray, J.B.; Arnold, J.R.P.; Stoddard, B.L.; Klug, A. Capturing the Structure of a Catalytic RNA Intermediate: The Hammerhead Ribozyme. Science 1996, 274, 2065–2069. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horning, D.P.; Joyce, G.F. Amplification of RNA by an RNA polymerase ribozyme. Proc. Natl. Acad. Sci. USA 2016, 113, 9786–9791. [Google Scholar] [CrossRef] [Green Version]
- Doudna, J.A.; Couture, S.; Szostak, J.W. A Multisubunit Ribozyme That Is a Catalyst of and Template for Complementary Strand RNA synthesis. Science 1991, 251, 1605–1608. [Google Scholar] [CrossRef]
- Joyce, G.F. Directed Evolution of Nucleic Acid Enzymes. Annu. Rev. Biochem. 2004, 73, 791–836. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walker, S.I. Origins of life: A problem for physics, a key issues review. Rep. Prog. Phys. 2017, 80, 092601. [Google Scholar] [CrossRef]
- Ameta, S.; Matsubara, Y.J.; Chakraborty, N.; Krishna, S.; Thutupalli, S. Self-Reproduction and Darwinian Evolution in Autocatalytic Chemical Reaction Systems. Life 2021, 11, 308. [Google Scholar] [CrossRef]
- Sievers, D.; von Kiedrowski, G. Self-replication of complementary nucleotide-based oligomers. Nature 1994, 369, 221–224. [Google Scholar] [CrossRef]
- Derr, J.; Manapat, M.L.; Rajamani, S.; Leu, K.; Xulvi-Brunet, R.; Joseph, I.; Nowak, M.A.; Chen, I.A. Prebiotically plausible mechanisms increase compositional diversity of nucleic acid sequences. Nucleic Acids Res. 2012, 40, 4711–4722. [Google Scholar] [CrossRef] [Green Version]
- Leu, K.; Kervio, E.; Obermayer, B.; Turk-MacLeod, R.M.; Yuan, C.; Luevano, J.M.; Chen, E.; Gerland, U.; Richert, C.; Chen, I.A. Cascade of Reduced Speed and Accuracy after Errors in Enzyme-Free Copying of Nucleic Acid Sequences. J. Am. Chem. Soc. 2013, 135, 354–366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manapat, M.L.; Chen, I.A.; Nowak, M.A. The basic reproductive ratio of life. J. Theor. Biol. 2010, 263, 317–327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanavarioti, A.; White, D.H. Kinetic analysis of the template effect in ribooligoguanylate elongation. Orig. Life Evol. Biosph. 1987, 17, 333–349. [Google Scholar] [CrossRef] [PubMed]
- Yakovchuk, P. Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucl. Acids Res. 2006, 34, 564–574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- SantaLucia, J., Jr.; Hicks, D. The Thermodynamics of DNA Structural Motifs. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 415–440. [Google Scholar] [CrossRef] [Green Version]
- Turner, D.H.; Mathews, D.H. NNDB: The nearest neighbor parameter database for predicting stability of nucleic acid secondary structure. Nucleic Acids Res. 2010, 38, D280–D282. [Google Scholar] [CrossRef]
- Rajamani, S.; Ichida, J.K.; Antal, T.; Treco, D.A.; Leu, K.; Nowak, M.A.; Szostak, J.W.; Chen, I.A. Effect of Stalling after Mismatches on the Error Catastrophe in Nonenzymatic Nucleic Acid Replication. J. Am. Chem. Soc. 2010, 132, 5880–5885. [Google Scholar] [CrossRef]
- Leu, K.; Obermayer, B.; Rajamani, S.; Gerland, U.; Chen, I.A. The prebiotic evolutionary advantage of transferring genetic information from RNA to DNA. Nucleic Acids Res. 2011, 39, 8135–8147. [Google Scholar] [CrossRef] [Green Version]
- Blain, J.C.; Szostak, J.W. Progress toward synthetic cells. Annu. Rev. Biochem. 2014, 83, 615–640. [Google Scholar] [CrossRef] [Green Version]
- Szostak, J.W. The eightfold path to non-enzymatic RNA replication. J. Syst. Chem. 2012, 3, 2. [Google Scholar] [CrossRef] [Green Version]
- Sosson, M.; Richert, C. Enzyme-free genetic copying of DNA and RNA sequences. Beilstein J. Org. Chem. 2018, 14, 603–617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, L.; O’Flaherty, D.K.; Szostak, J.W. Assembly of a Ribozyme Ligase from Short Oligomers by Nonenzymatic Ligation. J. Am. Chem. Soc. 2020, 142, 15961–15965. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; O’Flaherty, D.K.; Szostak, J.W. Template-Directed Copying of RNA by Non-enzymatic Ligation. Angew. Chem. Int. Ed. 2020, 132, 15812–15817. [Google Scholar] [CrossRef]
- Zielinski, W.S.; Orgel, L.E. Autocatalytic synthesis of a tetranucleotide analogue. Nature 1987, 327, 346–347. [Google Scholar] [CrossRef]
- Zielinski, W.S.; Orgel, L.E. Oligoaminudeoside phosphoramidates. Oligomeilzation of dimers of 3′-amino-3′-deoxy-nucleotides (GC and CG) in aqueous solution. Nucleic Acids Res. 1987, 15, 1699–1715. [Google Scholar] [CrossRef] [Green Version]
- von Kiedrowski, G. A Self-Replicating Hexadeoxynucleotide. Angew. Chem. Int. Ed. 1986, 25, 932–935. [Google Scholar] [CrossRef]
- Sosson, M.; Pfeffer, D.; Richert, C. Enzyme-free ligation of dimers and trimers to RNA primers. Nucleic Acids Res. 2019, 47, 3836–3845. [Google Scholar] [CrossRef]
- Hänle, E.; Richert, C. Enzyme-Free Replication with Two or Four Bases. Angew. Chem. Int. Ed. 2018, 57, 8911–8915. [Google Scholar] [CrossRef]
- Deck, C.; Jauker, M.; Richert, C. Efficient enzyme-free copying of all four nucleobases templated by immobilized RNA. Nat. Chem. 2011, 3, 603–608. [Google Scholar] [CrossRef]
- Jauker, M.; Griesser, H.; Richert, C. Copying of RNA Sequences without Pre-Activation. Angew. Chem. Int. Ed. 2015, 54, 14559–14563. [Google Scholar] [CrossRef] [Green Version]
- Kervio, E.; Hochgesand, A.; Steiner, U.E.; Richert, C. Templating efficiency of naked DNA. Proc. Natl. Acad. Sci. USA 2010, 107, 12074–12079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prywes, N.; Blain, J.C.; Del Frate, F.; Szostak, J.W. Nonenzymatic copying of RNA templates containing all four letters is catalyzed by activated oligonucleotides. eLife 2016, 5, e17756. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, L.; Prywes, N.; Tam, C.P.; O’Flaherty, D.K.; Lelyveld, V.S.; Izgu, E.C.; Pal, A.; Szostak, J.W. Enhanced Nonenzymatic RNA Copying with 2-Aminoimidazole Activated Nucleotides. J. Am. Chem. Soc. 2017, 139, 1810–1813. [Google Scholar] [CrossRef]
- Kudella, P.W.; Tkachenko, A.V.; Salditt, A.; Maslov, S.; Braun, D. Structured sequences emerge from random pool when replicated by templated ligation. Proc. Natl. Acad. Sci. USA 2021, 118, e2018830118. [Google Scholar] [CrossRef] [PubMed]
- Rosenberger, J.H.; Göppel, T.; Kudella, P.W.; Braun, D.; Gerland, U.; Altaner, B. Self-Assembly of Informational Polymers by Templated Ligation. Phys. Rev. X 2021, 11, 031055. [Google Scholar] [CrossRef]
- Dill, K.A.; Bromberg, S. Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience, 2nd ed.; Garland Science: London, UK; New York, NY, USA, 2011. [Google Scholar]
- Kervio, E.; Sosson, M.; Richert, C. The effect of leaving groups on binding and reactivity in enzyme-free copying of DNA and RNA. Nucleic Acids Res. 2016, 44, 5504–5514. [Google Scholar] [CrossRef]
- Walton, T.; Szostak, J.W. A Kinetic Model of Nonenzymatic RNA Polymerization by Cytidine-5′-phosphoro-2-aminoimidazolide. Biochemistry 2017, 56, 5739–5747. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, G.K.; Lad, C.; Wyman, P.; Williams, N.H.; Wolfenden, R. The time required for water attack at the phosphorus atom of simple phosphodiesters and of DNA. Proc. Natl. Acad. Sci. USA 2006, 103, 4052–4055. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Ding, D.; Szostak, J.W. The virtual circular genome model for primordial RNA replication. RNA 2021, 27, 1–11. [Google Scholar] [CrossRef]
- Lindahl, T.; Andersson, A. Rate of chain breakage at apurinic sites in double-stranded deoxyribonucleic acid. Biochemistry 1972, 11, 3618–3623. [Google Scholar] [CrossRef]
- Li, Y.; Breaker, R.R. Kinetics of RNA Degradation by Specific Base Catalysis of Transesterification Involving the 2′-Hydroxyl Group. J. Am. Chem. Soc. 1999, 121, 5364–5372. [Google Scholar] [CrossRef]
- Komiyama, M.; Takeda, N.; Shigekawa, H. Hydrolysis of DNA and RNA by lanthanide ions: Mechanistic studies leading to new applications. Chem. Commun. 1999, 16, 1443–1451. [Google Scholar] [CrossRef]
- Basile, L.A.; Raphael, A.L.; Barton, J.K. Metal-activated hydrolytic cleavage of DNA. J. Am. Chem. Soc. 1987, 109, 7550–7551. [Google Scholar] [CrossRef]
- Hopfield, J.J. Kinetic Proofreading: A New Mechanism for Reducing Errors in Biosynthetic Processes Requiring High Specificity. Proc. Natl. Acad. Sci. USA 1974, 71, 4135–4139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rauzan, B.; McMichael, E.; Cave, R.; Sevcik, L.R.; Ostrosky, K.; Whitman, E.; Stegemann, R.; Sinclair, A.L.; Serra, M.J.; Deckert, A.A. Kinetics and Thermodynamics of DNA, RNA, and Hybrid Duplex Formation. Biochemistry 2013, 52, 765–772. [Google Scholar] [CrossRef]
- Ouldridge, T.E. The importance of thermodynamics for molecular systems, and the importance of molecular systems for thermodynamics. Nat. Comput. 2018, 17, 3–29. [Google Scholar] [CrossRef] [Green Version]
- Jhunjhunwala, A.; Ali, Z.; Bhattacharya, S.; Halder, A.; Mitra, A.; Sharma, P. On the Nature of Nucleobase Stacking in RNA: A Comprehensive Survey of Its Structural Variability and a Systematic Classification of Associated Interactions. J. Chem. Inf. Model. 2021, 61, 1470–1480. [Google Scholar] [CrossRef]
- Luther, A.; Brandsch, R.; von Kiedrowski, G. Surface-promoted replication and exponential amplification of DNA analogues. Nature 1998, 396, 245–248. [Google Scholar] [CrossRef]
- Keil, L.M.R.; Möller, F.M.; Kieß, M.; Kudella, P.W.; Mast, C.B. Proton gradients and pH oscillations emerge from heat flow at the microscale. Nat. Commun. 2017, 8, 1897. [Google Scholar] [CrossRef]
- Mariani, A.; Bonfio, C.; Johnson, C.M.; Sutherland, J.D. pH-Driven RNA Strand Separation under Prebiotically Plausible Conditions. Biochemistry 2018, 57, 6382–6386. [Google Scholar] [CrossRef] [Green Version]
- Kreysing, M.; Keil, L.; Lanzmich, S.; Braun, D. Heat flux across an open pore enables the continuous replication and selection of oligonucleotides towards increasing length. Nat. Chem. 2015, 7, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Damer, B.; Deamer, D. The Hot Spring Hypothesis for an Origin of Life. Astrobiology 2020, 20, 429–452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mast, C.B.; Braun, D. Thermal Trap for DNA Replication. Phys. Rev. Lett. 2010, 104, 188102. [Google Scholar] [CrossRef] [PubMed]
- Ianeselli, A.; Mast, C.B.; Braun, D. Periodic Melting of Oligonucleotides by Oscillating Salt Concentrations Triggered by Microscale Water Cycles Inside Heated Rock Pores. Angew. Chem. Int. Ed. 2019, 131, 13289–13294. [Google Scholar] [CrossRef]
- Tkachenko, A.V.; Maslov, S. Spontaneous emergence of autocatalytic information-coding polymers. J. Chem. Phys. 2015, 143, 045102. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Gibson, M.A.; Bruck, J. Efficient Exact Stochastic Simulation of Chemical Systems with Many Species and Many Channels. J. Phys. Chem. A 2000, 104, 1876–1889. [Google Scholar] [CrossRef]
- Krapivsky, P.L.; Redner, S.; Ben-Naim, E. A Kinetic View of Statistical Physics; CBO9780511780516; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef] [Green Version]
- Obermayer, B.; Krammer, H.; Braun, D.; Gerland, U. Emergence of Information Transmission in a Prebiotic RNA Reactor. Phys. Rev. Lett. 2011, 107, 018101. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.; Bapat, N.V.; Derr, J.; Rajamani, S.; Sengupta, S. Emergence of ribozyme and tRNA-like structures from mineral-rich muddy pools on prebiotic earth. J. Theor. Biol. 2020, 506, 110446. [Google Scholar] [CrossRef]
- Matsubara, Y.J.; Kaneko, K. Optimal size for emergence of self-replicating polymer system. Phys. Rev. E 2016, 93, 032503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gonçalves da Silva, L.H.; Hochberg, D. Open flow non-enzymatic template catalysis and replication. Phys. Chem. Chem. Phys. 2018, 20, 14864–14875. [Google Scholar] [CrossRef]
- Fellermann, H.; Tanaka, S.; Rasmussen, S. Sequence selection by dynamical symmetry breaking in an autocatalytic binary polymer model. Phys. Rev. E 2017, 96, 062407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanaka, S.; Fellermann, H.; Rasmussen, S. Structure and selection in an autocatalytic binary polymer model. EPL 2014, 107, 28004. [Google Scholar] [CrossRef]
- Matsubara, Y.J.; Kaneko, K. Kinetic Selection of Template Polymer with Complex Sequences. Phys. Rev. Lett. 2018, 121, 118101. [Google Scholar] [CrossRef] [Green Version]
- Mizuuchi, R.; Lehman, N. Limited Sequence Diversity Within a Population Supports Prebiotic RNA Reproduction. Life 2019, 9, 20. [Google Scholar] [CrossRef] [Green Version]
- Tkachenko, A.V.; Maslov, S. Onset of natural selection in populations of autocatalytic heteropolymers. J. Chem. Phys. 2018, 149, 134901. [Google Scholar] [CrossRef] [Green Version]
- Tupper, A.; Shi, K.; Higgs, P. The Role of Templating in the Emergence of RNA from the Prebiotic Chemical Mixture. Life 2017, 7, 41. [Google Scholar] [CrossRef] [Green Version]
- Anderson, P.W. Suggested model for prebiotic evolution: The use of chaos. Proc. Natl. Acad. Sci. USA 1983, 80, 3386–3390. [Google Scholar] [CrossRef] [Green Version]
- Morasch, M.; Braun, D.; Mast, C.B. Heat-Flow-Driven Oligonucleotide Gelation Separates Single-Base Differences. Angew. Chem. Int. Ed. 2016, 55, 6676–6679. [Google Scholar] [CrossRef]
- Zhou, L.; Kim, S.C.; Ho, K.H.; O’Flaherty, D.K.; Giurgiu, C.; Wright, T.H.; Szostak, J.W. Non-enzymatic primer extension with strand displacement. eLife 2019, 8, e51888. [Google Scholar] [CrossRef] [PubMed]
- Mutschler, H.; Taylor, A.I.; Porebski, B.T.; Lightowlers, A.; Houlihan, G.; Abramov, M.; Herdewijn, P.; Holliger, P. Random-sequence genetic oligomer pools display an innate potential for ligation and recombination. eLife 2018, 7, e43022. [Google Scholar] [CrossRef] [PubMed]
- Tupper, A.S.; Higgs, P.G. Rolling-circle and strand-displacement mechanisms for non-enzymatic RNA replication at the time of the origin of life. J. Theor. Biol. 2021, 527, 110822. [Google Scholar] [CrossRef] [PubMed]
- Blokhuis, A.; Lacoste, D. Length and sequence relaxation of copolymers under recombination reactions. J. Chem. Phys. 2017, 147, 094905. [Google Scholar] [CrossRef] [Green Version]
- Göppel, T.; Palyulin, V.V.; Gerland, U. The efficiency of driving chemical reactions by a physical non-equilibrium is kinetically controlled. Phys. Chem. Chem. Phys. 2016, 18, 20135–20143. [Google Scholar] [CrossRef] [Green Version]
- Göppel, T.; Obermayer, B.; Chen, I.A.; Gerland, U. A kinetic error filtering mechanism for enzyme-free copying of nucleic acid sequences. Evol. Biol. 2021. preprint. [Google Scholar] [CrossRef]
- Mast, C.B.; Schink, S.; Gerland, U.; Braun, D. Escalation of polymerization in a thermal gradient. Proc. Natl. Acad. Sci. USA 2013, 110, 8030–8035. [Google Scholar] [CrossRef] [Green Version]
- Walker, S.I.; Grover, M.A.; Hud, N.V. Universal Sequence Replication, Reversible Polymerization and Early Functional Biopolymers: A Model for the Initiation of Prebiotic Sequence Evolution. PLoS ONE 2012, 7, e34166. [Google Scholar] [CrossRef]
- Nowak, M.A.; Ohtsuki, H. Prevolutionary dynamics and the origin of evolution. Proc. Natl. Acad. Sci. USA 2008, 105, 14924–14927. [Google Scholar] [CrossRef] [Green Version]
- Andrieux, D.; Gaspard, P. Nonequilibrium generation of information in copolymerization processes. Proc. Natl. Acad. Sci. USA 2008, 105, 9516–9521. [Google Scholar] [CrossRef] [Green Version]
- Manapat, M.; Ohtsuki, H.; Bürger, R.; Nowak, M.A. Originator dynamics. J. Theor. Biol. 2009, 256, 586–595. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wachtershauser, G. An all-purine precursor of nucleic acids. Proc. Natl. Acad. Sci. USA 1988, 85, 1134–1135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levy, M.; Miller, S.L. The stability of the RNA bases: Implications for the origin of life. Proc. Natl. Acad. Sci. USA 1998, 95, 7933–7938. [Google Scholar] [CrossRef] [Green Version]
- Rogers, J.; Joyce, G.F. A ribozyme that lacks cytidine. Nature 1999, 402, 323–325. [Google Scholar] [CrossRef] [PubMed]
- Reader, J.S.; Joyce, G.F. A ribozyme composed of only two different nucleotides. Nature 2002, 420, 841–844. [Google Scholar] [CrossRef]
- Schlosser, K.; Li, Y. DNAzyme-mediated catalysis with only guanosine and cytidine nucleotides. Nucleic Acids Res. 2009, 37, 413–420. [Google Scholar] [CrossRef]
- Joyce, G.F.; Schwartz, A.W.; Miller, S.L.; Orgel, L.E. The case for an ancestral genetic system involving simple analogues of the nucleotides. Proc. Natl. Acad. Sci. USA 1987, 84, 4398–4402. [Google Scholar] [CrossRef] [Green Version]
- Schoning, K.U. Chemical Etiology of Nucleic Acid Structure: The alpha -Threofuranosyl-(3’rightarrow 2’) Oligonucleotide System. Science 2000, 290, 1347–1351. [Google Scholar] [CrossRef]
- Hud, N.V. Searching for lost nucleotides of the pre-RNA World with a self-refining model of early Earth. Nat. Commun. 2018, 9, 5171. [Google Scholar] [CrossRef]
- Hud, N.; Cafferty, B.; Krishnamurthy, R.; Williams, L. The Origin of RNA and “My Grandfather’s Axe”. Chem. Biol. 2013, 20, 466–474. [Google Scholar] [CrossRef] [Green Version]
- Joyce, G.F. The antiquity of RNA-based evolution. Nature 2002, 418, 214–221. [Google Scholar] [CrossRef] [PubMed]
- Orgel, L.E. Did template-directed nucleation precede molecular replication? Orig. Life Evol. Biosph. 1986, 17, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Higgs, P.G.; Lehman, N. The RNA World: Molecular cooperation at the origins of life. Nat. Rev. Genet. 2015, 16, 7–17. [Google Scholar] [CrossRef] [PubMed]
- Wachowius, F.; Attwater, J.; Holliger, P. Nucleic acids: Function and potential for abiogenesis. Q. Rev. Biophys. 2017, 50, e4. [Google Scholar] [CrossRef]
- Georgiadis, M.M.; Singh, I.; Kellett, W.F.; Hoshika, S.; Benner, S.A.; Richards, N.G.J. Structural Basis for a Six Nucleotide Genetic Alphabet. Proc. Natl. Acad. Sci. USA 2015, 137, 6947–6955. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, P.E. DNA Analogues with Nonphosphodiester Backbones. Annu. Rev. Biophys. Biomol. Struct. 1995, 24, 167–183. [Google Scholar] [CrossRef]
- Ura, Y.; Beierle, J.M.; Leman, L.J.; Orgel, L.E.; Ghadiri, M.R. Self-Assembling Sequence-Adaptive Peptide Nucleic Acids. Science 2009, 325, 73–77. [Google Scholar] [CrossRef]
- Lescrinier, E.; Esnouf, R.; Schraml, J.; Busson, R.; Heus, H.; Hilbers, C.; Herdewijn, P. Solution structure of a HNA–RNA hybrid. Chem. Biol. 2000, 7, 719–731. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.C.; O’Flaherty, D.K.; Giurgiu, C.; Zhou, L.; Szostak, J.W. The Emergence of RNA from the Heterogeneous Products of Prebiotic Nucleotide Synthesis. J. Am. Chem. Soc. 2021, 143, 3267–3279. [Google Scholar] [CrossRef]
- Cafferty, B.J.; Fialho, D.M.; Khanam, J.; Krishnamurthy, R.; Hud, N.V. Spontaneous formation and base pairing of plausible prebiotic nucleotides in water. Nat. Commun. 2016, 7, 11328. [Google Scholar] [CrossRef] [Green Version]
- Kolb, V.; Dworkin, J.; Miller, S. Alternative bases in the RNA world: The prebiotic synthesis of urazole and its ribosides. J. Mol. Evol. 1994, 38, 549–557. [Google Scholar] [CrossRef] [PubMed]
- Piccirilli, J.A.; Benner, S.A.; Krauch, T.; Moroney, S.E.; Benner, S.A. Enzymatic incorporation of a new base pair into DNA and RNA extends the genetic alphabet. Nature 1990, 343, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.C.; O’Flaherty, D.K.; Zhou, L.; Lelyveld, V.S.; Szostak, J.W. Inosine, but none of the 8-oxo-purines, is a plausible component of a primordial version of RNA. Proc. Natl. Acad. Sci. USA 2018, 115, 13318–13323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.J.; Cai, X.; Szostak, J.W. N2′→ P3′ Phosphoramidate Glycerol Nucleic Acid as a Potential Alternative Genetic System. J. Am. Chem. Soc. 2009, 131, 2119–2121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Flaherty, D.K.; Zhou, L.; Szostak, J.W. Nonenzymatic Template-Directed Synthesis of Mixed-Sequence 3′-NP-DNA up to 25 Nucleotides Long Inside Model Protocells. J. Am. Chem. Soc. 2019, 141, 10481–10488. [Google Scholar] [CrossRef] [Green Version]
- Heuberger, B.D.; Pal, A.; Del Frate, F.; Topkar, V.V.; Szostak, J.W. Replacing Uridine with 2-Thiouridine Enhances the Rate and Fidelity of Nonenzymatic RNA Primer Extension. J. Am. Chem. Soc. 2015, 137, 2769–2775. [Google Scholar] [CrossRef] [Green Version]
- Winnacker, M.; Kool, E.T. Artificial Genetic Sets Composed of Size-Expanded Base Pairs. Angew. Chem. Int. Ed. 2013, 52, 12498–12508. [Google Scholar] [CrossRef]
- Nelson, K.E.; Levy, M.; Miller, S.L. Peptide nucleic acids rather than RNA may have been the first genetic molecule. Proc. Natl. Acad. Sci. USA 2000, 97, 3868–3871. [Google Scholar] [CrossRef] [Green Version]
- Orgel, L. A Simpler Nucleic Acid. Science 2000, 290, 1306–1307. [Google Scholar] [CrossRef]
- Colville, B.W.F.; Powner, M.W. Selective Prebiotic Synthesis of α-Threofuranosyl Cytidine by Photochemical Anomerization. Angew. Chem. Int. Ed. 2021, 60, 10526–10530. [Google Scholar] [CrossRef]
- Szathmáry, E.; Smith, J.M. The major evolutionary transitions. Nature 1995, 374, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Blokhuis, A.; Lacoste, D.; Nghe, P. Universal motifs and the diversity of autocatalytic systems. Proc. Natl. Acad. Sci. USA 2020, 117, 25230–25236. [Google Scholar] [CrossRef] [PubMed]
- Nghe, P.; Hordijk, W.; Kauffman, S.A.; Walker, S.I.; Schmidt, F.J.; Kemble, H.; Yeates, J.A.M.; Lehman, N. Prebiotic network evolution: Six key parameters. Mol. Biosyst. 2015, 11, 3206–3217. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24. [Google Scholar] [CrossRef]
- Lincoln, T.A.; Joyce, G.F. Self-Sustained Replication of an RNA Enzyme. Science 2009, 323, 1229–1232. [Google Scholar] [CrossRef] [Green Version]
- Hordijk, W.; Hein, J.; Steel, M. Autocatalytic Sets and the Origin of Life. Entropy 2010, 12, 1733–1742. [Google Scholar] [CrossRef]
- Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Hordijk, W.; Steel, M.; Kauffman, S. The Structure of Autocatalytic Sets: Evolvability, Enablement, and Emergence. Acta Biotheor. 2012, 60, 379–392. [Google Scholar] [CrossRef]
- Vasas, V.; Fernando, C.; Santos, M.; Kauffman, S.; Szathmáry, E. Evolution before genes. Biol. Direct 2012, 7, 1. [Google Scholar] [CrossRef] [Green Version]
- Vaidya, N.; Manapat, M.L.; Chen, I.A.; Xulvi-Brunet, R.; Hayden, E.J.; Lehman, N. Spontaneous network formation among cooperative RNA replicators. Nature 2012, 491, 72–77. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]

| System | RNA | DNA | ||
|---|---|---|---|---|
| Nucleotides | A, U | C, G | A, T | C, G |
| −1.74 | −5.00 | −1.40 | −3.26 | |
| −0.46 | 0.60 | 0.42 | −0.65 | |
| Process | Parameter | Value |
|---|---|---|
| hybridization | 1 | |
| dehybridization | ||
| 7 | ||
| ligation | 10 | |
| , | ||
| hydrolysis | 18.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Göppel, T.; Rosenberger, J.H.; Altaner, B.; Gerland, U. Thermodynamic and Kinetic Sequence Selection in Enzyme-Free Polymer Self-Assembly inside a Non-equilibrium RNA Reactor. Life 2022, 12, 567. https://doi.org/10.3390/life12040567
Göppel T, Rosenberger JH, Altaner B, Gerland U. Thermodynamic and Kinetic Sequence Selection in Enzyme-Free Polymer Self-Assembly inside a Non-equilibrium RNA Reactor. Life. 2022; 12(4):567. https://doi.org/10.3390/life12040567
Chicago/Turabian StyleGöppel, Tobias, Joachim H. Rosenberger, Bernhard Altaner, and Ulrich Gerland. 2022. "Thermodynamic and Kinetic Sequence Selection in Enzyme-Free Polymer Self-Assembly inside a Non-equilibrium RNA Reactor" Life 12, no. 4: 567. https://doi.org/10.3390/life12040567







