An Enhanced SEIR Model for Prediction of COVID-19 with Vaccination Effect
Abstract
:1. Introduction
- To enhance SEIR Model with effect different versions of severity.
- To predict the susceptibility, infection and recovered using enhanced model with no social distancing is considered.
- To predict the susceptibility, infection and recovered using enhanced model with social distancing is considered.
- To predict the susceptibility, infection and recovered using enhanced model with social distancing with vaccination is considered.
2. Background
- N = total number of population of a geographical location, (S + I + R = N)
- β is the average number of contacts per person per time
- γ is the transition rate assumed to be proportional to the number of infectious individuals
3. Related Work
Novelty of the Proposed Research Work
4. Proposed Method
5. Result and Discussion
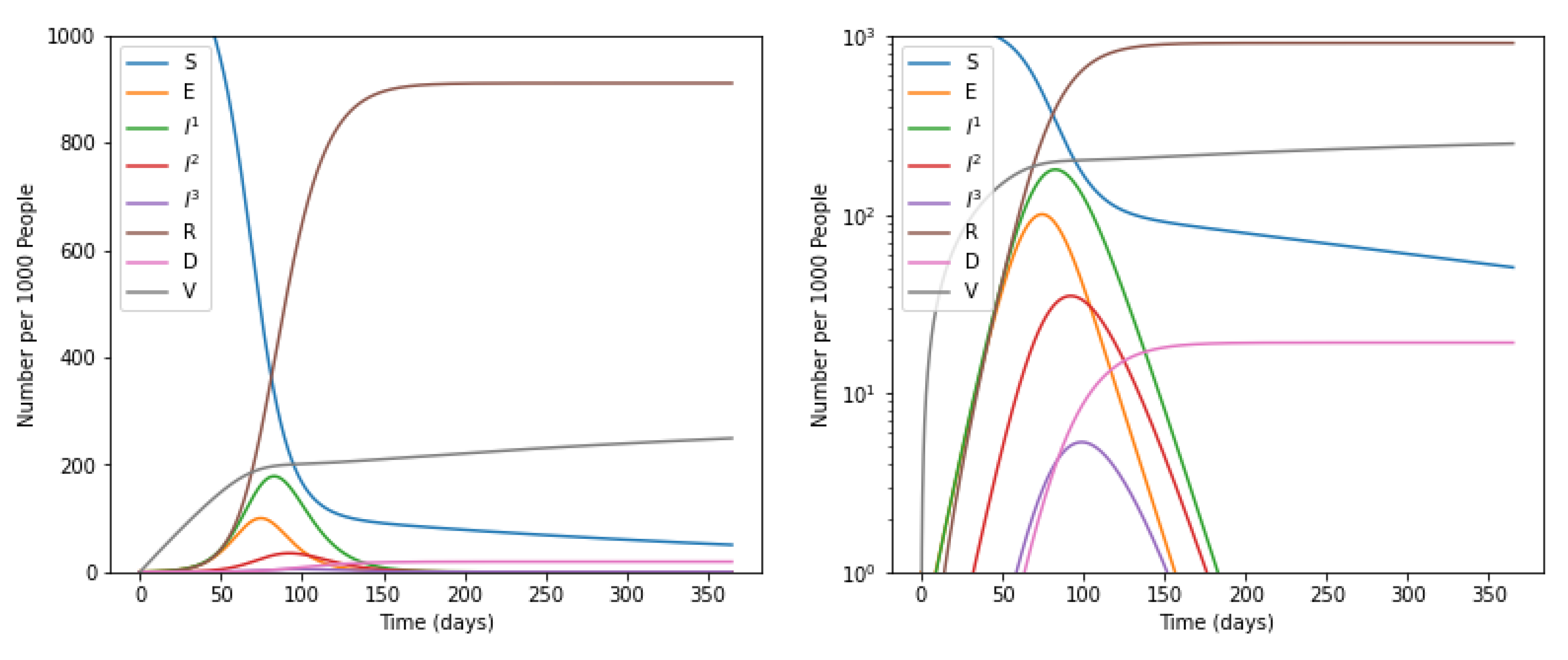
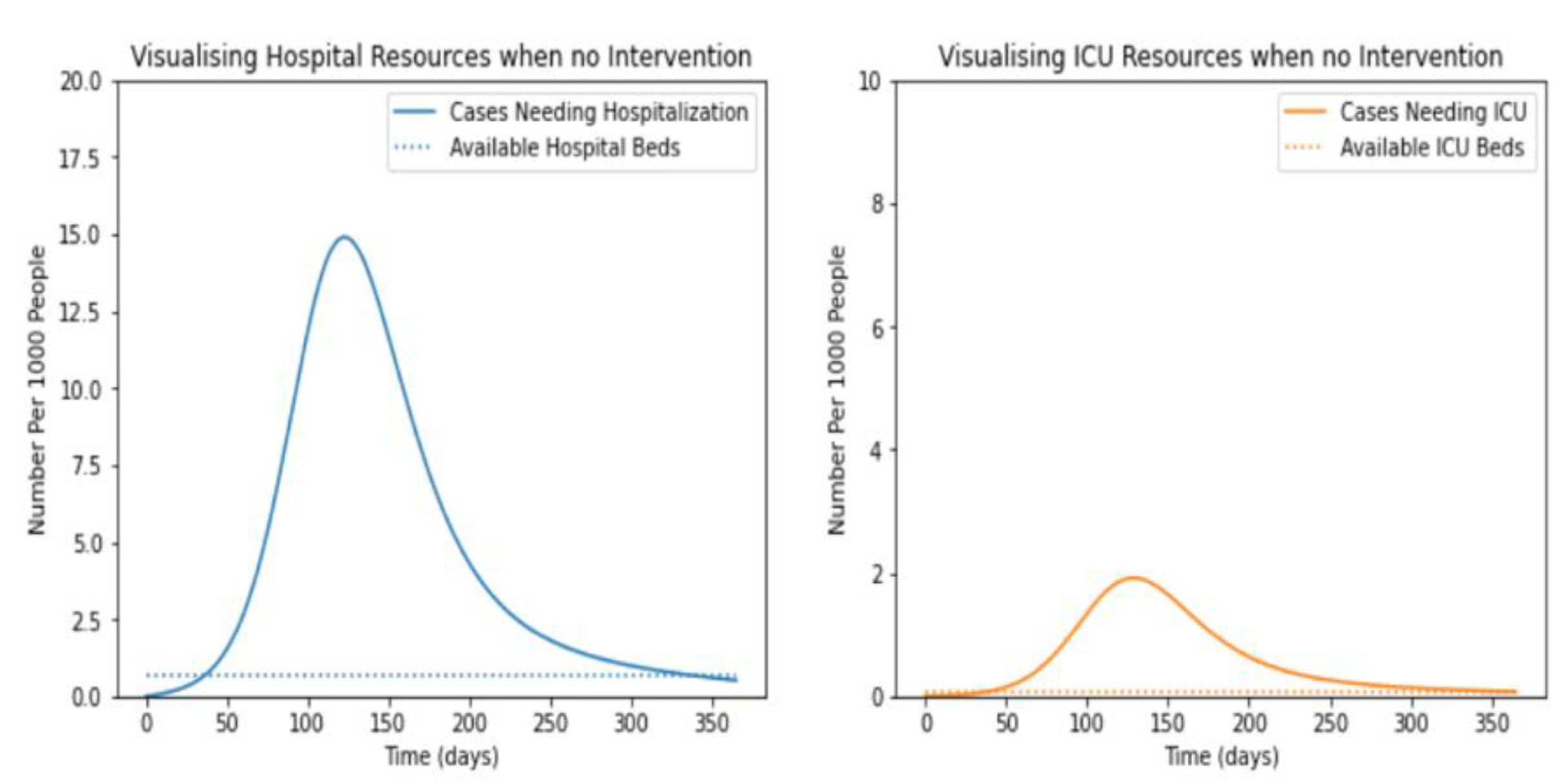
5.1. Without Intervention of Social Distancing
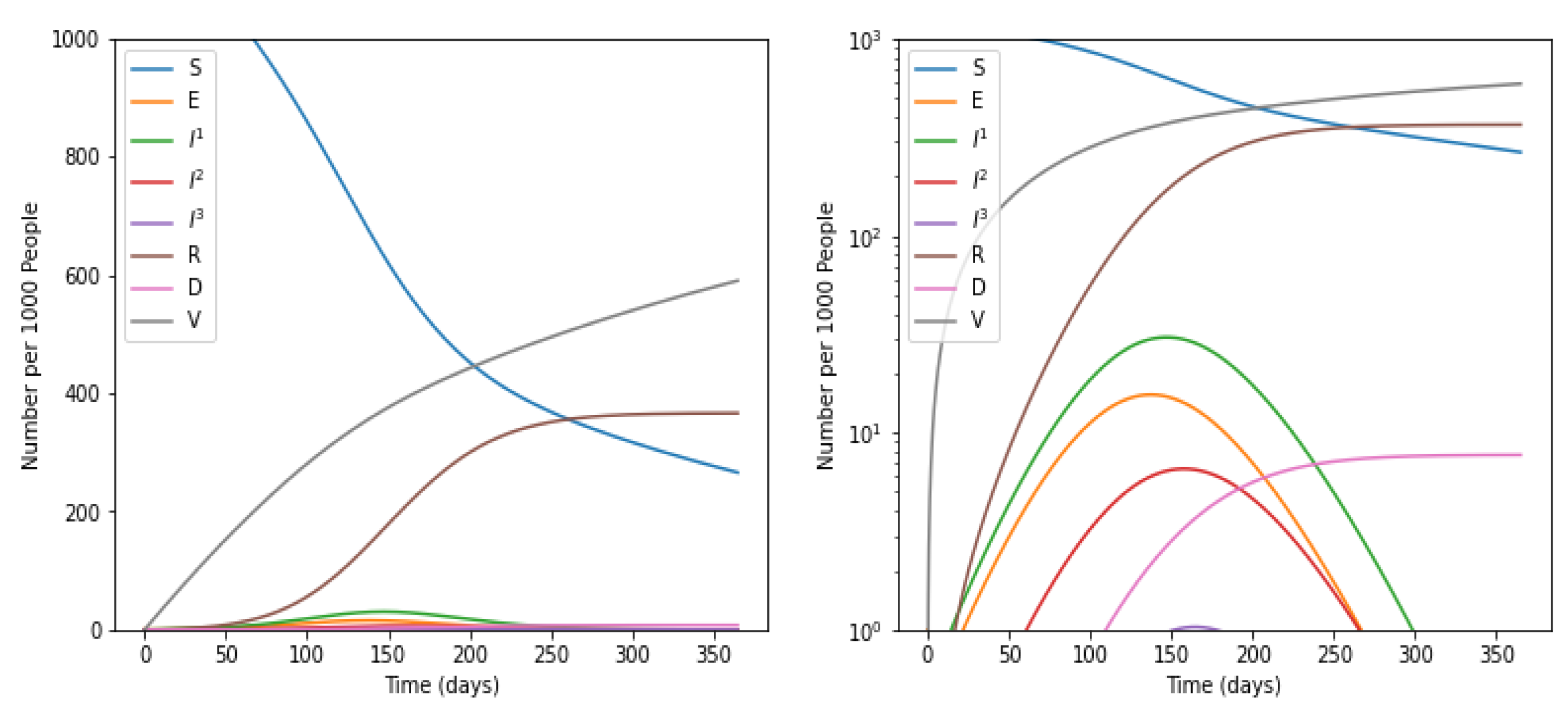
5.2. With Intervention of Social Distancing
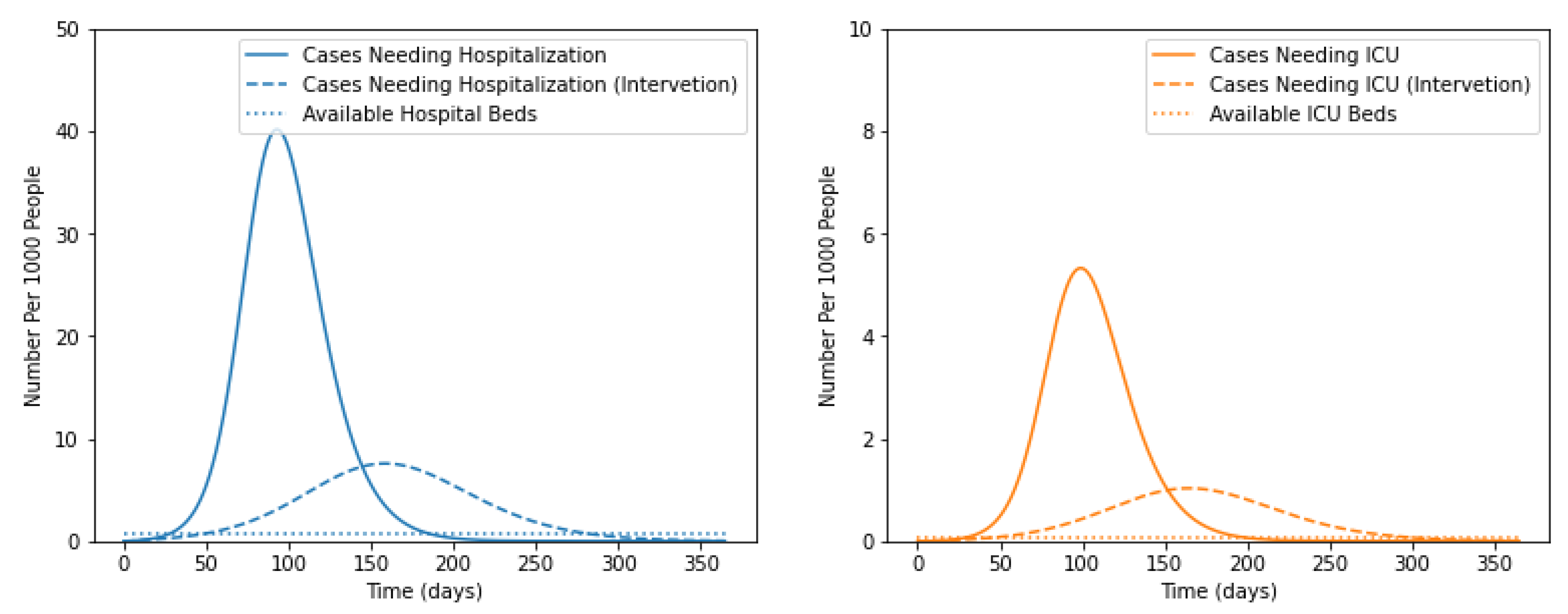
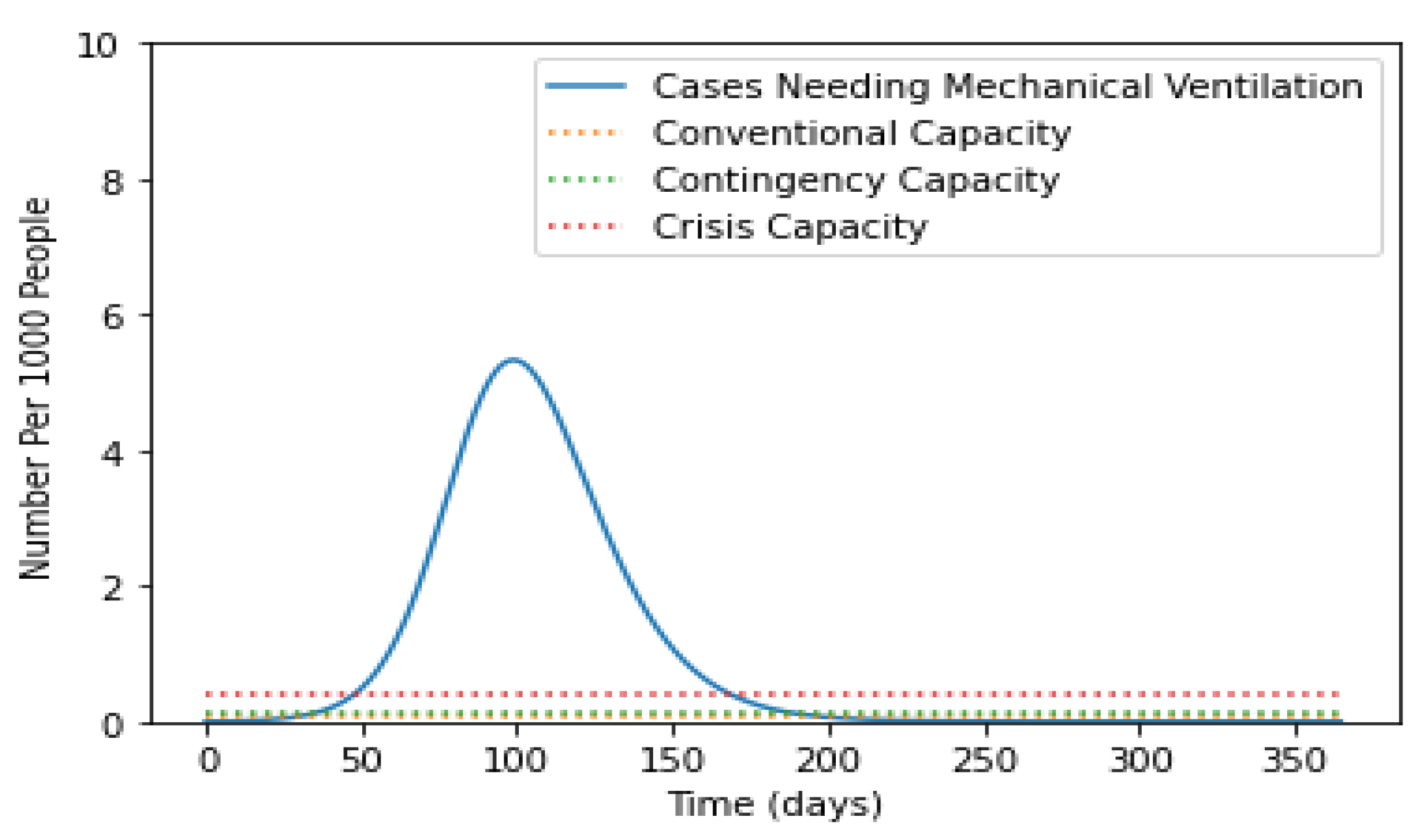
5.3. Impact of Social Distancing and Vaccination on the Number of Infectious Cases
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Topic: GDP of World. Available online: https://data.worldbank.org/indicator/NY.GDP.MKTP.KD.ZG?end=2020&start=1961&view=chart (accessed on 23 December 2021).
- Topic: COVID-19 Cases. Available online: https://covid19.who.int/ (accessed on 12 December 2021).
- Topic: Approved Vaccines. Available online: https://covid19.trackvaccines.org/agency/who/ (accessed on 10 December 2021).
- Topic: Countries with Vaccine. Available online: https://www.who.int/ (accessed on 1 December 2021).
- Weiss, H.H. The SIR model and the foundations of public health. Mater. Math. 2013, 2013, 1–17. [Google Scholar]
- Li, M.Y.; Muldowney, J.S. Global stability for the SEIR model in epidemiology. Math. Biosci. 1995, 125, 155–164. [Google Scholar] [CrossRef]
- Luo, W.; Peng Tay, W. Finding an infection source under the SIS model. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, USA, 26–31 May 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar]
- Fernández-Villaverde, J.; Jones, C.I. Estimating and Simulating a SIRD Model of COVID-19 for Many Countries, States, and Cities; No. w27128; National Bureau of Economic Research: Cambridge, MA, USA, 2020. [Google Scholar]
- Bichara, D.; Iggidr, A.; Sallet, G. Global analysis of multi-strains SIS, SIR and MSIR epidemic models. J. Appl. Math. Comput. 2014, 44, 273–292. [Google Scholar] [CrossRef] [Green Version]
- Qiao, M.; Liu, A.; Foryś, U. Qualitative analysis of the SICR epidemic model with impulsive vaccinations. Math. Methods Appl. Sci. 2013, 36, 695–706. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, H. Modeling the Epidemic Dynamics and Control of COVID-19 Outbreak in China; Quantitative Biology: Beijing, China, 2020; pp. 1–9. [Google Scholar]
- Singh, P.; Gupta, A. Generalized SIR (GSIR) epidemic model: An improved framework for the predictive monitoring of COVID-19 pandemic. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Niu, R.; Wong, E.W.M.; Chan, Y.-C.; Van Wyk, M.A.; Chen, G. Modeling the COVID-19 pandemic using an SEIHR model with human migration. IEEE Access 2020, 8, 195503–195514. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Saad, D. Impact of presymptomatic transmission on epidemic spreading in contact networks: A dynamic message-passing analysis. Phys. Rev. E 2021, 103, 052303–052313. [Google Scholar] [CrossRef]
- Marpaung, F.; Rangkuti, Y.M.; Sinaga, M.S. The analysis of optimal singular controls for SEIR model of tuberculosis. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2014; Volume 1635, No. 1. [Google Scholar]
- Safarishahrbijari, A.; Lawrence, T.; Lomotey, R.; Liu, J.; Waldner, C.; Osgood, N. Particle filtering in a SEIRV simulation model of H1N1 influenza. In Proceedings of the 2015 Winter Simulation Conference (WSC), Huntington Beach, CA, USA, 6–9 December 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Ghostine, R.; Gharamti, M.; Hassrouny, S.; Hoteit, I. An extended seir model with vaccination for forecasting the COVID-19 pandemic in saudi arabia using an ensemble kalman filter. Mathematics 2021, 9, 636. [Google Scholar] [CrossRef]
- Li, Y.; Ge, L.; Zhou, Y.; Cao, X.; Zheng, J. Toward the Impact of Non-pharmaceutical Interventions and Vaccination on the COVID-19 Pandemic with Time-Dependent SEIR Model. Front. Artif. Intell. 2021, 4, 26. [Google Scholar] [CrossRef]
- Li, H.; Wang, J. Global Dynamics of an SEIR Model with the Age of Infection and Vaccination. Mathematics 2021, 9, 2195. [Google Scholar] [CrossRef]
- Wang, X.; Wu, H.; Tang, S. Assessing Age-Specific Vaccination Strategies and Post-Vaccination Reopening Policies for COVID-19 Control Using SEIR Modeling Approach. medRxiv 2021. [Google Scholar] [CrossRef]
- Rajapaksha, R.N.U.; Wijesinghe, M.S.D.; Jayasooriya, S.P.; Gunawardana, B.I.; Weerasinghe, W.P.C. An Extended Susceptible-Exposed-Infected-Recovered (SEIR) Model with Vaccination for Forecasting the COVID-19 Pandemic in Sri Lanka. medRxiv 2021. [Google Scholar] [CrossRef]
- Markovič, R.; Šterk, M.; Marhl, M.; Perc, M.; Gosak, M. Socio-demographic and health factors drive the epidemic progression and should guide vaccination strategies for best COVID-19 containment. Results Phys. 2021, 26, 104433. [Google Scholar] [CrossRef] [PubMed]
- Mahata, A.; Paul, S.; Mukherjee, S.; Roy, B. Stability analysis and Hopf bifurcation in fractional order SEIRV epidemic model with a time delay in infected individuals. Part. Differ. Equ. Appl. Math. 2022, 5, 100282. [Google Scholar] [CrossRef]
- Al Ataby, A.; Jiang, S.; Al-Naima, F. COVID-19 Cases Estimation in the UK Using Improved SEIR Models. In Proceedings of the 2021 14th International Conference on Developments in eSystems Engineering (DeSE), Sharjah, United Arab Emirates, 7–10 December 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Regis-Hernández, F.; Mora-Vargas, J.; Sánchez-Partida, D.; Ruiz, A. Optimising Distribution of Limited COVID-19 Vaccines: Analysing Impact in Argentine. In Humanitarian Logistics from the Disaster Risk Reduction Perspective; Springer: Cham, Switzerland, 2022; pp. 273–291. [Google Scholar]
- Feng, A.; Obolski, U.; Stone, L.; He, D. Modelling COVID-19 Vaccine Breakthrough Infections in Highly Vaccinated Israel-the effects of waning immunity and third vaccination dose. medRxiv 2022. [Google Scholar] [CrossRef]
- Nana-Kyere, S.; Boateng, F.A.; Jonathan, P.; Donkor, A.; Hoggar, G.K.; Titus, B.D.; Kwarteng, D.; Adu, I.K. Global Analysis and Optimal Control Model of COVID-19. Comput. Math. Methods Med. 2022, 2022, 1–20. [Google Scholar] [CrossRef]
- Singh, V.; Poonia, R.C.; Kumar, S.; Dass, P.; Agarwal, P.; Bhatnagar, V.; Raja, L. Prediction of COVID-19 corona virus pandemic based on time series data using Support Vector Machine. J. Discret. Math. Sci. Cryptogr. 2020, 23, 1583–1597. [Google Scholar] [CrossRef]
- Bhatnagar, V.; Poonia, R.C.; Nagar, P.; Kumar, S.; Singh, V.; Raja, L.; Dass, P. Descriptive analysis of COVID-19 patients in the context of India. J. Interdiscip. Math. 2021, 24, 489–504. [Google Scholar] [CrossRef]
- Kumari, R.; Kumar, S.; Poonia, R.C.; Singh, V.; Raja, L.; Bhatnagar, V.; Agarwal, P. Analysis and predictions of spread, recovery, and death caused by COVID-19 in India. Big Data Min. Anal. 2021, 4, 65–75. [Google Scholar] [CrossRef]
- Kou, G.; Xu, Y.; Peng, Y.; Shen, F.; Chen, Y.; Chang, K.; Kou, S. Bankruptcy prediction for SMEs using transactional data and two-stage multiobjective feature selection. Decis. Support Syst. 2021, 140, 113429. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Z.; Yan, L.; Wen, F. Forecasting the volatility of EUA futures with economic policy uncertainty using the GARCH-MIDAS model. Financ. Innov. 2021, 7, 1–19. [Google Scholar] [CrossRef]
- Li, B.; Xu, Z. Insights into financial technology (FinTech): A bibliometric and visual study. Financ. Innov. 2021, 7, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Ke, J. Pricing, management and decision-making of financial markets with artificial intelligence: Introduction to the issue. Financ. Innov. 2021, 7, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, P.; Nieto, J.J.; Ruzhansky, M.; Torres, D.F. Analysis of Infectious Disease Problems (COVID-19) and Their Global Impact; Agarwal, P., Nieto, J.J., Ruzhansky, M., Torres, D.F., Eds.; Springer: Singapore, 2021. [Google Scholar]
- Otaki, J.M.; Wataru, N.; Morikazu, N. Nonself Mutations in the Spike Protein Suggest an Increase in the Antigenicity and a Decrease in the Virulence of the Omicron Variant of SARS-CoV-2. bioRxiv 2022, 2, 407–418. [Google Scholar] [CrossRef]
- Vega, R.; Leonardo, F.; Russell, G. SIMLR: Machine Learning inside the SIR model for COVID-19 Forecasting. Forecasting 2022, 4, 72–94. [Google Scholar] [CrossRef]

| S. N. | Name of Company | Name of Vaccine |
|---|---|---|
| 1 | Moderna | mRNA-1273 |
| 2 | Pfizer/BioNTech | BNT162b2 |
| 3 | Janssen (Johnson & Johnson) | Ad26.COV2.S |
| 4 | Oxford/AstraZeneca | AZD1222 |
| 5 | Serum Institute of India | Covishield |
| 6 | Bharat Biotech | Covaxin |
| 7 | Sinopharm (Beijing) | BBIBP-CorV (Vero Cells) |
| 8 | Sinovac | CoronaVac |
| S. N. | Name of Country | % of Population Fully Vaccination |
|---|---|---|
| 1 | India | 37.3% |
| 2 | United States | 60.8% |
| 3 | Brazil | 65.6% |
| 4 | Indonesia | 37.7% |
| 5 | Japan | 77.9% |
| 6 | Russia | 42.6% |
| 7 | Germany | 69.5% |
| 8 | United Kingdom | 69.5% |
| 9 | France | 71.0% |
| 10 | Iran | 57.3% |
| 11 | Saudi Arabia | 65.5% |
| 12 | Egypt | 16.4% |
| 13 | South Africa | 25.8% |
| 14 | United Arab Emirates | 91.1% |
| 15 | Nigeria | 1.9% |
| S. N. | Acronym | Name of Model | Parameter Added | Definition |
|---|---|---|---|---|
| 1 | SIS [7] | Susceptible-Infectious-Susceptible | Simplest form | Immunity does not build |
| 2 | SIRD [8] | Susceptible-Infectious-Recovered-Deceased | Deceased | D is the mortality rate |
| 3 | MSIR [9] | Maternal-Susceptible-Infectious-Recovered | Maternally Derived Immune | Newborn babies which are immune to a specific disease, such as measles |
| 4 | SICR [10] | Susceptible-Infectious-Carrier-Recovered | Carrier | It is applicable on those where infection resides in the body forever, such as TB |
| 5 | SUQC [11] | Susceptible-Unquarantined, Quarantine-Confirmed | Unquarantined, Quarantine | Number of people who are quarantined and unquarantined. |
| 6 | GSIR [12] | Generalized-Susceptible-Infectious-Recovered | Generalized | Assumed that throughout time, many waves of varied peak amplitude and form arise and fade away |
| 7 | SEIHR [13] | Generalized-Susceptible-Infectious-Hospitalized-Recovered | Hospitalized | Number of persons hospitalized |
| 8 | SCEIR [14] | Susceptible-Exposed-Infectious-Recovered-Removed | Confined | When an individual is experiencing lockdown |
| 9 | ISSEIR [15] | Interacting Subpopulation- Susceptible-Exposed-Infectious-Recovered | Interacting Subpopulation | Separate SEIR model between each subgroup of the population |
| 10 | SEIRV [16] | Susceptible-Infectious-Recovered-Vaccination | Vaccination | When the population is vaccinated |
| Name of Coefficient | Definition |
|---|---|
| Total population (comprising 1000 individuals in this research) | |
| S | Susceptible individuals |
| Rate at which one infected in class I1 contact susceptible and infect all of them. Thus, the susceptible individuals changed to exposed individuals. | |
| Rate at which one infected in class I2 contact susceptible and infect all of them. Thus, the susceptible individuals changed to exposed individuals. | |
| Rate at which one infected in class I3 contact susceptible and infect all of them. Thus, the susceptible individuals changed to exposed individuals. | |
| I1 | Rate of mild infection and hospitalization not required. |
| I2 | Rate of severe infection and hospitalization is required. |
| I3 | Rate of critical infection and I.C.U. is required. |
| E | Set of exposed individuals; they are infected but not asymptotic and infectious. |
| V | Set of vaccinated persons. |
| Rate at which infected individuals in class I1 recovered from the disease and immunity is developed. | |
| Rate at which infected individuals in class I2 recovered from the disease and immunity is developed. | |
| Rate at which infected individuals in class I3 recover from the disease and immunity is developed. | |
| p1 | Rate at which one infected in class I1 is shifted to class I2. |
| p2 | Rate at which one infected in class I2 is shifted to class I3. |
| R | Set of individuals who have recovered from the disease and are now immune. |
| λ | Rate of natural (those who are not deceased from the COVID-19). |
| The death rate of individuals in the most severe stage of disease. | |
| Ψ | The rate at which individuals are vaccinated |
| η | Vaccine inefficacy |
| D | Set of removed populations |
| Coefficient | Crude Birth Rate (σ) | λ | η | ψ |
|---|---|---|---|---|
| 0.0 | 0.00025 | 0.0 | 0.0 | |
| α | 0.2 | - | - | - |
| γ | 0.0 | 0.08 | 0.06818182 | 0.08571429 |
| 0.0 | 0.02 | 0.02272727 | - | |
| 0.057142857 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poonia, R.C.; Saudagar, A.K.J.; Altameem, A.; Alkhathami, M.; Khan, M.B.; Hasanat, M.H.A. An Enhanced SEIR Model for Prediction of COVID-19 with Vaccination Effect. Life 2022, 12, 647. https://doi.org/10.3390/life12050647
Poonia RC, Saudagar AKJ, Altameem A, Alkhathami M, Khan MB, Hasanat MHA. An Enhanced SEIR Model for Prediction of COVID-19 with Vaccination Effect. Life. 2022; 12(5):647. https://doi.org/10.3390/life12050647
Chicago/Turabian StylePoonia, Ramesh Chandra, Abdul Khader Jilani Saudagar, Abdullah Altameem, Mohammed Alkhathami, Muhammad Badruddin Khan, and Mozaherul Hoque Abul Hasanat. 2022. "An Enhanced SEIR Model for Prediction of COVID-19 with Vaccination Effect" Life 12, no. 5: 647. https://doi.org/10.3390/life12050647
APA StylePoonia, R. C., Saudagar, A. K. J., Altameem, A., Alkhathami, M., Khan, M. B., & Hasanat, M. H. A. (2022). An Enhanced SEIR Model for Prediction of COVID-19 with Vaccination Effect. Life, 12(5), 647. https://doi.org/10.3390/life12050647









