PhyloM: A Computer Program for Phylogenetic Inference from Measurement or Binary Data, with Bootstrapping
Abstract
:1. Introduction
2. Materials and Methods
2.1. Algorithm for Computing the Pairwise Distance Matrix from Measurement Data
2.2. Algorithm for Computing the Pairwise Distance Matrix from Binary Data
2.3. Genome Tree Reconstruction
2.4. Metabolic Measurement Data
3. Results
3.1. Input File
3.2. Distance Matrix
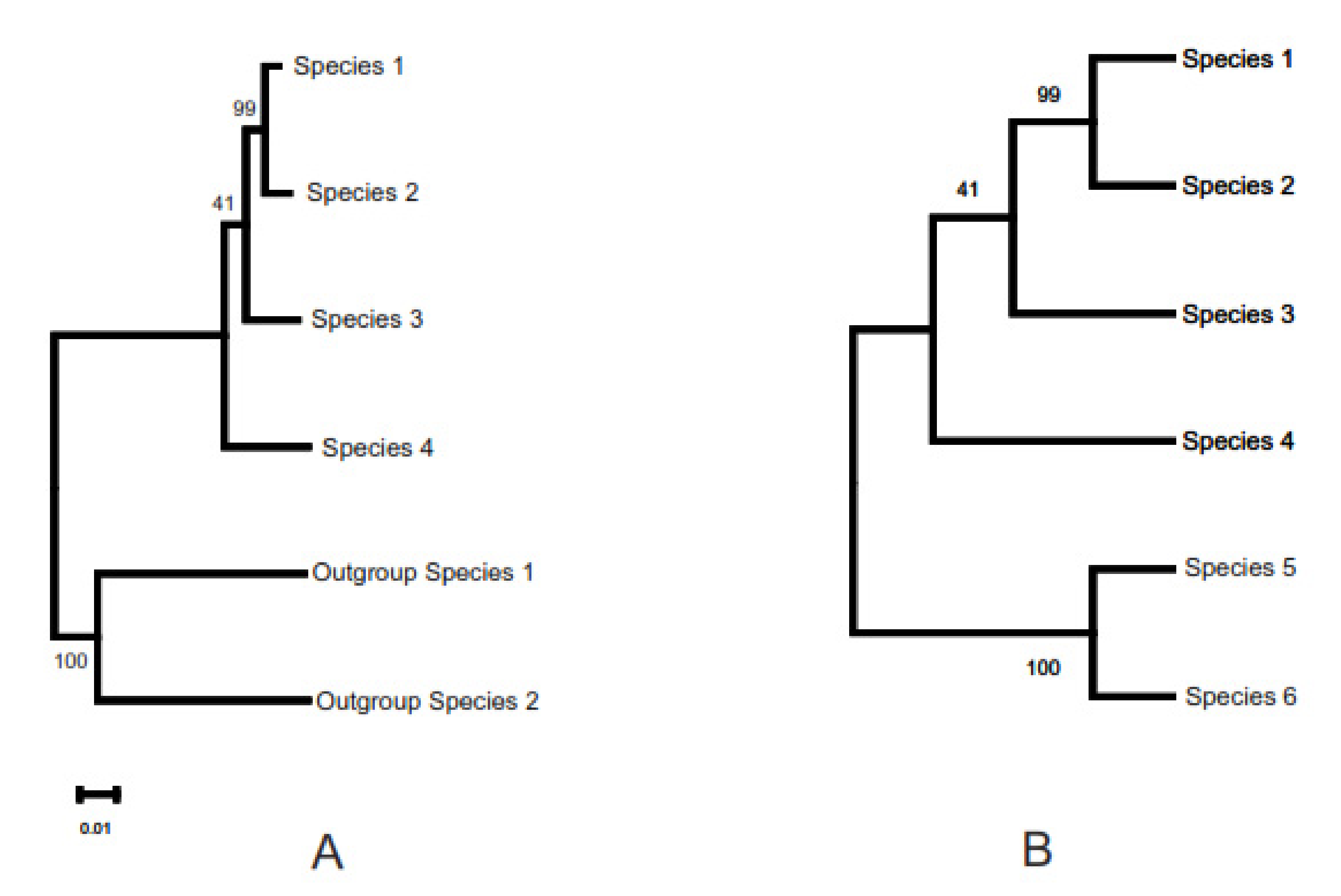
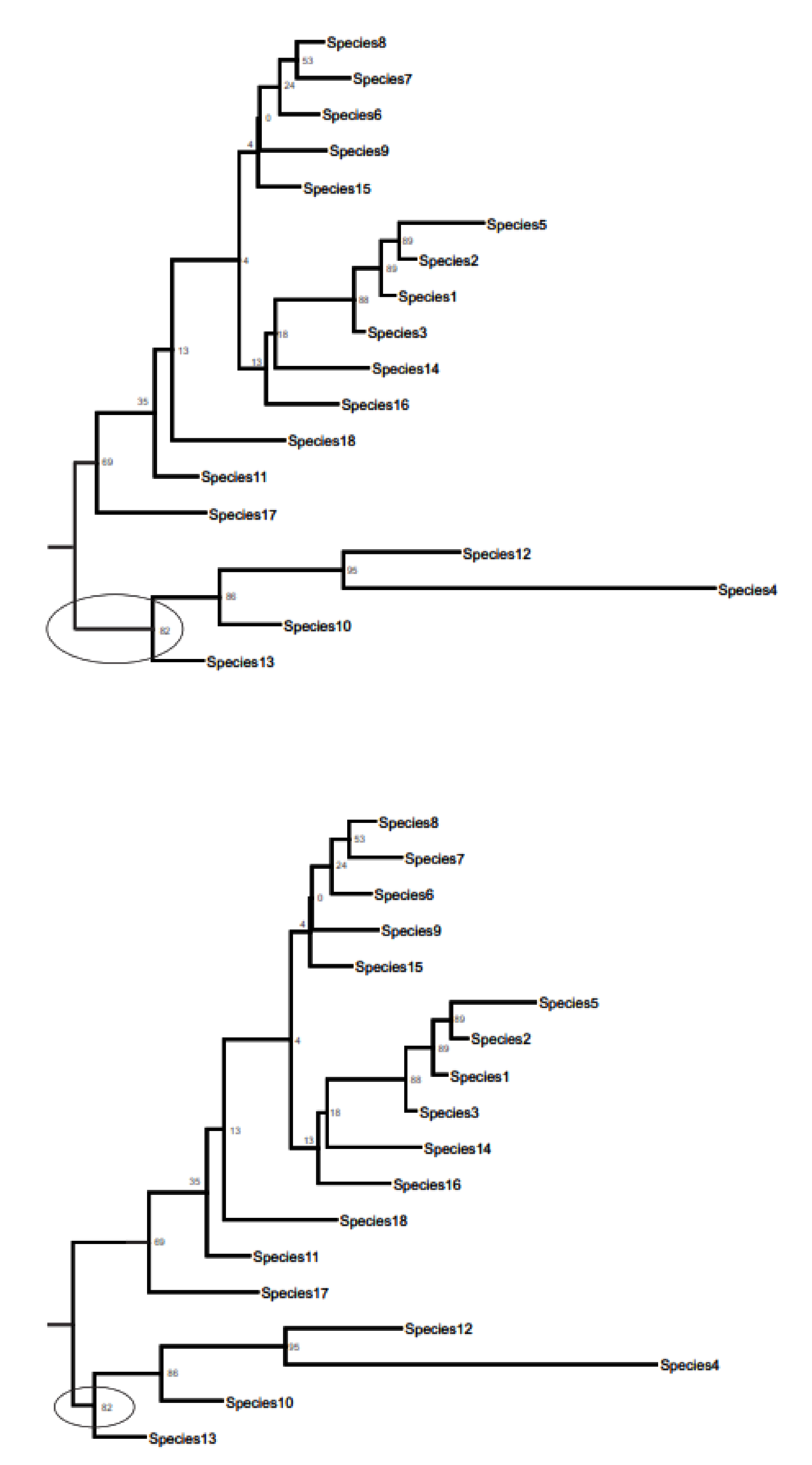
3.3. Phylogenetic Inference
4. Discussion
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soby, S.D.; Gadagkar, S.R.; Contreras, C.; Caruso, F.L. Chromobacterium vaccinii sp. nov., isolated from native and cultivated cranberry (Vaccinium macrocarpon Ait.) bogs and irrigation ponds. Int. J. Syst. Evol. Microbiol. 2013, 63, 1840–1846. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Felsenstein, J. Confidence limits on phylogenies: An approach using the bootstrap. Evolution 1985, 39, 783–791. [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Stecher, G.; Kumar, S. MEGA11: Molecular Evolutionary Genetics Analysis Version 11. Mol. Biol. Evol. 2021, 38, 3022–3027. [Google Scholar] [CrossRef] [PubMed]
- Felsenstein, J. PHYLIP: Phylogeny Inference Package; University of Washington: Seattle, WA, USA, 1995. [Google Scholar]
- Swofford, D.L. PAUP*: Phylogenetic Analysis Using Parsimony (and Other Methods); Sinauer Associates: Sunderland, MA, USA, 1998. [Google Scholar]
- Huelsenbeck, J.P.; Ronquist, F. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics 2001, 17, 754–755. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Z.H.; Rannala, B. Molecular phylogenetics: Principles and practice. Nat. Rev. Genet. 2012, 13, 303–314. [Google Scholar] [CrossRef] [PubMed]
- Saitou, N.; Nei, M. The Neighbor-Joining Method—A New Method for Reconstructing Phylogenetic Trees. Jpn. J. Genet. 1987, 61, 611. [Google Scholar]
- Dwivedi, B.; Gadagkar, S.R. Phylogenetic inference under varying proportions of indel-induced alignment gaps. BMC Evol. Biol. 2009, 9, 211. [Google Scholar] [CrossRef] [Green Version]
- Criscuolo, A.; Berry, V.; Douzery, E.J.P.; Gascuel, O. SDM: A fast distance-based approach for (super) tree building in phylogenomics. Syst. Biol. 2006, 55, 740–755. [Google Scholar] [CrossRef] [Green Version]
- Mihaescu, R.; Levy, D.; Pachter, L. Why Neighbor-Joining Works. Algorithmica 2009, 54, 1–24. [Google Scholar] [CrossRef]
- Kuhner, M.K.; Felsenstein, J. A simulation comparison of phylogeny algorithms under equal and unequal evolutionary rates. Mol. Biol. Evol. 1994, 11, 459–468. [Google Scholar]
- Kumar, S.; Gadagkar, S.R. Efficiency of the neighbor-joining method in reconstructing deep and shallow evolutionary relationships in large phylogenies. J. Mol. Evol. 2000, 51, 544–553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nei, M.; Kumar, S. Molecular Evolution and Phylogenetics; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Strimmer, K.; von Haeseler, A.; Salemi, M. Genetic distances and nucleotide substitution models. In The Phylogenetic Handbook—A Practical Approach to Phylogenetic Analysis and Hypothesis Testing, 2nd ed.; Lemey, P., Salemi, M., Vandamme, A.-M., Eds.; Cambridge University Press: Cambridge, MA, USA, 2009. [Google Scholar] [CrossRef]
- Ohno, S. An argument for the genetic simplicity of man and other mammals. J. Hum. Evol. 1972, 1, 651–662. [Google Scholar] [CrossRef]
- King, M.C.; Wilson, A.C. Evolution at two levels in humans and chimpanzees. Science 1975, 188, 107–116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, Y.; Xu, L.; Jovanovic, B.D.; Helenowski, I.B.; Kelly, D.L.; Catalona, W.J.; Yang, X.J.; Pins, M.; Bergan, R.C. The methodology used to measure differential gene expression affects the outcome. J. Biomol. Tech. 2007, 18, 321–330. [Google Scholar] [PubMed]
- Emerson, J.J.; Li, W.H. The genetic basis of evolutionary change in gene expression levels. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 2581–2590. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Corona, B.A.; Fruth, S.; Ofoegbu, O.; Wunderlich, Z. The mode of expression divergence in Drosophila fat body is infection-specific. Genome Res. 2021, 31, 12. [Google Scholar] [CrossRef]
- Josephs, E.B.; Lee, Y.W.; Wood, C.W.; Schoen, D.J.; Wright, S.I.; Stinchcombe, J.R. The Evolutionary Forces Shaping Cis- and Trans-Regulation of Gene Expression within a Population of Outcrossing Plants. Mol. Biol. Evol. 2020, 37, 2386–2393. [Google Scholar] [CrossRef]
- Brown, K.E.; Kelly, J.K. Genome-wide association mapping of transcriptome variation in Mimulus guttatus indicates differing patterns of selection on cis- versus trans-acting mutations. Genetics 2022, 220, 14. [Google Scholar] [CrossRef]
- Gadagkar, S.R.; Call, G.B. Computational tools for fitting the Hill equation to dose-response curves. J. Pharmacol. Toxicol. Methods 2015, 71, 68–76. [Google Scholar] [CrossRef] [Green Version]
- Keck, F.; Rimet, F.; Bouchez, A.; Franc, A. phylosignal: An R package to measure, test, and explore the phylogenetic signal. Ecol. Evol. 2016, 6, 2774–2780. [Google Scholar] [CrossRef]
- Hohna, S.; Landis, M.J.; Heath, T.A.; Boussau, B.; Lartillot, N.; Moore, B.R.; Huelsenbeck, J.P.; Ronquist, F. RevBayes: Bayesian Phylogenetic Inference Using Graphical Models and an Interactive Model-Specification Language. Syst. Biol. 2016, 65, 726–736. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lazarus: The Professional Free Pascal RAD IDE. Version 1.8.4. Available online: https://www.lazarus-ide.org/.
- Davis, J.J.; Wattam, A.R.; Aziz, R.K.; Brettin, T.; Butler, R.; Butler, R.M.; Chlenski, P.; Conrad, N.; Dickerman, A.; Dietrich, E.M.; et al. The PATRIC Bioinformatics Resource Center: Expanding data and analysis capabilities. Nucleic Acids Res. 2020, 48, D606–D612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davis, J.J.; Gerdes, S.; Olsen, G.J.; Olson, R.; Pusch, G.D.; Shukla, M.; Vonstein, V.; Wattam, A.R.; Yoo, H. PATtyFams: Protein Families for the Microbial Genomes in the PATRIC Database. Front. Microbiol. 2016, 7, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stamatakis, A. RAxML version 8: A tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 2014, 30, 1312–1313. [Google Scholar] [CrossRef] [PubMed]
- Edgar, R.C. MUSCLE: Multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004, 32, 1792–1797. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cock, P.J.A.; Antao, T.; Chang, J.T.; Chapman, B.A.; Cox, C.J.; Dalke, A.; Friedberg, I.; Hamelryck, T.; Kauff, F.; Wilczynski, B.; et al. Biopython: Freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics 2009, 25, 1422–1423. [Google Scholar] [CrossRef] [PubMed]
- Stamatakis, A.; Hoover, P.; Rougemont, J. A Rapid Bootstrap Algorithm for the RAxML Web Servers. Syst. Biol. 2008, 57, 758–771. [Google Scholar] [CrossRef]
- Maddison, W.P.; Maddison, D.R. Mesquite: A Modular System for Evolutionary Analysis; Version 3.31. 2017.




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gadagkar, S.R. PhyloM: A Computer Program for Phylogenetic Inference from Measurement or Binary Data, with Bootstrapping. Life 2022, 12, 719. https://doi.org/10.3390/life12050719
Gadagkar SR. PhyloM: A Computer Program for Phylogenetic Inference from Measurement or Binary Data, with Bootstrapping. Life. 2022; 12(5):719. https://doi.org/10.3390/life12050719
Chicago/Turabian StyleGadagkar, Sudhindra R. 2022. "PhyloM: A Computer Program for Phylogenetic Inference from Measurement or Binary Data, with Bootstrapping" Life 12, no. 5: 719. https://doi.org/10.3390/life12050719
APA StyleGadagkar, S. R. (2022). PhyloM: A Computer Program for Phylogenetic Inference from Measurement or Binary Data, with Bootstrapping. Life, 12(5), 719. https://doi.org/10.3390/life12050719





