Sub-Nanosecond Dynamics of Pathologically Relevant Bio-Macromolecules Observed by Incoherent Neutron Scattering
Abstract
:1. Introduction
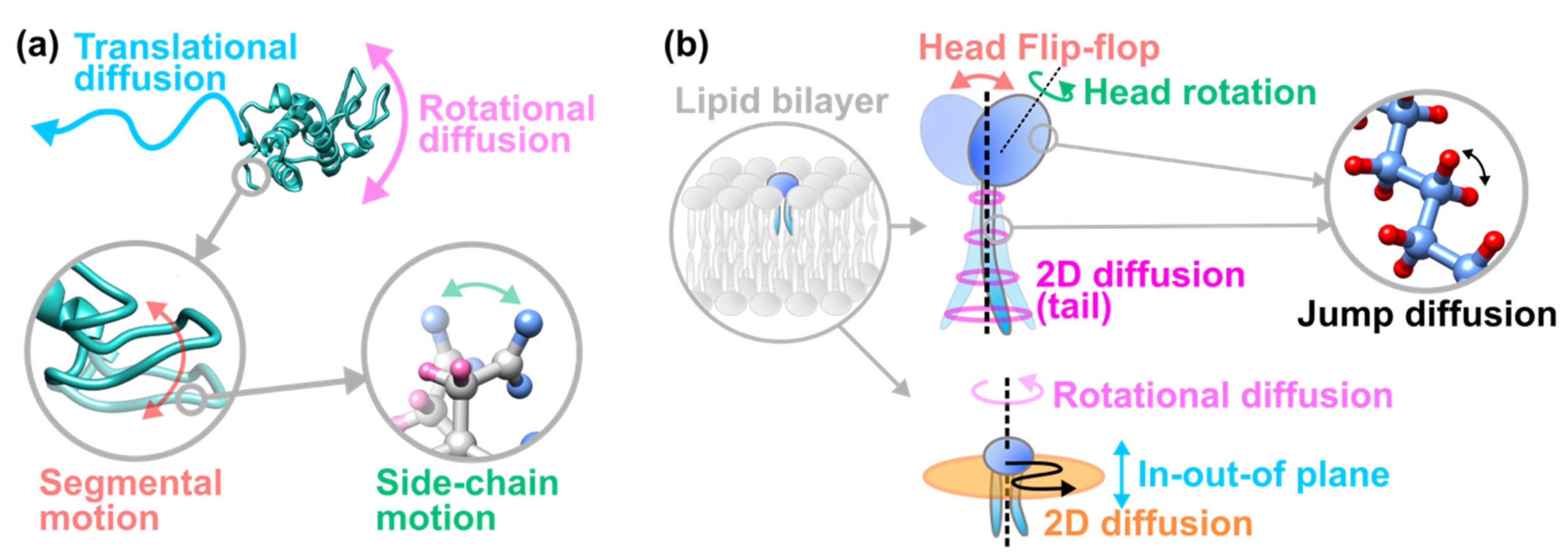
2. Basic Information on Incoherent Neutron Scattering
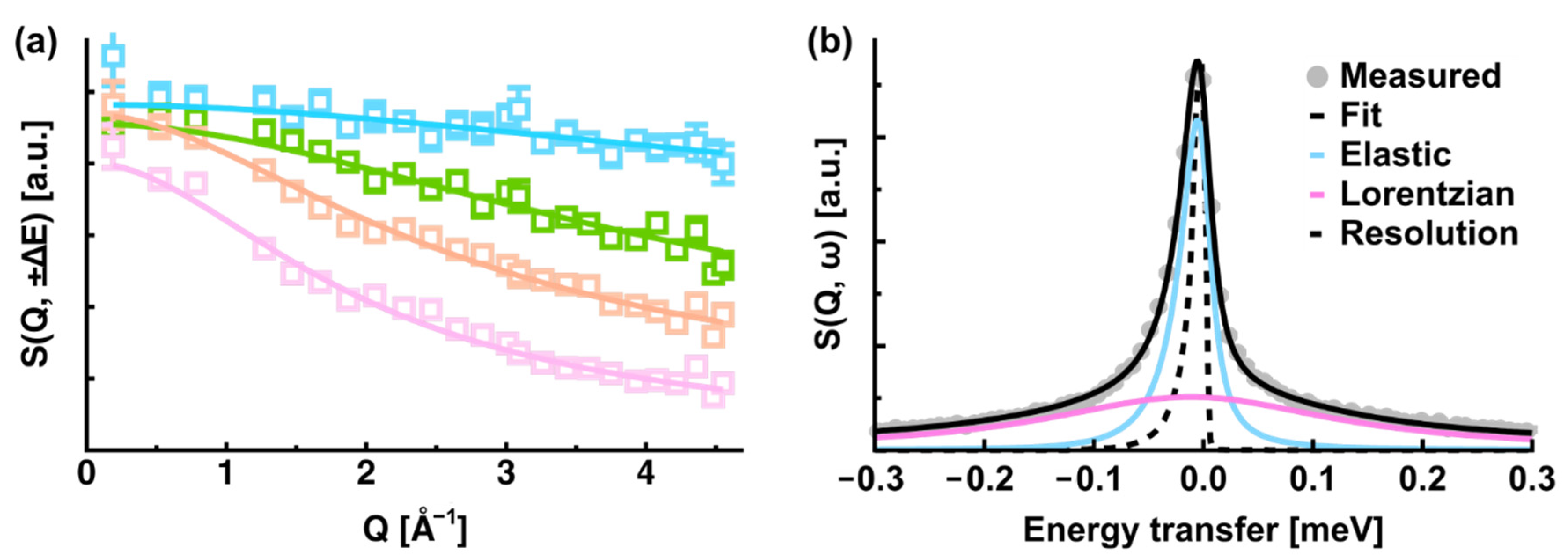
3. iNS Studies on Pathologically Relevant Bio-Macromolecules
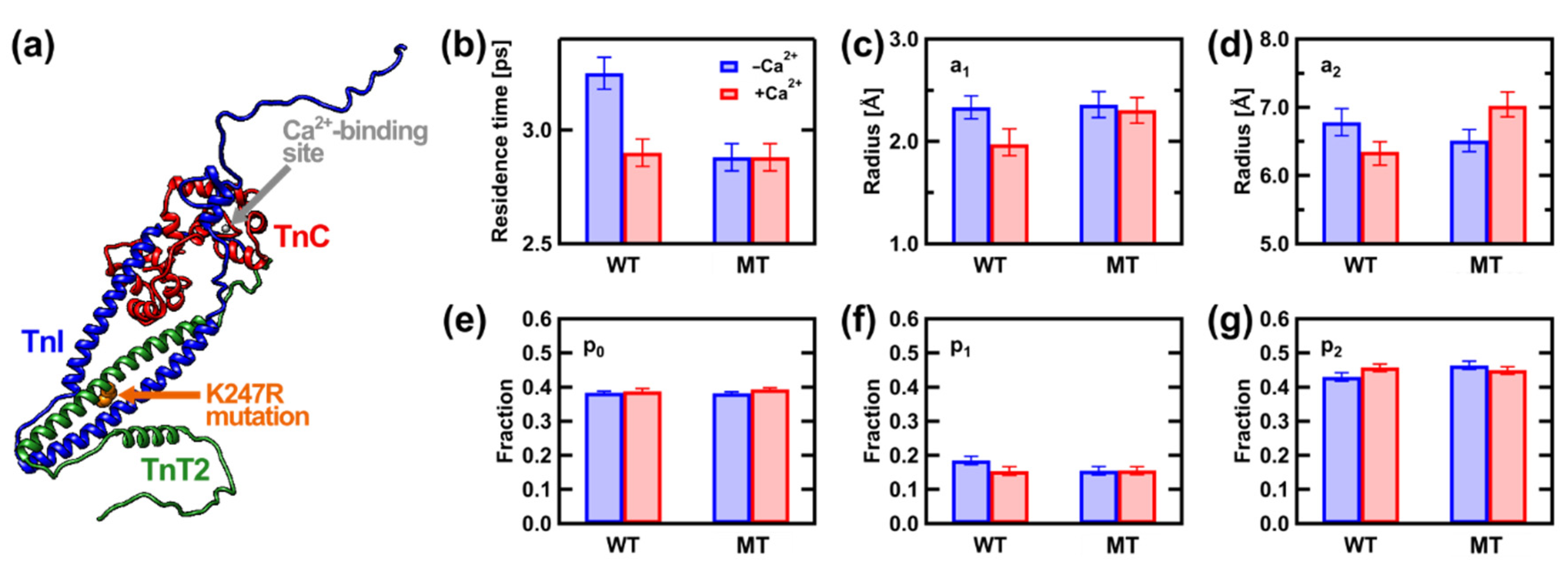
3.1. Protein Mutants as a Cause of Cardiomyopathy
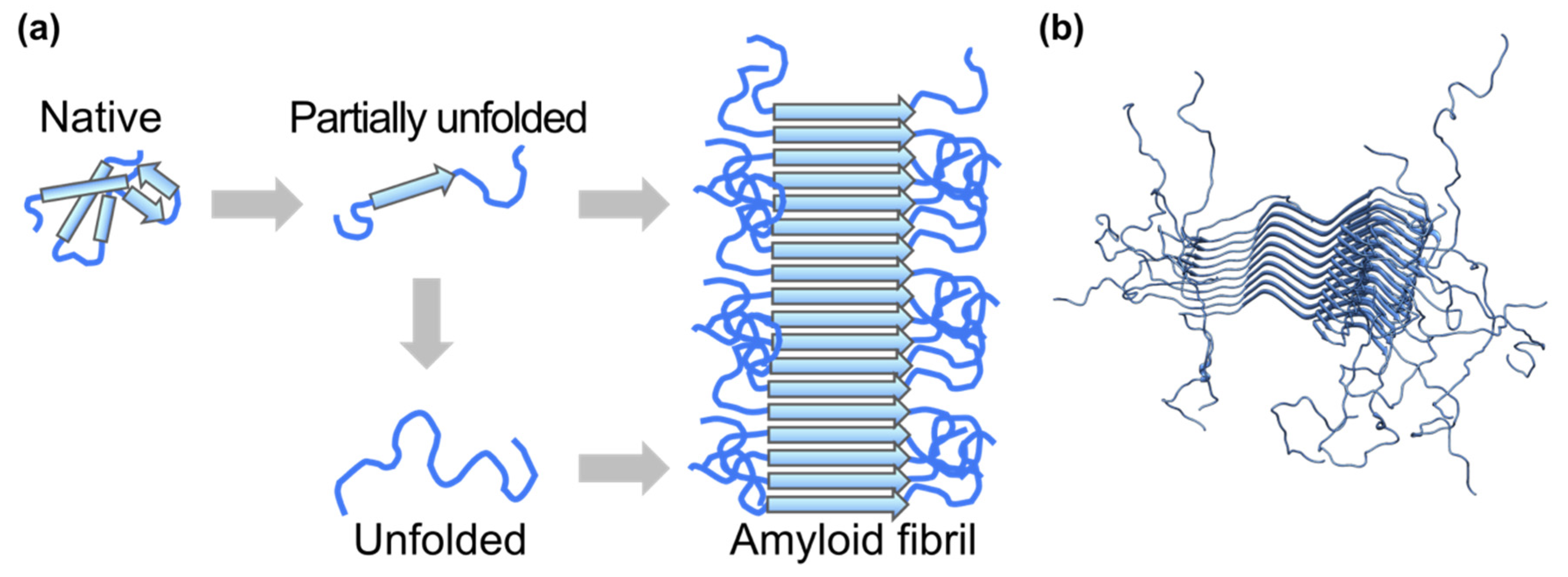
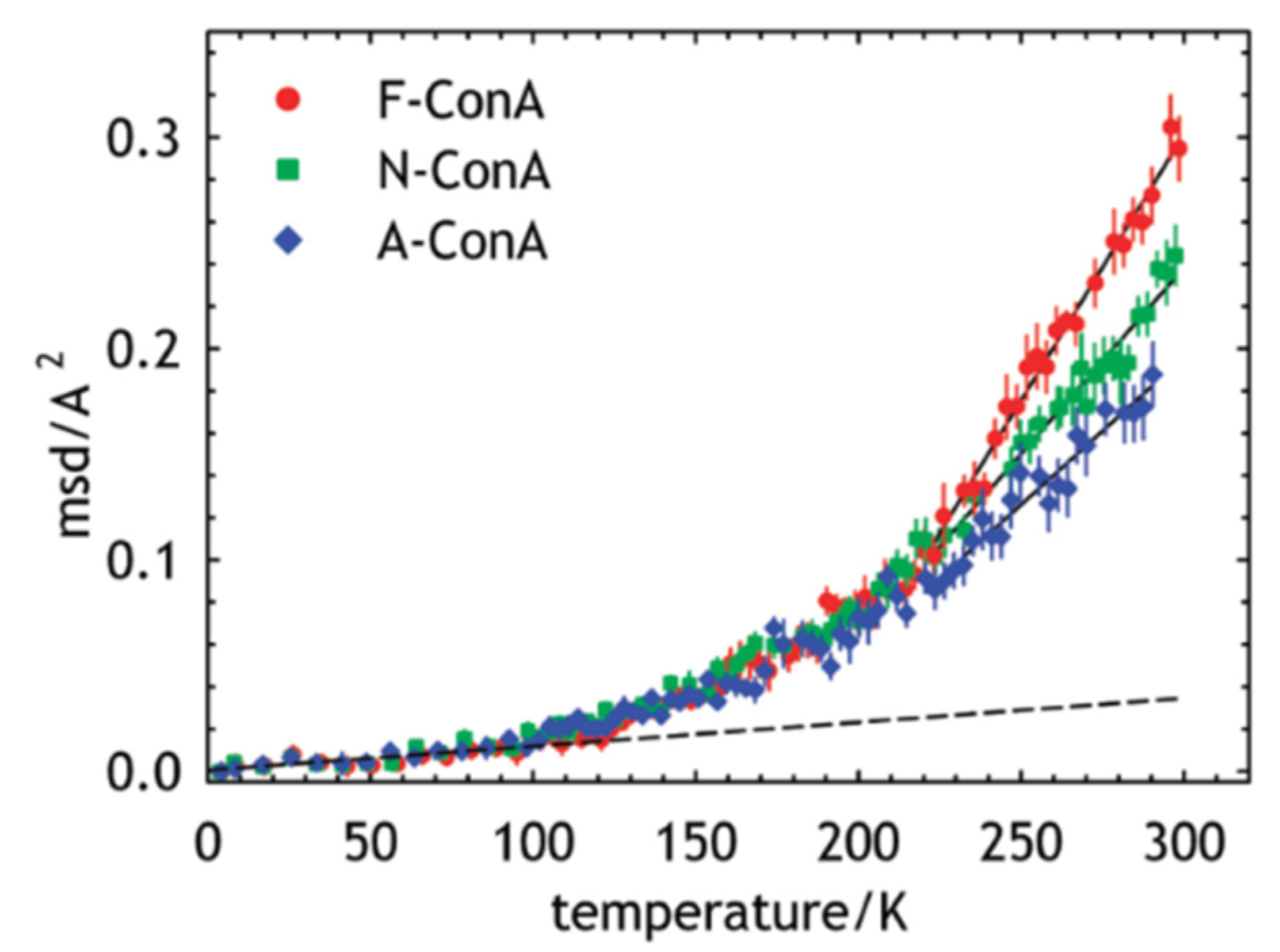
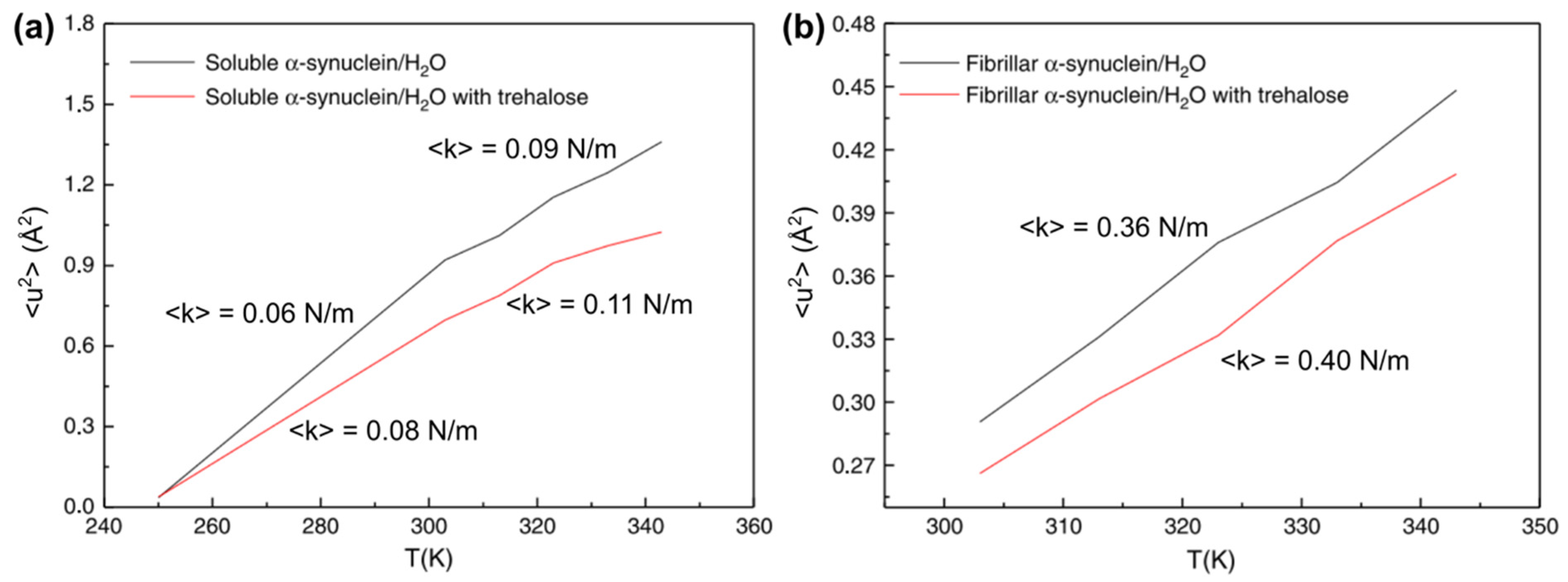
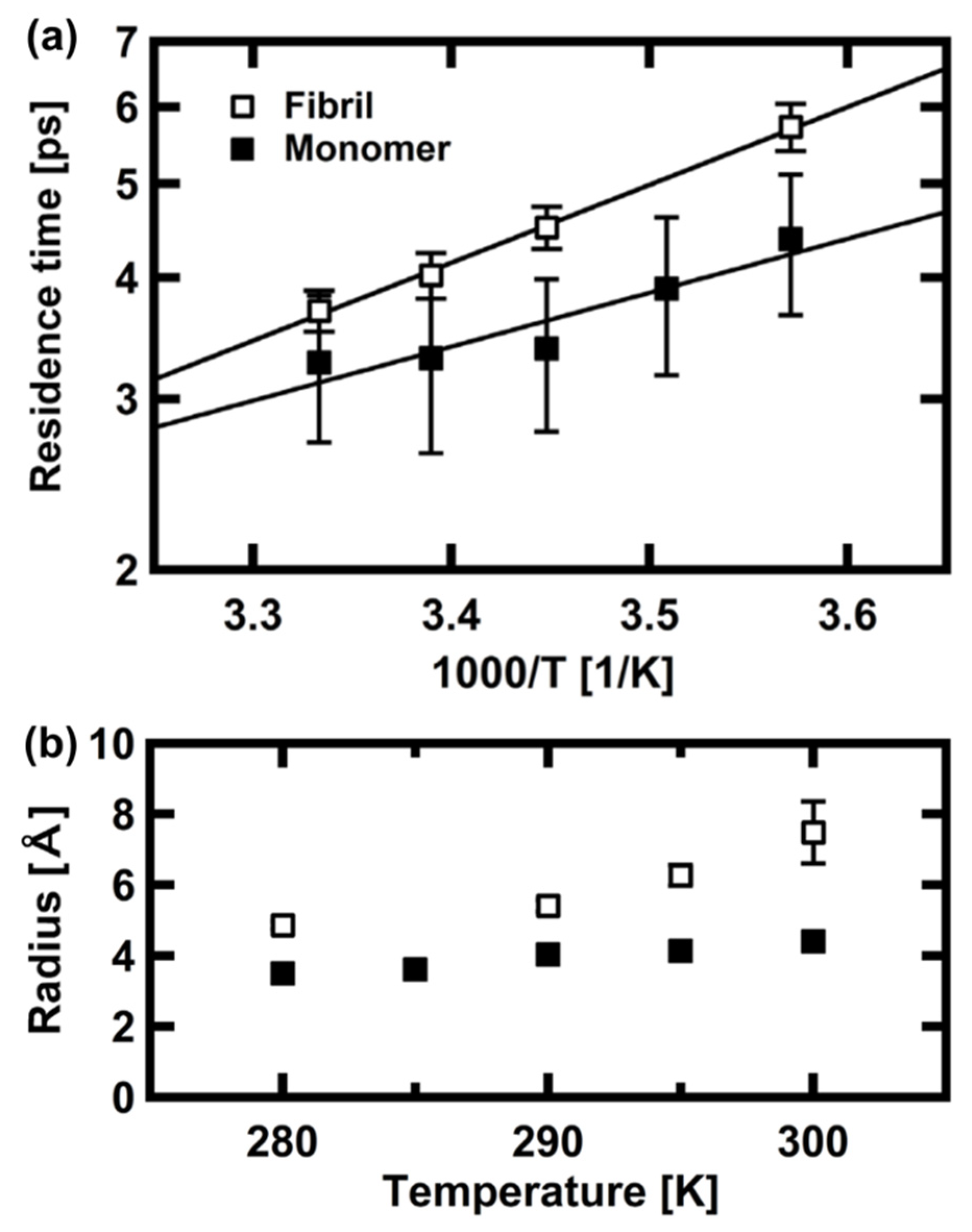
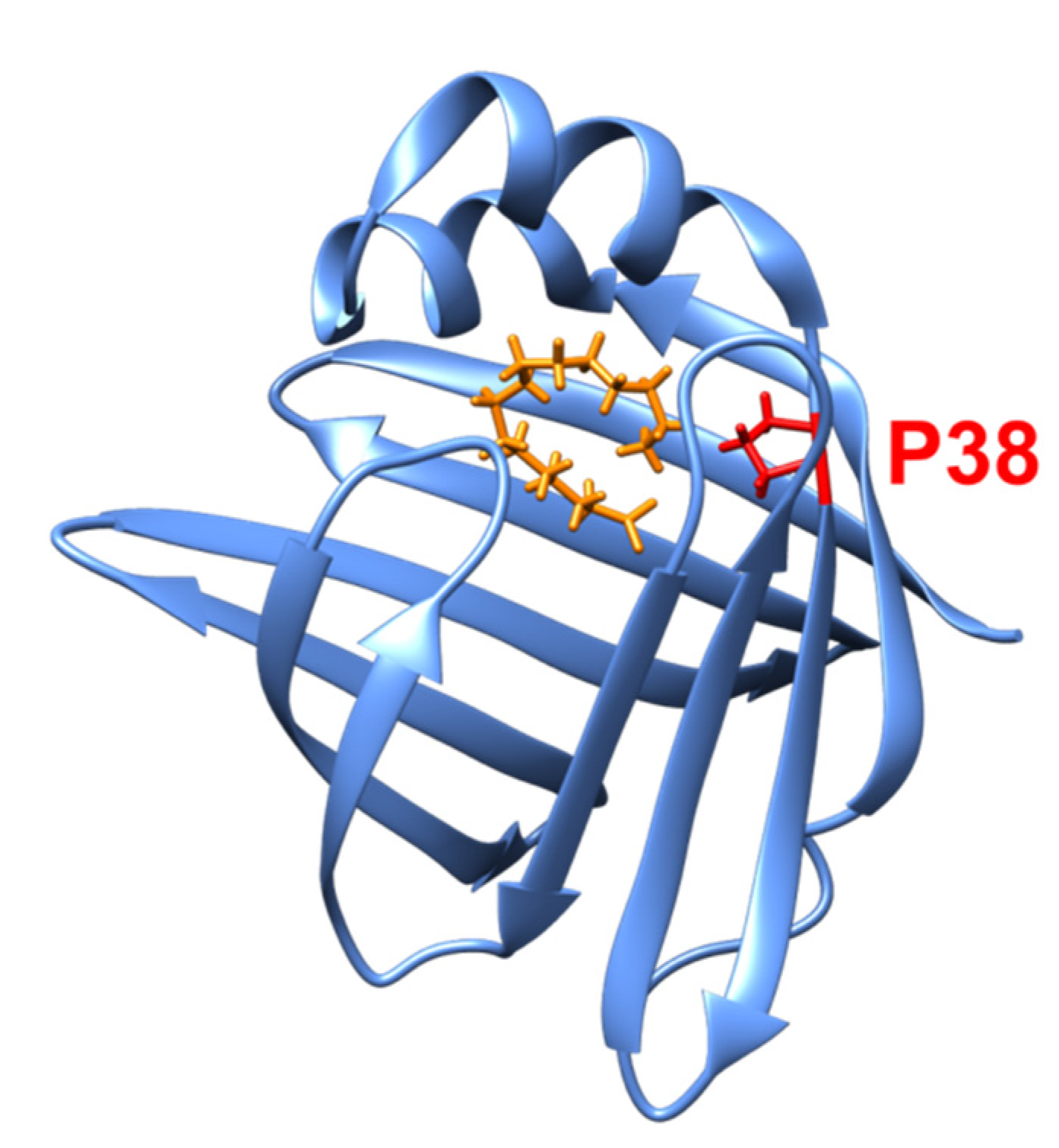
3.2. Proteins Related to Amyloidosis
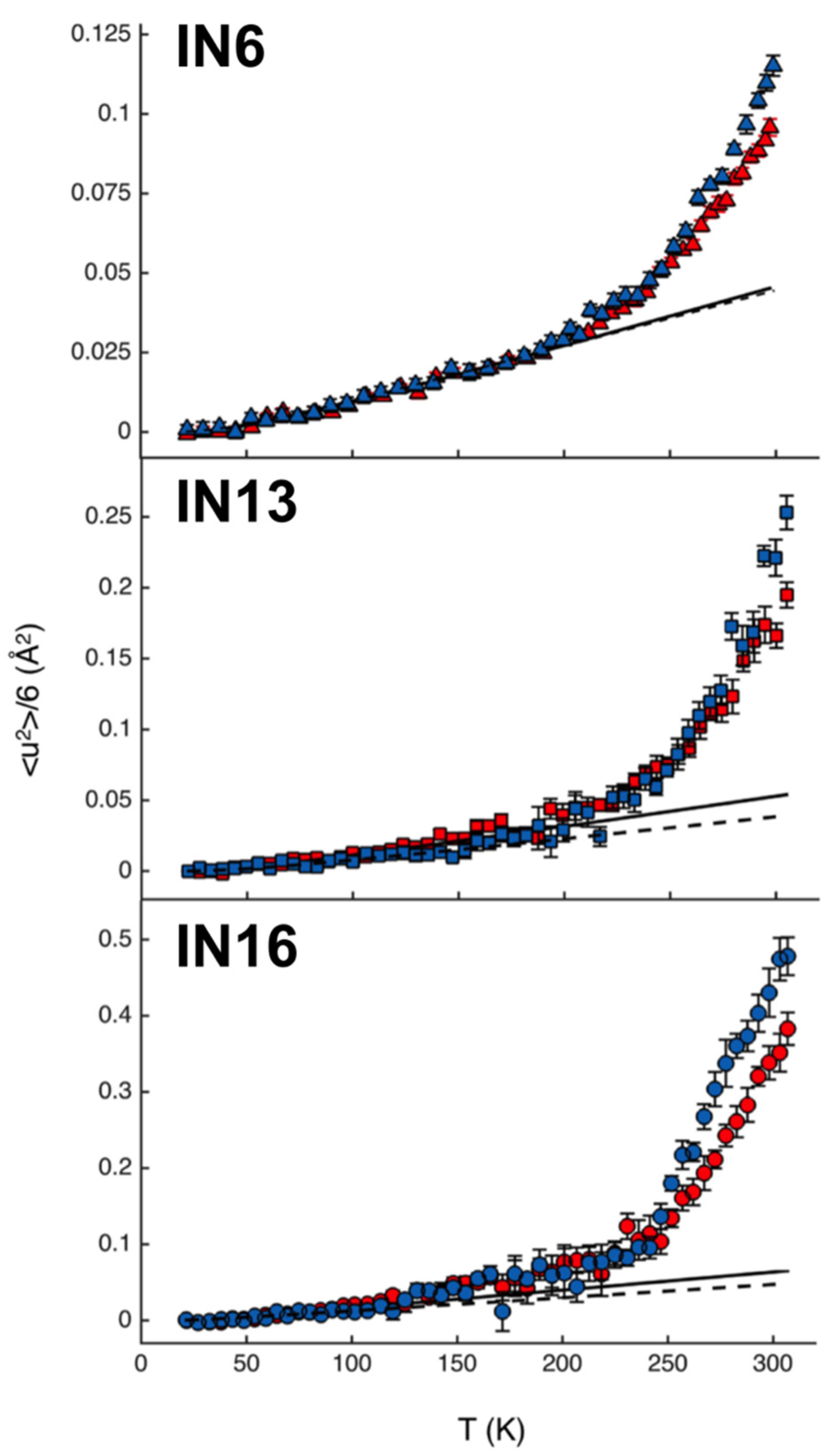
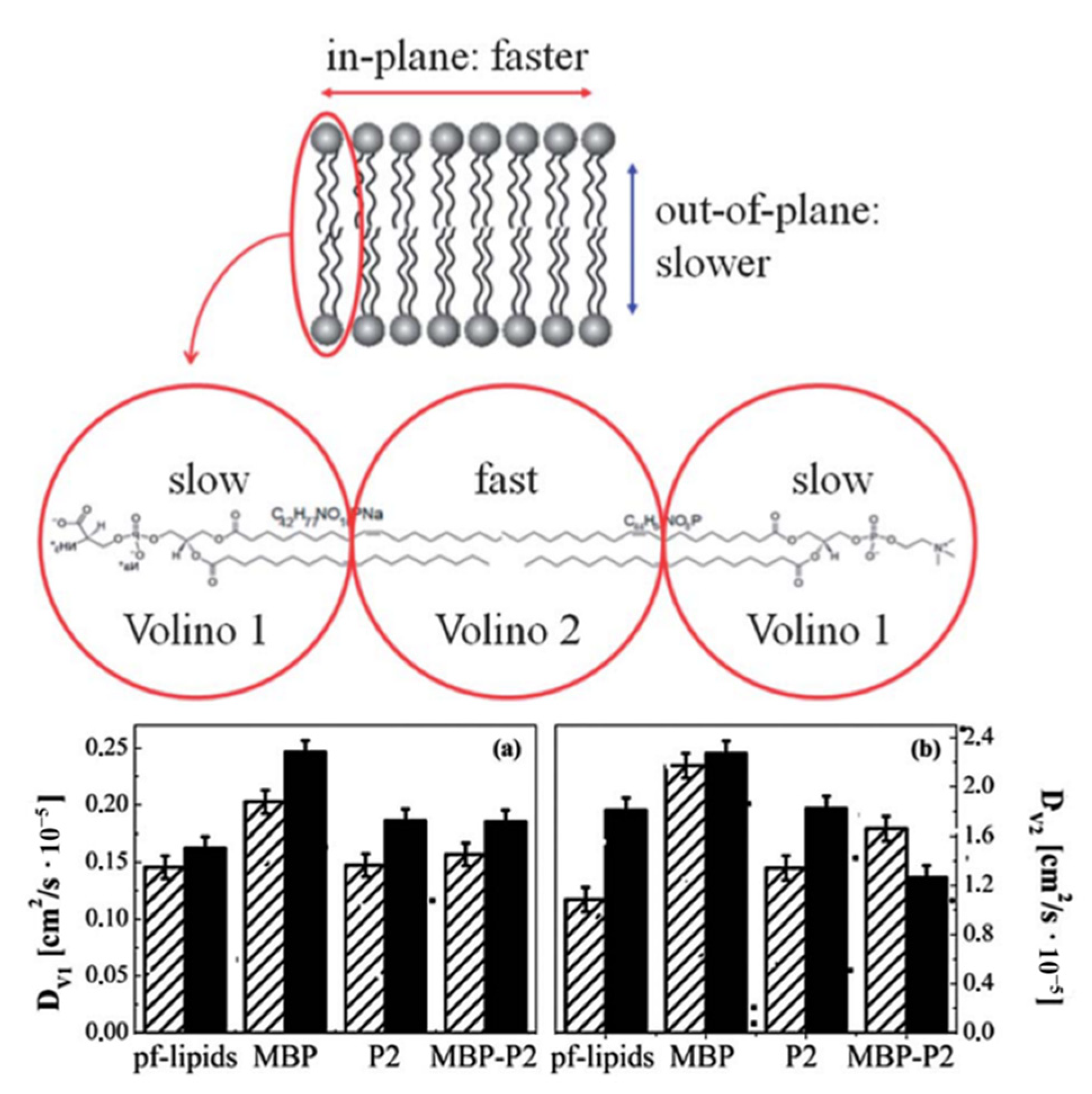
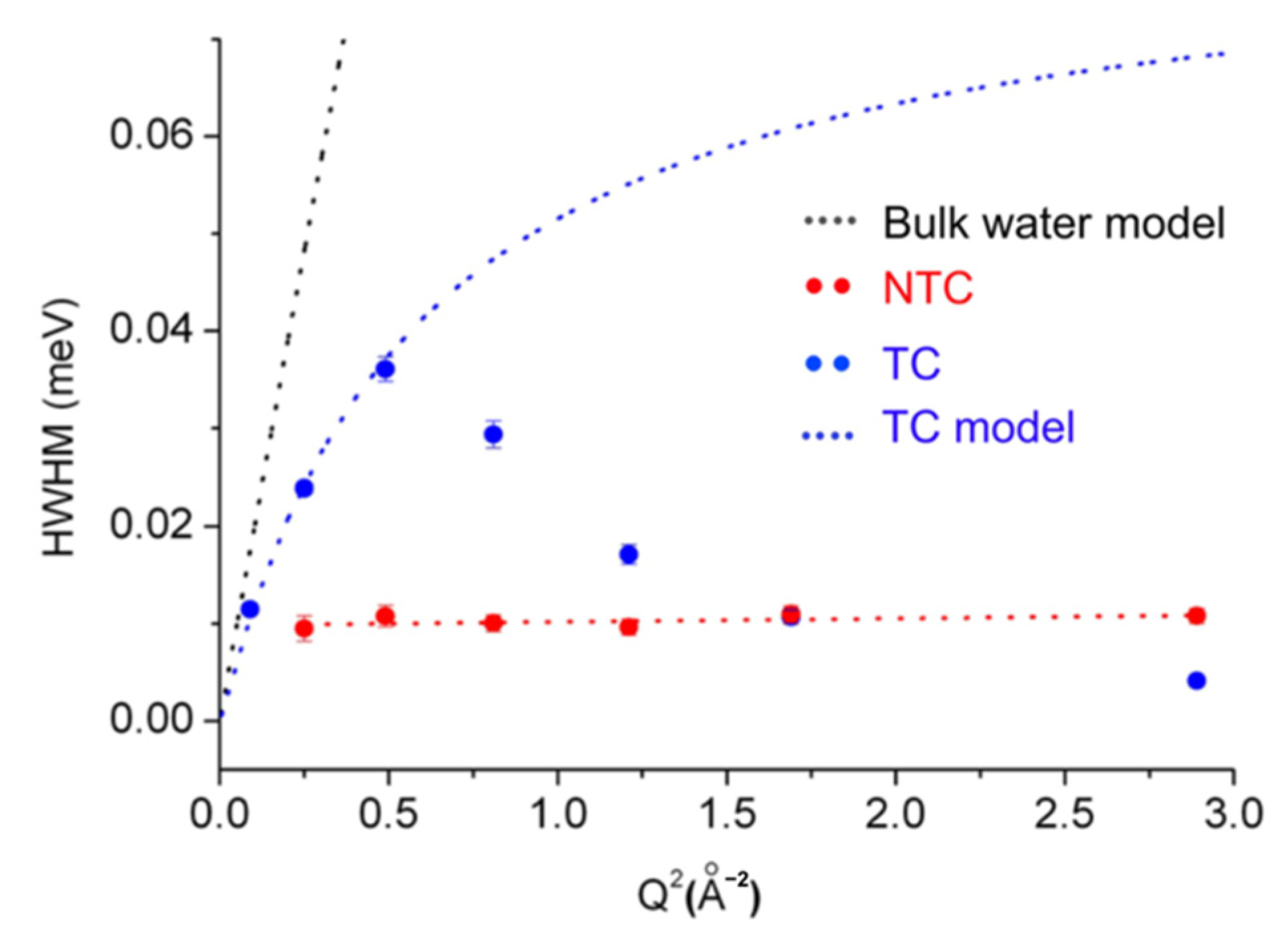
3.3. Model System Mimicking Myelin
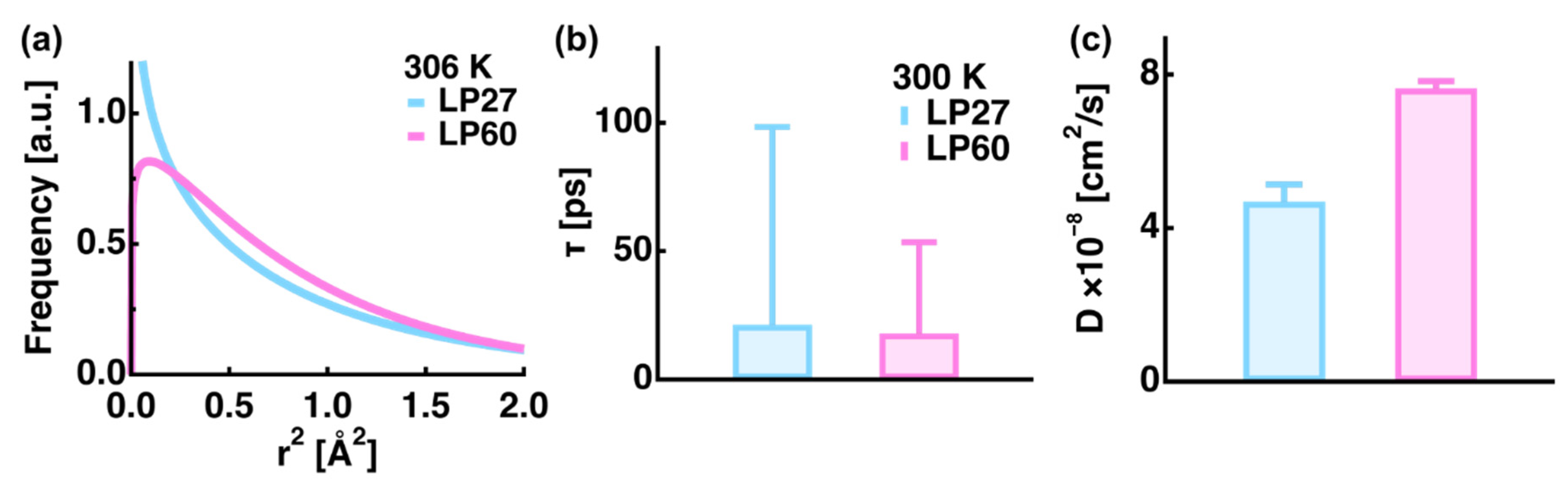
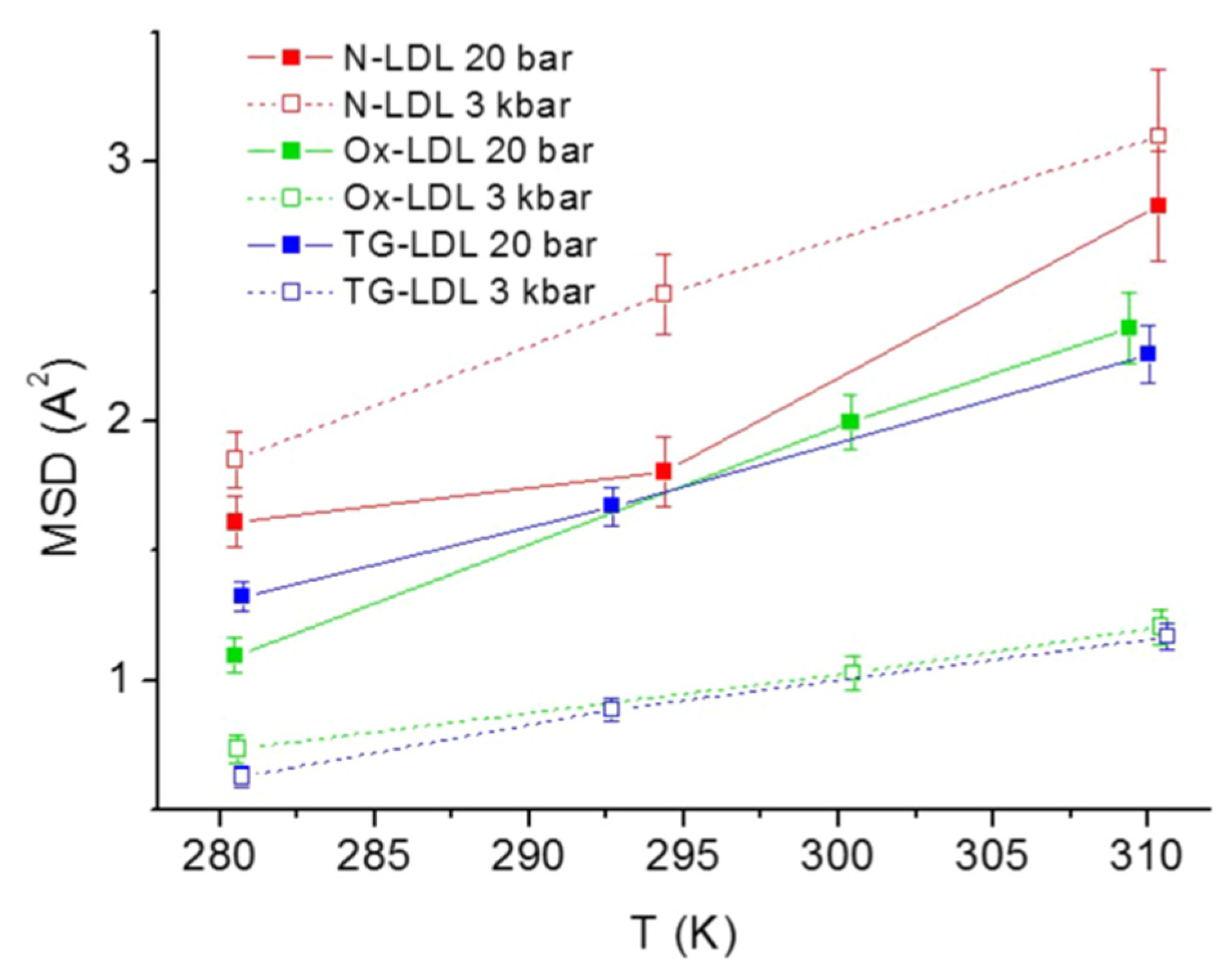
3.4. Low-Density Lipoprotein in Terms of Pathology
3.5. Brain Tissue and Cancer Cell
4. Future Perspective
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alberts, B.; Alexander, J.; Julian, L.; Martin, R.; Keith, R.; Peter, W. Molecular Biology of the Cell, 5th ed.; Garland Science: New York, NY, USA, 2008. [Google Scholar]
- Milo, R.; Phillips, R. Cell Biology by the Numbers; Garland Science: New York, NY, USA, 2015; ISBN 9780815345374. [Google Scholar]
- Fenimore, P.W.; Frauenfelder, H.; McMahon, B.H.; Young, R.D. Bulk-solvent and hydration-shell fluctuations, similar to alpha- and beta-fluctuations in glasses, control protein motions and functions. Proc. Natl. Acad. Sci. USA 2004, 101, 14408–14413. [Google Scholar] [CrossRef] [PubMed]
- Bée, M. Quasielastic Neutron Scattering; Adam Hilger: Bristol, UK; Philadelphia, PA, USA, 1988; ISBN 9780852743713. [Google Scholar]
- Zaccai, G. How Soft Is a Protein? A Protein Dynamics Force Constant Measured by Neutron Scattering. Science 2000, 288, 1604–1607. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.A.; Lei, M.; Thai, V.; Kerns, S.J.; Karplus, M.; Kern, D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature 2007, 450, 913–916. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.C. Protein dynamics: Comparison of simulations with inelastic neutron scattering experiments. Q. Rev. Biophys. 1991, 24, 227–291. [Google Scholar] [CrossRef]
- Gabel, F.; Bicout, D.; Lehnert, U.; Tehei, M.; Weik, M.; Zaccai, G. Protein dynamics studied by neutron scattering. Q. Rev. Biophys. 2002, 35, 327–367. [Google Scholar] [CrossRef]
- Sakai, V.G.; Arbe, A. Quasielastic neutron scattering in soft matter. Curr. Opin. Colloid Interface Sci. 2009, 14, 381–390. [Google Scholar] [CrossRef]
- Doster, W.; Cusack, S.; Petry, W. Dynamical transition of myoglobin revealed by inelastic neutron scattering. Nature 1989, 337, 754–756. [Google Scholar] [CrossRef]
- Pfeiffer, W.; Henkel, T.; Sackmann, E.; Knoll, W.; Richter, D. Local Dynamics of Lipid Bilayers Studied by Incoherent Quasi-Elastic Neutron Scattering. Europhys. Lett. 1989, 8, 201–206. [Google Scholar] [CrossRef]
- Grimaldo, M.; Roosen-Runge, F.; Zhang, F.; Schreiber, F.; Seydel, T. Dynamics of proteins in solution. Q. Rev. Biophys. 2019, 52, e7. [Google Scholar] [CrossRef]
- Pounot, K.; Appel, M.; Beck, C.; Weik, M.; Schirò, G.; Fichou, Y.; Seydel, T.; Schreiber, F. High-resolution Neutron Spectroscopy to Study Picosecond-nanosecond Dynamics of Proteins and Hydration Water. JoVE 2022, 182, e63664. [Google Scholar] [CrossRef] [PubMed]
- Bicout, D.J.; Cisse, A.; Matsuo, T.; Peters, J. The dynamical Matryoshka model: 1. Incoherent neutron scattering functions for lipid dynamics in bilayers. Biochim. Biophys. Acta-Biomembr. 2022, 1864, 183944. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, T.; Cisse, A.; Plazanet, M.; Natali, F.; Marek, M.; Ollivier, J.; Bicout, D.J.; Peters, J. The dynamical Matryoshka model: 3. Diffusive nature of the atomic motions contained in a new dynamical model for deciphering local lipid dynamics. BBA-Biomembr. 2022, 1864, 183949. [Google Scholar] [CrossRef] [PubMed]
- Squires, G.L. Introduction to the Theory of Thermal Neutron Scattering; Cambridge University Press: Cambridge, UK, 1978; ISBN 978-1-107-64406-9. [Google Scholar]
- Matsuo, T.; Peters, J. Chapter 2: Introduction to incoherent neutron scattering: A powerful technique to investigate the dynamics of bio-macromolecules. In Analytical Techniques for the Elucidation of Protein Function; Hojo, H., Sharma, R., Suetake, I., Eds.; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 2022; ISBN 9781119886327. [Google Scholar]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Rahman, A.; Singwi, K.; Sjölander, A. Theory of Slow Neutron Scattering by Liquids. I. Phys. Rev. 1962, 126, 986–996. [Google Scholar] [CrossRef]
- Gabel, F. Protein dynamics in solution and powder measured by incoherent elastic neutron scattering: The influence of Q-range and energy resolution. Eur. Biophys. J. 2005, 34, 1–12. [Google Scholar] [CrossRef]
- Stadler, A.M.; Unruh, T.; Namba, K.; Samatey, F.; Zaccai, G. Correlation between supercoiling and conformational motions of the bacterial flagellar filament. Biophys. J. 2013, 105, 2157–2165. [Google Scholar] [CrossRef]
- Peters, J.; Kneller, G.R. Motional heterogeneity in human acetylcholinesterase revealed by a non-Gaussian model for elastic incoherent neutron scattering. J. Chem. Phys. 2013, 139, 165102. [Google Scholar] [CrossRef]
- Singwi, K.; Sjölander, A. Diffusive Motions in Water and Cold Neutron Scattering. Phys. Rev. 1960, 119, 863–871. [Google Scholar] [CrossRef]
- Volino, F.; Dianoux, A.J. Neutron incoherent scattering law for diffusion in a potential of spherical symmetry: General formalism and application to diffusion inside a sphere. Mol. Phys. 1980, 41, 271–279. [Google Scholar] [CrossRef]
- Matsuo, T.; De Francesco, A.; Peters, J. Molecular Dynamics of Lysozyme Amyloid Polymorphs Studied by Incoherent Neutron Scattering. Front. Mol. Biosci. 2022, 8, 812096. [Google Scholar] [CrossRef] [PubMed]
- Ebashi, S.; Endo, M.; Otsuki, I. Control of muscle contraction. Q. Rev. Biophys. 1969, 2, 351–384. [Google Scholar] [CrossRef] [PubMed]
- Harada, K.; Morimoto, S. Inherited cardiomyopathies as a troponin disease. Jpn. J. Physiol. 2004, 54, 307–318. [Google Scholar] [CrossRef]
- Yanaga, F.; Morimoto, S.; Ohtsuki, I. Ca2+ sensitization and potentiation of the maximum level of myofibrillar ATPase activity caused by mutations of troponin T found in familial hypertrophic cardiomyopathy. J. Biol. Chem. 1999, 274, 8806–8812. [Google Scholar] [CrossRef]
- Tobacman, L.S.; Lin, D.; Butters, C.; Landis, C.; Back, N.; Pavlov, D.; Homsher, E. Functional consequences of troponin T mutations found in hypertrophic cardiomyopathy. J. Biol. Chem. 1999, 274, 28363–28370. [Google Scholar] [CrossRef] [PubMed]
- Maeda, Y.; Nitanai, Y.; Oda, T. From the crystal structure of troponin to the mechanism of calcium regulation of muscle contraction. Adv. Exp. Med. Biol. 2007, 592, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, F.; Maeda, K.; Chatake, T.; Maeda, Y.; Fujiwara, S. Functional aberration of myofibrils by cardiomyopathy-causing mutations in the coiled-coil region of the troponin-core domain. Biochem. Biophys. Res. Commun. 2009, 382, 205–209. [Google Scholar] [CrossRef]
- Takeda, S.; Yamashita, A.; Maeda, K.; Maeda, Y. Structure of the core domain of human cardiac troponin in the Ca2+-saturated form. Nature 2003, 424, 35–41. [Google Scholar] [CrossRef]
- Takahashi, N.; Shibata, K.; Kawakita, Y.; Nakajima, K.; Inamura, Y.; Nakatani, T.; Nakagawa, H.; Fujiwara, S.; Sato, J.T.; Tsukushi, I.; et al. Repetition Rate Multiplication: RRM, an Advanced Measuring Method Planed for the Backscattering Instrument,DNAat the MLF, J-PARC. J. Phys. Soc. Jpn. 2011, 80, SB007. [Google Scholar] [CrossRef]
- Matsuo, T.; Tominaga, T.; Kono, F.; Shibata, K.; Fujiwara, S. Modulation of the picosecond dynamics of troponin by the cardiomyopathy-causing mutation K247R of troponin T observed by quasielastic neutron scattering. Biochim. Biophys. Acta Proteins. Proteom. 2017, 1865, 1781–1789. [Google Scholar] [CrossRef]
- Ortega, A.; Amoros, D.; Garcia de la Torre, J. Prediction of hydrodynamic and other solution properties of rigid proteins from atomic- and residue-level models. Biophys. J. 2011, 101, 892–898. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, T.; Takeda, S.; Oda, T.; Fujiwara, S. Structures of the troponin core domain containing the cardiomyopathy-causing mutants studied by small-angle X-ray scattering. Biophys. Phys. 2015, 12, 145–158. [Google Scholar] [CrossRef] [PubMed]
- Stadler, A.M.; Stingaciu, L.; Radulescu, A.; Holderer, O.; Monkenbusch, M.; Biehl, R.; Richter, D. Internal Nanosecond Dynamics in the Intrinsically Disordered Myelin Basic Protein. J. Am. Chem. Soc. 2014, 136, 6987–6994. [Google Scholar] [CrossRef]
- Fujiwara, S.; Araki, K.; Matsuo, T.; Yagi, H.; Yamada, T.; Shibata, K.; Mochizuki, H. Dynamical Behavior of Human α-Synuclein Studied by Quasielastic Neutron Scattering. PLoS ONE 2016, 11, e0151447. [Google Scholar] [CrossRef]
- Fujiwara, S.; Matsuo, T.; Sugimoto, Y.; Shibata, K. Segmental Motions of Proteins under Non-native States Evaluated Using Quasielastic Neutron Scattering. J. Phys. Chem. Lett. 2019, 10, 7505–7509. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, T.; Natali, F.; Plazanet, M.; Zaccai, G.; Fujiwara, S. Dynamics of Cardiomyopathy-causing Mutant of Troponin Measured by Neutron Scattering. J. Phys. Soc. Jpn. 2013, 82, SA0201–SA0205. [Google Scholar] [CrossRef]
- Matsuo, T.; Kono, F.; Fujiwara, S. Effects of the cardiomyopathy-causing E244D mutation of troponin T on the structures of cardiac thin filaments studied by small-angle X-ray scattering. J. Struct. Biol. 2019, 205, 196–205. [Google Scholar] [CrossRef] [PubMed]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera--a visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed]
- Iadanza, M.G.; Jackson, M.P.; Hewitt, E.W.; Ranson, N.A.; Radford, S.E. A new era for understanding amyloid structures and disease. Nat. Rev. Mol. Cell Biol. 2018, 19, 755–773. [Google Scholar] [CrossRef]
- Geddes, A.J.; Parker, K.D.; Atkins, E.D.; Beighton, E. “Cross-beta” conformation in proteins. J. Mol. Biol. 1968, 32, 343–358. [Google Scholar] [CrossRef]
- Tuttle, M.D.; Comellas, G.; Nieuwkoop, A.J.; Covell, D.J.; Berthold, D.A.; Kloepper, K.D.; Courtney, J.M.; Kim, J.K.; Barclay, A.M.; Kendall, A.; et al. Solid-state NMR structure of a pathogenic fibril of full-length human α-synuclein. Nat. Struct. Mol. Biol. 2016, 23, 409–415. [Google Scholar] [CrossRef] [PubMed]
- Schirò, G.; Vetri, V.; Frick, B.; Militello, V.; Leone, M.; Cupane, A. Neutron Scattering Reveals Enhanced Protein Dynamics in Concanavalin A Amyloid Fibrils. J. Phys. Chem. Lett. 2012, 3, 992–996. [Google Scholar] [CrossRef] [PubMed]
- Frick, B.; Gonzalez, M. Five years operation of the second generation backscattering spectrometer IN16—a retrospective, recent developments and plans. Phys. B Condens. Matter 2001, 301, 8–19. [Google Scholar] [CrossRef]
- Fujiwara, S.; Yamada, T.; Matsuo, T.; Takahashi, N.; Kamazawa, K.; Kawakita, Y.; Shibata, K. Internal Dynamics of a Protein That Forms the Amyloid Fibrils Observed by Neutron Scattering. J. Phys. Soc. Jpn. 2013, 82, SA019. [Google Scholar] [CrossRef]
- Bousset, L.; Brewee, C.; Melki, R.; Migliardo, F. Dynamical properties of alpha-synuclein in soluble and fibrillar forms by Quasi Elastic Neutron Scattering. Biochim. Biophys. Acta 2014, 1844, 1307–1316. [Google Scholar] [CrossRef]
- Telling, M.T.F.; Andersen, K.H. Spectroscopic characteristics of the OSIRIS near-backscattering crystal analyser spectrometer on the ISIS pulsed neutron source. Phys. Chem. Chem. Phys. 2005, 7, 1255–1261. [Google Scholar] [CrossRef]
- Carlile, C.J.; Adams, M.A. The design of the IRIS inelastic neutron spectrometer and improvements to its analysers. Phys. B Condens. Matter 1992, 182, 431–440. [Google Scholar] [CrossRef]
- Fichou, Y.; Schiro, G.; Gallat, F.X.; Laguri, C.; Moulin, M.; Combet, J.; Zamponi, M.; Hartlein, M.; Picart, C.; Mossou, E.; et al. Hydration water mobility is enhanced around tau amyloid fibers. Proc. Natl. Acad. Sci. USA 2015, 112, 6365–6370. [Google Scholar] [CrossRef]
- Hoyer, W.; Antony, T.; Cherny, D.; Heim, G.; Jovin, T.M.; Subramaniam, V. Dependence of α-Synuclein Aggregate Morphology on Solution Conditions. J. Mol. Biol. 2002, 322, 383–393. [Google Scholar] [CrossRef]
- Fujiwara, S.; Kono, F.; Matsuo, T.; Sugimoto, Y.; Matsumoto, T.; Narita, A.; Shibata, K. Dynamic Properties of Human alpha-Synuclein Related to Propensity to Amyloid Fibril Formation. J. Mol. Biol. 2019, 431, 3229–3245. [Google Scholar] [CrossRef]
- Tycko, R. Neuron Amyloid polymorphism: Structural basis and neurobiological relevance. Neuron 2015, 86, 632–645. [Google Scholar] [CrossRef] [PubMed]
- Mossuto, M.F.; Dhulesia, A.; Devlin, G.; Frare, E.; Kumita, J.R.; de Laureto, P.P.; Dumoulin, M.; Fontana, A.; Dobson, C.M.; Salvatella, X. The Non-Core Regions of Human Lysozyme Amyloid Fibrils Influence Cytotoxicity. J. Mol. Biol. 2010, 402, 783–796. [Google Scholar] [CrossRef] [PubMed]
- Mocanu, M.M.; Ganea, C.; Siposova, K.; Filippi, A.; Demjen, E.; Marek, J.; Bednarikova, Z.; Antosova, A.; Baran, I.; Gazova, Z. Polymorphism of hen egg white lysozyme amyloid fibrils influences the cytotoxicity in LLC-PK1 epithelial kidney cells. Int. J. Biol. Macromol. 2014, 65, 176–187. [Google Scholar] [CrossRef] [PubMed]
- Rahimi Araghi, L.; Dee, D.R. Cross-Species and Cross-Polymorph Seeding of Lysozyme Amyloid Reveals a Dominant Polymorph. Front. Mol. Biosci. 2020, 7, 206. [Google Scholar] [CrossRef]
- Natali, F.; Peters, J.; Russo, D.; Barbieri, S.; Chiapponi, C.; Cupane, A.; Deriu, A.; Di Bari, M.T.; Farhi, E.; Gerelli, Y.; et al. IN13 Backscattering Spectrometer at ILL: Looking for Motions in Biological Macromolecules and Organisms. Neutron News 2008, 19, 14–18. [Google Scholar] [CrossRef]
- Yoshiike, Y.; Akagi, T.; Takashima, A. Surface structure of amyloid-β fibrils contributes to cytotoxicity. Biochemistry 2007, 46, 9805–9812. [Google Scholar] [CrossRef]
- Rossor, A.M.; Polke, J.M.; Houlden, H.; Reilly, M.M. Clinical implications of genetic advances in Charcot-Marie-Tooth disease. Nat. Rev. Neurol. 2013, 9, 562–571. [Google Scholar] [CrossRef] [PubMed]
- Waksman, B.H. Demyelinating disease: Evolution of a paradigm. Neurochem. Res. 1999, 24, 491–495. [Google Scholar] [CrossRef]
- Laulumaa, S.; Kursula, P.; Natali, F. Neutron scattering studies on protein dynamics using the human myelin peripheral membrane protein P2. EPJ Web Conf. 2015, 83, 02010. [Google Scholar] [CrossRef]
- Laulumaa, S.; Nieminen, T.; Lehtimäki, M.; Aggarwal, S.; Simons, M.; Koza, M.M.; Vattulainen, I.; Kursula, P.; Natali, F. Dynamics of the Peripheral Membrane Protein P2 from Human Myelin Measured by Neutron Scattering—A Comparison between Wild-Type Protein and a Hinge Mutant. PLoS ONE 2015, 10, e0128954. [Google Scholar] [CrossRef]
- Zenker, J.; Stettner, M.; Ruskamo, S.; Domènech-Estévez, E.; Baloui, H.; Médard, J.-J.; Verheijen, M.H.G.; Brouwers, J.F.; Kursula, P.; Kieseier, B.C.; et al. A role of peripheral myelin protein 2 in lipid homeostasis of myelinating Schwann cells. Glia 2014, 62, 1502–1512. [Google Scholar] [CrossRef] [PubMed]
- IN6: Cold Neutron Time-Focussing Time-of-Flight Spectrometer IN6- Sharp; Institut Laue-Langevin: Grenoble, France. Available online: https://www.ill.eu/users/instruments/instruments-list/sharp/description/instrument-layout (accessed on 11 August 2022).
- Knoll, W.; Natali, F.; Peters, J.; Nanekar, R.; Wang, C.; Kursula, P. Dynamic properties of a reconstituted myelin sheath. Spectroscopy 2010, 24, 585–592. [Google Scholar] [CrossRef]
- Knoll, W.; Peters, J.; Kursula, P.; Gerelli, Y.; Ollivier, J.; Deme, B.; Telling, M.; Kemner, E.; Natali, F.; Soft, M. Structural and dynamical properties of reconstituted myelin sheaths in the presence of myelin proteins MBP and P2 studied by neutron scattering. Soft Matter 2014, 10, 519–529. [Google Scholar] [CrossRef]
- D16: High-Resolution Diffractometer with Variable Vertical Focusing; Institut Laue-Langevin: Grenoble, France. Available online: https://www.ill.eu/users/instruments/instruments-list/d16/description/instrument-layout (accessed on 11 August 2022).
- Jacques, O.; Mutka, H.; Didier, L. The new cold neutron time-of-flight spectrometer IN5. Neutron News 2010, 21, 22–25. [Google Scholar] [CrossRef]
- Time-Of-Flight Spectrometer NEAT. Available online: https://helmholtz-berlin.de/forschung/oe/ce/elektrochemische-energiespeicherung/forschung/laufzeit/neat_en.html (accessed on 11 August 2022).
- Peters, J.; Martinez, N.; Lehofer, B.; Prassl, R. Low-density lipoproteins investigated under high hydrostatic pressure by elastic incoherent neutron scattering. Eur. Phys. J. E Soft Matter 2017, 40, 68. [Google Scholar] [CrossRef] [PubMed]
- Prassl, R.; Schuster, B.; Laggner, P.; Flamant, C.; Nigon, F.; Chapman, M.J. Thermal stability of apolipoprotein B100 in low-density lipoprotein is disrupted at early stages of oxidation while neutral lipid core organization is conserved. Biochemistry 1998, 37, 938–944. [Google Scholar] [CrossRef]
- Cisse, A.; Schachner-Nedherer, A.-L.; Appel, M.; Beck, C.; Ollivier, J.; Leitinger, G.; Prassl, R.; Kornmueller, K.; Peters, J. Dynamics of Apolipoprotein B-100 in Interaction with Detergent Probed by Incoherent Neutron Scattering. J. Phys. Chem. Lett. 2021, 12, 12402–12410. [Google Scholar] [CrossRef]
- Appel, M.; Frick, B.; Magerl, A. First results with the neutron backscattering and TOF spectrometer option BATS on IN16B. Phys. B Condens. Matter 2019, 562, 6–8. [Google Scholar] [CrossRef]
- Frey, L.; Lakomek, N.A.; Riek, R.; Bibow, S. Micelles, Bicelles, and Nanodiscs: Comparing the Impact of Membrane Mimetics on Membrane Protein Backbone Dynamics. Angew. Chem. Int. Ed. 2017, 56, 380–383. [Google Scholar] [CrossRef]
- Cissé, A.; Matsuo, T.; Plazanet, M.; Natali, F.; Koza, M.M.; Olivier, J.; Bicout, D.J.; Peters, J. The dynamical Matryoshka model: 2. A new modelling of local lipid dynamics at the sub-nanosecond timescale in phospholipid membranes. BBA-Biomembr. 2022, 1864, 183950. [Google Scholar] [CrossRef]
- Padhani, A.R.; Liu, G.; Koh, D.M.; Chenevert, T.L.; Thoeny, H.C.; Takahara, T.; Dzik-Jurasz, A.; Ross, B.D.; Van Cauteren, M.; Collins, D.; et al. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: Consensus and recommendations. Neoplasia 2009, 11, 102–125. [Google Scholar] [CrossRef] [PubMed]
- Natali, F.; Gerelli, Y.; Stelletta, C.; Peters, J. Anomalous proton dynamics of water molecules in neural tissue as seen by quasi-elastic neutron scattering. Impact on medical imaging techniques. AIP Conf. Proc. 2013, 1518, 551–557. [Google Scholar] [CrossRef]
- Natali, F.; Dolce, C.; Peters, J.; Stelletta, C.; Demé, B.; Ollivier, J.; Boehm, M.; Leduc, G.; Piazza, I.; Cupane, A.; et al. Anomalous water dynamics in brain: A combined diffusion magnetic resonance imaging and neutron scattering investigation. J. R. Soc. Interface 2019, 16, 20190186. [Google Scholar] [CrossRef] [PubMed]
- Martins, M.L.; Dinitzen, A.B.; Mamontov, E.; Rudić, S.; Pereira, J.E.M.; Hartmann-Petersen, R.; Herwig, K.W.; Bordallo, H.N. Water dynamics in MCF-7 breast cancer cells: A neutron scattering descriptive study. Sci. Rep. 2019, 9, 6–13. [Google Scholar] [CrossRef]
- Mamontov, E.; Herwig, K.W. A time-of-flight backscattering spectrometer at the Spallation Neutron Source, BASIS. Rev. Sci. Instrum. 2011, 82, 85109. [Google Scholar] [CrossRef]
- Matsuo, T.; Arata, T.; Oda, T.; Nakajima, K.; Ohira-Kawamura, S.; Kikuchi, T.; Fujiwara, S. Difference in the hydration water mobility around F-actin and myosin subfragment-1 studied by quasielastic neutron scattering. Biochem. Biophys. Rep. 2016, 6, 220–225. [Google Scholar] [CrossRef]
- Marques, M.P.M.; Santos, I.P.; Batista de Carvalho, A.L.M.; Mamede, A.P.; Martins, C.B.; Figueiredo, P.; Sarter, M.; Sakai, V.G.; Batista de Carvalho, L.A.E. Water dynamics in human cancer and non-cancer tissues. Phys. Chem. Chem. Phys. 2022, 24, 15406–15415. [Google Scholar] [CrossRef]
- Wood, K.; Frolich, A.; Paciaroni, A.; Moulin, M.; Hartlein, M.; Zaccai, G.; Tobias, D.J.; Weik, M. Coincidence of dynamical transitions in a soluble protein and its hydration water: Direct measurements by neutron scattering and MD simulations. J. Am. Chem. Soc. 2008, 130, 4586–4587. [Google Scholar] [CrossRef]
- Kang, J.; Lim, L.; Lu, Y.; Song, J. A unified mechanism for LLPS of ALS/FTLD-causing FUS as well as its modulation by ATP and oligonucleic acids. PLOS Biol. 2019, 17, e3000327. [Google Scholar] [CrossRef]
- Matsuo, T. Viewing SARS-CoV-2 Nucleocapsid Protein in Terms of Molecular Flexibility. Biology 2021, 10, 454. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsuo, T.; Peters, J. Sub-Nanosecond Dynamics of Pathologically Relevant Bio-Macromolecules Observed by Incoherent Neutron Scattering. Life 2022, 12, 1259. https://doi.org/10.3390/life12081259
Matsuo T, Peters J. Sub-Nanosecond Dynamics of Pathologically Relevant Bio-Macromolecules Observed by Incoherent Neutron Scattering. Life. 2022; 12(8):1259. https://doi.org/10.3390/life12081259
Chicago/Turabian StyleMatsuo, Tatsuhito, and Judith Peters. 2022. "Sub-Nanosecond Dynamics of Pathologically Relevant Bio-Macromolecules Observed by Incoherent Neutron Scattering" Life 12, no. 8: 1259. https://doi.org/10.3390/life12081259
APA StyleMatsuo, T., & Peters, J. (2022). Sub-Nanosecond Dynamics of Pathologically Relevant Bio-Macromolecules Observed by Incoherent Neutron Scattering. Life, 12(8), 1259. https://doi.org/10.3390/life12081259






