Automatic Differentiation for Inverse Problems in X-ray Imaging and Microscopy
Abstract
:1. Introduction
1.1. Paper Scope
1.2. Potential Uses of Automatic Differentiation
1.3. Computational Imaging Problem Statement
1.4. Compressive Sensing
1.5. Single Image Super Resolution
1.6. Tomography
1.7. Ptychography
2. Materials and Methods
2.1. Compressive Sensing
| Listing 1. Example implementation for Compressive Sensing gradient-based optimisation. |
 |
| Listing 2. AD implementation for the CS problem. |
 |
2.2. Single Image Super Resolution
2.3. Tomography
2.4. Ptychography
3. Results
3.1. CS Reconstructions
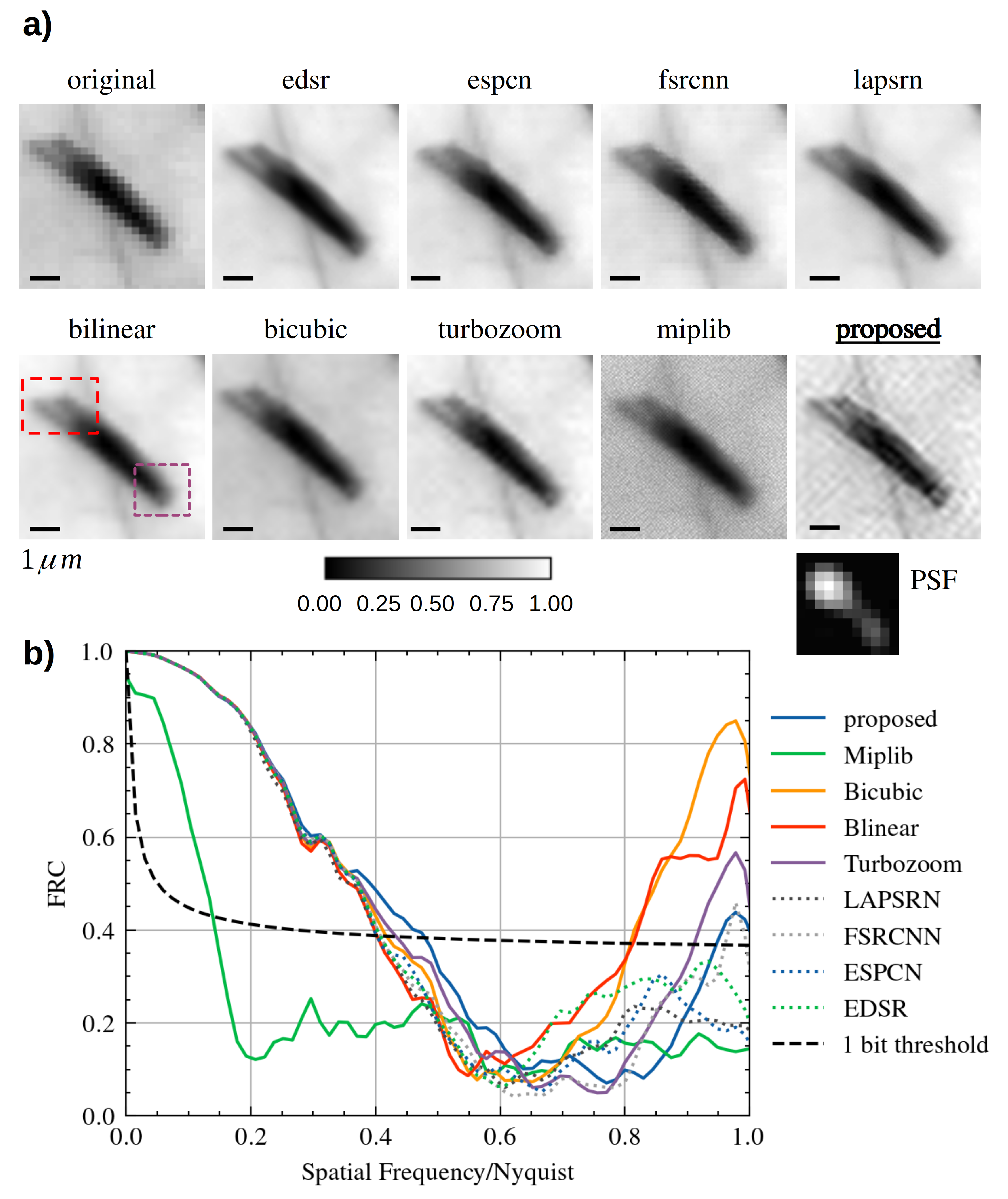
3.2. SISR Reconstructions
3.3. Micro/Nano—Tomography Reconstructions
3.4. Ptychography Reconstructions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Automatic Differentiation |
| CCD | Charge-Coupled Device |
| CNN | Convolutional Neural Network |
| CS | Compressive Sensing |
| CT | Computed Tomography |
| DCT | Discrete Cosine Transform |
| DWT | Discrete Wavelets Transform |
| DL | Deep Learning |
| FOV | Field Of View |
| FRC | Fourier Ring Correlation |
| FZP | Fresnel Zone Plate |
| GPU | Graphics Processing Unit |
| PSF | Point Spread Function |
| SISR | Single Image Super Resolution |
| STXM | Scanning Transmission X-ray Microscopy |
| XRF | X-ray Fluorescence |
References
- De Andrade, V.; Nikitin, V.; Wojcik, M.; Deriy, A.; Bean, S.; Shu, D.; Mooney, T.; Peterson, K.; Kc, P.; Li, K.; et al. Fast X-ray Nanotomography with Sub-10 nm Resolution as a Powerful Imaging Tool for Nanotechnology and Energy Storage Applications. Adv. Mater. 2021, 33, 2008653. [Google Scholar] [CrossRef] [PubMed]
- Candes, E.; Wakin, M. An Introduction To Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Chen, H.; He, X.; Qing, L.; Wu, Y.; Ren, C.; Sheriff, R.E.; Zhu, C. Real-world single image super-resolution: A brief review. Inf. Fusion 2022, 79, 124–145. [Google Scholar] [CrossRef]
- Rodenburg, J.M.; Faulkner, H.M. A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 2004, 85, 4795–4797. [Google Scholar] [CrossRef] [Green Version]
- McCloskey, S. Computational Imaging. Adv. Comput. Vis. Pattern Recognit. 2022, 10, 41–62. [Google Scholar] [CrossRef]
- Guizar-Sicairos, M.; Fienup, J.R. Phase retrieval with transverse translation diversity: A nonlinear optimization approach. Opt. Express 2008, 16, 7264. [Google Scholar] [CrossRef] [PubMed]
- Thibault, P.; Guizar-Sicairos, M. Maximum-likelihood refinement for coherent diffractive imaging. New J. Phys. 2012, 14, 63004. [Google Scholar] [CrossRef]
- Donato, S.; Arana Peña, L.M.; Bonazza, D.; Formoso, V.; Longo, R.; Tromba, G.; Brombal, L. Optimization of pixel size and propagation distance in X-ray phase-contrast virtual histology. J. Instrum. 2022, 17, C05021. [Google Scholar] [CrossRef]
- Brombal, L.; Arana Peña, L.M.; Arfelli, F.; Longo, R.; Brun, F.; Contillo, A.; Di Lillo, F.; Tromba, G.; Di Trapani, V.; Donato, S.; et al. Motion artifacts assessment and correction using optical tracking in synchrotron radiation breast CT. Med. Phys. 2021, 48, 5343–5355. [Google Scholar] [CrossRef]
- Bartholomew-Biggs, M.; Brown, S.; Christianson, B.; Dixon, L. Automatic differentiation of algorithms. J. Comput. Appl. Math. 2000, 124, 171–190. [Google Scholar] [CrossRef] [Green Version]
- Güneş Baydin, A.; Pearlmutter, B.A.; Andreyevich Radul, A.; Mark Siskind, J. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Margossian, C.C. A review of automatic differentiation and its efficient implementation. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1305. [Google Scholar] [CrossRef] [Green Version]
- Guzzi, F.; Kourousias, G.; Gianoncelli, A.; Billè, F.; Carrato, S. A parameter refinement method for ptychography based on deep learning concepts. Condens. Matter 2021, 6, 36. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Li, T.M.; Gharbi, M.; Adams, A.; Durand, F.; Ragan-Kelley, J. Differentiable programming for image processing and deep learning in halide. ACM Trans. Graph. 2018, 37, 139:1’139:13. [Google Scholar] [CrossRef] [Green Version]
- Rios, L.M.; Sahinidis, N.V. Derivative-free optimization: A review of algorithms and comparison of software implementations. J. Glob. Optim. 2013, 56, 1247–1293. [Google Scholar] [CrossRef] [Green Version]
- Guzzi, F.; De Bortoli, L.; Molina, R.S.; Marsi, S.; Carrato, S.; Ramponi, G. Distillation of an end-to-end oracle for face verification and recognition sensors. Sensors 2020, 20, 1369. [Google Scholar] [CrossRef] [Green Version]
- Laue, S. On the Equivalence of Forward Mode Automatic Differentiation and Symbolic Differentiation. 2019. Available online: http://xxx.lanl.gov/abs/1904.02990 (accessed on 16 February 2023).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef] [Green Version]
- Andrew, G.; Gao, J. Scalable training of L1-regularized log-linear models. In Proceedings of the ACM International Conference Proceeding Series; Association for Computing Machinery: New York, NY, USA, 2007; Volume 227, ICML ’07; pp. 33–40. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive Sensing [Lecture Notes]. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, C.; Zhao, D.; Gao, W. Image compressive sensing recovery using adaptively learned sparsifying basis via L0 minimization. Signal Process. 2014, 103, 114–126. [Google Scholar] [CrossRef] [Green Version]
- Gianoncelli, A.; Bonanni, V.; Gariani, G.; Guzzi, F.; Pascolo, L.; Borghes, R.; Billè, F.; Kourousias, G. Soft x-ray microscopy techniques for medical and biological imaging at twinmic–elettra. Appl. Sci. 2021, 11, 7216. [Google Scholar] [CrossRef]
- Kourousias, G.; Billè, F.; Borghes, R.; Alborini, A.; Sala, S.; Alberti, R.; Gianoncelli, A. Compressive Sensing for Dynamic XRF Scanning. Sci. Rep. 2020, 10, 9990. [Google Scholar] [CrossRef] [PubMed]
- Kourousias, G.; Billè, F.; Borghes, R.; Pascolo, L.; Gianoncelli, A. Megapixel scanning transmission soft X-ray microscopy imaging coupled with compressive sensing X-ray fluorescence for fast investigation of large biological tissues. Analyst 2021, 146, 5836–5842. [Google Scholar] [CrossRef]
- Vetal, A.P.; Singh, D.; Singh, R.K.; Mishra, D. Reconstruction of apertured Fourier Transform Hologram using compressed sensing. Opt. Lasers Eng. 2018, 111, 227–235. [Google Scholar] [CrossRef]
- Orović, I.; Papić, V.; Ioana, C.; Li, X.; Stanković, S. Compressive Sensing in Signal Processing: Algorithms and Transform Domain Formulations. Math. Probl. Eng. 2016, 2016, 7616393. [Google Scholar] [CrossRef] [Green Version]
- Pilastri, A.L.; Tavares, J.M.R. Reconstruction algorithms in compressive sensing: An overview. In Proceedings of the 11th Edition of the Doctoral Symposium in Informatics Engineering (DSIE-16), Porto, Portugal, 3 February 2016; pp. 127–137. [Google Scholar]
- Peyré, G. The numerical tours of signal processing part 2: Multiscale processings. Comput. Sci. Eng. 2011, 13, 68–71. [Google Scholar] [CrossRef]
- Li, S.; Qi, H. A Douglas-Rachford Splitting Approach to Compressed Sensing Image Recovery Using Low-Rank Regularization. IEEE Trans. Image Process. 2015, 24, 4240–4249. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching Pursuits With Time-Frequency Dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Cai, T.T.; Wang, L. Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, W.; Wu, Y. Efficient implementations for orthogonal matching pursuit. Electronics 2020, 9, 1507. [Google Scholar] [CrossRef]
- Damelin, S.B.; Hoang, N.S. On Surface Completion and Image Inpainting by Biharmonic Functions: Numerical Aspects. Int. J. Math. Math. Sci. 2018, 2018, 3950312. [Google Scholar] [CrossRef] [Green Version]
- Telea, A. An Image Inpainting Technique Based on the Fast Marching Method. J. Graph. Tools 2004, 9, 23–34. [Google Scholar] [CrossRef]
- Bertalmío, M.; Bertozzi, A.L.; Sapiro, G. Navier-Stokes, fluid dynamics, and image and video inpainting. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001; Volume 1, p. I. [Google Scholar] [CrossRef] [Green Version]
- Genser, N.; Seiler, J.; Schilling, F.; Kaup, A. Signal and Loss Geometry Aware Frequency Selective Extrapolation for Error Concealment. In Proceedings of the 2018 Picture Coding Symposium, PCS 2018—Proceedings, San Francisco, CA, USA, 24–27 June 2018; pp. 159–163. [Google Scholar] [CrossRef]
- Seiler, J.; Kaup, A. Complex-valued frequency selective extrapolation for fast image and video signal extrapolation. IEEE Signal Process. Lett. 2010, 17, 949–952. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S. Deep Learning for Image Super-Resolution: A Survey. Inf. Fusion 2021, 43, 3365–3387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guarnieri, G.; Fontani, M.; Guzzi, F.; Carrato, S.; Jerian, M. Perspective registration and multi-frame super-resolution of license plates in surveillance videos. Forensic Sci. Int. Digit. Investig. 2021, 36, 301087. [Google Scholar] [CrossRef]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2Noise: Learning image restoration without clean data. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; PMLR: London, UK, 2018; Volume 7, pp. 4620–4631. [Google Scholar]
- Vicente, A.N.; Pedrini, H. A learning-based single-image super-resolution method for very low quality license plate images. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2016—Conference Proceedings, Budapest, Hungary, 9–12 October 2016; pp. 515–520. [Google Scholar] [CrossRef]
- Papyan, V.; Elad, M. Multi-Scale Patch-Based Image Restoration. IEEE Trans. Image Process. 2016, 25, 249–261. [Google Scholar] [CrossRef]
- Brifman, A.; Romano, Y.; Elad, M. Turning a denoiser into a super-resolver using plug and play priors. In Proceedings of the International Conference on Image Processing, ICIP, Phoenix, AZ, USA, 25–28 September 2016; Volume 2016, pp. 1404–1408. [Google Scholar] [CrossRef]
- Eilers, P.H.; Ruckebusch, C. Fast and simple super-resolution with single images. Sci. Rep. 2022, 12, 11241. [Google Scholar] [CrossRef]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Boissonnat, J.D., Chenin, P., Cohen, A., Gout, C., Lyche, T., Mazure, M.L., Schumaker, L.L., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 6920. [Google Scholar] [CrossRef]
- Sen, P.; Darabi, S. Compressive image super-resolution. In Proceedings of the Conference Record—Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2009; pp. 1235–1242. [Google Scholar] [CrossRef]
- Freeman, W.T.; Jones, T.R.; Pasztor, E.C. Example-based super-resolution. IEEE Comput. Graph. Appl. 2002, 22, 56–65. [Google Scholar] [CrossRef] [Green Version]
- Glasner, D.; Bagon, S.; Irani, M. Super-resolution from a single image. In Proceedings of the IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 349–356. [Google Scholar] [CrossRef] [Green Version]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; IEEE Computer Society: Washington, DC, USA, 2017; Volume 2017-July, pp. 1132–1140. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; IEEE Computer Society: Washington, DC, USA, 2016; Volume 2016-December, pp. 1874–1883. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9906. [Google Scholar] [CrossRef] [Green Version]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; IEEE Computer Society: Washington, DC, USA, 2017; Volume 2017-January, pp. 5835–5843. [Google Scholar] [CrossRef] [Green Version]
- Bruno, P.; Calimeri, F.; Marte, C.; Manna, M. Combining Deep Learning and ASP-Based Models for the Semantic Segmentation of Medical Images. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Moschoyiannis, S., Peñaloza, R., Vanthienen, J., Soylu, A., Roman, D., Eds.; Springer International Publishing: Cham, Switzerland, 2021; Volume 12851 LNCS, pp. 95–110. [Google Scholar] [CrossRef]
- Vo, T.H.; Nguyen, N.T.K.; Kha, Q.H.; Le, N.Q.K. On the road to explainable AI in drug-drug interactions prediction: A systematic review. Comput. Struct. Biotechnol. J. 2022, 20, 2112–2123. [Google Scholar] [CrossRef]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in interpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef] [Green Version]
- Yang, X. An Overview of the Attention Mechanisms in Computer Vision. J. Phys. Conf. Ser. 2020, 1693, 12173. [Google Scholar] [CrossRef]
- Hounsfield, G.N. Computerized transverse axial scanning (tomography): I. Description of system. Br. J. Radiol. 1973, 46, 1016–1022. [Google Scholar] [CrossRef]
- Szczykutowicz, T.P.; Toia, G.V.; Dhanantwari, A.; Nett, B. A Review of Deep Learning CT Reconstruction: Concepts, Limitations, and Promise in Clinical Practice. Curr. Radiol. Rep. 2022, 10, 101–115. [Google Scholar] [CrossRef]
- Pereiro, E.; Nicolás, J.; Ferrer, S.; Howells, M.R. A soft X-ray beamline for transmission X-ray microscopy at ALBA. J. Synchrotron Radiat. 2009, 16, 505–512. [Google Scholar] [CrossRef]
- Withers, P.J.; Bouman, C.; Carmignato, S.; Cnudde, V.; Grimaldi, D.; Hagen, C.K.; Maire, E.; Manley, M.; Du Plessis, A.; Stock, S. X-ray computed tomography. Nat. Rev. Methods Prim. 2021, 1, 18. [Google Scholar] [CrossRef]
- Morgan, K.S.; Siu, K.K.; Paganin, D.M. The projection approximation versus an exact solution for X-ray phase contrast imaging, with a plane wave scattered by a dielectric cylinder. Opt. Commun. 2010, 283, 4601–4608. [Google Scholar] [CrossRef]
- Soleimani, M.; Pengpen, T. Introduction: A brief overview of iterative algorithms in X-ray computed tomography. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140399. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, C. Relaxation of the Crowther criterion in multislice tomography. Opt. Lett. 2018, 43, 4811. [Google Scholar] [CrossRef]
- Dowd, B.A.; Campbell, G.H.; Marr, R.B.; Nagarkar, V.V.; Tipnis, S.V.; Axe, L.; Siddons, D.P. Developments in synchrotron x-ray computed microtomography at the National Synchrotron Light Source. Dev. X-ray Tomogr. II 1999, 3772, 224–236. [Google Scholar] [CrossRef] [Green Version]
- Gordon, R.; Bender, R.; Herman, G.T. Algebraic Reconstruction Techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theor. Biol. 1970, 29, 471–481. [Google Scholar] [CrossRef]
- Gianoncelli, A.; Vaccari, L.; Kourousias, G.; Cassese, D.; Bedolla, D.E.; Kenig, S.; Storici, P.; Lazzarino, M.; Kiskinova, M. Soft X-Ray Microscopy Radiation Damage On Fixed Cells Investigated With Synchrotron Radiation FTIR Microscopy. Sci. Rep. 2015, 5, 10250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frachon, T.; Weber, L.; Hesse, B.; Rit, S.; Dong, P.; Olivier, C.; Peyrin, F.; Langer, M. Dose fractionation in synchrotron radiation x-ray phase micro-tomography. Phys. Med. Biol. 2015, 60, 7543–7566. [Google Scholar] [CrossRef] [Green Version]
- Mori, I.; Machida, Y.; Osanai, M.; Iinuma, K. Photon starvation artifacts of X-ray CT: Their true cause and a solution. Radiol. Phys. Technol. 2013, 6, 130–141. [Google Scholar] [CrossRef] [PubMed]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar] [CrossRef]
- van der Sluis, A.; van der Vorst, H.A. SIRT- and CG-type methods for the iterative solution of sparse linear least-squares problems. Linear Algebra Its Appl. 1990, 130, 257–303. [Google Scholar] [CrossRef] [Green Version]
- Gregor, J.; Benson, T. Computational analysis and improvement of SIRT. IEEE Trans. Med. Imaging 2008, 27, 918–924. [Google Scholar] [CrossRef] [PubMed]
- Kupsch, A.; Lange, A.; Hentschel, M.P.; Lück, S.; Schmidt, V.; Grothausmann, R.; Hilger, A.; Manke, I. Missing wedge computed tomography by iterative algorithm DIRECTT. J. Microsc. 2016, 261, 36–45. [Google Scholar] [CrossRef]
- Sorrentino, A.; Nicolás, J.; Valcárcel, R.; Chichón, F.J.; Rosanes, M.; Avila, J.; Tkachuk, A.; Irwin, J.; Ferrer, S.; Pereiro, E. MISTRAL: A transmission soft X-ray microscopy beamline for cryo nano-tomography of biological samples and magnetic domains imaging. J. Synchrotron Radiat. 2015, 22, 1112–1117. [Google Scholar] [CrossRef] [PubMed]
- Guay, M.D.; Czaja, W.; Aronova, M.A.; Leapman, R.D. Compressed sensing electron tomography for determining biological structure. Sci. Rep. 2016, 6, 27614. [Google Scholar] [CrossRef] [Green Version]
- Moebel, E.; Kervrann, C. A Monte Carlo framework for missing wedge restoration and noise removal in cryo-electron tomography. J. Struct. Biol. X 2020, 4, 100013. [Google Scholar] [CrossRef]
- Xu, J.; Mahesh, M.; Tsui, B.M. Is Iterative Reconstruction Ready for MDCT? J. Am. Coll. Radiol. 2009, 6, 274–276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, G.; Liu, Y.; Zhang, R.; Xin, H.L. A joint deep learning model to recover information and reduce artifacts in missing-wedge sinograms for electron tomography and beyond. Sci. Rep. 2019, 9, 12803. [Google Scholar] [CrossRef] [Green Version]
- Sorzano, C.O.S.; Messaoudi, C.; Eibauer, M.; Bilbao-Castro, J.R.; Hegerl, R.; Nickell, S.; Marco, S.; Carazo, J.M. Marker-free image registration of electron tomography tilt-series. BMC Bioinform. 2009, 10, 124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gürsoy, D.; Hong, Y.P.; He, K.; Hujsak, K.; Yoo, S.; Chen, S.; Li, Y.; Ge, M.; Miller, L.M.; Chu, Y.S.; et al. Rapid alignment of nanotomography data using joint iterative reconstruction and reprojection. Sci. Rep. 2017, 7, 11818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bogensperger, L.; Kobler, E.; Pernitsch, D.; Kotzbeck, P.; Pieber, T.R.; Pock, T.; Kolb, D. A joint alignment and reconstruction algorithm for electron tomography to visualize in-depth cell-to-cell interactions. Histochem. Cell Biol. 2022, 157, 685–696. [Google Scholar] [CrossRef]
- Frank, J.; McEwen, B.F. Alignment by Cross-Correlation. In Electron Tomography; Frank, J., Ed.; Springer: Boston, MA, USA, 1992; pp. 205–213. [Google Scholar] [CrossRef]
- Kremer, J.R.; Mastronarde, D.N.; McIntosh, J.R. Computer visualization of three-dimensional image data using IMOD. J. Struct. Biol. 1996, 116, 71–76. [Google Scholar] [CrossRef] [Green Version]
- Sorzano, C.O.; de Isidro-Gómez, F.; Fernández-Giménez, E.; Herreros, D.; Marco, S.; Carazo, J.M.; Messaoudi, C. Improvements on marker-free images alignment for electron tomography. J. Struct. Biol. X 2020, 4, 100037. [Google Scholar] [CrossRef]
- Yu, H.; Xia, S.; Wei, C.; Mao, Y.; Larsson, D.; Xiao, X.; Pianetta, P.; Yu, Y.S.; Liu, Y. Automatic projection image registration for nanoscale X-ray tomographic reconstruction. J. Synchrotron Radiat. 2018, 25, 1819–1826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Hu, J.; Jiang, Z.; Zhang, K.; Liu, P.; Wang, C.; Yuan, Q.; Pianetta, P.; Liu, Y. Automatic 3D image registration for nano-resolution chemical mapping using synchrotron spectro-tomography. J. Synchrotron Radiat. 2021, 28, 278–282. [Google Scholar] [CrossRef]
- Jun, K.; Yoon, S. Alignment Solution for CT Image Reconstruction using Fixed Point and Virtual Rotation Axis. Sci. Rep. 2017, 7, 41218. [Google Scholar] [CrossRef] [Green Version]
- Han, R.; Wang, L.; Liu, Z.; Sun, F.; Zhang, F. A novel fully automatic scheme for fiducial marker-based alignment in electron tomography. J. Struct. Biol. 2015, 192, 403–417. [Google Scholar] [CrossRef]
- Han, R.; Wan, X.; Wang, Z.; Hao, Y.; Zhang, J.; Chen, Y.; Gao, X.; Liu, Z.; Ren, F.; Sun, F.; et al. AuTom: A novel automatic platform for electron tomography reconstruction. J. Struct. Biol. 2017, 199, 196–208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woolcot, T.; Kousi, E.; Wells, E.; Aitken, K.; Taylor, H.; Schmidt, M.A. An evaluation of systematic errors on marker-based registration of computed tomography and magnetic resonance images of the liver. Phys. Imaging Radiat. Oncol. 2018, 7, 27–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, R.; Li, G.; Gao, X. Robust and ultrafast fiducial marker correspondence in electron tomography by a two-stage algorithm considering local constraints. Bioinformatics 2021, 37, 107–117. [Google Scholar] [CrossRef] [PubMed]
- Han, R.; Bao, Z.; Zeng, X.; Niu, T.; Zhang, F.; Xu, M.; Gao, X. A joint method for marker-free alignment of tilt series in electron tomography. Bioinformatics 2019, 35, i249–i259. [Google Scholar] [CrossRef] [Green Version]
- Guzzi, F.; Kourousias, G.; Gianoncelli, A.; Pascolo, L.; Sorrentino, A.; Billè, F.; Carrato, S. Improving a rapid alignment method of tomography projections by a parallel approach. Appl. Sci. 2021, 11, 7598. [Google Scholar] [CrossRef]
- Di, Z.W.; Chen, S.; Gursoy, D.; Paunesku, T.; Leyffer, S.; Wild, S.M.; Vogt, S. Optimization-based simultaneous alignment and reconstruction in multi-element tomography. Opt. Lett. 2019, 44, 4331–4334. [Google Scholar] [CrossRef]
- Odstrčil, M.; Holler, M.; Raabe, J.; Guizar-Sicairos, M. Alignment methods for nanotomography with deep subpixel accuracy. Opt. Express 2019, 27, 36637–36652. [Google Scholar] [CrossRef] [Green Version]
- Guizar-Sicairos, M.; Thibault, P. Ptychography: A solution to the phase problem. Phys. Today 2021, 74, 42–48. [Google Scholar] [CrossRef]
- Pfeiffer, F. X-ray ptychography. Nat. Photonics 2018, 12, 9–17. [Google Scholar] [CrossRef]
- Paganin, D.; Gureyev, T.E.; Mayo, S.C.; Stevenson, A.W.; Nesterets, Y.I.; Wilkins, S.W. X-ray omni microscopy. J. Microsc. 2004, 214, 315–327. [Google Scholar] [CrossRef] [PubMed]
- Abbey, B.; Nugent, K.A.; Williams, G.J.; Clark, J.N.; Peele, A.G.; Pfeifer, M.A.; De Jonge, M.; McNulty, I. Keyhole coherent diffractive imaging. Nat. Phys. 2008, 4, 394–398. [Google Scholar] [CrossRef] [Green Version]
- Rodenburg, J. The theory of super-resolution electron microscopy via Wigner-distribution deconvolution. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1992, 339, 521–553. [Google Scholar] [CrossRef]
- Maiden, A.M.; Rodenburg, J.M. An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy 2009, 109, 1256–1262. [Google Scholar] [CrossRef]
- Maiden, A.; Johnson, D.; Li, P. Further improvements to the ptychographical iterative engine. Optica 2017, 4, 736–745. [Google Scholar] [CrossRef]
- Marchesini, S.; Tu, Y.C.; Wu, H.T. Alternating projection, ptychographic imaging and phase synchronization. Appl. Comput. Harmon. Anal. 2016, 41, 815–851. [Google Scholar] [CrossRef] [Green Version]
- Thibault, P.; Dierolf, M.; Menzel, A.; Bunk, O.; David, C.; Pfeiffer, F. High-Resolution Scanning X-ray Diffraction Microscopy. Science 2008, 321, 379–382. [Google Scholar] [CrossRef]
- Pelz, P.M.; Qiu, W.X.; Bücker, R.; Kassier, G.; Miller, R.J.D. Low-dose cryo electron ptychography via non-convex Bayesian optimization. Sci. Rep. 2017, 7, 9883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spence, J.; Weierstall, U.; Howells, M. Coherence and sampling requirements for diffractive imaging. Ultramicroscopy 2004, 101, 149–152. [Google Scholar] [CrossRef]
- Vartanyants, I.; Robinson, I. Origins of decoherence in coherent X-ray diffraction experiments. Opt. Commun. 2003, 222, 29–50. [Google Scholar] [CrossRef]
- Thibault, P.; Menzel, A. Reconstructing state mixtures from diffraction measurements. Nature 2013, 494, 68–71. [Google Scholar] [CrossRef]
- Li, P.; Batey, D.J.; Edo, T.B.; Parsons, A.D.; Rau, C.; Rodenburg, J.M. Multiple mode x-ray ptychography using a lens and a fixed diffuser optic. J. Opt. 2016, 18, 054008. [Google Scholar] [CrossRef]
- Shi, X.; Burdet, N.; Batey, D.; Robinson, I. Multi-Modal Ptychography: Recent Developments and Applications. Appl. Sci. 2018, 8, 1054. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Ning, S.; Zhang, F. Numerical and experimental study of partial coherence for near-field and far-field ptychography. Opt. Express 2021, 29, 40652–40667. [Google Scholar] [CrossRef] [PubMed]
- Maiden, A.; Humphry, M.; Sarahan, M.; Kraus, B.; Rodenburg, J. An annealing algorithm to correct positioning errors in ptychography. Ultramicroscopy 2012, 120, 64–72. [Google Scholar] [CrossRef]
- Zhang, F.; Peterson, I.; Vila-Comamala, J.; Diaz, A.; Berenguer, F.; Bean, R.; Chen, B.; Menzel, A.; Robinson, I.K.; Rodenburg, J.M. Translation position determination in ptychographic coherent diffraction imaging. Opt. Express 2013, 21, 13592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandula, O.; Elzo Aizarna, M.; Eymery, J.; Burghammer, M.; Favre-Nicolin, V. PyNX.Ptycho: A computing library for X-ray coherent diffraction imaging of nanostructures. J. Appl. Crystallogr. 2016, 49, 1842–1848. [Google Scholar] [CrossRef]
- Guzzi, F.; Kourousias, G.; Billè, F.; Pugliese, R.; Reis, C.; Gianoncelli, A.; Carrato, S. Refining scan positions in Ptychography through error minimisation and potential application of Machine Learning. J. Instrum. 2018, 13, C06002. [Google Scholar] [CrossRef]
- Dwivedi, P.; Konijnenberg, A.P.; Pereira, S.F.; Meisner, J.; Urbach, H.P. Position correction in ptychography using hybrid input–output (HIO) and cross-correlation. J. Opt. 2019, 21, 035604. [Google Scholar] [CrossRef]
- Guzzi, F.; Kourousias, G.; Billè, F.; Pugliese, R.; Gianoncelli, A.; Carrato, S. A modular software framework for the design and implementation ofptychography algorithms. PeerJ Comput. Sci. 2022, 8, e1036. [Google Scholar] [CrossRef] [PubMed]
- Du, M.; Kandel, S.; Deng, J.; Huang, X.; Demortiere, A.; Nguyen, T.T.; Tucoulou, R.; De Andrade, V.; Jin, Q.; Jacobsen, C. Adorym: A multi-platform generic X-ray image reconstruction framework based on automatic differentiation. Opt. Express 2021, 29, 10000. [Google Scholar] [CrossRef]
- Du, M.; Nashed, Y.S.; Kandel, S.; Gürsoy, D.; Jacobsen, C. Three dimensions, two microscopes, one code: Automatic differentiation for x-ray nanotomography beyond the depth of focus limit. Sci. Adv. 2020, 6, eaay3700. [Google Scholar] [CrossRef] [Green Version]
- Shenfield, A.; Rodenburg, J.M. Evolutionary determination of experimental parameters for ptychographical imaging. J. Appl. Phys. 2011, 109, 124510. [Google Scholar] [CrossRef] [Green Version]
- Loetgering, L.; Rose, M.; Keskinbora, K.; Baluktsian, M.; Dogan, G.; Sanli, U.; Bykova, I.; Weigand, M.; Schütz, G.; Wilhein, T. Correction of axial position uncertainty and systematic detector errors in ptychographic diffraction imaging. Opt. Eng. 2018, 57, 1. [Google Scholar] [CrossRef]
- Loetgering, L.; Du, M.; Eikema, K.S.E.; Witte, S. zPIE: An autofocusing algorithm for ptychography. Opt. Lett. 2020, 45, 2030. [Google Scholar] [CrossRef]
- Guzzi, F.; Kourousias, G.; Billè, F.; Pugliese, R.; Gianoncelli, A.; Carrato, S. A Deep Prior Method for Fourier Ptychography Microscopy. In Proceedings of the 2021 44th International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 27 September–1 October 2021; pp. 1781–1786. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, Z. Pytorch-DCT. 2018. Available online: https://github.com/zh217/torch-dct (accessed on 13 February 2023).
- Feinman, R. Pytorch-Minimize. 2021. Available online: https://github.com/rfeinman/pytorch-minimize (accessed on 13 February 2023).
- Koho, S.; Tortarolo, G.; Castello, M.; Deguchi, T.; Diaspro, A.; Vicidomini, G. Fourier ring correlation simplifies image restoration in fluorescence microscopy. Nat. Commun. 2019, 10, 3103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Chambolle, A.; Duval, V.; Peyré, G.; Poon, C. Geometric properties of solutions to the total variation denoising problem. Inverse Probl. 2016, 33, 015002. [Google Scholar] [CrossRef] [Green Version]
- Cotter, F. Uses of Complex Wavelets in Deep Convolutional Neural Networks; Apollo—University of Cambridge Repository: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- A Wavelet Tour of Signal Processing; Elsevier: Amsterdam, The Netherlands, 1999. [CrossRef]
- E. Riba, D.; Mishkin, D.P.E.R.; Bradski, G. Kornia: An Open Source Differentiable Computer Vision Library for PyTorch. In Proceedings of the Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; 2020. [Google Scholar]
- Nashed, Y.S.; Peterka, T.; Deng, J.; Jacobsen, C. Distributed Automatic Differentiation for Ptychography. Procedia Comput. Sci. 2017, 108, 404–414. [Google Scholar] [CrossRef]
- Kandel, S.; Maddali, S.; Allain, M.; Hruszkewycz, S.O.; Jacobsen, C.; Nashed, Y.S.G. Using automatic differentiation as a general framework for ptychographic reconstruction. Opt. Express 2019, 27, 18653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stockmar, M.; Cloetens, P.; Zanette, I.; Enders, B.; Dierolf, M.; Pfeiffer, F.; Thibault, P. Near-field ptychography: Phase retrieval for inline holography using a structured illumination. Sci. Rep. 2013, 3, 1927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paganin, D.M. Coherent X-ray Optics; Oxford Series on Synchrotron Radiation; Oxford University Press: London, UK, 2013. [Google Scholar]
- Gianoncelli, A.; Kourousias, G.; Merolle, L.; Altissimo, M.; Bianco, A. Current status of the TwinMic beamline at Elettra: A soft X-ray transmission and emission microscopy station. J. Synchrotron Radiat. 2016, 23, 1526–1537. [Google Scholar] [CrossRef] [PubMed]
- Cammisuli, F.; Giordani, S.; Gianoncelli, A.; Rizzardi, C.; Radillo, L.; Zweyer, M.; Da Ros, T.; Salomé, M.; Melato, M.; Pascolo, L. Iron-related toxicity of single-walled carbon nanotubes and crocidolite fibres in human mesothelial cells investigated by Synchrotron XRF microscopy. Sci. Rep. 2018, 8, 706. [Google Scholar] [CrossRef] [Green Version]
- Gürsoy, D.; De Carlo, F.; Xiao, X.; Jacobsen, C. TomoPy: A framework for the analysis of synchrotron tomographic data. J. Synchrotron Radiat. 2014, 21, 1188–1193. [Google Scholar] [CrossRef] [Green Version]
- Pouchard, L.; Juhas, P.; Park, G.; Dam, H.V.; Campbell, S.I.; Stavitski, E.; Billinge, S.; Wright, C.J. Provenance Infrastructure for Multi-modal X-ray Experiments and Reproducible Analysis. In Handbook on Big Data and Machine Learning in the Physical Sciences; World Scientific Publishing Co Pte Ltd.: Singapore, 2020; Chapter 15; pp. 307–331. [Google Scholar] [CrossRef]
- Dullin, C.; di Lillo, F.; Svetlove, A.; Albers, J.; Wagner, W.; Markus, A.; Sodini, N.; Dreossi, D.; Alves, F.; Tromba, G. Multiscale biomedical imaging at the SYRMEP beamline of Elettra—Closing the gap between preclinical research and patient applications. Phys. Open 2021, 6, 100050. [Google Scholar] [CrossRef]
- Tavella, S.; Ruggiu, A.; Giuliani, A.; Brun, F.; Canciani, B.; Manescu, A.; Marozzi, K.; Cilli, M.; Costa, D.; Liu, Y.; et al. Bone Turnover in Wild Type and Pleiotrophin-Transgenic Mice Housed for Three Months in the International Space Station (ISS). PLoS ONE 2012, 7, e33179. [Google Scholar] [CrossRef]
- MessaoudiI, C.; Boudier, T.; Sorzano, C.O.S.; Marco, S. TomoJ: Tomography software for three-dimensional reconstruction in transmission electron microscopy. BMC Bioinform. 2007, 8, 288. [Google Scholar] [CrossRef] [Green Version]
- Guzzi, F.; Bille‘, F.; Carrato, S.; Gianoncelli, A. Kourousias, G Automatic Differentiation Methods for Computational Microscopy Experiments—Code. 2023. Available online: https://vuo.elettra.eu/pls/vuo/open_access_data_portal.show_view_investigation?FRM_ID=10664 (accessed on 16 February 2023).






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzzi, F.; Gianoncelli, A.; Billè, F.; Carrato, S.; Kourousias, G. Automatic Differentiation for Inverse Problems in X-ray Imaging and Microscopy. Life 2023, 13, 629. https://doi.org/10.3390/life13030629
Guzzi F, Gianoncelli A, Billè F, Carrato S, Kourousias G. Automatic Differentiation for Inverse Problems in X-ray Imaging and Microscopy. Life. 2023; 13(3):629. https://doi.org/10.3390/life13030629
Chicago/Turabian StyleGuzzi, Francesco, Alessandra Gianoncelli, Fulvio Billè, Sergio Carrato, and George Kourousias. 2023. "Automatic Differentiation for Inverse Problems in X-ray Imaging and Microscopy" Life 13, no. 3: 629. https://doi.org/10.3390/life13030629
APA StyleGuzzi, F., Gianoncelli, A., Billè, F., Carrato, S., & Kourousias, G. (2023). Automatic Differentiation for Inverse Problems in X-ray Imaging and Microscopy. Life, 13(3), 629. https://doi.org/10.3390/life13030629





