Integrating Finite Element Death Technique and Bone Remodeling Theory to Predict Screw Loosening Affected by Radiation Treatment after Mandibular Reconstruction Surgery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Finite Element Model Generation
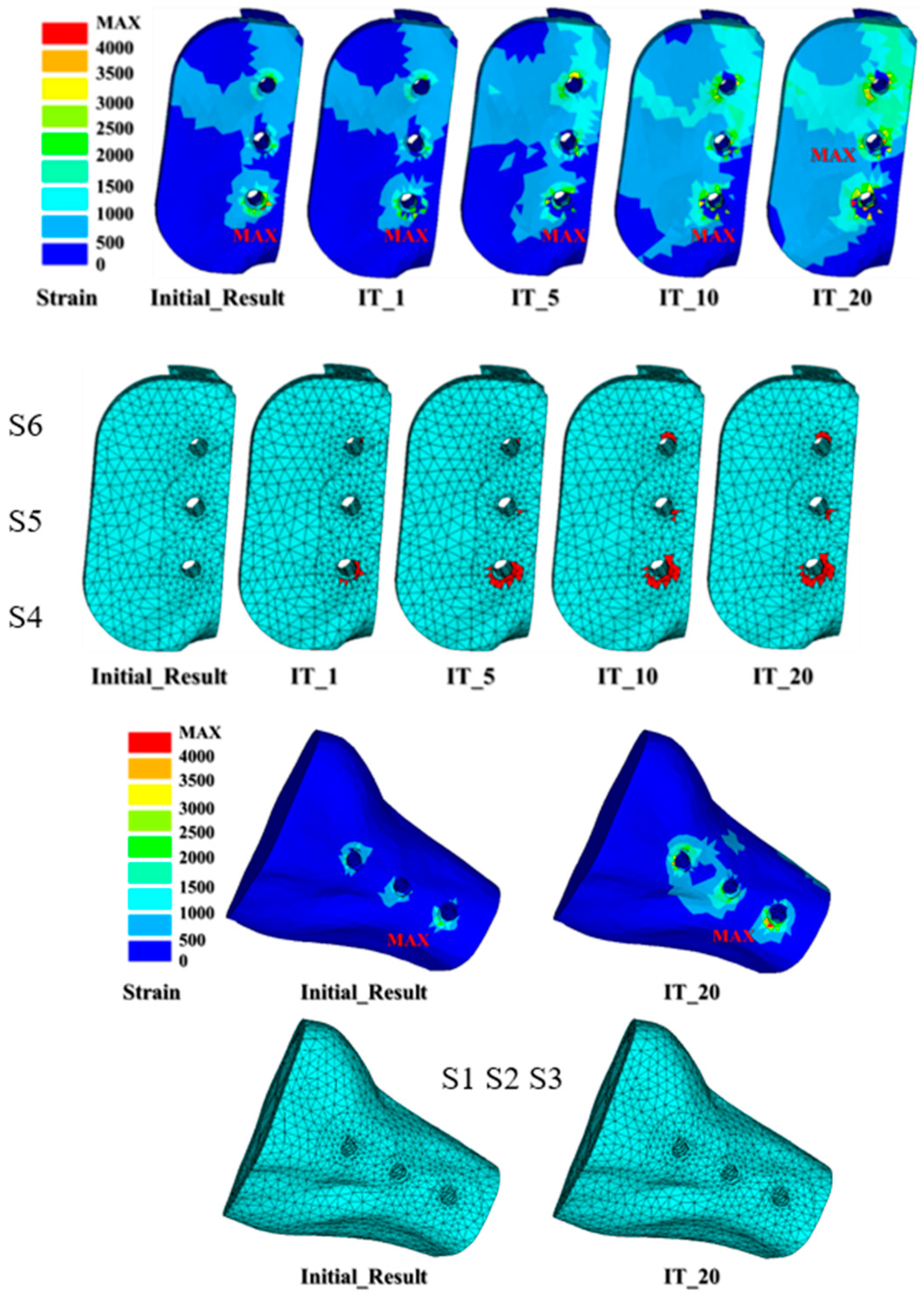
2.2. Micro-Crack Propagation Simulation Using Element Death Analysis
2.3. Mandibular Reconstruction Surgery and Radiation Treatment
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, C.H.; Wu, C.H.; Lin, C.L. Design of a patient-specific mandible reconstruction implant with dental prosthesis for metal 3D printing using integrated weighted topology optimization and finite element analysis. J. Mech. Behav. Biomed. Mater. 2020, 105, 103700. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, H.G.; Ham, M.J.; Hong, D.G.K.; Kim, S.G.; Rotaru, H. Custom implant for reconstruction of mandibular continuity defect. J. Oral Maxillofac. Surg. 2018, 76, 1370–1376. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.; Harrison, P.; Cheng, A.; Bray, B.; Bell, R.B. Fibular reconstruction of the maxilla and mandible with immediate implant-supported prosthetic rehabilitation: JAW in a day. Oral Maxillofac. Surg. Clin. N. Am. 2019, 31, 369–986. [Google Scholar] [CrossRef]
- Toure, G.; Gouet, E. Use of a 3-dimensional custom-made porous titanium prosthesis for mandibular body reconstruction with prosthetic dental rehabilitation and lipofilling. J. Oral Maxillofac. Surg. 2019, 77, 1305–1313. [Google Scholar] [CrossRef]
- Chiapasco, M.; Colletti, G.; Romeo, E.; Zaniboni, M.; Brusati, R. Long-term results of mandibular reconstruction with autogenous bone grafts and oral implants after tumor resection. Clin. Oral Implants Res. 2008, 19, 1074–1080. [Google Scholar] [CrossRef]
- Vajgel, A.; Camargo, I.B.; Willmersdorf, R.B.; de Melo, T.M.; Laureano Filho, J.R.; Vasconcellos, R.J. Comparative finite element analysis of the biomechanical stability of 2.0 fixation plates in atrophic mandibular fractures. J. Oral Maxillofac. Surg. 2013, 71, 335–342. [Google Scholar] [CrossRef] [PubMed]
- Bujtár, P.; Simonovics, J.; Váradi, K.; Sándor, G.K.B.; Avery, C.M.E. The biomechanical aspects of reconstruction for segmental defects of the mandible: A finite element study to assess the optimization of plate and screw factors. J. Cranio Maxillofac. Surg. 2014, 42, 855–862. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Shen, L.; Li, J.; Liang, R.; Tian, W.; Tang, W. Optimal design of an individual endoprosthesis for the reconstruction of extensive mandibular defects with finite element analysis. J. Cranio Maxillofac. Surg. 2014, 42, 73–78. [Google Scholar] [CrossRef] [PubMed]
- De Felice, F.; Musio, D.; Tombolini, V. Osteoradionecrosis and intensity modulated radiation therapy: An overview. Crit. Rev. Oncol. Hematol. 2016, 107, 39–43. [Google Scholar] [CrossRef]
- Marx, R.E. Osteoradionecrosis: A new concept of its pathophysiology. J. Oral Maxillofac. Surg. 1993, 41, 283–288. [Google Scholar] [CrossRef]
- Monika, D.P.; Both, S.; Alexander, C.W.; Amit, M.; Sunday, O.A. Onest of mandible and tibia osteoradionecrosis: A comparative pilot study in the rat. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. 2013, 115, 201–211. [Google Scholar]
- Patrik, C.; Keita, I.; Rafaa, E.; Stephanie, B.; Elisabeth, S.R.; Roland, D.C.; Bert van, R. Bone remodeling in humans is load-driven but not lazy. Nat. Commun. 2014, 5, 4855. [Google Scholar]
- Frost, H.M. From Wolff’s law to the Utah paradigm: Insights about bone physiology and its clinical applications. Anat. Rec. 2001, 262, 398–419. [Google Scholar] [CrossRef] [PubMed]
- Frost, H.M. On our age-related bone loss: Insights from a new paradigm. J. Bone Miner. Res. 1997, 12, 1539–1546. [Google Scholar] [CrossRef]
- Huiskes, R.; Weinans, H.; Grootenboer, H.J.; Dalstra, M.; Fudala, B.; Slooff, T.J. Adaptive bone-remodeling theory applied to prosthetic-design analysis. J. Biomech. 1997, 20, 1135–1150. [Google Scholar] [CrossRef] [Green Version]
- Huiskes, R.; Weinans, H.; van Rietbergen, B. The relationship between stress shielding and bone resorption around total hip stems and the effects of flexible materials. Clin. Orthop. Relat. Res. 1992, 274, 124–134. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.L.; Lin, Y.H.; Chang, S.H. Multi-factorial analysis of variables influencing the bone loss of an implant placed in the maxilla: Prediction using FEA and SED bone remodeling algorithm. J. Biomech. 2010, 43, 644–651. [Google Scholar] [CrossRef] [PubMed]
- Watson, P.J.; Gröning, F.; Curtis, N.; Fitton, L.C.; Herrel, A.; McCormack, S.W.; Fagan, M.J. Masticatory biomechanics in the rabbit: A multi-body dynamics analysis. J. R. Soc. Interface 2014, 11, 20140564. [Google Scholar] [CrossRef] [Green Version]
- Atali, O.; Varol, A.; Basa, S.; Ergun, C.; Hartomacıoğlu, S. Comparison and validation of finite element analysis with a servo-hydraulic testing unit for a biodegradable fixation system in a rabbit model. Int. J. Oral Maxillofac. Surg. 2014, 43, 32–39. [Google Scholar] [CrossRef]
- Prendergast, P.J.; Taylor, D. Prediction of bone adaptation using gamage accumulation. J. Biomech. 1994, 27, 1067–1076. [Google Scholar] [CrossRef]
- Poort, L.J.; Ludlage, J.H.B.; Lie, N.; Böckmann, R.A.; Odekerken, J.C.E.; Hoebers, F.J.; Kessler, P.A.W.H. The histological and histomorphometric changes in the mandible after radiotherapy: An animal model. J. Craniomaxillofac. Surg. 2017, 45, 716–721. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.L.; Lin, C.-L.; Sun, M.T.; Chang, Y.H. 3D micro-crack propagation simulation at enamel/adhesive interface using FE submodeling and element death techniques. Ann. Biomed. Eng. 2010, 38, 2004–2012. [Google Scholar] [CrossRef] [PubMed]
- Sciubba, J.J.; Goldenberg, D. Oral complications of radiotherapy. Lancet Oncol. 2006, 7, 175–183. [Google Scholar] [CrossRef]
- Yu, T.; Gao, H.; Liu, T.; Huang, Y.; Wang, C. Effects of immediately static loading on osteointegration and osteogenesis around 3D-printed porous implant: A histological and biomechanical study. Mater. Sci. Eng. 2020, 108, 110406. [Google Scholar] [CrossRef] [PubMed]
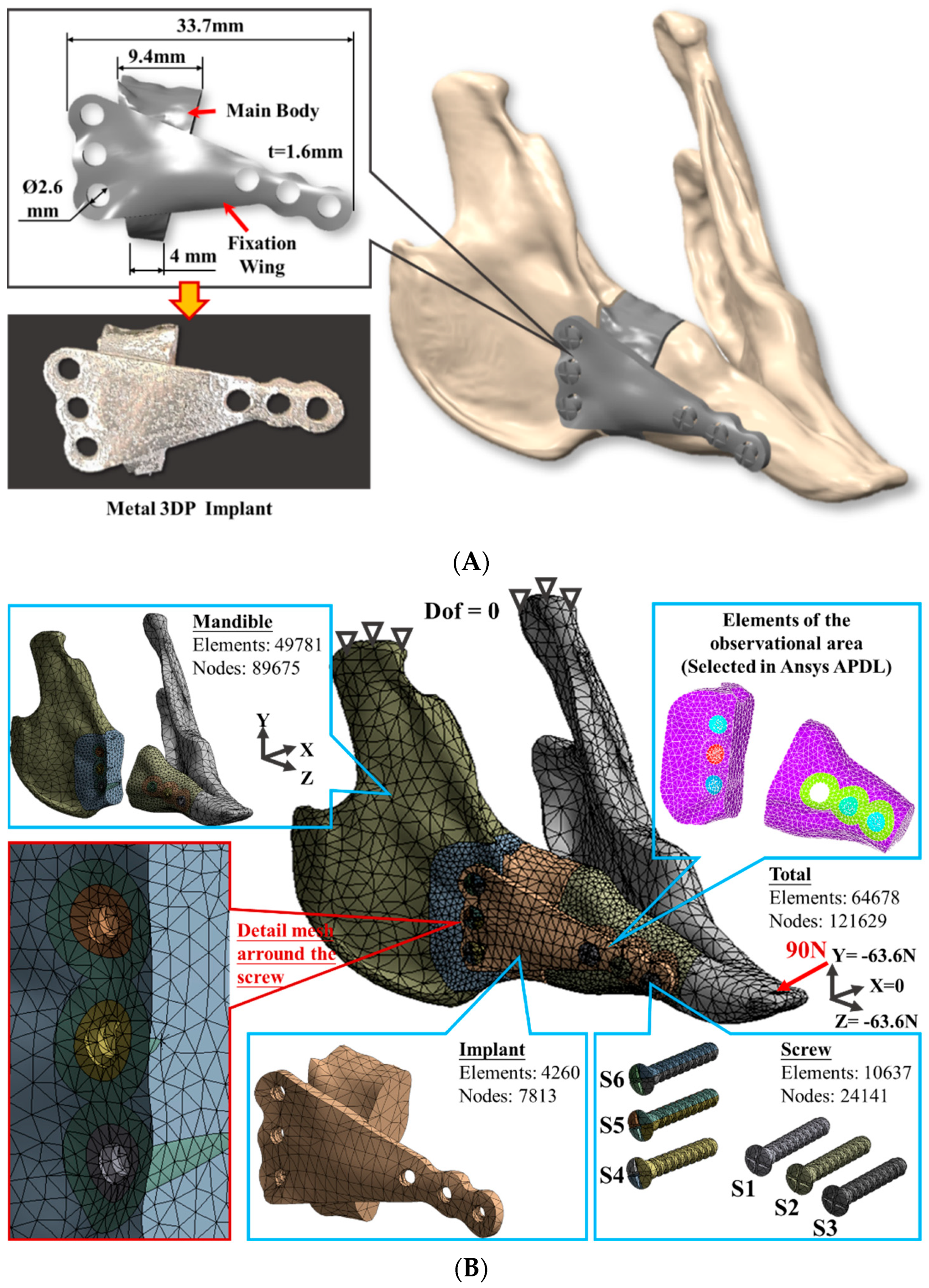






| Material | Young’s Modulus | Poisson’s Ratio |
|---|---|---|
| Cortical Bone | 13,700 MPa | 0.3 |
| Cancellous Bone | 1370 MPa | 0.3 |
| Implants (Ti-6Al-4V) | 110,000 MPa | 0.35 |
| Bone Screw (Ti-6Al-4V) | 110,000 MPa | 0.35 |
| S4_Dis. | S5_Dis. | S6_Dis. | S4_% | S5_% | S6_% | |
|---|---|---|---|---|---|---|
| Initial results | 0.000683 | 0.000596 | 0.000522 | |||
| IT_1 | 0.000685 | 0.000597 | 0.000522 | 0.29 | 0.17 | 0.00 |
| IT_5 | 0.000687 | 0.000598 | 0.000523 | 0.59 | 0.34 | 0.19 |
| IT_10 | 0.000688 | 0.000598 | 0.000523 | 0.73 | 0.34 | 0.19 |
| IT_20 | 0.000688 | 0.000598 | 0.000523 | 0.73 | 0.34 | 0.19 |
| S1 | S2 | S3 | S4 | S5 | S6 | |
|---|---|---|---|---|---|---|
| Initial results | 0 | 0 | 0 | 0 | 0 | 0 |
| IT_1 | 0 | 0 | 0 | 46 | 1 | 5 |
| IT_5 | 0 | 0 | 0 | 121 | 6 | 10 |
| IT_10 | 0 | 0 | 0 | 160 | 9 | 23 |
| IT_20 | 0 | 0 | 0 | 164 | 10 | 23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.-J.; Hsieh, K.-H.; Lin, C.-L. Integrating Finite Element Death Technique and Bone Remodeling Theory to Predict Screw Loosening Affected by Radiation Treatment after Mandibular Reconstruction Surgery. Diagnostics 2020, 10, 844. https://doi.org/10.3390/diagnostics10100844
Wu L-J, Hsieh K-H, Lin C-L. Integrating Finite Element Death Technique and Bone Remodeling Theory to Predict Screw Loosening Affected by Radiation Treatment after Mandibular Reconstruction Surgery. Diagnostics. 2020; 10(10):844. https://doi.org/10.3390/diagnostics10100844
Chicago/Turabian StyleWu, Le-Jung, Kai-Hung Hsieh, and Chun-Li Lin. 2020. "Integrating Finite Element Death Technique and Bone Remodeling Theory to Predict Screw Loosening Affected by Radiation Treatment after Mandibular Reconstruction Surgery" Diagnostics 10, no. 10: 844. https://doi.org/10.3390/diagnostics10100844
APA StyleWu, L.-J., Hsieh, K.-H., & Lin, C.-L. (2020). Integrating Finite Element Death Technique and Bone Remodeling Theory to Predict Screw Loosening Affected by Radiation Treatment after Mandibular Reconstruction Surgery. Diagnostics, 10(10), 844. https://doi.org/10.3390/diagnostics10100844






