Next Article in Journal
RNA-Based Multiplexing Assay for Routine Testing of Fusion and Splicing Variants in Cytological Samples of NSCLC Patients
Next Article in Special Issue
Simulated Radiation Dose Reduction in Whole-Body CT on a 3rd Generation Dual-Source Scanner: An Intraindividual Comparison
Previous Article in Journal
Deportalization, Venous Congestion, Venous Deprivation: Serial Measurements of Volumes and Functions on Morphofunctional 99mTc-Mebrofenin SPECT-CT
Previous Article in Special Issue
COPD Imaging on a 3rd Generation Dual-Source CT: Acquisition of Paired Inspiratory-Expiratory Chest Scans at an Overall Reduced Radiation Risk
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Diagnostics
Volume 11
Issue 1
10.3390/diagnostics11010014
diagnostics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Optimization of the Maximum Skin Dose Measurement Technique Using Digital Imaging and Communication in Medicine—Radiation Dose Structured Report Data for Patients Undergoing Cerebral Angiography

by
Koichi Morota
1,2,
Takashi Moritake
2,*,
Keisuke Nagamoto
2,3,
Satoru Matsuzaki
1,2,
Koichi Nakagami
2,3,
Lue Sun
4 and
Naoki Kunugita
5
1
Department of Radiology, Shinkomonji Hospital, 2-5 Dairishinmachi, Moji-ku, Kitakyushu, Fukuoka 800-0057, Japan
2
Department of Radiobiology and Hygiene Management, Institute of Industrial Ecological Sciences, University of Occupational and Environmental Health, Japan, 1-1 Iseigaoka, Yahatanishi-ku, Kitakyushu, Fukuoka 807-8555, Japan
3
Department of Radiology, Hospital of the University of Occupational and Environmental Health, Japan, 1-1 Iseigaoka, Yahatanishi-ku, Kitakyushu, Fukuoka 807-8556, Japan
4
Health and Medical Research Institute, Department of Life Science and Biotechnology, National Institute of Advanced Industrial Science and Technology (AIST), Central 6, 1-1-1 Higashi, Tsukuba, Ibaraki 305-8566, Japan
5
Department of Occupational and Community Health Nursing, School of Health Sciences, University of Occupational and Environmental Health, Japan, 1-1 Iseigaoka, Yahatanishi-ku, Kitakyushu, Fukuoka 807-8555, Japan
*
Author to whom correspondence should be addressed.
Diagnostics 2021, 11(1), 14; https://doi.org/10.3390/diagnostics11010014
Submission received: 5 November 2020 / Revised: 4 December 2020 / Accepted: 18 December 2020 / Published: 23 December 2020
(This article belongs to the Special Issue Assessment of Radiation Dose in X-ray and CT Exams)
Browse Figures
Versions Notes

Abstract

:
Understanding the maximum skin dose is important for avoiding tissue reactions in cerebral angiography. In this study, we devised a method for using digital imaging and communication in medicine—radiation dose structured report (DICOM-RDSR) data to accurately estimate the maximum skin dose from the total air kerma at the patient entrance reference point (Total Ka,r). Using a test data set (n = 50), we defined the mean ratio of the maximum skin dose obtained from measurements with radio-photoluminescence glass dosimeters (RPLGDs) to the Total Ka,r as the conversion factor, CFKa,constant, and compared the accuracy of the estimated maximum skin dose obtained from multiplying Total Ka,r by CFKa,constant (Estimation Model 1) with that of the estimated maximum skin dose obtained from multiplying Total Ka,r by the functional conversion factor CFKa,function (Estimation Model 2). Estimation Model 2, which uses the quadratic function for the ratio of the fluoroscopy Ka,r to the Total Ka,r (Ka,r ratio), provided an estimated maximum skin dose closer to that obtained from direct measurements with RPLGDs than compared with that determined using Estimation Model 1. The same results were obtained for the validation data set (n = 50). It was suggested the quadratic function for the Ka,r ratio provides a more accurate estimate of the maximum skin dose in real time.

1. Introduction

The advances in interventional radiology (IVR) technology in recent years have resulted in an increased number of patients undergoing lengthy procedures, and the increased radiation exposure of patients is becoming a great concern. Although neurointerventional radiology (NIR) has a number of practical benefits for patients, including being less physically invasive than surgical treatment and requiring a shorter time in hospital, there have been numerous reported cases of tissue reactions (deterministic effects), such as hair loss, under increased radiation exposure doses [1,2,3,4,5].
The most important factor in managing patient radiation exposure dose is to ascertain the maximum skin dose (Dskin,max) during an IVR procedure [6], and assessing the Dskin,max in real time is important to avoid damaging the patient’s skin [7]. The reported methods for measuring doses in real time include measuring the dose at the crystalline lens of the eye using a metal–oxide–semiconductor field-effect transistor (MOSFET) dosimeter [8] and attaching up to four photoluminescence sensors (of non-toxic phosphor) to the patient’s back to measure the skin dose [9]. Because both methods show up on X-ray fluoroscopy and involve a limited number of measurement sensors, these sensors must not only be placed at locations where they do not interfere with X-ray fluoroscopy but also require the location of the maximum dose to be predicted in advance. Both methods also involve wired measurements, and their value for estimating Dskin,max is limited. Wireless dosimeter systems utilizing plastic scintillators have recently been developed [8,10,11]. Because these systems are not made of metal, they do not show up using X-ray fluoroscopy, and their absence of cables increases their convenience. If the number of points that can be measured simultaneously were increased, this method would become more widespread [10]. A method of mapping the exposure dose on a diagram of the human body using the biplane dose tracking system (Biplane-DTS), developed by the angiography device manufacturer Canon Medical Systems, Inc. (formerly Toshiba Medical Systems, Co.), was also reported [12]. However, although it is extremely useful to be able to visualize the dose in real time, the device-specific nature of this system means that it can only be used in limited situations. A method for estimating the dose on the patient’s body surface by performing a real-time Monte Carlo simulation using a high-speed graphics processing unit (GPU) has also been reported [13], but this system can also only currently be used in a specific facility.
When considering alternative means of direct Dskin, max measurements in real time, the correlation between the indirect measurement value, the air kerma at the patient entrance reference point (Ka,r) displayed on the device, and the directly measured Dskin, max has been widely discussed [14,15,16,17,18,19,20]. For directly measuring Dskin,max, methods using thermoluminescent dosemeters (TLDs) [14,15,20] and Gafchromic film [15,16,17,18,19,20] have been reported. It was shown that the correlation between Ka,r and the directly measured Dskin,max is high, and if the Ka,r values are measured accurately, Dskin,max can be sufficiently predicted by indirect measurement through Ka,r. We previously estimated the Dskin,max for patients undergoing NIR using a RADIREC® system (Chiyoda Technol Corporation, Tokyo, Japan) (Scheme 1a) [3,21,22,23,24,25]. However, the greatest disadvantages of using the RADIREC system, a passive dosimeter system with 64 radio-photoluminescence glass dosimeters (RPLGDs) (GD-302M, Chiyoda Technol Corporation, Tokyo, Japan), for measuring the dose in a single patient are the time and effort required to obtain readouts from the RPLGDs, which make it impracticable to ascertain the Dskin,max in real time during NIR and to take measures at the right time to avoid damaging patient skin. As an alternative method, we analyzed the Dskin,max measured by the RADIREC system (Dskin,max,RPLGD) and the total air kerma at the patient entrance reference point (Total Ka,r) in the same patient among an appropriate number of patients (approximately 50). We used the ratio of the Dskin,max,RPLGD and the Total Ka,r (Dskin,max,RPLGD/Total Ka,r) as the Total Ka,r to the Dskin,max,Ka conversion factor (CFKa,constant) (Scheme 1b) [21,22,23,24,25]. Using this CFKa,constant enabled the Dskin,max (Dskin,max,Ka) to be estimated from the Total Ka,r in real time during procedures, thereby enabling the operator to be warned when the dose approaches the thresholds for skin reddening and hair loss at 2 and 3 Gy, respectively.
The Total Ka,r value must be recorded in a Digital Imaging and Communication in Medicine—Radiation Dose Structured Report (DICOM-RDSR) (Table 1) [26]. As this value is constantly displayed on the angiography monitor during procedures, setting the CFKa,constant before commencing the procedure would make any subsequent estimates of the Dskin,max,Ka in real time simpler and more convenient. However, because the irradiation angle during the procedure varies markedly between patients, the value of Dskin,max/Total Ka,r also varies markedly, and converting Total Ka,r to Dskin,max,Ka using a single fixed value (CFKa,constant), as in Estimation Model 1 (Scheme 1b), naturally generates large errors. Therefore, we developed a technique to convert Dskin,max,Ka by applying a conversion factor corrected in real time using DICOM-RDSR data for the individual patient concerned (CFKa,function), as in Estimation Model 2 (Scheme 1c).
In this study, to optimize the process for estimating Dskin,max,Ka to establish a method that would bring the value of Dskin,max,Ka estimated indirectly from the Total Ka,r value closer to the more directly estimated Dskin,max,RPLGD value, we first analyzed the factors giving rise to variation in the Dskin,max,RPLGD/Total Ka,r ratio and then devised a new method for correcting for this variation. Finally, we validated the efficacy of this new correction method using a separately prepared validation data set. Our objective was to improve the accuracy with which the Dskin,max for patients undergoing NIR can be estimated from the Total Ka,r to help prevent skin damage by providing the operator with real-time Dskin,max measurements during NIR procedures. This method may provide a new means of utilizing DICOM-RDSR data.

2. Materials and Methods

2.1. Data Sets

The test data set comprised 50 patients who underwent cerebral angiography in our hospital between October 2015 and July 2016 (diagnostic cerebral angiography: 43 cases; NIR: 7 cases), and the validation data set comprised 50 patients who underwent cerebral angiography in our hospital between August 2016 and September 2017 (diagnostic cerebral angiography: 43 cases; NIR: 7 cases) (Table 2).

2.2. X-ray Equipment

Angiography was performed using a single-plane angiography system (BRANSIST Safire VC9 Slender, Shimadzu Co., Kyoto, Japan) equipped with a flat-panel detector. The tube voltage and tube current were adjusted via auto exposure control, and scanning was conducted at a fluoroscopy pulse rate of 15 pulses/s and an exposure frame rate of 3 frames/s. A 1.5 mm Al + 0.6 mm Cu filter was automatically selected and applied during fluoroscopy, and a 1.0 mm Al filter was applied during exposure.

2.3. Dosimetry of Skin Dose for Patients Who Undergo NIR Procedures

The skin dose (Dskin,RPLGD) from the patient’s head to their neck was measured using the RADIREC® system [3,21,22,23,24,25]. This system consists of 64 RPLGDs (GD-302M, Chiyoda Technol, Corporation, Tokyo, Japan), which are passive dosimeters, placed on a special cap that covers the entire circumference of the head. The maximum skin dose (Dskin,max,RPLGD) can thus be obtained from the dose distribution and measurements at these 64 points [24,25].

2.4. RPLGD X-Ray Energy Calibration

Firstly, to obtain the energy responses of the RPLGDs under the fluoroscopy settings, the X-ray tube voltage was increased from 60 to 120 kVp in 10 kVp increments, and the X-ray effective energy at each tube voltage was measured using the aluminum half-value layer method [27] with an ionization chamber dosimeter (AE-1322 exposure ratemeter, Applied Engineering Inc., Kiyose, Tokyo, Japan), which is calibrated annually by the Japan Quality Assurance Organization (JQA), Japan’s secondary standard body. Secondly, under the same fluoroscopy settings, the ionization chamber and the five RPLGDs were simultaneously exposed to X-rays in free air at tube voltage values from 60 to 120 kVp in 10 kVp increments. Thirdly, under the exposure settings, simultaneous irradiation of the ionization chamber and the five RPLGDs was performed using the same method as described above. Finally, the RPLGD energy compensation factors (CFRPLGD) for the X-ray effective energies were calculated by dividing the ionization chamber dosimeter measurements by the RPLGD readings, and the CFRPLGD (y) values were fitted to a quadratic equation (Equation (1)) for the X-ray effective energy [keV] (x) (Figure 1):
y = 0.0002x2 − 0.0147x + 0.5270

2.5. Direct Estimation Method: Estimation of Dskin,max,RPLGD from RPLGD Measurements

In the cerebral angiography of actual patients, the tube voltage changes constantly in response to factors including the objective and procedure, scanning site, and patient’s position. Hence, the X-ray effective energy is also constantly changing. For this reason, we first calculated the CFRPLGD from Equation (1) using the representative effective energies for fluoroscopy and the exposure obtained from the individual DICOM-RDSR data for the 50 patients in the test data set; then, we calculated the weighted calibration factor (CFRPLGD,weighted) from the fluoroscopy Ka,r and the exposure Ka,r. We next defined the Total CFRPLGD,weighted as the mean CFRPLGD,weighted for all 50 patients and converted the RPLGD readout values to Dskin,RPLGD according to Equation (2) below (Scheme 1a):
Dskin,RPLGD = Total CFRPLGD,weighted × RPLGD readout value
While using the RADIREC system, we assumed that the maximum value of all Dskin,RPLGD values at the 64 dose monitoring points were Dskin,max,RPLGD.

2.6. Indirect Estimation Method: Estimation of Dskin,max from Total Ka,r by Applying an Arbitrary Constant as a Conversion Factor (CFKa,const) (Estimation Model 1)

The mean value of the ratio between Dskin,max,RPLGD and Total Ka,r (Dskin,max,RPLGD/Total Ka,r) for the 50 patients in the test data set was defined as CFKa,constant, and Dskin,max,Ka was estimated using Equation (3) below (Scheme 1b):
Dskin,max,Ka = CFKa,constant × Total Ka,r

2.7. Indirect Estimation Method: Estimation of Dskin,max from Total Ka,r by Applying an Arbitrary Function as a Conversion Factor (CFKa,function) (Estimation Model 2)

We analyzed the associations between the Dskin,max,RPLGD/Total Ka,r and the Total Ka,r, Fluoroscopy Ka,r, Exposure Ka,r, Fluoroscopy Time, Number of DSA, Number of Frames, and the Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio) in the various combinations from the DICOM-RDSR data recorded for the 50 patients in the test data set. In light of the results, we used the Total Ka,r to Dskin,max,Ka conversion factor (CFKa,function), an arbitrary function that minimizes the error between the estimated Dskin,max,Ka and the Dskin,max,RPLGD, to estimate the Dskin,max,Ka for each individual patient according to Equation (4) (Scheme 1c):
Dskin,max,Ka = CFKa,function × Total Ka,r

2.8. Comparison of the Accuracy of the Estimation of Dskin,max,Ka under Estimation Models 1 and 2

Using the 50 patient test data set, we carried out a regression analysis between the values of Dskin,max,Ka estimated indirectly using the two maximum skin dose estimation models above (Estimation Models 1 and 2) and the value of Dskin,max,RPLGD estimated directly from RPLGD readouts. We calculated the root mean squared error (RMSE), mean absolute error (MAE), and coefficient of determination (R2) between Dskin,max,Ka and Dskin,max,RPLGD, and compared the goodness of fit of the two estimation models.

2.9. Validation of the Accuracy of Estimation Models 1 and 2 Using the Validation Data Set

Using the 50 patient validation data set, after first determining that there was little variation in CFRPLGD,weighted, we determined the Total CFRPLGD,weighted. We then compared the goodness of fit of the two maximum skin dose estimation models (Estimation Models 1 and 2) via the same method as that used for the test data set.

2.10. Statistical Analysis

SPSS (Version 25. SPSS Inc., Chicago, IL, USA) was used for statistical analyses. Differences between the mean values of the test data set and the validation data set were tested for significance using Welch’s t-test, with p < 0.05 regarded as indicating significance.

2.11. Ethical Approval

This study was approved by the Ethics Committee of Shinkomonji Hospital (Approval No. 27004, 10 June 2015).

3. Results

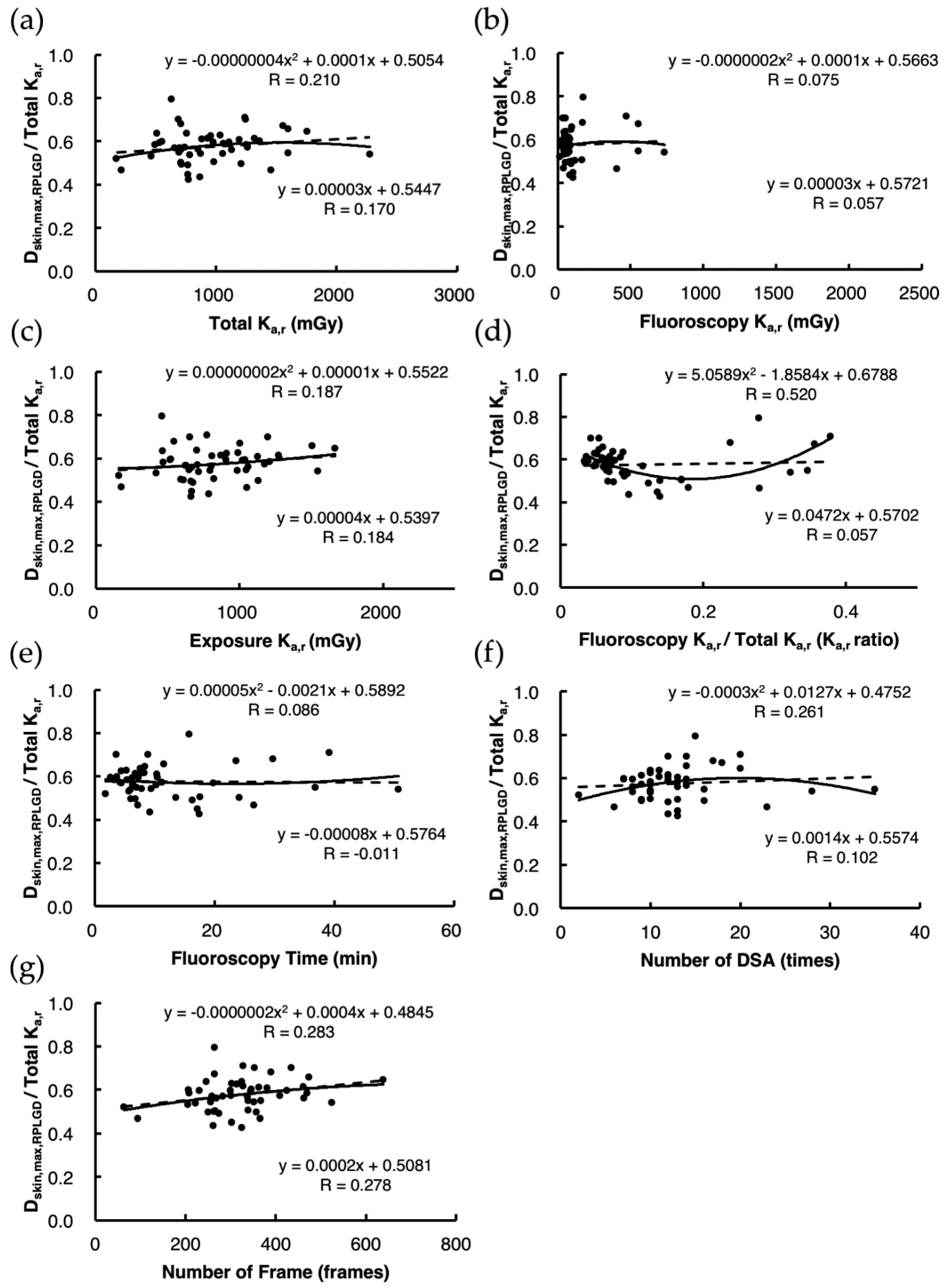
3.1. Direct Estimation of Dskin,max,RPLGD

Table 3 shows the values of CFRPLGD,weighted, the RPLGD compensation factors weighted by the Ka,r for fluoroscopy, and the exposure obtained from the DICOM-RDSR data for the 50 patients in the test data set. CFRPLGD,weighted exhibited little variation at 0.272 ± 0.004 (mean ± standard deviation; range: 0.267−0.284), suggesting that, in practical terms, the effect of patient differences on CFRPLGD,weighted is negligible, so a value of 0.272 for Total CFRPLGD,weighted was adopted. The highest of the Dskin,RPLGD values at the 64 sites calculated for each patient was used as Dskin,max,RPLGD.

3.2. Indirect Estimation of Dskin,max,Ka Using Estimation Model 1

The Dskin,max,RPLGD/Total Ka,r for the 50 patients in the test data set was 0.575 ± 0.075 (mean ± standard deviation; range: 0.425−0.795), so a value of 0.575 for CFKa,constant was used to estimate Dskin,max,Ka using Equation (3).

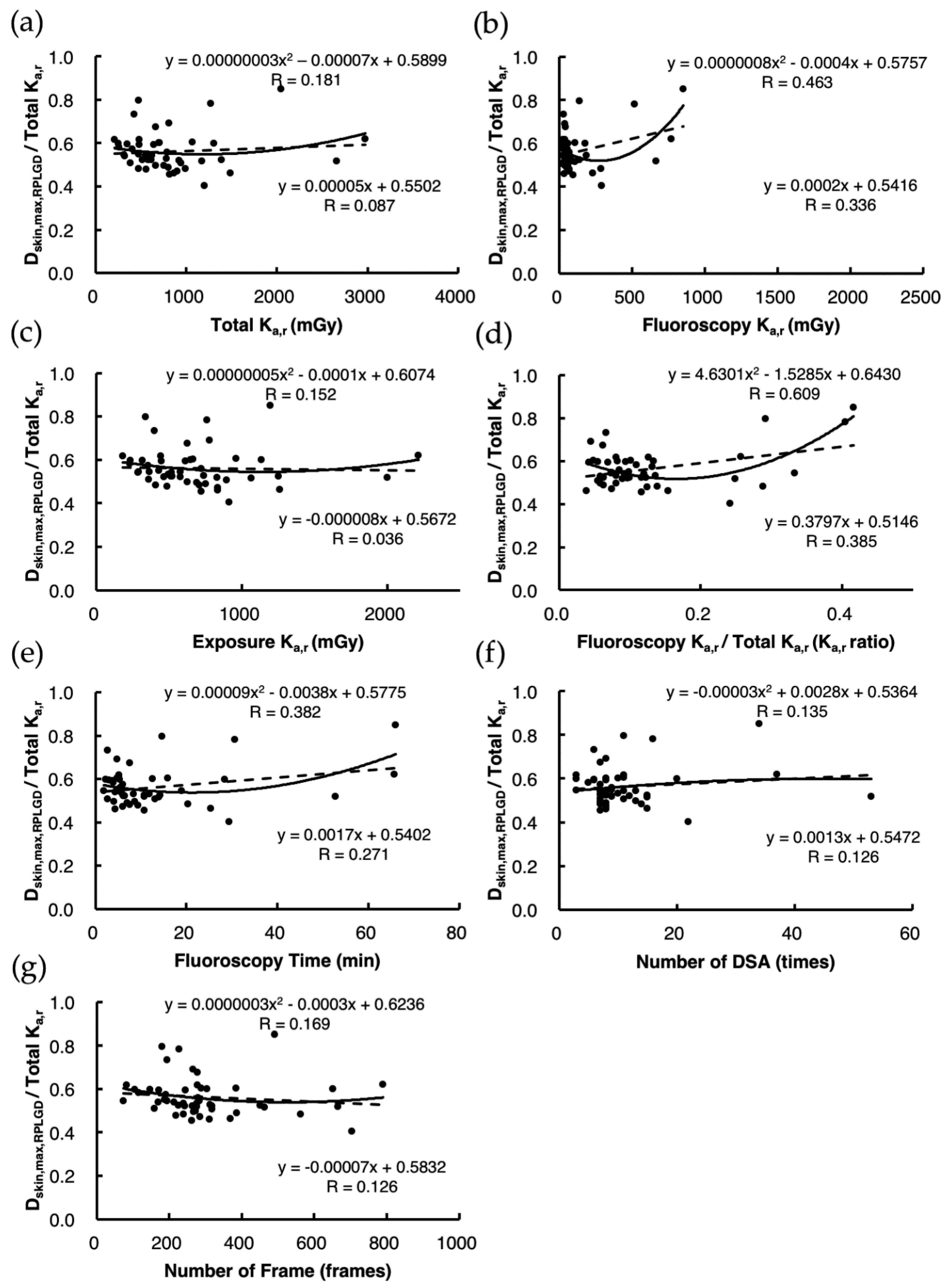
3.3. Indirect Estimation of Dskin,max,Ka Using Estimation Model 2

A linear regression analysis of the 50 patients in the test data set did not show any significant correlation between Total Ka,r, Fluoroscopy Ka,r, Exposure Ka,r, Fluoroscopy Time, Number of DSA, Number of Frames, or Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio) and Dskin,max,RPLGD/Total Ka,r (Figure 2). However, quadratic regression analysis identified a moderate correlation (R = 0.520) for Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio) alone (Figure 2d), so Equation (5) was used as the CFKa,function:
CFKa,function = 5.0589 × (Fluoroscopy Ka,r/Total Ka,r)2 − 1.8584 × (Fluoroscopy Ka,r/Total Ka,r) + 0.6788
Dskin,max,Ka was estimated using Equations (4) and (5).

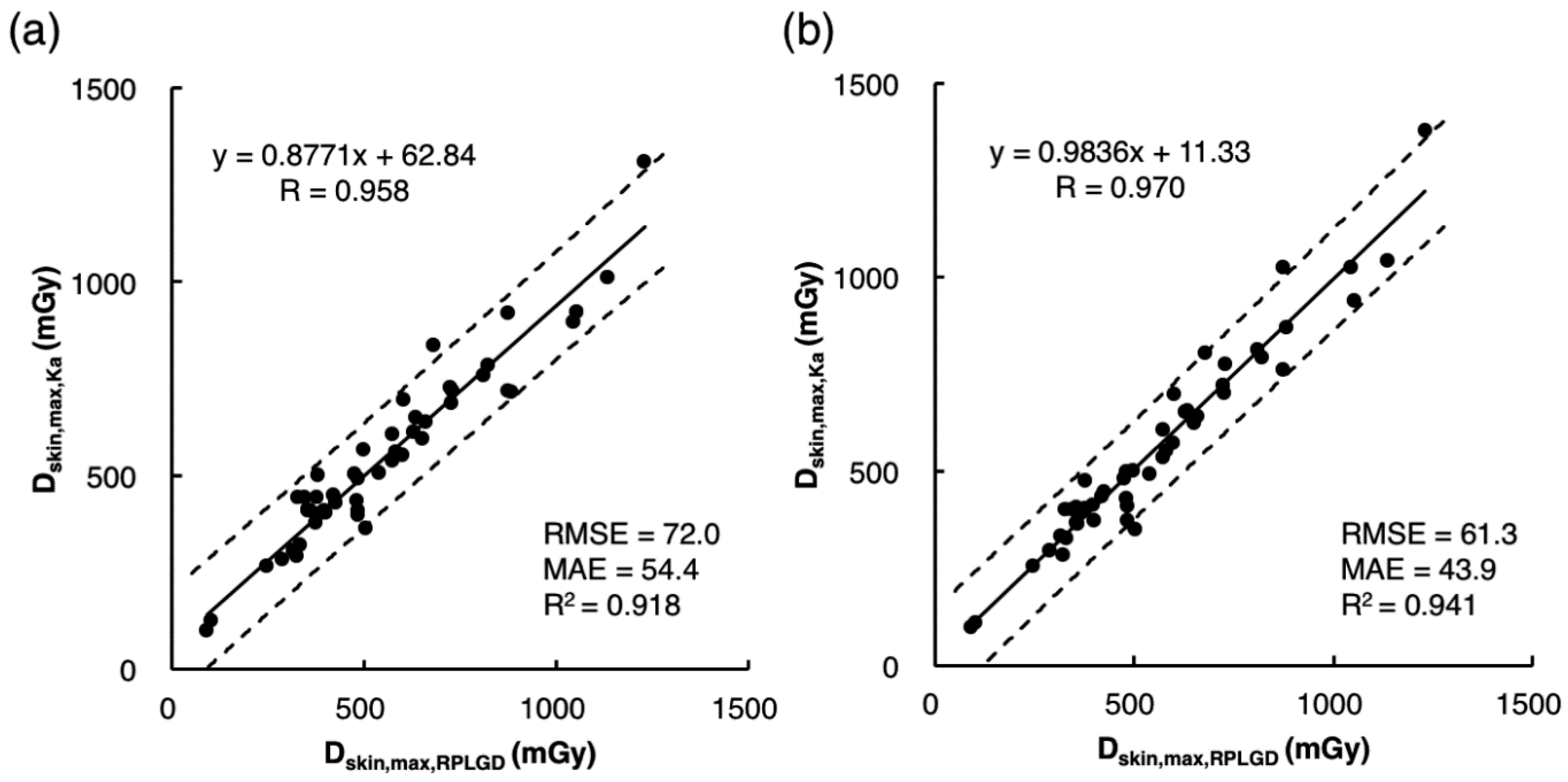
3.4. Comparison of the Accuracy of Dskin,max,Ka Estimated Using Estimation Models 1 and 2

Using the 50 patient test data set, we analyzed the correlations between the values of Dskin,max,Ka estimated using Estimation Models 1 and 2 and Dskin,max,RPLGD. We found that the correlation was high for both estimation methods (Model 1, R = 0.958; Model 2, R = 0.970) but that Estimation Model 2, which used CFKa,function as the conversion factor for individual patients, exhibited a better goodness of fit than Estimation Model 1 in terms of RMSE, MAE, and R2, demonstrating the superiority of Estimation Model 2 (Figure 3).

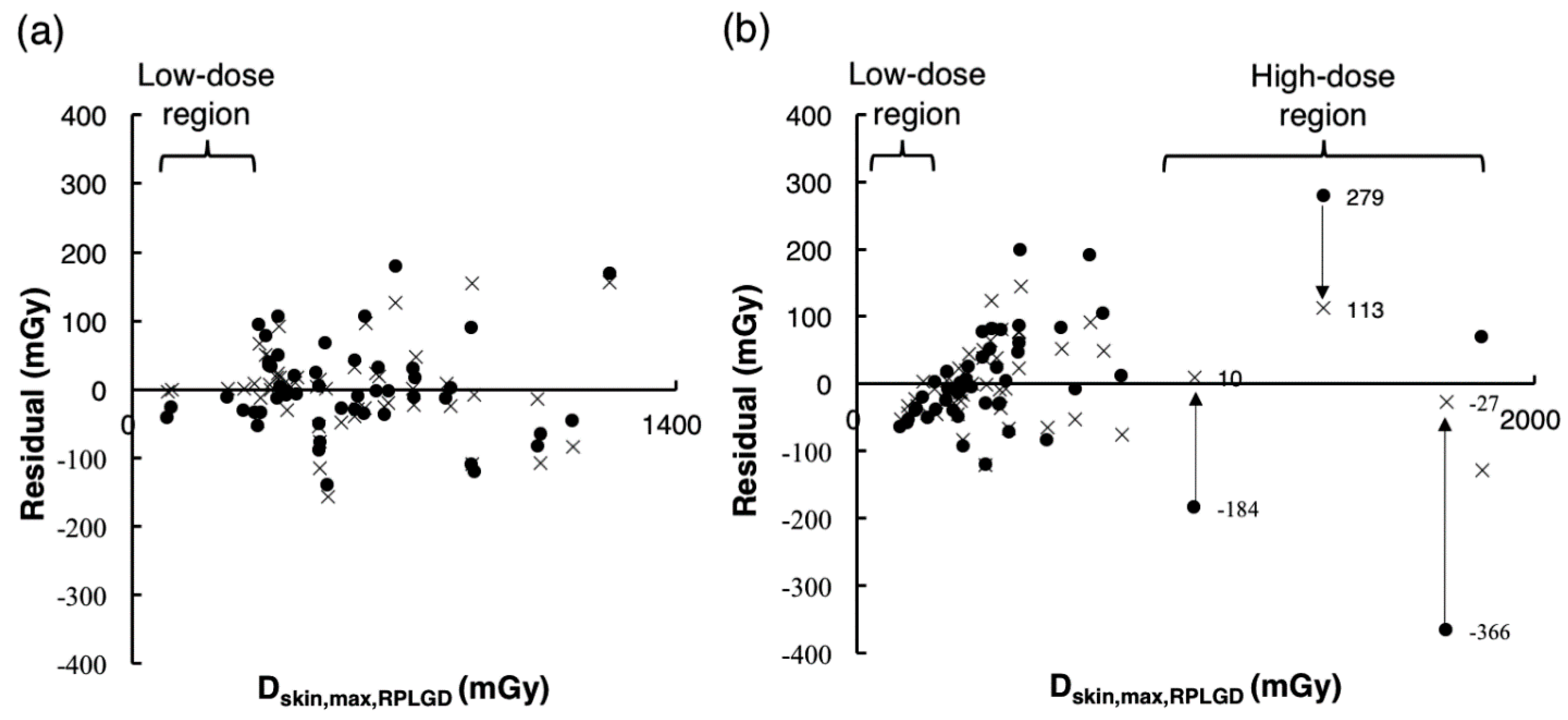
3.5. Validation of the Accuracy of Estimates Using Estimation Models 1 and 2 under the Validation Data Set

In the 50 patient validation data set, CFRPLGD,weighted exhibited little variation at 0.273 ± 0.004 (mean ± standard deviation; range: 0.270−0.287) (Table 4), so a value of 0.273 for Total CFRPLGD,weighted was adopted. Dskin,max,RPLGD/Total Ka,r was 0.562 ± 0.089 (mean ± standard deviation; range: 0.403−0.850), so a value of 0.562 was used for CFKa,constant. As in the test data set, linear regression did not show any significant correlation between Total Ka,r, Fluoroscopy Ka,r, Exposure Ka,r, Fluoroscopy Time, Number of DSA, Number of Frames, or Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio), or Dskin,max,RPLGD/Total Ka,r (Figure 4). However, quadratic regression identified a moderate correlation (R = 0.609) for Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio) (Figure 4d), so the quadratic equation shown as Equation (6) was used as the CFKa,function:
CFKa,function = 4.6301 × (Fluoroscopy Ka,r/Total Ka,r)2 − 1.5285 × (Fluoroscopy Ka,r/Total Ka,r) + 0.6430
Analysis of the correlations between the values of Dskin,max,Ka estimated by Estimation Models 1 and 2 using these values and Dskin,max,RPLGD showed that although the correlations were high for both estimation methods (Model 1, R = 0.951; Model 2, R = 0.984), Estimation Model 2, which used CFKa,function as the conversion factor for individual patients, exhibited a better goodness of fit than Estimation Model 1 in terms of the RMSE, MAE, and R2, demonstrating the superiority of Estimation Model 2 (Figure 5).

4. Discussion

Two factors are important for reducing the occurrence of radiation damage in patients undergoing IVR: minimizing stochastic effects, such as carcinogenesis and genetic effects, and avoiding tissue reactions, such as hair loss and skin injury [6].
One method for reducing the stochastic effects of IVR is to use the diagnostic reference level (DRL) to keep the radiation dose administered to the patient “as low as reasonably achievable (ALARA)” while guaranteeing the image quality required for diagnostic imaging [28,29,30]. Countries belonging to the European Union (EU) are required to establish DRLs [31], and individual countries have adopted DRLs appropriate to their situations. In the United States, organizations including the American College of Radiology (ACR), the American Association of Physicists in Medicine (AAPM), and the National Council on Radiation Protection and Measurements (NCRP) require that both image quality and dose be optimized using both the DRL, defined as the 75th percentile of the dose distribution of a number of representative facilities, and the achievable dose, defined as the 50th percentile, although not all states have adopted this approach [32]. The first Japanese DRLs were issued on 7 June 2015 by the Japan Network for Research and Information on Medical Exposure (J-RIME) [33], and these DRLs were revised five years later on 3 July 2020. With respect to NIR, the revised version includes the DRL values for the Ka,r and air kerma area product (PKA) for the imaging of six major patient groups for the three purposes of preoperative diagnostic angiography, postoperative diagnostic angiography, and endovascular treatment [34]. However, the establishment of DRLs and dose optimization by individual institutions are not directly helpful for avoiding tissue reactions. Rather, what is important is to be aware of the threshold levels in advance (reddening: 2 Gy; hair loss: 3 Gy), monitoring the Dskin,max in real time during NIR procedures, and informing the operator, as required, if this value approaches the threshold value [6].
A wide range of data is acquired for DICOM-RDSR, including the tube current and voltage, scanning data (such as exposure time and number of exposures), distance from the X-ray focal point to the detector, open area of the irradiation aperture, entrance angle, area dose, and patient entrance reference point dose. Because these data are acquired automatically for each fluoroscopy and exposure event, they can be used to manage medical radiation exposure for patients undergoing IVR [35,36,37,38,39,40,41], and case studies of patient dose monitoring in multiple institutions have been reported [35,36,41]. In particular, Total Ka,r is constantly displayed on the angiography system monitor during treatment procedures, and its recording in DICOM-RDSR is also obligatory [26], meaning that it can be used to estimate the Dskin,max simply and in real time at every medical facility where NIR is performed. In NIR, however, because the direction of X-ray irradiation and the extent of irradiation are constantly changing, the accurate estimation of Dskin,max is not necessarily simple, and the discrepancy between the values of Total Ka,r and Dskin,max mean that each individual institution should use its own conversion coefficient.
We previously analyzed Dskin,max,RPLGD using the RADIREC system and estimated Dskin,max,Ka intraoperatively in real time by multiplying the Total Ka,r by the mean Dskin,max,RPLGD/Total Ka,r ratio as CFKa,constant (Schema 1b). However, Total Ka,r is the sum of all the X-ray entrance angles, and as the X-ray entrance angles are completely different for each patient, the Dskin,max,Ka is often larger or smaller than the actual Dskin,max,RPLGD. Theoretically, if the X-ray entrance angle does not change at all during the procedure, the value of Dskin,max,RPLGD/Total Ka,r increases and approaches 1. Conversely, if the X-ray entrance angle varies widely, the ratio will be lower. However, to our best knowledge, no index that provides an appropriate indication of variation in the X-ray entrance angle has yet been reported, and ours is the first study to demonstrate that a quadratic equation for the Ka,r ratio can adequately explain the variation in the value of Dskin,max,RPLGD/Total Ka,r.
Figure 6 shows the residue plots for directly estimated Dskin,max,RPLGD and indirectly estimated Dskin,max,Ka. Applying the CFKa,function to the Ka,r ratio quadratic equations (see Equation (5) for the test data set and Equation (6) for the validation data set) and estimating the individual Dskin,max,Ka for each patient revealed a strong corrective effect in the high-dose region of the validation data set and a weak corrective effect in the low-dose regions of the test data set and the validation data set (Figure 6). This may be because radiation exposure is high in therapeutic NIR procedures, such as cerebral aneurysm coil embolization, in which the Ka,r ratio is high because fluoroscopy is conducted over long periods from the same X-ray entrance angle, and the Dskin,max,RPLGD/Total Ka,r also increases (Figure 4d), and application of a high CFKa,function value can be used to correct Dskin,max,Ka appropriately. Conversely, the procedure that most commonly involves a low radiation dose is diagnostic cerebral angiography, a standard procedure in which most of the radiation dose comes from exposure at the same X-ray entrance angle (mainly via posterior–anterior and/or left–right projection), resulting in a low Ka,r ratio and increasing the Dskin,max,RPLGD/Total Ka,r (Figure 2d and Figure 4d). As in the case of a high radiation dose, a high CFKa,function value can also be applied for appropriate correction of Dskin,max,Ka. Applying CFKa,function weighted by the Ka,r ratio therefore facilitates more accurate estimation of Dskin,max,Ka.
In this study, our objective was to construct a CFKa,function using the Fluoroscopy Ka,r and the Total Ka,r data recorded in the DICOM-RDSR, but as X-ray entrance angle data are also recorded for each fluoroscopy and exposure event, analysis of these data may also enable us to develop an index of the degree of variation in the X-ray entrance angle, potentially further increasing the accuracy of estimating Dskin,max,Ka. As DICOM-RDSR is currently obligatory for all angiography systems both in Japan and overseas, it is a tool that is readily available in most institutions. Further studies should be conducted to explore other potential uses of DICOM-RDSR to reduce patient radiation exposure.

5. Conclusions

In this study, it was suggested that multiplying a conversion factor using the quadratic function for the ratio of Fluoroscopy Ka,r/Total Ka,r for each patient by the Total Ka,r provides a more accurate estimate than multiplying with a constant conversion factor during cerebral angiography, including NIR procedures, in real time.

Author Contributions

Conceptualization, K.M. and T.M.; methodology, K.M. and T.M.; validation, K.M., T.M., and K.N. (Keisuke Nagamoto); formal analysis, K.M. and T.M.; investigation, K.M.; data curation, T.M., S.M., K.N. (Keisuke Nagamoto), K.N. (Koichi Nakagami), and L.S.; writing—original draft preparation, K.M.; writing—review and editing, T.M. and K.N. (Keisuke Nagamoto); visualization, K.M. and T.M.; supervision, L.S. and N.K.; project administration, T.M.; funding acquisition, T.M. and N.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by a Grant-in-Aid for Scientific Research (number 18H03376 to T.M.) and by a grant from the Japanese Ministry of Health, Labour and Welfare (number 180501-1 to N.K. and T.M.).

Acknowledgments

The authors would like to thank Miho Itonaga, Tomomi Konari, Fumiko Kawagoe, and Kimi Kihara for their technical support and assistance. We would also like to thank all medical staff who participated in this project.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wagner, L.K.; Eifel, P.J.; Geise, R.A. Potential Biological Effects Following High X-ray Dose Interventional Procedures. J. Vasc. Interv. Radiol. 1994, 5, 71–84. [Google Scholar] [CrossRef]
  2. Mooney, R.B.; McKinstry, C.S.; A Kamel, H. Absorbed dose and deterministic effects to patients from interventional neuroradiology. Br. J. Radiol. 2000, 73, 745–751. [Google Scholar] [CrossRef] [PubMed]
  3. Hayakawa, M.; Moritake, T.; Kataoka, F.; Takigawa, T.; Koguchi, Y.; Miyamoto, Y.; Akahane, K.; Matsumaru, Y. Direct measurement of patient’s entrance skin dose during neurointerventional procedure to avoid further radiation-induced skin injuries. Clin. Neurol. Neurosurg. 2010, 112, 530–536. [Google Scholar] [CrossRef] [PubMed]
  4. Magrassi, L.; Bongetta, D.; D’Ercole, L.; Lisciandro, F.; Arienta, C.; Thyrion, F.Z. Neuroembolization may expose patients to radiation doses previously linked to tumor induction. Acta Neurochir. 2012, 154, 33–41. [Google Scholar] [CrossRef] [PubMed]
  5. Corrigall, R.S.; Martin, C.J.; Scott, I. Observations of tissue reactions following neuroradiology interventional procedures. J. Radiol. Prot. 2020, 40, N9–N15. [Google Scholar] [CrossRef]
  6. ICRP. Avoidance of radiation injuries from medical interventional procedures. ICRP Publ. 2000, 85, 1–53. [Google Scholar]
  7. Miller, N.L.; Balter, S.; Noonan, P.T.; Georgia, J.D. Minimizing Radiation-induced Skin Injury in Interventional Radiology Procedures. Radiology 2002, 2002, 329–336. [Google Scholar] [CrossRef] [Green Version]
  8. Safari, M.J.; Wong, J.H.; Kadir, K.A.; Thorpe, N.K.; Cutajar, D.L.; Petasecca, M.; Lerch, M.L.; Rosenfeld, A.B.; Ng, K.H. Real-time eye lens dose monitoring during cerebral angiography procedures. Eur. Radiol. 2016, 26, 79–86. [Google Scholar] [CrossRef] [Green Version]
  9. Kato, M.; Chida, K.; Nakamura, M.; Toyoshima, H.; Terata, K.; Abe, Y. New real-time patient radiation dosimeter for use in radiofrequency catheter ablation. J. Radiat. Res. 2019, 60, 215–220. [Google Scholar] [CrossRef] [Green Version]
  10. Inaba, Y.; Chida, K.; Murabayashi, Y.; Endo, M.; Otomo, K.; Zuguchi, M. An initial investigation of a wireless patient radiation dosimeter for use in interventional radiology. Radiol. Phys. Technol. 2020, 13, 321–326. [Google Scholar] [CrossRef]
  11. Sato, F.; Honda, T.; Haga, Y.; Inaba, Y.; Kaga, Y.; Chida, K. Basic characteristic evaluation of the real-time model MOSFET dosimeter. Bull. Sch. Health Sci. Tohoku Univ. 2017, 26, 57–65. [Google Scholar]
  12. Rana, V.K.; Rudin, S.; Bednarek, D.R. A tracking system to calculate patient skin dose in real-time during neurointerventional procedures using a biplane X-ray imaging system. Med. Phys. 2016, 43, 5131. [Google Scholar] [CrossRef]
  13. Takata, T.; Kotoku, J.; Maejima, H.; Kumagai, S.; Arai, N.; Kobayashi, T.; Shiraishi, K.; Yamamoto, M.; Kondo, H.; Furui, S. Fast skin dose estimation system for interventional radiology. J. Radiat. Res. 2018, 59, 233–239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Bor, D.; Sancak, T.; Olgar, T.; Elcim, Y.; Adanali, A.; Sanlıdilek, U.; Akyar, S. Comparison of effective doses obtained from dose–area product and air kerma measurements in interventional radiology. Br. J. Radiol. 2004, 77, 315–322. [Google Scholar] [CrossRef] [PubMed]
  15. Farah, J.; Trianni, A.; Ciraj-Bjelac, O.; Clairand, I.; De Angelis, C.; Delle Canne, S.; Hadid, L.; Huet, C.; Jarvinen, H.; Negri, A. Characterization of XR-RV3 GafChromic® films in standard laboratory and in clinical conditions and means to evaluate uncertainties and reduce errors. Med. Phys. 2015, 42, 4211–4226. [Google Scholar] [CrossRef]
  16. Habib Geryes, B.; Hadid-Beurrier, L.; Waryn, M.J.; Jean-Pierre, A.; Farah, J. Benchmarking the DACS-integrated Radiation Dose Monitor(R) skin dose mapping software using XR-RV3 Gafchromic(R) films. Med. Phys. 2018, 45, 4683–4692. [Google Scholar] [CrossRef] [PubMed]
  17. Jones, A.K.; Ensor, J.E.; Pasciak, A.S. How accurately can the peak skin dose in fluoroscopy be determined using indirect dose metrics? Med. Phys. 2014, 41, 071913. [Google Scholar] [CrossRef] [Green Version]
  18. Khoury, H.; Garzon, W.; Andrade, G.; Lunelli, N.; Kramer, R.; de Barros, V.; Huda, A. Radiation exposure to patients and medical staff in hepatic chemoembolisation interventional procedures in Recife, Brazil. Radiat. Prot. Dosim. 2015, 165, 263–267. [Google Scholar] [CrossRef]
  19. Krajinović, M.; Dobrić, M.; Ciraj-Bjelac, O. Skin dose mapping in interventional cardiology: A practical solution. Radiat. Prot. Dosim. 2020, 188, 508–515. [Google Scholar] [CrossRef]
  20. Bor, D.; Olgar, T.; Toklu, T.; Caglan, A.; Onal, E.; Padovani, R. Patient doses and dosimetric evaluations in interventional cardiology. Phys. Med. 2009, 25, 31–42. [Google Scholar] [CrossRef]
  21. Nishizawa, K.; Moritake, T.; Matsumaru, Y.; Tsuboi, K.; Iwai, K. Dose measurement for patients and physicians using a glass dosemeter during endovascular treatment for brain disease. Radiat. Prot. Dosim. 2003, 107, 247–252. [Google Scholar] [CrossRef] [PubMed]
  22. Moritake, T.; Matsumaru, Y.; Takigawa, T.; Nishizawa, K.; Matsumura, A.; Tsuboi, K. Dose measurement on both patients and operators during neurointerventional procedures using photoluminescence glass dosimeters. Am. J. Neuroradiol. 2008, 29, 1910–1917. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Moritake, T.; Hayakawa, M.; Matsumaru, Y.; Takigawa, T.; Koguchi, Y.; Miyamoto, Y.; Mizuno, Y.; Chida, K.; Akahane, K.; Tsuboi, K.; et al. Precise mapping system of entrance skin dose during endovascular embolization for cerebral aneurysm. Radiat. Meas. 2011, 46, 2103–2106. [Google Scholar] [CrossRef]
  24. Kawauchi, S.; Chida, K.; Moritake, T.; Matsumaru, Y.; Hamada, Y.; Sakuma, H.; Yoda, S.; Sun, L.; Sato, M.; Tsuruta, W. Estimation of Patient Lens Dose Associated with C-Arm Cone-Beam Computed Tomography Usage during Interventional Neuroradiology. Radiat. Prot. Dosim. 2018, 184, 138–147. [Google Scholar] [CrossRef] [PubMed]
  25. Kawauchi, S.; Chida, K.; Moritake, T.; Hamada, Y.; Matsumaru, Y.; Tsuruta, W.; Sato, M.; Hosoo, H.; Sun, L. Treatment of Internal Carotid Aneurysms Using Pipeline Embolization Devices: Measuring the Radiation Dose of the Patient and Determining the Factors Affecting It. Radiat. Prot. Dosim. 2020. [Google Scholar] [CrossRef] [PubMed]
  26. IEC 60601-2-43, e. Medical Electrical Equipment Part 2-43, 2nd ed.; Particular Requirements for the Basic Safety and Essential Performance of X-Ray Equipment for Interventional Procedures; International Electrotechnical Commission: Geneva, Switzerland, 2010. [Google Scholar]
  27. Hubbell, J.H.; Seltzer, S.M. Tables of X-Ray Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients from 1 keV to 20 MeV for Elements Z = 1 to 92 and 48 Additional Substances of Dosimetric Interest. Physical Reference Data (NISTIR 5632); National Institute of Standards and Technology: Gaithersburg, MD, USA, 1995.
  28. ICRP. Safety in Medicine; International Commission for Radiological Protection (ICRP) Publication 73; Pergamon Press: Oxford, UK; New York, NY, USA, 1996. [Google Scholar]
  29. ICRP. Diagnostic Reference Levels in Medical Imaging. Ann. Icrp 2017, 1–144. [Google Scholar]
  30. ICRP. ICRP Publication 105. Radiation protection in medicine. Ann. Icrp 2007, 37, 1–63. [Google Scholar] [CrossRef]
  31. Directive, C. 97/43/Euratom of 30 June 1997 on health protection of individuals against the dangers of ionizing radiation in relation to medical exposure, and repealing Directive 84/466/Euratom. Off. J. Eur. Communities L 1997, 180, 7. [Google Scholar]
  32. ACR. ACR–AAPM–SPR Practice Parameter for Diagnostic Reference Levels and Achievable Doses In medical X-Ray Imaging; ACR: Hong Kong, China, 2018. [Google Scholar]
  33. J-RIME. Diagnostic Reference Levels Based on Latest Surveys in Japan–Japan DRLs 2015. Available online: http://www.radher.jp/J-RIME/report/DRLhoukokusyoEng.pdf (accessed on 22 December 2020).
  34. J-RIME. Diagnostic Reference Levels Based on Latest Surveys in Japan–Japan DRLs 2020. Available online: http://www.radher.jp/J-RIME/report/JapanDRL2020_jp.pdf (accessed on 22 December 2020).
  35. Vano, E.; Fernandez Soto, J. Patient dose management in digital radiography. Biomed. Imaging Interv. J. 2007, 3, e26. [Google Scholar] [CrossRef]
  36. Vano, E.; Ten, J.I.; Fernandez, J.M.; Prieto, C.; Ordiales, J.M.; Martinez, D. Quality control and patient dosimetry in digital radiology. On line system: New features and transportability. Radiat. Prot. Dosim. 2008, 129, 144–146. [Google Scholar] [CrossRef]
  37. Ten, J.I.; Fernandez, J.M.; Vano, E. Automatic management system for dose parameters in interventional radiology and cardiology. Radiat. Prot. Dosim. 2011, 147, 325–328. [Google Scholar] [CrossRef] [PubMed]
  38. Khodadadegan, Y.; Zhang, M.; Pavlicek, W.; Paden, R.G.; Chong, B.; Schueler, B.A.; Fetterly, K.A.; Langer, S.G.; Wu, T. Automatic monitoring of localized skin dose with fluoroscopic and interventional procedures. J. Digit. Imaging 2011, 24, 626–639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  39. Matthews, L.; Dixon, M.; Rowles, N.; Stevens, G. A practical method for skin dose estimation in interventional cardiology based on fluorographic DICOM information. Radiat. Prot. Dosim. 2015, 168, 381–387. [Google Scholar] [CrossRef] [PubMed]
  40. Omar, A.; Bujila, R.; Fransson, A.; Andreo, P.; Poludniowski, G. A framework for organ dose estimation in X-ray angiography and interventional radiology based on dose-related data in DICOM structured reports. Phys. Med. Biol. 2016, 61, 3063–3083. [Google Scholar] [CrossRef] [PubMed]
  41. Vano, E.; Ten, J.I.; Fernandez-Soto, J.M.; Sanchez-Casanueva, R.M. Experience with patient dosimetry and quality control online for diagnostic and interventional radiology using DICOM services. Am. J. Roentgenol. 2013, 200, 783–790. [Google Scholar] [CrossRef]
Diagnostics 11 00014 sch001 550
Scheme 1. Schema of the methods used for estimating the maximum skin dose (Dskin,max) in neurointerventional radiology (NIR) patients. (a) Direct estimation method using radio-photoluminescence glass dosimeters (RPLGDs) in the RADIREC® system (Dskin,max,RPLGD). Methods for indirectly estimating the maximum skin dose from the Total Ka,r displayed by the angiography system (Dskin,max,Ka): (b) Estimation Model 1, applying a constant as the conversion factor (CFKa,constant) and (c) Estimation Model 2, applying an individual conversion factor obtained by means of a function (CFKa,function).
Scheme 1. Schema of the methods used for estimating the maximum skin dose (Dskin,max) in neurointerventional radiology (NIR) patients. (a) Direct estimation method using radio-photoluminescence glass dosimeters (RPLGDs) in the RADIREC® system (Dskin,max,RPLGD). Methods for indirectly estimating the maximum skin dose from the Total Ka,r displayed by the angiography system (Dskin,max,Ka): (b) Estimation Model 1, applying a constant as the conversion factor (CFKa,constant) and (c) Estimation Model 2, applying an individual conversion factor obtained by means of a function (CFKa,function).
Diagnostics 11 00014 sch001
Diagnostics 11 00014 g001 550
Figure 1. Relationship between X-ray effective energy and the radio-photoluminescence glass dosimeter (RPLGD) energy compensation factor (CFRPLGD). The symbols ● and × show the data obtained under simultaneous X-ray exposure to the ionization chamber and RPLGDs under settings of fluoroscopy and exposure, respectively. CFRPLGD (y) was fitted to the following quadratic equation for X-ray effective energy (x): y = 0.0002x2 − 0.0147x + 0.5270 (R = 0.999) (solid line).
Figure 1. Relationship between X-ray effective energy and the radio-photoluminescence glass dosimeter (RPLGD) energy compensation factor (CFRPLGD). The symbols ● and × show the data obtained under simultaneous X-ray exposure to the ionization chamber and RPLGDs under settings of fluoroscopy and exposure, respectively. CFRPLGD (y) was fitted to the following quadratic equation for X-ray effective energy (x): y = 0.0002x2 − 0.0147x + 0.5270 (R = 0.999) (solid line).
Diagnostics 11 00014 g001
Diagnostics 11 00014 g002 550
Figure 2. Analysis of factors affecting Dskin,max,RPLGD /Total Ka,r using the test data set (n = 50). The broken lines indicate linear regression, and the solid lines indicate quadratic regression. We analyzed the correlations between Dskin,max,RPLGD/Total Ka,r and the following DICOM-RDSR parameters: (a) Total Ka,r; (b) Fluoroscopy Ka,r; (c) Exposure Ka,r; (d) Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio); (e) Fluoroscopy Time; (f) Number of DSA; (g) Number of frames.
Figure 2. Analysis of factors affecting Dskin,max,RPLGD /Total Ka,r using the test data set (n = 50). The broken lines indicate linear regression, and the solid lines indicate quadratic regression. We analyzed the correlations between Dskin,max,RPLGD/Total Ka,r and the following DICOM-RDSR parameters: (a) Total Ka,r; (b) Fluoroscopy Ka,r; (c) Exposure Ka,r; (d) Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio); (e) Fluoroscopy Time; (f) Number of DSA; (g) Number of frames.
Diagnostics 11 00014 g002
Diagnostics 11 00014 g003 550
Figure 3. Investigation of the accuracy of the two indirect methods for estimating Dskin,max,Ka using the test data set (n = 50). (a) Correlation between the value of Dskin,max,Ka indirectly estimated using an arbitrary constant CFKa,constant (Estimation Model 1) and Dskin,max,RPLGD directly estimated using radio-photoluminescence glass dosimeters (RPLGDs); (b) correlation between the value of Dskin,max,Ka indirectly estimated using an arbitrary quadratic function CFKa,function (Estimation Model 2) and Dskin,max,RPLGD directly estimated using RPLGDs. The broken lines indicate 95% predictive intervals.
Figure 3. Investigation of the accuracy of the two indirect methods for estimating Dskin,max,Ka using the test data set (n = 50). (a) Correlation between the value of Dskin,max,Ka indirectly estimated using an arbitrary constant CFKa,constant (Estimation Model 1) and Dskin,max,RPLGD directly estimated using radio-photoluminescence glass dosimeters (RPLGDs); (b) correlation between the value of Dskin,max,Ka indirectly estimated using an arbitrary quadratic function CFKa,function (Estimation Model 2) and Dskin,max,RPLGD directly estimated using RPLGDs. The broken lines indicate 95% predictive intervals.
Diagnostics 11 00014 g003
Diagnostics 11 00014 g004 550
Figure 4. Analysis of the factors affecting Dskin,max,RPLGD /Total Ka,r using the validation data set (n = 50). The broken lines indicate linear regression, and the solid lines indicate quadratic regression. We analyzed the correlations between Dskin,max,RPLGD/Total Ka,r and the following Digital Imaging and Communication in Medicine—Radiation Dose Structured Report parameters: (a) Total Ka,r; (b) Fluoroscopy Ka,r; (c) Exposure Ka,r; (d) Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio); (e) Fluoroscopy Time; (f) Number of DSA; and (g) Number of frames.
Figure 4. Analysis of the factors affecting Dskin,max,RPLGD /Total Ka,r using the validation data set (n = 50). The broken lines indicate linear regression, and the solid lines indicate quadratic regression. We analyzed the correlations between Dskin,max,RPLGD/Total Ka,r and the following Digital Imaging and Communication in Medicine—Radiation Dose Structured Report parameters: (a) Total Ka,r; (b) Fluoroscopy Ka,r; (c) Exposure Ka,r; (d) Fluoroscopy Ka,r/Total Ka,r (Ka,r ratio); (e) Fluoroscopy Time; (f) Number of DSA; and (g) Number of frames.
Diagnostics 11 00014 g004
Diagnostics 11 00014 g005 550
Figure 5. Investigation of the accuracy of the two indirect methods of estimating Dskin,max,Ka using the validation data set (n = 50). (a) Correlation between the value of Dskin,max,Ka estimated indirectly using an arbitrary constant CFKa,constant (Estimation Model 1) and Dskin,max,RPLGD directly estimated using RPLGDs; (b) correlation between the value of Dskin,max,Ka estimated indirectly using an arbitrary quadratic function CFKa,function (Estimation Model 2) and Dskin,max,RPLGD directly estimated using radio-photoluminescence glass dosimeters (RPLGDs). The broken lines indicate 95% predictive intervals.
Figure 5. Investigation of the accuracy of the two indirect methods of estimating Dskin,max,Ka using the validation data set (n = 50). (a) Correlation between the value of Dskin,max,Ka estimated indirectly using an arbitrary constant CFKa,constant (Estimation Model 1) and Dskin,max,RPLGD directly estimated using RPLGDs; (b) correlation between the value of Dskin,max,Ka estimated indirectly using an arbitrary quadratic function CFKa,function (Estimation Model 2) and Dskin,max,RPLGD directly estimated using radio-photoluminescence glass dosimeters (RPLGDs). The broken lines indicate 95% predictive intervals.
Diagnostics 11 00014 g005
Diagnostics 11 00014 g006 550
Figure 6. Residue plots of directly estimated Dskin,max RPLGD and indirectly estimated Dskin,max,Ka. The residues of Dskin,max RPLGD − Dskin,max,Ka are plotted for (a) the test data set (n = 50) and (b) the validation data set (n = 50). The circles ● indicate the differences between the Dskin,max,Ka estimated using the CFKa,constant (Estimation Model 1) and Dskin,max RPLGD, and the crosses × indicate the differences between Dskin,max,Ka estimated using the CFKa,function (Estimation Model 2) and Dskin,max RPLGD. In the low-dose region of the test data set and the low-dose and high-dose regions of the validation data set, the residues with negative values when estimated using Estimation Model 1 were close to zero when Estimation Model 2 was used, highlighting the corrective effect of CFKa,function.
Figure 6. Residue plots of directly estimated Dskin,max RPLGD and indirectly estimated Dskin,max,Ka. The residues of Dskin,max RPLGD − Dskin,max,Ka are plotted for (a) the test data set (n = 50) and (b) the validation data set (n = 50). The circles ● indicate the differences between the Dskin,max,Ka estimated using the CFKa,constant (Estimation Model 1) and Dskin,max RPLGD, and the crosses × indicate the differences between Dskin,max,Ka estimated using the CFKa,function (Estimation Model 2) and Dskin,max RPLGD. In the low-dose region of the test data set and the low-dose and high-dose regions of the validation data set, the residues with negative values when estimated using Estimation Model 1 were close to zero when Estimation Model 2 was used, highlighting the corrective effect of CFKa,function.
Diagnostics 11 00014 g006
Table
Table 1. Example of a DICOM—Radiation Dose Structured Report (DICOM-RDSR) at our hospital.
Table 1. Example of a DICOM—Radiation Dose Structured Report (DICOM-RDSR) at our hospital.
Acquisition No.No. of FramesFluoroscopy
/Exposure		LAO
/RAO
(Degree)		CAUD
/CRAN
(Degree)		Tube
Voltage
(kV)		Tube
Current
(mA)		Pulse Width
(ms)		SID
(mm)		Ka,r
(mGy)		Collimated
Field
Size
(m2)		Pulse
Rate
(Pulse/s)		Fluoroscopy
Time
(s)
1819FluoroscopyLAO 0CRAN 0766.966.79767.710.0231554.6
228FluoroscopyRAO 30CRAN 0827.966.710410.340.020151.9
311ExposureRAO 30CRAN 071654.041.4100537.390.021NA−
4195FluoroscopyRAO 30CRAN 0827.966.710052.630.0211513.0
51938FluoroscopyRAO 30CRAN 0827.966.7100526.040.02115129.2
643FluoroscopyLAO 0CRAN 20848.266.79500.680.018152.9
7104FluoroscopyLAO 0CRAN 20838.166.79191.540.019156.9
814FluoroscopyLAO 0CRAN 25838.166.79040.190.020151.0
928ExposureLAO 0CRAN 2570642.039.090486.060.020NA−
10329FluoroscopyLAO 0CRAN 0787.266.79573.560.0181521.9
∙∙∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙∙∙∙
6130FluoroscopyLAO 0CRAN 0766.766.710163.020.021152.0
62767FluoroscopyLAO 0CRAN 0817.866.710169.890.0211551.1
DICOM: Digital Imaging and Communication in Medicine; LAO: left anterior oblique; RAO: right anterior oblique; CAUD: caudal; CRAN: cranial; SID: source image receptor distance; Ka,r: air kerma at the patient entrance reference point.
Table
Table 2. Data set characteristics.
Table 2. Data set characteristics.
Test Data SetValidation Data Setp-Value *
Period of investigationOctober 2015–July 2016August 2016–September 2017
Number of cases (NIR)50 (7)50 (7)
Men20 (40%)24 (48%)
Women30 (60%)26 (52%)
Age, y [range] 57.5 ± 13.9 [30–78]62.8 ± 14.4 [33–88]N.S.
BMI, kg·m−2 [range]22.5 ± 3.1 [16.8–32.4]−23.5 ± 3.8 [16.9–33.4]N.S.
Dskin,max,RPLGD, mGy552.4 ± 250.3457.9 ± 353.6N.S.
Total Ka,r, mGy951.2 ± 398.2807.8 ± 548.5N.S.
Fluoroscopy Ka,r, mGy117.3 ± 151.8124.5 ± 185.5N.S.
Exposure Ka,r, mGy833.9 ± 322.7683.3 ± 397.5p = 0.04
Fluoroscopy Time, min11.9 ± 10.112.7 ± 14.4N.S.
Number of DSA12.7 ± 5.411.3 ± 8.8N.S.
Number of Frames 322.8 ± 100.5297.8 ± 155.9N.S.
All data are expressed as the mean ± standard deviation; * Welch’s t-test; N.S.: not significant; NIR: neurointerventional radiology; BMI: body mass index; Dskin,max,RPLGD: the maximum absorbed dose to the most heavily irradiated localized region that was obtained using 64 radio-photoluminescence glass dosimeters placed on the surface of the head and neck of the patient (RADIREC® system); Ka,r: air kerma of the primary X-ray beam measured under specific conditions and expressed as the equivalent value at the patient entrance reference point; Total Ka,r = Fluoroscopy Ka,r + Exposure Ka,r; DSA: digital subtraction angiography.
Table
Table 3. Radio-photoluminescence glass dosimeter (RPLGD) energy compensation factors weighted by the ratio of the dose at the patient entrance reference point (Ka,r ratio) (test data set: n = 50).
Table 3. Radio-photoluminescence glass dosimeter (RPLGD) energy compensation factors weighted by the ratio of the dose at the patient entrance reference point (Ka,r ratio) (test data set: n = 50).
Case No.FluoroscopyExposureKa,r RatioCFRPLGD,weighted
Tube Voltage *
(kV)		Effective Energy **
(keV)		CFRPLGD ***
(a)		Tube Voltage *
(kV)		Effective Energy **
(keV)		CFRPLGD ***
(b)		Fluoroscopy Ka,r/Total Ka,r
(c)		Exposure Ka,r/Total Ka,r
(d)
179.351.80.30269.429.10.2690.0740.9260.271
274.950.50.29568.628.90.2690.0740.9260.271
383.853.10.31171.029.40.2680.2780.7220.280
∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙
4873.250.00.29268.028.80.2700.0870.9130.272
4974.850.50.29568.328.80.2700.1390.8610.273
5074.350.30.29468.428.80.2690.0460.9540.271
Mean76.851.10.29870.029.20.2680.1120.8880.272
S.D.3.41.00.0062.00.40.0010.0910.0910.004
Range69.7—87.349.0—54.20.287—0.31867.5—76.228.7—30.50.265—0.2700.034—0.3780.622—0.9660.267—0.284
CFRPLGD: RPLGD energy compensation factor; RPLGD: radio-photoluminescence glass dosimeter; CFRPLGD,weighted: Ka,r ratio weighted RPLGD energy compensation factor obtained by the equation as follows: CFRPLGD,weighted = (a) × (c) + (b) × (d); * Mean tube voltage for each patient derived from DICOM-RDSR; ** Effective energy value for the mean tube voltage for each patient. Calculated by interpolation from the NIST Standard Reference Database 126 [27] data; *** Calculated from the CFRPLGD X-ray effective energy function (Equation (1)) shown in Figure 1.
Table
Table 4. RPLGD energy compensation factors weighted by the Ka,r ratio (validation data set: n = 50).
Table 4. RPLGD energy compensation factors weighted by the Ka,r ratio (validation data set: n = 50).
Case No.FluoroscopyExposureKa,r RatioCFRPLGD,weighted
Tube Voltage *
(kV)		Effective Energy **
(keV)		CFRPLGD ***
(a)		Tube Voltage *
(kV)		Effective Energy **
(keV)		CFRPLGD ***
(b)		Fluoroscopy Ka,r/Total Ka,r
(c)		Exposure Ka,r/Total Ka,r
(d)
5176.7 51.0 0.298 69.3 29.0 0.269 0.055 0.945 0.270
5280.0 52.0 0.303 70.0 29.2 0.268 0.075 0.925 0.271
5377.6 51.3 0.299 68.8 28.9 0.269 0.136 0.864 0.273
∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙
∙∙∙∙∙∙∙∙∙∙
9873.1 50.0 0.292 67.9 28.7 0.270 0.120 0.880 0.272
9974.8 50.5 0.295 70.1 29.2 0.268 0.097 0.903 0.271
10075.8 50.7 0.296 69.2 29.0 0.269 0.292 0.708 0.277
Mean77.3 51.2 0.299 69.3 29.0 0.269 0.124 0.876 0.273
S.D.2.9 0.8 0.005 1.5 0.3 0.001 0.090 0.090 0.004
Range73.1—85.950.0—53.70.292—0.31567.7—78.428.7—31.00.264—0.2700.039—0.4160.584—0.9610.270—0.287
CFRPLGD: RPLGD energy compensation factor; CFRPLGD,weighted: Ka,r ratio weighted RPLGD energy compensation factor obtained by the equation as follows: CFRPLGD,weighted = (a) × (c) + (b) × (d); * Mean tube voltage for each patient derived from DICOM-RDSR; ** Effective energy value for the mean tube voltage for each patient. Calculated by interpolation from the NIST Standard Reference Database 126 [27] data; *** Calculated from the CFRPLGD X-ray effective energy function (Equation (1)) shown in Figure 1.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Morota, K.; Moritake, T.; Nagamoto, K.; Matsuzaki, S.; Nakagami, K.; Sun, L.; Kunugita, N. Optimization of the Maximum Skin Dose Measurement Technique Using Digital Imaging and Communication in Medicine—Radiation Dose Structured Report Data for Patients Undergoing Cerebral Angiography. Diagnostics 2021, 11, 14. https://doi.org/10.3390/diagnostics11010014

AMA Style

Morota K, Moritake T, Nagamoto K, Matsuzaki S, Nakagami K, Sun L, Kunugita N. Optimization of the Maximum Skin Dose Measurement Technique Using Digital Imaging and Communication in Medicine—Radiation Dose Structured Report Data for Patients Undergoing Cerebral Angiography. Diagnostics. 2021; 11(1):14. https://doi.org/10.3390/diagnostics11010014

Chicago/Turabian Style

Morota, Koichi, Takashi Moritake, Keisuke Nagamoto, Satoru Matsuzaki, Koichi Nakagami, Lue Sun, and Naoki Kunugita. 2021. "Optimization of the Maximum Skin Dose Measurement Technique Using Digital Imaging and Communication in Medicine—Radiation Dose Structured Report Data for Patients Undergoing Cerebral Angiography" Diagnostics 11, no. 1: 14. https://doi.org/10.3390/diagnostics11010014

APA Style

Morota, K., Moritake, T., Nagamoto, K., Matsuzaki, S., Nakagami, K., Sun, L., & Kunugita, N. (2021). Optimization of the Maximum Skin Dose Measurement Technique Using Digital Imaging and Communication in Medicine—Radiation Dose Structured Report Data for Patients Undergoing Cerebral Angiography. Diagnostics, 11(1), 14. https://doi.org/10.3390/diagnostics11010014

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop