A Novel Approach on Microwave Hyperthermia
Abstract
1. Introduction
2. Materials and Methods
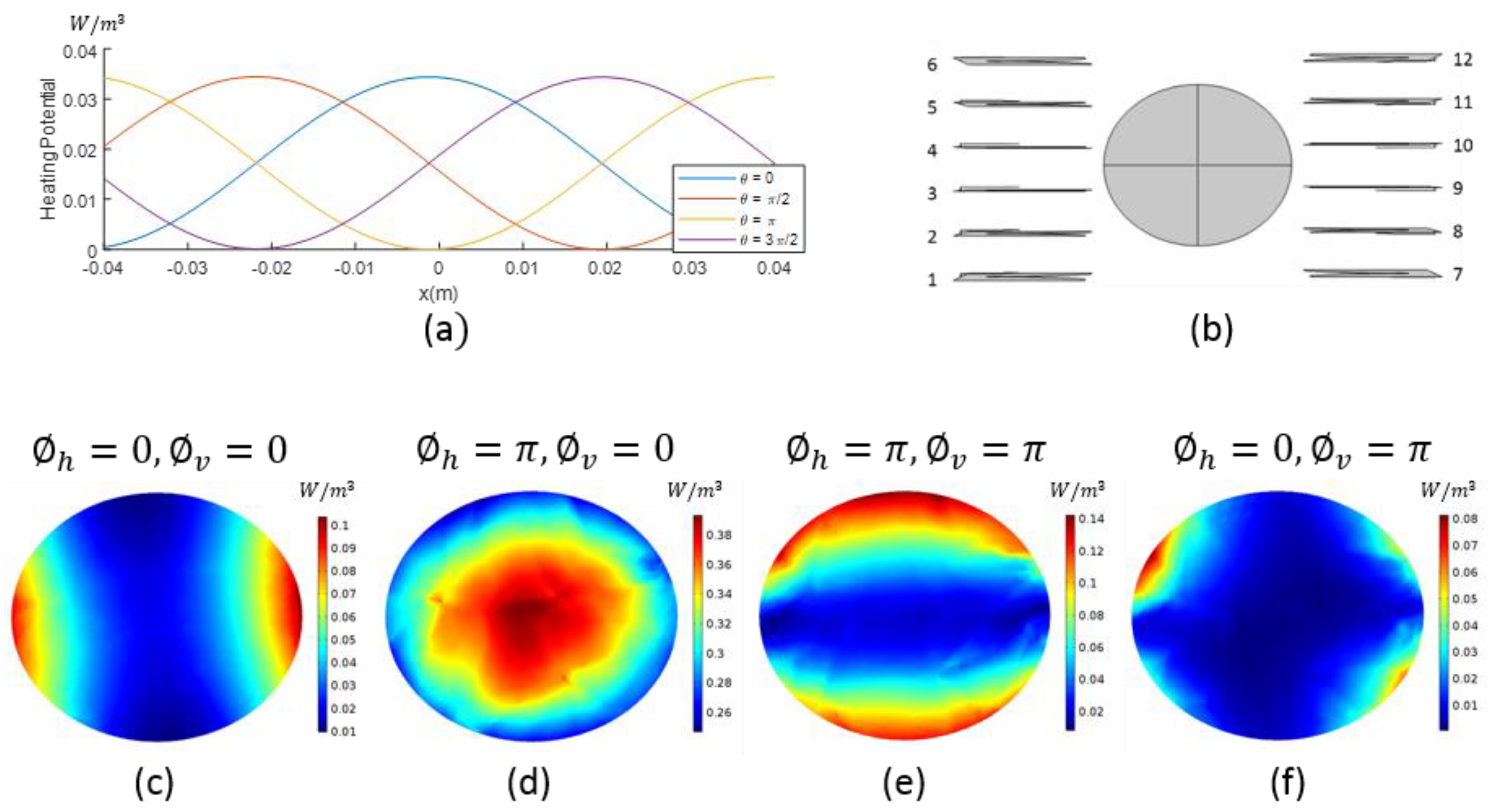
2.1. Heating Potential
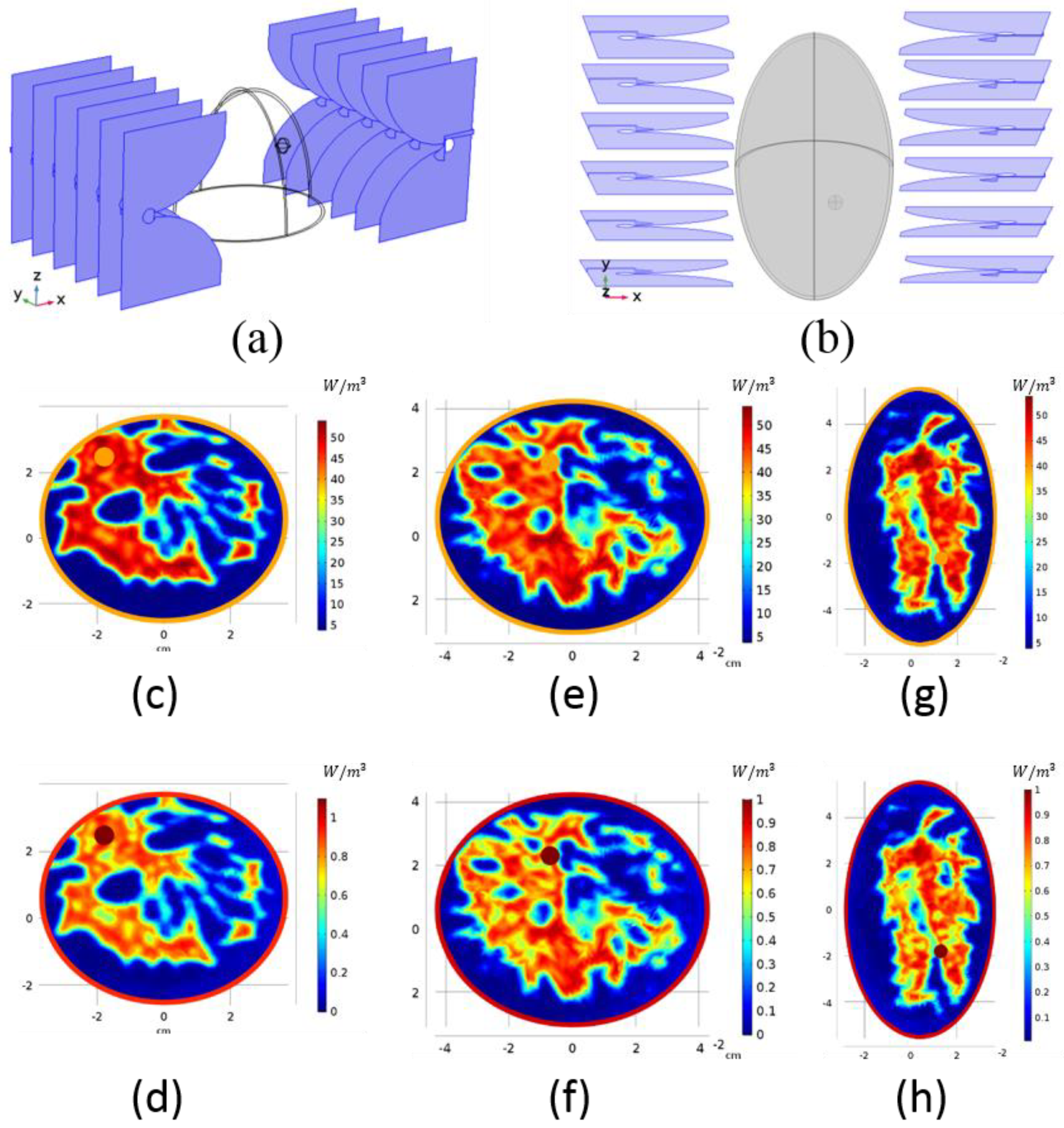
2.2. Antenna Configuration
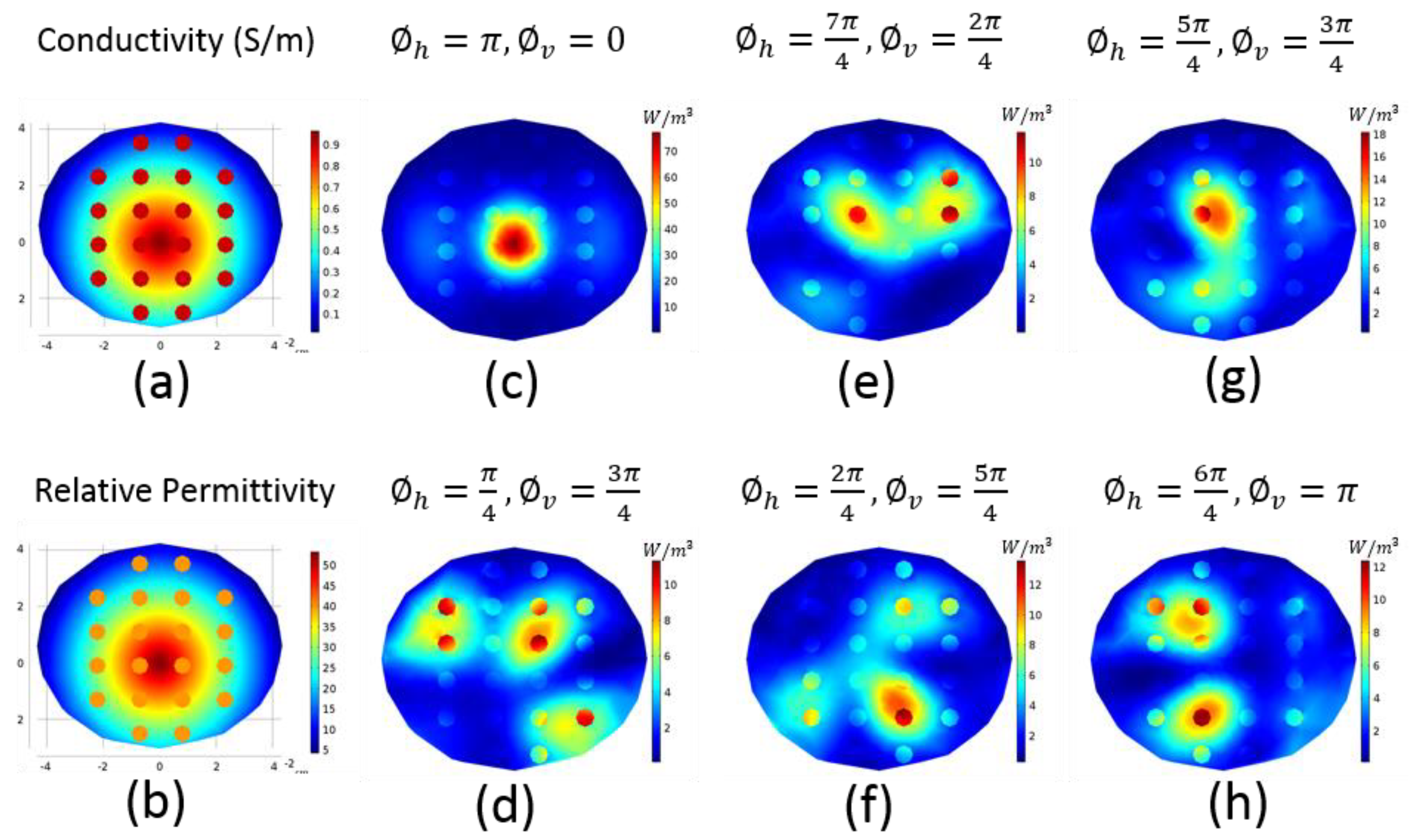
2.3. Focusing
2.4. Realistic Numeric Phantoms
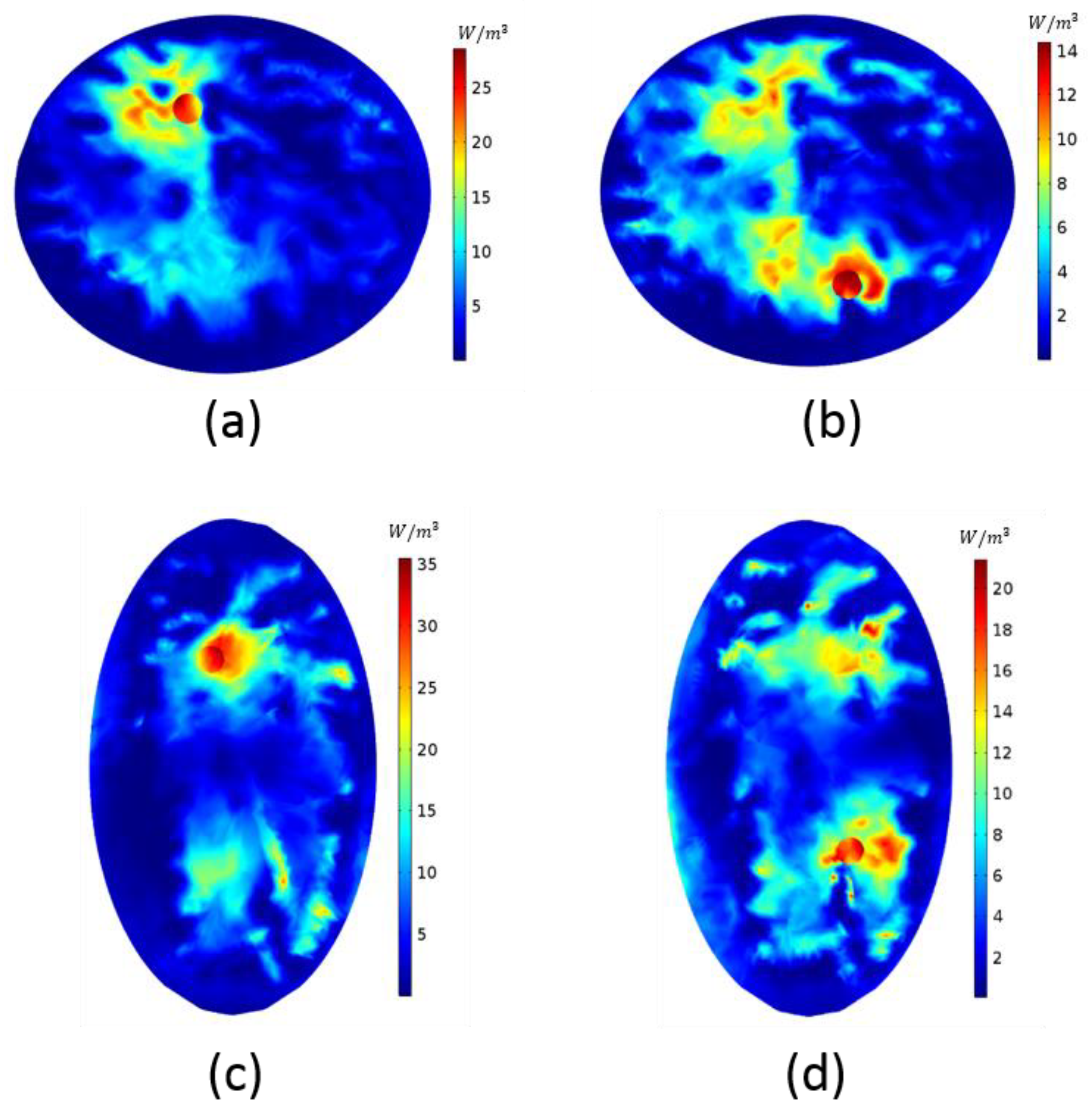
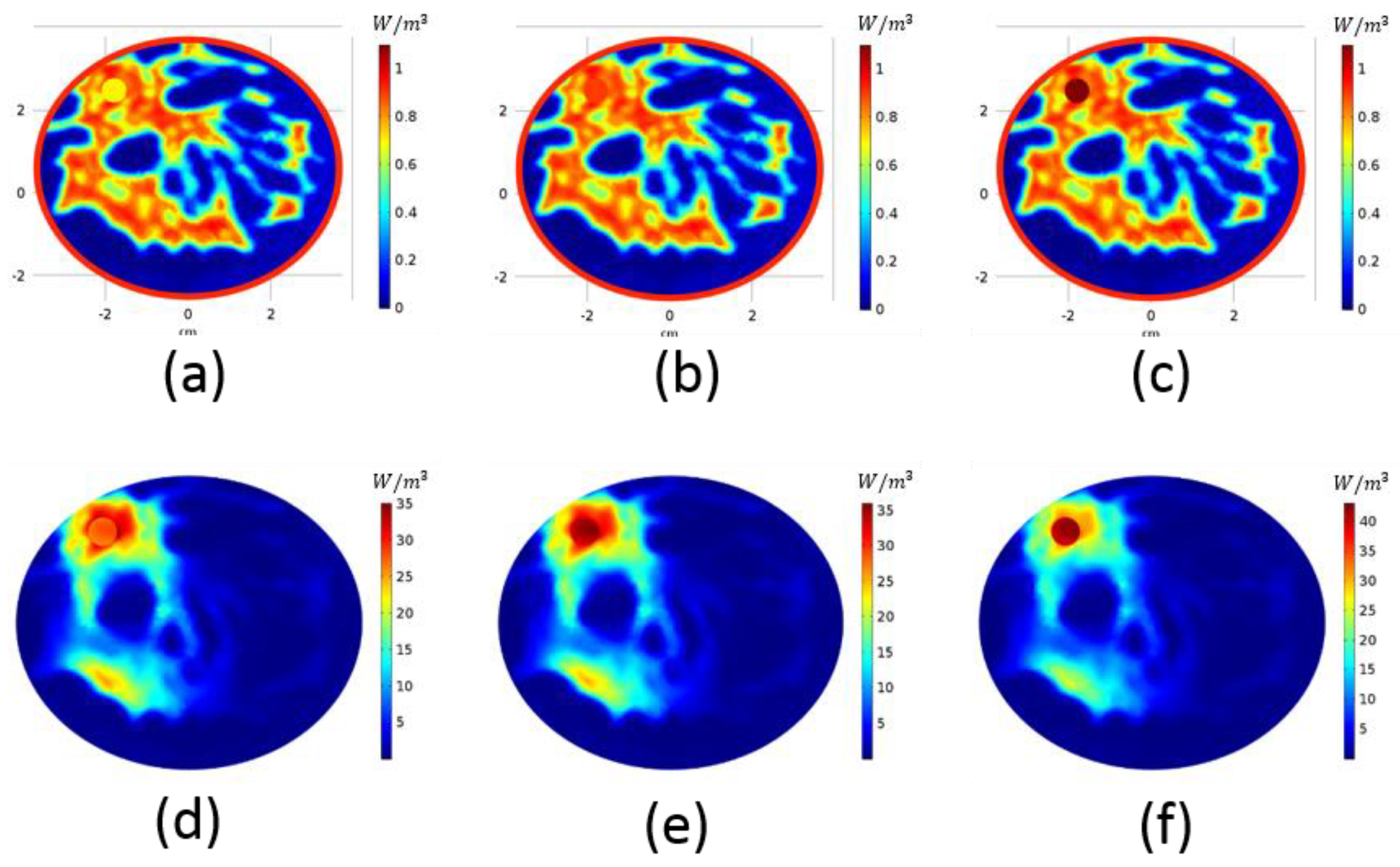
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- National Cancer Institute. Chemotherapy to Treat Cancer. 2021. Available online: https://www.cancer.gov/about-cancer/treatment/types/chemotherapy (accessed on 10 November 2020).
- Issels, R.D. Hyperthermia adds to chemotherapy. Eur. J. Cancer 2008, 44, 2546–2554. [Google Scholar] [CrossRef]
- Iero, D.; Isernia, T.; Morabito, A.F.; Catapano, I.; Crocco, L. Optimal Constrained Field Focusing for Hyperthermia Cancer Therapy: A Feasibility Assessment on Realistic Phantoms. Prog. Electromagn. Res. 2010, 102, 125–141. [Google Scholar] [CrossRef][Green Version]
- Iero, D.A.M.; Crocco, L.; Isernia, T. Thermal and Microwave Constrained Focusing for Patient-Specific Breast Cancer Hyperthermia: A Robustness Assessment. IEEE Trans. Antennas Propag. 2013, 62, 814–821. [Google Scholar] [CrossRef]
- Iero, D.A.M.; Crocco, L.; Isernia, T. Advances in 3-D electromagnetic focusing: Optimized time reversal and optimal constrained power focusing. Radio Sci. 2017, 52, 166–175. [Google Scholar] [CrossRef]
- Bellizzi, G.G.; Crocco, L.; Battaglia, G.M.; Isernia, T. Multi-Frequency Constrained SAR Focusing for Patient Specific Hyperthermia Treatment. IEEE J. Electromagn. RF Microw. Med. Biol. 2017, 1, 74–80. [Google Scholar] [CrossRef]
- ElKayal, H.A.; Ismail, N.E.; Lotfy, M. Microwaves for breast cancer treatments. Alex. Eng. J. 2015, 54, 1105–1113. [Google Scholar] [CrossRef][Green Version]
- Curto, S.; Garcia-Miquel, A.; Suh, M.; Vidal, N.; Lopez-Villegas, J.M.; Prakash, P. Design and characterisation of a phased antenna array for intact breast hyperthermia. Int. J. Hyperth. 2017, 34, 250–260. [Google Scholar] [CrossRef]
- Merunka, I.; Fiser, O.; Vojackova, L.; Vrba, J.; Vrba, D. Utilization Potential of Balanced Antipodal Vivaldi Antenna for Microwave Hyperthermia Treatment of Breast Cancer. In Proceedings of the 8th European Conference On Antennas And Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014. [Google Scholar]
- Fenn, A.J. An adaptive microwave phased array for targeted heating of deep tumours in intact breast: Animal study results. Int. J. Hyperth. 1999, 15, 45–61. [Google Scholar] [CrossRef] [PubMed]
- Dooley, W.C.; Vargas, H.I.; Fenn, A.J.; Tomaselli, M.B.; Harness, J.K. Focused Microwave Thermotherapy for Preoperative Treatment of Invasive Breast Cancer: A Review of Clinical Studies. Ann. Surg. Oncol. 2009, 17, 1076–1093. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Abbosh, A.; Crozier, S. Microwave Hyperthermia for Breast Cancer Treatment Using Electromagnetic and Thermal Focusing Tested on Realistic Breast Models and Antenna Arrays. IEEE Trans. Antennas Propag. 2015, 63, 4426–4434. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Abbosh, A.; Crozier, S. Three-Dimensional Microwave Hyperthermia for Breast Cancer Treatment in a Realistic Environment Using Particle Swarm Optimization. IEEE Trans. Biomed. Eng. 2017, 64, 1335–1344. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Abbosh, A.M.; Crozier, S. 3-D Focused Microwave Hyperthermia for Breast Cancer Treatment With Experimental Validation. IEEE Trans. Antennas Propag. 2017, 65, 3489–3500. [Google Scholar] [CrossRef]
- Burfeindt, M.J.; Zastrow, E.; Hagness, S.C.; Van Veen, B.D.; Medow, J.E. Microwave beamforming for non-invasive patient-specific hyperthermia treatment of pediatric brain cancer. Phys. Med. Biol. 2011, 56, 2743. [Google Scholar] [CrossRef] [PubMed]
- Ghahremani, F.H.; Sazgarnia, A.; Bahreyni-Toosi, M.H.; Rajabi, O.; Aledavood, A. Efficacy of microwave hyperthermia and chemotherapy in the presence of gold nanoparticles: An in vitro study on osteosarcoma. Int. J. Hyperth. 2011, 27, 625–636. [Google Scholar] [CrossRef] [PubMed]
- Saito, K.; Yoshimura, H.; Ito, K.; Aoyagi, Y.; Horita, H. Clinical trials of interstitial microwave hyperthermia by use of coaxial-slot antenna with two slots. IEEE Trans. Microw. Theory Tech. 2004, 52, 1987–1991. [Google Scholar] [CrossRef]
- Van der Heijden, A.; Kiemeney, L.; Gofrit, O.; Nativ, O.; Sidi, A.; Leib, Z.; Colombo, R.; Naspro, R.; Pavone, M.; Baniel, J.; et al. Preliminary European Results of Local Microwave Hyperthermia and Chemotherapy Treatment in Intermediate or High Risk Superficial Transitional Cell Carcinoma of the Bladder. Eur. Urol. 2004, 46, 65–72. [Google Scholar] [CrossRef]
- Martin, G.T.; Haddad, M.G.; Cravalho, E.G.; Bowman, H.F. Thermal model for the local microwave hyperthermia treatment of benign prostatic hyperplasia. IEEE Trans. Biomed. Eng. 1992, 39, 836–844. [Google Scholar] [CrossRef]
- Giombini, A.; Giovannini, V.; Cesare, A.D.; Pacetti, P.; Ichinoseki-Sekine, N.; Shiraishi, M.; Naito, H.; Maffulli, N. Hyperthermia induced by microwave diathermy in the management of muscle and tendon injuries. Br. Med. Bull. 2007, 83, 379–396. [Google Scholar] [CrossRef] [PubMed]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1998, 85, 5–34. [Google Scholar] [CrossRef] [PubMed]
- Zastrow, E.; Davis, S.K.; Lazebnik, M.; Kelcz, F.; Van Veen, B.D.; Hagness, S.C. Development of Anatomically Realistic Numerical Breast Phantoms With Accurate Dielectric Properties for Modeling Microwave Interactions With the Human Breast. IEEE Trans. Biomed. Eng. 2008, 55, 2792–2800. [Google Scholar] [CrossRef] [PubMed]
- UWCEM–Phantom Repository. Uwcem.Ece.Wisc.Edu. Available online: https://uwcem.ece.wisc.edu/phantomRepository.html (accessed on 10 November 2020).
- Haynes, M.; Stang, J.; Moghaddam, M. Real-time Microwave Imaging of Differential Temperature for Thermal Therapy Monitoring. IEEE Trans. Biomed. Eng. 2014, 61, 1787–1797. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Stang, J.; Haynes, M.; Leuthardt, E.; Moghaddam, M. Real-Time Three-Dimensional Microwave Monitoring of Interstitial Thermal Therapy. IEEE Trans. Biomed. Eng. 2017, 65, 528–538. [Google Scholar] [CrossRef] [PubMed]
- Scapaticci, R.; LoPresto, V.; Pinto, R.; Cavagnaro, M.; Crocco, L. Monitoring Thermal Ablation via Microwave Tomography: An Ex Vivo Experimental Assessment. Diagnostics 2018, 8, 81. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altintas, G.; Akduman, I.; Janjic, A.; Yilmaz, T. A Novel Approach on Microwave Hyperthermia. Diagnostics 2021, 11, 493. https://doi.org/10.3390/diagnostics11030493
Altintas G, Akduman I, Janjic A, Yilmaz T. A Novel Approach on Microwave Hyperthermia. Diagnostics. 2021; 11(3):493. https://doi.org/10.3390/diagnostics11030493
Chicago/Turabian StyleAltintas, Gulsah, Ibrahim Akduman, Aleksandar Janjic, and Tuba Yilmaz. 2021. "A Novel Approach on Microwave Hyperthermia" Diagnostics 11, no. 3: 493. https://doi.org/10.3390/diagnostics11030493
APA StyleAltintas, G., Akduman, I., Janjic, A., & Yilmaz, T. (2021). A Novel Approach on Microwave Hyperthermia. Diagnostics, 11(3), 493. https://doi.org/10.3390/diagnostics11030493







