The Reconstruction of Magnetic Particle Imaging: Current Approaches Based on the System Matrix
Abstract
:1. Introduction
2. MPI Principle
3. The Theory of SM-Based MPI
3.1. Current SM Construction Methods
3.2. The Theory of SM-Based MPI
4. Current SM-Based MPI Reconstruction Methods
4.1. SM-Based MPI Reconstruction Based on the State-of-the-Art Tikhonov Regularization
4.2. SM-Based MPI Reconstruction Based on the Improved Methods
4.3. SM-Based MPI Reconstruction Methods to Subtract the Background Signal
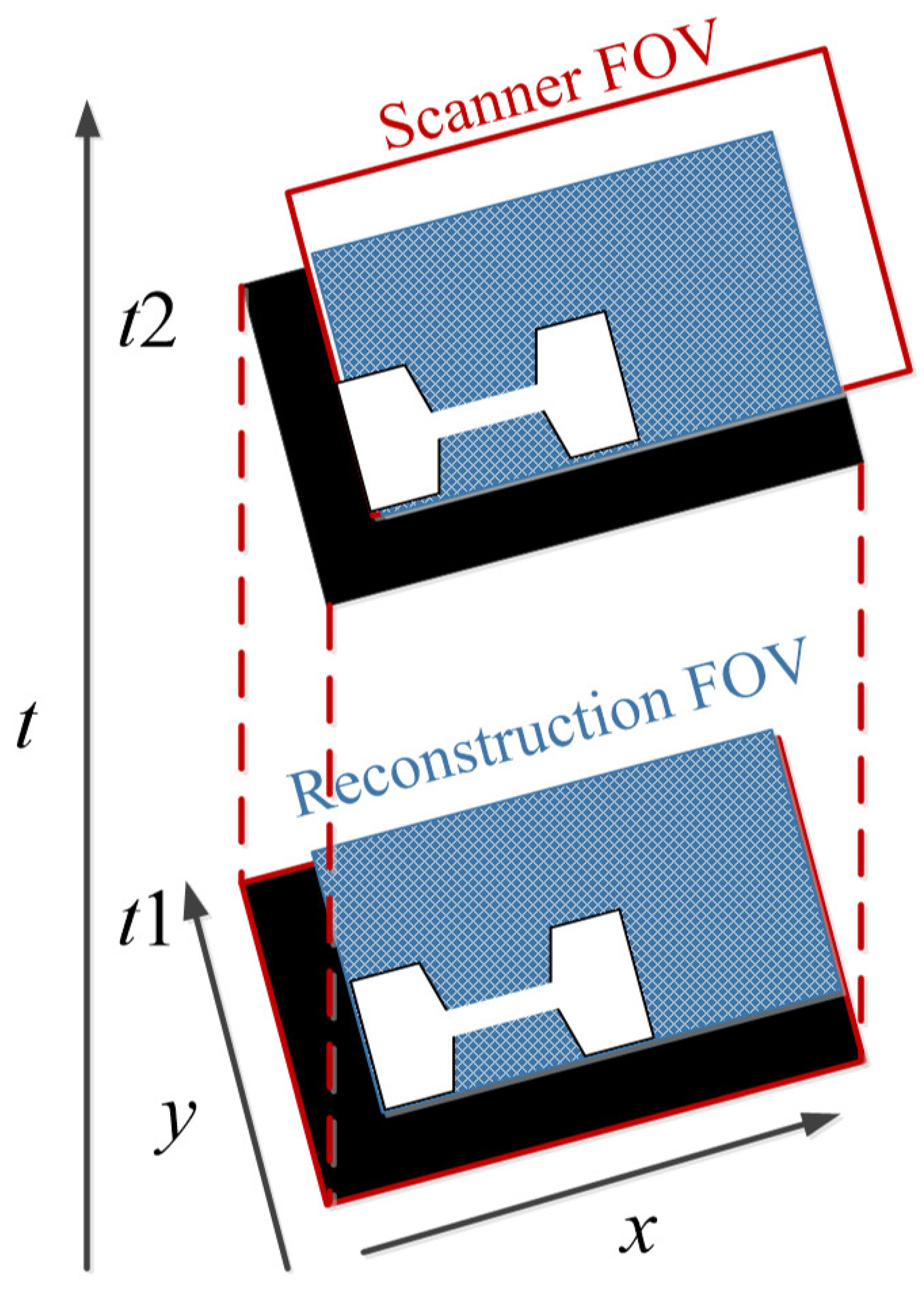
4.4. SM-Based MPI Reconstruction Approaches to Expand the Spatial Coverage
4.5. Matrix Transformations to Accelerate SM-Based MPI Reconstruction
5. Current Phantoms Used for SM-Based MPI Reconstruction
6. Performance Indicators for MPI Reconstruction
7. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Bulte, J.W. Superparamagnetic iron oxides as MPI tracers: A primer and review of early applications. Adv. Drug Deliv. Rev. 2019, 138, 293–301. [Google Scholar] [CrossRef] [PubMed]
- Gleich, B.; Weizenecker, J. Tomographic imaging using the nonlinear response of magnetic particles. Nat. Cell Biol. 2005, 435, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Goodwill, P.W.; Conolly, S.M. Multidimensional x-space magnetic particle imaging. IEEE Trans. Med. Imaging 2011, 30, 1581–1590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weizenecker, J.; Gleich, B.; Rahmer, J.; Dahnke, H.; Borgert, J. Three-dimensional real-time in vivo magnetic particle imaging. Phys. Med. Biol. 2009, 54, L1–L10. [Google Scholar] [CrossRef]
- Sattel, T.F.; Knopp, T.; Biederer, S.; Gleich, B.; Weizenecker, J.; Borgert, J.; Buzug, T.M. Single-sided device for magnetic particle imaging. J. Phys. D Appl. Phys. 2009, 42, 022001. [Google Scholar] [CrossRef] [Green Version]
- Grafe, K.; Von Gladiss, A.; Bringout, G.; Ahlborg, M.; Buzug, T.M. 2D Images Recorded With a Single-Sided Magnetic Particle Imaging Scanner. IEEE Trans. Med. Imaging 2016, 35, 1056–1065. [Google Scholar] [CrossRef]
- Meribout, M.; Kalra, M.; Alhmoudi, F.; Alhosani, A.; Almurshidi, M. A portable system for two dimensional magnetic particle imaging. Measurement 2020, 152, 152. [Google Scholar] [CrossRef]
- Le, T.-A.; Bui, M.P.; Yoon, J. System Design of a rabbit scale 3D magnetic particle imaging system with amplitude modulation. Int. J. Magn. Part. Imaging 2020, 6, 1–3. [Google Scholar]
- Zheng, Y.; Huang, J.; Zhu, T.; Li, R.; Wang, Z.; Ma, F.; Zhu, J. Stem Cell Tracking Technologies for Neurological Regenerative Medicine Purposes. Stem Cells Int. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Han, X.; Li, Y.; Liu, W.; Chen, X.; Song, Z.; Wang, X.; Deng, Y.; Tang, X.; Jiang, Z. The Applications of Magnetic Particle Imaging: From Cell to Body. Diagnostics 2020, 10, 800. [Google Scholar] [CrossRef]
- Song, G.; Chen, M.; Zhang, Y.; Cui, L.; Qu, H.; Zheng, X.; Wintermark, M.; Liu, Z.; Rao, J. Janus Iron Oxides @ Semiconducting Polymer Nanoparticle Tracer for Cell Tracking by Magnetic Particle Imaging. Nano Lett. 2018, 18, 182–189. [Google Scholar] [CrossRef]
- Jung, K.O.; Jo, H.; Yu, J.H.; Gambhir, S.S.; Pratx, G. Development and MPI tracking of novel hypoxia-targeted theranostic exosomes. Biomaterials 2018, 177, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Tay, Z.W.; Chandrasekharan, P.; Zhou, X.Y.; Yu, E.; Zheng, B.; Conolly, S. In vivo tracking and quantification of inhaled aerosol using magnetic particle imaging towards inhaled therapeutic monitoring. Theranostics 2018, 8, 3676–3687. [Google Scholar] [CrossRef] [PubMed]
- Yu, E.Y.; Chandrasekharan, P.; Berzon, R.; Tay, Z.W.; Zhou, X.; Khandhar, A.P.; Ferguson, R.M.; Kemp, S.; Zhen, B.; Goodwill, P.; et al. Magnetic Particle Imaging for Highly Sensitive, Quantitative, and Safe in Vivo Gut Bleed Detection in a Murine Model. ACS Nano 2017, 11, 12067–12076. [Google Scholar] [CrossRef] [PubMed]
- Israel, L.L. A Nanomedicine Approach to Manage Cancer—Imaging Pancreatic Cancer Using Targeted Iron Oxide Nanoparticles. EBioMedicine 2018, 30, 7–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tay, Z.W.; Chandrasekharan, P.; Chiu-Lam, A.; Hensley, D.W.; Dhavalikar, R.; Zhou, X.Y.; Yu, E.Y.; Goodwill, P.W.; Zheng, B.; Rinaldi, C.; et al. Magnetic Particle Imaging-Guided Heating in Vivo Using Gradient Fields for Arbitrary Localization of Magnetic Hyperthermia Therapy. ACS Nano 2018, 12, 3699–3713. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhang, Y.; Steinberg, G.; Qu, H.; Huang, S.; Cheng, M.; Bliss, T.; Du, F.; Rao, J.; Song, G.; et al. A Review of Magnetic Particle Imaging and Perspectives on Neuroimaging. Am. J. Neuroradiol. 2019, 40, 206–212. [Google Scholar] [CrossRef]
- Top, C.B.; Güngör, A.; Ilbey, S.; Güven, H.E. Trajectory analysis for field free line magnetic particle imaging. Med. Phys. 2019, 46, 1592–1607. [Google Scholar] [CrossRef] [Green Version]
- Borgert, J.; Gleich, B.; Buzug, T.M. Magnetic Particle Imaging; Springer Handbook of Medical Technology: Berlin/Heidelberg, Germany, 2011; pp. 461–476. [Google Scholar]
- Weizenecker, J.; Gleich, B.; Borgert, J. Magnetic particle imaging using a field free line. J. Phys. D Appl. Phys. 2008, 41, 105009. [Google Scholar] [CrossRef]
- Knopp, T.; Erbe, M.; Biederer, S.; Sattel, T.F.; Buzug, T.M. Efficient generation of a magnetic field-free line. Med. Phys. 2010, 37, 3538. [Google Scholar] [CrossRef]
- Bente, K.; Weber, M.; Graeser, M.; Sattel, T.F.; Erbe, M.; Buzug, T.M. Electronic Field Free Line Rotation and Relaxation Deconvolution in Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2014, 34, 644–651. [Google Scholar] [CrossRef] [PubMed]
- Ilbey, S.; Top, C.B.; Gungor, A.; Cukur, T. Comparison of System-Matrix-Based and Projection-Based Reconstructions for Field Free Line Magnetic Particle Imaging. Int. J. Mag. Part. Imaging 2017, 3, 1. [Google Scholar]
- Top, C.B.; Gungor, A. Tomographic Field Free Line Magnetic Particle Imaging with an Open-Sided Scanner Configuration. IEEE Trans. Med. Imaging 2020, 39, 4164–4173. [Google Scholar] [CrossRef]
- Kluth, T. Mathematical models for magnetic particle imaging. Inverse Probl. 2018, 34, 083001. [Google Scholar] [CrossRef] [Green Version]
- Goodwill, P.W.; Saritas, E.U.; Croft, L.R.; Kim, T.N.; Krishnan, K.M.; Schaffer, D.V.; Conolly, S.M. X-Space MPI: Magnetic Nanoparticles for Safe Medical Imaging. Adv. Mater. 2012, 24, 3870–3877. [Google Scholar] [CrossRef] [Green Version]
- Kurt, S.; Muslu, Y.; Saritas, E.U. Partial FOV Center Imaging (PCI): A Robust X-Space Image Reconstruction for Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2020, 39, 3441–3450. [Google Scholar] [CrossRef] [PubMed]
- Ozaslan, A.A.; Alacaoglu, A.; Demirel, O.B.; Çukur, T.; Saritas, E.U. Fully automated gridding reconstruction for non-Cartesian x-space magnetic particle imaging. Phys. Med. Biol. 2019, 64, 165018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmiester, L.; Moddel, M.; Erb, W.; Knopp, T. Direct Image Reconstruction of Lissajous-Type Magnetic Particle Imaging Data Using Chebyshev-Based Matrix Compression. IEEE Trans. Comput. Imaging 2017, 3, 671–681. [Google Scholar] [CrossRef]
- März, T.; Weinmann, A. Model-based reconstruction for magnetic particle imaging in 2D and 3D. Inverse Probl. Imaging 2016, 10, 1087–1110. [Google Scholar] [CrossRef] [Green Version]
- Erb, W.; Weinmann, A.; Ahlborg, M.; Brandt, C.; Bringout, G.; Buzug, T.M.; Frikel, J.; Kaethner, C.; Knopp, T.; März, T.; et al. Mathematical analysis of the 1D model and reconstruction schemes for magnetic particle imaging. Inverse Probl. 2018, 34, 055012. [Google Scholar] [CrossRef] [Green Version]
- Kaethner, C.; Erb, W.; Ahlborg, M.; Szwargulski, P.; Knopp, T.; Buzug, T.M. Non-Equispaced System Matrix Acquisition for Magnetic Particle Imaging Based on Lissajous Node Points. IEEE Trans. Med. Imaging 2016, 35, 2476–2485. [Google Scholar] [CrossRef]
- Von Gladiss, A.; Graeser, M.; Behrends, A.; Chen, X.; Buzug, T.M. Efficient hybrid 3D system calibration for magnetic particle imaging systems using a dedicated device. Sci. Rep. 2020, 10, 18432. [Google Scholar] [CrossRef] [PubMed]
- Panagiotopoulos, N.; Vogt, F.M.; Barkhausen, J.; Buzug, T.M.; Duschka, R.L.; Lüdtke-Buzug, K.; Ahlborg, M.; Bringout, G.; Debbeler, C.; Graeser, M.; et al. Magnetic particle imaging: Current developments and future directions. Int. J. Nanomed. 2015, 10, 3097–3114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rahmer, J.; Weizenecker, J.; Gleich, B.; Borgert, J. Signal encoding in magnetic particle imaging: Properties of the system function. BMC Med. Imaging 2009, 9, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knopp, T.; Sattel, T.F.; Biederer, S.; Rahmer, J.; Weizenecker, J.; Gleich, B.; Borgert, J.; Buzug, T.M. Model-Based Reconstruction for Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2009, 29, 12–18. [Google Scholar] [CrossRef]
- Knopp, T.; Gdaniec, N.; Möddel, M. Magnetic particle imaging: From proof of principle to preclinical applications. Phys. Med. Biol. 2017, 62, R124–R178. [Google Scholar] [CrossRef]
- Szwargulski, P.; Moddel, M.; Gdaniec, N.; Knopp, T. Efficient Joint Image Reconstruction of Multi-Patch Data Reusing a Single System Matrix in Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2019, 38, 932–944. [Google Scholar] [CrossRef] [PubMed]
- Straub, M.; Schulz, V. Joint Reconstruction of Tracer Distribution and Background in Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2018, 37, 1192–1203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meribout, M.; Al Hosani, E.; Kalra, M.; Saeid, I. An NIR-Based Probe for Submilligram Measurement of Solid Contaminants in Gas Pipelines. IEEE Photonics J. 2016, 8, 1–15. [Google Scholar] [CrossRef]
- Franke, J.; Heinen, U.; Lehr, H.; Weber, A.; Jaspard, F.; Ruhm, W.; Heidenreich, M.; Schulz, V. System Characterization of a Highly Integrated Preclinical Hybrid MPI-MRI Scanner. IEEE Trans. Med. Imaging 2016, 35, 1993–2004. [Google Scholar] [CrossRef]
- Ilbey, S.; Top, C.B.; Gungor, A.; Cukur, T.; Saritas, E.U.; Guven, H.E. Fast System Calibration With Coded Calibration Scenes for Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2019, 38, 2070–2080. [Google Scholar] [CrossRef]
- Grüttner, M.; Knopp, T.; Franke, J.; Heidenreich, M.; Rahmer, J.; Halkola, A.; Kaethner, C.; Borgert, J.; Buzug, T.M. On the formulation of the image reconstruction problem in magnetic particle imaging. Biomed. Tech. Eng. 2013, 58, 583–591. [Google Scholar] [CrossRef]
- Baltruschat, I.M.; Szwargulski, P.; Griese, F.; Grosser, M.; Werner, R.; Knopp, T. 3d-SMRnet: Achieving a New Quality of MPI System Matrix Recovery by Deep Learning. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; pp. 74–82. [Google Scholar]
- Storath, M.; Brandt, C.; Hofmann, M.; Knopp, T.; Salamon, J.; Weber, A.; Weinmann, A. Edge Preserving and Noise Reducing Reconstruction for Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2016, 36, 74–85. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Ma, X.; Liao, H.; Liang, Z.; Li, F.; Tian, J.; Ling, D. Artificially Engineered Cubic Iron Oxide Nanoparticle as a High-Performance Magnetic Particle Imaging Tracer for Stem Cell Tracking. ACS Nano 2020, 14, 2053–2062. [Google Scholar] [CrossRef]
- Ferguson, R.M.; Khandhar, A.P.; Kemp, S.J.; Arami, H.; Saritas, E.U.; Croft, L.R.; Konkle, J.; Goodwill, P.W.; Halkola, A.; Rahmer, J.; et al. Magnetic Particle Imaging With Tailored Iron Oxide Nanoparticle Tracers. IEEE Trans. Med. Imaging 2015, 34, 1077–1084. [Google Scholar] [CrossRef] [PubMed]
- Knopp, T.; Biederer, S.; Sattel, T.; Weizenecker, J.; Gleich, B.; Borgert, J.; Buzug, T.M. Trajectory analysis for magnetic particle imaging. Phys. Med. Biol. 2008, 54, 385–397. [Google Scholar] [CrossRef]
- Vogel, P.; Ruckert, M.A.; Jakoc, P.M.; Behr, V.C. MPI—Initial Experiments with an Ultrahigh Resolution MPI. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Graeser, M.; von Gladiss, A.; Friedrich, T.; Buzug, T.M. SNR and Discretization Enhancement for System Matrix Determination by Decreasing the Gradient in Magnetic Particle Imaging. Int. J. Mag. Part. Imaging 2017, 3, 1. [Google Scholar]
- Takagi, T.; Tsuchiya, H.; Hatsuda, T.; Ishihara, Y. Image Reconstruction Method Using Orthonormal Basis by Singular Value Decomposition for Magnetic Particle Imaging. Trans. Jpn. Soc. Med. Biol. Eng. 2016, 53, 276–282. [Google Scholar]
- Vandenplas, J.; Eding, H.; Bosmans, M.; Calus, M.P.L. Computational strategies for the preconditioned conjugate gradient method applied to ssSNPBLUP, with an application to a multivariate maternal model. Genet. Sel. Evol. 2020, 52, 24. [Google Scholar] [CrossRef]
- Hsieh, S.S.; Hoffman, J.M.; Noo, F. Accelerating iterative coordinate descent using a stored system matrix. Med. Phys. 2019, 46, e801–e809. [Google Scholar] [CrossRef] [PubMed]
- Gräfe, K.; Bringout, G.; Graeser, M.; Sattel, T.F.; Buzug, T.M. System Matrix Recording and Phantom Measurements with a Single-Sided Magnetic Particle Imaging Device. IEEE Trans. Magn. 2015, 51, 1–3. [Google Scholar] [CrossRef]
- Knopp, T.; Sattel, T.F.; Beiderer, S.; Weizenecker, J.; Gleich, B.; Borgert, J.; Buzug, M.T. Weighted iterative reconstruction for magnetic particle imaging. Phys. Med. Biol. 2010, 55, 1577–1589. [Google Scholar] [CrossRef]
- Kluth, T.; Jin, B. Enhanced reconstruction in magnetic particle imaging by whitening and randomized SVD approximation. Phys. Med. Biol. 2019, 64, 125026. [Google Scholar] [CrossRef] [Green Version]
- Chambolle, A.; Lions, P.-L. Image recovery via total variation minimization and related problems. Numer. Math. 1997, 76, 167–188. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef] [Green Version]
- Ting, M.; Raich, R.; Hero, I.A.O. Sparse Image Reconstruction for Molecular Imaging. IEEE Trans. Image Process. 2009, 18, 1215–1227. [Google Scholar] [CrossRef]
- Keller, S.H.; Svarer, C.; Sibomana, M. Attenuation correction for the HRRT PET-scanner using transmission scatter correction and total variation regularization. IEEE Trans. Med. Imaging 2013, 32, 1611–1621. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Z.; Ma, J.; Lu, H.; Wang, K.; Zhang, H.; Moore, W. Total variation-stokes strategy for sparse-view X-ray CT image reconstruction. IEEE Trans. Med. Imaging 2014, 33, 749–763. [Google Scholar] [CrossRef]
- Brandt, C.; Seppanen, A. Recovery from Errors Due to Domain Truncation in Magnetic Particle Imaging: Approximation Error Modeling Approach. J. Math. Imaging Vis. 2018, 60, 1196–1208. [Google Scholar] [CrossRef]
- Aggarwal, H.K.; Mani, M.P.; Jacob, M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans. Med. Imaging 2018, 38, 394–405. [Google Scholar] [CrossRef]
- Chae, B.G. Neural Network Image Reconstruction for Magnetic Particle Imaging. ETRI J. 2017, 39, 841–850. [Google Scholar] [CrossRef] [Green Version]
- Hashimoto, F.; Ohba, H.; Ote, K.; Kakimoto, A.; Tsukada, H.; Ouchi, Y. 4D deep image prior: Dynamic PET image denoising using an unsupervised four-dimensional branch convolutional neural network. Phys. Med. Biol. 2020, 66, 015006. [Google Scholar] [CrossRef] [PubMed]
- Dittmer, S.; Kluth, T.; Maass, P.; Baguer, D.O. Regularization by Architecture: A Deep Prior Approach for Inverse Problems. J. Math. Imaging Vis. 2020, 62, 456–470. [Google Scholar] [CrossRef] [Green Version]
- Them, K.; Kaul, M.G.; Jung, C.; Hofmann, M.; Mummert, T.; Werner, F.; Knopp, T. Sensitivity Enhancement in Magnetic Particle Imaging by Background Subtraction. IEEE Trans. Med. Imaging 2015, 35, 893–900. [Google Scholar] [CrossRef] [PubMed]
- Paysen, H.; Kosch, O.; Wells, J.; Loewa, N.; Wiekhorst, F. Characterization of noise and background signals in a magnetic particle imaging system. Phys. Med. Biol. 2020. [Google Scholar] [CrossRef]
- Knopp, T.; Them, K.; Kaul, M.; Gdaniec, N. Joint reconstruction of non-overlapping magnetic particle imaging focus-field data. Phys. Med. Biol. 2015, 60, L15–L21. [Google Scholar] [CrossRef] [Green Version]
- Gdaniec, N.; Szwargulski, P.; Knopp, T. Fast multiresolution data acquisition for magnetic particle imaging using adaptive feature detection. Med. Phys. 2017, 44, 6456–6460. [Google Scholar] [CrossRef]
- Tay, Z.W.; Hensley, D.; Ma, J.; Chandrasekharan, P.; Zheng, B.; Goodwill, P.; Conolly, S. Pulsed Excitation in Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2019, 38, 2389–2399. [Google Scholar] [CrossRef] [PubMed]
- Saritas, E.U.; Goodwill, P.W.; Conolly, S.M. Effects of pulse duration on magnetostimulation thresholds. Med. Phys. 2015, 42, 3005–3012. [Google Scholar] [CrossRef] [Green Version]
- Szwargulski, P.; Gdaniec, N.; Graeser, M.; Moddel, M.; Griese, F.; Krishnan, K.M.; Buzug, T.M.; Knopp, T. Moving table magnetic particle imaging: A stepwise approach preserving high spatio-temporal resolution. J. Med. Imaging 2018, 5, 046002. [Google Scholar] [CrossRef]
- Lampe, J.; Bassoy, C.; Rahmer, J.; Weizenecker, J.; Voss, H.; Gleich, B.; Borgert, J. Fast reconstruction in magnetic particle imaging. Phys. Med. Biol. 2012, 57, 1113–1134. [Google Scholar] [CrossRef]
- Knopp, T.; Weber, A. Local System Matrix Compression for Efficient Reconstruction in Magnetic Particle Imaging. Adv. Math. Phys. 2015, 2015, 1–7. [Google Scholar] [CrossRef]
- Knopp, T.; Hofmann, M. Online reconstruction of 3D magnetic particle imaging data. Phys. Med. Biol. 2016, 61, N257–N267. [Google Scholar] [CrossRef]
- Rahmer, J.; Weizenecker, J.; Gleich, B.; Borgert, J. Analysis of a 3-D System Function Measured for Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2012, 31, 1289–1299. [Google Scholar] [CrossRef]
- Weber, A.; Knopp, T. Symmetries of the 2D magnetic particle imaging system matrix. Phys. Med. Biol. 2015, 60, 4033–4044. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shin, H.-C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep Convolutional Neural Networks for Computer-Aided Detection: CNN Architectures, Dataset Characteristics and Transfer Learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoo, S.; Gujrathi, I.; Haider, M.A.; Khalvati, F. Prostate Cancer Detection using Deep Convolutional Neural Networks. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]




| Year | Journal | Phantoms | Description |
|---|---|---|---|
| 2016 | IEEE Transactions on Medical Imaging |  | The size of the cube-shaped calibration sample size is 2 × 2 × 2 mm3. The calibration sample is moved in vertical and horizontal steps of 2 mm over the 30 × 30 mm2 FOV [6]. |
| 2017 | IEEE Transactions on Medical Imaging |  | Three different phantoms with one percent Gaussian noise are used to evaluate the reconstruction quality: a simulated stenosis, overlapping ellipses, and a vascular tree [45]. |
| 2018 | Journal of Mathematical Imaging and Vision |  | The first is a typical resolution phantom with round objects of different size and concentration. The second includes three ellipses with different size and concentration. The third simulates a situation where objects cannot be covered by a single FOV [62]. |
| 2019 | IEEE Transactions on Medical Imaging |  | The first is the filled 3D-printed model, which consists of four rectangles with different sizes. The second is the UKE phantom. The letters of the phantom are located in different planes in the y direction [38]. |
| 2019 | Physics in Medicine & Biology |  | These two phantoms are from the open MPI datasets (www.tuhh.de/ibi/research/open-mpi-data.html (accessed on 7 October 2020)). The first is a cone and the second consists of five tubes with a common origin on one side of the phantom [56]. |
| 2019 | Measurement |  | Real images are used to study MPI reconstruction, which represent the different mouse organs: the lungs, left kidney, right kidney, and reproductive system [7]. |
| Journal | Indicator | Equation and Description |
|---|---|---|
| Measurement | the absolute mean error | The absolute mean error is a quantitative evaluation [7]. It considers eventual image transforms, such as rotation, translation, and zoom transform [45]. Therefore, it is fairer. |
| IEEE Transactions on Medical Imaging | NRMSE | The NRMSE is an objective evaluation index of image quality based on pixel error. It reflects the degree of difference between the reconstructed image and the original image [45]. The smaller the NRMSE, the better the reconstruction quality. |
| IEEE Transactions on Medical Imaging | SSIM | SSIM (I, U) = L(I,U) × C(I,U) × S(I,U) where uI and uU represent the mean values of images I and U, respectively. σI and σI represent the standard deviations of image I and U. σIU represents the image I and U covariance. C1, C2, and C3 are constants to prevent the denominator from being 0 and maintain stability. SSIM takes the similarity of local structures into account [45], therefore, it is more suitable for perceiving visual quality. The SSIM is limited by 1, and a higher SSIM means a better reconstruction result [79]. |
| Physics in Medicine & Biology | The reconstruction time t | The reconstruction time represents the solution time of equation , where and represent the truncated system matrix and truncated measurement, respectively. The shorter t is, the better the reconstruction performance. The reconstruction time is always the mean of the execution time for 100 times [56]. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Jiang, Z.; Han, X.; Wang, X.; Tang, X. The Reconstruction of Magnetic Particle Imaging: Current Approaches Based on the System Matrix. Diagnostics 2021, 11, 773. https://doi.org/10.3390/diagnostics11050773
Chen X, Jiang Z, Han X, Wang X, Tang X. The Reconstruction of Magnetic Particle Imaging: Current Approaches Based on the System Matrix. Diagnostics. 2021; 11(5):773. https://doi.org/10.3390/diagnostics11050773
Chicago/Turabian StyleChen, Xiaojun, Zhenqi Jiang, Xiao Han, Xiaolin Wang, and Xiaoying Tang. 2021. "The Reconstruction of Magnetic Particle Imaging: Current Approaches Based on the System Matrix" Diagnostics 11, no. 5: 773. https://doi.org/10.3390/diagnostics11050773
APA StyleChen, X., Jiang, Z., Han, X., Wang, X., & Tang, X. (2021). The Reconstruction of Magnetic Particle Imaging: Current Approaches Based on the System Matrix. Diagnostics, 11(5), 773. https://doi.org/10.3390/diagnostics11050773






