A Machine Learning Decision Support System (DSS) for Neuroendocrine Tumor Patients Treated with Somatostatin Analog (SSA) Therapy
Abstract
1. Introduction
2. Results
2.1. Cohort of Patients
2.2. Data Cleaning
2.3. Classification Models
- Model 1: predicts whether the patient will progress after 12 months;
- Model 2: predicts whether the patient will progress after 18 months;
- Model 3: predicts whether the patient will progress either after 12 or 18 months or not at all.
2.4. Imbalance Analysis of the Dataset
2.5. Fixing the Data Imbalance
2.6. Feature Selection
2.7. ML Algorithms
2.8. Hyperparameter Tuning
3. Discussion
4. Materials and Methods
4.1. Patient Population and Methods
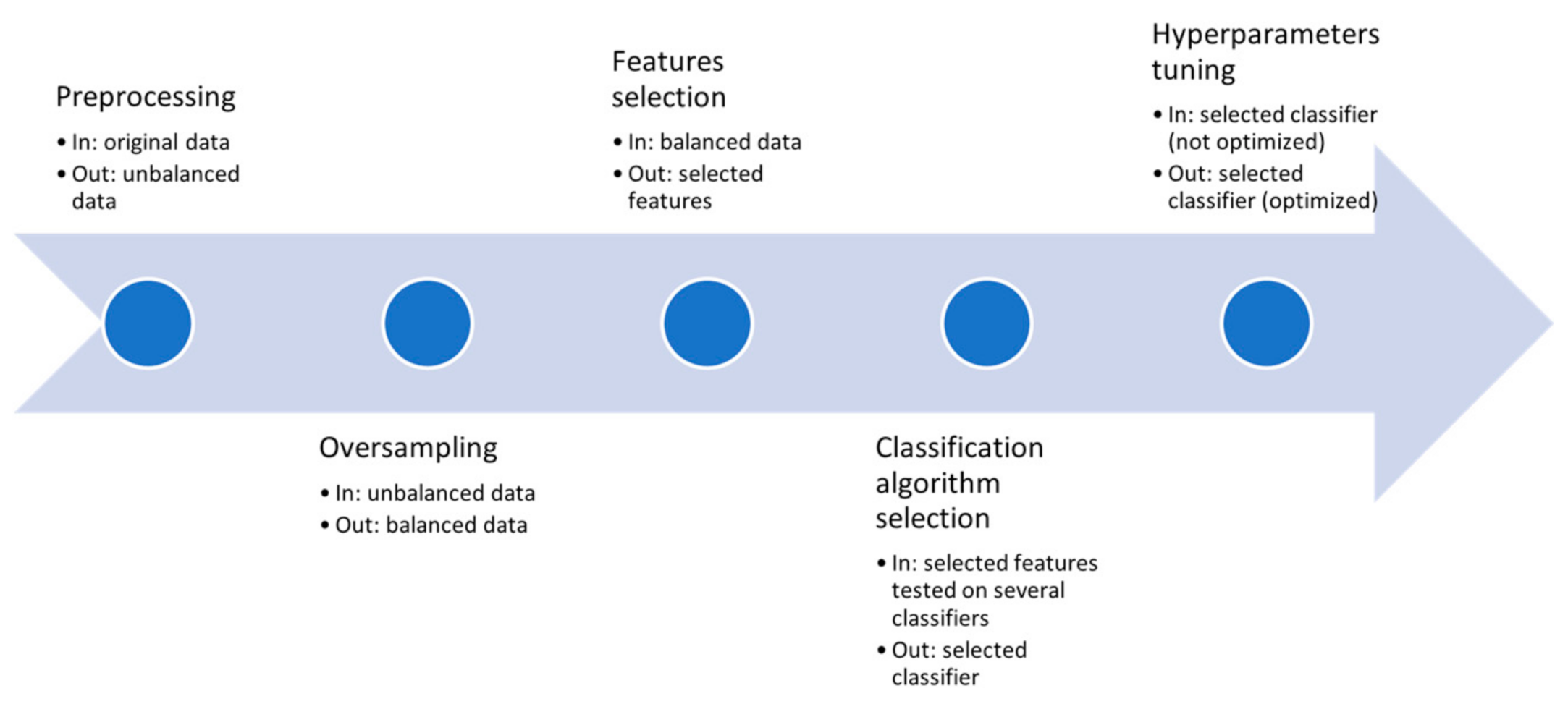
4.2. Pre-Processing and Oversampling
- Each example of the minority class is considered and the K-Nearest Neighbors belonging to the same class are identified.
- A line between the considered example and its K-Nearest Neighbor is drawn;
- Synthetic examples are randomly generated along those line segments.
- SMOTE works also for multi-class classification problems [45].
4.3. Feature Selection
4.4. ML Algorithms
- Logistic Regression (LR): this algorithm falls in the family of statistical models. They are diffusely used in ML to predict the risk of developing a certain disease. Although this method models the probability of an output given an input and therefore should not be properly considered as a classifier, it can still be profitably used as such by setting cutoff thresholds [50].
- Decision Tree (DT): this is a structure similar to a flowchart where each internal node holds a test linked through arches (outcome of tests) to other nodes. The children nodes, or “leaves”, represent decisions or classes. DTs are often used in ensemble methods [51], techniques that combine multiple models or algorithms to achieve better predictive performances. A recent evolution is represented in the C5.0 algorithm, which includes feature selection and reduced pruning errors [52,53].
- Random Forest (RF): introduced by Breiman in 2001 [54], it is an ensemble method widely used also in the field of bioinformatics, metagenomics and genomic data analysis [55]. It is a combination of several algorithms for classification or regression, providing enhanced performances and gaining the predictive power of a single DT [56]. The final prediction is obtained as the average or the majority of the estimations from the single DTs. RF shows sound performances and simplified parameter tuning [57].
- Support Vector Machine (SVM): SVMs are often the chosen algorithm thanks to their excellent performance as supervised binary classifiers. They were first introduced by Boser et al. [58]. The binary classes of training data are represented by two subsets (’regions’) of features. This is done by using a linear hyperplane of equation [59]:wtx + b = 0.
- Naïve Bayes (NB): grounded on the well-known Bayes’ theorem, these probabilistic classifiers have been used in ML since the very beginning and are still often used in clinical decision support systems for their neatness.
- Multinomial Naïve Bayes (MNB): an NB variation with the features representing the frequencies with which a few events have been generated by a multinomial distribution.
- K-Nearest Neighbors (k-NN): an object is ranked by the majority of its neighbors’ votes. K is a small positive integer. If K = 1 then the object is assigned to its neighbor’s class. Typically, for binary classifications, K is not even to avoid finding situations of equality. This method can also be used for regression techniques by assigning to the object the average of the values of the K closest objects. A drawback is due to the predominance of the classes with more objects. This can be compensated with weighing techniques based on distance.
- Gradient Boosting (GB): this produces a predictive model in the form of a set of weak predictive models, typically DTs. It constructs a model similar to boosting methods and generalizes them allowing the optimization of an arbitrary differentiable loss function. Boosting algorithms are views as iterative descending functional gradient algorithms, optimizing a cost function over a space function pointing to a direction with a negative gradient.
- Extremely Randomized Tree Classifier: based on the idea that randomized DTs show a performance as good as classical ones. In the extreme case, fully randomized trees are built whose structures are independent of the output values of the learning sample [60]. This approach provides good accuracy and computational efficiency.
- Multi-Layer Perceptron (MLP): this is an artificial neural network model, mapping sets of input data into a set of appropriate output data. A direct graph is made up of multiple layers of nodes, each fully connected to the next. The nodes or ’neurons’ are provided with a non-linear activation function. If compared with a traditional standard perceptron, MLPs can distinguish data that are not linearly separable [61].
4.5. ML Performance Measures
- Accuracy: this is a widely used method for assessing how effective one classifier is in predicting the correct classes. It is defined as the sum of all of the true positives (TPs) and true negatives (TNs) divided by all samples, TP + TN + false positives (FPs) + false negatives (FNs).
- Precision: in a classification task, the precision is, for a class, defined as TP divided by the total number of elements labeled as positives (i.e., TP + FP). In a binary classifier, this parameter can be also called sensitivity.
- Recall: this is defined as the number of TPs divided by the total amount of “real” positives that includes the TP and the FN.
- F1-score: this is a score computed as the harmonic mean of precision and recall. Its best value is 1, meaning perfect precision and recall.
4.6. ML Validation
4.7. Hyperparameter Tuning
4.8. Workflow
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Tables
| Patients Number | 74 | 100% |
|---|---|---|
| Age (years) | ||
| Median | 68 | |
| Range | 24–90 | |
| >70 | 57 | 77% |
| ≥70 | 17 | 23% |
| Sex | ||
| M | 45 | 61% |
| F | 29 | 39% |
| Performance status (ECOG) | ||
| 0–1 | 73 | 99% |
| 2 | 1 | 1% |
| Primary site | ||
| Pancreas | 30 | 41% |
| Gastrointestinal | 44 | 59% |
| Functioning NET | ||
| Yes | 22 | 30% |
| No | 52 | 70% |
| Grade | ||
| G1 | 26 | 35% |
| G2 | 46 | 62% |
| NA | 2 | 3% |
| Ki67 | ||
| <2% | 19 | 26% |
| 2–20% | 51 | 69% |
| ≥20% | 2 | 2.5% |
| NA | 2 | 2.5% |
| Stage | ||
| Locally advanced | 2 | 3% |
| Metastatic | 72 | 97% |
| Primary on site | ||
| Yes | 31 | 42% |
| No | 43 | 58% |
| Number of metastatic sites | ||
| 0 | 2 | 3% |
| 1 | 46 | 62% |
| >1 | 26 | 35% |
| Metastatic sites | ||
| Liver | 63 | 85% |
| Lung | 5 | 7% |
| Bone | 3 | 4% |
| Type of SSA | ||
| Lanreotide | 34 | 46% |
| Octreotide LAR | 40 | 54% |
| Adverse events G3-G4 | ||
| Yes | 1 | 1% |
| No | 73 | 99% |
| PFS > 12 months | ||
| Yes | 53 | 72% |
| No | 17 | 23% |
| NA | 4 | 5% |
| PFS > 18 months | ||
| Yes | 43 | 58% |
| No | 27 | 37% |
| NA | 4 | 5% |
| Model | 12 Month Progression | 18 Month Progression | No Progression |
|---|---|---|---|
| 1 | 17 | NA | 53 |
| 2 | NA | 27 | 43 |
| 3 | 17 | 10 | 43 |
| Algorithm | Parameter | Parameter Values |
|---|---|---|
| Logistic regression | solvers | ‘newton-cg’, ‘lbfgs’, ‘liblinear’ |
| penalty | I2 | |
| c_values | 100, 10, 1.0, 0.1, 0.01 | |
| Multinomial NB | alpha | 1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.1, 0.01, 0.001, 0.0001, 0.00001 |
| fit_prior | True, False | |
| class_prior | None, (0.5, 0.5), (0.4, 0.6), (0.45, 0.55), (0.6, 0.4), (0.1, 0.9), (0.2, 0.8) | |
| MLP | hidden_layer_sizes | (50, 50, 50), (50, 100, 50), (100) |
| activation | ‘tanh’, ‘relu’ | |
| solver | ‘sgd’, ‘adam’ | |
| alpha | 0.0001, 0.05 | |
| learning_date | ‘constant’, ‘adaptive’ | |
| SVC | C | 0.1, 1, 10, 100, 1000 |
| gamma | 1, 0.1, 0.01, 0.001, 0.0001 | |
| kernel | rbf | |
| K-Nearest Neighbors | n_neighbors | 3, 5, 11, 19 |
| weights | uniform, distance | |
| metric | ‘euclidean’, ‘manhattan’ |
References
- Yao, J.C.; Hassan, M.; Phan, A.; Dagohoy, C.; Leary, C.; Mares, J.E.; Abdalla, K.E.; Fleming, J.B.; Vauthey, J.N.; Rashid, A.; et al. One hundred years after “carcinoid”: Epidemiology of and prognostic factors for neuroendocrine tumors in 35,825 cases in the United States. J. Clin. Oncol. 2008, 26, 3063–3072. [Google Scholar] [CrossRef]
- Tsikitis, V.L.; Wertheim, B.C.; Guerrero, M.A. Trends of incidence and survival of gastrointestinal neuroendocrine tumors in the United States: A seer analysis. J. Cancer 2012, 3, 292–302. [Google Scholar] [CrossRef]
- Hallet, J.; Law, C.H.L.; Cukier, M.; Saskin, R.; Liu, N.; Singh, S. Exploring the rising incidence of neuroendocrine tumors: A population-based analysis of epidemiology, metastatic presentation, and outcomes. Cancer 2015, 121, 589–597. [Google Scholar] [CrossRef]
- Klimstra, D.S. Pathology reporting of neuroendocrine tumors: Essential elements for accurate diagnosis, classification, and staging. Semin. Oncol. 2013, 40, 23–36. [Google Scholar] [CrossRef]
- Marx, S.; Spiegel, A.M.; Skarulis, M.C.; Doppman, J.L.; Collins, F.S.; Liotta, L.A. Multiple endocrine neoplasia type 1: Clinical and genetic topics. Ann. Intern. Med. 1998, 129, 484–494. [Google Scholar] [CrossRef]
- Donis-Keller, H.; Dou, S.; Chi, D.; Carlson, K.M.; Toshima, K.; Lairmore, T.C.; Howe, J.R.; Moley, J.F.; Goodfellow, P.; Wells, S.A., Jr. Mutations in the RET proto-oncogene are associated with MEN 2A and FMTC. Hum. Mol. Genet. 1993, 2, 851–856. [Google Scholar] [CrossRef]
- Anlauf, M.; Garbrecht, N.; Bauersfeld, J.; Schmitt, A.; Henopp, T.; Komminoth, P.; Heitz, P.U.; Perren, A.; Klöppel, G. Hereditary neuroendocrine tumors of the gastroenteropancreatic system. Virchows Arch. 2007, 451, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, R.; Osamura, R.; Klöppel, G. WHO Classification of Tumours of Endocrine Organs; International Agency for Research on Cancer (IARC): Lyon, France, 2017. [Google Scholar]
- Hochwald, S.N.; Zee, S.; Conlon, K.C.; Colleoni, R.; Louie, O.; Brennan, M.F.; Klimstra, D.S. Prognostic factors in pancreatic endocrine neoplasms: An analysis of 136 cases with a proposal for low-grade and intermediate-grade groups. J. Clin. Oncol. 2002, 20, 2633–2642. [Google Scholar] [CrossRef] [PubMed]
- Panzuto, F.; Boninsegna, L.; Fazio, N.; Campana, D.; Brizzi, M.P.; Capurso, G.; Scarpa, A.; De Braud, F.; Dogliotti, L.; Tomassetti, P.; et al. Metastatic and locally advanced pancreatic endocrine carcinomas: Analysis of factors associated with disease progression. J. Clin. Oncol. 2011, 29, 2372–2377. [Google Scholar] [CrossRef] [PubMed]
- Panzuto, F.; Nasoni, S.; Falconi, M.; Corleto, V.D.; Capurso, G.; Cassetta, S.; Di Fonzo, M.; Tornatore, V.; Milione, M.; Angeletti, S.; et al. Prognostic factors and survival in endocrine tumor patients: Comparison between gastrointestinal and pancreatic localization. Endocr. Relat. Cancer 2005, 12, 1083–1092. [Google Scholar] [CrossRef]
- Pape, U.F.; Jann, H.; Müller-Nordhorn, J.; Bockelbrink, A.; Berndt, U.; Willich, S.N.; Koch, M.; Röcken, C.; Rindi, G.; Wiedenmann, B. Prognostic relevance of a novel TNM classification system for upper gastroenteropancreatic neuroendocrine tumors. Cancer 2008, 113, 256–265. [Google Scholar] [CrossRef] [PubMed]
- Rindi, G.; Bordi, C.; La Rosa, S.; Solcia, E.; Delle Fave, G. Gruppo Italiano Patologi Apparato Digerente (GIPAD); Società Italiana di Anatomia Patologica e Citopatologia Diagnostica/International Academy of Pathology, Italian division (SIAPEC/IAP). Gastroenteropancreatic (neuro) endocrine neoplasms: The histology report. Dig. Liver Dis. 2011, 43, 356–360. [Google Scholar]
- van Velthuysen, M.L.F.; Groen, E.J.; van der Noort, V.; van de Pol, A.; Tesselaar, M.E.T.; Korse, C.M. Grading of neuroendocrine neoplasms: Mitoses and Ki-67 are both essential. Neuroendocrinology 2014, 100, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Amin, M.N.; Edge, S.B.; Greene, A.J.C.C. Cancer Staging Manual; Springer: New York, NY, USA, 2017. [Google Scholar]
- Chagpar, R.; Chiang, J.Y.; Xing, Y.; Cormier, J.N.; Feig, B.W.; Rashid, A.; Chang, G.J.; You, Y.N. Neuroendocrine tumors of the colon and rectum: Prognostic relevance and comparative performance of current staging systems. Ann. Surg. Oncol. 2012, 20, 1170–1178. [Google Scholar] [CrossRef] [PubMed]
- Landry, C.S.; Brock, G.; Scoggins, C.R.; McMasters, K.M.; Martin, R.C.G., II. A proposed staging system for small bowel carcinoid tumors based on an analysis of 6380 patients. Am. J. Surg. 2008, 196, 896–903. [Google Scholar] [CrossRef]
- Landry, C.; Brock, G.; Scoggins, C.R.; McMasters, K.M.; Martin, R.C.G., II. A proposed staging system for gastric carcinoid tumors based on an analysis of 1543 patients. Ann. Surg. Oncol. 2008, 16, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Gou, S.; Liu, Z.; Ye, Z.; Wang, C. Assessment of the American Joint Commission on Cancer 8th Edition Staging System for patients with pancreatic neuroendocrine tumors: A surveillance, epidemiology, and end results analysis. Cancer Med. 2018, 7, 626–634. [Google Scholar] [CrossRef]
- Curran, T.; Pockaj, B.A.; Gray, R.J.; Halfdanarson, T.R.; Wasif, N. Importance of lymph node involvement in pancreatic neuroendocrine tumors: Impact on survival and implications for surgical resection. J. Gastrointest. Surg. 2015, 19, 152–160. [Google Scholar] [CrossRef]
- Klimstra, D.; Modlin, I.R.; Adsay, N.V.; Chetty, R.; Deshpande, V.; Gönen, M.; Jensen, R.T.; Kidd, M.; Kulke, M.H.; Lloyd, R.V.; et al. Pathology reporting of neuroendocrine tumors: Application of the delphic consensus process to the development of a minimum pathology data set. Am. J. Surg. Pathol. 2010, 34, 300–313. [Google Scholar] [CrossRef]
- Ballian, N.; Loeffler, A.G.; Rajamanickam, V.; Norstedt, P.A.; Weber, S.M.; Cho, C.S. A simplified prognostic system for resected pancreatic neuroendocrine neoplasms. HPB 2009, 11, 422–428. [Google Scholar] [CrossRef]
- Ter-Minassian, M.; Chan, J.A.; Hooshmand, S.M.; Brais, L.K.; Daskalova, A.; Heafield, R.; Buchanan, L.; Qian, Z.R.; Fuchs, C.S.; Lin, X.; et al. Clinical presentation, recurrence, and survival in patients with neuroendocrine tumors: Results from a prospective institutional database. Endocr. Relat. Cancer 2013, 20, 187–196. [Google Scholar] [CrossRef]
- Qian, Z.R.; Ter-Minassian, M.; Chan, J.A.; Imamura, Y.; Hooshmand, S.M.; Kuchiba, A.; Morikawa, T.; Brais, L.K.; Daskalova, A.; Heafield, R.; et al. Prognostic significance of MTOR pathway component expression in neuroendocrine tumors. J. Clin. Oncol. 2013, 31, 3418–3425. [Google Scholar] [CrossRef]
- Francis, J.M.; Kiezun, A.; Ramos, A.H.; Serra, S.; Pedamallu, C.S.; Qian, Z.R.; Banck, M.S.; Kanwar, R.; Kulkarni, A.A.; Karpathakis, A.; et al. Somatic mutation of CDKN1B in small intestine neuroendocrine tumors. Nat. Genet. 2013, 45, 1483–1486. [Google Scholar] [CrossRef]
- Kim, H.S.; Lee, H.S.; Nam, K.H.; Choi, J.; Kim, W.H. p27 Loss is associated with poor prognosis in gastroenteropancreatic neuroendocrine tumors. Cancer Res. Treat. 2014, 46, 383–392. [Google Scholar] [CrossRef]
- Khan, M.S.; Kirkwood, A.; Tsigani, T.; Garcia-Hernandez, J.; Hartley, J.A.; Caplin, M.E.; Meyer, T. Circulating tumor cells as prognostic markers in neuroendocrine tumors. J. Clin. Oncol. 2013, 31, 365–372. [Google Scholar] [CrossRef]
- Thorson, A.K. Studies on carcinoid disease. Acta Med. Scand. 1958, 334, 1–132. [Google Scholar]
- Vinik, A.I.; Wolin, E.M.; Liyanage, N.; Gomez-Panzani, E.; Fisher, G.A. ELECT Study Group. Evaluation of lanreotide depot/autogel efficacy and safety as a carcinoid syndrome treatment (ELECT): A randomized, doubleblind, placebo-controlled trial. Endocr. Pract. 2016, 22, 1068–1080. [Google Scholar] [CrossRef] [PubMed]
- Rinke, A.; Müller, H.H.; Schade-Brittinger, C.; Klose, K.J.; Barth, P.; Wied, M.; Mayer, C.; Aminossadati, B.; Pape, U.F.; Bläker, M.; et al. PROMID Study group placebo-controlled, double-blind, prospective, randomized study on the effect of octreotide lar in the control of tumor growth in patients with metastatic neuroendocrine midgut tumors: A report from the PROMID study group. J. Clin. Oncol. 2009, 27, 4656–4663. [Google Scholar] [CrossRef] [PubMed]
- Rinke, A.; Wittenberg, M.; Schade-Brittinger, C.; Aminossadati, B.; Ronicke, E.; Gress, T.M.; Müller, H.H.; Arnold, R. PROMID study group placebo-controlled, double-blind, prospective, randomized study on the effect of octreotide lar in the control of tumor growth in patients with metastatic neuroendocrine midgut tumors (PROMID): Results of long-term survival. Neuroendocrinology 2017, 104, 26–32. [Google Scholar] [CrossRef] [PubMed]
- Caplin, M.E.; Pavel, M.; Ćwikła, J.B.; Phan, A.T.; Raderer, M.; Sedláčková, E.; Cadiot, G.; Wolin, E.M.; Capdevila, J.; Wall, L.; et al. Lanreotide in metastatic enteropancreatic neuroendocrine tumors. N. Engl. J. Med. 2014, 371, 224–233. [Google Scholar] [CrossRef] [PubMed]
- Caplin, M.E.; Pavel, M.; Ćwikła, J.B.; Phan, A.T.; Raderer, M.; Sedláčková, E.; Cadiot, G.; Wolin, E.M.; Capdevila, J.; Wall, L.; et al. Anti-tumour effects of lanreotide for pancreatic and intestinal neuroendocrine tumours: The CLARINET open-label extension study. Endocr. Relat. Cancer 2016, 23, 191–199. [Google Scholar] [CrossRef]
- Paulson, A.S.; Bergsland, E.K. Systemic therapy for advanced carcinoid tumors: Where do we go from here? J. Natl. Compr. Cancer Netw. 2012, 10, 785–793. [Google Scholar] [CrossRef][Green Version]
- Bini, S.A. Artificial intelligence, machine learning, deep learning, and cognitive computing: What do these terms mean and how will they impact health care. J. Arthroplast. 2018, 33, 2358–2361. [Google Scholar] [CrossRef]
- Kumar, S.S.; Awan, K.H.; Patil, S.; Sk, I.B.; Raj, A.T. Potential role of machine learning in oncology. J. Contemp. Dent. Pract. 2019, 20, 529–530. [Google Scholar]
- Syed, T.; Doshi, A.; Guleria, S.; Syed, S.; Shah, T. Artificial intelligence and its role in identifying esophageal neoplasia. Dig. Dis. Sci. 2020, 65, 3448–3455. [Google Scholar] [CrossRef] [PubMed]
- Niu, P.H.; Zhao, L.L.; Wu, H.L.; Zhao, D.B.; Chen, Y.T. Artificial intelligence in gastric cancer: Application and future perspectives. World J. Gastroenterol. 2020, 26, 5408. [Google Scholar] [CrossRef]
- Ousefi, B.; Akbari, H.; Maldague, X.P. Detecting vasodilation as potential diagnostic biomarker in breast cancer using deep learning-driven thermomics. Biosensors 2020, 10, 164. [Google Scholar] [CrossRef] [PubMed]
- Polónia, A.; Campelos, S.; Ribeiro, A.; Aymore, I.; Pinto, D.; Biskup-Fruzynska, M.; Campilho, A. Artificial intelligence improves the accuracy in histologic classification of breast lesions. Am. J. Clin. Pathol. 2020, 155, 527–536. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Edwards, A.V.; Newstead, G.M. Artificial intelligence applied to breast MRI for improved diagnosis. Radiology 2021, 298, 38–46. [Google Scholar] [CrossRef]
- Goehler, A.; Hsu TM, H.; Lacson, R.; Gujrathi, I.; Hashemi, R.; Chlebus, G.; Khorasani, R. Three-dimensional neural network to automatically assess liver tumor burden change on consecutive liver MRIs. J. Am. Coll. Radiol. 2020, 17, 1475–1484. [Google Scholar] [CrossRef]
- Sun, Y.; Wong, A.K.; Kamel, M.S. Classification of imbalanced data: A review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. Int. J. Pattern Recognit. Artif. Intell. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Sridhar, S.; Kalaivani, A. A Survey on Methodologies for Handling Imbalance Problem in Multiclass Classification. In Advances in Smart System Technologies; Springer: Singapore, 2021; pp. 775–790. [Google Scholar]
- Remeseiro, B.; Bolon-Canedo, V. A review of feature selection methods in medical applications. Comput. Biol. Med. 2019, 112, 103375. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Gupta, S.; Chan, Y.H.; Rajapakse, J.C.; Alzheimer’s Disease Neuroimaging Initiative. Obtaining leaner deep neural networks for decoding brain functional connectome in a single shot. Neurocomputing 2021, in press. Available online: https://www.sciencedirect.com/science/article/pii/S0925231221000977 (accessed on 27 April 2021). [CrossRef]
- Amin, N.; McGrath, A.; Chen, Y.P. FexRNA: Exploratory data analysis and feature selection of non-coding RNA. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021. Available online: https://pubmed.ncbi.nlm.nih.gov/33539302/ (accessed on 27 April 2021). [CrossRef] [PubMed]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001; Volume 1.10. [Google Scholar]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Rutvija, P. C5.0 algorithm to improved decision tree with feature selection and reduced error pruning. Int. J. Comput. Appl. 2015, 117, 18–21. [Google Scholar]
- Iadanza, E.; Mudura, V.; Melillo, P.; Gherardelli, M. An automatic system supporting clinical decision for chronic obstructive pulmonary disease. Health Technol. 2020, 10, 487–498. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Qi, Y. Random forest for bioinformatics. In Ensemble Machine Learning; Springer: New York, NY, USA, 2012; pp. 307–323. [Google Scholar]
- Rokach, L. Decision forest: Twenty years of research. Inf. Fusion 2016, 27, 111–125. [Google Scholar] [CrossRef]
- Genuer, R. Random forests for Big Data. Big Data Res. 2017, 1, 28–46. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the 5th Annual Workshop on Computational Learning Theory, COLT’92, Pittsburgh, PA, USA, 27–29 July 1992; ACM Press: New York, NY, USA, 1992. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. Int. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Browne, M.W. Cross-validation methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef]
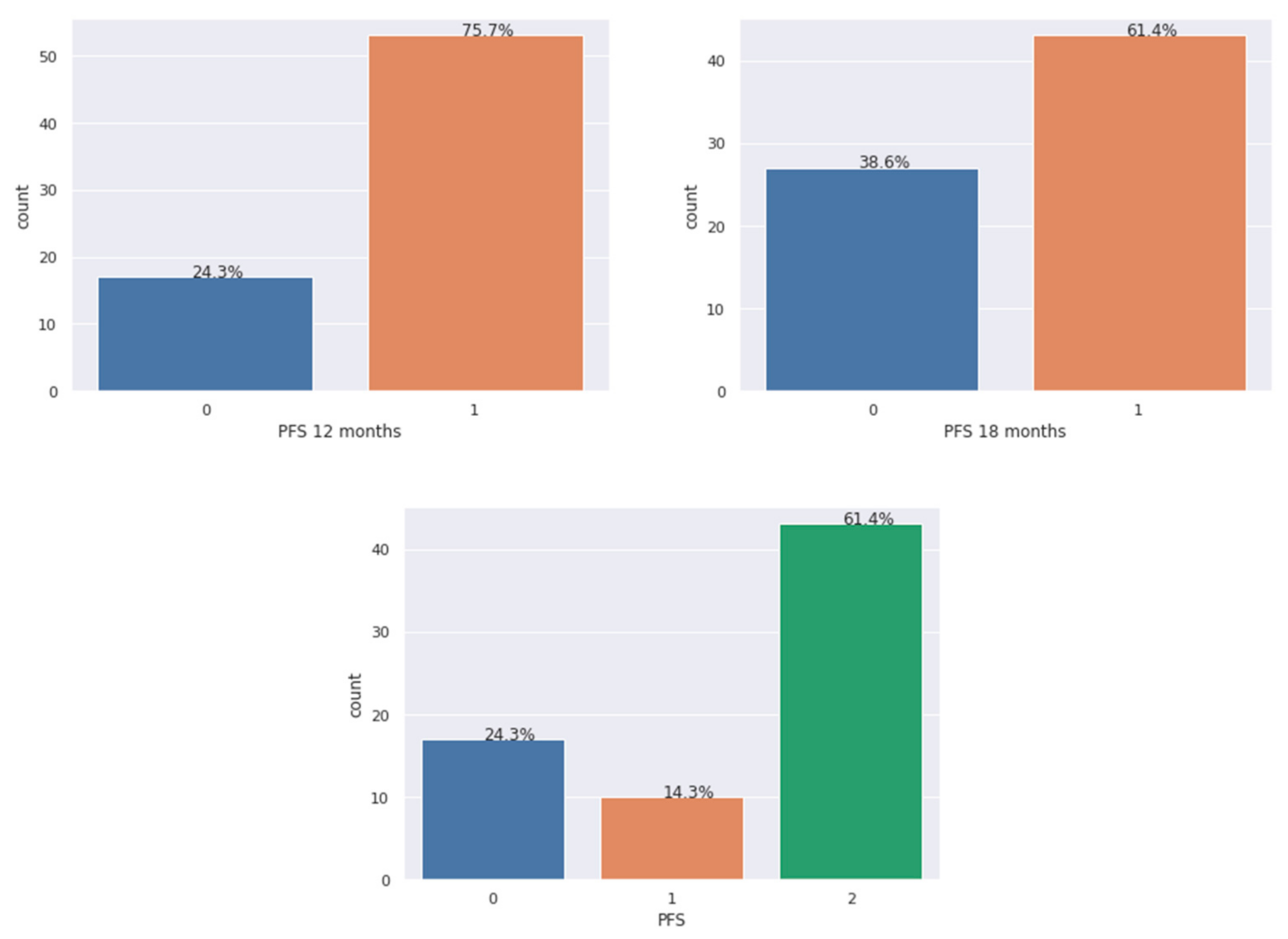
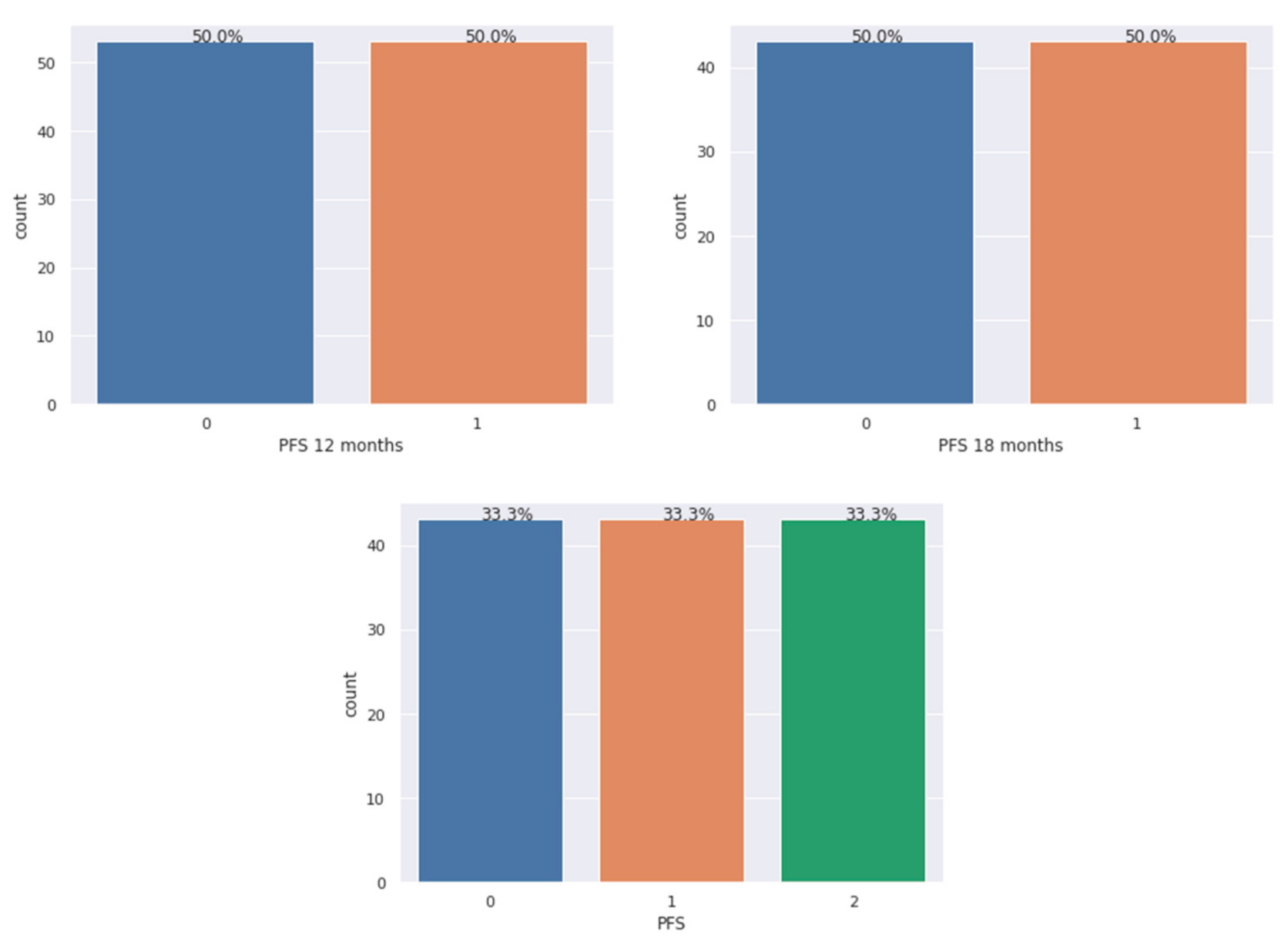
| Model | Outcome 1 | Outcome 2 | Outcome 3 |
|---|---|---|---|
| 1 | 0 (progression within 12 months) | 1 (progression free after 12 months) | NA |
| 2 | 0 (progression within 18 months) | 1 (progression free after 18 months) | NA |
| 3 | 0 (progression within 12 months) | 1 (progression between 12 and 18 months) | 2 (progression free after 18 months) |
| Model 1 | Model 2 | Model 3 | ||||||
|---|---|---|---|---|---|---|---|---|
| Features | Score | Features | Score | Features | Score | |||
| 1 | GENDER | 6 | 1 | AGE70 | 6 | 1 | NET | 6 |
| 2 | PinSITE | 6 | 2 | NET | 6 | 2 | PinSITE | 6 |
| 3 | NMETA | 6 | 3 | PinSITE | 6 | 3 | NMETA | 6 |
| 4 | BONEMETA | 6 | 4 | Ki67 | 6 | 4 | SSA | 6 |
| 5 | Ki67 | 6 | 5 | SSA | 6 | 5 | PSITE | 5 |
| 6 | LIVERMETA | 4 | 6 | LIVERMETA | 4 | 6 | Ki67 | 5 |
| 7 | AGE | 3 | 7 | AEG3-4 | 4 | 7 | AGE70 | 4 |
| 8 | PSITE | 3 | 8 | AGE | 3 | 8 | BONEMETA | 3 |
| 9 | STAGE | 3 | 9 | NMETA | 3 | |||
| 10 | GRADE | 3 | ||||||
| 11 | AEG3-4 | 3 | ||||||
| Algorithm | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| Average (St.Dev.) | Average (St.Dev.) | Average (St.Dev.) | Average (St.Dev.) | |
| Logistic regression | ||||
| Model 1 | 79.5% (11.8%) | 86.5% (18.3%) | 74% (16.5%) | 77.9% (12.7%) |
| Model 2 | 70.4% (20.1%) | 76% (23%) | 66.5% (25.3%) | 67.7% (21.6%) |
| Model 3 | 75.4% (22.8%) | 78.7% (18.6%) | 75.5% (22.8%) | 75.1% (22.7%) |
| Random Forest | ||||
| Model 1 | 84.4% (14%) | 88.1% (18.7%) | 81.3% (14.8%) | 83.7% (14.5%) |
| Model 2 | 70.3% (21.1%) | 70.3% (22.6%) | 66.5% (19.8%) | 69.4% (18.3%) |
| Model 3 | 73.8% (27.1%) | 75% (28%) | 75.3% (25%) | 75.2% (26.2%) |
| SVC | ||||
| Model 1 | 87.1% (12.3%) | 88.6% (17.5%) | 88.7% (9.3%) | 87.6% (11.2%) |
| Model 2 | 74% (17.6%) | 74.5% (21.2%) | 74% (20%) | 73.5% (18.8%) |
| Model 3 | 76.2% (25.2%) | 77.5% (24.3%) | 76.2% (25.2%) | 75.3% (26.1%) |
| Gaussian Naïve Bayes | ||||
| Model 1 | 51% (4.6%) | 25% (40.3%) | 5.7% (8.7%) | 9% (13.9%) |
| Model 2 | 48.9% (4.2%) | 4.3% (12.9%) | 7.5% (22.5%) | 5.5% (16.4%) |
| Model 3 | 55.9% (12.7%) | 45% (22%) | 55.2% (14.4%) | 46% (15.4%) |
| K-Nearest Neighbors (3) | ||||
| Model 1 | 84.3% (14.7%) | 87.4% (18.2%) | 83.3% (13%) | 84.4% (13.5%) |
| Model 2 | 71.3% (14.1%) | 72.6% (18.6%) | 71% (21.1%) | 70% (15.7%) |
| Model 3 | 65.3% (22.5%) | 69.6% (20.1%) | 65.5% (22.5%) | 64.4% (22%) |
| Decision Trees | ||||
| Model 1 | 84.5% (16.3%) | 89% (18.5%) | 79.7% (21.3%) | 82% (16.5%) |
| Model 2 | 69% (18.5%) | 66.8% (30.9%) | 58% (30.2%) | 67.6% (23.7%) |
| Model 3 | 73.8% (21.5%) | 77.4% (18.6%) | 74% (21.9%) | 73.5% (21.6%) |
| Gradient Boosting | ||||
| Model 1 | 83.5% (15.6%) | 85.5% (20%) | 83.3% (18.1%) | 83.1% (16.6%) |
| Model 2 | 59.9% (23.8%) | 61% (31%) | 60% (32.3%) | 57.4% (29.2%) |
| Model 3 | 76.1% (22.4%) | 76.1% (24.1%) | 76% (22.8%) | 75.2% (23.7%) |
| Extra Trees | ||||
| Model 1 | 85.2% (10%) | 89.5% (16.3%) | 85.3% (10.6%) | 85.1% (9.2%) |
| Model 2 | 65.6% (18.2%) | 66.3% (21.3%) | 69% (19.1%) | 63% (19.8%) |
| Model 3 | 72.2% (24.3%) | 73.7% (25.8%) | 73% (25.2%) | 70.5% (26.4%) |
| MultinomialNB | ||||
| Model 1 | 82.2% (12.7%) | 86.8% (15.9%) | 81.7% (20.2%) | 81.2% (13.8%) |
| Model 2 | 76.1% (13.1%) | 73.6% (14.4%) | 78.5% (22.6%) | 75% (16.3%) |
| Model 3 | 68.3% (14.7%) | 71.5% (14.8%) | 67.8% (14.5%) | 65.9% (14.7%) |
| MLP | ||||
| Model 1 | 86.9% (9.3%) | 86.9% (17.1%) | 86.7% (8.8%) | 85% (12.4%) |
| Model 2 | 67.9% (20.4%) | 74.5% (21.7%) | 66.5% (25.3%) | 64.6% (21.7%) |
| Model 3 | 76.9% (22.3%) | 78% (23.7%) | 78.5% (22.6%) | 78.2% (22.4%) |
| Algorithm | Initial Accuracy (Default Parameter Setting) | Accuracy after Hyperparameters Tuning (Average and Std) |
|---|---|---|
| Logistic regression | ||
| Model 1 | 79.5% | 83.6% (1.08%) |
| Model 2 | 70.4% | 72% (0.9%) |
| Model 3 | 75.4% | 76.3% (0.3%) |
| MultinomialNB | ||
| Model 1 | 82.2% | 82.5% (0.8%) |
| Model 2 | 76.1% | 77.3% (0.7%) |
| Model 3 | 68.3% | 70% (0.5%) |
| MLP | ||
| Model 1 | 86.9% | 86.7% (0.7%) |
| Model 2 | 67.9% | 71.7% (1.03%) |
| Model 3 | 76.9% | 77.7% (0.6%) |
| SVC | ||
| Model 1 | 87.1% | 86.2% (0.5%) |
| Model 2 | 74% | 73.6% (1.33%) |
| Model 3 | 76.2% | 77.4% (0.8%) |
| KNNeighbors | ||
| Model 1 | 84.3% | 85.2% (0.7%) |
| Model 2 | 71.3% | 72.9% (1.15%) |
| Model 3 | 65.3% | 77.3% (0.96%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasic Telalovic, J.; Pillozzi, S.; Fabbri, R.; Laffi, A.; Lavacchi, D.; Rossi, V.; Dreoni, L.; Spada, F.; Fazio, N.; Amedei, A.; et al. A Machine Learning Decision Support System (DSS) for Neuroendocrine Tumor Patients Treated with Somatostatin Analog (SSA) Therapy. Diagnostics 2021, 11, 804. https://doi.org/10.3390/diagnostics11050804
Hasic Telalovic J, Pillozzi S, Fabbri R, Laffi A, Lavacchi D, Rossi V, Dreoni L, Spada F, Fazio N, Amedei A, et al. A Machine Learning Decision Support System (DSS) for Neuroendocrine Tumor Patients Treated with Somatostatin Analog (SSA) Therapy. Diagnostics. 2021; 11(5):804. https://doi.org/10.3390/diagnostics11050804
Chicago/Turabian StyleHasic Telalovic, Jasminka, Serena Pillozzi, Rachele Fabbri, Alice Laffi, Daniele Lavacchi, Virginia Rossi, Lorenzo Dreoni, Francesca Spada, Nicola Fazio, Amedeo Amedei, and et al. 2021. "A Machine Learning Decision Support System (DSS) for Neuroendocrine Tumor Patients Treated with Somatostatin Analog (SSA) Therapy" Diagnostics 11, no. 5: 804. https://doi.org/10.3390/diagnostics11050804
APA StyleHasic Telalovic, J., Pillozzi, S., Fabbri, R., Laffi, A., Lavacchi, D., Rossi, V., Dreoni, L., Spada, F., Fazio, N., Amedei, A., Iadanza, E., & Antonuzzo, L. (2021). A Machine Learning Decision Support System (DSS) for Neuroendocrine Tumor Patients Treated with Somatostatin Analog (SSA) Therapy. Diagnostics, 11(5), 804. https://doi.org/10.3390/diagnostics11050804







