Impact of the Noise Penalty Factor on Quantification in Bayesian Penalized Likelihood (Q.Clear) Reconstructions of 68Ga-PSMA PET/CT Scans
Abstract
1. Introduction
2. Materials and Methods
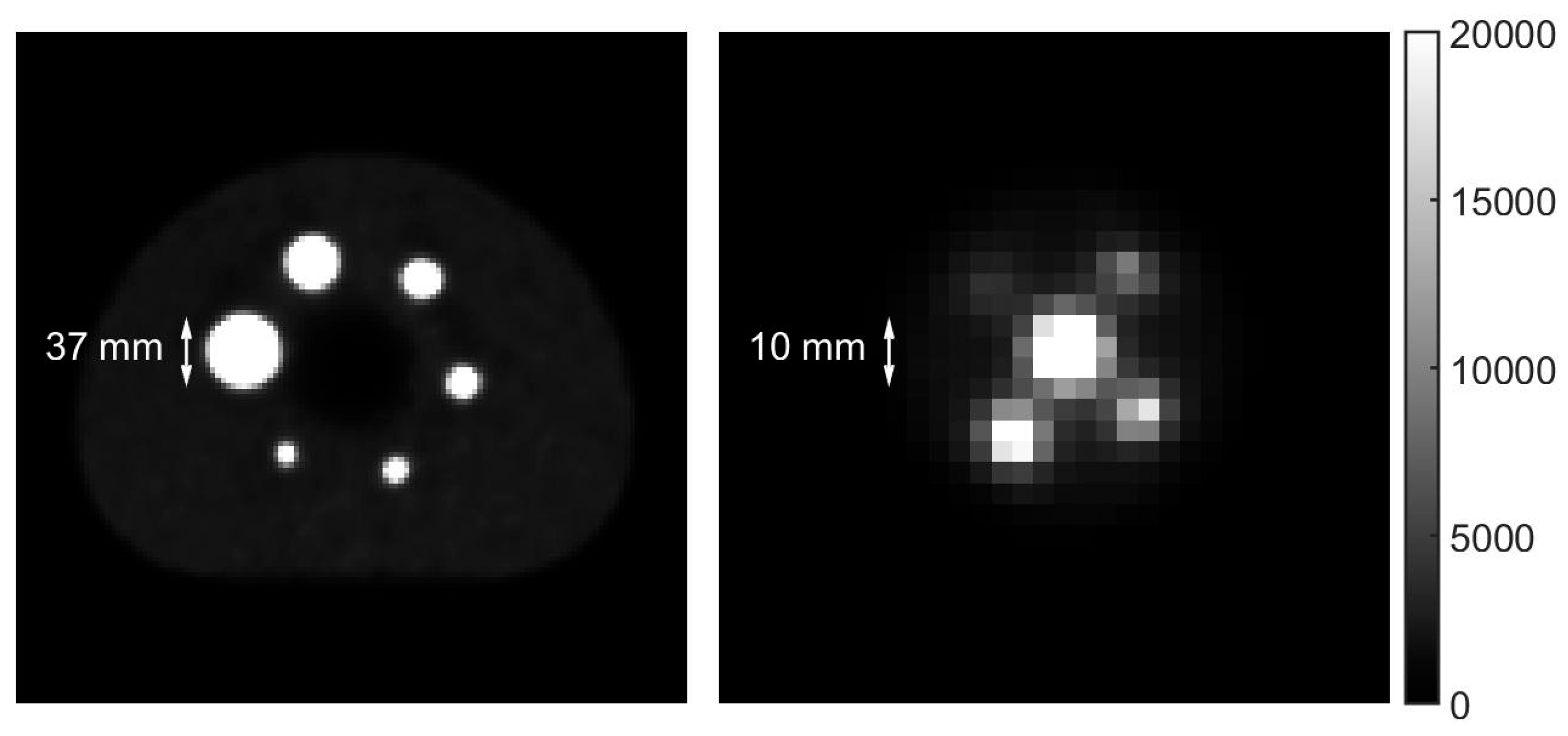
2.1. Phantom Preparation and Scanning Procedure
2.2. BPL Reconstructions
2.3. Background Variability
2.4. Activity Recovery Coefficients
3. Results
3.1. Background Variability
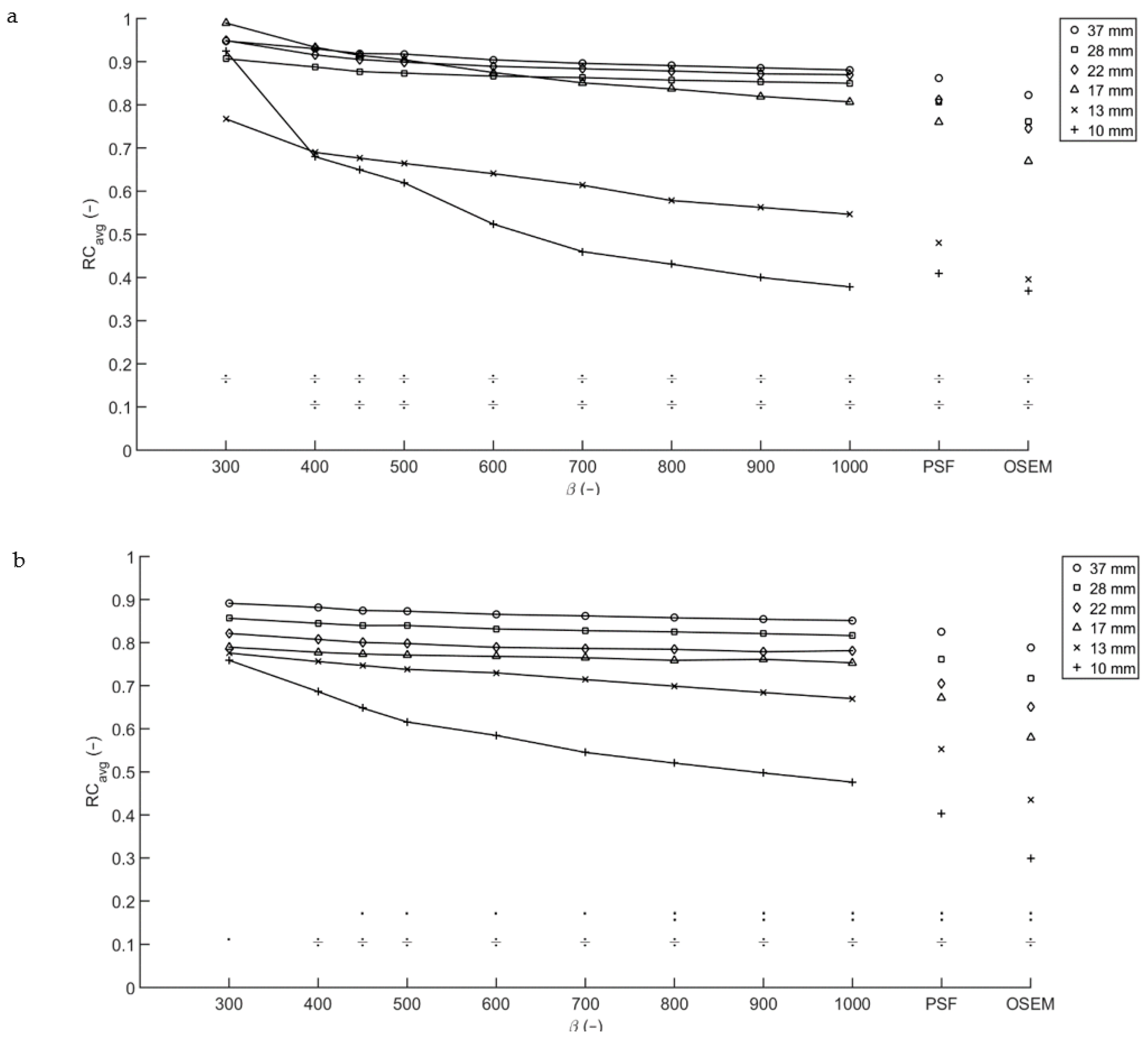
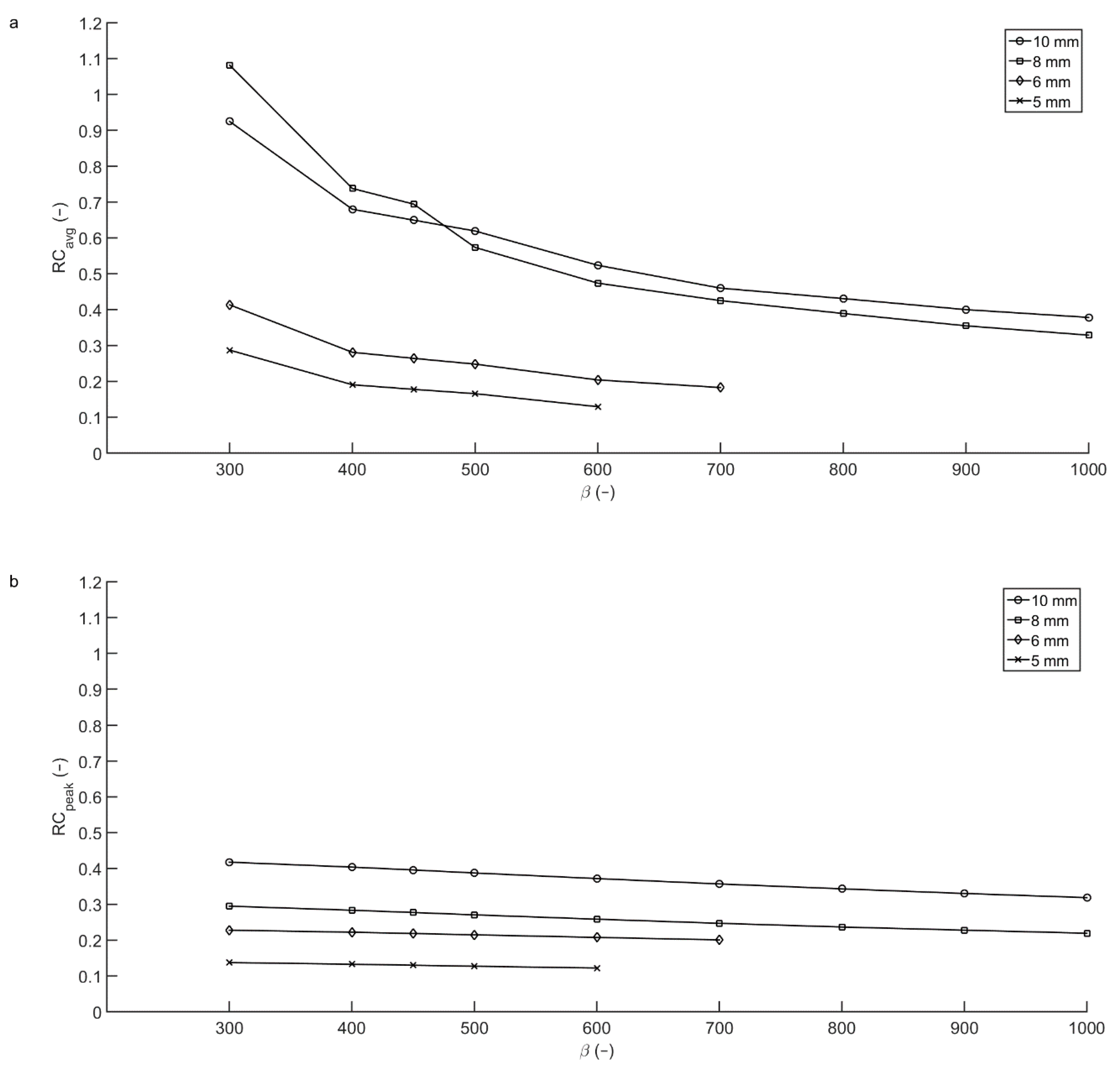
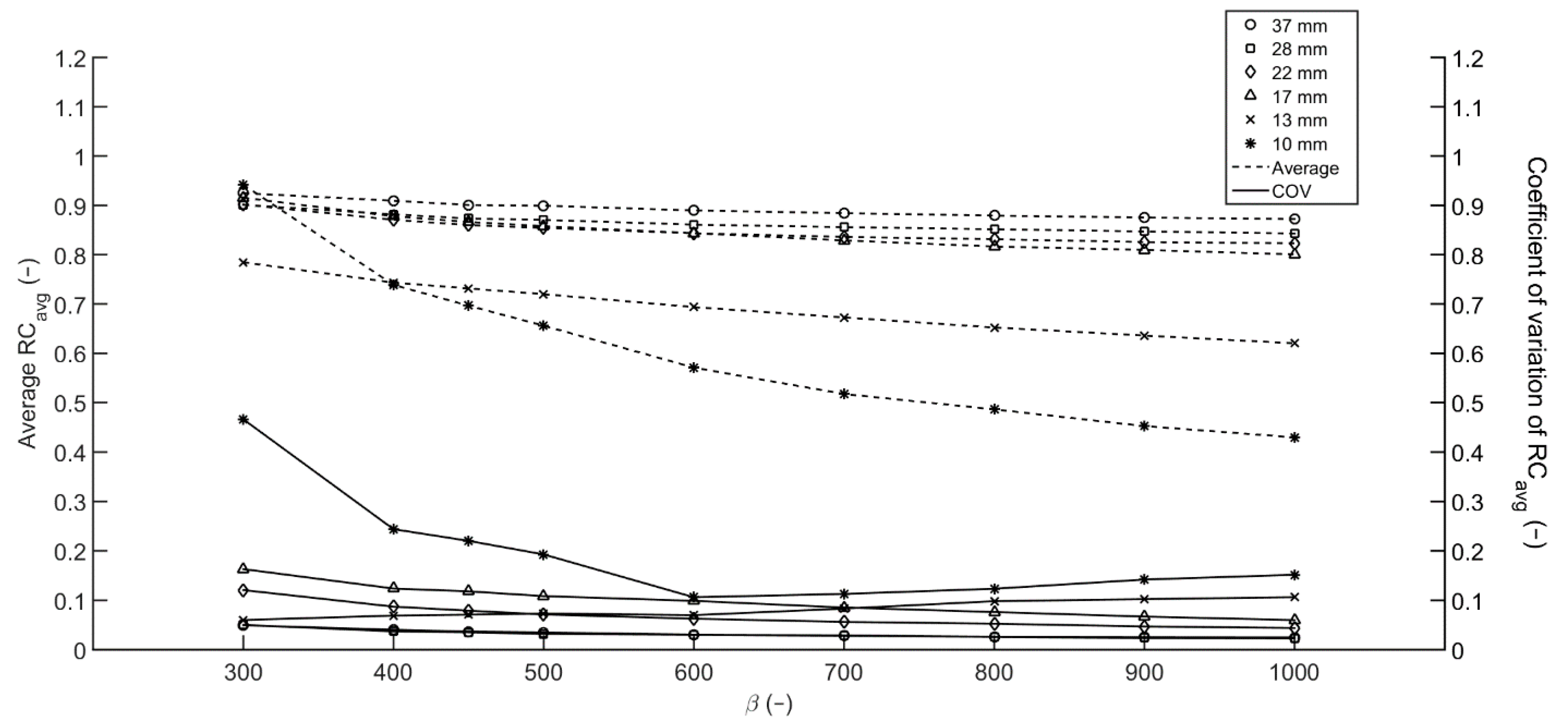
3.2. Contrast Recovery
3.2.1. NEMA IEC Image Quality Phantom
3.2.2. Micro Hollow Sphere Phantom
3.3. Reproducibility
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Global Burden of Disease Cancer Collaboration; Fitzmaurice, C.; Allen, C.; Barber, R.M.; Barregard, L.; Bhutta, Z.A.; Brenner, H.; Dicker, D.J.; Chimed-Orchir, O.; Dandona, R.; et al. Global, Regional, and National Cancer Incidence, Mortality, Years of Life Lost, Years Lived With Disability, and Disability-Adjusted Life-years for 32 Cancer Groups, 1990 to 2015. JAMA Oncol. 2017, 3, 524–548. [Google Scholar] [CrossRef]
- Mottet, N.; Bellmunt, J.; Bolla, M.; Joniau, S.; Mason, M.; Matveev, V.; Schmid, H.-P.; Van der Kwast, T.; Wiegel, T.; Zattoni, F.; et al. EAU Guidelines on Prostate Cancer. Part II: Treatment of Advanced, Relapsing, and Castration-Resistant Prostate Cancer. Eur. Urol. 2011, 59, 572–583. [Google Scholar] [CrossRef]
- Boellaard, R.; Delgado-Bolton, R.; Oyen, W.J.G.; Giammarile, F.; Tatsch, K.; Eschner, W.; Verzijlbergen, F.J.; Barrington, S.F.; Pike, L.C.; Weber, W.A.; et al. FDG PET/CT: EANM procedure guidelines for tumour imaging: Version 2.0. Eur. J. Nucl. Med. Mol. Imaging 2015, 42, 328–354. [Google Scholar] [CrossRef]
- Fraum, T.J.; Fowler, K.J.; Crandall, J.P.; Laforest, R.A.; Salter, A.; An, H.; Jacobs, M.A.; Grigsby, P.W.; Dehdashti, F.; Wahl, R.L. Measurement Repeatability of 18F-FDG PET/CT Versus 18F-FDG PET/MRI in Solid Tumors of the Pelvis. J. Nucl. Med. 2019, 60, 1080–1086. [Google Scholar] [CrossRef] [PubMed]
- Kurland, B.F.; Peterson, L.M.; Shields, A.T.; Lee, J.H.; Byrd, D.W.; Novakova-Jiresova, A.; Muzi, M.; Specht, J.M.; Mankoff, D.A.; Linden, H.M.; et al. Test–Retest Reproducibility of 18F-FDG PET/CT Uptake in Cancer Patients Within a Qualified and Calibrated Local Network. J. Nucl. Med. 2018, 60, 608–614. [Google Scholar] [CrossRef] [PubMed]
- Kramer, G.M.; Frings, V.; Hoetjes, N.; Hoekstra, O.S.; Smit, E.F.; De Langen, A.J.; Boellaard, R. Repeatability of Quantitative Whole Body 18F-FDG PET/CT Uptake Measures as Function of Uptake Interval and Lesion Selection in Non-Small Cell Lung Cancer Patients. J. Nucl. Med. 2016, 57, 1343–1349. [Google Scholar] [CrossRef] [PubMed]
- Velasquez, L.M.; Boellaard, R.; Kollia, G.; Hayes, W.; Hoekstra, O.S.; Lammertsma, A.A.; Galbraith, S.M. Repeatability of 18F-FDG PET in a Multicenter Phase I Study of Patients with Advanced Gastrointestinal Malignancies. J. Nucl. Med. 2009, 50, 1646–1654. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Liu, C.; Wei, Y.; Meng, J.; Zhang, Y.; Gan, H.; Xu, X.-P.; Wan, F.; Pan, J.; Ma, X.; et al. A Prospective Trial of 68Ga-PSMA and 18F-FDG PET/CT in Nonmetastatic Prostate Cancer Patients with an Early PSA Progression During Castration. Clin. Cancer Res. 2020, 26, 4551–4558. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; Jiang, X.; Wang, X.; Chen, S.; Shen, T.; You, J.; Lu, H.; Liao, H.; Li, Z.; et al. Intra-Individual Comparison of 18F-PSMA-1007 and 18F-FDG PET/CT in the Evaluation of Patients With Prostate Cancer. Front. Oncol. 2021, 10. [Google Scholar] [CrossRef] [PubMed]
- Kuyumcu, S.; Has-Simsek, D.; Iliaz, R.; Sanli, Y.; Buyukkaya, F.; Akyuz, F.; Turkmen, C. Evidence of Prostate-Specific Membrane Antigen Expression in Hepatocellular Carcinoma Using 68Ga-PSMA PET/CT. Clin. Nucl. Med. 2019, 44, 702–706. [Google Scholar] [CrossRef] [PubMed]
- Moses, W.W. Fundamental limits of spatial resolution in PET. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers, Detect. Assoc. Equip. 2011, 648, S236–S240. [Google Scholar] [CrossRef]
- Soret, M.; Bacharach, S.L.; Buvat, I. Partial-Volume Effect in PET Tumor Imaging. J. Nucl. Med. 2007, 48, 932–945. [Google Scholar] [CrossRef] [PubMed]
- Kessler, R.M.; Ellis, J.R.; Eden, M. Analysis of Emission Tomographic Scan Data: Limitations Imposed by Resolution and Background. J. Comput. Assist. Tomogr. 1984, 8, 514–522. [Google Scholar] [CrossRef]
- Hoffman, E.J.; Huang, S.-C.; Phelps, M.E. Quantitation in Positron Emission Computed Tomography. J. Comput. Assist. Tomogr. 1979, 3, 299–308. [Google Scholar] [CrossRef]
- Van Der Vos, C.S.; Koopman, D.; Rijnsdorp, S.; Arends, A.J.; Boellaard, R.; Van Dalen, J.A.; Lubberink, M.; Willemsen, A.T.M.; Visser, E.P. Quantification, improvement, and harmonization of small lesion detection with state-of-the-art PET. Eur. J. Nucl. Med. Mol. Imaging 2017, 44, 4–16. [Google Scholar] [CrossRef]
- Eckerman, K.; Endo, A. PREFACE. Ann. ICRP 2008, 38, 9–10. [Google Scholar] [CrossRef]
- Bailey, D.L.; Townsend, D.W.; Valk, P.E.; Maisey, M.N. (Eds.) Positron Emission Tomography – Basic Sciences; Springer: London, UK, 2005. [Google Scholar]
- Levin, C.S.; Hoffman, E.J. Calculation of positron range and its effect on the fundamental limit of positron emission tomography system spatial resolution. Phys. Med. Biol. 1999, 44, 781–799. [Google Scholar] [CrossRef] [PubMed]
- Cal-Gonzalez, J.; Vaquero, J.J.; Herraiz, J.L.; Pérez-Liva, M.; Soto-Montenegro, M.L.; Peña-Zalbidea, S.; Desco, M.; Udías, J.M. Improving PET Quantification of Small Animal [68Ga]DOTA-Labeled PET/CT Studies by Using a CT-Based Positron Range Correction. Mol. Imaging Biol. 2018, 20, 584–593. [Google Scholar] [CrossRef]
- Disselhorst, J.A.; Brom, M.; Laverman, P.; Slump, C.H.; Boerman, O.C.; Oyen, W.J.G.; Gotthardt, M.; Visser, E.P. Image-Quality Assessment for Several Positron Emitters Using the NEMA NU 4-2008 Standards in the Siemens Inveon Small-Animal PET Scanner. J. Nucl. Med. 2010, 51, 610–617. [Google Scholar] [CrossRef] [PubMed]
- Prasad, V.; Steffen, I.G.; Diederichs, G.; Makowski, M.R.; Wust, P.; Brenner, W. Biodistribution of [68Ga]PSMA-HBED-CC in Patients with Prostate Cancer: Characterization of Uptake in Normal Organs and Tumour Lesions. Mol. Imaging Biol. 2016, 18, 428–436. [Google Scholar] [CrossRef] [PubMed]
- Afshar-Oromieh, A.; Malcher, A.; Eder, M.; Eisenhut, M.; Linhart, H.G.; Hadaschik, B.A.; Holland-Letz, T.; Giesel, F.L.; Kratochwil, C.; Haufe, S.; et al. PET imaging with a [68Ga]gallium-labelled PSMA ligand for the diagnosis of prostate cancer: Biodistribution in humans and first evaluation of tumour lesions. Eur. J. Nucl. Med. Mol. Imaging 2013, 40, 486–495. [Google Scholar] [CrossRef]
- Eder, M.; Schäfer, M.; Bauder-Wüst, U.; Hull, W.-E.; Wängler, C.; Mier, W.; Haberkorn, U.; Eisenhut, M. 68Ga-Complex Lipophilicity and the Targeting Property of a Urea-Based PSMA Inhibitor for PET Imaging. Bioconjugate Chem. 2012, 23, 688–697. [Google Scholar] [CrossRef]
- Hudson, H.; Larkin, R. Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans. Med Imaging 1994, 13, 601–609. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.; Ross, S.G.; Asma, E.; Miao, J.; Jin, X.; Cheng, L.; Wollenweber, S.D.; Manjeshwar, R.M. Quantitative comparison of OSEM and penalized likelihood image reconstruction using relative difference penalties for clinical PET. Phys. Med. Biol. 2015, 60, 5733–5751. [Google Scholar] [CrossRef] [PubMed]
- Howard, B.A.; Morgan, R.; Thorpe, M.P.; Turkington, T.G.; Oldan, J.; James, O.G.; Borges-Neto, S. Comparison of Bayesian penalized likelihood reconstruction versus OS-EM for characterization of small pulmonary nodules in oncologic PET/CT. Ann. Nucl. Med. 2017, 31, 623–628. [Google Scholar] [CrossRef] [PubMed]
- Chilcott, A.K.; Bradley, K.M.; McGowan, D.R. Effect of a Bayesian Penalized Likelihood PET Reconstruction Compared With Ordered Subset Expectation Maximization on Clinical Image Quality Over a Wide Range of Patient Weights. Am. J. Roentgenol. 2018, 210, 153–157. [Google Scholar] [CrossRef]
- Riet, J.T.; Rijnsdorp, S.; Roef, M.J.; Arends, A.J. Evaluation of a Bayesian penalized likelihood reconstruction algorithm for low-count clinical 18F-FDG PET/CT. EJNMMI Phys. 2019, 6, 1–14. [Google Scholar] [CrossRef]
- Teoh, E.J.; McGowan, D.R.; MacPherson, R.E.; Bradley, K.M.; Gleeson, F.V. Phantom and Clinical Evaluation of the Bayesian Penalized Likelihood Reconstruction Algorithm Q.Clear on an LYSO PET/CT System. J. Nucl. Med. 2015, 56, 1447–1452. [Google Scholar] [CrossRef]
- Teoh, E.J.; McGowan, D.R.; Schuster, D.M.; Tsakok, M.T.; Gleeson, F.V.; Bradley, K.M. Bayesian penalised likelihood reconstruction (Q.Clear) of 18F-fluciclovine PET for imaging of recurrent prostate cancer: Semi-quantitative and clinical evaluation. Br. J. Radiol. 2018. [Google Scholar] [CrossRef]
- Rowley, L.M.; Bradley, K.M.; Boardman, P.; Hallam, A.; McGowan, D.R. Optimization of Image Reconstruction for 90 Y Selective Internal Radiotherapy on a Lutetium Yttrium Orthosilicate PET/CT System Using a Bayesian Penalized Likelihood Reconstruction Algorithm. J. Nucl. Med. 2017, 58, 658–664. [Google Scholar] [CrossRef]
- Berliner, C.; Tienken, M.; Frenzel, T.; Kobayashi, Y.; Helberg, A.; Kirchner, U.; Klutmann, S.; Beyersdorff, D.; Budäus, L.; Wester, H.-J.; et al. Detection rate of PET/CT in patients with biochemical relapse of prostate cancer using [68Ga]PSMA I&T and comparison with published data of [68Ga]PSMA HBED-CC. Eur. J. Nucl. Med. Mol. Imaging 2016, 44, 670–677. [Google Scholar] [CrossRef]
- Schmuck, S.; Nordlohne, S.; Von Klot, C.-A.; Henkenberens, C.; Sohns, J.M.; Christiansen, H.; Wester, H.-J.; Ross, T.L.; Bengel, F.M.; Derlin, T. Comparison of standard and delayed imaging to improve the detection rate of [68Ga]PSMA I&T PET/CT in patients with biochemical recurrence or prostate-specific antigen persistence after primary therapy for prostate cancer. Eur. J. Nucl. Med. Mol. Imaging 2017, 44, 960–968. [Google Scholar] [CrossRef] [PubMed]
- Sahlmann, C.-O.; Meller, B.; Bouter, C.; Ritter, C.O.; Ströbel, P.; Lotz, J.; Trojan, L.; Meller, J.; Hijazi, S. Biphasic 68Ga-PSMA-HBED-CC-PET/CT in patients with recurrent and high-risk prostate carcinoma. Eur. J. Nucl. Med. Mol. Imaging 2015, 43, 898–905. [Google Scholar] [CrossRef]
- EARL Accreditation Manual Version 2.1 (Oct 2020). Available online: http://earl.eanm.org/html/img/pool/MASTER_EARL_Manual_Oct2020_2.1.pdf (accessed on 5 May 2021).
- Nuyts, J.; Beque, D.; Dupont, P.; Mortelmans, L. A concave prior penalizing relative differences for maximum-a-posteriori reconstruction in emission tomography. IEEE Trans. Nucl. Sci. 2002, 49, 56–60. [Google Scholar] [CrossRef]
- D’Amico, A.V.; Whittington, R.; Malkowicz, S.B.; Schultz, D.; Blank, K.; Broderick, G.A.; Tomaszewski, J.E.; Renshaw, A.A.; Kaplan, I.; Beard, C.J.; et al. Biochemical Outcome After Radical Prostatectomy, External Beam Radiation Therapy, or Interstitial Radiation Therapy for Clinically Localized Prostate Cancer. JAMA 1998, 280, 969–974. [Google Scholar] [CrossRef]
- Koerber, S.A.; Utzinger, M.T.; Kratochwil, C.; Kesch, C.; Haefner, M.F.; Katayama, S.; Mier, W.; Iagaru, A.H.; Herfarth, K.; Haberkorn, U.; et al. 68Ga-PSMA-11 PET/CT in Newly Diagnosed Carcinoma of the Prostate: Correlation of Intraprostatic PSMA Uptake with Several Clinical Parameters. J. Nucl. Med. 2017, 58, 1943–1948. [Google Scholar] [CrossRef]
- Sachpekidis, C.; Bäumer, P.; Kopka, K.; Hadaschik, B.A.; Hohenfellner, M.; Kopp-Schneider, A.; Haberkorn, U.; Dimitrakopoulou-Strauss, A. 68Ga-PSMA PET/CT in the evaluation of bone metastases in prostate cancer. Eur. J. Nucl. Med. Mol. Imaging 2018, 45, 904–912. [Google Scholar] [CrossRef]
- Beheshti, M.; Paymani, Z.; Brilhante, J.; Geinitz, H.; Gehring, D.; Leopoldseder, T.; Wouters, L.; Pirich, C.; Loidl, W.; Langsteger, W. Optimal time-point for 68Ga-PSMA-11 PET/CT imaging in assessment of prostate cancer: Feasibility of sterile cold-kit tracer preparation? Eur. J. Nucl. Med. Mol. Imaging 2018, 45, 1188–1196. [Google Scholar] [CrossRef]
- Lindström, E.; Sundin, A.; Trampal, C.; Lindsjö, L.; Ilan, E.; Danfors, T.; Antoni, G.; Sörensen, J.; Lubberink, M. Evaluation of Penalized-Likelihood Estimation Reconstruction on a Digital Time-of-Flight PET/CT Scanner for18F-FDG Whole-Body Examinations. J. Nucl. Med. 2018, 59, 1152–1158. [Google Scholar] [CrossRef] [PubMed]
- Wagner, T.; Gellee, S.; Page, J.; Sanghera, B.; Payoux, P. Impact of the Point Spread Function on Maximum Standardized Uptake Value Measurements in Patients with Pulmonary Cancer. World J. Nucl. Med. 2014, 13, 128–131. [Google Scholar] [CrossRef]
- Yamashita, S.; Yamamoto, H.; Nakaichi, T.; Yoneyama, T.; Yokoyama, K. Comparison of image quality between step-and-shoot and continuous bed motion techniques in whole-body 18F-fluorodeoxyglucose positron emission tomography with the same acquisition duration. Ann. Nucl. Med. 2017, 31, 686–695. [Google Scholar] [CrossRef] [PubMed]
- Bärwolf, R.; Zirnsak, M.; Freesmeyer, M. Breath-hold and free-breathing F-18-FDG-PET/CT in malignant melanoma—detection of additional tumoral foci and effects on quantitative parameters. Med. 2017, 96, e5882. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Schmidtlein, C.R.; Burger, I.A.; Ridge, C.A.; Solomon, S.B.; Humm, J.L. Assessing and accounting for the impact of respiratory motion on FDG uptake and viable volume for liver lesions in free-breathing PET using respiration-suspended PET images as reference. Med Phys. 2014, 41, 091905. [Google Scholar] [CrossRef] [PubMed]
- Akamatsu, G.; Ikari, Y.; Nishida, H.; Nishio, T.; Ohnishi, A.; Maebatake, A.; Sasaki, M.; Senda, M. Influence of Statistical Fluctuation on Reproducibility and Accuracy of SUVmax and SUVpeak: A Phantom Study. J. Nucl. Med. Technol. 2015, 43, 222–226. [Google Scholar] [CrossRef] [PubMed]
- Boellaard, R.; Krak, N.C.; Hoekstra, O.S.; A Lammertsma, A. Effects of noise, image resolution, and ROI definition on the accuracy of standard uptake values: A simulation study. J. Nucl. Med. 2004, 45, 1519–1527. [Google Scholar]
- Messerli, M.; Stolzmann, P.; Egger-Sigg, M.; Trinckauf, J.; D’Aguanno, S.; Burger, I.A.; Von Schulthess, G.K.; Kaufmann, P.A.; Huellner, M.W. Impact of a Bayesian penalized likelihood reconstruction algorithm on image quality in novel digital PET/CT: Clinical implications for the assessment of lung tumors. EJNMMI Phys. 2018, 5, 1–13. [Google Scholar] [CrossRef]
- Mansor, S.; Pfaehler, E.; Heijtel, D.; Lodge, M.A.; Boellaard, R.; Yaqub, M. Impact of PET/CT system, reconstruction protocol, data analysis method, and repositioning on PET/CT precision: An experimental evaluation using an oncology and brain phantom. Med Phys. 2017, 44, 6413–6424. [Google Scholar] [CrossRef]
- Munk, O.L.; Tolbod, L.P.; Hansen, S.B.; Bogsrud, T.V. Point-spread function reconstructed PET images of sub-centimeter lesions are not quantitative. EJNMMI Phys. 2017, 4, 5. [Google Scholar] [CrossRef]
- Cherry, S.R.; Sorenson, J.A.; Phelps, M.E. Physics in Nuclear Medicine, 4th ed.Saunders: Philadelphia, PA, USA, 2012. [Google Scholar]
- Derenzo, S.E. Precision measurement of annihilation point spread distributions for medically important positron emitters. In Proceedings of the 5th International Conference on Positron Annihilation, Lake Yamanaka, Japan, 8–11 April 1979. [Google Scholar]
- Derenzo, S.E. Mathematical Removal of Positron Range Blurring in High Resolution Tomography. IEEE Trans. Nucl. Sci. 1986, 33, 565–569. [Google Scholar] [CrossRef]
| [32] Mean ± SD | [22] Median (Range) | [33] Mean ± SD (Range) | [34] Median (Range) | |
|---|---|---|---|---|
| Lymph node metastases | 21.0 ± 27.4 | 65.2 ± 65.7 (5.3–486.4) | 12.2 (3.8–62.2) | |
| Bone metastases | 24.7 ± 34.2 | 84.4 ± 75.1 (3.8–355) | 34 (6.8–40) | |
| Local recurrences | 15.7 ± 10.1 | 43.3 ± 33.5 (10.7–144.3) | ||
| Axillary lymph nodes | 3 (1.3–8.5) | |||
| Primary tumor | 18.5 (6.7–92) | |||
| Other metastases | 16.7 ± 14.1 | |||
| Total lesions | 21.1 ± 27.4 | 18.8 (2.4–158.3) | 7.8 (1.5–35) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rijnsdorp, S.; Roef, M.J.; Arends, A.J. Impact of the Noise Penalty Factor on Quantification in Bayesian Penalized Likelihood (Q.Clear) Reconstructions of 68Ga-PSMA PET/CT Scans. Diagnostics 2021, 11, 847. https://doi.org/10.3390/diagnostics11050847
Rijnsdorp S, Roef MJ, Arends AJ. Impact of the Noise Penalty Factor on Quantification in Bayesian Penalized Likelihood (Q.Clear) Reconstructions of 68Ga-PSMA PET/CT Scans. Diagnostics. 2021; 11(5):847. https://doi.org/10.3390/diagnostics11050847
Chicago/Turabian StyleRijnsdorp, Sjoerd, Mark J. Roef, and Albert J. Arends. 2021. "Impact of the Noise Penalty Factor on Quantification in Bayesian Penalized Likelihood (Q.Clear) Reconstructions of 68Ga-PSMA PET/CT Scans" Diagnostics 11, no. 5: 847. https://doi.org/10.3390/diagnostics11050847
APA StyleRijnsdorp, S., Roef, M. J., & Arends, A. J. (2021). Impact of the Noise Penalty Factor on Quantification in Bayesian Penalized Likelihood (Q.Clear) Reconstructions of 68Ga-PSMA PET/CT Scans. Diagnostics, 11(5), 847. https://doi.org/10.3390/diagnostics11050847






